Известия РАН. Теория и системы управления, 2021, № 2, стр. 106-125

Введение. Современный этап развития радиотехнических систем различного назначения связан с разработкой и применением крупногабаритных раскрывающихся антенн-рефлекторов, устанавливаемых на космических аппаратах (КА). При этом возникают новые задачи управления. Так как антенны доставляются на космические орбиты в сложенном состоянии, то необходимо правильно реализовать процесс раскрытия и обеспечить функционирование проектируемой механической системы. Несмотря на значительные успехи в области проектирования раскрывающихся крупногабаритных трансформируемых конструкций космического базирования [1, 2], важной остается задача их плавного и надежного раскрытия.

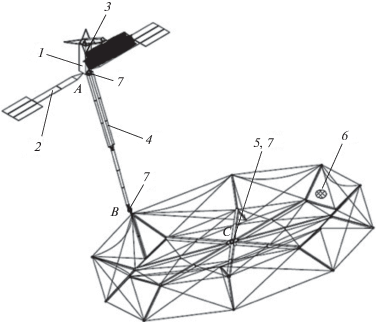
Крупногабаритный трансформируемый рефлектор (КТР) космического базирования (рис. 1) с использованием вантовой системы состоит из КА (1), относительно которого разворачиваются элементы солнечных батарей (2), обеспечивающих энергией установку, системы (3), облучающей отражающую поверхность. Также в состав рефлектора входит штанга (4), выдвигающая рефлектор (5) на необходимое расстояние, и сетеполотно (6), формирующие необходимую диаграмму направленности. В точках A, B и C находятся двигатели (7), которые переводят КТР из сложенного транспортировочного положения в развернутое штатное.

В общем виде задача раскрытия КТР на каждом этапе решается за счет воздействия на конструкцию исполнительных механизмов (актюаторов). В настоящеe время развертывание различных видов крупногабаритных рефлекторов (ферменных, зонтичных, кольцевых и др.) производится за счет энергии пружин или деформированных упругих элементов [3, 4]. Очевидные недостатки данного способа: невозможность осуществления синтеза управления при процессе раскрытия, необходимость создания макета и проведения дополнительных расчетов для определения степени сжатия пружин или закручивания элементов, наличие колебаний и прогибов конструкции.

Альтернативой классическим могут являться автоматические системы, в которых энергия для развертывания элементов рефлектора производится за счет приводов, в частности электрической машины. Для раскрытия рефлекторов расчет динамики и прочности конструкции является одним из определяющих факторов. В процессе приведения КТР в рабочее состояние и после его завершения возникают высокие напряжения в элементах конструкции в результате импульсных воздействий со стороны управляющего органа, а также механизмов упора и фиксации. Вследствие чего могут возникать колебания всего спутника, что приведет к длительному времени неактивности аппарата или даже к его выходу из строя. Решение задачи минимизации колебаний конструкции является не тривиальным и требует особого подхода к каждой рассматриваемой системе [5, 6].

Точность поддержания заданной формы обеспечивает высокое качество передаваемого сигнала. В условиях открытого космоса конструкция подвержена различным возмущающим воздействиям, таким, как перепад температур, радиация, и возникает задача настройки и поддержания формы радиоотражающего сетеполотна.

Ввиду больших затрат на проведение испытаний в космической отрасли важным является этап математического моделирования. Поэтому возникает задача построения адекватной математической модели [7, 8]. А.А. Красовский в работе [9] писал: “Разработка математических моделей требуемого уровня адекватности, их идентификация и сертификация (верификация) для многих новых процессов, объектов и технологий требует очень высоких интеллектуальных и материальных затрат. Для ряда объектов и процессов создание верифицированных математических моделей невозможно без натурных испытаний, а объекты и процессы не могут быть доведены до натурных испытаний без таких математических моделей (т.е. возникает “порочный круг”)”.

1. Описание системы и постановка задачи. При развертывании КТР имеют место поступательное и вращательное движения. Развертывание происходит поэтапно по соответствующим видам движения. Для описания динамики воспользуемся уравнением Лагранжа второго рода с учетом диссипативных сил [7].

1.1. Раскрытие спицы рефлектора. Вращательное движение встречается при раскрытии штанг и спиц. Математические модели динамики, описанные системой дифференциальных уравнений, на всех этих этапах аналогичны друг другу, а конструкции отличаются только массогабаритными параметрами.

Рассмотрим разворот спицы. Примем, что один актюатор разворачивает только одну спицу в одной плоскости (рис. 2). Спица одним концом жестко закреплена за силовой каркас рефлектора.

Система дифференциальных уравнений первого порядка для определения прогиба спицы $h$ при ее повороте на угол ${\varphi }$ имеет вид [7] ${{{\mathbf{\dot {X}}}}_{{\text{р}}}} = {\mathbf{f}}({{{\mathbf{X}}}_{{\text{р}}}},u,t)$, где ${{{\mathbf{X}}}_{{\text{р}}}} = {{({\varphi }\;{\omega }\;h\;{{V}_{{{\text{изг}}}}})}^{{\text{T}}}}$ – вектор состояния процесса раскрытия, $u$ – вектор управления, $t$ – время, $\omega $ – угловая скорость поворота спицы, V_изг – линейная скорость изгиба спицы. В поэлементном виде система представляется следующим образом:

где M_п – полезный момент, создаваемый бесколлекторной машиной; ${{U}_{1}}$ – напряжение питания бесколлекторной машины; M_тр – момент трения; M_упор – момент, создаваемый упором; M_ф – момент, создаваемый фиксатором; I – момент инерции спицы; $E$ – модуль упругости; I_изг – изгибной момент инерции; ${\rho }$ – плотность материала спицы; $S$ – площадь спицы в поперечном сечении; ${\gamma }$ – коэффициент затухания; M – общий момент, действующий на спицу: M = M_п – ${{M}_{{{\text{тр}}}}} - {{M}_{{{\text{упор}}}}}$ – M_ф. С учетом функций Крылова [10] значения ${{\partial }^{4}}h{\text{/}}\partial {{l}^{4}}$, исходя из граничных условий при l = 0 и l = a, определяются как где ${{{\omega }}_{{{{{\text{c}}}_{{{\text{изг }}k}}}}}}$ – k-я собственная частота изгибных колебаний; ${{K}_{3}} = 0.5({\text{ch}}{{Z}_{k}} - \cos {{Z}_{k}})$; ${{K}_{4}} = 0.5({\text{sh}}{{Z}_{k}} - \sin {{Z}_{k}})$; ${{Z}_{k}} = l\rho S{\omega }_{{{{{\text{c}}}_{{{\text{изг }}k}}}}}^{2}{\text{/}}(E{{I}_{{{\text{изг}}}}})$; С, D – коэффициенты, определяемые из граничных условий задачи. Для определения $\partial M{\text{/}}\partial l$ примем, что полный момент силы M создается на радиусе вала двигателя R_дв, приводящего систему в движение; ${{\left. {\partial M{\text{/}}\partial l} \right|}_{{l = {{R}_{{{\text{дв}}}}}}}}$ = M/R_дв, R_дв = 0.5 м.

Моменты, действующие на спицу при раскрытии, определяются как [7]

где ${{k}_{{{\text{у}}{\text{.упор(ф)}}}}}$ – коэффициент жесткости упругой компоненты модели упора (фиксатора); ${{c}_{{{\text{д}}{\text{.упор(ф)}}}}}$ – коэффициент демпфирования вязкой компоненты модели упора (фиксатора); $\Delta {\varphi } = {\varphi } - {{{\varphi }}_{f}}$ – относительный угол, соответствующий моменту t_f  установки на упор (фиксатор) спицы при достижении конечного угла раскрытия ${{{\varphi }}_{f}}$; ${{H}_{{{\text{упор}}}}}(\Delta {\varphi })$ – функция, которая принимает значение 1 (при $\Delta {\varphi }$ > 0) или 0 (при $\Delta {\varphi } < 0$); ${{H}_{{\text{ф}}}}(\Delta {\varphi })$ – функция, которая принимает значение 1 (при $\Delta {\varphi } < 0$) или 0 (при $\Delta {\varphi } > 0$) при условии, что спица уже достигла ${{{\varphi }}_{f}}$, т.е. сработал упор и ${{H}_{{{\text{упор}}}}}(\Delta {\varphi }) = 1$; m_фаз – число фаз ротора; p – число пар полюсов магнитного поля, E₀ – действующее значение электродвижущей силы (ЭДС) на обмотке статора; $\vartheta $ – угол рассогласования (между U₁ и E₀, для двигателя находится в пределах [0, π/2])); ${{{\omega }}_{1}}$ – угловая скорость вращения ротора двигателя; ${{X}_{{{\text{cинхр}}}}}$ – синхронное сопротивление (${{X}_{{{\text{cинхр}}}}} = {{X}_{{\sigma }}} + {{X}_{a}}$, где X_σ и X_a – индуктивные сопротивления рассеяния и реакции якоря соответственно).

Исходя из результатов численного моделирования, полученных в [7], система (1.1) написана в предположении, что момент инерции постоянный. Угловые скорости ${\omega }$ при раскрытии спицы не превышают 10^–2 рад/с, тогда при рассматриваемых параметрах (m = 32 кг – масса спицы, a = = 30 м – длина спицы) центробежная сила ${{F}_{{\text{ц}}}} = m{{{\omega }}^{2}}a = 4.7 \times {{10}^{{ - 2}}}$ Н. Нормальное напряжение в поперечном сечении $\sigma = {{F}_{{\text{ц}}}}{\text{/}}S = 6$ Н/м². Из закона Гука сила упругости ${{F}_{{\text{у}}}} = k\Delta l$ [11], где $k = ES{\text{/}}a$, $\varepsilon = \Delta l{\text{/}}a$, т.е. $\sigma = E\varepsilon $ и относительное удлинение $\varepsilon = \sigma {\text{/}}E = 5 \times {{10}^{{ - 11}}}$. Следовательно, абсолютное удлинение $\Delta l = 1.5 \times {{10}^{{ - 9}}}$ м. Возникающая при этом сила Кориолиса ${{F}_{{\text{К}}}} = 2m{\omega }\Delta \dot {l}$ не превышает ${{F}_{{\text{К}}}} = {{10}^{{ - 11}}}$ Н, где $\Delta \dot {l} = {{10}^{{ - 11}}}$ м/с – скорость удлинения спицы в процессе ее поворота, определенная из результатов моделирования. Закон Гука при изгибе $\sigma = {{M}_{{{\text{изг}}}}}{\text{/}}W$ [11], где M_изг – момент изгиба, W – момент сопротивления изгибу. Для наибольшего нормального напряжения на поверхности изгиба на половине длины спицы (${{M}_{{{\text{изг}}}}} = 0.25{{F}_{{\text{К}}}}a = 15 \times {{10}^{{ - 12}}}$ Нм, $W = \pi {{D}^{4}}{\text{/}}8 = 0.22$ Нм) получаем $\sigma = {{M}_{{{\text{изг}}}}}{\text{/}}W = 7 \times {{10}^{{ - 11}}}$. При данных порядках величин момент инерции можно считать постоянным.

Для решения системы уравнений необходимо выполнить интегрирование как по времени, так и по длине. Конструктивно спица имеет вид цилиндрической трубы с внешним радиусом R и изготовлена из материала с плотностью ρ и модулем упругости E. За исполнительный двигатель был взят А2212 Brushless Inrunner. Напряжение питания U₁, $\left| {{{U}_{1}}} \right| \leqslant {{U}_{1}}_{{\max }}$ выберем в качестве управления и будем изменять его значения для достижения конечного угла раскрытия.

Момент трения рассчитывается динамически в процессе моделирования системы по формуле [12] ${{M}_{{{\text{тр}}}}} = {{{\varphi }}_{{ish}}}{{{\varphi }}_{{rs}}}{{M}_{{rr}}} + {{M}_{{sl}}} + {{M}_{{seal}}} + {{M}_{{drag}}}$, где ${{{\varphi }}_{{ish}}}$ – коэффициент уменьшения за счет нагрева смазочного материала, ${{{\varphi }}_{{rs}}}$ – коэффициент уменьшения в режиме кинематического голодания, где ${{M}_{{rr}}}$ – момент трения качения, ${{M}_{{sl}}}$ – момент трения скольжения, ${{M}_{{seal}}}$ – момент трения уплотнений, ${{M}_{{drag}}}$ – момент трения за счет сопротивления смазки, взбалтывания, разбрызгивания и пр.

Примем, что спица является тонкостенным кольцом в плоскости изгиба. При этом в сложенном состоянии звенья жестко закреплены и никаких дополнительных перемещений звеньев относительного друг друга не происходит.

Требуется найти такое управление $U_{1}^{*}$, которое переведет систему (1.1) из начального состояния ${{{\mathbf{X}}}_{{\text{р}}}}(0)$ в конечное ${{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}})$ при минимизации прогиба спицы h при ограничении на управление U₁ за конечное время t_f.

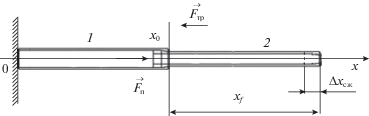
1.2. Выдвижение спицы рефлектора. Одним из этапов развертывания КТР является выдвижение спицы (рис. 3). Необходимо выдвинуть спицу рефлектора космического базирования длиной x_выдв и массой m_выдв из начального транспортировочного положения x₀ в конечное заданное x_f.

Система дифференциальных уравнений, описывающих динамику выдвижения спицы, имеет вид [7] ${{{\mathbf{\dot {X}}}}_{{\text{в}}}} = {\mathbf{f}}({{{\mathbf{X}}}_{{\text{в}}}},u,t)$, где ${{{\mathbf{X}}}_{{\text{в}}}} = {{(x\;\;V\;\Delta {{x}_{{{\text{сж}}}}}\;{{V}_{{{\text{сж}}}}})}^{{\text{T}}}}$ – вектор состояния процесса выдвижения, x – длина  выдвижения спицы; V – линейная скорость выдвижения спицы, $\Delta {{x}_{{{\text{сж}}}}}$ – продольная деформация, V_сж – линейная скорость сжатия спицы. В поэлементном виде система представляется следующим образом:

где ${{F}_{{\text{п}}}}$ – полезная сила; ${{F}_{{{\text{тр}}}}}$ – сила трения, ${{F}_{{{\text{упор}}}}}$ – сила, создаваемая упором; ${{F}_{{\text{ф}}}}$ – сила, создаваемая фиксатором; ${{m}_{{{\text{выдв}}}}}$ – масса выдвигаемой части; $F$ – общая сила, действующая на спицу: $F = {{F}_{{\text{п}}}} - {{F}_{{{\text{тр}}}}} - {{F}_{{{\text{упор}}}}} - {{F}_{{\text{ф}}}}$. С учетом функций Крылова [7, 10] значение ${{\partial }^{2}}\Delta {{x}_{{{\text{сж}}}}}{\text{/}}\partial {{x}^{2}}$, исходя из граничных условий при x = 0 и $x = {{x}_{{{\text{выдв}}}}}$, равно ${{\partial }^{2}}\Delta {{x}_{{{\text{сж}}}}}{\text{/}}\partial {{x}^{2}} = \rho {\omega }_{{{{{\text{c}}}_{{{\text{прод }}k}}}}}^{2}\sin ({{{\omega }}_{{{{{\text{c}}}_{{{\text{прод }}k}}}}}}t){\text{/}}Е$, где ${{{\omega }}_{{{{{\text{c}}}_{{{\text{прод }}k}}}}}}$ – k-я собственная частота продольных колебаний. В работе [7] показано, что тогда можно записать

Для описания F_п можно использовать уравнение, аналогичное M_п в системе (1.1). Для создания F_п необходимо учитывать конструкцию передачи, например цепную, зубчатую и т.д., что само по себе является отдельной технической задачей. Для полного описания также необходимо учитывать люфты и “мертвые” зоны механизма. Ввиду всего вышесказанного уравнение для F_п будет состоять из уравнения типа M_п в системе (1.1), умноженного на коэффициент k_f, который отвечает за преобразование вращающего момента в толкающую силу ${{F}_{{\text{п}}}} = {{k}_{f}}{{M}_{{\text{п}}}}.$ Аналогично этапу раскрытия спицы учтем воздействие механизмов упора и фиксации.

При выдвижении спицы необходимо минимизировать сжатие $\Delta {{х}_{{{\text{сж}}}}}$, так как оно является эффективным показателем нагрузок, оказываемых на спицу. Силу трения F_тр примем равной константе. Соединение между звеньями 1 и 2 можно считать без наличия люфтов.

Управление выдвижением происходит за счет изменения напряжения питания электродвигателя $u = {{U}_{1}}$, $\left| {{{U}_{1}}} \right| \leqslant {{U}_{1}}_{{\max }}$. Требуется найти такое управление $U_{1}^{*}$, которое переведет систему (1.3) из начального состояния ${{{\mathbf{X}}}_{{\text{в}}}}(0)$ в конечное ${{{\mathbf{X}}}_{{\text{в}}}}({{t}_{f}})$ при минимизации сжатия спицы $\Delta {{x}_{{{\text{сж}}}}}$ и ограничении на управление U₁ за конечное время ${{t}_{f}}$.

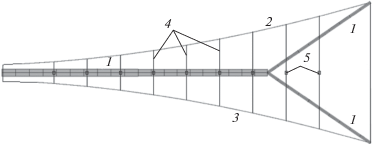
1.3. Настройка формы радиоотражающей поверхности. Рассмотрим процесс настройки формы радиоотражающей поверхности. На рис. 4 представлена одна спица в сечении: 1 – спица, 2 и 3 – внешняя и задняя сетка, 4 – ванты, в которых установлены актюаторы. Необходимо, изменяя длину вант 4 с помощью актюаторов 5, задать желаемую форму радиоотражающего сетеполотна 2.

Для определения формы радиоотражающего сетеполотна в пространстве удобно представить ее в виде мембраны. Тогда дифференциальное уравнение мембраны можно описать уравнением Лапласа [8]

где x, y, z – оси координат, q – распределенная нагрузка, S_м – площадь поверхности мембраны.

В качестве актюаторов рассматривались пьезопривод, двигатель постоянного тока (ДПТ). Система дифференциальных уравнений, описывающих пьезоэлемент с исполнительным органом, имеет вид [13] ${{{\mathbf{\dot {X}}}}_{{{\text{пэ}}}}} = {\mathbf{f}}({{{\mathbf{X}}}_{{{\text{пэ}}}}},u,t)$, где ${{{\mathbf{X}}}_{{{\text{пэ}}}}} = {{(\Delta {{l}_{{{\text{пэ}}}}}\;{{V}_{{{\text{пэ}}}}}\;{{U}_{{{\text{пэ}}}}})}^{{\text{T}}}}$ – вектор состояния пьезоэлемента; $\Delta {{l}_{{{\text{пэ}}}}}$ – изменение длины (ход) пьезоактюатора; V_пэ – скорость выдвижения пьезоактюатора; U_пэ – напряжение, приложенное к электродам пьезоактюатора, или

где K₀ – коэффициент обратного пьезоэффекта, ${{F}_{{{\text{cтат}}}}}$ – статическое усилие, ${{K}_{{{\text{у}}{\text{.}}\;{\text{пэ}}}}}$ – коэффициент упругости пьезоактюатора, ${{K}_{{{\text{д}}{\text{.}}\;{\text{пэ}}}}}$ – коэффициент внутреннего демпфирования пьезоактюатора, e_n – напряжение от источника ЭДС, ${{C}_{0}}$ – емкость, ${{R}_{{{\text{внут}}}}}$ – внутреннее сопротивление, K_n – коэффициент прямого пьезоэффекта, ${{m}_{\Sigma }}$ – суммарная масса, состоящая из массы самого пьезоактюатора и перемещаемой массы.

Задача управления пьезоактюатором состоит в приведении его из начального положения ${{{\mathbf{X}}}_{{{\text{пэ}}}}}(0)$ в заданное конечное состояние ${{{\mathbf{X}}}_{{{\text{пэ}}}}}(t{}_{f})$ при ограничении на управление, за которое принято напряжение от источника ЭДС e_n, $\left| {{{e}_{n}}} \right| \leqslant {{e}_{n}}_{{\;\max }}$.

Система уравнений, описывающая ДПТ с учетом угла поворота вала, имеет вид [14] ${{{\mathbf{\dot {X}}}}_{{{\text{ДПТ}}}}} = {\mathbf{f}}({{{\mathbf{X}}}_{{{\text{ДПТ}}}}}$, u, t), где ${{{\mathbf{X}}}_{{{\text{дпт}}}}} = {{({{{\varphi }}_{{{\text{вал}}}}}\;{{{\omega }}_{{{\text{вал}}}}}\;{{I}_{{\text{я}}}})}^{{\text{T}}}}$ – вектор состояния ДПТ; ${{{\varphi }}_{{{\text{вал}}}}}$ – угол поворота вала двигателя; ${{{\omega }}_{{{\text{вал}}}}}$ – угловая скорость вращения вала двигателя; I_я – ток якоря, или

где k_m – коэффициент пропорциональности (постоянная момента двигателя), ${{M}_{{{\text{внеш}}}}}$ – момент внешних сил, J_я – момент инерции ротора двигателя, U_ДПТ – внешнее напряжение ДПТ, R_я – активное сопротивление обмотки якоря, ${{k}_{e}}$ – коэффициент пропорциональности (постоянная ЭДС двигателя), L_я – индуктивность якорной обмотки. В качестве редуктора рассматривается диск радиуса ${{R}_{{{\text{ред}}}}}$, который одевается непосредственно на вал двигателя и обеспечивает изменение длины ванты на длину $\Delta {{l}_{{{\text{ДПТ}}}}} = {{{\varphi }}_{{{\text{вал}}}}}{{R}_{{{\text{ред}}}}}{\pi /180}^\circ $.

Задача управления ДПТ состоит в приведении его из начального положения ${{{\mathbf{X}}}_{{{\text{ДПТ}}}}}(0)$ в заданное конечное состояние ${{{\mathbf{X}}}_{{{\text{ДПТ}}}}}(t{}_{f})$ при ограничении на управление, за которое принято внешнeе напряжение питания ${{U}_{a}}$, $\left| {{{U}_{a}}} \right| \leqslant {{U}_{a}}_{{\max }}$.

2. Разработка стратегий управления. Оптимизация процесса создания и поддержания формы КТР космического базирования является сложной задачей. Построение устойчивых алгоритмов поиска оптимальной траектории в реальном масштабе времени затруднено, а зачастую невозможно ввиду трудности обеспечения сходимости решений, возникающих из принципа максимума [15, 16] двухточечных краевых задач. Поэтому требуется разработать методику и алгоритмы, которые позволят получать надежное решение задачи оптимизации траектории в реальном времени движения.

Одним из возможных подходов к решению задачи синтеза оптимального управления является разработка алгоритма оптимизации движения с коррекцией параметров структуры управления [17–19]. При этом управление может вычисляться в реальном времени в процессе раскрытия как функция текущих значений фазовых координат. В этом случае из применения принципа максимума определяется структура управления, параметры которой оптимизируются во вспомогательной задаче.

Системы (1.1) и (1.3) содержат в правых частях уравнений частные производные. Примем, что параметры колебаний данных систем вычисляются на конце спицы, т.е. при l = a. Также будем считать первую форму колебаний на конце спицы, так как первая форма вносит самый большой вклад в амплитуду колебаний, а на конце спицы они максимальны. Тогда частные производные ${{\partial }^{4}}h{\text{/}}\partial {{l}^{4}}$, ${{\partial }^{4}}{{V}_{{{\text{изг}}}}}{\text{/}}\partial {{l}^{4}}$, ${{\partial }^{2}}\Delta {{x}_{{{\text{сж}}}}}{\text{/}}\partial {{x}^{2}}$, $\partial {{V}_{{{\text{сж}}}}}{\text{/}}\partial x$ примут конкретные значения, что позволяет применять принцип максимума Понтрягина, который был разработан применительно к системам обыкновенных дифференциальных уравнений.

Рассмотрим задачи разворота, выдвижения спицы и настройки сетеполотна при наличии наблюдений по полным данным и при отсутствии возмущений.

2.1. Раскрытие спицы рефлектора. Используем принцип максимума для поиска оптимального управления с учетом постановки задачи минимизации прогиба h на всем времени развертывания. В качестве целевого рассмотрим интегротерминальный функционал:

где ${{{\mathbf{V}}}_{f}} = 0.5{{\left[ {{{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}}) - {{{\mathbf{X}}}_{{\text{р}}}}_{{\;f}}} \right]}^{{\text{T}}}}{\mathbf{\rho }}\left[ {{{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}}) - {{{\mathbf{X}}}_{{\text{р}}}}_{{\;f}}} \right]$; ${{f}_{0}} = 0.5{{h}^{2}}{\text{/}}k_{{\text{р}}}^{2}$; ${\mathbf{\rho }} = {\text{diag}}({{{\rho }}_{1}},{{{\rho }}_{2}},{{{\rho }}_{3}},{{{\rho }}_{4}})$, k_p – коэффициенты этапа раскрытия; ${{{\mathbf{X}}}_{{\text{р}}}}_{{\;f}} = {{({{{\varphi }}_{f}}\;{{{\omega }}_{f}}\;{{h}_{f}}\;{{V}_{{{\text{изг}}\;f}}})}^{{\text{T}}}}$ – заданные конечные значения соответствующих переменных процесса раскрытия. В системе уравнений (1.1) прогиб h зависит и от времени, и от длины, поэтому для упрощения вычислений в первом приближении прогиб можно принять равным $h(l) = M{{l}^{2}}{\text{/}}(2E{{I}_{{{\text{изг}}}}})$, где M – общий момент, действующий на спицу [20]. Так как $M = E{{I}_{{{\text{изг}}}}}{{\partial }^{2}}h{\text{/}}\partial {{l}^{2}}$, то $h(l) = 0.5{{l}^{2}}{{\partial }^{2}}h{\text{/}}\partial {{l}^{2}}$. Исходя из (1.2) получим ${{{{\partial }^{2}}h} \mathord{\left/ {\vphantom {{{{\partial }^{2}}h} {\partial {{l}^{2}}}}} \right. \kern-0em} {\partial {{l}^{2}}}} = {{\alpha }^{2}}[A{{K}_{1}}({{Z}_{k}}) + B{{K}_{2}}({{Z}_{k}})]$, где $\alpha = \rho S{\omega }_{{{\text{c}}{{{\text{ }}}_{{{\text{изг }}k}}}}}^{2}{\text{/}}(E{{I}_{{{\text{изг}}}}})$; ${{K}_{1}} = 0.5({\text{ch}}Z + \cos Z)$, ${{K}_{2}} = 0.5({\text{sh}}Z + \sin Z)$, A, B – коэффициенты, определяемые из граничных условий задачи. Проделав данные преобразования получаем выражение для первого приближения прогиба в виде $h(l) = 0.5{{l}^{2}}{{\alpha }^{2}}[A{{K}_{1}}({{Z}_{k}}) + B{{K}_{2}}({{Z}_{k}})]$, подставив в него значения коэффициентов A, B получим уравнение идентичное (1.2). Данное упрощение является допустимым, поскольку принимается, что максимальный прогиб достигается на конце спицы. Спица в каждый момент времени жестко закреплена одним концом, а второй конец является свободным. На спицу действует момент, приложенный к закрепленному концу спицы.

Поскольку в терминальную часть функционала (2.1) входят требования не только к конечным значениям угла φ и прогиба h, но и к их производным, то механизмы упора и фиксатора при оптимальном управлении будут нести в себе только функции собственно фиксации спиц при достижении упора и не приводить к колебаниям в этих механизмах.

С учетом сделанных допущений гамильтониан системы (1.1) примет вид $H = {{{\mathbf{P}}}^{T}}{\mathbf{f}}({{{\mathbf{X}}}_{{\text{р}}}}) + {{f}_{0}}$, где ${\mathbf{P}} = {{[{{P}_{{\varphi }}}\;{{P}_{{\omega }}}\;{{P}_{h}}\;{{P}_{{{{V}_{{{\text{изг}}}}}}}}]}^{{\text{T}}}}$ – вектор сопряженных переменных, или

Найдем сопряженные переменные:

Так как на управление наложено ограничение $\left| {{{U}_{1}}} \right| \leqslant {{U}_{{1\;\max }}}$, то оно определяется из условия [16] $\partial H{\text{/}}\partial {{U}_{1}} = 0$:

при $\left| {{{U}_{1}}} \right| < {{U}_{{1\;\max }}}$ или ${{U}_{1}} = {{U}_{{1\;\max }}}{\text{sign}}{{U}_{1}}$ при $\left| {{{U}_{1}}} \right| \geqslant {{U}_{{1\;\max }}}$, где $A = {{m{}_{{{\text{фаз}}}}p{{E}_{0}}\sin \vartheta } \mathord{\left/ {\vphantom {{m{}_{{{\text{фаз}}}}p{{E}_{0}}\sin \vartheta } {{\text{(}}{{{\omega }}_{1}}{{X}_{{{\text{cинхр}}}}}}}} \right. \kern-0em} {{\text{(}}{{{\omega }}_{1}}{{X}_{{{\text{cинхр}}}}}}})$.

2.2. Выдвижение спицы рефлектора. Аналогично этапу раскрытия спицы рассмотрим этап выдвижения. Исходя из постановки задачи, целевой критерий примем в виде

где ${{{\mathbf{V}}}_{f}} = 0.5{{\left[ {{{{\mathbf{X}}}_{{\text{в}}}}({{t}_{f}}) - {{{\mathbf{X}}}_{{\text{в}}}}_{{\;f}}} \right]}^{{\text{T}}}}{\mathbf{\rho }}\left[ {{{{\mathbf{X}}}_{{\text{в}}}}({{t}_{f}}) - {{{\mathbf{X}}}_{{\text{в}}}}_{{\;f}}} \right]$; ${{f}_{0}} = 0.5\Delta x_{{{\text{сж}}}}^{2}{\text{/}}k_{{\text{в}}}^{2}$; ${{{\mathbf{X}}}_{{{\text{в}}\;}}}_{f} = {{({{x}_{f}}\;{{V}_{f}}\;\Delta {{x}_{{{\text{сж}}\;f}}}\;{{V}_{{{\text{сж}}\;f}}})}^{{\text{T}}}}$ – заданные конечные значения соответствующих переменных; ${\mathbf{\rho }} = {\text{diag}}({{{\rho }}_{1}},{{{\rho }}_{2}},{{{\rho }}_{3}},{{{\rho }}_{4}})$, k_в – коэффициенты этапа выдвижения.

В первом приближении сжатие $\Delta {{x}_{{{\text{сж}}}}}$ можно принять равным [20] $\Delta {{x}_{{{\text{сж}}}}} = Fl{\text{/}}(ES)$, где F – общая сила, действующая на спицу. Для оптимального управления по критерию (2.4) при наличии в системе упора и фиксатора аналогично случаю раскрытия спицы гамильтониан системы (1.3) примет вид $H = {{{\mathbf{P}}}^{{\text{T}}}}{\mathbf{f}}({{{\mathbf{X}}}_{{\text{в}}}}) + {{f}_{0}}$, где ${\mathbf{P}} = {{[{{P}_{x}}\;{{P}_{V}}\;{{P}_{{\Delta {{x}_{{{\text{сж}}}}}}}}\;{{P}_{{{{V}_{{{\text{сж}}}}}}}}]}^{{\text{T}}}}$ – вектор сопряженных переменных, или

Найдем сопряженные переменные

и управление с учетом ограничения $\left| {{{U}_{1}}} \right| \leqslant {{U}_{{1\;\max }}}$ из условия $\partial H{\text{/}}{{U}_{1}} = 0{\text{:}}$при $\left| {{{U}_{1}}} \right| < {{U}_{{1\;\max }}}$ или ${{U}_{1}} = {{U}_{{1\;\max }}}{\text{sign}}{{U}_{1}}$ при $\left| {{{U}_{1}}} \right| \geqslant {{U}_{{1\;\max }}}$, где $B = {{k}_{f}}{{m{}_{{{\text{фаз}}}}p{{E}_{0}}\sin \vartheta } \mathord{\left/ {\vphantom {{m{}_{{{\text{фаз}}}}p{{E}_{0}}\sin \vartheta } {({{{\omega }}_{1}}{{X}_{{{\text{cинхр}}}}})}}} \right. \kern-0em} {({{{\omega }}_{1}}{{X}_{{{\text{cинхр}}}}})}}$.

2.3. Настройка формы радиоотражающей поверхности. Примем, что необходимо перенастроить форму радиоотражающего сетеполотна. Для этого по формуле (1.4) определяется текущее состояние фронтальной сети. Вычисляются необходимые размеры вант для задания желаемой формы радиоотражающего сетеполотна. С помощью актюаторов в каждой точке происходит изменение длины ванты.

Рассмотрим в качестве исполнительного органа пьезоактюатор. При оптимизации перевода системы из одного положения в другое с фиксированным начальным и конечным состоянием выберем критерий J = t_f.

Гамильтониан системы (1.5) имеет вид $H = {{{\mathbf{P}}}^{{\text{T}}}}{\mathbf{f}}({{{\mathbf{X}}}_{{{\text{пэ}}}}})$, где ${\mathbf{P}} = {{[{{P}_{{\Delta {{l}_{{{\text{пэ}}}}}}}}\;{{P}_{{{{V}_{{{\text{пэ}}}}}}}}\;{{P}_{{{{U}_{{{\text{пэ}}}}}}}}]}^{{\text{T}}}}$ – вектор сопряженных переменных, или

Найдем сопряженные переменные

При решении задачи оптимальности по быстродействию системы дифференциальных уравнений (1.5) структура управления, согласно принципу максимума, при наличии ограничения на управление $\left| {{{e}_{n}}} \right| \leqslant {{e}_{n}}_{{\max }}$ примет вид

При выборе в качестве актюатора ДПТ для задачи, аналогичной пьезоактюатору, получим следующий гамильтониан системы (1.6): $H = {{{\mathbf{P}}}^{{\text{T}}}}{\mathbf{f}}({{{\mathbf{X}}}_{{{\text{ДПТ}}}}})$, где ${\mathbf{P}} = {{[{{P}_{{I{}_{{\text{я}}}}}}\;{{P}_{{{{{\omega }}_{{{\text{вал}}}}}}}}\;{{P}_{{{{{\varphi }}_{{{\text{вал}}}}}}}}]}^{{\text{T}}}}$ – вектор сопряженных переменных, или

Сопряженные переменные

При оптимизации по быстродействию системы дифференциальных уравнений (1.6) структура управления при наличии ограничения на управление $\left| {{{U}_{{{\text{ДПТ}}}}}} \right| \leqslant {{U}_{{{\text{ДПТ}}}}}{{\,}_{{\max }}}$ примет вид ${{U}_{{{\text{ДПТ}}}}}(t)$ = = $ - {{U}_{{{\text{ДПТ}}\,}}}_{{\max }}{\text{sign}}{{P}_{{{{I}_{{\text{я}}}}}}}(t).$

Решение перечисленных задач раскрытия и выдвижения спиц рефлектора, настройки сетеполотна с использованием принципа максимума позволяет выявить структуру оптимального управления. Используя момент времени τ_i переключения структуры управления в качестве параметров, представим структуру управления в виде:

где $i = \overline {1,r} $, i – номер участка структуры управления, r – количество переключений управления в структуре, ${{{\mathbf{l}}}^{{\text{T}}}}(t,{{{\tau }}_{i}}) = [l(t,{{{\tau }}_{1}})\;l(t,{{{\tau }}_{2}}) \ldots l(t,{{{\tau }}_{r}})]$, $\Delta {{u}_{i}} = - {{u}_{i}} + {{u}_{{i + 1}}}$, ${{u}_{i}}(t) = {{u}_{1}}(t)$ при $t < {{{\tau }}_{1}}$. Здесь u_i и ${{u}_{{i + 1}}}$ – управления на предыдущем и последующем участках этой структуры относительно τ₁ соответственно, а $l(t,{{{\tau }}_{i}})$ – единичные функции.

К исходным системам (1.1), (1.3), (1.5), (1.6) добавляются уравнения ${\mathbf{\dot {\tau }}} = {\mathbf{w}}$, где ${\mathbf{\tau }} = {{({{{\tau }}_{1}}\,{{{\tau }}_{2}}\,...\,{{{\tau }}_{r}})}^{{\text{T}}}}$; ${\mathbf{w}} = {{\left( {{{w}_{1}}\,\,{{w}_{2}}\,\,...\,\,{{w}_{r}}} \right)}^{{\text{T}}}}$ – векторы новых переменных, принимаемых за управления.

Вспомогательную задачу можно решать с минимизацией критерия

или критерия где ${\mathbf{k}} = {\text{diag}}({{k}_{1}},{{k}_{2}},{{k}_{3}},{{k}_{4}})$.

Тогда уравнения для обобщенного вектора состояния запишутся как

При свободном времени окончания t_f оно также является корректируемым параметром: ${\mathbf{\tau }} = {{({{{\tau }}_{1}}\;{{{\tau }}_{2}}\; \ldots {{{\tau }}_{r}}\;{{t}_{f}})}^{{\text{T}}}}$. Введением нового вектора управления w исходная задача оптимизации по определению u решается косвенно – через нахождение этого вектора w.

Для обеспечения развертывания крупногабаритного рефлектора космического базирования с мягким выходом к упорам можно также использовать алгоритм последовательной оптимизации по иерархии целевых функционалов [21].

3. Моделирование. Рассмотрим отдельно задачи для раскрытия, выдвижения спиц и настройки сетеполотна.

3.1. Раскрытие спиц рефлектора. Рассмотрим первый этап развертывания КТР – раскрытие спиц. При раскрытии системы не оказывается никаких возмущающих воздействий и управление осуществляется по полным данным. Процесс получения информации с датчиков (без ошибок) происходит непрерывно.

Спица разворачивается из начального траспортировочного положения при значении угла поворота ${{{\varphi }}_{0}} = 0$ и фиксируется при достижении заданного угла ${{{\varphi }}_{f}} = {\pi /}2$. Спица в начальном положении находится в состоянии покоя, соответсвенно угловая скорость ω₀ = 0, прогиб ${{h}_{0}} = 0$ и скорость изгиба ${{V}_{{{\text{из}}{{{\text{г}}}_{0}}}}} = 0$. Конечные значения угловой скорости ${{{\omega }}_{f}} = 0$, прогиба ${{h}_{f}} = 0$ и скорости изгиба ${{V}_{{{\text{из}}{{{\text{г}}}_{f}}}}} = 0$. Примем время раскрытия ${{t}_{f}} = 130$ с, максимальная допустимая амплитуда прогиба ${{h}_{{\max }}} = 10$ мм. Значение коэффициента затухания примем ${\gamma } = 0.04$ c [7]. Первая собственная частота изгибных колебаний для случая заделанного левого и свободного правого концов [10] ${{{\omega }}_{{{\text{c}}{{{\text{ }}}_{{{\text{изг 1}}}}}}}} = 14.465$ Гц. Число фаз ротора $m{}_{{{\text{фаз}}}}$ = 2, число пар полюсов магнитного поля $p$ = 2, действующее значение ЭДС на обмотке статора ${{E}_{0}}$ = 2.5 В, синхронное сопротивление ${{X}_{{{\text{cинхр}}}}}$ = = $22 \times {{10}^{{ - 3}}}$ Ом, угол рассогласования между полем ротора и статора $\vartheta $ = ${\pi /}10$ при любой нагрузке. Коэффициенты ${{k}_{{{\text{у}}{\text{.упор}}}}} = {{k}_{{{\text{у}}{\text{.ф}}}}} = 100$, ${{с}_{{{\text{д}}{\text{.упор}}}}} = 30$, ${{с}_{{{\text{д}}{\text{.ф}}}}} = 25$.

Были выбраны следующие параметры спицы при моделировании: материал пластик QHF – 0140: плотность материала ${\rho } = 1600$ кг/м³, модуль упругости (Юнга) $E = 1.2 \times {{10}^{{11}}}$ Па, длина спицы a = 9.75 м, масса спицы (всех вложенных звеньев) m = 32 кг. Рассматривается спица с сечением в виде кольца с внешним радиусом R = 0.26 м и внутренним радиусом r = 0.25 м. Момент инерции I будет равняться $I = \frac{1}{2}m{{R}^{2}} + \frac{1}{3}m{{a}^{2}} = 1015.4$ кг ⋅ м². Изгибной момент инерции I_изг = = $\pi {{R}^{3}}\delta = 5.52 \times {{10}^{{ - 4}}}$ м⁴, где $\delta $ = 0.01 м – толщина стенки спицы.

В качестве регулятора было рассмотрено применение различной структуры (пропорционально-интегрально-дифференцирующего) ПИД-регулятора, в том числе с ограничениями на управление. Измерению и вычислению доступны $\Delta {{{\mathbf{X}}}_{{\text{р}}}} = {{{\mathbf{X}}}_{{\text{р}}}}_{{\;f}} - {{{\mathbf{X}}}_{{\text{р}}}}(t)$, интеграл $\int_0^t {\Delta {{{\mathbf{X}}}_{{\text{р}}}}dt} $ и производная $\Delta {{{\mathbf{\dot {X}}}}_{{\text{р}}}}$.

Проанализировав работу различной структуры ПИД-регулятора, выберем в качестве наилучшего (пропорционально-интегральный) ПИ-регулятор, так как его использование обеспечило удовлетворительное качество переходного процесса. Для перевода системы из начального состояния ${{{\mathbf{X}}}_{{\text{р}}}}(0) = {{(0\;0\;0\;0)}^{{\text{T}}}}$ в конечное ${{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}}) = {{({\pi /2}\;0\;0\;0)}^{{\text{T}}}}$ с отсутствием перерегулирования по углу разворота φ потребовалось ${{t}_{f}} = 462.2$ с, что больше заданного времени развертывания, равного 130 с. Максимальное значение величины прогиба h составило ${{h}_{{\max }}} = 1.35 \times {{10}^{{ - 5}}}$ м.

Можно настроить ПИ-регулятор таким образом, чтобы система достигала конечного значения ${{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}}) = {{({\pi /2}\;0\;0\;0)}^{{\text{T}}}}$ за ${{t}_{f}} = 130$ с, но из-за наличия в системе упора и фиксатора колебания спицы продолжаются больше заданного времени (340 с) при максимальной величине прогиба ${{h}_{{\max }}} = 0.0018$ м.

При оптимальном управлении краевая задача (1.1), (2.2), (2.3) решалась методом Ньютона [15] с использованием вектора невязок:

Здесь для более быстрой сходимости метода Ньютона при получении решения поставленной задачи можно считать фиксированным правый конец траектории. Это позволяет не включать в вектор невязок значения сопряженных переменных на правом конце траектории при сохранении условий оптимальности. Данное упрощение допустимо, поскольку метод Ньютона используется для выявления структуры оптимального управления.

Интегрирование проводилось методом Эйлера с шагом Δt = 0.01 с при ${{k}_{{\text{р}}}} = 1 \times {{10}^{{ - 7}}}$. Были приняты начальные условия для компонент вектора сопряженных переменных P(t₀): ${{P}_{{\varphi }}}({{t}_{0}}) = 0$, ${{P}_{{\omega }}}({{t}_{0}}) = - 20$, ${{P}_{h}}({{t}_{0}}) = - 0.1$, ${{P}_{{{{V}_{{{\text{изг}}}}}}}}({{t}_{0}}) = - 1$ при приращениях для сопряженных переменных ΔP|_φ = 0.1, ΔP|_ω = 1, ΔP|_h = 0.01, Δ$P{{{\text{|}}}_{{{{V}_{{{\text{изг}}}}}}}}$ = 0.1 в процедуре численного определения частных производных от вектора невязок. Итерационная процедура выполнялась с точностью $\left\| {{{{\mathbf{Z}}}_{{\text{Н}}}}(t,{{t}_{f}})} \right\| \leqslant 0.001$. При заданных начальных условиях за 13 итераций были получены оптимальные начальные значения сопряженных переменных ${{P}_{{\varphi }}}{{({{t}_{0}})}_{{{\text{опт}}}}} = 0.1$, ${{P}_{{\omega }}}{{({{t}_{0}})}_{{{\text{опт}}}}} = - 10$, ${{P}_{h}}{{({{t}_{0}})}_{{{\text{опт}}}}} = - 0.01$, ${{P}_{{{{V}_{{{\text{изг}}}}}}}}{{({{t}_{0}})}_{{{\text{опт}}}}} = - 1.909$.

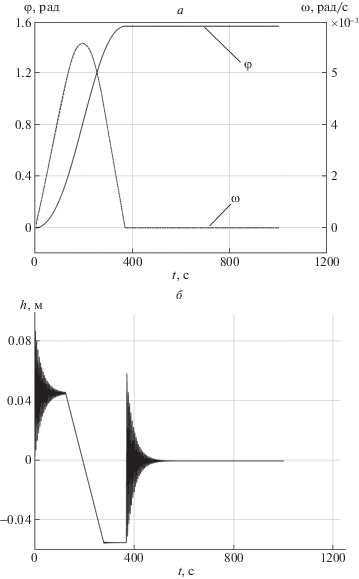
Как видно из рис. 5, а и б, удалось добиться перевода системы из заданного начального положения в заданное конечное за ${{t}_{f}} = 133$ с, причем данное время является минимально возможным для поставленных условий задачи. Максимальное значение величины прогиба h составило ${{h}_{{\max }}} = 1.583 \times {{10}^{{ - 4}}}$ м, что на порядок меньше по сравнению с ПИ-регулятором при одинаковых условиях.

Значение величины невязки $\left\| {{{{\mathbf{Z}}}_{{\text{Н}}}}(t,{{t}_{f}})} \right\|$ необходимо выбирать не более 0.001, так как в системе присутствуют упор и фиксатор, и даже небольшое расхождение по углу раскрытия спицы φ и угловой скоростью ω приводит к колебательному процессу или же спица не доходит до своего конечного значения. При выбранных оптимальных начальных значениях сопряженных переменных значение невязки составило не более 10^–5.

Представим сигнал управления U₁ в виде, когда возможно два переключения (из решения задачи методом Ньютона следует одно переключение):

где ${{P}_{{{\omega }\;0}}} = {{P}_{{\omega }}}(0)$, $\Delta {{U}_{{{{1}_{1}}}}} = 2{{U}_{{1\;}}}_{{\max }}{\text{sign}}({{P}_{{{\omega }\;0}}})$, $\Delta {{U}_{{{{1}_{2}}}}} = - {{U}_{{1\;}}}_{{\max }}{\text{sign}}({{P}_{{{\omega }\;0}}})$, а $l(t,{{{\tau }}_{1}})$, $l(t,{{{\tau }}_{2}})$ – функции вида [21]

Здесь c – коэффициент, при неограниченном возрастании которого функция $l(t,{{{\tau }}_{i}})$ приближается к единичной функции Хэвисайда.

Запишем гамильтониан вспомогательной задачи оптимизации с учетом (2.7) и (2.8):

Система канонических уравнений имеет вид

где ${\delta }(t,{{{\tau }}_{1}})$, ${\delta }(t,{{{\tau }}_{2}})$ – функции вида ${\delta }(t,{{{\tau }}_{i}}) = {{\partial l(t,{{{\tau }}_{i}})} \mathord{\left/ {\vphantom {{\partial l(t,{{{\tau }}_{i}})} {\partial {{{\tau }}_{i}}}}} \right. \kern-0em} {\partial {{{\tau }}_{i}}}} = - {{2c{{e}^{{ - 2c(t - {{{\tau }}_{i}})}}}} \mathord{\left/ {\vphantom {{2c{{e}^{{ - 2c(t - {{{\tau }}_{i}})}}}} {{{{(1 + {{e}^{{ - 2c(t - {{{\tau }}_{i}})}}})}}^{2}}}}} \right. \kern-0em} {{{{(1 + {{e}^{{ - 2c(t - {{{\tau }}_{i}})}}})}}^{2}}}}$. Составляющие вектора управления ${{w}_{1}}(t) = - k_{1}^{2}{{P}_{{{{{\tau }}_{1}}}}}({{{\tau }}_{1}})$, ${{w}_{2}}(t) = - k_{2}^{2}{{P}_{{{{{\tau }}_{2}}}}}({{{\tau }}_{2}})$.

Расчеты показали, что характер зависимостей ${\varphi }(t),{\omega }(t),h(t)$ соответствуют графикам на рис. 5. Алгоритм оптимизации с коррекцией параметров структуры управления позволяет обеспечить успешное выполнение поставленной задачи без затруднений в сходимости. При этом τ₁ стремится к оптимальному времени смены предельных значений управления U₁, полученного из метода Ньютона (рис. 5, б), а ${{{\tau }}_{2}}$ стремится к конечному времени, при котором система достигает заданных значений [17].

Прогибы конструкции незначительны и не превышают величины ${{h}_{{\max }}} = 0.002$ м. При использовании оптимального регулятора время затухания колебаний составляет 5 с. Это объясняется достаточной жесткостью конструкции.

Исходя из [7] наибольший интерес представляет минимизация прогиба и колебаний при полностью раскрытой спице, так как в данном случае спица более склонна к переходному процессу с длительными затухающими колебаниями. При данных условиях изменится длина, момент инерции, первая собственная частота спицы: $a = 29.01$ м, $I \approx 8978$ кг ⋅ м², ${{{\omega }}_{{{{{\text{c}}}_{{{\text{изг }}1}}}}}} = 1.432$ Гц. На двигатель также подается напряжение питания U₁ не более ${{U}_{1}}_{{\max }}$ = 12 В.

Увеличение момента инерции почти в 9 раз делает систему “более” инерционной, вследствие чего увеличивается время раскрытия. Поэтому необходимо корректно выбрать конечное время. Проанализируем время раскрытия спицы от минимально до максимально возможного. Для этого была решена задача максимального быстродействия, время перевода системы (1.1) из начального состояния ${{{\mathbf{X}}}_{{\text{р}}}}(0) = {{(0\;0\;0\;0)}^{{\text{T}}}}$ в конечное ${{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}}) = {{({\pi /2}\;0\;0\;0)}^{{\text{T}}}}$ составило ${{t}_{f}} = 900$ с, конечное значение по углу разворота ${\varphi }$ и угловой скорости разворота ${\omega }$ было достигнуто за 356 с (рис. 6, а). Затухающие колебания свободного конца спицы длились 544 с (рис. 6, б). Максимальное значение величины прогиба ${{h}_{{\max }}} = 0.148$ м.

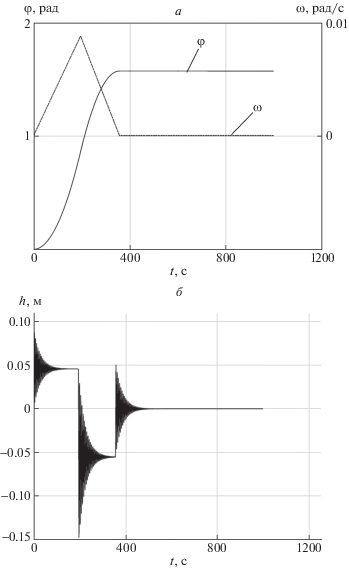
Для оценки времени раскрытия был рассмотрен вариант раскрытия спицы при использовании ПИД-регулятора при переходном процессе без перерегулирования. Время перевода системы (1.1) из начального состояния в конечное ${{t}_{f}} = 1590$ с, при этом конечное значение по углу разворота ${\varphi }$ и угловой скорости разворота ${\omega }$ было достигнуто за 1369 с. Затухающие колебания свободного конца спицы длились 221 с. Максимальное значение величины прогиба ${{h}_{{\max }}} = 0.008$ м.

Поскольку прогиб спицы прямо пропорционален приложенному моменту, то для получения минимальной величины прогиба необходимо так управлять спицей, чтобы момент был минимален. Напряжение питания, необходимое для преодоления момента трения, ${{U}_{1}} = 1.12$ В. При данном напряжении разворот спицы из начального состояния ${{{\mathbf{X}}}_{{\text{р}}}}(0) = {{(0\;0\;0\;0)}^{{\text{T}}}}$ в конечное ${{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}}) = {{({\pi /2}\;0\;0\;0)}^{{\text{T}}}}$ произойдет за ${{t}_{f}} = 28042$ с, при этом конечное значение по углу разворота ${\varphi }$ и угловой скорости разворота ${\omega }$ будет достигнуто за 27830 с. Затухающие колебания свободного конца спицы будут длиться 212 с. Максимальное значение величины прогиба ${{h}_{{\max }}} = 0.006$ м.

Для удобства обозначим: ${{t}_{f}} = {{T}_{f}} + {{t}_{{{\text{затух}}}}}$, ${{T}_{f}}$ – время раскрытия по углу разворота φ и угловой скорости разворота ${\omega }$, t_затух – время затухания колебаний спицы после постановки ее на упор и фиксатор. Исходя из полученных данных, необходимо выбирать время разворота спицы по углу разворота φ и угловой скорости разворота ω в пределах от 356 до 1369 с.

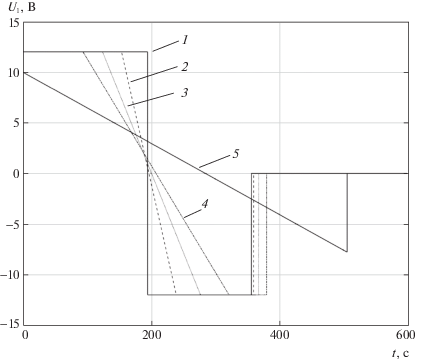
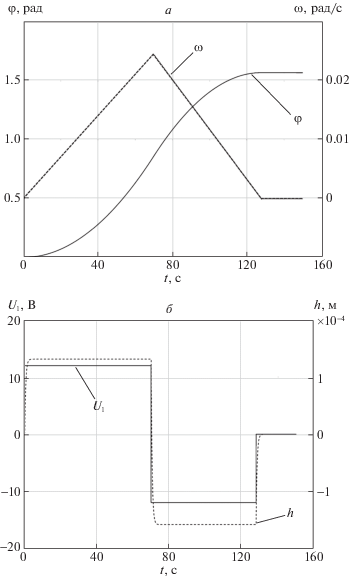
При этом с увеличением T_f  вид оптимального управления будет изменяться, например, от релейного переключения до управления с линейным участком убывания (рис. 7). Кривая 1 – ${{T}_{f}}\, = \,356$ с, ${{t}_{f}}\, = \,936$ с; кривая 2 – ${{T}_{f}} = 360$ с, ${{t}_{f}} = 940$ с; кривая 3 – ${{T}_{f}} = 368$ с, ${{t}_{f}} = 948$ с; кривая 4 – ${{T}_{f}} = 380$ с, ${{t}_{f}} = 960$ с; кривая 5 – ${{T}_{f}} = 506$ с, ${{t}_{f}} = 1200$ с.

При этом в случаях, где управление достигает максимального значения ±12 В, величина прогиба ${{h}_{{\max }}}$ одинакова, чем меньше напряжение питания (кривая 5), тем меньше прогиб и быстрее затухающий процесс. Так для случая ${{T}_{f}} = 506$ с значение ${{h}_{{\max }}} = 0.07$ м. При достаточно большом выборе t_f можно получить переходную характеристику, аналогичную минимально возможному прогибу (${{t}_{f}} = 28042$ с).

Расчеты показали, что управление раскрытием с максимальным быстродействием приводит к заметному увеличению времени затухания t_затух колебаний. Поэтому целесообразно применить алгоритм коррекции структуры управления, в которой переход между предельными значениями управлений разных знаков осуществляется по плавно изменяющейся кривой.

Для использования алгоритма с коррекцией параметров структуры управления примем, что ${{T}_{f}} = 368$ с. За управление выберем функцию вида (3.1) путем домножения ее на 24 и прибавления к ней 12, с коэффициентом c = 0.017.

На рис. 8 представлены характеристики динамики развертывания полностью раскрытой спицы при применении алгоритма коррекции параметров структуры управления для рассмотренного случая ${{T}_{f}}$ = 368 с (кривая 3 на рис. 7) с выходом в конечное положение ${{{\mathbf{X}}}_{{\text{р}}}}({{t}_{f}})$ за ${{t}_{f}} = 948$ с.

3.2. Выдвижение спиц рефлектора. Рассмотрим этап выдвижения спицы (рис. 3). Первая собственная частота продольных колебаний для случая заделанного левого и свободного правого концов [10] 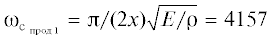Гц. Значение коэффициента затухания примем ${\gamma } = 0.04$ c [7]. Коэффициент k_f примем для рассматриваемого случая равным 1. Начальное значение длины выдвижения ${{х}_{0}} = 0$. Спица фиксируется при достижении расстояния, равного ее длине, за исключением участка стыковки первого и второго звеньев, поэтому конечное значение длины ${{х}_{f}} = 9.5$ м. Поскольку спица в начальном положении находится в состоянии покоя, то соответственно линейная скорость ${{V}_{0}} = 0$, сжатие $\Delta {{х}_{{{\text{сж}}\;{\text{0}}}}} = 0$, скорость сжатия ${{V}_{{{\text{сж}}\;0}}} = 0$. Для задания сил упора ${{F}_{{{\text{упор}}}}}$ и фиксатора ${{F}_{{\text{ф}}}}$ необходимо определить коэффициенты ${{k}_{{{\text{у}}{\text{. упор(ф)}}}}}$ и ${{c}_{{{\text{д}}{\text{. упор(ф)}}}}}$. Исходя из экспериментальных данных примем ${{k}_{{{\text{у}}{\text{. упор}}}}} = {{k}_{{{\text{у}}{\text{. ф}}}}} = 100$, ${{c}_{{{\text{д}}{\text{. упор}}}}} = 50$, ${{c}_{{{\text{д}}{\text{. ф}}}}} = 15$. Примем время раскрытия ${{t}_{f}} = 100$ с, максимальная допустимая амплитуда сжатия $\Delta {{x}_{{{\text{сж}}\;{\text{max}}}}} = 1$ мм.

Измерениям доступен вектор переменных состояния ${{{\mathbf{X}}}_{{\text{в}}}}$. Для перевода системы из начального состояния ${{{\mathbf{X}}}_{{\text{в}}}}(0) = {{(0\;0\;0\;0)}^{{\text{T}}}}$ в конечное ${{{\mathbf{X}}}_{{\text{в}}}}({{t}_{f}}) = {{(9.5\;0\;{\text{0}}\;0)}^{{\text{T}}}}$ с отсутствием перерегулирования по длине выдвижения x при работе ПИ-регулятора потребовалось ${{t}_{f}} = 113$ с, что больше заданного времени развертывания. Максимальное значение величины сжатия спицы $\Delta {{x}_{{{\text{сж}}}}}$ составило Δx_{сж max} = $0.5 \times {{10}^{{ - 6}}}$ м. Можно настроить ПИ-регулятор таким образом, чтобы система достигала конечного значения ${{{\mathbf{X}}}_{{\text{в}}}}({{t}_{f}}) = {{(9.5\;0\;{\text{0}}\;0)}^{{\text{T}}}}$ за ${{t}_{f}} = 100$ с, но из-за наличия в системе упора и фиксатора колебания спицы продолжаются больше заданного времени (105 с) при максимальной величине сжатия спицы $\Delta {{x}_{{{\text{сж}}}}} = 1.42 \times {{10}^{{ - 5}}}$ м. Особенностью продольных колебаний в отличие от поперечных, возникающих при развороте спицы, является их высокая частота и быстрое время затухания.

При оптимальном управлении краевая задача (1.3), (2.4), (2.5) решалась методом Ньютона с использованием вектора невязок

Расчет проводился при ${{k}_{{\text{в}}}} = 1 \times {{10}^{{ - 10}}}$, шаг $\Delta t = 0.0001$ c, начальные условия для компонент вектора сопряженных переменных P(t₀) и приращениях для сопряженных переменных составляют: ${{P}_{x}}({{t}_{0}}) = - 0.01$, ${{P}_{V}}({{t}_{0}}) = 100$, ${{P}_{{\Delta {{x}_{{{\text{сж}}}}}}}}({{t}_{0}}) = - 0.0001$, ${{P}_{{{{V}_{{{\text{сж}}}}}}}}({{t}_{0}}) = 300$, ΔP|_x = 0.1, ΔP|_V = 10, $\Delta P{{{\text{|}}}_{{\Delta {{x}_{{{\text{сж}}}}}}}} = 0.0001$, $\Delta P{{{\text{|}}}_{{{{V}_{{{\text{сж}}}}}}}} = 1$ в процедуре численного определения частных производных от вектора невязок в методе Ньютона.

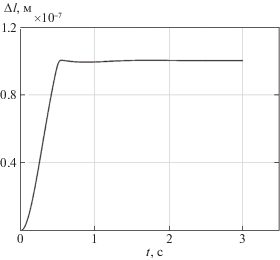
На рис. 9, а и б для данного варианта представлены оптимальные характеристики. Как видно из графиков, удалось добиться перевода системы из заданного начального положения в заданное конечное за ${{t}_{f}} = 100$ с за 7 итераций. Максимальное значение величины сжатия спицы Δx_сж = = $8 \times {{10}^{{ - 7}}}$ м, что на 2 порядка меньше по сравнению с ПИ-регулятором при одинаковых условиях. Время затухания колебаний спицы составило 3 с.

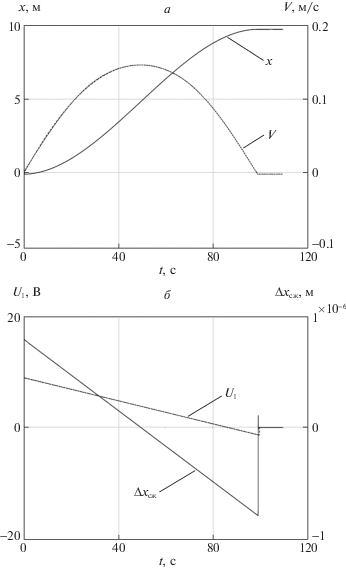
В соответствии с рис. 9, б можно структуру сигнала управления U₁ представить линейной функцией ${{U}_{1}} = at + b$, где a и b – коэффициенты. Тогда в качестве оптимизируемых параметров можно выбрать коэффициенты a и b. При этом удается добиться перевода выдвигающегося элемента из начального состояния в конечное при ограничении на управление.

Отметим, что в данной задаче сжатие конструкции незначительно и не превышает величины $\Delta {{x}_{{{\text{сж}}\;{\text{max}}}}} = 8 \times {{10}^{{ - 7}}}$ м. При этом с использованием оптимального регулятора время затухания колебаний составляет 3 с.

Можно сделать вывод, что с помощью оптимального регулятора удается снизить значение сжатия на порядок. Тем не менее, ни при каких рассматриваемых условиях задачи $\Delta {{x}_{{{\text{сж}}}}}$ не превышает установленное граничное значение в 1 мм как при использовании ПИ-регулятора, так и оптимального регулятора.

Применение алгоритма коррекции параметров структуры управления обеспечивает высокую сходимость решения задачи, но в отличие от коррекции моментов времени переключения структуры параметры a и b необходимо выбирать в небольшом диапазоне от оптимальных значений.

3.3. Настройка формы радиоотражающей поверхности. Использование алгоритмов оптимального управления как для пьезоактюатора, так и для ДПТ при настройке формы радиоотражающего сетеполотна подробно рассмотрено в [23, 24]. При выборе, например, пьезоактюатора применение алгоритма с коррекцией параметров структуры управления в виде (2.6) позволяет осуществить линейное перемещение без возникновения колебательного процесса, а время достижения конечного состояния существенно меньше, чем с помощью ПИД-регулятора, и составляет t ≈ 0.6 с (рис. 10) вместо 2 с.

Задача управления состоит в приведении пьезоактюатора из начального положения ($\Delta {{l}_{{{\text{пэ}}}}}_{{\;0}} = 0$ м; ${{V}_{{{\text{пэ}}\;{\text{0}}}}} = 0$ м/с; ${{U}_{{{\text{пэ}}\;{\text{0}}}}} = 0$ В) в заданное конечное состояние ($\Delta {{l}_{{{\text{пэ}}}}}_{{\;f}} = 1 \times {{10}^{{ - 7}}}$ м; ${{V}_{{{\text{пэ}}\;f}}} = 0$ м/с; ${{U}_{{{\text{пэ}}\;f}}} = 0$ В) при ограничении на управление, за которое принято напряжение от источника ЭДС ${{e}_{n}} = \pm 10$ B. Коэффициент обратного пьезоэффекта ${{K}_{0}} = 38 \times {{10}^{{ - 9}}}$, статическое усилие ${{F}_{{{\text{cтат}}}}} = {{10}^{{ - 8}}}$ Н, коэффициент упругости ${{K}_{{{\text{у}}{\text{.}}\;{\text{пэ}}}}} = 4.4$, коэффициент внутреннего демпфирования ${{K}_{{{\text{д}}{\text{.}}\;{\text{пэ}}}}} = 1$, емкость ${{C}_{0}} = 1.17 \times {{10}^{{ - 6}}}$ Ф, внутреннее сопротивление ${{R}_{{{\text{внут}}}}} = 102.5$ Ом, коэффициент прямого пьезоэффекта K_n = K₀, суммарная масса ${{m}_{\Sigma }} = 0.25$ кг.

Предложенный алгоритм для управления ДПТ помимо повышения быстродействия позволяет снизить энергетические затраты, что является важным в условиях ограниченного запаса энергии при работе в космическом пространстве.

Для настройки формы радиоотражающего сетеполотна научно-исследовательской лабораторией и студенческим конструкторским бюро БГТУ “ВОЕНМЕХ” им. Д.Ф. Устинова были изготовлены макетные образцы фасеты (части радиоотражающего сетеполотна) КТР (рис. 11). При проведении эксперимента в качестве актюаторов применялся ДПТ, аналогичный рассмотренному выше. Для определения усилий и длин оттяжки вант использовалась методика на основе уравнения Лапласа для мембраны [8].

Предлагаемый алгоритм коррекции параметров структуры управления применяется для выбранного в качестве актюатора ДПТ. Отсутствие постоянной силы тяжести в космическом пространстве не усложняет решение данной задачи. Меняются условия для использования методики на основе уравнения Лапласа для мембраны. При наземных испытаниях в правую часть уравнения (1.4) добавляется составляющая силы тяжести. Алгоритм управления ДПТ не нуждается в корректировке, так как его сравнение с ПИД-структурой происходит в одинаковых условиях.

Применение алгоритма коррекции параметров структуры управления позволило более чем в 2 раза сократить время настройки по сравнению с ПИД-регулятором, а также прийти в заданное значение без перерегулирования, что соответствует результатам моделирования. Ввиду плавного подхода к конечному значению удалось повысить энергоэффективность использования ДПТ. Выигрыш в затратах мощности при управлении одним актюатором составил ≈15% (0.495 Вт против 0.583 Вт).

Данные эксперимента позволяют сделать вывод о возможности уменьшения емкости источников питания за счет уменьшения потребления мощности актюаторов. Это дает возможность уменьшить массогабаритные размеры энергонакопительных элементов и освободить место для полезной нагрузки.

Оптимальное управление с разработанными алгоритмами для данных актюаторов значительно ускоряет переходный процесс и, как следствие, поддерживает заданную форму сетеполотна с необходимой точностью.

Заключение. В статье был выполнен поиск и разработка стратегий управления процессами раскрытия и настройки КТР. Реализованы в соответствующих программах для ЭВМ математические модели этапов развертывания КТР. Для развертывания, выдвижения спиц, а также управления актюаторами для настройки сетеполотна показано преимущество использования алгоритма с коррекцией параметров структуры управления. Для всех этапов применение разработанных алгоритмов позволяет добиться необходимой точности и качества регулирования системы. Решена задача улучшения характеристик развертывания КТР путем включения в контур управления бортового компьютера с программным обеспечением, допускающим реализацию алгоритмов оптимального управления. При этом для получения оптимальной динамики используется математическая модель.

В дальнейшем в математической модели можно учесть люфты в соединениях. Учет действующих на исследуемую систему возмущений и шумов предполагаемых датчиков приводит к сложным задачам обработки результатов измерений и их планирования [16, 25, 26]. В перспективе целесообразно произвести стабилизацию имитационной модели раскрытия КТР (или реального процесса) посредством самоорганизующегося оптимального регулятора с экстраполяцией (СОРЭ) А.А. Красовского [27, 28]. СОРЭ целесообразно применять при отсутствии математических моделей или для обеспечения оптимальных режимов, полученных с помощью математических моделей. В этом случае СОРЭ уменьшает отклонения динамики имитационной модели (или реального КТР) от оптимальной опорной траектории при использовании информационной модели соответствующих отклонений. Это позволит адаптировать решения, полученные для математических моделей, к реальным объектам и приближает результаты теории оптимального управления к решению практических задач.