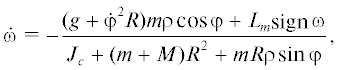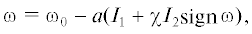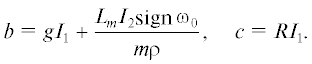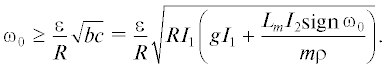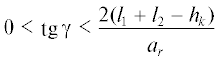Известия РАН. Теория и системы управления, 2021, № 2, стр. 156-176

Введение. Характерной особенностью дикой лесистой местности являются различного рода завалы. Часто встречаются завалы из стволов упавших деревьев. Бывают также искусственные завалы, предназначенные для ограничения проезда колесных или гусеничных транспортных средств. Принципиальная возможность преодоления хотя бы простейших завалов из стволов деревьев и бревен выделяет шагающие машины и, в частности, инсектоморфные роботы как перспективное транспортное средство для работы в естественной среде. Такой робот контактирует с опорой стопами ног. Применение для повышения надежности опоры в стопах ног аппарата таких специальных средств, как вакуумные присоски, магнитные контактные устройства и средства химической адгезии [1–3], представляется в рассматриваемом случае нецелесообразным. Особенность преодоления завалов состоит в том, что робот, наступая на отдельные предметы и создавая дополнительную нагрузку на опору, может ее разрушить. Поэтому проблемы выбора опорных точек на бревнах и направлений опорных усилий в процессе преодоления препятствия требуют специального исследования.

Существует очень много видов завалов из бревен [4]. В предлагаемой работе рассмотрим лишь некоторые простейшие варианты препятствий. Например, это могут быть отдельные бревна, лежащие на горизонтальной в среднем поверхности. Если бревен несколько, то в зависимости от расстояний между ними они могут образовывать препятствия различной сложности. В качестве математической модели бревен возьмем шероховатые однородные прямые круговые цилиндры различного радиуса. Опорную поверхность представим горизонтальной шероховатой опорной плоскостью.

Задача преодоления препятствия в виде отдельного цилиндра, лежащего на шероховатой горизонтальной плоскости, сводится в наиболее общем случае к задаче о равновесии цилиндра под действием силы тяжести и сил, приложенных к поверхности цилиндра. Ясно, что цилиндр не покатится, если линии действия этих сил пройдут через образующую цилиндра, касающуюся опорной плоскости, а если линии действия сил окажутся внутри соответствующего конуса трения, то не возникнет и проскальзывания цилиндра относительно опорной плоскости. В этом случае отдельный цилиндр будет достаточно хорошей опорой.

Препятствие в виде двух цилиндров, целиком лежащих на плоскости, преодолевается как последовательность отдельных цилиндров, если они не касаются друг друга и лежат на достаточном расстоянии. Задача несколько усложняется, если расстояние между цилиндрами сравнимо с половиной длины корпуса. Если цилиндры параллельны и касаются, то они образуют более надежную опору, чем один цилиндр, поскольку на линии их касания возникает сила трения, препятствующая их встречному качению. Для того, чтобы использовать эту силу трения, достаточно направить линию действия внешней силы в какую-нибудь точку площадки между проекциями осей цилиндров на опорную плоскость.

В дальнейшем ограничимся случаем, когда завал образован не более чем тремя цилиндрами. Равновесие системы и возможность ее использования в качестве опоры для шагающего робота будут исследоваться в предположении, что сухое трение и трение качения в контактах системы ограничены. Предлагаемая статья развивает результаты работ [5–10] и увеличивает набор препятствий, которые инсектоморфный робот теоретически может преодолеть. С целью выявления некоторых принципиальных особенностей алгоритма управления для преодоления завалов в статье рассматриваются следующие простейшие локомоционные задачи. На горизонтальной плоскости лежит либо один цилиндр, либо три параллельных одинаковых прямых круговых шероховатых цилиндра. Первоначально робот движется в направлении, перпендикулярном осям цилиндров. В общем случае он не видит участок опорной плоскости за препятствием. Если в процессе движения робота будет установлено, что опорная плоскость за препятствием непосредственно по курсу движения робота непригодна для наступания, то робот, находясь на препятствии, должен изменить свое положение на нем так, чтобы спуститься с препятствия в доступном для опоры месте. В статье представлен конструктивно построенный алгоритм решения сформулированных задач. Этот алгоритм был отработан на программном комплексе “Универсальный механизм” [11] с учетом полной динамики системы в целом. Приведенные результаты компьютерного моделирования свидетельствуют о принципиальной реализуемости предложенного алгоритма. Полная динамическая модель робота формируется автоматически средствами комплекса “Универсальный механизм” [11].

1. Механическая модель системы. Конструкция робота совпадает с принятой в [5]. Твердый корпус робота имеет форму прямоугольного параллелепипеда массы $m$, $a$ – его боковая сторона (длина), b – передний или задний край (ширина), $c$ – высота параллелепипеда. По бокам корпуса симметрично прикреплены шесть одинаковых инсектоморфных ног. Точки прикрепления ног с каждой стороны корпуса расположены на одинаковом расстоянии друг от друга. Отдельная нога состоит из двух твердых звеньев: бедра длины ${{l}_{1}}$, массы ${{m}_{1}}$ и голени длины ${{l}_{2}}$, массы ${{m}_{2}}$. Допускается касание роботом поверхности опоры и окружающих предметов только стопами, ноги робота не должны иметь взаимных пересечений во все время движения.

Программные значения шарнирных углов генерируются алгоритмом управления с учетом информации о реализовавшейся конфигурации робота при его движении. Реализация программных значений шарнирных углов осуществляется так же, как в [5] с помощью простейшей модели электроприводов с самоиндукцией. Предполагается, что роботу известны: собственное положение относительно препятствий, несущая способность участков поверхности, выбираемых для опоры, шарнирные углы, скорости перемещения как самого робота, так и объектов, выбираемых для опоры.

Цилиндры, образующие препятствия, могут свободно перекатываться по плоскости. На них действует сухое кулоновское трение и трение качения. Если какие-нибудь реакции выходят за ограничивающие их пределы, то возникает соответствующее проскальзывание.

Траектории переносов ног формируются в виде плоских шаговых циклов [5, 6], адаптируемых в зависимости от поверхностей препятствий, скорости движения робота, предписанных следовых точек. Движения ног, соответствующие шаговым циклам, сглаживаются, чтобы сохранить непрерывность как самого движения, так и его скорости [5].

Наличие силового момента в опорных точках не предполагается. Реакции в них должны удовлетворять условию малой деформации опорной поверхности и должны принадлежать конусам кулоновского трения с заданным коэффициентом [5]. Коэффициент трения предполагается равным единице. Программное движение создается в виде последовательности событий, в начале каждого из которых в некоторой абсолютной системе координат $O\xi \eta \zeta $ определяются траектории перемещений стоп и точек их крепления к корпусу.

2. Постановки задач. Решаемые задачи формулируются следующим образом.

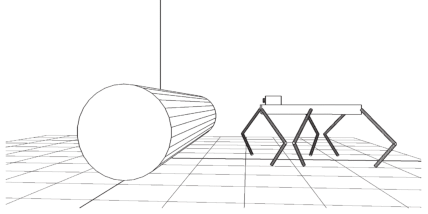
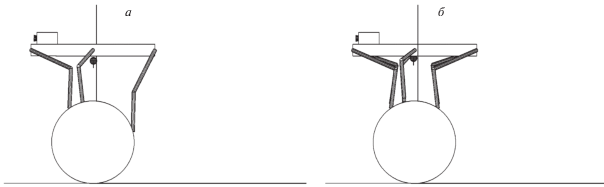
Задача 1 (“Ряд цилиндров”). Поперек трассы под прямым углом расположены три цилиндра, диаметры которых равны половине клиренса робота. Расстояние между осями цилиндров сравнимо с половиной длины корпуса (рис. 1). Робот должен преодолеть эту полосу препятствий.

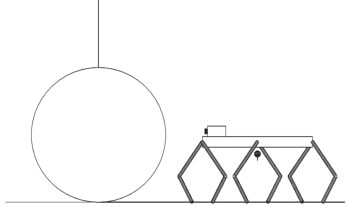
Задача 2 (“Толстый цилиндр”). Шестиногий робот идет вдоль прямолинейной трассы по горизонтальной плоскости. Поперек трассы под прямым углом лежит одиночный цилиндр, по высоте сравнимый с маршевой высотой робота, так что робот не может ни перешагнуть его, ни увидеть расположенную за цилиндром и примыкающую к нему область горизонтальной опорной плоскости (рис. 2). Робот должен забраться на цилиндр и, если за цилиндром имеется достаточно хорошая опора, продолжить движение поперек цилиндра, а если за цилиндром опора ненадежная, то переместиться вдоль цилиндра, так чтобы обойти ненадежный участок, а затем спуститься на опорную плоскость.

Задача 3 (“Большой цилиндр”). Шестиногий робот идет вдоль прямолинейной трассы по горизонтальной плоскости. Поперек трассы под прямым углом лежит одиночный цилиндр настолько большого радиуса, что робот не может, имея точки опоры средних и задних ног на плоскости, дотянуться до вершины цилиндра (рис. 3). Как и в задаче 2, робот должен забраться на цилиндр и, если за цилиндром имеется достаточно хорошая опора, продолжить движение поперек цилиндра, а если за цилиндром опора ненадежная, то переместиться вдоль цилиндра, так чтобы обойти ненадежный участок и слезть с цилиндра.

Рассмотрим методику преодоления препятствий для каждой задачи.

3. Преодоление препятствий в задачах 1 и 2. 3.1. Задача “Ряд цилиндров”. Диаметры цилиндров и расстояния между ними в задаче 1 выбраны таким образом, что робот, преодолевая препятствие, будет вынужден наступить хотя бы на один цилиндр. Движение робота имеет структуру волновой походки “галоп”. Перечислим характерные этапы движения в этом случае.

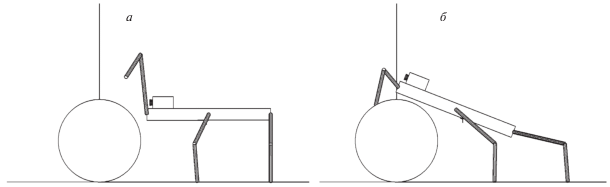
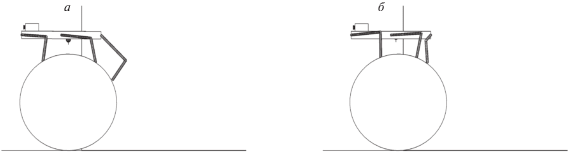
Этап 1.1. Приблизившись к препятствию походкой “трешки”, робот перестраивает положение ног для походки “галоп” и готовится к переносу передних ног через ближайший к нему (первый) цилиндр (рис. 4, а).

Этап 1.2. Передними ногами робот перешагивает через первый цилиндр, продвигает корпус вперед по ходу движения и делает шаг задними ногами (рис. 4, б).

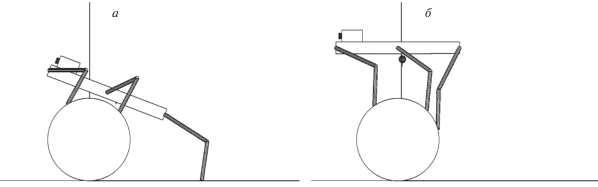
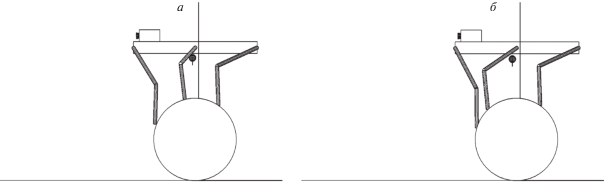
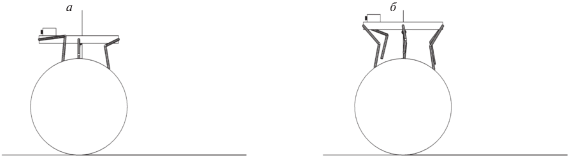
Этап 1.3. Робот переносит средние ноги и вынужден поставить их на первый цилиндр (рис. 5, а). Если проскальзывание цилиндра относительно опорной плоскости не возникает, а робот образует жесткую фигуру, то цилиндр будет надежной опорой, несмотря на то что проекция точки опоры на горизонтальную плоскость может оказаться вне опоры цилиндра.

Этап 1.4. Робот делает очередной шаг передними ногами и ставит их на средний цилиндр. Задние ноги продолжают опираться об опорную плоскость (рис. 5, б).

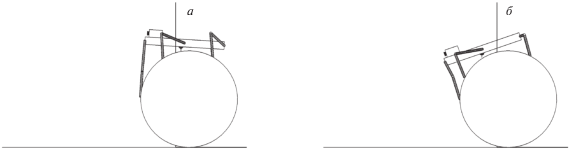
Этап 1.5. Задние ноги переносятся в точку опоры на плоскости поближе к первому цилиндру. Во время их переноса робот опирается передними и средними ногами о средний и первый цилиндры соответственно. При этом существенно, чтобы точки опоры передних ног проецировались относительно вертикальной плоскости, проходящей через опорную образующую среднего цилиндра, со стороны, противоположной, чем проекции точек опоры средних ног относительно вертикальной плоскости, проходящей через опорную образующую первого цилиндра (принцип устойчивой опоры) (рис. 6, а). В этом случае моменты сил, действующих со стороны робота на цилиндры при опоре, будут иметь разные знаки и система стабилизации робота будет удерживать цилиндры от раскатывания в разные стороны.

Этап 1.6. Средние ноги ставятся в промежуток между первым и средним цилиндрами (рис. 6, б).

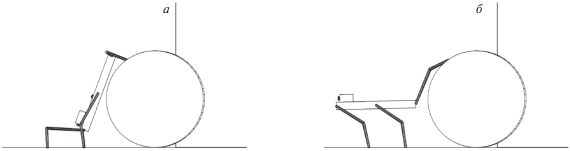
Этап 1.7. Передние ноги ставятся на последний цилиндр. Корпус продвигается вперед, подготавливая перенос задних ног (рис. 7, а).

Этап 1.8. Задние ноги перешагивают через первый цилиндр (рис. 7, б).

Этап 1.9. Средние ноги перешагивают через средний цилиндр, а за ними перешагивают передние ноги через последний цилиндр (рис. 8, а). Все ноги робота стоят на плоскости. Передние ноги находятся за препятствием, средние ноги стоят между последним и средним цилиндрами, задние ноги – между первым и средним цилиндрами.

Этап 1.10. Корпус робота продвигается вперед, сначала задние ноги ставятся на средний цилиндр, затем средние ноги ставятся на последний цилиндр, потом передние ноги переносятся вперед в следующую точку опоры на плоскости. Во время переноса передних ног робот стоит на среднем и заднем цилиндрах (рис. 8, б). При этом относительно последнего и среднего цилиндров должен соблюдаться принцип устойчивой опоры, как при выполнении этапа 1.5.

Этап 1.11. После постановки передних ног на плоскость корпус продвигается вперед и, начиная с задних ног, запускается волна переносов ног (рис. 9, а) с перешагиванием через цилиндры так, чтобы робот целиком оказался за препятствием (рис. 9, б).

3.2. Задача “Толстый цилиндр”. Задача 2 имеет много общего с задачей преодоления препятствия в виде шара [5]. Основная разница состоит в том, что цилиндр может катиться по плоскости только в направлении, перпендикулярном к оси цилиндра, тогда как шар может катиться в любом направлении. Кроме того, трение качения цилиндра будет больше, чем трение качения шара при прочих равных условиях. Указанные обстоятельства облегчают решение задачи 2. Рассмотрим последовательные этапы преодоления цилиндра, диаметр которого сравним с маршевой высотой робота.

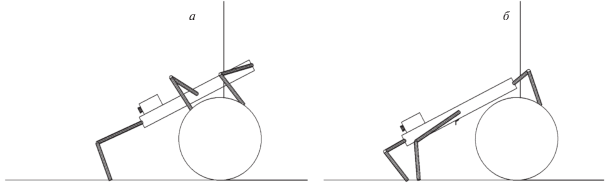
Этап 2.1. Приблизившись к препятствию походкой “трешки”, робот перестраивает положение ног для походки “галоп” и, продвигая корпус по направлению к цилиндру, готовится к переносу на него передних ног (рис. 10, а).

Этап 2.2. Робот ставит передние ноги на верхнюю часть цилиндра, приводит корпус в наклонное положение и продвигает его вперед так, чтобы центр масс корпуса проектировался в опорный многоугольник передних и средних ног. Тем самым готовится перенос задних ног (рис. 10, б).

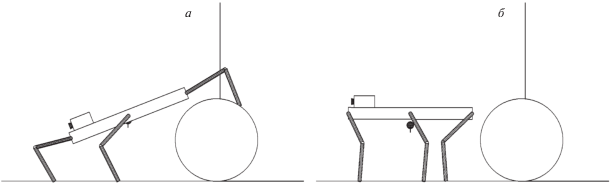
Этап 2.3. В соответствии с правилом волновой походки робот переносит задние ноги поближе к цилиндру, затем переносит средние и продвигает корпус вперед вдоль его оси, подготавливая перенос задних ног на цилиндр (рис. 11, а).

Этап 2.4. Робот продолжает продвигать корпус вдоль своей оси до тех пор, пока задние ноги не будут полностью выпрямлены. Затем происходит перенос задних ног на поверхность цилиндра. Одновременно осуществляется поворот и подъем корпуса, чтобы привести его в горизонтальное положение на маршевой высоте над поверхностью цилиндра (рис. 11, б).

Этап 2.5. Робот видит, что за цилиндром спуск невозможен. Он переносит средние ноги в более удобную позицию для движения вдоль оси цилиндра походкой “трешки” (рис. 12, а).

Этап 2.6. Робот идет походкой “трешки” по цилиндру вдоль его оси до тех пор, пока опорная площадка за цилиндром окажется пригодной для спуска с цилиндра (рис. 12, б). Центр масс робота проектируется в малую окрестность верхней точки цилиндра.

Этап 2.7. Обнаружив за цилиндром достаточно надежную площадку для спуска, робот начинает спуск с цилиндра и переносит на цилиндр поближе к опорной плоскости сначала стопы передних (рис. 13, а), а за ними – стопы средних ног (рис. 13, б).

Этап 2.8. Робот приседает, одновременно с этим наклоняется, переносит передние ноги на опорную плоскость и продвигает корпус по касательной к цилиндру (рис. 14, а).

Этап 2.9. Корпус продвигается далее по касательной с одновременным переносом средних ног на опорную плоскость (рис. 14, б).

Этап 2.10. Робот переносит передние ноги в более удобные точки опоры на горизонтальной плоскости, одновременно приподнимает корпус и переносит его вперед, так чтобы его центр масс проектировался в опорный многоугольник передних и средних ног (рис. 15, а).

Этап 2.11. Корпус робота выравнивается. Задние ноги переносятся на опорную плоскость, завершая преодоление препятствия (рис. 15, б).

Перейдем к анализу задачи 3 о преодолении препятствия в виде большого цилиндра. Она аналогична задаче о преодолении шара большого диаметра [5] с той существенной разницей, что на шаре робот, создавая давление ногами на шар перпендикулярно поверхности, имеет возможность за счет обхвата шара ногами легче создать необходимое сцепление ног с поверхностью шара. Возможность обхвата цилиндра может быть эффективно реализована лишь перпендикулярно образующей, что ослабляет сцепление робота с поверхностью цилиндра. Трудность задачи в том, что когда центр масс робота находится не над вершиной цилиндра, то из-за момента силы тяжести цилиндр может покатиться, а робот из-за этого может упасть.

4. Динамика залезания на большой цилиндр. Пусть однородный шероховатый круговой цилиндр радиуса $R$ и массы $M$ лежит на горизонтальной опорной плоскости. Центр масс $C$ цилиндра расположен на его оси. Предположим, что цилиндр не может скользить по плоскости вдоль образующей, а может только катиться по плоскости в общем случае с проскальзыванием перпендикулярно образующей цилиндра. Движение цилиндра будет в этом случае плоскопараллельным. Через центр масс $C$ проведем вертикальную плоскость перпендикулярно оси цилиндра. В сечении получим круговой диск $D$, касающийся плоскости в точке A. Движение цилиндра интерпретируется как качение диска в неподвижной вертикальной плоскости $O\eta \zeta $ по горизонтальной прямой $O\eta $ правоориентированной декартовой неподвижной системы координат $O\xi \eta \zeta $ с направляющими векторами ${{{\mathbf{e}}}_{\xi }}$, ${{{\mathbf{e}}}_{\eta }}$, ${{{\mathbf{e}}}_{\zeta }}$ соответственно. Начало координат принадлежит опорной плоскости. Рассмотрим случай, когда радиус цилиндра настолько велик, что робот должен вскарабкаться на него, не опираясь на опорную плоскость, прежде, чем он окажется на вершине цилиндра.

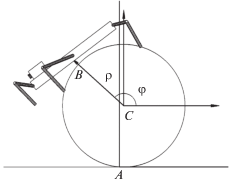
С диском $D$ свяжем подвижную систему координат $C\xi \eta \zeta $. Движение корпуса робота предполагается параллельным плоскости $O\eta \zeta $ таким образом, что продольная ось корпуса в любой момент времени движения направлена по касательной к цилиндру, а плоскость $C\eta \zeta $ служит плоскостью симметрии корпуса. Точки опоры ног на цилиндре также будем располагать симметрично относительно $C\eta \zeta $. Положение фигуры, полученной сечением робота плоскостью $C\eta \zeta $, будем характеризовать постоянным радиусом $\rho $ между точкой $C$ и центром масс $B$ робота и переменным углом $\varphi $ между осью $C\eta $ и направлением из центра диска $D$ в точку $B$ (рис. 16, а).

Воспользуемся теоремой об изменении кинетического момента ${{{\mathbf{K}}}_{A}}$ цилиндра вместе с роботом, взятого относительно подвижной точки $A$ [5, 12]:

где $t$ – время, ${{{\mathbf{v}}}_{A}}$ – вектор скорости точки A, ${\mathbf{Q}}$ – вектор количества движения системы, “$ \times $” – знак векторного умножения, $m$ – масса робота, ${\mathbf{g}}$ – вектор ускорения силы тяжести, $\rho $ – радиус-вектор центра масс $B$ робота, имеющий начало в точке C, $L$ – момент трения качения. Предполагается, что $\rho > R$ и ${\text{|}}L{\text{|}} \leqslant {{L}_{m}}$. Выражение в правой части для момента силы тяжести робота относительно точки A справедливо из-за того, что радиус CA в любой момент времени параллелен силе тяжести.

Будем считать, что цилиндр не имеет вертикальной составляющей угловой скорости, а его движение параллельно плоскости $O\eta \zeta $. Тогда кинетический момент ${{{\mathbf{K}}}_{c}}$ цилиндра относительно точки $A$ выражается формулой

так как центр диска всегда проектируется в точку A. При условии, что угол между отрезком ${\mathbf{CB}}$ и продольной осью корпуса остается постоянным, кинетический момент ${{{\mathbf{K}}}_{r}}$ робота относительно точки A имеет вид [12]

где

${\mathbf{K}}_{r}^{*}$ – кинетический момент робота относительно его центра масс, ${{{\mathbf{v}}}_{r}}$ – скорость точки B, ${{\rho }_{{AB}}}$ – вектор из точки A в точку B. Пренебрегая для простоты кинетическим моментом движения ног относительно корпуса и обозначая через ${{J}_{r}}$ момент инерции всего робота относительно его центра масс, получим выражение

С учетом сказанного уравнение (4.1) в проекции на ось $C\xi $ принимает вид

Пусть робот залезает на цилиндр с постоянной угловой скоростью $\dot {\varphi } \ne 0$. Если при этом цилиндр остается неподвижным, то из (4.2) получим

До тех пор, пока робот залезает на первоначально покоящийся цилиндр в соответствии с рис. 16, имеем $\cos \varphi \geqslant 0$. Таким образом, согласно свойствам трения качения, при

цилиндр при залезании робота будет оставаться неподвижным. Наиболее критичным для равновесия цилиндра будет начальный момент залезания, когда cosφ максимален. Если в этот момент равновесие цилиндра не нарушилось, то оно сохранится и в дальнейшем движении. Из формулы (4.4) также следует, что корпус робота при залезании должен располагаться как можно ближе к цилиндру, а скорость залезания должна быть как можно меньше.

Пусть теперь в начале залезания робота на цилиндр неравенство (4.4) не выполнено, а цилиндр имеет угловую скорость ω₀. Угловая скорость цилиндра при его качении подчиняется уравнению

которое можно проинтегрировать: где ω₀ – начальная угловая скорость цилиндра,

Аналитические выражения для интегралов ${{I}_{1}}(\varphi ,\varepsilon )$ и ${{I}_{2}}(\varphi ,\varepsilon )$ могут быть найдены стандартными методами и здесь не приводятся. Отметим лишь, что при ${{\varphi }_{0}} \leqslant \varphi \leqslant \pi {\text{/}}2$ для $\forall \varepsilon = {\text{const}} > 0$ функции ${{I}_{1}}(\varphi ,\varepsilon )$ и ${{I}_{2}}(\varphi ,\varepsilon )$ монотонно возрастают, причем $0 \leqslant {{I}_{1}} \leqslant {{I}_{2}}$.

По смыслу задачи при достижении роботом вершины цилиндра ($\varphi = \pi {\text{/}}2$) цилиндр должен быть в покое (ω = 0). Вместе с тем остановка цилиндра может произойти и раньше при некотором значении угла ${{\varphi }_{0}} < \varphi = {{\varphi }_{s}} < \pi {\text{/}}2$. Пусть это значение задано. Для него получим уравнение, связывающее начальную угловую скорость ω₀ цилиндра и постоянную угловую скорость $\dot {\varphi }$ перемещения робота по цилиндру:

С учетом (4.6) уравнение (4.7) можно представить в виде

где

Следовательно,

Минимальное значение начальной угловой скорости цилиндра достигается при $\dot {\varphi } = \sqrt {b{\text{/}}c} $. Если значение ${{\omega }_{0}}$ больше минимального, то уравнение (4.7) будет иметь два корня относительно $\dot {\varphi }$, из которых следует выбирать наименьший.

При условии, что $\varepsilon \ll 1$, интегралы ${{I}_{1}}$ и ${{I}_{2}}$ можно вычислить приближенно с точностью до членов первого порядка малости по ε. При ${{\varphi }_{0}} = 0$ получим

В частности, если потребовать, чтобы цилиндр остановился в тот момент, когда робот окажется в близкой окрестности вершины цилиндра, то в формуле (4.9) можно принять

5. Динамика слезания робота с большого цилиндра. Как и прежде, предполагается, что круговой шероховатый цилиндр радиуса $R$ и массы M может катиться по горизонтальной плоскости без проскальзывания и отскоков под действием трения качения. В начальный момент времени робот покоится на вершине неподвижного цилиндра, его корпус ориентирован горизонтально, а все шесть ног опираются о цилиндр, образуя в проекции на горизонтальную плоскость симметричный опорный многоугольник. Радиус цилиндра настолько велик, что робот не может, находясь на вершине, наступить на опорную плоскость. Он может начать спуск непосредственно из состояния покоя, либо предварительно разогнав цилиндр так, чтобы он в начальный момент времени имел угловую скорость ${{\omega }_{0}}$ [5]. Пусть робот при слезании с цилиндра выполняет плоскопараллельное движение вдоль вертикальной плоскости. Если сила тяжести и трение качения отсутствуют, то кинетический момент системы в целом относительно опорной образующей цилиндра сохраняется. Поэтому движение робота вдоль поверхности цилиндра будет вызывать приращение кинетического момента цилиндра относительно опорной образующей. Это приращение по направлению будет противоположно кинетическому моменту робота относительно той же образующей. Вместе с тем в реальности под действием силы тяжести робота и трения качения кинетический момент системы меняется. В этом случае момент силы тяжести будет сонаправлен кинетическому моменту робота и, следовательно, будет разгонять цилиндр в направлении движения робота. Можно оценить, какая должна быть скорость робота, чтобы скорость цилиндра в момент окончания маневра оказалась минимальной.

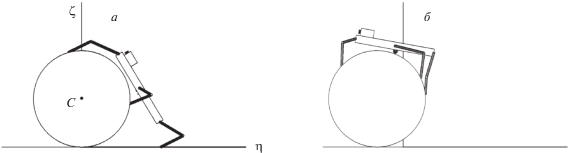
Поступим аналогично тому, как это было сделано в разд. 4. Возьмем систему координат $C\xi \eta \zeta $ с началом C, совпадающим в любой момент времени с центром диска $D$ (рис. 17) и с осями, параллельными осям абсолютной системы координат $O\xi \eta \zeta $. Ось $C\eta $ направлена в сторону, противоположную предполагаемой начальной скорости робота, и не меняет своей ориентации в процессе движения. Ось $C\zeta $ направлена вертикально вверх. Ось $C\xi $ образует с двумя указанными осями правую тройку, так что с положительного направления оси $C\xi $ вращение цилиндра, индуцированное качением цилиндра в сторону движения робота, будет видно происходящим против хода часовой стрелки. Пусть ${{{\mathbf{e}}}_{\xi }}$, ${{{\mathbf{e}}}_{\eta }}$, ${{{\mathbf{e}}}_{\zeta }}$ – единичные направляющие векторы указанных координатных осей.

Движение корпуса робота предполагается происходящим параллельно плоскости $O\eta \zeta $, причем продольная ось корпуса в любой момент времени движения параллельна касательной к цилиндру, а плоскость $C\eta \zeta $ служит плоскостью симметрии корпуса. Точки опоры ног на цилиндре также будем располагать симметрично относительно плоскости $C\eta \zeta $. Положение фигуры, полученной сечением робота плоскостью $C\eta \zeta $, будем характеризовать постоянным радиусом $\rho $ между точкой C и центром масс $B$ робота и переменным углом $\varphi $ между осью $C\eta $ и направлением из центра C в точку $B$ (рис. 17).

Воспользуемся уравнением (4.2). Пусть робот слезает с цилиндра с постоянной угловой скоростью $\dot {\varphi } > 0$. Тогда для угловой скорости цилиндра имеем выражение (4.5), где ${{\omega }_{0}}$ – проекция начальной угловой скорости цилиндра на ось $B\xi $, ${{\varphi }_{0}} = \pi {\text{/}}2$ – начальное угловое положение робота. При этих условиях имеем ${{I}_{1}} \leqslant 0$, ${{I}_{2}} \geqslant 0$. Финальное положение робота на цилиндре определим углом ${{\varphi }_{f}} > \pi {\text{/}}2$. По смыслу задачи при $\varphi = {{\varphi }_{f}}$ цилиндр должен иметь минимально возможную абсолютную величину угловой скорости $\omega = {{\omega }_{f}}$ для того, чтобы облегчить роботу переход с цилиндра на опорную плоскость. Формулу (4.5) можно представить в виде

где b и $c$ выражаются формулами (4.8), из которых следует, что в рассматриваемом случае $c < 0$, а знак коэффициента b зависит от величины коэффициента трения качения и от знака начальной угловой скорости ${{\omega }_{0}}$ цилиндра. Таким образом, нулевое значение скорости ${{\omega }_{f}}$ может быть достигнуто лишь при

Заметим, что случай $b > 0$ реализуется при достаточно большом значении ${{L}_{m}}$ предельного трения качения:

Например, для ${{\varphi }_{f}} = \pi $ получим

Если неравенство (5.3) выполнено, то робот может спуститься с цилиндра даже при ${{\omega }_{0}} = 0$. Для этого достаточно выбрать скорость ${{v}_{r}} = \rho \dot {\varphi }$ движения робота по цилиндру в соответствии с неравенством

Это ограничение в виде неравенства следует из (5.1), поскольку момент трения качения имеет пассивную природу и возникает лишь по мере необходимости воспрепятствовать возникновению движения. Грунты, удовлетворяющие (5.3), можно назвать мягкими, поскольку именно для мягких грунтов характерны большие значения постоянной ${{L}_{m}}$, и возможен спуск с покоящегося цилиндра. Для твердых грунтов, для которых неравенство (5.3) нарушено, спуск с покоящегося цилиндра невозможен, и для безопасности перед спуском необходимо цилиндру придать иногда заметную угловую скорость.

Приведенные формулы дают грубую оценку динамики робота при слезании с цилиндра из-за того, что они не учитывают движение ног при движении робота. Вместе с тем они дают качественно верную картину явления и могут быть использованы для предварительного анализа рациональности применяемых алгоритмов построения движения.

6. Исходная позиция перед большим цилиндром. Формулы (4.4) и (4.9) показывают, что если предельная величина трения качения невелика, то для возможности залезания на цилиндр робот должен толкнуть цилиндр в том же направлении, в котором он приближается к цилиндру, и придать цилиндру достаточно большую начальную скорость. В начале толчка корпус робота должен быть ориентирован по касательной к цилиндру. Будем считать, что передняя часть корпуса должна оказаться выше задней. Тогда из соображений дотягивания ног до опорной плоскости очевидно, что в толчке должны участвовать задние ноги. После отделения всех стоп от опорной плоскости передние и средние ноги должны надежно обхватывать цилиндр, чтобы робот мог перемещать корпус относительно цилиндра без проскальзывания стоп по поверхности цилиндра. Поскольку на перенос ног требуется конечное время, заключаем, что к началу толчка передние и средние ноги должны уже находиться на цилиндре и толчок осуществляется лишь задними ногами. Для залезания будем использовать походку “галоп”, располагая точки опоры симметрично относительно плоскости $C\eta \zeta $.

Пусть робот приблизился к цилиндру и стоит рядом с ним в симметричной позе, соответствующей походке “галоп”. Корпус горизонтален, а его передний край находится на расстоянии $\sigma $ от цилиндра, соответствующем началу маневра залезания на цилиндр. Средние и задние ноги перенесены вперед, так что центр масс робота проектируется в опорный многоугольник, образованный средними и задними стопами. Робот имеет возможность перенести на цилиндр стопы передних ног.

Основная цель подготовительного этапа состоит в том, чтобы расположить корпус по касательной к цилиндру в вертикальной плоскости. При этом для уверенной опоры стопы передних ног должны оказаться вблизи верхней точки цилиндра. Для надежности обхвата цилиндра после начального толчка стопы средних ног необходимо расположить на цилиндре на достаточном расстоянии от точек опоры передних ног [5]. Чтобы придать корпусу требуемую скорость вместе с цилиндром, точки опоры задних ног целесообразно разместить на опорной плоскости на продолжении продольной оси корпуса. Возможность выполнения подготовительного этапа обеспечивается следующим кинематическим свойством системы робот–цилиндр.

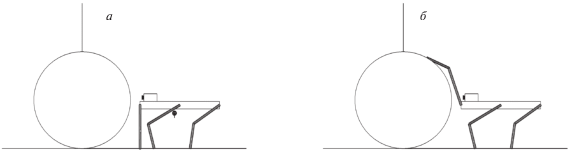
Предположим, что робот поставил стопы передних ног на цилиндр и давит на него так, что линия действия сил, приложенных к цилиндру со стороны стоп ног, принадлежит двугранному углу сухого трения с ребром в опорной образующей цилиндра (рис. 16, б). Тангенс половины угла трения ${{\chi }_{f}}$ равен коэффициенту трения. Тогда цилиндр способен лишь перекатываться по опорной плоскости без проскальзывания. Покажем, что если робот перемещается, сохраняя точки контакта между передними стопами и цилиндром, а также расстояние между передними стопами на цилиндре и неподвижными точками опоры других ног, находящихся на опорной плоскости, то цилиндр должен оставаться в покое [5]. Действительно, при виртуальном перекатывании цилиндра движение опирающихся о него стоп будет перпендикулярным кратчайшему отрезку, соединяющему расположенные на нем стопы с опорной образующей цилиндра. Указанный отрезок и отрезок, проходящий через стопы передних ног и точки опоры на плоскости, не параллельны. Следовательно, проекция перемещения стоп передних ног на отрезок, соединяющий стопы передних ног со стопами, которые опираются на плоскость, будет ненулевой, что противоречит условию сохранения расстояний между опорными стопами. Отмеченное свойство позволяет точки опоры передних ног на цилиндре использовать с целью переноса других ног.

Примем, что в начале подготовительного этапа корпус робота ориентирован горизонтально. Выполнение поворота корпуса в положение, при котором его продольная ось ориентирована по требуемой касательной к цилиндру, должно происходить с таким расчетом, чтобы средние ноги смогли дотянуться до опорной плоскости. С целью осуществления поворота корпуса аналогично [5] потребуем, чтобы передний край корпуса робота двигался с постоянной скоростью по вертикальной окружности радиуса $R{\kern 1pt} ' = R + \sigma $ с центром в точке $C$ (рис. 16), а средняя точка корпуса выполняла бы вынужденное движение по прямой, составляющей с осью $O\eta $ угол $ - \gamma $. Движение передней точки корпуса зададим параметрически

где ${{h}_{k}}$ есть высота корпуса над опорной плоскостью перед началом выполнения маневра поворота корпуса. Найдем зависимости от параметра s координат ${{\eta }_{m}}(s)$, ${{\zeta }_{m}}(s)$ средней точки корпуса и координат ${{\eta }_{r}}(s)$, ${{\zeta }_{r}}(s)$ его задней точки. При $s = {{s}_{0}}$ имеем где a – длина корпуса робота. Обозначим

Движение средней точки корпуса по прямой определено соотношениями

Из них для $\Delta {{\zeta }_{m}}$ получаем уравнение

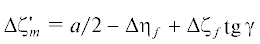решение которого где вместе с (6.1) дает искомую зависимость. Координаты задней точки корпуса заданы равенствами

Очевидно, что условие дотягивания средних ног до опорной плоскости ограничивает значения параметра γ: $\mathop {{\text{tg}}}\nolimits_ \gamma < 2({{l}_{1}} + {{l}_{2}} - {{h}_{k}}){\text{/}}a$. Задняя точка корпуса не должна опускаться ниже опорной плоскости. Поэтому возникает ограничение

Подходящая величина γ позволяет расширить диапазон значений параметра s, при которых неравенство (6.3) выполняется. Из формулы (6.2) следует, что указанное расширение диапазона для s возникает при γ > 0. Таким образом, значение γ должно принадлежать интервалу

с тем расчетом, чтобы можно было осуществить поворот корпуса, не нарушая неравенство (6.3). Вместе с тем интуитивно ясно, что чем выше удалось поднять корпус робота на подготовительном этапе, тем легче ему будет взобраться на вершину цилиндра впоследствии. Поэтому значение $\gamma $ следует выбирать максимально допустимым с учетом сохранения достаточного запаса статической устойчивости при опоре на средние и задние ноги.

Поворот корпуса робота следует продолжать до тех пор, пока расстояние между цилиндром и корпусом не станет равным заданной величине $\sigma {\kern 1pt} ' \leqslant \sigma $. При выполнении этого условия уже можно начать движение корпуса по касательной к цилиндру. Для реализации поворота необходимо задать функцию $s(t)$. Тогда радиус-векторы

соответственно передней точки корпуса и средней его точки будут функциями времени. Условие окончания вращения корпуса можно выразить формулой

7. Перелезание через большой цилиндр. Из формулы (4.9) следует, что если коэффициент трения качения мал, то залезть на большой цилиндр можно, лишь придав ему ненулевую начальную угловую скорость. Опишем последовательность этапов подготовки начального толчка с целью разгона цилиндра до необходимой скорости. На каждом этапе учитывается условие статической устойчивости в смысле принадлежности опорному многоугольнику проекции центра масс робота на опорную плоскость. Опорный многоугольник в данном случае получается как выпуклая оболочка проекций всех точек опоры на опорную плоскость.

На рис. 18, а показана исходная позиция робота перед началом подготовительного этапа. Центр масс робота проектируется в опорный многоугольник средних и задних ног. Робот приготовился к постановке передних ног на цилиндр. На рис. 18, б изображена позиция робота после постановки передних ног на цилиндр. Корпус робота в этот момент времени еще горизонтален. Из этой позиции робот начинает поворот корпуса.

В процессе поворота все точки опоры сохраняются. На рис. 19, а показана позиция робота после поворота корпуса. Центр масс робота проектируется в опорный многоугольник, образованный передними и средними ногами, что дает возможность начать перенос задних ног в позицию, удобную для выполнения толчка цилиндра. После переноса задних ног (целевая позиция показана на рис. 19, б) можно осуществить последовательность переносов, обеспечивающих достаточный контакт робота с цилиндром после толчка. Перемещаются средние ноги в позицию, указанную на рис. 19, б, чтобы обеспечить статическую устойчивость при переносе передних ног. Передние ноги ставятся практически на верхнюю часть цилиндра (позиция на рис. 20, а). Подготовительный этап заканчивается переносом средних ног на цилиндр (рис. 20, а). Расстояние между точками опоры передних и средних ног на цилиндре выбирается достаточным, чтобы в них при отталкивании не возникало проскальзывания относительно цилиндра.

Разгон цилиндра реализуется при отсутствии проскальзывания в его точке контакта с опорной поверхностью. Скорость центра масс цилиндра ${{v}_{*}}$ должна быть получена за время $T{\kern 1pt} *$ опорной фазы задних ног из положения, приведенного на рис. 20, а в момент времени ${{t}_{s}}$. Программное движение цилиндра формируется в предположении постоянства ускорения его центра масс. Пусть в момент времени ${{t}_{s}}$ центр масс цилиндра имеет скорость ${{v}_{B}} = 0$. На рис. 20, а неподвижная система координат $O\xi \eta \zeta $ соответствует положению цилиндра в момент ${{t}_{s}}$. При положительной угловой скорости цилиндра движение его центра масс будет происходить в отрицательном направлении оси $O\eta $. Программный закон движения цилиндра во время отталкивания задними ногами от горизонтальной опорной плоскости выражается координатами ${{\xi }_{b}}(t)$, ${{\eta }_{b}}(t)$, ${{\zeta }_{b}}(t)$ и углом поворота $\psi (t)$ цилиндра вокруг оси $C\xi $:

так что каждая точка цилиндра, имеющая в момент времени t_s координаты $\xi ({{t}_{s}})$, $\eta ({{t}_{s}})$, $\zeta ({{t}_{s}})$, будет описывать обобщенную циклоиду, параллельную плоскости $O\eta \zeta $:

Формулы (7.1) и (7.2) дают возможность рассчитать программные положения стоп опирающихся о цилиндр передних и средних ног в любой момент времени при разгоне цилиндра.

Для расчета шарнирных углов требуется еще задать программный закон движения корпуса робота. Потребуем, чтобы во время толчка корпус робота двигался параллельно своему положению, достигнутому к моменту ${{t}_{s}}$ (рис. 20, а), а расстояние от осевой линии корпуса до цилиндра при этом не менялось. В соответствии с разд. 4 за время $T{\kern 1pt} *$ корпус робота должен продвинуться относительно цилиндра на вектор $\Delta {\mathbf{r}}(t) = {{{\mathbf{r}}}_{c}}(t) - {{{\mathbf{r}}}_{c}}({{t}_{s}})$ так, чтобы ближайшая к цилиндру точка осевой линии корпуса совпала с серединой корпуса. Этот замысел реализуется формулой

где $\lambda ({{t}_{s}}) = 0$, $\lambda ({{t}_{s}} + T{\kern 1pt} *) = 1$, “$ \cdot $” – знак скалярного умножения векторов. Полностью поступательное движение корпуса при толчке определено тем, что величина $\Delta {\mathbf{r}}(t)$ добавляется к радиус-вектору любой точки корпуса, полученному к моменту ${{t}_{s}}$.

После отталкивания цилиндр и робот движутся совместно, а задние ноги выполняют перенос своих стоп на цилиндр. В процессе переноса задних ног корпус перемещается относительно поверхности цилиндра вверх с опережением (см. разд. 4), используя передние и средние ноги. Движение цилиндра замедляется. После переноса стоп задних ног на цилиндр робот оказывается в позиции, показанной на рис. 20, б. Затем осуществляются переносы стоп средних и задних ног таким образом, чтобы стопы средних ног оказались в точках на цилиндре, соответствующих окончанию залезания. Эта позиция робота и цилиндра представлена на рис. 21, а. Точки опоры ног на цилиндре расставляются с тем расчетом, чтобы не было взаимных пересечений ног при переносах. Движение корпуса относительно цилиндра вблизи его поверхности продолжается до тех пор, когда центр масс робота окажется внутри опорного многоугольника передних и средних ног с достаточным запасом. К этому моменту скорость цилиндра практически исчезает. Далее происходит перенос задних ног в их финальное положение относительно цилиндра (рис. 21, б). После этого робот переставляет средние ноги в симметричную позу (рис. 22, а) и окончательно останавливает цилиндр с использованием алгоритма стабилизации, изложенного в [5].

Забравшись на вершину, робот обнаруживает, что сразу за препятствием отсутствует возможность наступить на опорную плоскость и поэтому он начинает движение вбок по цилиндру (рис. 22, б). Пройдя несколько шагов по цилиндру (рис. 23, а), робот останавливается, а затем начинает спускаться с него (рис. 23, б). Центр масс робота после остановки проецируется в близкую окрестность точек опоры средних ног. Поэтому сначала робот переносит средние ноги назад для обеспечения статической устойчивости при переносе задних ног, а затем переносит задние ноги поближе к вершине цилиндра. После этой подготовки начинается спуск с цилиндра. Сначала переносятся средние ноги вперед так, чтобы можно было поднять передние ноги (рис. 24, а). Потом переносятся передние ноги (позиция на рис. 24, б). Стопы средних ног переносятся за вершину цилиндра (рис. 24, б), а затем одновременно с движением корпуса вперед переносятся снова передние ноги (рис. 25, а). Вслед за этим снова переносятся средние ноги с одновременным смещением и поворотом корпуса по касательной к цилиндру (рис. 25, б). Сам цилиндр при этом начинает вращаться в сторону движения робота. После этого упомянутое движение корпуса продолжается, а передние ноги ставятся на опорную плоскость (рис. 26, а). Движение корпуса при этом останавливается. Частый перенос передних и средних ног связан с необходимостью сохранения статической устойчивости, а также с необходимостью отсутствия взаимного пересечения ног. После этого корпус движется параллельно самому себе, а средние ноги ставятся на опорную поверхность (позиция на рис. 26, б). Настала очередь переносить задние ноги. Но поставить их сразу на опорную плоскость невозможно. Поэтому они сначала ставятся на цилиндр, чтобы облегчить необходимые маневры передними и средними ногами (рис. 26, б). Затем переносятся средние ноги поближе к передним (позиция на рис. 27, а). После переноса средних ног происходит перенос передних (рис. 27, а), а затем осуществляется продвижение корпуса вперед с одновременным его поворотом (рис. 27, б). Теперь освободилось место для постановки задних ног (рис. 28, а), и их можно поставить (рис. 28, б). Преодоление препятствия завершено.

8. Компьютерное моделирование. Компьютерное моделирование осуществлялось аналогично тому, как это было описано в [5, 7]. Управление роботом и закон взаимодействия стоп ног с цилиндрами реализованы в виде DLL-библиотеки, подключенной к программному комплексу “Универсальный механизм” [11]. Тем самым создается виртуальная среда обитания робота. Неподвижная опорная поверхность в ней представлена горизонтальной плоскостью. Опорная плоскость, цилиндры и ноги робота взаимодействуют друг с другом, согласно модели трения, основанной на вязкоупругом взаимодействии тел в точках контакта. Управление движением реализуется посредством компьютерного моделирования работы электромеханических приводов шарнирных углов. Выполнение требуемого движения робота осуществляется, как и в реальности, лишь в результате подачи значения управляющего электрического напряжения на модели электромеханических приводов. Соотношение размеров корпуса и звеньев ног имеет вид

Соотношения размеров корпуса и радиуса цилиндра имеют вид

для задач 1–3 соответственно. Массы корпуса робота и звеньев ног относятся как

Соотношения масс робота и цилиндров имеют вид

для задач 1–3 соответственно.

Управляющие моменты в шарнирах были ограничены по модулю значениями 60 Н · м (задача 1), 80 Н · м (задача 2), 400 Н · м (задача 3).

Представление о движении корпуса робота и его ног возникает в результате численного интегрирования дифференциальных уравнений полной трехмерной динамики робота. Поскольку в точках контакта объектов предполагается силовое взаимодействие, механическая система имеет 42 степени свободы для задачи 1 и 30 степеней свободы для задач 2, 3. Уравнения динамики синтезируются автоматически [11]. Результаты компьютерного моделирования отображаются на экране монитора в виде движения геометрических образов исследуемых материальных объектов.

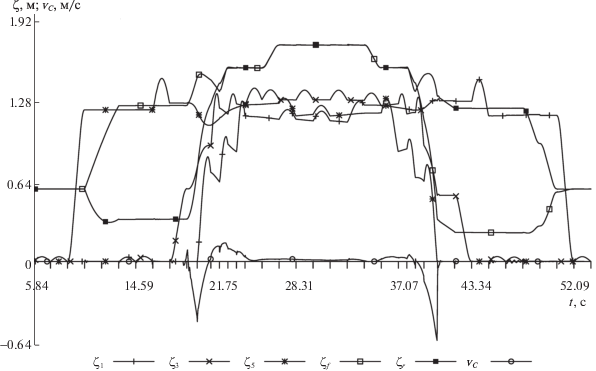
На рис. 29, 30 представлены графики изменения по времени вертикальных координат нечетных стоп ${{\zeta }_{1}}$, ${{\zeta }_{3}}$, ${{\zeta }_{5}}$, а также передней и задней точек корпуса ${{\zeta }_{f}}$, ${{\zeta }_{r}}$. На рис. 30 дополнительно приведена горизонтальная скорость цилиндра ${{v}_{C}}$. Все величины даны в абсолютной системе координат $O\xi \eta \zeta $.

Заключение. Представлено решение новой задачи о преодолении инсектоморфным роботом препятствий в виде одиночных цилиндров крупных радиусов и совокупности отдельно лежащих цилиндров небольшого радиуса. Для препятствия в виде ряда отдельно лежащих цилиндров, диаметры которых равны половине клиренса робота, описан принцип расположения точек опоры на цилиндрах, обеспечивающий устойчивую опору.

Для задачи о преодолении цилиндра, диаметр которого сравним с маршевой высотой робота, построен конструктивный алгоритм залезания на цилиндр, движения робота вбок и слезания с учетом малости области постановки стоп на вершине препятствия.

Для преодоления цилиндра, диаметр которого не позволяет роботу дотянуться до вершины парой передних ног, имея точки опоры остальных ног на плоскости, на основе теоремы об изменении кинетического момента механической системы робот–цилиндр относительно точки опоры цилиндра о горизонтальную плоскость найдены условия реализуемости указанного маневра. Дана оценка величины скорости движения робота по цилиндру, обеспечивающая слезание. Построен конструктивный алгоритм залезания на цилиндр с отталкиванием от опорной плоскости, движения робота вбок и слезания.

Предложенные алгоритмы формирования движения робота при преодолении указанных препятствий были отработаны средствами компьютерного моделирования в программной среде, реализующей расчет взаимодействия трехмерной полной динамической модели робота и окружающих его объектов с учетом сил кулоновского трения и моделей электромеханических приводов в шарнирах робота. Показано, что предложенные программные движения реализуемы при коэффициенте трения, не превышающем 1.

Стабилизация движения робота в окрестности программного движения построена по принципу кусочно-формируемой с дискретностью шага интегрирования обратной связи. Обратная связь рассчитывается по рассогласованиям реальных и программных шарнирных углов с требованием минимальных значений угловых скоростей. Возникающие в шарнирных углах переходные процессы не разрушают требуемое программное движение робота на всех этапах движения системы.