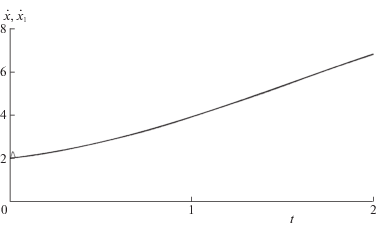Известия РАН. Теория и системы управления, 2021, № 4, стр. 46-56

Введение. В статье описывается задача управления системой нелинейных обыкновенных дифференциальных уравнений. Суть задачи состоит в построении алгоритма формирования управления по принципу обратной связи, который гарантировал бы отслеживание траекторией заданной системы траектории другой системы, подверженной влиянию неизвестного возмущения. В работе исследуем задачу, в которой предполагается, что измеряются (с ошибкой) в дискретные моменты времени не все, а часть фазовых координат заданной управляемой системы. Кроме того, полагаем, что неизвестное возмущение является элементом пространства функций, суммируемых с квадратом евклидовой нормы, т.е. может быть неограниченным. Учитывая данную особенность задачи, конструируем устойчивый к информационным помехам и погрешностям вычислений алгоритм решения, который основан на сочетании элементов теории некорректных задач с известным в теории позиционных дифференциальных игр методом экстремального сдвига. Предлагаемый алгоритм содержит два блока: блок реконструкции в темпе “реального времени” ненаблюдаемых координат, а также блок управления, использующий результаты работы блока реконструкции в качестве входа.

1. Постановка задачи. Рассматривается нелинейная система дифференциальных уравнений

с начальным состоянием

Здесь $0 < \vartheta < + \infty $ – конечный момент времени, $x \in {{R}^{n}}$ – измеряемая часть полного фазового вектора системы, $y \in {{R}^{N}}$ – неизмеряемая часть, ${v} \in {{R}^{r}}$ – возмущение,  f₁ и f₂₁ – липшицевые функции с константой Липшица L, C – стационарная матрица соответствующей размерности. Назовем систему (1.1) возмущенной. Система (1.1) подвержена воздействию некоторого возмущения ${v}( \cdot ) \in {{L}_{2}}(T;{{R}^{r}})$. Как это возмущение ${v}( \cdot )$, так и отвечающее ему решение системы (1.1) ${{z}_{1}}( \cdot ;{{z}_{{10}}},{v}( \cdot )) = \left\{ {{{x}_{1}}( \cdot ;{{z}_{{10}}},{v}( \cdot )),{{y}_{1}}( \cdot ;{{z}_{{10}}},{v}( \cdot ))} \right\}$, где ${{z}_{1}} = \left\{ {{{x}_{1}},{{y}_{1}}} \right\}$, ${{z}_{{10}}} = \left\{ {{{x}_{{10}}},{{y}_{{10}}}} \right\}$, неизвестны.

Наряду с системой (1.1) имеется еще одна система того же вида

с начальным состоянием и управлением $u \in {{R}^{r}}$. Назовем её следящей. Начальные состояния систем (1.1) и (1.2) полагаем в дальнейшем известными.

В дискретные, достаточно частые, моменты времени

измеряется часть фазовых состояний системы (1.1), а именно состояния ${{x}_{1}}({{\tau }_{i}}) = {{x}_{1}}({{\tau }_{i}};{{z}_{{10}}},{v}( \cdot ))$, а также состояния $x({{\tau }_{i}}) = x({{\tau }_{i}};{{z}_{0}},u( \cdot ))$ системы (1.2). Состояния ${{x}_{1}}({{\tau }_{i}})$ измеряются с ошибкой. Результаты измерений – векторы $\xi _{i}^{h} \in {{R}^{n}},$ $i \in \overline {0,{{m}_{h}} - 1} $, удовлетворяют неравенствам

Здесь $h \in (0,1)$ – уровень погрешности измерения, символ $| \cdot {{|}_{n}}$ означает евклидову норму в пространстве Rⁿ. Для простоты ограничимся случаем, когда состояния $x({{\tau }_{i}})$ и $y({{\tau }_{i}})$ системы (1.2) измеряются точно. Будем предполагать

Неравенства (1.3) означают, что состояния ${{x}_{1}}({{\tau }_{i}})$ измеряются с ошибкой. В свою очередь неравенства (1.4) говорят о том, что начальные состояния следящей и возмущенной систем близки.

Обсуждаемая в работе задача состоит в построении алгоритма формирования управления $u = {{u}^{h}}( \cdot )$ системой (1.2), позволяющего осуществлять отслеживание решением $z( \cdot ) = \left\{ {x( \cdot ),y( \cdot )} \right\}$ этой системы решение ${{z}_{1}}( \cdot ) = \left\{ {{{x}_{1}}( \cdot ),{{y}_{1}}( \cdot )} \right\}$ системы (1.1), т.е. обеспечить малость величины ${{\sup }_{{t \in T}}}{{\left| {z(t) - {{z}_{1}}(t)} \right|}_{{n + N}}}$. Таким образом, рассматривается задача, состоящая в построении алгоритма, который по текущим измерениям величин ${{x}_{1}}({{\tau }_{i}})$ и $z({{\tau }_{i}})$ в “реальном времени” формирует (по принципу обратной связи) управление $u = {{u}^{h}}( \cdot )$ в правой части системы (1.2), такое, что отклонение решения системы (1.2) $z( \cdot ) = z( \cdot ;{{z}_{0}},{{u}^{h}}( \cdot )) = \left\{ {x({{\tau }_{i}};{{z}_{0}},u( \cdot )),y({{\tau }_{i}};{{z}_{0}},u( \cdot ))} \right\}$ $({{z}_{0}} = \left\{ {{{x}_{0}},{{y}_{0}}} \right\})$ от решения системы (1.1) ${{z}_{1}}( \cdot ) = {{z}_{1}}( \cdot ;{{z}_{{10}}},{v}( \cdot ))$ в метрике пространства $C(T;{{R}^{{n + N}}})$ мало при достаточной малости измерительной погрешности h и периода дискретизации δ.

Задача слежения – одна из классических задач теории управления. Она исследовалась многими авторами (см., например, [1–5]). В данной работе мы рассмотрим случай измерения части координат. При этом укажем алгоритм решения, который основан на методе динамического обращения, развитом в [6, 7], а также известном в теории позиционного управления методе экстремального сдвига [8]. В связи с неполнотой информации (а именно с возможностью измерения в моменты ${{\tau }_{i}}$ не всего фазового состояния системы (1.1) – $\{ {{x}_{1}}({{\tau }_{i}}),{{y}_{1}}({{\tau }_{i}})\} $, а лишь его части – ${{x}_{1}}({{\tau }_{i}})$), наряду с блоком управления, нами будет использоваться дополнительный блок – блок динамического восстановления неизмеряемых координат. Последний будет играть роль поставщика недостающей информации о текущем фазовом состоянии системы (1.1). Эта информация оперативно передается на блок управления, формирующий $u$ по принципу обратной связи. Среди последних работ, где сначала оценивается часть координат, а затем все координаты подаются на вход контура управления, следует отметить [9].

Другие задачи отслеживания решений дифференциальных уравнений, основанные на методе экстремального сдвига, обсуждались, например, в [10–15]. При этом в работах [10–12] рассматривался случай измерения “всех” координат. Случай измерения части фазовых координат обсуждался в публикациях [13] (линейная система обыкновенных дифференциальных уравнений), [14] (система с последействием), [15] (система с распределенными параметрами).

2. Метод решения. Перейдем к описанию метода решения рассматриваемой задачи. Пусть для каждого $h \in (0,1)$ фиксировано семейство ${{\Delta }_{h}}$ разбиений отрезка $T$ контрольными моментами времени ${{\tau }_{{h,i}}}$:

Как было отмечено выше, при решении задачи слежения будут использоваться два блока.

Первый (вспомогательный) блок – блок реконструкции, содержит управляемую систему и закон формирования управления $u_{0}^{h}( \cdot )$ этой системой по принципу обратной связи ${{U}_{0}}$. Динамика системы описывается векторным дифференциальным уравнением

с начальным условием $w_{1}^{h}(0) = {{x}_{0}}.$ Здесь управление $u_{0}^{h}( \cdot )$ задается формулой $\xi _{i}^{h}$ – результат измерения компоненты ${{x}_{1}}({{\tau }_{i}})$ (см. (1.3)), п.в. – почти всех. При i = 0 полагаем $\xi _{0}^{h} = {{x}_{0}}.$ Закон ${{U}_{0}}( \cdot , \cdot , \cdot ):T \times {{R}^{n}} \times {{R}^{n}} \mapsto {{R}^{n}}$ конструируется таким образом, что при соответствующем согласовании параметров h и $\delta (h)$ управление $u_{0}^{h}( \cdot )$, стоящее в правой части системы (2.2), позволяет с помощью некоторого отображения ${{U}_{1}}:T \times {{R}^{n}} \times {{R}^{n}} \to {{R}^{N}}$ сконструировать функцию $u_{1}^{h}( \cdot )$: являющуюся приближением (в метрике пространства непрерывных функций) неизмеряемой части фазовой траектории $y_{1}^{{}}( \cdot )$.

Второй (основной) блок – блок управления системой (1.2), содержит закон U(·, ·, ·) : $T \times {{R}^{N}} \times {{R}^{N}} \mapsto {{R}^{r}}$ формирования управления $u = {{u}^{h}}( \cdot )$. Закон U конструируется таким образом, что при соответствующем согласовании ряда параметров управление $u = {{u}^{h}}( \cdot )$ вида

обеспечивает отслеживание решения системы (1.2) решением системы (1.2).

На рис. 1 изображена блок-схема алгоритма решения задачи.

3. Алгоритм решения. Укажем алгоритм решения рассматриваемой задачи. Фиксируем некоторoе семейство ${{\Delta }_{h}}$ (2.1), а также две функции $\alpha (h):(0,1) \to (0,1)$ и ${{\alpha }_{1}}(h):(0,1) \to (0,1)$.

Пусть $M \subset {{R}^{n}}$ – область, в которой остаются первые $n$ фазовых координат решения системы (1.1), порожденного неизвестным возмущением ${v}( \cdot )$, т.е.

Условие. В области $T \times M$ функция $y \to F = {{f}_{1}}(t,x,y)$ имеет обратную функцию $y = f_{{1y}}^{{ - 1}}(t,x$, F), которая является липшицевой функцией по совокупности переменных с постоянной Липшица L_y.

Кроме того, полагаем, что функция  f₁ – дифференцируема, а компонента $x( \cdot )$ решения системы (1.2) обладает следующим свойством: $\ddot {x}( \cdot ) \in {{L}_{2}}(T;{{R}^{n}})$.

До начала работы алгоритма фиксируем величину $h \in (0,1)$, числа ${{\alpha }_{1}} = {{\alpha }_{1}}(h),$ $\alpha = \alpha (h)$ и разбиение ${{\Delta }_{h}} = \left\{ {{{\tau }_{{h,i}}}} \right\}_{{i = 0}}^{{{{m}_{h}}}}$ вида (2.1). Работу алгоритма разобьем на однотипные шаги. В течение i-го шага, осуществляемого на промежутке времени ${{\delta }_{i}} = [{{\tau }_{i}},{{\tau }_{{i + 1}}})$, ${{\tau }_{i}} = {{\tau }_{{h,i}}}$, выполняются следующие операции. Сначала, в момент ${{\tau }_{i}}$, вычисляются векторы $u_{{0i}}^{h},$ $u_{{1i}}^{h}$ и $u_{i}^{h}$ по формулам (2.3)–(2.5), в которых

Здесь символ “T” означает транспонирование. Затем на вход системы (2.2) при всех $t \in {{\delta }_{i}}$ подается управление $u_{0}^{h}(t)$ вида (2.3), (3.1), а на вход системы (1.2) – управление $u = {{u}^{h}}(t)$ вида (2.5), (3.1). Под действием этих управлений решение системы (1.2) переходит из состояния $z({{\tau }_{i}})$ в состояние $z({{\tau }_{{i + 1}}})$, а решение системы (2.2) – из состояния $w_{1}^{h}({{\tau }_{i}})$ в состояние $w_{1}^{h}({{\tau }_{{i + 1}}})$. Работа алгоритма заканчивается в момент $\vartheta $.

Оказывается, что при определенном согласовании величин $h,\,\,\delta (h),\,\;\alpha (h)$ и ${{\alpha }_{1}}(h)$ построенное таким образом управление $u = {{u}^{h}}( \cdot )$ решает обсуждаемую задачу слежения.

Прежде чем перейти к доказательству этого факта, приведем два вспомогательных утверждения. Заметим, что встречающиеся далее постоянные ${{c}_{j}},\;{{C}_{j}}$ зависят от структуры системы (1.2) и не зависят от $h,\;\alpha ,\;{{\alpha }_{1}},\;\delta $.

Лемма 1 [10]. Пусть неотрицательная функция $\varphi ( \cdot )$ при всех $i \in \overline {0,{{m}_{h}} - 1} $ удовлетворяет неравенствам

где ${{\tau }_{i}} \in \Delta = \left\{ {{{\tau }_{i}}} \right\}_{{i = 0}}^{m}$, $p = {\text{const}} > 0,$ $G( \cdot ) \in {{L}_{\infty }}(T;R)$. Тогда справедливы неравенства

Символ $| \cdot |$ здесь означает модуль числа.

Лемма 2. Пусть $\alpha (h) \to 0,$ $\delta (h) \to 0,$ $(h + \delta (h)){{\alpha }^{{ - 1}}}(h) \to 0$ при $h \to 0$, причем $\delta ({{h}_{1}}) \leqslant \delta ({{h}_{2}})$, если ${{h}_{1}} \leqslant {{h}_{2}}$. Тогда можно указать такое число ${{h}_{0}} \in (0,1)$, что при всех $h \in (0,{{h}_{0}})$ верно неравенство

где ${{\nu }^{h}} = \nu (h,\alpha (h),$ $\delta (h)) = \alpha (h) + (h + \delta (h)){{\alpha }^{{ - 1}}}(h)$.

Доказательство леммы 2 приведено в Приложении.

Теорема. Пусть выполнены условия леммы 2. Пусть также ${{\alpha }_{1}}(h) \to 0$ при $h \to 0$ и ${{\delta }^{\gamma }}(h) \leqslant {{C}_{1}}\alpha _{1}^{2}(h)$ при некотором $\gamma \in (0,1)$. Тогда можно указать ${{h}_{1}} \in (0,{{h}_{0}})$, такое, что при всех $h \in (0,{{h}_{1}})$ верно неравенство

где ${{\varepsilon }_{1}}(t) = {\text{|}}z(t) - {{z}_{1}}(t){\text{|}}_{{n + N}}^{2},$ ${{\alpha }_{1}} = {{\alpha }_{1}}(h),$ $\delta = \delta (h),$ ${{\nu }^{h}} = \nu (h,\alpha (h),\delta (h))$.

Доказательство теоремы приведено в Приложении.

Следствие. Если $\gamma = 1{\text{/}}2,$ δ = h, $\alpha = {{h}^{{1/2}}},$ ${{\alpha }_{1}} = {{h}^{{1/2}}}$, то справедливо неравенство

Замечание. Пусть неточно измеряются состояния $x({{\tau }_{i}})$ системы (1.2), т.е. в моменты ${{\tau }_{i}}$ находятся величины $\psi _{i}^{h} \in {{R}^{n}}$, такие, что

В этом случае блок реконструкции следует дополнить системой

с начальным состоянием $w_{2}^{h}(0) = {{x}_{{10}}}$. При этом управление ${{{v}}^{{h(1)}}}(t)$ будем вычислять по правилу

В свою очередь управление ${{u}^{h}}(t)$ вычисляется по формуле (2.5), в которой вместо вектора $y({{\tau }_{i}})$ стоит вектор

т.е.

При этом теорема и следствие будут справедливыми.

4. Примеры. Пример 1. Рассматриваются две материальные точки единичной массы, которые двигаются по прямой под действием внешних сил. Силы гравитации, а также сопротивления среды отсутствуют. Поэтому уравнения движения точек, согласно второму закону Ньютона, имеют вид

и

Здесь $x(t)\;({{x}_{1}}(t))$ – путь, пройденный к моменту t первой (второй) точкой, $\dot {x}(t)({{\dot {x}}_{1}}(t))$ – скорость первой (второй) точки, $u( \cdot )({v}( \cdot ))$ – сила воздействия на первую (вторую) точку. В начальный момент времени ($t = 0)$ состояния точек и их скоростей изменения близки:

Сила ${v}( \cdot )$, действующая на вторую точку, неизвестна. Известно лишь, что она удовлетворяет условию ${v}( \cdot ) \in {{L}_{2}}(T;R)$. В дискретные моменты времени ${{\tau }_{i}},{{\tau }_{i}} = {{\tau }_{{i - 1}}} + \delta ,$ ${{\tau }_{0}} = 0$, измеряются пути, пройденные каждой из точек, т.е. определяются числа $\xi _{i}^{h}$ и $\psi _{i}^{h}$, такие, что

Необходимо указать алгоритм формирования управления $u( \cdot )$ по принципу обратной связи

такой, что первая точка отслеживает движение второй, т.е. величина мала при малых величинах погрешности измерения h и расстояния между узлами измерения фазовых положений точек $\delta = {{\tau }_{i}} - {{\tau }_{{i - 1}}}$.

Для решения сформулированной задачи был использован описанный выше алгоритм. Уравнение (4.1) сводилось к виду (1.2) заменой переменных $y(t) = \dot {x}(t)$, а уравнение (4.2) – к виду (1.1) заменой ${{y}_{1}}(t) = {{\dot {x}}_{1}}(t)$. Полученные системы решались методом Эйлера с шагом $\delta $.

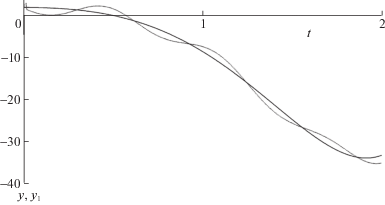
В моменты ${{\tau }_{i}} = i\delta $ числа ${v}_{i}^{h}$, $u_{{1i}}^{h}$ и $u_{i}^{h}$ вычислялись по формулам (2.3)–(2.5) и (3.1). В ходе эксперимента полагалось ${v}(t) = 1 + \sin (2t),$ $\vartheta = 2$, ${{x}_{0}} = {{x}_{{10}}} = 2$, ${{y}_{0}} = {{y}_{{10}}} = 2$, $\alpha = {{\alpha }_{1}} = 0.002$, $\xi _{i}^{h} = {{x}_{1}}({{\tau }_{i}})$ + + hcos(10t), $\psi _{i}^{h} = x({{\tau }_{i}}) + h$. Результаты вычислительного эксперимента показаны на рис. 2, 3. Рисунок 2 отвечает случаю $h = 0.01$, $\delta = 0.002$, в то время как рисунок 3 – случаю $h = 0.001$, $\delta = 0.002$. На рисунках сплошная линия изображает $\dot {x}( \cdot )$, пунктирная линия – ${{\dot {x}}_{1}}( \cdot )$. Как показал эксперимент, графики кривых $x( \cdot )$ и ${{x}_{1}}( \cdot )$ во втором случае практически совпадают.

Пример 2. Аналогичная задача решалась для систем вида

и

Системы (4.3)–(4.4) решались методом Эйлера с шагом δ. В ходе эксперимента полагалось $v(t) = {{t}^{2}},$ ϑ = 2, ${{x}_{0}} = 2$, ${{y}_{0}} = 2$, $\alpha = {{\alpha }_{1}} = 0.002$, $\xi _{i}^{h} = {{x}_{1}}({{\tau }_{i}}) + hcos(10t)$, $x_{{10}}^{{}} = {{x}_{0}}$, $y_{{10}}^{{}} = {{y}_{0}} + h$. Результаты эксперимента приведены на рис. 4, 5. Рисунок 4 отвечает случаю $h = 0.5$, $\delta = 0.002$, а рисунок 5 – случаю h = 0.1, $\delta = 0.002$. На указанных рисунках сплошная линия изображает $y( \cdot )$, пунктирная линия –${{y}_{1}}( \cdot )$.