Известия РАН. Теория и системы управления, 2021, № 5, стр. 18-26

Введение. Изучается задача управления механической системой, представляющей собой твердое тело с прицепленным к нему упругим звеном. В математическом описании системы упругое звено моделируется горизонтальной цепочкой из $n$ линейных осцилляторов, т.е. последовательно присоединенными с помощью пружин $n$ точечными массами (рис. 1). Несущее тело перемещается вдоль горизонтальной прямой под действием ограниченной управляющей силы и неконтролируемого возмущения, например силы сухого трения. Предполагается, что координата и скорость несущего тела, а также координата первой массы в цепочке в каждый момент времени известны, а фазовые переменные, описывающие динамику остальных масс, не доступны для измерений. Требуется перенести несущее тело в заданное терминальное положениe за конечное (нефиксированное) время и полностью погасить колебания осцилляторов. Искомое управление должно удовлетворять наложенным на его модуль ограничениям.

Рассматриваемая модель (с малым числом осцилляторов) применима, например, для описания прецизионной поворотной платформы, устанавливаемой на орбитальном космическом аппарате и предназначенной для изменения ориентации закрепленного на ней объекта. В [1] построен алгоритм управления такой платформой с учетом неполноты информации о динамических параметрах данной механической системы, действующего в ней трения и законах движения основания. В [2] решена задача, аналогичная рассматриваемой ниже, для случая n = 2, т.е. для цепочки из двух осцилляторов.

Изучение линейной цепочки осцилляторов восходит к классической работе [3]. Отметим, что исследуемую систему отличает дефицит управлений, так как она состоит из n + 1 твердых тел, совершающих поступательные горизонтальные перемещения, и имеет n + 1 степень свободы, тогда как управляющее воздействие скалярно. Некоторые методы решения задач управления механическими системами с дефицитом управляющих параметров представлены в [4]. Наличие неконтролируемых внешних возмущений приводит к необходимости искать управление в форме обратной связи, при этом невозможность измерить текущие координаты и скорости точечных масс из цепочки существенно затрудняет решение задачи. Время движения системы к равновесию должно быть конечно, поэтому изучаемую ниже задачу управления можно отнести к классу задач о стабилизации за конечное время, которые являются предметом активного исследования [5, 6].

1. Постановка задачи и уравнения движения. Динамика системы, представленной на рис. 1, описывается уравнениями

Здесь x₀ – координата несущего тела на прямой, ${{m}_{0}}$ – его масса, x_i – координата точечной массы m_i, ${{k}_{i}} > 0$ – жесткость пружины, соединяющей массы ${{m}_{{i - 1}}}$ и ${{m}_{i}},\;i = \overline {1,n} $.

На управляющую силу u и возмущение ${v}$ накладываются ограничения

Предполагается, что в каждый момент времени известны текущие значения фазовых переменных ${{x}_{0}},{{\dot {x}}_{0}},{{x}_{1}}$, т.е. координата и скорость несущего тела и координата первой массы, а остальные переменные ${{x}_{i}},{{\dot {x}}_{i}}$ не доступны для измерений.

В [7] предложен закон управления, удовлетворяющий ограничению (1.2) и приводящий систему (1.1) в заданное терминальное состояние покоя за конечное (нефиксированное) время из некоторой окрестности этого терминального состояния в предположении, что все фазовые переменные ${{x}_{i}},{{\dot {x}}_{i}}$, $i = \overline {0,n} $, в каждый момент времени известны. Там же вычислено время перемещения всей системы из одного состояния покоя в другое с помощью указанного закона управления и найдена асимптотика этого времени при $n \to \infty $. Используемый подход основан на методике, развитой в [8].

Ниже показано, что данное управление оказывается эффективным в случае неполного измерения вектора текущего фазового состояния цепочки осцилляторов. Вычислено время, за которое система остановится в начале координат, для некоторых начальных состояний и найдена асимптотика этого времени в зависимости от числа осцилляторов n.

В дальнейшем через $e_{k}^{s}$ будем обозначать единичный вектор размерности k, у которого координата с номером s равна 1, а остальные координаты равны 0.

Представим систему (1.1) в векторной форме

где

Положим $N = 2n + 2$ и перепишем систему (1.3) в форме Коши

Здесь и в дальнейшем квадратные скобки обозначают блочную матрицу или вектор, $I$ – единичная матрица.

2. Управляемость и наблюдаемость. Покажем сначала, что пара $(\widetilde A,\widetilde b)$ управляема. Установим для этого справедливость следующих утверждений.

Утверждение 1. Для любой квадратной $(k \times k)$-матрицы A и k-вектора b системы

и управляемы или нет одновременно.

Действительно, система второго порядка (2.1) эквивалентна системе первого порядка:

Для последней матрица управляемости Калмана имеет вид

После перестановки столбцов получаем

где $K = [b\;Ab \ldots {{A}^{{k - 1}}}b]$ – матрица управляемости Калмана для системы (2.2) . Отсюда следует равенство ${\text{rk}}\widetilde K = {\text{rk}}\widetilde K{\kern 1pt} ' = 2{\text{rk}}K$ и справедливость утверждения 1.

Утверждение 2. Если A – трехдиагональная $(k \times k)$-матрица

где ${{a}_{i}} \ne 0,$ $i = \overline {1,k - 1} ,$ то пара $(A,e_{k}^{1})$ управляема.

Так как матрица управляемости Калмана $K = [e_{k}^{1}\;Ae_{k}^{1} \ldots {{A}^{{k - 1}}}e_{k}^{1}]$ – верхнетреугольная с ненулевыми диагональными элементами ${{K}_{{11}}} = 1,$ ${{K}_{{jj}}} = {{a}_{1}}{{a}_{2}} \ldots {{a}_{{j - 1}}},$ $j\; \geqslant \;1$, то ${\text{rk}}K = k$.

Из приведенных утверждений вытекает, что пара $({{A}_{0}},m_{0}^{{ - 1}}e_{{n + 1}}^{1})$ и, следовательно, система (1.4) управляемы.

Для проверки наблюдаемости системы (1.4) рассмотрим систему уравнений, описывающую лишь динамику цепочки осцилляторов (исключая несущее тело):

Здесь трехдиагональная матрица A₁ получена из матрицы A₀ удалением первых строки и столбца.

По предположению координата и скорость ${{x}_{0}},{{\dot {x}}_{0}}$ несущего тела и координата ${{x}_{1}} = \langle e_{{2n}}^{1},\bar {x}\rangle $ первой массы в цепочке доступны измерению (здесь и далее угловые скобки означают скалярное произведение). Рассуждая как и выше и используя трехдиагональную структуру матрицы A₁, можно показать, что пара $(\bar {A},e_{{2n}}^{1})$ наблюдаема.

Таким образом, по результатам наблюдений переменных ${{x}_{0}},\;{{\dot {x}}_{0}},\;{{x}_{1}}$ все остальные, не доступные для измерений, фазовые переменные системы могут быть вычислены с помощью стандартной процедуры [9–11]. В дальнейшем считаем, что фазовый вектор системы (1.4) в каждый момент времени известен.

3. Алгоритм построения управления. Для приведения системы (1.4) в начало координат используем подход, развитый в [8] и примененный в [7] для управления движением цепочки осцилляторов. Этот подход позволяет построить закон управления в форме обратной связи, т.е. как функцию вектора текущего фазового состояния $\tilde {x}$, удовлетворяющий ограничению (1.2) и при некоторых предположениях относительно ρ останавливающий систему (1.4) в начале координат за конечное время. Изложим кратко алгоритм построения такого управления.

Приведем сначала систему (1.4) к нормальной форме Фробениуса. Матрица управляемости Калмана для системы (1.4) имеет вид

Положим

У вектора $A_{0}^{j}e_{{n + 1}}^{1}$ на $(j + 1)$-м месте стоит число

и нули на последующих местах, $j = \overline {0,n} $. Следовательно, вектор f ортогонален всем столбцам матрицы $\widetilde K$, за исключением последнего.

Составим построчно матрицу

Преобразование $Z = S\widetilde X$ приводит систему (1.4) к нормальной форме Фробениуса

где ${{\alpha }_{i}}$ – коэффициенты характеристического полинома матрицы $\widetilde A,\;i = \overline {1,N} $.

Сделаем еще одно преобразование координат

и обозначим через u_c новую управляющую функцию

Система (3.3) примет вид

Определим теперь управляющую функцию u_c следующим образом:

Здесь функция T(z) задается неявно уравнением

с положительно определенной матрицей Q и диагональной матрицей δ(T):

В [8] установлено:

1) для любого d > 0 уравнение (3.8) имеет единственное положительное решение $T(z)$;

2) производная функции $T(z)$ в силу системы (3.6), управляемой по закону (3.5), в отсутствие возмущений, т.е. при $v = 0$, удовлетворяет равенству

которое означает, что время движения системы из точки z до начала координат равно $T(z)$;

3) управляющая функция ${{u}_{c}}(z)$ ограничена:

Из соотношения (3.9) вытекает, что выбором постоянной d в уравнении (3.8) можно обеспечить выполнение любого наперед заданного ограничения на модуль управляющей функции ${{u}_{c}}(z)$, а в некоторой окрестности нуля, в силу соотношения (3.5), – и ограничения (1.2) на управляющую функцию $u(x)$ для исходной системы.

В [7] показано, что если величина ρ в (1.2) удовлетворяет соотношению

то выполнено неравенство $\dot {T}\;\leqslant \; - {\kern 1pt} \sigma $ для некоторого $\sigma > 0$. Следовательно, время движения системы $\tau (z)$ от точки z до 0 конечно и $\tau (z) = O(T(z))$.

4. Оценка времени движения. Пусть $v = 0$. Вычислим время движения системы (2.6) из начального состояния

до нуля. Таким образом, в начальный момент времени все массы находятся в точке x = 0, имеют одинаковую скорость $\eta $ и их необходимо остановить в начале координат.

В переменных z начальное состояние системы ${{\widetilde X}^{0}}$ соответствует вектору

Здесь матрицы $S$ и ${{S}_{1}}$ заданы выражениями (3.2) и (3.4). Время, за которое управление (3.5) переводит z⁰ в нуль, равно $T({{z}^{0}})$. Оно определяется из уравнения (3.8), которое в данном случае принимает вид

и сводится к вычислению элемента ${{Q}_{{N - 1N - 1}}}$ матрицы Q. Такое вычисление может быть проведено с помощью соотношения между матрицей Q и ортогональными полиномами [12]. Здесь – матрица коэффициентов полиномов Якоби:

Из (4.1) и (4.2) вытекает

Старший коэффициент полинома ${{P}_{{N - 2}}}(x)$ и коэффициент при степени N – 2 полинома ${{P}_{{N - 1}}}(x)$ равны

В итоге получаем следующее выражение для $T({{z}^{0}})$:

где

Приведем уравнение, из которого вычисляется время перехода в нуль из начального состояния более общего вида, а именно

В канонических переменных z данное начальное состояние соответствует вектору

Время движения $T = T({{z}^{0}})$ до нуля под действием управления (3.5) определяется из следующего аналога уравнения (4.1):

5. Асимптотическая оценка времени движения при $N \to \infty $. Для перехода к пределу $N \to \infty $ в выражении для времени движения $T({{z}^{0}})$ примем следующие допущения о том, как ведут себя параметры системы (1.1) при больших $N$ (или $n$). Будем считать, что массы ${{m}_{i}}$ и жесткости ${{k}_{i}}$ имеют вид ${{m}_{i}} = {{\rho }_{i}}{\text{/}}n,$ ${{k}_{i}} = {{\kappa }_{i}}n$, где ${{\rho }_{i}} = O(1),$ ${{\kappa }_{i}}^{{ - 1}} = O(1)$ при $n \to \infty $. Это означает, что в пределе конечномерная динамическая система (1.1) описывает продольные колебания упругого стержня, а принятые допущения соответствуют конечной плотности массы и конечности модуля Юнга у предельной сплошной среды.

В формуле (4.3) для вычисления времени движения единственная величина, зависящая от параметров динамической системы (1.1), – это $\Omega $ из (3.1) . Для определения асимптотической оценки $T({{z}^{0}})$ важна лишь асимптотика величины ${{\Omega }^{{1/N}}}$, которая при сделанных предположениях имеет вид

Для оценки $Q_{{N - 1N - 1}}^{{1/2N}}$ достаточно использовать грубую форму формулы Стирлинга

применение которой дает соотношения

Остальные величины, входящие в формулу (4.3) для $T({{z}^{0}})$, постоянны при $N \to \infty $. Поэтому

т.е. время движения остается равномерно ограниченным.

Можно получить асимптотическую оценку при $N \to \infty $ времени движения $T = T({{z}^{0}})$ до нуля под действием управления (3.5) из начального состояния (4.4). Для этого нужно изучить асимптотику при $N \to \infty $ решения T уравнения (4.5). Вычисления, аналогичные проделанным выше, показывают, что уравнения (4.5) можно записать в виде

где коэффициенты a_ij имеют асимптотическую оценку $a_{{ij}}^{{1/N}} = O(1)$. Отсюда следует, что для времени движения T верна асимптотическая оценка

6. Численное моделирование. Приведем результаты компьютерного моделирования динамики системы, состоящей из несущего тела и двух осцилляторов, при следующих значениях параметров:

Изучался случай, когда в начальный момент времени все массы находятся в точке x = 0 и имеют одинаковую скорость: ${{x}_{i}} = 0,$ ${{\dot {x}}_{i}} = 0.2\;{\text{м/с}},$ $i = 0,1,2$. Предполагалось, что возмущения отсутствуют, т.е. $v = 0$. Величина d в уравнении (3.8) была выбрана равной $d = 10$. Система переводилась в начало координат.

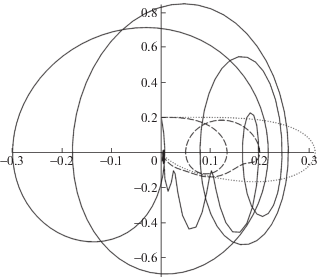
Рисунок 2 описывает поведение фазовых траекторий всех трех масс системы, движущейся под действием предложенного управления. Сплошная линия отвечает несущей массе ${{m}_{0}}$, штриховая – массе ${{m}_{1}}$, а пунктирная – массе ${{m}_{2}}$. По оси абсцисс отложены координаты масс, по оси ординат – скорости. Полное время движения составило $ \approx {\kern 1pt} 6.44$ с.

На рис. 3 представлены графики зависимости от времени управляющих функций, реализовавшихся вдоль полученной траектории системы. Сплошная линия здесь отвечает управлению $u(t)$, применяемому к исходной системе (1.1), а штриховая – управлению ${{u}_{c}}(t)$, заданному выражением (3.7). Разность между значениями этих функций определяется слагаемым

в выражении (3.5) и стремится к нулю по мере приближения системы к терминальному состоянию равновесия. При выбранном в уравнении (3.8) параметре d, как видно из рисунка, максимальная абсолютная величина управления приблизительно равна 8 H.

Заключение. В работе применен развитый ранее подход к синтезу управления в линейных системах для перемещения тела, несущего цепочку осцилляторов произвольной длины. Показано, что для приведения такой системы в заданное состояние покоя за конечное время достаточно измерять лишь текущее фазовое состояние несущего тела и координату массы первого осциллятора, остальные фазовые переменные системы могут быть определены на основе этих измерений. Для некоторых начальных состояний вычислено время движения и найдена асимптотика этого времени при увеличении числа осцилляторов. Полученные асимптотические оценки говорят о перспективах предельного перехода от управления конечномерной системой к управлению движением сплошной среды.