Известия РАН. Теория и системы управления, 2021, № 5, стр. 5-17

Введение. Существуют разные способы построения регуляторов [1–4], в том числе способ, основанный на применении аппарата линейных матричных неравенств [1]. В задаче стабилизации по состоянию предполагают, что состояние системы доступно измерению и управление строят в виде линейной обратной связи по состоянию. С помощью современных программ (например, программ для инженерных расчетов Matlab) можно получить параметры такого регулятора. Вместе с тем возможна ситуация, когда полученное решение физически не может быть реализовано. Это связано с тем, что синтез линейных законов управления на основе линейной модели управляемого объекта может быть эффективно применен только там, где линейная модель более или менее адекватно описывает реальный объект, т.е. в ограниченной области фазового пространства. Заметим также, что в реальных условиях работы система должна находиться в области ее допустимых состояний. В связи с этим возникает необходимость учитывать в модели ограничение на фазовые переменные объекта и управление. Проблема синтеза управления при заданных ограничениях является сложной и актуальной в настоящее время [2, 3, 5].

В работах [2, 3] рассмотрена и решена задача синтеза управления по состоянию, которое обеспечивает стабилизацию динамического объекта при ограничениях на фазовые и управляющие переменные. В фазовом пространстве получена область допустимых начальных состояний системы, при которых регулятор стабилизирует систему. Однако в реальных ситуациях состояние системы измеряется, как правило, с ошибкой. Поэтому открытым остается вопрос о возможности применения полученного в [2, 3] регулятора в указанной ситуации.

В статье обсуждаются вопросы по оценке области допустимых начальных состояний линейной динамической системы, при которых регулятор, полученный в задаче синтеза управления по состоянию при ограничениях на фазовые и управляющие переменные, будет обеспечивать стабилизацию также и в случае наличия ошибки в измеряемом состоянии. Сформулированы достаточные условия, позволяющие оценить множество допустимых начальных состояний динамической системы. Подход к решению основан на применении метода квадратичных функций Ляпунова и аппарата линейных матричных неравенств. Ключевым моментом в доказательстве теоремы является использование неущербности S-процедуры при двух ограничениях [6]. В качестве примеров приведены две задачи: стабилизация перевернутого маятника и задача о движении ферромагнитного тела в электромагнитном подвесе.

1. Предварительные сведения. Рассмотрим управляемый объект

где $x \in {{R}^{n}}$ – состояние системы, $u \in {{R}^{l}}$ – управление, ${{z}_{i}} \in {{R}^{{{{m}_{i}}}}}$ – управляемые выходы системы; A, B, ${{C}_{i}}$ и ${{D}_{i}}$ – заданные матрицы соответствующих размеров.

Задача о стабилизации объекта (1.1) с помощью управления в виде линейной обратной связи по состоянию

обеспечивающего асимптотическую устойчивость замкнутой системы (1.1)–(1.3) и выполнение при заданных значениях ${{\gamma }_{i}}$ ограничений обсуждалась в работах [2, 3]. С помощью техники линейных матричных неравенств и неущербности S-процедуры для квадратичных неравенств были сформулированы условия на множество начальных состояний, стартуя из которых фазовые траектории системы (1.1), замкнутой управлением (1.3), асимптотически приближались к нулевому состоянию и не выходили за границы множества, задаваемого ограничениями (1.4). Для решения задачи синтеза управления в [3] проводится анализ линейной системы с фазовым ограничением. Рассматривается асимптотически устойчивая линейная система где матрица A – гурвицева, т.е. все собственные значения этой матрицы имеют строго отрицательные действительные части. Ставится задача поиска множества начальных состояний $x(0)$ = x₀, из которых стартует фазовая траектория, не выходя за пределы множества, задаваемого ограничением при $\gamma > 0$.

Заметим, что если функция $V = {{x}^{{\text{T}}}}{{Y}^{{ - 1}}}x$ с матрицей $Y = {{Y}^{{\text{T}}}} > 0$ является квадратичной функцией Ляпунова системы (1.5), тогда все траектории этой системы, выходящие из множества $E(Y) = \{ x:{{x}^{{\text{T}}}}{{Y}^{{ - 1}}}x \leqslant 1\} $, ограниченного эллипсоидом ${{x}^{{\text{T}}}}{{Y}^{{ - 1}}}x \leqslant 1$, вписанным в область фазового пространства, которая задана неравенством $\left| z \right| \leqslant \gamma $, удовлетворяют ограничению (1.6). В работе показано, что область фазового пространства, определяемая объединением всех таких множеств E(Y) при всевозможных функциях Ляпунова указанного вида, можно характеризовать в терминах линейных матричных неравенств. Справедлива следующая теорема.

Теорема 1. Если матрица $Y = {{Y}^{{\text{T}}}} > 0$ удовлетворяет системе линейных матричных неравенств

тогда все траектории системы (1.5) с начальными условиями $x(0) \in E(Y)$ удовлетворяют ограничениям (1.6).

Заметим, что матриц Y, удовлетворяющих системе матричных неравенств (1.7), очень много. Это в свою очередь означает, что “много” множеств начальных состояний, определяемых соответствующими эллипсоидами. Поэтому возникает желание найти множество, которое является “максимальным” в соответствии с некоторым критерием. В частности, в качестве критериев для поиска множества, обладающего в некотором смысле “максимальными” размерами, могут выступать максимизация следа матрицы Y  при ограничениях, задаваемых линейными матричными неравенствами (1.7), или максимизация объема соответствующего эллипсоида.

В случае анализа асимптотически устойчивой линейной системы с несколькими ограничениями определим множество начальных состояний “наибольшего” размера как множество, полученное пересечением эллипсоидов с “максимальными” размерами, отвечающих каждому из этих ограничений.

Ключевым моментом при решении задачи стабилизации объекта (1.1) в классе линейных обратных связей по состоянию (1.3) при ограничениях (1.4) является выбор единой квадратичной функции Ляпунова замкнутой системы с учетом ограничений и применение неущербности S-процедуры при одном ограничении [7]. Это позволяет представить достаточные условия для поиска матрицы параметров регулятора (1.3) в терминах линейных матричных неравенств. Использование S-процедуры при одном ограничении – это прием, который позволяет заменить два неравенства для квадратичных форм эквивалентным им единственным неравенством. Он состоит в следующем. Рассмотрим неравенство

для всех $x \in {{R}^{n}}$, удовлетворяющих неравенству где $F(x)$ и $G(x)$ – квадратичные формы. Тогда можно составить квадратичную форму и рассмотреть неравенство при некотором $\lambda \geqslant 0$. Эквивалентная замена неравенств (1.8) и (1.9) неравенством (1.10) называется S-процедурой.

Очевидно, что из выполнения (1.10) следует выполнение (1.8) при условии (1.9). Но верно и обратное утверждение. При условии, что существует ${{x}_{0}}$, для которого $G({{x}_{0}}) < 0$, выполнение неравенства (1.8) при условии (1.9) влечет существование $\lambda > 0$, при котором верно неравенство

В этом случае говорят, что S-процедура неущербна для одного ограничения. Данный прием в работах [2, 3] авторы применяют для каждого индекса i, что позволяет свести процесс нахождения единой функции Ляпунова замкнутой системы к решению системы линейных матричных неравенств.

Если функция $V = {{x}^{{\text{T}}}}{{Y}^{{ - 1}}}x$ с матрицей $Y = {{Y}^{{\text{T}}}} > 0$ является единой квадратичной функцией Ляпунова системы (1.1), замкнутой управлением (1.3), тогда все траектории этой системы, выходящие из множества $E(Y) = \{ x:{{x}^{{\text{T}}}}{{Y}^{{ - 1}}}x \leqslant 1\} $, ограниченного эллипсоидом ${{x}^{{\text{T}}}}{{Y}^{{ - 1}}}x \leqslant 1$, вписанным в область фазового пространства, которая задана неравенствами $\left| {{{z}_{i}}} \right| \leqslant {{\gamma }_{i}}$, $i = \overline {1,N} $, удовлетворяют ограничениям (1.4). Можно показать [2, 3], что в этом случае справедлива следующая теорема.

Теорема 2. Если матрицы $Y = {{Y}^{{\text{T}}}} > 0$, Z и величины ${{\gamma }_{i}} > 0$, $i = \overline {1,N} $, удовлетворяют системе линейных матричных неравенств

тогда все траектории системы (1.1), замкнутой управлением (1.3) с начальными условиями $x(0) \in E(Y)$, удовлетворяют ограничениям (1.4). Матрица параметров закона управления (1.3) для динамической системы с ограничениями вычисляется как

Заметим, что если матрица параметров закона управления (1.12) найдена, то для всех начальных состояний $x(0) \in \bigcap\limits_{i = 1}^N {E({{Y}_{i}})} $ фазовые траектории системы (1.1), замкнутой управлением (1.3), будут асимптотически приближаться к нулевому состоянию и не выходить за границы множества, задаваемого ограничениями (1.4). Здесь множества $E({{Y}_{i}}) = \{ x:{{x}^{{\text{T}}}}{{Y}_{i}}^{{ - 1}}x \leqslant 1\} $ получены как множества начальных состояний $x(0) = {{x}_{0}}$ для асимптотически устойчивой линейной системы, при которых фазовая траектория не выйдет за пределы множества, задаваемого ограничением $\mathop {\max }\limits_{t \geqslant 0} \left| {{{z}_{i}}(t)} \right| \leqslant {{\gamma }_{i}}$. При этом желательно выбирать множества $E({{Y}_{i}})$, обладающие в некотором смысле “максимальными” размерами (например, в смысле максимизации следа матрицы Y или максимизации объема соответствующего эллипсоида).

Как отмечалось выше, ключевым моментом при решении задачи стабилизации объекта (1.1) в классе линейных обратных связей по состоянию (1.3) при ограничениях (1.4) является выбор единой квадратичной функции Ляпунова замкнутой системы с учетом ограничений. Это связано с тем, что в противном случае, выбирая свою функцию Ляпунова для каждого ограничения $\mathop {\max }\limits_{t \geqslant 0} \left| {{{z}_{i}}(t)} \right| \leqslant {{\gamma }_{i}}$, приходим к системе билинейных матричных неравенств

где I – единичная матрица соответствующего размера, относительно неизвестных матриц X_i = = ${{X}_{i}}^{{\text{T}}} > 0$, $i = \overline {1,N} $, и K, для которых задача поиска решений существенно усложняется.

Заметим, что полученный в работах [2, 3] результат не позволяет указать “полное” множество начальных состояний, фазовые траектории из которых не нарушают ограничений. В качестве примера рассмотрим управляемый перевернутый маятник

при ограничениях на $\varphi $ – угол отклонения звена маятника от вертикали и управление $u$

Представим уравнение и ограничения в виде (1.1), (1.2), где

Для объекта (1.13) найдено управление

которое обеспечивает асимптотическую устойчивость замкнутой системы (1.13), (1.15) и выполнение ограничений (1.14). Управление (1.15) получено в результате поиска матрицы Y, имеющей максимальный след и удовлетворяющей системе линейных матричных неравенств (1.11).

На рис. 1 и 2 в фазовой плоскости пунктиром отмечены ограничения

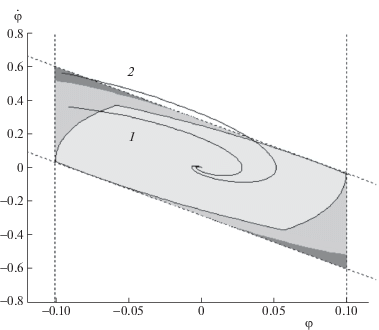
На рис. 1 эллипс 1 ограничивает оценку множества начальных состояний, при выборе которых управление (1.15) обеспечивает стабилизацию перевернутого маятника при первом ограничении, т.е. на угол отклонения маятника φ. Эллипс 2 ограничивает оценку множества начальных состояний, при выборе которых управление обеспечивает стабилизацию при втором ограничении, т.е. при ограничении на управление. В пересечении эллипсов получим оценку области допустимых начальных состояний, для которых управление стабилизирует объект при двух ограничениях. На рис. 1 и 2 данная область отмечена светло-серым цветом. Можно построить и проанализировать фазовый портрет замкнутой системы. На рис. 2 серым цветом отмечено множество  допустимых  начальных  состояний,  стартуя  из  которых фазовые траектории системы (1.13), замкнутой  управлением (1.15), асимптотически приближаются к нулевому состоянию и не выходят за границы множества, задаваемого ограничениями (1.14). В качестве примера приведена траектория 1 для начального состояния $\varphi = - 0.09$, $\dot {\varphi } = 0.36$. Темным цветом на рис. 2 отмечено множество начальных состояний, при выборе которых фазовые траектории системы выйдут за границы области (1.16). В качестве примера приведена траектория 2 для начального состояния $\varphi = - 0.095$, $\dot {\varphi } = 0.56$.

2. Постановка задачи. Предположим, что для объекта (1.1), (1.2) решена задача стабилизации с ограничениями на фазовые и управляющие переменные и найден закон управления $u = Kx$. В реальной ситуации состояние динамической системы всегда измеряется с некоторой ошибкой. В этой связи введем переменную

измеряемый выход системы, где I – единичная матрица размера $n \times n$, а матрица $\Delta (t)$ определяет относительные ошибки измерения фазовых переменных и в любой момент времени удовлетворяет матричному неравенству ($\delta \ne 0$ – заданный параметр), представляющему ограничения на допустимые значения ошибок измерения. Рассмотрим задачу стабилизации системы (1.1), (1.2) регулятором при ограничениях на фазовые и управляющие переменные (1.4). Возникает следующий вопрос: как скажутся ошибки измерения фазовых переменных на выполнении ограничений (1.4)? Другими словами, как изменится множество начальных состояний системы, для которых регулятор (2.2) обеспечивает стабилизацию при ограничениях (1.4) и в случае наличия ошибки в измеряемом выходе (2.1)?

3. Оценка области допустимых начальных состояний в случае наличия ошибки в измеряемом состоянии. Рассмотрим ситуацию, когда состояние системы (1.1) измеряется с ошибкой. Представим измеряемый выход системы (2.1) в виде

где $w = \Delta (t)x$. Так как матрица неопределенности $\Delta (t)$ удовлетворяет условию ${{\Delta }^{{\text{T}}}}\Delta \leqslant {{\delta }^{2}}I$, то

Обозначив $\bar {A} = A + BK$, $\bar {B} = BK$, ${{\bar {C}}_{i}} = {{C}_{i}} + {{D}_{i}}K$, ${{\bar {D}}_{i}} = {{D}_{i}}K$, запишем замкнутую систему (1.1), (1.2), (2.2), (3.1) в виде

Сформулируем достаточные условия для поиска области допустимых начальных состояний динамической системы, при которых управление (2.2) с матрицей параметров регулятора $K$, полученной в задаче синтеза управления при ограничениях на фазовые и управляющие переменные без учета ошибки в измеряемом выходе, будет обеспечивать стабилизацию и в случае наличия ошибки в измеряемом выходе.

Рассмотрим вспомогательную задачу. Пусть требуется найти множество допустимых начальных состояний, при которых полученный регулятор (2.2) обеспечивает для каждого индекса i стабилизацию системы (3.3) при одном ограничении $\mathop {\max }\limits_{t \geqslant 0} \left| {{{z}_{i}}(t)} \right| \leqslant {{\gamma }_{i}}$. Справедлива следующая теорема.

Теорема 3. Пусть матрица ${{X}_{i}} = X_{i}^{{\text{T}}} > 0$ и величины ${{\mu }_{1}} > 0$, ${{\mu }_{2}} > 0$, $\delta > 0$, ${{\gamma }_{i}} > 0$ удовлетворяют системе матричных неравенств

Тогда все траектории замкнутой системы (3.3) с начальными условиями $x(0) \in E({{X}_{i}})$, E(X_i) = = $\{ x:{{x}^{{\text{T}}}}{{X}_{i}}x \leqslant 1\} $ удовлетворяют ограничению $\mathop {\max }\limits_{t \geqslant 0} \left| {{{z}_{i}}(t)} \right| \leqslant {{\gamma }_{i}}$.

Доказательство. В область фазового пространства, заданную неравенством $\left| {{{z}_{i}}} \right| \leqslant {{\gamma }_{i}}$, впишем эллипсоид ${{x}^{{\text{T}}}}{{X}_{i}}x = 1$. Покажем, что выполнение первого неравенства системы (3.5) обеспечивает выполнение условия, что квадратичная функция $V = {{x}^{{\text{T}}}}{{X}_{i}}x$ с матрицей ${{X}_{i}} = {{X}_{i}}^{{\text{T}}} > 0$ является функцией Ляпунова для замкнутой системы. На любой траектории замкнутой системы (3.3) верно условие

Согласно неущербности S-процедуры при одном ограничении, неравенство (3.6) выполнено для всех x, w, таких, что ${{\left| x \right|}^{2}} + {{\left| w \right|}^{2}} \ne 0$, удовлетворяющих неравенству (3.2), тогда и только тогда, когда для некоторого числа ${{\mu }_{1}} > 0$ и для всех x, w выполнено неравенство

Запишем его в виде

Это неравенство эквивалентно первому неравенству системы (3.5).

Покажем, что любое решение второго неравенства системы (3.5) обеспечивает выполнение условия $\left| {{{z}_{i}}(t)} \right| \leqslant {{\gamma }_{i}}$. Для квадратичных форм справедлива S-процедура при двух ограничениях [6]. Теорема утверждает следующее. Пусть даны квадратичные формы $F(x) = {{x}^{{\text{T}}}}{{A}_{0}}x$, ${{G}_{1}}(x) = {{x}^{{\text{T}}}}{{A}_{1}}x$, ${{G}_{2}}(x) = {{x}^{{\text{T}}}}{{A}_{2}}x$, где $x \in {{R}^{n}}$, ${{A}_{i}} = {{A}_{i}}^{{\text{T}}} \in {{R}^{{n \times n}}}$, $i = 0,1,2$, и числа a₀, a₁, a₂. Составим квадратичную форму $S(x) = F(x) - {{\tau }_{1}}{{G}_{1}}(x) - {{\tau }_{2}}{{G}_{2}}(x)$ и рассмотрим систему неравенств

при некоторых ${{\tau }_{1}} \geqslant 0$, ${{\tau }_{2}} \geqslant 0$. Рассмотрим неравенство которое для всех $x \in {{R}^{n}}$ удовлетворяет системе неравенств

Тогда из неравенств (3.7) следует неравенство (3.8) при условии (3.9).

Обратно, в случае если $n \geqslant 3$, существуют числа ${{\tau }_{3}}$, ${{\tau }_{4}}$ и вектор ${{x}_{*}} \in {{R}^{n}}$, такие, что

то выполнение неравенства (3.8) при условии (3.9) влечет существование чисел ${{\tau }_{1}} \geqslant 0$, ${{\tau }_{2}} \geqslant 0$, при которых верно условие (3.7).

Применим этот результат для решения задачи. Согласно неущербности S-процедуры, при двух ограничениях выполнение неравенства $\mathop {\max }\limits_{t \geqslant 0} \left| {{{z}_{i}}(t)} \right| \leqslant {{\gamma }_{i}}$ при условии (3.2) и условии ${{x}^{{\text{T}}}}{{X}_{i}}x \leqslant 1$ для всех x, w, таких, что ${{\left| x \right|}^{2}} + {{\left| w \right|}^{2}} \ne 0$, эквивалентно существованию чисел ${{\mu }_{2}} \geqslant 0$, ${{\mu }_{3}} \geqslant 0$, при которых верно неравенство

При этом должны существовать числа ${{\mu }_{4}}$, ${{\mu }_{5}}$ и вектор ${{(\begin{array}{*{20}{c}} {x_{*}^{{\text{T}}}}&{w_{*}^{{\text{T}}}} \end{array})}^{{\text{T}}}}$, такие, что

и

Запишем неравенство (3.10) в виде

Неравенство (3.13) верно для всех x, w. Значит,

Следовательно,

Запишем неравенство (3.14) в виде

Матричное неравенство (3.15) эквивалентно второму матричному неравенству в системе (3.5).

Найдем числа μ₄, μ₅, удовлетворяющие неравенству (3.11). Перепишем условие (3.11) в виде ${{\mu }_{5}}$ > 0, ${{\mu }_{4}}{{X}_{i}} - {{\mu }_{5}}{{\delta }^{2}}I > 0$. Следовательно, с учетом ${{X}_{i}} = {{X}_{i}}^{{\text{T}}} > 0$ для выполнения этих неравенств достаточно выбрать ${{\mu }_{4}} = {{2{{\delta }^{2}}} \mathord{\left/ {\vphantom {{2{{\delta }^{2}}} {{{\lambda }_{{\min }}}({{X}_{i}})}}} \right. \kern-0em} {{{\lambda }_{{\min }}}({{X}_{i}})}}$, где в знаменателе фигурирует минимальное собственное число матрицы; μ₅ = 1.

Найдем вектор ${{(\begin{array}{*{20}{c}} {x_{*}^{{\text{T}}}}&{w_{*}^{{\text{T}}}} \end{array})}^{{\text{T}}}}$, удовлетворяющий неравенствам (3.12). Так как $V = {{x}^{{\text{T}}}}(t){{X}_{i}}x(t)$ – квадратичная функция Ляпунова, то для всех $x \in E({{X}_{i}})$ выполнено неравенство ${{x}^{{\text{T}}}}(t){{X}_{i}}x(t) \leqslant 1$. Следовательно, первое неравенство (3.12) верно, если точка ${{x}_{*}}$ лежит внутри эллипсоида $E({{X}_{i}})$. В силу неравенства (3.2) для выполнения второго неравенства (3.12) выберем ${{w}_{*}} = {{\delta {{x}_{*}}} \mathord{\left/ {\vphantom {{\delta {{x}_{*}}} 2}} \right. \kern-0em} 2}$. Теорема 3 доказана.

Обозначим через X_i множество всех матриц X_i, удовлетворяющих неравенствам (3.5). Максимальную по всем ${{X}_{i}} \in {{{\rm X}}_{i}}$ область $E(X_{i}^{*})$ найдем путем минимизации следа матрицы X_i. Эта операция является стандартной в пакете программ для инженерных расчетов Matlab [8] с использованием приложения CVX. Заметим, что не удается получить в терминах линейных матричных неравенств условия для построения множеств $E({{Y}_{i}}) = \{ x:{{x}^{{\text{T}}}}{{Y}_{i}}^{{ - 1}}x \leqslant 1\} $, $i = \overline {1,N} $, что позволило бы максимизировать объемы соответствующих эллипсоидов.

Пусть каждая из матриц X_i, $i = \overline {1,N} $, имеет минимальный след и является решением системы (3.5) для значения ${{\gamma }_{i}}$. Тогда все траектории замкнутой системы (3.3) с начальными условиями $x(0) \in E({{X}_{i}})$, $E({{X}_{i}}) = \{ x:{{x}^{{\text{T}}}}{{X}_{i}}x \leqslant 1\} $ будут удовлетворять ограничению $\mathop {\max }\limits_{t \geqslant 0} \left| {{{z}_{i}}(t)} \right| \leqslant {{\gamma }_{i}}$. Следовательно, для всех начальных состояний $x(0) \in \bigcap\limits_{i = 1}^N {E({{X}_{i}})} $, управление с заданной матрицей параметров регулятора K стабилизирует замкнутую систему при ограничениях (1.4).

4. Стабилизация перевернутого маятника. В качестве примера рассмотрим управляемый перевернутый маятник

при ограничениях на φ – угол отклонения звена маятника от вертикали и управление $u$

Численное решение получено в пакете Matlab. Для объекта (4.1) решен ряд задач. Как было указано выше, в случае решения задачи стабилизации при отсутствии ошибки в измеряемом выходе найдено управление

которое обеспечивает асимптотическую устойчивость замкнутой системы (4.1), (4.3) и выполнение ограничений на фазовую переменную и управление (4.2). Управление (4.3) получено в результате поиска матрицы Y, имеющей максимальный след и удовлетворяющей системе линейных матричных неравенств (1.11).

На рис. 3 в фазовой плоскости пунктиром отмечены ограничения

Оценим изменение оценки области допустимых начальных состояний динамической системы, при которых управление (4.3) будет обеспечивать стабилизацию и в случае наличия ошибки в измеряемом выходе. Обозначим через ${{\Sigma }_{\delta }}$ оценку множества допустимых начальных состояний, для которых управление стабилизирует систему при значении $\delta $. На рис. 3 приведены области ${{\Sigma }_{0}}$, ${{\Sigma }_{{0.05}}}$, ${{\Sigma }_{{0.1}}}$, ${{\Sigma }_{{0.2}}}$, соответствующие значениям δ = 0, $\delta = 0.05$, $\delta = 0.1$, $\delta = 0.2$, и показано пересечение этих областей. Из рисунка следует, что область ${{\Sigma }_{{0.2}}}$ лежит внутри области ${{\Sigma }_{{0.1}}}$, которая в свою очередь лежит внутри области ${{\Sigma }_{{0.05}}}$, а область ${{\Sigma }_{{0.05}}}$ лежит внутри ${{\Sigma }_{0}}$.

Проведенные вычисления показывают, что эллипсы, отвечающие за ограничения на угол отклонения звена маятника при значениях δ = 0, $\delta = 0.05$, $\delta = 0.1$ и $\delta = 0.2$, близки друг к другу. Таким образом, на размер области ${{\Sigma }_{\delta }}$ допустимых начальных состояний оказывает влияние как значение величины параметра $\delta $, так и наличие в задаче ограничения на управление.

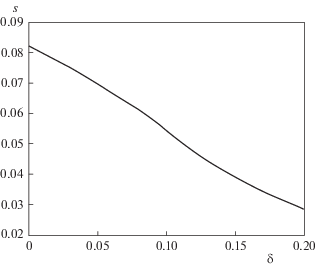
Вычислим зависимость площади $S$ области ${{\Sigma }_{\delta }}$ от величины $\delta $, которая определяет величину ошибки в изменяемом выходе. На рис. 4 представлен график этой зависимости. В частности, получены значения $S(0) = 0.0819$, $S(0.05) = 0.0696$, $S(0.1) = 0.0541$, $S(0.2) = 0.0285$. Таким образом, при относительно небольших значениях $\delta $ размеры области допустимых начальных состояний могут существенно уменьшиться.

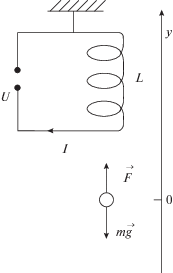
5. Стабилизация тела в электромагнитном подвесе. Уравнения движения тела в электромагнитном подвесе одностороннего действия, изображенном на рис. 5, имеют вид

где $m$ – масса вывешенного тела, $y$ – координата вывешенного тела, $g$ – ускорение свободного падения, $\psi $ – потокосцепление обмотки электромагнита, I – сила тока в электромагните, $R$ – сопротивление в цепи электромагнита, $U$ – напряжение, подаваемое на электромагнит.

Первое уравнение системы (5.1) описывает второй закон Ньютона для вывешенного тела. Второе уравнение следует из закона Кирхгофа для электрической цепи электромагнита. Известно [9], что величина потокосцепления $\psi $ связана с током $I$ и величиной индуктивности электромагнита $L(y)$ выражением $\psi = L(y)I$, где $L(y) = {{{{C}_{L}}} \mathord{\left/ {\vphantom {{{{C}_{L}}} {(\delta - y)}}} \right. \kern-0em} {(\delta - y)}}$. Здесь ${{C}_{L}}$ – конструктивный параметр, $\delta $ – величина номинального зазора между электромагнитом и вывешенным телом. Также известно, что выражение для силы $F(y,I)$, действующей на тело, можно представить в виде F(y, I) = = ${{\partial W} \mathord{\left/ {\vphantom {{\partial W} {\partial y}}} \right. \kern-0em} {\partial y}}$, где коэнергия системы

Перепишем уравнения (5.1) в виде

Состояние равновесия системы (5.2) определяется равенствами y = 0, $\dot {y} = 0$, $I = {{I}_{C}}$, где I_C = = $\sqrt {{{2{{\delta }^{2}}mg} \mathord{\left/ {\vphantom {{2{{\delta }^{2}}mg} {{{C}_{L}}}}} \right. \kern-0em} {{{C}_{L}}}}} $. Перейдем к безразмерным величинам. Введем новое безразмерное время $t\, = \,\sqrt {{{2g} \mathord{\left/ {\vphantom {{2g} \delta }} \right. \kern-0em} \delta }} t{\kern 1pt} '$ и, обозначив

запишем систему (5.2) в виде где

Линеаризуем систему в окрестности состояния равновесия. Получим

где

Численное решение получено в пакете Matlab. Пусть значение параметра системы α = 7.5. Для объекта (5.4) решен ряд задач. В случае отсутствия ошибки в измеряемом выходе системы найдено управление

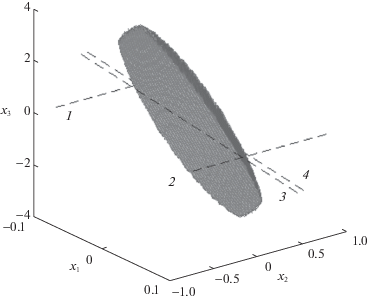
которое обеспечивает асимптотическую устойчивость замкнутой системы (5.4), (5.5) и выполнение ограничений где ${{x}_{1}}$ – величина, пропорциональная смещению тела. Управление (5.5) получено в результате поиска матрицы Y, имеющей максимальный след и удовлетворяющей системе линейных матричных неравенств (1.11).

Оценим область допустимых начальных состояний динамической системы, при которых управление (5.5) будет обеспечивать стабилизацию и в случае наличия ошибки в измеряемом выходе. Решение системы линейных матричных неравенств (3.5) при заданном параметре $\delta $ будут определять два множества допустимых начальных состояний $E({{X}_{1}})\, = \,\{ x\,:\,{{x}^{{\text{T}}}}{{X}_{1}}x\, \leqslant \,1\} $, E(X₂) = $\{ x\,:\,{{x}^{{\text{T}}}}{{X}_{2}}x\, \leqslant \,1\} $ для первого и второго ограничений (5.6) соответственно. На рис. 6 представлено множество, полученное пересечением эллипсоидов $E({{X}_{1}})$ и $E({{X}_{2}})$ при значении параметра δ = 0. Пунктирными линиями 1 и 2 изображены при ${{x}_{3}} = 0$ прямые ${{x}_{1}} = - 0.1$ и ${{x}_{1}} = 0.1$ соответственно. Пунктирные линии 3 и 4 соответствуют при ${{x}_{3}} = 0$ прямым $u = - 1$ и u = 1.

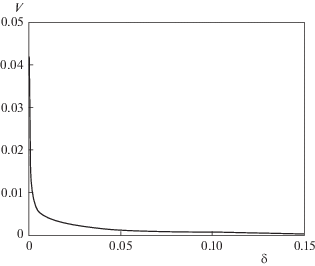
Впишем в множество $E({{X}_{1}}) \cap E({{X}_{2}})$ эллипсоид, имеющий наибольший объем. На рис. 7 представлен график зависимости объема $V$ данного эллипсоида от величины $\delta $. В частности, получены значения $V(0) = 0.0481$, $V(0.05) = 0.0014$, $V(0.1) = 0.0008$, $V(0.15) = 0.0003$. Проведенные исследования показывают, что на размеры области $E({{X}_{1}}) \cap E({{X}_{2}})$ наибольшее влияние оказывает наличие в задаче ограничения на управления. Так, при изменении значения параметра $\delta $ от 0 до 0.1 объем эллипсоида $E({{X}_{1}})$ меняется от 0.4678 до 0.1303. В то же время объем эллипсоида $E({{X}_{2}})$ меняется от 0.1161 до 0.0008. Таким образом, при относительно небольших значениях $\delta $ размеры области допустимых начальных состояний существенно уменьшаются.

Заключение. Поставлена и решена задача по оценке области допустимых начальных состояний линейной динамической системы, при которых регулятор, полученный в задаче синтеза управления по состоянию при ограничениях на фазовые и управляющие переменные, будет обеспечивать стабилизацию и в случае, когда измерение состояния системы производится с ошибкой. В терминах линейных матричных неравенств сформулированы условия, позволяющие оценить множество допустимых начальных состояний динамической системы. В качестве примеров рассмотрены задачи стабилизации перевернутого маятника и движения тела в электромагнитном подвесе. Численные эксперименты подтверждают теоретические результаты.

Заметим, что при решении практических задач управления реальными физическими объектами полная информация о состоянии системы обычно недоступна измерению. В связи с этим возникает нетривиальная задача стабилизации динамических объектов по измеряемому выходу системы. В дальнейшем планируется рассмотреть ситуацию, когда измеряется часть фазовых переменных или их линейная комбинация. Предполагается решить задачу стабилизации с помощью статического регулятора при ограничениях на фазовые и управляющие переменные, а также оценить область допустимых начальных состояний для полученного регулятора при наличии ошибки в измерениях выходных переменных.