Известия РАН. Теория и системы управления, 2021, № 5, стр. 91-104
ВЕТРОТУРБИНА ТИПА ДАРЬЕ–МАГНУСА: ДИНАМИКА И УПРАВЛЕНИЕ
Л. А. Климина *
НИИ механики МГУ
Москва, Россия
* E-mail: klimina@imec.msu.ru
Поступила в редакцию 01.03.2021
После доработки 27.03.2021
Принята к публикации 31.05.2021
Аннотация
При вращении ротора Дарье формируется сила, родственная силе Магнуса: перпендикулярная скорости набегающего потока. В работе она вычисляется на основе квазистатической модели аэродинамического воздействия и сравнивается с аналогичной силой, действующей на ротор Савониуса. Эта сила позволяет использовать ротор Дарье как элемент ветроэнергетической установки, работающей на основе эффекта Магнуса. Математическая модель такой ветротурбины с горизонтальным валом и двумя вращающимися лопастями в форме роторов Дарье представлена в форме динамической системы пятого порядка. В качестве коэффициента усиления управляющего воздействия в модели выступает параметр, который характеризует полезную внешнюю электрическую нагрузку в локальной цепи электрогенератора установки. В результате проведенного анализа установлено, что ветротурбина может обладать, как минимум, тремя типами рабочих режимов. Из них два характеризуются синхронизацией средних угловых скоростей роторов Дарье, в общем случае средняя скорость вращения центрального вала с ними несоизмерима. На третьем типе режимов скорости собственного вращения роторов Дарье несоизмеримы. Решена задача выбора управления, которое обеспечивает максимальную величину механической мощности на рабочем режиме ветротурбины.
Введение. Классический пример силы Магнуса: перпендикулярная скорости потока сила, действующая на сферическую или цилиндрическую поверхность, вращающуюся в потоке [1, 2]. Боковая сила, родственная силе Магнуса, формируется при авторотации некоторых ветротурбин, например ротора Савониуса, что было отмечено на заре конструирования подобных роторов и послужило поводом для расширения вариантов их применения в ветроэнергетических системах. Так, турбины, при авторотации которых формируется сила Магнуса, могут использоваться вместо цилиндров или наряду с ними в качестве роторных парусов, подобных парусу Флеттнера, для создания подъемной силы парящих объектов и летательных аппаратов [3–8], а также в качестве лопастей ветротурбин, работающих на основе эффекта Магнуса [9–14].
Подобного рода боковая сила присутствует и при авторотации в потоке так называемой ветротурбины Дарье. Однако этот эффект слабо отражен в литературе, например [8]. В отличие от случая ротора Савониуса, силы, действующие на ротор Дарье, могут быть оценены на основе применения гипотезы квазистатического обтекания для каждой из лопастей ротора. В работе получены соответствующие функции от угла поворота и угловой скорости ротора, построены числовые оценки для случая трехлопастной турбины с лопастями профиля RAF34.
Представляется актуальным проанализировать возможность использования турбин Дарье в качестве авторотирующих лопастей горизонтально-осевой ветроустановки, подобно тому, как в этом качестве применяются роторы Савониуса [9–13]. Необходимо отметить радикальное отличие использования ротора Дарье для формирования силы Магнуса от случая, когда в качестве лопастей турбины Дарье выступают цилиндры, формирующие силу Магнуса [14].
В работе построена математическая модель двухлопастной горизонтально-осевой ветроэнергетической установки, каждая лопасть которой представляет собой авторотирующую турбину Дарье, формирующую силу Магнуса. Назовем такое устройство ветротурбиной типа Дарье–Магнуса. Уравнения движения турбины представлены в форме автономной динамической системы пятого порядка. Варьируемый параметр модели, который характеризует полезную внешнюю электрическую нагрузку, рассматривается как коэффициент усиления управляющего воздействия (подобно работам [12, 15]). Определяется значение этого параметра, оптимальное с позиций максимизации средней механической мощности на рабочем режиме. При этом рабочему режиму может соответствовать достаточно нетривиальная траектория динамической системы пятого порядка, на которой угловые переменные монотонно растут, а угловые скорости остаются близки к постоянным значениям и не синхронизируются друг с другом или синхронизируются частично. Анализ таких режимов, не предполагающих полной синхронизации угловых скоростей элементов, проводится на основе методов [16, 17]. Подробный обзор альтернативных методов, которые могут быть применены для решения родственных задач, приведен в [18]. Краткий обзор дан, например, в [19], где при помощи модификации метода [17] описаны рабочие режимы ветротурбины с двумя противовращающимися роторами Савониуса.
Для ветроустановки типа Дарье–Магнуса являются естественными режимы, на которых происходит частичная синхронизация угловых скоростей: средние угловые скорости роторов Дарье – лопастей основной турбины – совпадают друг с другом, а средняя угловая скорость центрального вала не синхронизирована с ними. Таким образом, в соответствующей динамической системе возможен эффект частичной синхронизации, характерный для так называемых химерных состояний [20].
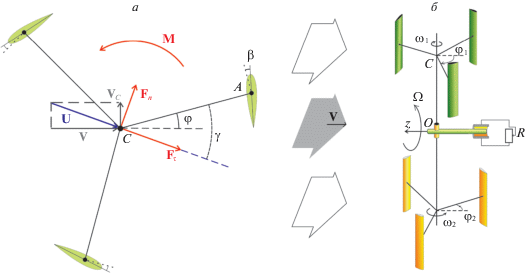
1. Описание системы и постановка задачи. Рассмотрим ротор Дарье с n-лопастями: сначала как самостоятельный объект, затем как составной элемент более сложной ветротурбины (рис. 1). Через геометрический центр C ротора проходит ось собственного вращения. Каждая лопасть ротора представляет собой крыло постоянного профиля, хорда которого составляет угол $\left( {\pi {\text{/}}2 + \beta } \right)$ с державкой AC, соединяющей лопасть с осью собственного вращения (рис. 1,a). Длина каждой державки равна r, характерная площадь каждой лопасти – S. Все лопасти профилированы одинаково. При численных расчетах будем использовать аэродинамические характеристики профиля RAF34 [21] и положим n = 3. Центр масс ротора расположен в геометрическом центре C конструкции. Масса ротора равна m, момент инерции относительно оси собственного вращения равен ${{J}_{C}}$. Другие два главных центральных момента инерции ротора считаем одинаковыми и обозначим ${{J}_{r}}$.
Рассмотрим ветротурбину с горизонтальным центральным валом Oz, с двумя радиальными лопастями, каждая из которых представляет собой ротор Дарье, закрепленный к центральному валу цилиндрическим шарниром (рис. 1,б). Ось собственного вращения ротора Дарье ортогональна неподвижной оси Oz; l – расстояние от оси Oz до центра C ротора. На горизонтальном валу турбины закреплен ротор электрогенератора. Момент инерции вала вместе с ротором генератора обозначим ${{J}_{O}}$. Генератор подключен к локальной электрической цепи с внешним сопротивлением R. Величину R можно рассматривать в качестве управления: варьировать ее с целью максимизации мощности, отбираемой турбиной у потока (аналогично работам [12, 15]). Ветротурбина расположена в стационарном потоке воздуха скорости V, плотности $\rho $, вектор V параллелен оси Oz.
Момент инерции J всей конструкции относительно оси Oz равен
Система имеет три степени свободы. Углы собственного вращения роторов Дарье обозначим ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$, угол поворота центрального вала всей конструкции является циклической координатой.
Подобная ветротурбина, но с тремя лопастями в форме роторов Савониуса рассмотрена в [11]. Вращение центрального вала должно поддерживаться боковыми силами, действующими на лопасти-роторы при их авторотации в потоке.
Задача данной работы состоит в том, чтобы оценить боковую силу и силу лобового сопротивления, действующие на ротор Дарье; с учетом этих сил построить математическую модель движения комбинированной ветротурбины; описать рабочие режимы устройства; построить управление внешним сопротивлением, обеспечивающее наличие установившегося рабочего режима, который характеризуется высоким значением механической мощности.
2. Силы, действующие на ротор Дарье при авторотации. Для определения боковой силы и силы сопротивления, действующих на ротор Дарье, воспользуемся квазистатической моделью (аналогично [22–27]). Рассмотрим отдельный ротор Дарье, совершающий вращение вокруг своей центральной оси С. Пусть ротор расположен в однородном потоке воздуха, скорость U которого ортогональна оси вращения ротора. Отличие между векторами U и V будет объяснено далее; оно вызвано тем, что ротор Дарье как элемент горизонтально-осевой турбины совершает более сложное движение в потоке.
Опишем воздействие потока на лопасть ротора Дарье. Пренебрегаем возможным перемещением центра давления (точки приложения аэродинамических сил) относительно лопасти. Считаем, что он всегда совпадает с точкой A, в которой конец державки закреплен к хорде лопасти. Воздушная скорость центра давления A представляет собой скорость точки А относительно системы отсчета, движущейся поступательно со скоростью U. Мгновенный угол атаки – угол между воздушной скоростью центра давления и хордой профиля – обозначим ${{\alpha }_{s}}$ для s-й из трех лопастей ротора ($s = 1,2,3$). Обозначим через $\gamma $ угол между одной из державок ротора и вектором U, тогда углы ${{\alpha }_{s}}$ вычисляются по формулам
Здесь $\lambda = {{U}^{{ - 1}}}r\dot {\gamma }$ – быстроходность ротора.
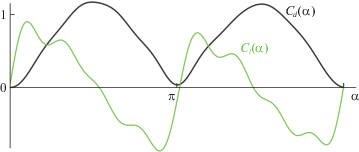
Аэродинамический профиль лопасти ротора Дарье характеризуется коэффициентами ${{C}_{d}}({{\alpha }_{s}})$ и ${{C}_{l}}({{\alpha }_{s}})$ силы сопротивления и подъемной (боковой) силы соответственно. При численных расчетах воспользуемся аппроксимациями (рис. 2) этих функций, которые соответствуют профилю RAF34 (экспериментальные данные взяты из [21]), и положим $\beta = 0.12$ (установочный угол лопастей). Сила ${{{\mathbf{F}}}_{d}}$ сопротивления и боковая (подъемная) сила ${{{\mathbf{F}}}_{l}}$, действующие на одну лопасть, направлены соответственно противоположно вектору воздушной скорости точки A и ортогонально ему. Их величины вычисляются по формулам
Силы, действующие на каждую из лопастей ротора, создают суммарный момент M относительно оси вращения С, а также формируют суммарную силу, приложенную в центре масс C ротора. Компоненты этой аэродинамической силы, направленные ортогонально скорости U потока и вдоль нее, обозначим ${{{\mathbf{F}}}_{n}}$ и ${{{\mathbf{F}}}_{\tau }}$ (рис. 1, а). Таким образом, ${{{\mathbf{F}}}_{n}}$ – аналог силы Магнуса, а ${{{\mathbf{F}}}_{\tau }}$ – сила лобового сопротивления ротора Дарье. Для суммарного момента и сил получаем
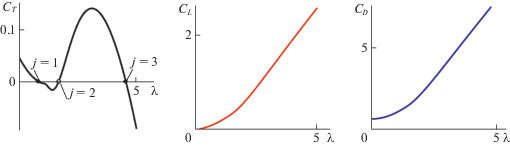
Здесь и далее CT, CL и CD – коэффициенты момента, боковой силы (аналог силы Магнуса) и силы лобового сопротивления, действующих на ротор Дарье (множитель 1.5 связан с тем, что ротор трехлопастной). Значения коэффициента CT обсуждаются в литературе весьма детально, поскольку именно информация о моменте требуется для оценки мощности, отбираемой у потока классическим ротором Дарье. Есть множество соответствующих работ, основанных на разнообразных моделях и на экспериментах по идентификации CT, например [4, 28–30]. Однако затруднительно найти в литературе какие-либо данные о силах ${{{\mathbf{F}}}_{n}}$ и ${{{\mathbf{F}}}_{\tau }}$, поскольку для классического ротора Дарье эти силы по существу не влияют на эффективность эксплуатации. В то же время эти силы можно использовать для обеспечения работы более сложных устройств, в конструкции которых задействован ротор Дарье. Вычислим средние за оборот значения коэффициентов CT, CL и CD в зависимости от быстроходности $\lambda $ ротора (рис. 3).
По сравнению с ротором Савониуса, например [31], более высокие значения боковой силы можно ожидать за счет большей скорости авторотации, но при этом и значения силы лобового сопротивления оказываются существенно выше. Интересно, что так же, как и в случае Савониуса, при нулевой угловой скорости ротора боковая сила принимает отрицательное значение (положительным выбрано направление, характерное для силы Магнуса). Вид функции осредненного CD качественно отличается: у ротора Савониуса аналогичная функция в широком диапазоне значений быстроходности близка к константе. С ростом $\lambda $ отношение средних значений CL к CD монотонно растет. Отметим, что выбор ненулевого установочного угла $\beta $ лопастей позволяет увеличить значения боковой силы.
3. Уравнения движения турбины с лопастями в форме роторов Дарье. Итак, получены выражения для аэродинамических сил, действующих на ротор Дарье в однородном потоке. При вращении комбинированной горизонтально-осевой турбины вокруг оси Oz поток, который приходит на лопасти роторов Дарье, строго говоря, не является однородным вдоль лопастей: воздушные скорости точек лопасти, расположенных ближе к Oz, меньше, чем у точек, более удаленных от Oz. Пренебрежем отличием между воздушными скоростями точек лопасти, считая, что расстояние OC значительно превосходит длину лопасти ротора Дарье и длину r державок, а также в свою очередь r существенно больше хорды профиля. Подобные предположения достаточно стандартны при применении квазистатической модели, например [22–25].
Для упрощения будем считать, что каждый ротор Дарье, выступающий в роли лопасти горизонтально-осевой турбины, воспринимает воздушный поток, скорость которого равна разности вектора V и абсолютной скорости ${{{\mathbf{V}}}_{C}}$ точки C (рис. 1,а). Вектор ${{{\mathbf{V}}}_{C}}$ ортогонален V и по величине равен $l\dot {\vartheta }$, где $\dot {\vartheta }$ – скорость вращения центрального вала ветротурбины вокруг оси Oz. Таким образом, при вычислении аэродинамических сил и моментов в выражения предыдущего параграфа подставляем следующую формулу для U:
Пусть угол ${{\varphi }_{i}}$ собственного вращения ротора Дарье отсчитывается от направления скорости V потока до одной из державок CA ротора. Угол между державкой CA ротора Дарье и вектором U (т.е. угол $\gamma $ в обозначениях предыдущего параграфа) составляет $({{\varphi }_{i}} + \operatorname{arctg} (l\dot {\vartheta }{\text{/}}V))$. При вычислении быстроходностей роторов Дарье пренебрегаем величиной ${{V}^{{ - 1}}}l\ddot {\vartheta }$ по сравнению с ${{V}^{{ - 1}}}r{{\dot {\varphi }}_{i}}$, иными словами, считаем, что угловая скорость центрального вала меняется достаточно медленно.
Помимо аэродинамических сил на систему действует электромеханический момент ${{M}_{e}}$, приложенный к центральному валу. Он описывает воздействие статора генератора на ротор, т.е. характеризует полезную электрическую нагрузку. Выражение для него аналогично работам [12, 13, 15]:
Здесь $\kappa $ – коэффициент электромеханического взаимодействия (константа, определяемая свойствами генератора), $\sigma $ – внутреннее сопротивление генератора (константа). Выражение для электромеханического момента основано на публикациях [23, 25], в которых предложена и проанализирована математическая модель, включающая уравнение изменения тока в локальной цепи генератора.
Перейдем к безразмерному времени $\tau = {{r}^{{ - 1}}}Vt$ и безразмерным переменным: ${{\omega }_{i}} = {{V}^{{ - 1}}}r{{\dot {\varphi }}_{i}}$, i = 1, 2, – безразмерные угловые скорости собственного вращения первого и второго роторов Дарье, $~\Omega = {{V}^{{ - 1}}}l\dot {\vartheta }$ – безразмерная угловая скорость центрального вала. До сих пор точкой обозначалась производная по времени t, далее точкой будем обозначать производную по безразмерному времени $\tau $.
Уравнения движения ветротурбины могут быть получены на основе формализма Лагранжа и представляются в форме динамической системы пятого порядка (можно сравнить с уравнениями [11, 12] для турбин с лопастями в виде роторов Савониуса):
(3.1)
$\left\{ \begin{gathered} {{{\dot {\varphi }}}_{1}} = {{\omega }_{1}}, \hfill \\ {{{\dot {\omega }}}_{1}} = a(1 + {{\Omega }^{2}}){{C}_{T}}\left( {{{\varphi }_{1}} + \operatorname{arctg} \Omega ,\frac{{{{\omega }_{1}}}}{{\sqrt {1 + {{\Omega }^{2}}} }}} \right), \hfill \\ {{{\dot {\varphi }}}_{2}} = {{\omega }_{2}}, \hfill \\ {{{\dot {\omega }}}_{2}} = a(1 + {{\Omega }^{2}}){{C}_{T}}\left( {{{\varphi }_{2}} + \operatorname{arctg} \Omega ,\frac{{{{\omega }_{2}}}}{{\sqrt {1 + {{\Omega }^{2}}} }}} \right), \hfill \\ \dot {\Omega } = b\sqrt {1 + {{\Omega }^{2}}} \sum\limits_{i = 1}^2 {\left( {{{C}_{L}}\left( {{{\varphi }_{i}} + \operatorname{arctg} \Omega ,\frac{{{{\omega }_{i}}}}{{\sqrt {1 + {{\Omega }^{2}}} }}} \right) - \Omega {{C}_{D}}\left( {{{\varphi }_{i}} + \operatorname{arctg} \Omega ,\frac{{{{\omega }_{i}}}}{{\sqrt {1 + {{\Omega }^{2}}} }}} \right)} \right)} - bk\Omega \,, \hfill \\ \end{gathered} \right.$Подсистемы, описывающие собственное вращение каждого из двух роторов Дарье, связаны друг с другом только через угловую скорость $~\Omega $ центрального вала. Роторы Дарье непосредственно друг с другом не взаимодействуют.
Следует отметить, что идентичность двух роторов Дарье (как и уравнений для $~{{\varphi }_{i}},{{\omega }_{i}}$), входящих в состав системы, наводит на мысль, что вполне достаточно рассматривать динамику одного из роторов, а не обоих. Однако для ротора Дарье характерно наличие пары притягивающих установившихся режимов (в отличие от ротора Савониуса, у которого такой режим единственен). Поэтому вполне возможна ситуация, когда в зависимости, например, от начальных условий один из роторов Дарье будет вращаться с высокой угловой скоростью, а другой – с низкой. Так что рассмотрение системы пятого порядка (а не третьего) существенно для выявления всех принципиально различных рабочих режимов устройства.
4. Установившиеся рабочие режимы. Рабочий режим ветроустановки представляет собой авторотацию по всем трем угловым координатам. Три обобщенные скорости на соответствующем решении системы могут совершать некоторые колебания около постоянных значений. Чем быстрее вращаются роторы Дарье, тем меньшее влияние успевает оказать изменение угла поворота каждого из роторов за оборот. Можно ожидать, что при высоких угловых скоростях роторов для практических приложений достаточно пользоваться уравнениями, усредненными по $~{{\varphi }_{i}}$, что существенно упростит анализ. Однако при небольших угловых скоростях влияние углов существенно и колебания угловых скоростей на низкоскоростных рабочих режимах могут быть значительными.
Для поиска режимов авторотации воспользуемся методом, предложенным в работе [17], где он описан для системы четвертого порядка. Обобщение этого подхода на систему (3.1) вполне очевидно (поскольку одна из обобщенных координат циклическая). Вычисление средних значений функций, отвечающих за перевязки между подсистемами, выполняется аналогично модификации [16]. Детали процедуры изложены далее в приложении к системе (3.1). Суть приема состоит в том, чтобы заменить функции, отвечающие за перевязки, их средними значениями, найти аттракторы (предельные циклы или неподвижные точки) отделившихся друг от друга подсистем, определить и учесть условия, при которых найденные аттракторы и принятые средние значения перевязок согласованы между собой.
Отметим, что при малых значениях параметров a и b приближения для угловых скоростей на установившихся режимах будут близки к константам, которые соответствуют притягивающим неподвижным точкам системы, формально усредненной по двум углам. В этом предельном случае применяемый подход совпадает с поиском притягивающих неподвижных точек усредненных уравнений (в качестве приближения для аттракторов полной системы). Такая методика поиска начального приближения для аттракторов системы с медленными переменными (частотами) восходит к классическим подходам [32, 33] и применяется во многих задачах механики [34]. Можно отметить востребованность методов, использующих численное продолжение таких приближений по параметрам: существуют различные варианты, например [35, 36].
4.1. Вспомогательные системы для роторов Дарье. В соответствии с выбранным алгоритмом [17] на первом этапе поиска аттракторов системы (3.1) формально заменим переменную $~\Omega $ константой $~\bar {\Omega }$ и рассмотрим любую из подсистем для $~{{\varphi }_{i}},{{\omega }_{i}}$. Индекс $~i$ в этой вспомогательной системе опускаем:
Заметим, что эту систему можно упростить: поскольку $~\bar {\Omega }$ в ней является константой, естественно сделать замену переменных и времени: $\gamma = \varphi + \operatorname{arctg} (\bar {\Omega })$, $~z = \omega {\text{/}}\sqrt {1 + {{{\bar {\Omega }}}^{2}}} $, $~s = \tau \sqrt {1 + {{{\bar {\Omega }}}^{2}}} $. В новых переменных получаем уравнения:
(4.1)
$\left\{ \begin{gathered} \frac{{d\gamma }}{{ds}} = z, \hfill \\ \frac{{dz}}{{ds}} = a{{C}_{T}}\left( {\gamma ,z} \right). \hfill \\ \end{gathered} \right.$Эта система представляет собой не что иное, как уравнения вращения ротора Дарье в однородном стационарном потоке (аналогично [22]).
Для системы (4.1), которая определена на цилиндре, находим предельные циклы, охватывающие фазовый цилиндр, т.е. 2π-периодические по γ. Используем для этого итерационный численно-аналитический метод, предложенный в [37], основанный на построении последовательных приближений локальных порождающих гамильтоновых систем. Отметим, что в [37] содержится обзор различных классов методов, которые можно использовать для поиска таких предельных циклов. Для предварительной локализации циклов эффективны, например, методы [38, 39]. Отметим, что можно проследить эволюцию циклов от бифуркаций особых точек системы, применяя такие подходы, как [40] в сочетании с [41].
Система (4.1) в зависимости от параметра a обладает одним или тремя циклами (в вырожденном случае – двумя, один из которых полуустойчивый). При относительно небольших значениях a ($a < {{a}_{{cr}}} \approx 16$) цикла три, те два из них, которые характеризуются наибольшими и наименьшими значениями фазовых скоростей, притягивающие. При $a = {{a}_{{cr}}}$ два цикла, расположенные ниже на фазовом цилиндре, сливаются. Далее рассмотрим для определенности a = 1. Такое значение a с позиций физического смысла довольно велико и может соответствовать, например, работе гидротурбины в потоке воды; в воздухе характерные значения этого параметра на три порядка меньше, что делает очевидной успешность процедуры усреднения.
Функции, описывающие предельные циклы на фазовом цилиндре, обозначим ${{\tilde {z}}^{j}}(\gamma )$, где индекс j = 1, 2, 3 соответствует нижнему (притягивающему), среднему (отталкивающему), верхнему (притягивающему) циклам. Значения z на том или ином цикле близки к значениям $\lambda $, отвечающим тому или иному корню функции ${{C}_{T}}(\lambda )$ (рис. 3). Для каждой из трех траекторий ${{\tilde {z}}^{j}}(\gamma )$ вычислим средние по времени за период значения $\bar {C}_{L}^{j}$ и $\bar {C}_{D}^{j}$ функций ${{C}_{L}}(\gamma ,z)$ и ${{C}_{D}}(\gamma ,z)$ вдоль этих траекторий. Приведем соответствующую формулу на примере $\bar {C}_{L}^{j}$ (в общем случае отличается от среднего по углу $\gamma $):
Для авторотации ротора Дарье с низкой угловой скоростью получаем: $\bar {C}_{L}^{1} \approx 0.12$, $\bar {C}_{D}^{1} \approx 0.92$; для случая высокоскоростной авторотации: $\bar {C}_{L}^{3} \approx 2.29$, $\bar {C}_{D}^{3} \approx 7.16$. Эти значения потребуются на следующем этапе алгоритма.
4.2. Вспомогательная система для скорости $~\Omega $ центрального вала. В уравнение системы (3.1), описывающее изменение переменной $~\Omega $, подставим вместо функций ${{C}_{L}}$ и ${{C}_{D}}$ найденные величины $\bar {C}_{L}^{j}$ и $\bar {C}_{D}^{j}$. Для двух различных $i$ значения индекса j могут быть выбраны независимо. Рассмотрим сочетания, отвечающие притягивающим траекториям вспомогательных систем (4.1), т.е. $j \ne 2$ (описание отталкивающих траекторий выходит за рамки данной работы, хотя оно тоже представляет интерес, например, для поиска элементов границ областей притяжения аттракторов, подобно работам [17, 19, 35, 36]). Подстановка констант $\bar {C}_{L}^{1}$, $\bar {C}_{D}^{1}$, $\bar {C}_{L}^{3}$, $\bar {C}_{D}^{3}$ вместо функций ${{C}_{L}}({{\gamma }_{1}},{{z}_{1}})$, ${{C}_{D}}({{\gamma }_{1}},{{z}_{1}})$, ${{C}_{L}}({{\gamma }_{2}},{{z}_{2}})$, ${{C}_{D}}({{\gamma }_{2}},{{z}_{2}})$ соответствует тому, что первый ротор Дарье авторотирует с низкой скоростью, а второй – с высокой. Подстановка констант $\bar {C}_{L}^{1}$, $\bar {C}_{D}^{1}$ для $i = 1,2$ отвечает низкоскоростному вращению обоих роторов Дарье. И, наконец, подстановка $\bar {C}_{L}^{3}$, $\bar {C}_{D}^{3}$ для $i = 1,2$ – высокой скорости авторотации обоих роторов.
В результате подстановки получаем уравнение вида
Здесь индексы ${{j}_{1}},{{j}_{2}}$ принимают значения 1 или 3.
Величина $\Omega {\text{*}}$ соответствует неподвижной точке этого уравнения, если
(4.2)
$k = \sqrt {1 + \Omega {\kern 1pt} {{*}^{2}}} (\bar {C}_{L}^{{{{j}_{1}}}} - \Omega {\kern 1pt} {\text{*}}\bar {C}_{D}^{{{{j}_{1}}}} + \bar {C}_{L}^{{{{j}_{2}}}} - \Omega {\kern 1pt} {\text{*}}\bar {C}_{D}^{{{{j}_{2}}}}){\text{/}}\Omega {\kern 1pt} {\text{*}}.$Для каждого k значение $\Omega {\kern 1pt} *$ при заданных ${{\bar {C}}_{L}}$ и ${{\bar {C}}_{D}}$ единственно, неподвижная точка притягивающая. Физический смысл имеют значения k > 0, так что на практике диапазон значений $\Omega {\kern 1pt} *$ ограничен.
4.3. Аттракторы полной динамической системы: приближения и численное исследование. Приближенные значения безразмерной скорости вращения центрального вала на рабочих режимах описываются диаграммой, построенной по формулам вида (4.2) (рис. 4, а). При каждом значении k можно ожидать, что у горизонтально-осевой ветротурбины с лопастями в форме роторов Дарье есть три принципиально различных притягивающих рабочих режима: на одном из них оба ротора Дарье авторотируют с высокой скоростью (красная кривая на рис. 4), на другом – с низкой (синяя кривая), на третьем один из роторов вращается быстро, другой – медленно (черная кривая).
Рис. 4.
Приближенные кривые, описывающие зависимость угловой скорости центрального вала и коэффициента мощности от коэффициента электрической нагрузки на рабочих режимах
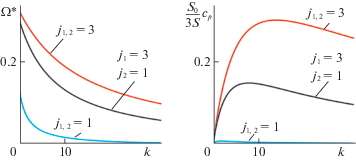
При достаточно большом моменте инерции J изменение переменной $\Omega $ за один оборот вала несущественно. При этом можно предполагать, что построенные диаграммы хорошо описывают рабочие режимы. Однако, строго говоря, требуется, как минимум прямая численная проверка того, что в полной системе пятого порядка существует аттрактор, проекции которого на фазовые плоскости расположены вблизи построенных приближений (кривых $\omega = {{\tilde {z}}^{j}}(\gamma ){\text{/}}\sqrt {1 + \Omega {\kern 1pt} {{*}^{2}}} $ и прямой $\Omega = \Omega {\kern 1pt} *$).
Для иллюстрации рассмотрим случай $b = 0.1$, k = 10. На рис. 5–7 черным пунктиром приведены построенные приближения для аттракторов полной системы, красным и зеленым цветом показаны проекции на фазовые плоскости траекторий, построенных путем прямого численного интегрирования уравнений (3.1) методом Рунге–Кутты. При этом начальные условия взяты из окрестностей трех приближений, построенных при данном k.
Рис. 5.
Сравнение траекторий, построенных прямым численным интегрированием полной системы, и приближений, полученных при анализе вспомогательных систем. Случай высокоскоростного режима
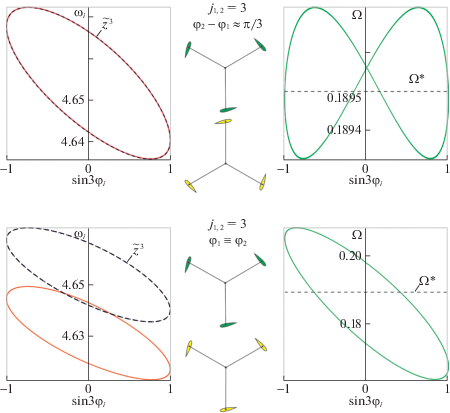
Рис. 6.
Случай низкоскоростного режима (вариант с ${{\varphi }_{2}} - {{\varphi }_{1}} \approx \pi {\text{/}}3$ получен при наличии дополнительного управления)
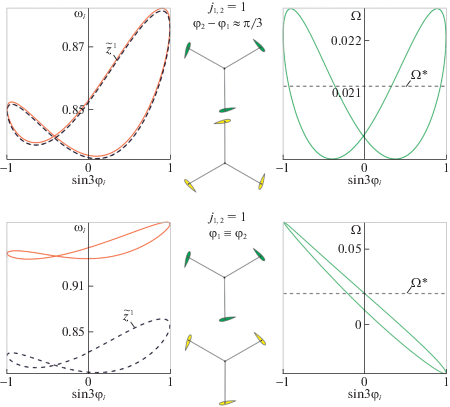
Для аттракторов, отвечающих авторотации обоих роторов Дарье с одинаковыми скоростями (рис. 5, 6), средние угловые скорости $d{{\varphi }_{1}}{\text{/}}dt = {{r}^{{ - 1}}}V{{\omega }_{1}}$ и $d{{\varphi }_{2}}{\text{/}}dt = {{r}^{{ - 1}}}V{{\omega }_{2}}$ совпадают друг с другом, а угловая скорость $d\vartheta {\text{/}}dt = {{l}^{{ - 1}}}V\Omega {\kern 1pt} *$, вообще говоря, не соизмерима с ними, т.е. можно говорить о частичной синхронизации элементов системы. Однако при определенном выборе отношения ${{l}^{{ - 1}}}r$ может быть реализована синхронизация по всем трем угловым скоростям.
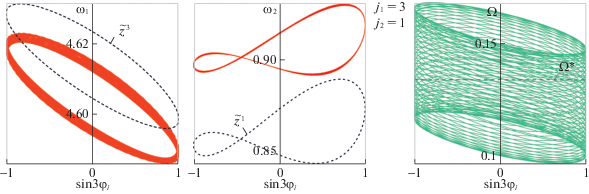
При численном исследовании в окрестности приближения, отвечающего высокоскоростной авторотации обоих роторов Дарье, обнаружено два существенно различных инвариантных многообразия полной системы (рис. 5). Одно из них – это близкий к периодическому аттрактор, на котором ${{\varphi }_{2}} - {{\varphi }_{1}} \approx \pi {\text{/}}3$ (соответственно существует и симметричный ему с ${{\varphi }_{1}} - {{\varphi }_{2}} \approx \pi {\text{/}}3$). Проекция этого аттрактора на плоскость $({{\varphi }_{i}},{{\omega }_{i}})$ с большой точностью совпадает с приближением ${{\tilde {z}}^{3}}(\gamma )$ (на рисунке визуально неотличимы). Второе – это периодическое решение, которое существует при ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$. В полной системе (3.1) оно неустойчиво, при искусственном ограничении вида ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$, т.е. в системе третьего порядка, оно притягивающее. Утверждать о наличии соответствующей траектории в полной системе можно в силу идентичности уравнений для двух роторов Дарье. При численном интегрировании полной системы (3.1) решение выходит в окрестность указанной траектории, только если ${{\varphi }_{1}}(0) = {{\varphi }_{2}}(0)$, ${{\omega }_{1}}(0) = {{\omega }_{2}}(0)$. При малейшем рассогласовании между начальными значениями углов собственного вращения или угловых скоростей двух роторов Дарье траектория уходит на аттрактор, на котором разница между двумя углами ${{\varphi }_{i}}$ близка к π/3 (отклонение от $\pi {\text{/}}3$ – в пределах 0.003). Заметим, что разница $\pi {\text{/}}3$ между углами ${{\varphi }_{i}}$ – это максимально возможное отличие в ориентации двух роторов Дарье, поскольку каждый из них трехлопастной.
На рис. 5 схематично изображено взаимное расположение лопастей роторов на двух различных режимах, если на каждый из роторов смотреть с конца его оси собственного вращения. В случае режима, на котором ${{\varphi }_{2}} - {{\varphi }_{1}} \approx \pi {\text{/}}3$, роторы движутся так, что фактически происходит дополнительное усреднение крутящего момента и сил по углу вращения. При этом сглаживаются колебания угловой скорости $\Omega $ на обороте. Напротив, для режима, на котором ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$, колебания сил и моментов за оборот не уменьшаются по сравнению со случаем единственного ротора Дарье, а возрастают. Колебания $\Omega $ на каждом периоде при этом значительно заметнее. То, что высокоскоростной режим с ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$ неустойчив в полной системе и разница между углами ${{\varphi }_{i}}$ устанавливается близкой к $\pi {\text{/}}3$, можно интерпретировать с физической точки зрения как самостоятельную подстройку системы, обеспечивающую “сглаживание” внешних воздействий и позволяющую “избегать” дополнительных колебаний.
Отметим, что если, исходя из идентичности лопастей, рассмотреть модель комбинированной турбины в форме системы третьего порядка, считая, что движения всех роторов Дарье идентичны, то в качестве основного рабочего режима будет получен режим, который в полной модели (в системе пятого порядка) неустойчив (высокоскоростной режим с ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$), и не будет выявлен рабочий режим, характеризующийся разницей $\pi {\text{/}}3$ между углами собственного вращения двух роторов Дарье. Это еще один аргумент в пользу того, что существенно учитывать в модели динамику каждого ротора Дарье, а не одного из них, несмотря на их идентичность.
Иначе обстоит дело в окрестности приближения, отвечающего низкоскоростному вращению обоих роторов Дарье: “низкоскоростная” периодическая траектория с ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$ является притягивающей. Ее проекции показаны на рис. 6. Близкая к периодической траектория с ${{\varphi }_{2}} - {{\varphi }_{1}} \approx \pi {\text{/}}3$ и ${{\omega }_{i}} < 1$ если и существует, то она неустойчива. Обнаружить ее прямым интегрированием системы (3.1) не удается. Силы и моменты, действующие на ротор Дарье, чувствительны к изменению угла ${{\varphi }_{i}}$ на π/3. Так что идентичность роторов Дарье не приводит к наличию в системе решения с ${{\varphi }_{2}} - {{\varphi }_{1}} \equiv \pi {\text{/}}3$. Можно предположить (по аналогии с траекторией, где ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$, для высокоскоростного случая), что для стабилизации такого решения достаточно только регулировать разность между углами ${{\varphi }_{i}}$.
Для численной проверки существования такого решения можно применить метод [35, 36], но это весьма ресурсоемкий подход, выходящий за рамки данного исследования. Ограничимся попыткой стабилизировать решение, существование которого мы предполагаем. Добавим в правую часть уравнения для ${{\dot {\omega }}_{1}}$ слагаемое вида $ - 0.004\left( {{{\varphi }_{1}} + \pi {\text{/}}3 - {{\varphi }_{2}}} \right)$ и аналогичное слагаемое в уравнение для ${{\dot {\omega }}_{2}}$. Тогда в окрестности приближения для низкоскоростного режима существует аттрактор, на котором разность $({{\varphi }_{2}} - {{\varphi }_{1}})$ колеблется около π/3 (отклонение от π/3 – в пределах 0.015). Проекции аттрактора изображены на рис. 6. Их отличия от построенного приближения значительно меньше, чем у аттрактора с ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$. По-видимому, это связано с тем, что при таком взаимном расположении двух роторов Дарье силомоментные характеристики сглаживаются – становятся ближе к своим средним за оборот значениям.
Отметим, что на режиме, характеризующемся низкими скоростями вращения роторов Дарье и равенством углов ${{\varphi }_{1}} \equiv {{\varphi }_{2}}$, переменная $\Omega $ не остается все время положительной: на каждом периоде есть этап возвратного движения центрального вала турбины.
Наконец, рассмотрим третий тип рабочих режимов, на котором один ротор Дарье авторотирует с высокой скоростью, а другой – с низкой. В системе (3.1) этому режиму отвечает аттрактор, на котором средние значения фазовых скоростей ${{\omega }_{1}}$ и ${{\omega }_{2}}$ несоизмеримы друг с другом, т.е. синхронизации роторов Дарье не происходит. Соответствующая траектория не является периодической (рис. 7). Проекции аттрактора на фазовые плоскости представляют собой некоторые области (траектория постепенно заполняет эти области). В проекции на плоскость $(\sin 3{{\varphi }_{1}},\Omega )$ показан некоторый участок траектории, чтобы ее структура была более наглядна. В общем случае и величина ${{l}^{{ - 1}}}r\Omega {\kern 1pt} *$ не соизмерима ни с одним из средних значений ${{\omega }_{i}}$. Однако за счет специального выбора отношения ${{l}^{{ - 1}}}r$ можно синхронизировать скорость $d\vartheta {\text{/}}dt$ вращения центрального вала с угловой скоростью того или иного ротора Дарье.
Рассмотренная система проявляет свойства частичной синхронизации элементов, что характерно для так называемых химерных состояний [20].
5. Управление рабочими режимами. Рассмотрим задачу выбора значения коэффициента k внешней электрической нагрузки, обеспечивающего близкую к максимальной механическую мощность на рабочем режиме ветротурбины. В системе имеет место дефицит управляющих воздействий [42]. Используем подход, примененный ранее в работах [12, 15]. Будем строить управление на основании проведенного выше анализа усредненных систем. Отметим, что разнообразные приемы, связанные с усреднением, в том числе достаточно нетривиальные подходы, востребованы в задачах теории управления, например [43].
Приближенные значения коэффициента cp механической мощности на рабочих режимах описываются формулами следующего вида (рис. 4):
(4.3)
${{c}_{p}} = \frac{P}{{{{P}_{0}}}} = \frac{{3S}}{{{{S}_{0}}}}\Omega {\kern 1pt} {\text{*}}\sqrt {1 + \Omega {\kern 1pt} {{*}^{2}}} (\bar {C}_{L}^{{{{j}_{1}}}} - \Omega {\kern 1pt} {\text{*}}\bar {C}_{D}^{{{{j}_{1}}}} + \bar {C}_{L}^{{{{j}_{2}}}} - \Omega {\kern 1pt} {\text{*}}\bar {C}_{D}^{{{{j}_{2}}}}).$Здесь $P$ – механическая мощность турбины, ${{P}_{0}} = 0.5\rho {{S}_{0}}{{V}^{3}}$ – мощность потока, проходящего через осевое сечение ветротурбины, ${{S}_{0}}$ – площадь осевого сечения.
Максимальные значения коэффициента мощности достигаются на рабочем режиме, на котором оба ротора Дарье авторотируют с одинаковыми высокими скоростями. Абсолютный максимум достигается на таком режиме при $k \approx 15$. Итак, стратегия управления состоит в том, чтобы при изменении условий функционирования ветроустановки поддерживать значение коэффициента k близким к найденному. Управление внешним сопротивлением R, которое обеспечивает, если возможно, желаемые значения k, обсуждается подробно в [12].
Заключение. В статье исследован вопрос о формировании силы, родственной силе Магнуса, при вращении ротора Дарье. Рассмотрена возможность применения роторов Дарье в качестве лопастей ветротурбины, работающей на основе эффекта Магнуса. Математическая модель такой энергетической установки представлена в форме автономной динамической системы пятого порядка. Эта система состоит из двух подсистем второго порядка, каждая из которых описывает собственное вращение одного из роторов Дарье, а также третьей подсистемы – уравнения первого порядка, описывающего вращение центрального вала основной турбины. Первые две подсистемы перевязаны друг с другом только посредством третьей. Для того чтобы приближенно описать аттракторы системы пятого порядка (отвечающие рабочим режимам ветротурбины), подсистемы формально отделяются друг от друга: вместо перевязок подставляются их усредненные значения (метод [17]). Проводится поиск аттракторов полученных таким образом вспомогательных подсистем второго и первого порядков. Затем найденные приближения используются для определения начальных условий, расположенных около аттракторов исходной системы пятого порядка. Выполняется численная проверка. Показано, что при значениях параметров модели, рассмотрение которых актуально для практических приложений, полученные приближения хорошо описывают аттракторы полной системы и могут быть использованы для оценки механической мощности на рабочих режимах устройства.
Отметим, что примененный алгоритм поиска аттракторов не чувствителен к тому, содержит ли область притяжения аттрактора окрестность хотя бы одной неподвижной точки или же аттрактор является скрытым (в смысле определения [44, 45]). Так, в рассмотренной задаче при достаточно малых значениях параметра a ни один из роторов Дарье не может без принудительного разгона перейти на высокоскоростной режим авторотации. Соответственно аттракторы, на которых хотя бы один из роторов Дарье авторотирует с высокой скоростью (${{\omega }_{i}} > \sqrt {1 + {{\Omega }^{2}}} $), являются скрытыми. Это касается, в частности, аттракторов, проекции которых на фазовые плоскости изображены на верхней части рис. 5 и на рис. 7.
Применение алгоритма [17] в данной задаче значительно упрощается тем, что вспомогательная подсистема второго порядка, описывающая собственное вращение ротора Дарье, после замены переменных не зависит от усредненного значения угловой скорости центрального вала составной турбины. Тем самым на промежуточном этапе анализа требуется найти предельные циклы только для системы второго порядка с фиксированными параметрами, нет необходимости в построении диаграммы циклов в зависимости от скорости центрального вала.
Для поиска аттракторов, соответствующих колебательным, а не ротационным движениям механической системы, при построении предельных циклов вспомогательных систем второго порядка можно использовать различные численно-аналитические алгоритмы, например итерационные методы [46, 47].
В результате применения алгоритма построены приближения для трех типов режимов: высокоскоростного (оба ротора Дарье вращаются с высокой скоростью), низкоскоростного, смешенного типа (только у одного из роторов Дарье скорость авторотации высокая).
В окрестности приближения, отвечающего высокоскоростной/низкоскоростной авторотации обоих роторов, обнаружен режим, который характеризуется идентичным движением двух роторов Дарье (${{\varphi }_{1}} \equiv {{\varphi }_{2}}$). В случае высоких скоростей такой режим неустойчив и из его окрестности система переходит на аттрактор, для которого разность между углами вращения роторов близка к $\pi {\text{/}}3$ (напомним, что каждый ротор трехлопастной, т.е. его лопасти расположены с шагом $2\pi {\text{/}}3$). В случае низких скоростей режим идентичного вращения притягивающий, предположительно низкоскоростной режим с близкой к $\pi {\text{/}}3$ разницей между углами ${{\varphi }_{i}}$ собственного вращения роторов Дарье тоже существует, но неустойчив (седлового типа).
Помимо этого обнаружен один режим в окрестности приближения, отвечающего высокоскоростной авторотации одного ротора и низкоскоростной другого. На нем скорости вращения двух роторов несоизмеримы.
Построено управление коэффициентом внешней электрической нагрузки, позволяющее реализовать режим, который характеризуется максимумом механической мощности.
Список литературы
Swanson W.M. The Magnus Effect: a Summary of Investigations to Date // J. Basic Eng. 1961. V. 83. № 3. P. 461–470.
Tsuji Y., Morikawa Y., Mizuno O. Experimental Measurement of the Magnus Force on a Rotating Sphere at Low Reynolds Numbers // J. Fluids Eng. 1985. V. 107. № 4. 484–488.
Прандтль Л. Эффект Магнуса и ветряной корабль // Успехи физ. наук. 1925. Т. 5. № 1. С. 1–27.
Paraschivoiu I. Wind Turbine Design: with Emphasis on Darrieus Concept. Monreal: Polytechnique International Pres., 2002.
Seifert J. A Review of the Magnus Effect in Aeronautics // Progress in Aerospace Sciences. 2012. V. 55. P. 17–45.
Ragheb M. Wind Energy Converters Concepts. Champaign, IL: University of Illinois at Urbana-Champaign, 2014.
https://omnidea.net/aerial-platforms.html.
Moreira R.A.L. Turbina Darrieus Numa Plataforma Aérea Por Efeito Magnus (Doctoral dissertation). Lisboa, 2017.
Savonius S.J. Rotor Adapted to be Driven by Wind or Flowing Water. U.S. Patent No. 1697574 A, 1929.
Akira I., Kawashima S., Nishizawa Y., Ushiyama I., Komatinovic N. A Study on Savonius Type Magnus Wind Turbine // European Wind Energy Conf. and Exhibition. 2007. https://www.researchgate.net/publication/240627785_A_Study_on_Savonius_Type_Magnus_Wind_Turbine.
Ишханян М.В., Климина Л.А., Привалова О.Г. Математическое моделирование ветротурбины, работающей на основе эффекта Магнуса // Мехатроника, автоматизация, управление. 2018. Т. 19. № 8. С. 523–528.
Ишханян М.В., Климина Л.А. Ветротурбина класса “Савониус-Магнус” с коническими лопастями: динамика и управление // Изв. РАН. ТиСУ. 2020. № 4. С. 160–168.
Климина Л.А., Шалимова Е.С., Досаев М.З., Селюцкий Ю.Д. Двойная ветротурбина, работающая на основе эффекта Магнуса // Вестн. МГУ. Сер. 1. Математика, механика. 2020. № 4. С. 65–69.
Викторов М.С., Маринин О.О., Смык А.Ф. Применение эффекта Магнуса в инфраструктуре дороги // Автомобиль. Дорога. Инфраструктура. 2019. Т. 19. № 1. С. 23.
Досаев М.З., Климина Л.А., Шалимова Е.С. Управление рабочими режимами шарнирной ветроустановки // Изв. РАН. ТиСУ. 2021. № 1. С. 169–176.
Климина Л.А. Метод формирования асинхронных автоколебаний в управляемой механической системе с двумя степенями свободы // ПММ. 2021. № 2. С. 152–171.
Климина Л.А. Метод формирования авторотаций в управляемой механической системе с двумя степенями свободы // Изв. РАН. ТиСУ. 2020. № 6. С. 3–14.
Schilder F., Osinga H.M., Vogt W. Continuation of Quasi-Periodic Invariant Tori // SIAM J. Applied Dynamical Systems. 2005. V. 4. № 3. P. 459–488.
Климина Л.А., Мастерова А.А., Самсонов В.А., Селюцкий Ю.Д. Численно-аналитический метод поиска авторотаций механической системы с двумя вращательными степенями свободы // Изв. РАН. МТТ. 2021. № 3. С. 128–142.
Ashwin P., Burylko O. Weak Chimeras in Minimal Networks of Coupled Phase Oscillators // Chaos: An Interdisciplinary J. of Nonlinear Science. 2015. V. 25. № 1. P. 013106.
Кравец А.С. Характеристики авиационных профилей. М.: Гос. изд. оборонной промышленности, 1939.
Klimina L., Lokshin B., Samsonov V. Parametrical Analysis of the Behavior of an Aerodynamic Pendulum with Vertical Axis of Rotation // Modelling, Simulation and Control of Nonlinear Engineering Dynamical Systems. Dordrecht: Springer, 2009. P. 211–220.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д. О динамике малой ветроэлектростанции // ДАН. 2007. Т. 416. № 1. С. 50–53.
Досаев М.З., Линь Ч.X., Лю В.Л., Самсонов В.А., Селюцкий Ю.Д. Качественный анализ стационарных режимов малых ветровых электростанций // ПММ. 2009. Т. 73. № 3. С. 368–374.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д., Вен-Лон Лю, Чин-Хуэй Линь. Бифуркации режимов функционирования малых ветроэлектростанций и оптимизация их характеристик // Изв. РАН. МТТ. 2009. № 2. С. 59–66.
Andronov P.R., Dosaev M.Z., Dynnikova G.Y., Selyutskii Y.D., Strekalov S.D. Modeling of Oscillating Wind Turbine // J. Machinery Manufacture and Reliability. 2009. V. 38. № 4. P. 383–387.
Selyutskiy Y.D., Holub A.P., Dosaev M.Z. Elastically Mounted Double Aerodynamic Pendulum // Intern. J. Structural Stability and Dynamics. 2019. V. 19. № 5. P. 1941007.
Sheldahl R.E. Comparison of Field and Wind-Tunnel Darrieus Wind-Turbine Data // J. of Energy. 1981. V. 5. № 4. P. 254–256.
Paraschivoiu I. Double-Multiple Streamtube Model for Darrieus Wind Turbines. NASA, Lewis Research Center Wind Turbine Dynamics, 1981. https://ntrs.nasa.gov/citations/19820015811.
Castelli M.R., Englaro A., Benini E. The Darrieus Wind Turbine: Proposal for a New Performance Prediction Model Based on CFD // Energy. 2011. V. 36. № 8. P. 4919–4934.
Bach G. Untersuchungen über Savonius-Rotoren und Verwandte Strömungsmaschinen // Forschung auf dem Gebiet des Ingenieurwesens A. 1931. B. 2. № 6. S. 218–231.
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. 2-е изд. М.: Наукa, 1974.
Волосов В.М., Моргунов Б.И. Метод осреднения в теории нелинейных колебательных систем. М.: Изд-во МГУ, 1971.
Акуленко Л.Д., Лещенко Д.Д., Черноусько Ф.Л. Быстрое движение вокруг неподвижной точки тяжелого твердого тела в сопротивляющейся среде // Изв. РАН. МТТ. 1982. № 3. С. 5–13.
Kamiyama K., Komuro M., Endo T. Bifurcation of Quasi-Periodic Oscillations in Mutually Coupled Hard-Type Oscillators: Demonstration of Unstable Quasi-Periodic Orbits // Intern. J. Bifurcation and Chaos. 2012. V. 22. № 6. P. 1230022.
Kamiyama K., Komuro M., Endo T. Algorithms for Obtaining a Saddle Torus Between two Attractors // Intern. J. Bifurcation and Chaos. 2013. V. 23. № 9. P. 1330032.
Климина Л.А. Метод построения периодических решений в управляемой динамической системе с цилиндрическим фазовым пространством // Изв. РАН. ТиСУ. 2020. № 2. С. 5–16.
Гринь А.А., Рудевич С.В. Признак Дюлака–Черкаса для установления точного числа предельных циклов автономных систем на цилиндре // Дифференц. уравнения. 2019. Т. 55. № 3. С. 328–336.
Гринь А.А. Трансверсальные кривые для установления точного числа предельных циклов // Дифференц. уравнения. 2020. Т. 56. № 4. С. 427–437.
Брюно А.Д. Локальный метод нелинейного анализа дифференциальных уравнений. М.: Наука, 1979. 252 с.
Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: Физматлит, 1998. 288 с.
Formalskii A.M. Stabilization and Motion Control of Unstable Objects. Berlin/Boston: Walter de Gruyter, 2015.
Aleksandrov A.Y., Tikhonov A.A. Averaging Technique in the Problem of Lorentz Attitude Stabilization of an Earth-pointing Satellite // Aerospace Science and Technology. 2020. V. 104. P. 105963.
Брагин В.О., Вагайцев В.И., Кузнецов Н.В., Леонов Г.А. Алгоритмы поиска скрытых колебаний в нелинейных системах. Проблемы Айзермана, Калмана и цепи Чуа // Изв. РАН. ТиСУ. 2011. № 4. С. 3–36.
Кузнецов Н.В. Теория скрытых колебаний и устойчивость систем управления // Изв. РАН. ТиСУ. 2020. № 5. С. 5–27.
Климина Л.А. Метод поиска периодических траекторий центрально-симметричных динамических систем на плоскости // Дифференц. уравнения. 2019. Т. 55. № 2. С. 159–168.
Климина Л.А., Селюцкий Ю.Д. Метод построения периодических решений в управляемой динамической системе второго порядка // Изв. РАН. ТиСУ. 2019. № 4. С. 3–15.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления