Известия РАН. Теория и системы управления, 2021, № 5, стр. 111-119

Введение. Данная работа продолжает исследования, начатые в [1]. На математической модели многопользовательской сети связи анализируются две различные стратегии распределения равноправных невзаимозаменяемых потоков разных видов, передаваемых между всеми узлами. Целью управления является эффективное использование ресурсов сети и взаимно-допустимое распределение межузловых потоков разных видов, которые могут одновременно передаваться между всеми парами. При уравнительной стратегии для всех корреспондентов определяются равные квоты на предельно допустимые межузловые потоки, которые передаются в сети одновременно [2]. Равнодолевая стратегия распределения предполагает, что значение квоты для каждой пары источник–приемник должно быть прямо пропорционально максимально возможному однопродуктовому потоку между соответствующими узлами [3]. В основу вычислительных экспериментов была положена процедура, при выполнении которой за конечное число шагов определяется финальное распределение совместно допустимых межузловых потоков и достигается полная загрузка всех ребер сети. Предложенную процедуру можно применять как для априорной оценки предельных функциональных возможностей сети, так и для анализа их изменения при целенаправленных разрушающих воздействиях.

1. Математическая модель. Для описания многопользовательской сетевой системы используется математическая запись модели передачи многопродуктового (МП-) потока. Структура сети $G(d)$ задается множествами $\left\langle {V,\;R,\;U} \right\rangle $: узлов (вершин) сети $V = \{ {{{v}}_{1}},{{{v}}_{2}},...,{{{v}}_{n}},...,{{{v}}_{N}}\} $; неориентированных ребер $R = \{ {{r}_{1}},{{r}_{2}},...,{{r}_{k}},...,{{r}_{E}}\} $ ⊂ V × V. Ребро ${{r}_{k}} = \left( {{{v}_{{{{n}_{k}}}}},\;{{v}_{{{{j}_{k}}}}}} \right)$ соединяет вершины ${{{v}}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$ (инцидентно вершинам ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$), которые для него служат концевыми. Предполагается, что в сети отсутствуют петли и сдвоенные ребра. Ребру r_k ставятся в соответствие две ориентированные дуги u_k, ${{u}_{{k + E}}}$ прямого и обратного направления из множества ориентированных дуг $U = \{ {{u}_{1}},{{u}_{2}},...,{{u}_{k}},...,{{u}_{{2E}}}\} $. Дуги $\{ {{u}_{k}},{{u}_{{k + E}}}\} $ определяют направление передачи потока по ребру ${{r}_{k}}$ между концевыми вершинами ${{v}_{{{{n}_{k}}}}}$, ${{v}_{{{{j}_{k}}}}}$.

Обозначим через $S({{v}_{n}})$ множество номеров исходящих дуг, по которым поток покидает узел ${{v}_{n}}$; $T({{v}_{n}})$ – множество номеров входящих дуг, по которым поток поступает в узел ${{v}_{n}}$. Состав множеств $S({{{v}}_{n}})$, $T({{{v}}_{n}})$ однозначно определяется в ходе выполнения следующей процедуры. Пусть некоторое ребро ${{r}_{k}} \in R$ соединяет вершины с номерами n и j, такими, что $n < j$. Тогда ориентированная дуга ${{u}_{k}} = ({{{v}}_{n}},{{{v}}_{j}})$ считается исходящей из вершины ${{{v}}_{n}}$ и ее номер k заносится в множество $S({{{v}}_{n}})$, ориентированная дуга ${{u}_{{k + E}}} = ({{{v}}_{j}},{{{v}}_{n}})$ – входящей для ${{{v}}_{n}}$ и ее номер $k + E$ помещается в список $T({{{v}}_{n}})$. Дуга ${{u}_{k}}$ является входящей для ${{{v}}_{j}}$ и ее номер k попадает в $T({{{v}}_{j}})$, а дуга ${{u}_{{k + E}}}$ – исходящей и номер $k + E$ вносится в список исходящих дуг $S({{{v}}_{j}})$.

Предполагается, что в сети между любой парой узлов могут передаваться потоки разных видов. Пара узлов-корреспондентов ${{p}_{m}}$ определяется упорядоченной парой вершин ${{p}_{m}} = ({{{v}}_{{{{s}_{m}}}}},{{{v}}_{{{{t}_{m}}}}})$, где вершина с номером ${{s}_{m}}$ является источником, а с номером ${{t}_{m}}$ – стоком или приемником потока m-го вида. В настоящей работе в сети из N узлов рассматривается $M = N(N - 1)$ независимых, невзаимозаменяемых и равноправных потоков различных видов, которые могут передаваться одновременно между парами узлов из множества $P = \{ {{p}_{1}},{{p}_{2}},...,{{p}_{M}}\} $.

Пусть ${{x}_{{mk}}}$ – величина потока m-го вида, который передается по дуге ${{u}_{k}}$ в прямом, а ${{x}_{{m(k + E)}}}$ – величина потока m-го вида, который передается по дуге ${{u}_{{k + E}}}$ в обратном направлении, ${{x}_{{mk}}} \geqslant 0$, ${{x}_{{m(k + E)}}} \geqslant 0$, $m = \overline {1,M} $, $k = \overline {1,E} $. Каждому ребру ${{r}_{k}} \in R$ приписывается число ${{d}_{k}}$, ограничивающее суммарный предельно допустимый поток, который можно передать по ребру ${{r}_{k}}$ в обоих направлениях. В исходной сети компоненты вектора пропускных способностей ${\mathbf{d}} = ({{d}_{1}},{{d}_{2}},...,{{d}_{k}},...,{{d}_{E}})$ – наперед заданные положительные числа, ${{d}_{k}} > 0$, $k = \overline {1,E} $. Вектором ${\mathbf{d}}$ определяются следующие ограничения на все потоки, передаваемые по ребру ${{r}_{k}}$:

Ограничения (1.1) задают множество векторов

с допустимыми значениями компонент дуговых потоков ${\mathbf{x}} = ({{x}_{{mk}}},{{x}_{{m(k + E)}}})$, $m = \overline {1,M} $, $k = \overline {1,E} $, соответствующих (1.1).

Обозначим через ${{z}_{m}}$ величину межузлового потока m-го вида, который поступает в сеть в узле с номером s_m и покидает из узла с номером t_m. Во всех узлах сети ${{v}_{n}} \in V$, $n = \overline {1,N} $, для всех видов потоков должны выполняться условия сохранения потоков:

Величина z_m равна входному межузловому потоку $m$-го вида, который может быть пропущен от источника к приемнику пары p_m при распределении потоков ${{x}_{{mi}}}$ по дугам сети.

Условия сохранения потоков в узлах сети (1.2) устанавливают взаимосвязь векторов x и ${\mathbf{z}} = ({{z}_{1}},{{z}_{2}},...,{{z}_{m}},..,{{z}_{M}})$. Ограничения (1.1), (1.2) задают множество допустимых значений компонент для векторов межузловых потоков z, принадлежащих множеству

2. Равнодолевое распределение при предельной загрузке сети. Рассмотрим итерационную процедуру распределения межузловых потоков, при одновременной передаче которых полностью используется пропускная способность всех ребер сети. Выполнение каждого шага разбивается на несколько этапов. На предварительном этапе каждого шага для некоторой пары узлов-корреспондентов ${{p}_{a}},a = \overline {1,M} $, определяется максимальный межузловой однопродуктовый поток [3], который можно передать независимо из вершины с номером ${{s}_{a}}$ в вершину с номером ${{t}_{a}}$ без учета всех остальных. В рамках рассматриваемой модели указанный способ называется монопольным режимом передачи потока для пары ${{p}_{a}}$.

На основе найденных максимальных значений для всех пар вычисляется предельно допустимое совместное распределение межузловых потоков и находятся ребра, пропускная способность которых используется полностью. Для остальных ребер рассчитывается остаточная (неиспользованная) пропускная способность. На последующих шагах вновь решается задача поиска максимального межузлового однопродуктового потока, но для сети с остаточными пропускными способностями. Снова находится предельно допустимое совместное распределение потоков, а также ребра, пропускная способность которых исчерпана полностью. Таким образом за конечное число итераций, не превосходящее общего числа ребер сети, определяется финальное распределение, при котором сумма реберных потоков всех видов оказывается равна сумме пропускных способностей. Описанный метод называется PLD-процедурой (от английского peak load distribution – распределение (потоков) при предельной загрузке (сети)).

На первом этапе первого шага (t = 1) для каждой пары ${{p}_{a}} \in P$ решается следующая задача.

Задача 1. Для некоторой фиксированной пары ${{p}_{a}} \in P$ найти

${\text{при}}\;{\text{дополнительных}}\;{\text{условиях:}}\;\;{{z}_{m}} = 0,\;m \ne a,\;m = \overline {1,M} .$

Обозначим через $(x_{{ak}}^{0}(1),x_{{a(k + E)}}^{0}(1))$, $k = \overline {1,E} $, потоки по ребрам сети, соответствующие оптимальному решению $z_{a}^{0}(1)$ задачи 1 – максимальному однопродуктовому межузловому потоку, который проходит по сети в монопольном режиме. Далее для краткости $z_{a}^{0}(1)$ называется передаваемым в монопольном режиме максимальным (МРМ-) потоком для пары p_a. Последовательное решение задачи 1 для каждой пары ${{p}_{m}}$, ${{p}_{m}} \in P$, позволяет сформировать вектор межузловых МРМ-потоков ${{{\mathbf{z}}}^{0}}(1) = (z_{1}^{0}(1),z_{2}^{0}(1),...$, $z_{m}^{0}(1)$, …, $z_{M}^{0}(1))$ и вектор дуговых потоков ${{{\mathbf{x}}}^{0}}(1) = (x_{{mk}}^{0}(1),x_{{m(k + E)}}^{0}(1))$, $m = \overline {1,M} $, $k = \overline {1,E} $.

На следующем этапе первого шага ${{{\mathbf{z}}}^{0}}(1),$ ${{{\mathbf{x}}}^{0}}(1)$ рассматриваются как некоторые векторы возможных направлений [4] для поиска совместно допустимого распределения МП-потока, при котором достигается предельно возможная загрузка одного или нескольких ребер.

Задача 2. Найти $\theta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(1) = \mathop {max}\limits_\theta \theta $

Решение $\theta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(1)$ задачи 2 – максимальная доля МРМ-потока, равная для всех ${{p}_{m}} \in P$. На основе $\theta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(1)$ вычисляются допустимые значения $z_{m}^{{**}}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)z_{m}^{0}(1),$ $m = \overline {1,M} $, равнодолевых квот на одновременную передачу потоков для всех пар источник–приемник ${{p}_{m}} \in P$ и дуговые потоки $x_{{mk}}^{{**}}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)x_{{mk}}^{0}(1)$, $x_{{m(k + E)}}^{{**}}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)x_{{m(k + E)}}^{0}(1)$, $m = \overline {1,M} $, $k = \overline {1,E} $. С формальной точки зрения $\theta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(1)$ – длина шага по возможному направлению ${{{\mathbf{z}}}^{0}}(1),$ ${{{\mathbf{x}}}^{0}}(1)$.

В рамках рассматриваемой модели отношение $z_{m}^{{**}}(1){\text{/}}z_{m}^{0}(1) = \theta {\kern 1pt} *{\kern 1pt} *(1)$ показывает, какую долю от МРМ-потока составляет выделенная квота $z_{m}^{{**}}(1)$. Поскольку по построению единственное оптимальное значение $\theta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(1)$ одинаково для всех пар ${{p}_{m}} \in P$, то указанное распределение называется равнодолевым распределением квот при одновременной передаче межузловых потоков для всех пар ${{p}_{m}} \in P$.

Для всех ребер сети определяется остаточная пропускная способность

На первом этапе второго шага (t = 2) для вектора d(2) и каждой пары ${{p}_{a}} \in P$ последовательно решается цепочка задач, аналогичных задаче 1.

Задача 3. Для некоторой фиксированной пары узлов p_a найти

Оптимальному решению задачи 3 (текущему МРМ-потоку $z_{a}^{0}(2)$) соответствует распределение потоков по ребрам сети $(x_{{ak}}^{0}(2),x_{{a(k + E)}}^{0}(2))$, ${{p}_{a}} \in P$, $k = \overline {1,E} $. Исходя из решения задачи 3 для всех ${{p}_{m}} \in P$ вычисляются коэффициенты

На втором этапе второго шага формулируется задача поиска “узкого места” в сети с заданными остаточными пропускными способностями ${{d}_{k}}(2),\;k = \overline {1,E} $, для определения максимально допустимого равнодолевого распределения квот.

Задача 4. Найти $\theta {\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(2) = \mathop {max}\limits_\theta \theta $

На основании найденного решения $\theta {\text{**}}(2)$ задачи 4 определяются результирующие межузловые потоки:

и для всех ребер сети вычисляется остаточная пропускная способность

На заключительном этапе текущего шага $t,t = \overline {2,T} ,$ $T \leqslant E$, осуществляется проверка условий:

– если после завершения очередного шага t окажется, что хотя бы для одного ${{r}_{k}} \in R$ величина остаточной пропускной способности ${{d}_{k}}(t + 1) > 0$, то переходим к шагу $t: = t + 1$;

– если же ${{d}_{k}}(t + 1) = 0$ для всех $k = \overline {1,E} $, то происходит останов, поскольку все пропускные способности сети полностью исчерпаны.

В ходе выполнения PLD-процедуры при равнодолевом распределении квот межузловых потоков на каждом шаге и предельной загрузке сети формируется финальный вектор распределения межузловых потоков ${\mathbf{z}}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(T)$. Далее вектор ${\mathbf{z}}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(T)$ будем называть PLES-потоком (от английского peak load equal share – предельная загрузка (сети) при равнодолевом распределении).

3. Уравнительное распределение потоков. При проведении PLD-процедуры допускается использование различных правил распределения межузловых потоков. Ниже рассматривается уравнительная стратегия распределения, при которой на каждом текущем шаге всем парам узлов-корреспондентов выделяются равные квоты на предельно допустимые потоки, которые могут передаваться по сети одновременно.

На первом этапе первого шага ($t = 1$) для всех ${{p}_{m}} \in P$ решается цепочка задач 1 и определяется МРМ-вектор

вектор дуговых потоков ${{{\mathbf{x}}}^{0}}(1) = (x_{{mk}}^{0}(1),x_{{m(k + E)}}^{0}(1))$, $m = \overline {1,M} $, $k = \overline {1,E} $, и вычисляются коэффициенты

На втором этапе первого шага формулируется задача поиска равных предельных квот на передачу потоков между всеми парами ${{p}_{m}} \in P$ и “узкого места” – ребер, пропускная способность которых при соответствующем распределении окажется полностью исчерпана.

Задача 5. Найти $\alpha {\kern 1pt} {\text{*}}(1) = \mathop {max}\limits_\alpha \alpha $

Решение задачи 5 – предельно допустимое значение (равное для всех) межузловых потоков $z_{m}^{*}(1) = \alpha {\kern 1pt} {\text{*(}}1)$, которые могут передаваться одновременно между всеми парами узлов-корреспондентов ${{p}_{m}},m = \overline {1,M} $. Соответствующие компоненты вектора дуговых потоков $x{\kern 1pt} {\text{*}}(1) = \alpha {\kern 1pt} {\text{*}}(1){{{\mathbf{x}}}^{0}}(1)$ равны $x_{{mk}}^{*}(1) = \alpha {\kern 1pt} {\text{*}}(1)\omega _{m}^{0}(1)x_{{mk}}^{0}(1),$ $x_{{m(k + E)}}^{*}(1) = \alpha {\kern 1pt} {\text{*}}(1)\omega _{m}^{0}(1)x_{{m(k + E)}}^{0}(1),$ $m = \overline {1,M} ,$ $k = \overline {1,E} ,$ и определяют допустимое уравнительное распределение дуговых потоков по ребрам сети. Для всех ребер сети вычисляется остаточная пропускная способность

На первом этапе второго шага (t = 2) для полученного вектора остаточных пропускных способностей ${{d}_{k}}(2)$ и для каждой пары ${{p}_{a}} \in P$ последовательно решается цепочка следующих задач, аналогичных задаче 1.

Задача 6. Для некоторой фиксированной пары узлов ${{p}_{a}}$ найти

Оптимальному решению задачи 6 (МРМ-потоку $z_{a}^{0}(2)$) соответствует распределение потоков по дугам сети $(x_{{ak}}^{0}(2),x_{{a(k + E)}}^{0}(2))$, $k = \overline {1,E} $.

После решения цепочки задач 6 для всех ${{p}_{m}},m = \overline {1,M} $, вычисляются коэффициенты

На втором этапе второго шага формулируется задача определения “узкого места” в сети с заданными остаточными пропускными способностями ${{d}_{k}}(2)$ при поиске максимальных равных квот на совместную передачу предельно допустимых потоков между всеми парами узлов-корреспондентов.

Задача 7. Найти $\alpha {\kern 1pt} {\text{*}}(2) = \mathop {max}\limits_\alpha \alpha $

Решение задачи 7 (квота $\alpha {\kern 1pt} {\text{*}}(2)$) определяет значение предельно допустимых межузловых потоков в сети $G(d(2))$ при фиксированных значениях компонент вектора $z{\kern 1pt} {\text{*}}(1)$. На основании $\alpha {\kern 1pt} {\text{*}}(2)$ на шаге t = 2 вычисляются результирующие межузловые потоки для всех пар ${{p}_{m}} \in P$:

и соответствующие дуговые потоки для $k = \overline {1,E} ,m = \overline {1,M} $:

Подсчитывается остаточная пропускная способность для $k = \overline {1,E} $:

На заключительном этапе текущего шага $t,t = \overline {2,T} ,$ $T \leqslant E$, осуществляется проверка условий:

– если после завершения очередного шага t окажется, что хотя бы для одного ${{r}_{k}} \in R$ величина остаточной пропускной способности ${{d}_{k}}(t + 1) > 0$, то переходим к шагу $t: = t + 1$;

– если же ${{d}_{k}}(t + 1) = 0$ для всех $k = \overline {1,E} $, то происходит останов, поскольку все пропускные способности сети полностью исчерпаны.

Далее финальный вектор $z{\kern 1pt} {\text{*}}(T)$ допустимых межузловых потоков, которые можно одновременно передать между всеми парами узлов-корреспондентов, называется PLED-потоком (от английского peak load equalitarian distribution – предельная загрузка (сети) при уравнительном распределении). Результирующие значения компонент PLED-потока $z_{m}^{*}(T),$ $m = \overline {1,M} $, определяются в ходе PLD-процедуры при пошаговом уравнительном распределении равных для всех пар ${{p}_{m}} \in P$ максимально допустимых квот на передачу потоков.

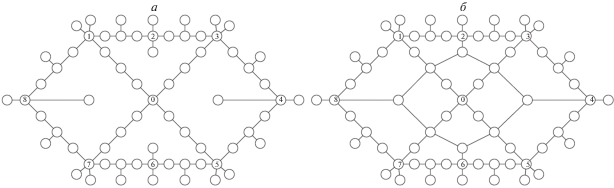
4. Вычислительный эксперимент. Вычислительные эксперименты с использованием PLD-процедуры проводились на моделях сетевых систем, представленных на рис. 1 (слева – базовая сеть, справа – кольцевая). В каждой сети имеется 69 узлов. Пропускные способности ребер – значения ${{d}_{k}}$, выбирались случайным образом из отрезка [900, 999] и совпадали для ребер, присутствующих в обеих сетях. В кольцевой сети пропускная способность каждого из добавленных ребер равна 900.

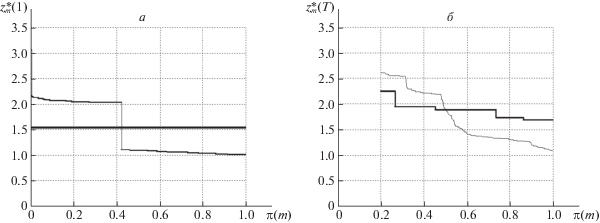
На рис. 2–5 тонкой линией указаны значения межузловых потоков $z_{m}^{{**}}(1),$ $z_{m}^{{**}}(T)$, полученные с использованием равнодолевого правила распределения, а жирной отмечены значения $z_{m}^{*}(1),$ $z_{m}^{*}(T)$, вычисленные для уравнительной стратегии. На диаграммах рис. 2–5 по вертикальной оси откладываются значения потоков (компонент векторов ${\mathbf{z}}{\kern 1pt} {\text{*}}(1)$, ${\mathbf{z}}{\kern 1pt} {\text{*}}(T)$, ${\mathbf{z}}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(1)$ и ${\mathbf{z}}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(T)$), упорядоченные по убыванию (не возрастанию). В соответствии с указанным порядком следования произведена перенумерация:

Для новых номеров пар узлов в упорядоченной последовательности вычисляются значения

которые откладываются по горизонтальной оси.

На диаграммах рис. 2, 3 слева представлены значения $z_{m}^{*}(1)$, полученные на первом шаге при выполнении PLD-процедуры. Прямая жирная линия, параллельная оси абсцисс, свидетельствует, что квоты, выделенные парам-корреспондентам на первом шаге при уравнительной стратегии, оказываются одинаковыми для всех ${{p}_{m}} \in P$. При равнодолевом распределении на первом шаге около половины пар получают меньше, а остальные – больше, чем при уравнительной стратегии. Из сравнения диаграмм на рис. 2, 3 следует, что указанная закономерность сохраняется и для финальных значений $z_{m}^{*}(T)$, $z_{m}^{{**}}(T)$ при полной загрузке сети. Значения $z_{m}^{*}(T)$, $z_{m}^{{**}}(T)$ указаны только для тех пар, у которых $\pi (i) \geqslant 0.2$ (80% от общего числа пар).

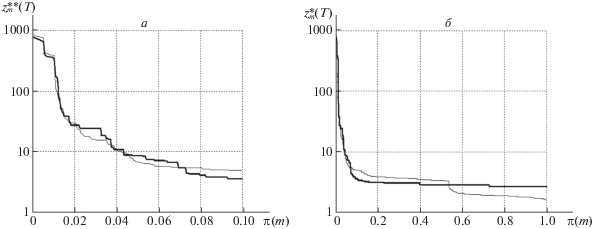
Диаграмма на рис. 3 справа свидетельствует, что при использовании уравнительной стратегии в кольцевой сети удается до останова распределять “почти равные” квоты на предельно допустимые межузловые потоки при полной загрузке сети. Финальные значения $z{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*(}}T)$ при равнодолевой стратегии распределения заметно отличаются от “почти равных” значений $z{\kern 1pt} {\text{*}}(T)$. Однако указанные различия становятся неразличимы для 2% пар-корреспондентов с большими значениями $z_{i}^{*}(T)$, $z_{i}^{{**}}(T)$ и $\pi (i) \leqslant 0.02$. На диаграммах по вертикальной оси для значений ${\mathbf{z}}{\kern 1pt} {\text{*}}(T)$, ${\mathbf{z}}{\kern 1pt} {\text{*}}{\kern 1pt} {\text{*}}(T)$ используется логарифмический масштаб (рис. 4, 5). Для большей наглядности на диаграммах слева приведены значения для 10% всех пар, для которых $\pi (i) \leqslant 0.1$.

На диаграммах рис. 2, 3 видно, что для 80% пар-корреспондентов разброс значений $z_{i}^{*}(T)$, $z_{i}^{{**}}(T)$ составляет 2–3 единицы, а сами значения не превосходят 5 единиц. Из анализа диаграмм рис. 4, 5 слева следует, что значения $z_{i}^{*}(T) \geqslant 10$ у 2% пар, а $z_{i}^{{**}}(T) \geqslant 10$ у 4% пар узлов-корреспондентов. При этом для 1% пар финальные значения $z_{i}^{*}(T)$, $z_{i}^{{**}}(T)$ превышают 100 при рекордных значениях чуть меньше 1000 единиц.

При использовании любого способа заполнения сети, начиная с некоторого шага, на многих ребрах остаточная пропускная способность ${{d}_{k}}(t)$ оказывается равна нулю. Сеть распадается на отдельные фрагменты, и локально для некоторых пар можно резко увеличить квоты на предельно допустимые потоки. В частности, остаточная пропускная способность ребер, соединяющих висячие вершины с сетью, может оказаться весьма значительной и на последних итерациях соответствующие квоты резко возрастут.

Результаты вычислительных экспериментов показывают, что PLD-процедура может быть использована для априорной оценки межузловых потоков при предельной загрузке сети.

Заключение. В ходе выполнения PLD-процедуры накапливается большое количество содержательно важных данных о структуре сети и маршрутах передачи потоков различных видов. В частности, на каждом этапе при решении задачи 1 определяются предельно допустимые дуговые потоки по ребрам соответствующего минимального разреза. Вектор-решение цепочки задач 1 – ${{x}_{0}}(1)$, для всех пар-корреспондентов содержит детализированную информацию о распределении всех видов потоков по дугам найденных минимальных разрезов при предельной загрузке ребер сети. Поскольку после решения задачи 2 для всех пар-корреспондентов фиксируются потоки $x{\text{*}}(1) = \theta {\kern 1pt} {\text{*}}(1){{x}_{0}}(1)$, то фактически маршруты передачи МРМ-потоков запоминаются и хранятся. На последующих этапах вектор остаточных пропускных способностей содержит хотя бы одну нулевую компоненту, а значения остальных становятся меньше исходных. В результате на каждом шаге найденные минимальные разрезы и маршруты передачи для многих видов потоков могут отличаться от зафиксированных ранее. Таким образом, в рамках PLD-процедуры фактически осуществляется поиск обходных путей соединения при достигнутой предельной загрузке одного из ребер.

В рамках формализма стандартной математической модели передачи многопродуктового потока PLD-процедура позволяет проследить взаимосвязь между максимальными значениями межузловых потоков и точкой на границе множества дуговых потоков $\mathcal{X}({\mathbf{d}})$ (см. (1.1)), в которой достигается полная загрузка всех ребер сети.