Известия РАН. Теория и системы управления, 2022, № 1, стр. 28-40
НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ ГИБРИДНЫХ СИСТЕМ ПЕРЕМЕННОЙ РАЗМЕРНОСТИ
А. С. Бортаковский *
МАИ (национальный исследовательский ун-т)
Москва, Россия
* E-mail: asbortakov@mail.ru
Поступила в редакцию 05.07.2021
После доработки 23.07.2021
Принята к публикации 26.07.2021
- EDN: OCHHGB
- DOI: 10.31857/S0002338821060056
Аннотация
Рассматривается задача оптимального управления гибридной системой, непрерывное движение которой чередуется с дискретными изменениями (переключениями), при которых меняется пространство состояний. Смена размерности пространства состояний происходит, например, при изменении количества управляемых объектов, что характерно, в частности, для задач управления группами подвижных объектов переменного состава. Моменты переключений заранее не заданы. Они определяются в результате минимизации функционала, при этом не исключаются процессы с мгновенными многократными переключениями. Доказаны необходимые условия оптимальности управления такими системами. Из-за наличия мгновенных многократных переключений эти условия отличаются от традиционных, в частности, уравнениями для вспомогательных переменных. Применение условий оптимальности демонстрируется на академическом примере.
Введение. Непрерывное движение гибридных систем переменной размерности (ГСПР) описывается дифференциальными уравнениями, а мгновенные изменения состояния (переключения) – рекуррентными уравнениями или включениями. В момент переключения меняется пространство состояний системы, в частности его размерность. Системы управления с изменяемым пространством состояний исследовались под разными названиями: составные системы [1, 2], системы с переменной размерностью [3], системы с разветвлением структур [4], ступенчатые системы [5], сложные (многоэтапные) процессы [6], системы со сменой фазового пространства [7], гибридные системы с промежуточными условиями [8, 9]. Большинство работ относятся к линейным системам и касаются вопросов устойчивости, управляемости и наблюдаемости [2, 4]. В задачах оптимального управления [1, 5, 7–9], как правило, моменты смены фазового пространства фиксированы или определяются промежуточными условиями, а переключения состояний неуправляемы. Количество переключений задано, а в первых работах [1, 5, 7] по этой тематике переключение единственное. Необходимые условия для гибридных систем с промежуточными условиями, обобщающие принцип максимума [10], получены в [8, 9]. В этих публикациях количество переключений задано, а сами переключения неуправляемы.
В статье рассматриваются задачи, в которых переключения состояний системы управляемы. Количество переключений задано, а моменты переключений – нет. Они определяются в результате минимизации функционала, в котором учитываются затраты на каждое переключение. При этом допускаются процессы с мгновенными многократными переключениями [11]. Такие процессы, как правило, исключаются в задачах оптимизации гибридных систем (ГС), несмотря на то, что именно они оказываются оптимальными не только в академических примерах, но и в приложениях, например в задачах группового управления.
Необходимые условия оптимальности управления динамическими системами, как правило, связаны с вычислением вариаций функционалов, определенных на траекториях движения. Для ГСПР такие вариации порождаются игольчатыми вариациями управления непрерывным движением системы, малыми вариациями управления переключениями, а также малыми вариациями моментов переключений. При доказательстве принципа максимума для непрерывных [10] или дискретных [12, 13] систем важную роль играют вспомогательные функции. Аналогичные функции используются для ГСПР. Между моментами переключений эти функции удовлетворяют сопряженной системе дифференциальных уравнений, а в моменты переключений – рекуррентным уравнениям. Из-за изменения размерности ГС приходится использовать разные наборы вспомогательных функций после каждого переключения.
Перечисленные вариации управлений непрерывным движением и переключениями – традиционные для непрерывных [10] и дискретных [12, 13] систем. Они порождают малые изменения траектории движения. Вариация моментов переключений приводит к необычным изменениям траектории. Возникают малые промежутки времени, на которых нельзя определить вариацию (даже отклонение) траектории, так как опорная и возмущенная траектории принадлежат разным пространствам состояний. Поэтому приходится преодолевать определенные технические трудности при вычислении вариации функционала.
Доказанные необходимые условия оптимальности ГСПР и ранее полученные достаточные условия [14] можно использовать для широкого круга задач управления с переключениями: непрерывно-дискретными [15], логико-динамическими, составными [1, 2], ступенчатыми системами [5], системами с промежуточными условиями [2, 8, 9, 16], с переменной или разветвляемой структурой [3, 4, 17, 18]. Применение необходимых условий оптимальности ГСПР демонстрируется на академическом примере.
1. Постановка задачи. Пусть на заданном промежутке времени $T = [{{t}_{0}},{{t}_{F}}]$ динамическая система совершает N переключений в моменты времени ti, $i = 1,...,N,$ образующие неубывающую конечную последовательность $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $:
(1.1)
${{t}_{0}} \leqslant {{t}_{1}} \leqslant ... \leqslant {{t}_{N}} \leqslant {{t}_{{N + 1}}}\mathop = \limits^\Delta {{t}_{F}}.$Между неравными последовательными моментами переключений состояние системы изменяется непрерывно, согласно дифференциальному уравнению:
(1.2)
${{\dot {x}}_{i}}(t) = {{f}_{i}}(t,{{x}_{i}}(t),{{u}_{i}}(t)),\quad t \in {{T}_{i}},\quad i \in \mathcal{N},$(1.3)
${{x}_{i}}({{t}_{i}}) = {{g}_{i}}({{t}_{i}},{{x}_{{i - 1}}}({{t}_{i}}),{{{v}}_{i}}),\quad i = 1,...,N.$В соотношениях (1.2) $\mathcal{N}\mathop = \limits^\Delta \,\{ \,i = 0,1,...,N\,{\mathbf{|}}\,{{t}_{i}} < {{t}_{{i + 1}}}\} $ – множество номеров ненулевых (по длине) частичных промежутков ${{T}_{i}}\, = \,\,[{{t}_{i}},{{t}_{{i + 1}}}]$ непрерывного изменения системы; ${{x}_{i}}(t)$ – состояние системы в момент времени $t \in {{T}_{i}}$, ${{x}_{i}}(t) \in {{X}_{i}} = {{\mathbb{R}}^{{{{n}_{i}}}}}$; ${{u}_{i}}(t)$ – управление непрерывным движением системы в момент времени $t \in {{T}_{i}}$, ${{u}_{i}}(t) \in {{U}_{i}} \subset {{\mathbb{R}}^{{{{p}_{i}}}}}$, Ui – заданное множество допустимых значений управления, $i \in \mathcal{N}$. При ${{t}_{i}} = {{t}_{{i + 1}}}$ дифференциальное уравнение (1.2) опускается ($i \notin \mathcal{N}$), функция ${{x}_{i}}( \cdot )$ определена в одной точке ${{x}_{i}}({{t}_{i}}) = {{x}_{i}}$, а значение ${{u}_{i}}({{t}_{i}})$ управления в этой точке несущественно. В уравнении (1.3) ${{{v}}_{i}}$ – управление переключением системы в момент ${{t}_{i}} \in \mathcal{T}$, ${{v}_{i}} \in {{V}_{i}} \subset {{\mathbb{R}}^{{{{q}_{i}}}}}$, ${{V}_{i}}$ – заданное множество допустимых управлений переключениями, $i = 1,...,N$. Функции fi : T × Xi × × ${{U}_{i}} \to {{\mathbb{R}}^{{{{n}_{i}}}}}$, $i = 0,1,...,N$, и ${{g}_{i}}:T \times {{X}_{{i - 1}}} \times {{V}_{i}} \to {{\mathbb{R}}^{{{{n}_{i}}}}}$, $i = 1,...,N$, непрерывны на всей области определения вместе с первыми частными производными по t и компонентам вектора xi. Возможное равенство последовательных моментов в (1.1) означает, что система совершает мгновенные многократные переключения [11].
Начальное состояние системы фиксировано ${{x}_{0}}({{t}_{0}}) = {{x}_{0}}$, а конечное определяется первым достижением терминальной поверхности $({{t}_{F}},{{x}_{N}}({{t}_{F}})) \in {{{\mathbf{\Gamma }}}_{N}}$, задаваемой системой уравнений
где ${{\Gamma }_{N}}:[{{t}_{0}}, + \infty ) \times {{X}_{N}} \to {{\mathbb{R}}^{{{{l}_{N}}}}}$ – непрерывно дифференцируемая вектор-функция. Аналогичные терминальные условия могут накладываться на левый конец траектории [19] либо на оба конца траектории одновременно (например, условие периодичности).Множество допустимых процессов ${{\mathcal{D}}_{0}}({{t}_{0}},{{x}_{0}})$ составляют четверки $d = (\mathcal{T},x( \cdot ),u( \cdot ),\{ {v}\} )$, включающие неубывающую последовательность $\mathcal{T}$ моментов переключений (1.1); последовательность $x( \cdot ) = \{ {{x}_{i}}( \cdot )\} _{{i = 0}}^{N}$ абсолютно непрерывных функций ${{x}_{i}}:{{T}_{i}} \to {{X}_{i}}$, $i \in \mathcal{N}$; последовательность $u( \cdot ) = \{ {{u}_{i}}( \cdot )\} _{{i = 0}}^{N}$ ограниченных измеримых функций ${{u}_{i}}:{{T}_{i}} \to {{U}_{i}}$; последовательность $\{ {v}\} = \{ {{{v}}_{i}}\} _{{i = 1}}^{N}$ векторов ${{{v}}_{i}} \in {{V}_{i}}$. Причем пары $({{x}_{i}}( \cdot ),{{u}_{i}}( \cdot ))$, $i \in \mathcal{N}$, удовлетворяют дифференциальному уравнению (1.2) почти всюду на промежутке Ti, тройки $({{x}_{{i - 1}}}({{t}_{i}}),{{x}_{i}}({{t}_{i}}),{{{v}}_{i}})$, $i = 1,...,N$, – рекуррентному уравнению (1.3). В начальный момент времени выполняется условие ${{x}_{0}}({{t}_{0}}) = {{x}_{0}}$, а в конечный – терминальное условие ${{\Gamma }_{N}}({{t}_{F}},{{x}_{N}}({{t}_{F}})) = 0$. Подчеркнем, что количество $N = {\text{|}}\mathcal{T}{\text{|}}$ переключений и моменты переключений $\mathcal{T} = \{ {{t}_{1}},...,{{t}_{N}}\} $ не фиксированы и у разных допустимых процессов могут не совпадать. При этом не исключается случай отсутствия переключений, когда $N = 0$ и $\mathcal{T} = \emptyset $ – пустое множество по определению.
На множестве ${{\mathcal{D}}_{0}}({{t}_{0}},{{x}_{0}})$ допустимых процессов задан функционал качества
(1.4)
${{I}_{0}}({{t}_{0}},{{x}_{0}},d) = \sum\limits_{i = 0}^N {\int\limits_{{{t}_{i}}}^{{{t}_{{i + 1}}}} {\,f_{i}^{0}(t,{{x}_{i}}(t),{{u}_{i}}(t))\,dt} } + \sum\limits_{i = 1}^N {g_{i}^{0}({{t}_{i}},{{x}_{{i - 1}}}({{t}_{i}}),{{{v}}_{i}})} + {{F}_{N}}({{t}_{F}},{{x}_{N}}({{t}_{F}})),$Требуется найти минимальное значение функционала (1.4) и оптимальный процесс d* = = $(\mathcal{T}*,x{\text{*}}( \cdot ),u*( \cdot ),\{ {v}*\} ) \in {{\mathcal{D}}_{0}}({{t}_{0}},{{x}_{0}})$, на котором это значение достигается:
(1.5)
${{I}_{0}}({{t}_{0}},{{x}_{0}},d*) = \mathop {\min }\limits_{d \in {{\mathcal{D}}_{0}}({{t}_{0}},{{x}_{0}})} {{I}_{0}}({{t}_{0}},{{x}_{0}},d).$Если наименьшее значение (1.5) не существует, то может быть поставлена задача нахождения минимизирующей последовательности допустимых процессов [19]. Количество переключений у процессов минимизирующей последовательности может оставаться конечным или неограниченно возрастать. Бесконечное количество переключений у оптимального процесса становится невозможным, если усилить условие ограниченности функции $g_{i}^{0}$ в (1.4), полагая $g_{i}^{0}(t,{{x}_{{i - 1}}},{{{v}}_{i}}) \geqslant {\text{const}}$ > 0. В этом случае каждое слагаемое $g_{i}^{0}$ в (1.4) можно рассматривать как затраты (или “штраф”) при переключении ${{x}_{{i - 1}}}({{t}_{i}}) \to {{x}_{i}}({{t}_{i}})$. Применение таких “штрафов” в функционале качества исключает фиктивные переключения, когда состояние не меняется ${{x}_{{i - 1}}}({{t}_{i}}) = {{x}_{i}}({{t}_{i}})$, а также последовательности процессов с неограниченным ростом числа переключений как неминимизирующие.
Отметим, что управляющие параметры в задаче (1.5) образуют “управляющий комплекс”, который включает: количество переключений N, моменты переключений ${{t}_{1}}$, …, ${{t}_{N}}$, управление непрерывным движением $u( \cdot )$, управление переключениями $\{ {v}\} $ и момент окончания процесса управления tF. Как правило, решение поставленной задачи I → min сводится к решению ряда задач ${{I}_{N}} \to \min $ с фиксированным числом переключений N, которое последовательно увеличивается: $N = 0,1,...$ Отметим, что в прикладных задачах количество переключений ограничено техническими требованиями.
2. Вариации функционала. Вывод условий оптимальности по методике [20] состоит в следующем: используя вариации управления, составляем уравнение для вариации траектории; выражаем вариацию функционала через вариации управления и траектории, исключаем из полученного выражения вариацию траектории, вводя вспомогательные переменные, удовлетворяющие дополнительным уравнениям и условиям трансверсальности (в форме [21]). Будем сравнивать значения функционала (1.5) на опорном (невозмущенном) допустимом процессе d = = $(\mathcal{T},x( \cdot ),u( \cdot ),\{ {v}\} )$ и возмущенном допустимом процессе $d = (\tilde {\mathcal{T}},\tilde {x}( \cdot ),\tilde {u}( \cdot ),\{ {\tilde {v}}\} )$. Для ГСПР используем два типа вариаций управляющих параметров: либо игольчатые вариации $\delta {{u}_{i}}( \cdot )$ управлений ${{u}_{i}}( \cdot )$, малые изменения $\delta {{{v}}_{i}}$ управления ${{{v}}_{i}}$ и малую вариацию $\delta {{t}_{F}}$ момента окончания, либо малые вариации $\delta {{t}_{i}}$ моментов переключений ti, $i = 1,...,N$.
2.1. Вариации управлений и момента окончания. Игольчатые вариации $\delta {{u}_{i}}( \cdot )$ управлений ${{u}_{i}}( \cdot )$ представляют собой конечные отклонения $\delta {{u}_{i}}(t) = {{\tilde {u}}_{i}}(t) - {{u}_{i}}(t)$ на множестве $T_{i}^{'} \subset {{T}_{i}}$ малой меры ${{\mu }_{i}}$, $i \in \mathcal{N}$. В остальных точках $t \in {{T}_{i}}{{\backslash }}T_{i}^{'}$ вариация $\delta {{u}_{i}}( \cdot )$ равна нулю. Величину $\mu = {{\mu }_{0}} + {{\mu }_{1}} + ... + {{\mu }_{N}}$ будем считать бесконечно малой первого порядка причем ${{\mu }_{i}} = 0$, $i \notin \mathcal{N}$. Предполагаем, что вариация $\delta {{t}_{F}} = {{\tilde {t}}_{F}} - {{t}_{F}}$ момента окончания и вариации $\delta {{{v}}_{i}} = {{{\tilde {v}}}_{i}} - {{{v}}_{i}}$ управлений переключениями имеют тот же порядок малости, т.е. $\delta {{t}_{F}}\sim \mu $ и ${\text{|}}{v}{\text{|}}\, = \,{\text{|}}{{{v}}_{1}}{\text{|}}\, + \,...\, + \,{\text{|}}{{{v}}_{N}}{\text{|}}\,\sim \,\mu $. Эти вариации порождают малые вариации $\delta x( \cdot ) = \tilde {x}( \cdot ) - x( \cdot )$ траектории, которые удовлетворяют уравнениям в вариациях:
(2.1)
$\delta {{\dot {x}}_{i}}(t) = {{f}_{{i\,{{x}_{i}}}}}[t]\,\delta {{x}_{i}}(t) + {{\tilde {f}}_{i}}[t] - {{f}_{i}}[t],\quad t \in {{T}_{i}},\quad i \in \mathcal{N},$(2.2)
$\delta {{x}_{i}}({{t}_{i}}) = {{g}_{{i\,{{x}_{{i - 1}}}}}}[{{t}_{i}}]\,\delta {{x}_{{i - 1}}}({{t}_{i}}) + {{g}_{{i\,{{{v}}_{i}}}}}[{{t}_{i}}]\,\delta {{{v}}_{i}},\quad i = 1,...,N.$Здесь и далее принято следующее [20]: аргумент t, заключенный в квадратные скобки, означает, что функция вычислена на опорном режиме в указанный момент времени. Например, ${{f}_{i}}[t] = {{f}_{i}}(t,{{x}_{i}}(t),{{u}_{i}}(t))$ – значение функции fi на опорном режиме; ${{f}_{{i\,{{x}_{i}}}}}[t] = {{f}_{{i\,{{x}_{i}}}}}(t,{{x}_{i}}(t),{{u}_{i}}(t))$ – матрица (Якоби) первых частных производных вектор-функции fi по компонентам вектора xi, вычисленная на опорном режиме. Знак “тильда” относится только к возмущенному управлению, т.е. ${{\tilde {f}}_{i}}[t] = {{f}_{i}}(t,{{x}_{i}}(t),{{\tilde {u}}_{i}}(t))$. Вариации $\delta x( \cdot )$ имеют порядок малости μ, а уравнения в вариациях (2.1), (2.2) выполняются с точностью $o(\mu )$.
Запишем вариацию функционала (1.4)
(2.3)
$\begin{gathered} \delta I = \sum\limits_{i = 0}^N {\int\limits_{{{t}_{i}}}^{{{t}_{{i + 1}}}} {\{ f_{{i\,{{x}_{i}}}}^{0}[t]\delta {{x}_{i}}(t) + \tilde {f}_{i}^{0}[t] - f_{i}^{0}[t]\} dt} + \sum\limits_{i = 1}^N {\{ g_{{i\,{{x}_{{i - 1}}}}}^{0}[{{t}_{i}}]\delta {{x}_{{i - 1}}}({{t}_{i}}) + g_{{i\,{{{v}}_{i}}}}^{0}[{{t}_{i}}]\delta {{{v}}_{i}}\} } } + \\ + \,\{ {{F}_{{N\,t}}}[{{t}_{F}}] + f_{N}^{0}[{{t}_{F}}]\} \delta {{t}_{F}} + {{F}_{{N\,{{x}_{N}}}}}[{{t}_{F}}]\delta {{x}_{{N\,F}}}, \\ \end{gathered} $Введем функции Гамильтона–Понтрягина (ГП) для непрерывного движения и переключений соответственно:
Здесь ${{\psi }_{i}} = (\psi _{i}^{1},...,\psi _{i}^{{{{n}_{i}}}})$ – вспомогательные переменные, $i = 1,...,N$. Предполагаем, что между моментами переключений функции ${{\psi }_{i}}:{{T}_{i}} \to {{\mathbb{R}}^{{{{n}_{i}}}}}$, $i \in \mathcal{N}$, абсолютно непрерывны и удовлетворяют сопряженным системам уравнений:
(2.4)
${{\dot {\psi }}_{i}}(t) = - \frac{{\partial \,{{H}_{i}}({{\psi }_{i}}(t),t,{{x}_{i}}(t),{{u}_{i}}(t))}}{{\partial \,{{x}_{i}}}},\quad i \in \mathcal{N},$(2.5)
${{\psi }_{{i - 1}}}({{t}_{i}}) = \frac{{\partial \,{{{\hat {H}}}_{i}}({{\psi }_{i}}({{t}_{i}}),{{t}_{i}},{{x}_{{i - 1}}}(t),{{{v}}_{i}})}}{{\partial \,{{x}_{{i - 1}}}}},\quad i = 1,...,N;$(2.6)
$\{ {{F}_{{N\,t}}}[{{t}_{F}}] - {{H}_{N}}[{{t}_{F}}]\} \delta {{t}_{F}} + \{ {{F}_{{N\,{{x}_{N}}}}}[{{t}_{F}}] + {{\psi }_{N}}({{t}_{F}})\} \,\delta {{x}_{{N\,F}}} = 0$Прибавляем к вариации (2.3) равенства
(2.7)
${{\psi }_{i}}(t)\,\delta {{x}_{i}}(t)\left. \, \right|_{{{{t}_{i}}}}^{{{{t}_{{i + 1}}}}} - \int\limits_{{{t}_{i}}}^{{{t}_{{i + 1}}}} {\{ {{{\dot {\psi }}}_{i}}(t)\,\delta {{x}_{i}}(t) + {{\psi }_{i}}(t)\,\delta {{{\dot {x}}}_{i}}(t)\} \,dt} = 0,\quad i = 0,1,...,N,$(2.8)
$ + \sum\limits_{i = 1}^N {\{ g_{{i\,{{x}_{{i - 1}}}}}^{0}[{{t}_{i}}]\;\delta {{x}_{{i - 1}}}({{t}_{i}}) + g_{{i\,{{{v}}_{i}}}}^{0}[{{t}_{i}}]\,\delta {{{v}}_{i}} + {{\psi }_{i}}({{t}_{{i + 1}}})\,\delta {{x}_{i}}({{t}_{{i + 1}}}) - {{\psi }_{i}}({{t}_{i}})\,\delta {{x}_{i}}({{t}_{i}})\} } + $В (2.8) учтено, что в начальный момент времени вариации траектории нет, т.е. $\delta {{x}_{0}}({{t}_{0}}) = 0$.
Рассмотрим сначала терминальные слагаемые, которые после подстановки δxN(tF) = δxNF – ‒ ${{f}_{N}}[{{t}_{F}}]\delta {{t}_{F}}$ можно преобразовать следующим образом:
Согласно условиям трансверсальности (2.6), это выражение равно нулю.
Теперь запишем подынтегральные слагаемые для одного промежутка $[{{t}_{i}},{{t}_{{i + 1}}}]$, $i \in \mathcal{N}$, подставляя для производных $\delta {{\dot {x}}_{i}}$ и ${{\dot {\psi }}_{i}}$ выражения из уравнений в вариациях (2.1) и сопряженной системы (2.4). Опуская индекс i (для сокращения записи), получаем
Следовательно, интегральные слагаемые вариации (2.8) имеют вид
Запишем слагаемые в (2.8), относящиеся к одному моменту переключений ti:
Подставляем вариацию (2.2) и группируем слагаемые с вариацией $\delta {{x}_{{i - 1}}}({{t}_{i}})$:
Учитывая (2.5), первое слагаемое равняется нулю. Второе – выражается через производную ${{\hat {H}}_{{i\,{{{v}}_{i}}}}}[{{t}_{i}}]$ функции ГП. Суммируя, получаем
Таким образом, вариация функционала (1.4) при варьировании управлений и момента окончания процесса управления имеет вид
(2.9)
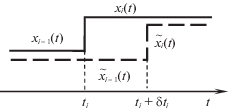
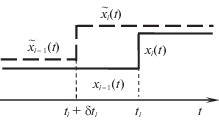
$\begin{gathered} \delta I = \sum\limits_{i = 0}^N {\int\limits_{{{t}_{i}}}^{{{t}_{{i + 1}}}} {\{ {{H}_{i}}({{\psi }_{i}}(t),t,{{x}_{i}}(t),{{u}_{i}}(t)) - {{H}_{i}}({{\psi }_{i}}(t),t,{{x}_{i}}(t),{{{\tilde {u}}}_{i}}(t))\} dt - } } \\ - \sum\limits_{i = 1}^N {\frac{{\partial \,{{{\hat {H}}}_{i}}({{\psi }_{i}}({{t}_{i}}),{{t}_{i}},{{x}_{{i - 1}}}({{t}_{i}}),{{{v}}_{i}})}}{{\partial {{{v}}_{i}}}}\delta {{{v}}_{i}}} . \\ \end{gathered} $2.2. Вариации моментов переключений. Будем варьировать только моменты переключений. Предполагаем, что вариации $\delta {{t}_{i}} = {{\tilde {t}}_{i}} - {{t}_{i}}$ моментов переключений ti, $i = 1,...,N$, настолько малы, что выполняются неравенства
Величину ${\text{|}}\delta t{\text{|}} = {\text{|}}\delta {{t}_{1}}{\text{|}} + ... + \,{\text{|}}\delta {{t}_{N}}{\text{|}}$ будем считать бесконечно малой первого порядка. На промежутках между моментами переключений ti и ${{t}_{i}} + \delta {{t}_{i}}$ вариации траектории $\delta x( \cdot )$ и управления $\delta u( \cdot )$ не определены, так как опорный и возмущенный процессы принадлежат разным пространствам. На рис. 1 и 2 изображены опорная (сплошная линия) и возмущенная (штриховая линия) траектории при вариации δti момента переключения ti. На рис. 1 представлен случай $\delta {{t}_{i}} > 0$, а на рис. 2 – случай $\delta {{t}_{i}} < 0$. На пересечениях $\Delta {{T}_{i}} = {{T}_{i}} \cap {{\tilde {T}}_{i}}$ промежутков ${{T}_{i}} = [{{t}_{i}},{{t}_{{i + 1}}}]$ и ${{\tilde {T}}_{i}} = [{{\tilde {t}}_{i}},{{\tilde {t}}_{{i + 1}}}]$, $i \in \mathcal{N}$, вариация $\delta {{x}_{i}}( \cdot )$ имеет тот же порядок малости, что и |δt|, а вариация управления нулевая. Уравнение в вариациях
(2.10)
$\delta {{\dot {x}}_{i}}(t) = {{f}_{{i\,{{x}_{i}}}}}[t]\,\delta {{x}_{i}}(t),\quad t \in \Delta {{T}_{i}},\quad i \in \mathcal{N},$Запишем вариацию функционала (1.4) при $\delta {{t}_{i}} > 0$, $i = 1,...,N$:
К этой вариации прибавляем равенства
Терминальные слагаемые будут равны нулю в силу условий трансверсальности (2.6)
Каждое подынтегральное выражение тоже равняется нулю, согласно уравнению в вариациях (2.10) и сопряженной системе (2.4):
Отметим, что в случае $\delta {{t}_{i}} < 0$ терминальные и интегральные члены вариации будут также нулевыми.
Запишем теперь слагаемые, относящиеся к одному моменту времени ti:
Преобразуем последнее слагаемое, подставляя вариацию
(2.11)
$\delta {{x}_{i}}({{t}_{i}} + \delta {{t}_{i}}) = {{g}_{{i\,{{x}_{{i - 1}}}}}}[{{t}_{i}}]\delta {{x}_{{i - 1}}}({{t}_{i}}) + \{ {{g}_{{i\,t}}}[{{t}_{i}}] + {{g}_{{i\,{{x}_{{i - 1}}}}}}[{{t}_{i}}]{{f}_{{i - 1}}}[{{t}_{i}}] - {{f}_{i}}[{{t}_{i}}]\} \delta {{t}_{i}}$Последнее слагаемое равно нулю, согласно уравнению (2.5). Оставшиеся члены записываем при помощи функции ГП:
Заменяя выражение в круглых скобках, согласно (2.5), получаем
При $\delta {{t}_{i}} < 0$ приходим к этой же формуле. Но в этом случае вместо замены (2.11) нужно использовать вариацию
Таким образом, вариация функционала при вариации моментов переключений имеет вид
(2.12)
$\begin{gathered} \delta I = \sum\limits_{i = 0}^N {\left\{ {{{H}_{i}}({{\psi }_{i}}({{t}_{i}}),{{t}_{i}},{{x}_{i}}({{t}_{i}}),{{u}_{i}}({{t}_{i}})) - {{H}_{{i - 1}}}({{\psi }_{{i - 1}}}({{t}_{i}}),{{t}_{i}},{{x}_{{i - 1}}}({{t}_{i}}),{{u}_{{i - 1}}}({{t}_{i}})){{ - }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}} \right.} \\ \left. { - \frac{\partial }{{\partial \,t}}{{{\hat {H}}}_{i}}({{\psi }_{i}}({{t}_{i}}),{{t}_{i}},{{x}_{{i - 1}}}({{t}_{i}}),{{{v}}_{i}})} \right\}\delta {{t}_{i}}. \\ \end{gathered} $3. Необходимые условия оптимальности. Полученные вариации (2.9) и (2.12) функционала (1.4), определенного на траекториях ГСПР, позволяют сформулировать необходимые условия оптимальности. Для учета неравенств (1.1) будем использовать метод Лагранжа [22, 23] снятия ограничений.
Теорема. Пусть оптимальный процесс $(\mathcal{T},x( \cdot ),u( \cdot ),\{ {v}\} )$ имеет N переключений в моменты t1, …, tN: ${{t}_{0}} \leqslant {{t}_{1}} \leqslant ... \leqslant {{t}_{N}} \leqslant {{t}_{F}}$. Тогда существуют функции ${{\psi }_{i}}( \cdot )$, $i = 0,1,...,N$, и такие числа λ0, λ1, …, λN+ 1, неравные нулю одновременно, что выполняются:
1) дифференциальные уравнения:
2) рекуррентные уравнения:
3) условие трансверсальности:
4) условие максимума функции ГП по управлению непрерывным движением
5) условие неположительности вариации функции ГП по управлению переключениями:
6) условие скачка функции ГП:
7) условие дополняющей нежесткости:
8) условие неотрицательности:
Доказательство. Если в качестве опорного процесса взять оптимальный, то вариации функционала (1.4) должны быть неотрицательными. Из неотрицательности вариации (2.9) следуют условия 4) и 5) теоремы. Действительно, возмущенное управление $\tilde {u}( \cdot )$ отличается от оптимального $u( \cdot )$ на множестве малой меры. Однако множество сколь угодно малой меры можно взять всюду плотным на T. Поэтому почти всюду на каждом промежутке интегрирования Ti выполняется неравенство
Чтобы снять ограничения ${{t}_{{i - 1}}} \leqslant {{t}_{i}}$, $i = 1,...,N + 1$, на моменты переключений используем принцип Лагранжа [22]. Функция Лагранжа для рассматриваемой задачи минимизации функционала (1.4) при ограничениях типа неравенств имеет вид
Заметим, что если из условий 4) и 5) теоремы удается выразить оптимальные управления ${{u}_{i}} = {{u}_{i}}({{\psi }_{i}},t,{{x}_{i}})$ и ${{{v}}_{i}} = {{{v}}_{i}}({{\psi }_{i}},{{t}_{i}},{{x}_{{i - 1}}})$ как функции времени, состояния и вспомогательных переменных, то, подставляя эти управления в уравнения движения и условия 1), 2) теоремы, получаем краевую задачу с промежуточными условиями. Ее решение зависит от ${{n}_{0}} + {{n}_{N}}$ произвольных постоянных, моментов переключений ${{t}_{1}},...,{{t}_{N}}$ и множителей ${{\lambda }_{0}},{{\lambda }_{1}},...,{{\lambda }_{{N + 1}}}$. Всего имеется ${{n}_{0}} + {{n}_{N}}$ + + 2N + 2 параметров. Остальные произвольные постоянные, получаемые при интегрировании дифференциальных уравнений движения (2.1) и сопряженных уравнений (2.4), связаны таким же количеством рекуррентных уравнений (2.2) и промежуточных условий (2.5). Начальные и конечные условия вместе с условиями трансверсальности дают ${{n}_{0}} + {{n}_{N}}$ уравнений, позволяющих исключить оставшиеся произвольные постоянные. Для нахождения остальных 2N + 2 параметров имеются $N$ условий 6) для скачка функции ГП и N + 1 условий дополняющей нежесткости. Этих условий хватает, так как коэффициенты λi определяются с точностью до положительного множителя. Как правило, систему дополняют либо равенством λ0 = 0 (вырожденный [22], нерегулярный [23] случаи), либо равенством λ0 = 1 (невырожденный, регулярный случаи). Таким образом, теорема, как и принцип максимума [10], дает “полную” систему условий, для нахождения процесса, который может быть оптимальным.
4. Пример. Рассмотрим движение группы объектов управления переменного состава на плоскости. Движение начинает один объект управления – носитель. При каждом переключении от него отделяется один объект, который продолжает самостоятельное управляемое движение к заданной цели. Количество управляемых объектов, а следовательно, и размерность гибридной системы увеличиваются с каждым переключением. Задача управления состоит в наискорейшем достижении всех заданных целей – терминальных положений объектов управления, т.е. решается задача многоцелевого быстродействия [15]. Применение необходимых условий оптимальности ГСПР покажем на простой задаче с одним переключением.
Пусть на промежутке времени $[0,T]$ система совершает одно переключение в момент ${{t}_{1}} \in [0,T]$. До переключения объект управления один – носитель. Его движение описывается уравнениями
В момент переключения t1 от носителя отделяется объект управления
(4.1)
${{x}_{1}}({{t}_{1}}) = {{x}_{0}}({{t}_{1}}),\quad {{y}_{1}}({{t}_{1}}) = {{y}_{0}}({{t}_{1}}),\quad x_{1}^{'}({{t}_{1}}) = {{x}_{0}}({{t}_{1}}),\quad y_{1}^{'}({{t}_{1}}) = {{y}_{0}}({{t}_{1}}).$Здесь x1, y1 – координаты носителя, а $x_{1}^{'}$, $y_{1}^{'}$ – координаты отделившегося объекта, которые, согласно (4.1), совпадают с координатами носителя.
После переключения движение системы описывается уравнениями
Момент окончания процесса управления определяется условиями
(4.2)
${{x}_{1}}(T) = {{x}_{T}},\quad {{y}_{1}}(T) = {{y}_{T}},\quad x_{1}^{'}(T) = x_{T}^{'},\quad y_{1}^{'}(T) = y_{T}^{'}.$Требуется найти наименьшее значение T и управление, на котором это значение достигается, т.е. решается задача группового быстродействия T → min.
По сравнению с общей постановкой задачи имеем:
Управление переключениями отсутствует, поэтому “управляющий комплекс” образуют управления непрерывным движением ${{\gamma }_{0}}( \cdot )$, ${{\gamma }_{1}}( \cdot )$, $\gamma _{1}^{'}( \cdot )$, момент переключения t1 и момент окончания T.
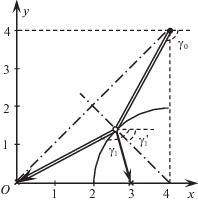
На рис. 3 траектория движения носителя изображена двойной линией, отделившегося объекта – полужирной линией, начальное состояние – полужирной точкой, конечные состояния носителя и отделившегося объектов – крестиками, точка разделения – окружностью. Направление движения указано стрелками.
Составляем функции ГП:
Записываем условия теоремы:
1) дифференциальные уравнения для вспомогательных переменных:
(4.3)
${{\dot {\psi }}_{{01}}} = 0,\quad {{\dot {\psi }}_{{02}}} = 0,\quad 0 \leqslant t \leqslant {{t}_{1}},\quad {{\dot {\psi }}_{{11}}} = 0,\quad {{\dot {\psi }}_{{12}}} = 0,\quad {{\dot {\psi }}_{{13}}} = 0,\quad {{\dot {\psi }}_{{14}}} = 0,\quad {{t}_{1}} \leqslant t \leqslant {{t}_{F}}.$Поскольку, согласно (4.3), вспомогательные функции постоянны, аргумент у этих функций далее не указывается;
2) рекуррентные уравнения для вспомогательных переменных:
(4.4)
${{\psi }_{{01}}} = {{\psi }_{{11}}} + {{\psi }_{{13}}},\quad {{\psi }_{{02}}} = {{\psi }_{{12}}} + {{\psi }_{{14}}};$3) условие трансверсальности:
(4.5)
$V{{\psi }_{{11}}}\cos {{\gamma }_{1}}(T) + V{{\psi }_{{12}}}\sin {{\gamma }_{1}}(T) + {v}{{\psi }_{{13}}}\cos \gamma _{1}^{'}(T) + {v}{{\psi }_{{14}}}\sin \gamma _{1}^{'}(T) - 1 = 0;$4) условие максимума функции ГП по управлению непрерывным движением, из которого следует равенство нулю производных функций ГП по γ0, γ1, $\gamma _{1}^{'}$:
(4.6)
${{\psi }_{{01}}}\sin {{\gamma }_{0}} - {{\psi }_{{02}}}\cos {{\gamma }_{0}} = 0,\quad {{\psi }_{{11}}}\sin {{\gamma }_{1}} - {{\psi }_{{12}}}\cos {{\gamma }_{1}} = 0,\quad {{\psi }_{{13}}}\sin \gamma _{1}^{'} - {{\psi }_{{14}}}\cos \gamma _{1}^{'} = 0.$Из этих равенств следует, что функции ${{\gamma }_{0}}( \cdot )$, ${{\gamma }_{1}}( \cdot )$, $\gamma _{1}^{'}( \cdot )$ – постоянны. Поэтому аргумент у этих функций далее не указывается;
5) условия неположительности вариации функции ГП по управлению переключениями нет, так как управление переключениями отсутствует;
6) условие скачка функции ГП:
7) условия дополняющей нежесткости: ${{\lambda }_{1}}( - {{t}_{1}}) = 0$, ${{\lambda }_{2}}({{t}_{1}} - T) = 0$;
8) условия неотрицательности: ${{\lambda }_{0}} \geqslant 0$, ${{\lambda }_{1}} \geqslant 0$, ${{\lambda }_{2}} \geqslant 0$.
Будем решать задачу при конкретных значениях параметров:
Разберем сначала крайние случаи, когда t1 = 0 или t1 = T. При t1 = 0 разделение объектов управления происходит в начальный момент времени. Тогда носитель достигает цели (начало координат) за время $T = 2\sqrt 2 $, а отделившийся объект приходит в конечное состояние (3, 0) – за время $T = \sqrt {17} $. Следовательно, терминальные условия (4.2) не выполняются. Случай t1 = T не подходит, так как в момент разделения t1 положение отделившегося объекта совпадает с положением носителя, а в конечный момент времени T – нет. Тогда $0 < {{t}_{1}} < T$ и из условий дополняющей нежесткости получаем ${{\lambda }_{1}} = 0$, ${{\lambda }_{2}} = 0$. Значит, ${{\lambda }_{0}} \ne 0$ из-за нетривиальности множителей Лагранжа. Поэтому задача невырожденная (регулярная) и можно взять ${{\lambda }_{0}} = 1$.
Обозначая через (x, y) координаты точки разделения, для невырожденной задачи из уравнений движения и терминальных условий получаем
(4.8)
$x + (T - {{t}_{1}})\cos \gamma _{1}^{'} = 3,\quad y + (T - {{t}_{1}})\sin \gamma _{1}^{'} = 0.$Система (4.8) вместе с условиями (4.4)–(4.7) для невырожденного случая (${{\lambda }_{1}} = {{\lambda }_{2}} = 0$, ${{\lambda }_{0}} = 1$) имеет 13 уравнений с 13 неизвестными: x, y, t1, T, ${{\gamma }_{0}}$, ${{\gamma }_{1}}$, $\gamma _{1}^{'}$, ψ01, ψ02, ψ11, ψ12, ψ13, ψ14. Найдем решение этой системы.
Исключая из последних четырех уравнений время T – t1 движения после разделения, приходим к равенству
Следовательно, точка разделения лежит на окружности Аполлония (см. рис. 3), так как отношение расстояний пройденных носителем и отделившимся объектом постоянно – равно отношению скоростей ($V{\text{/}}{v} = 2$).
Равенство (4.7) с учетом условия трансверсальности можно представить в виде $V{{\psi }_{{01}}}{\text{cos}}{{\gamma }_{0}}$ – ‒ Vψ02sinγ0 = 1. Решая это уравнение вместе с первым уравнением в (4.6) относительно ${{\psi }_{{01}}}$ и ${{\psi }_{{02}}}$, получаем
(4.9)
${{\psi }_{{01}}} = \frac{{\cos {{\gamma }_{0}}}}{V} = \frac{{x - 4}}{{2{{l}_{1}}}},\quad {{\psi }_{{02}}} = \frac{{\sin {{\gamma }_{0}}}}{V} = \frac{{y - 4}}{{2{{l}_{1}}}}.$Здесь ${{l}_{1}} = \sqrt {{{{(x - 4)}}^{2}} + {{{(y - 4)}}^{2}}} $ – длина пути до точки разделения (см. рис. 3). Из последних двух уравнений (4.6) находим ${{\psi }_{{12}}} = {{\psi }_{{11}}}{\text{tg}}{{\gamma }_{1}}$, ${{\psi }_{{14}}} = {{\psi }_{{13}}}{\text{tg}}\gamma _{1}^{'}$ и подставляем в уравнения (4.4) и в условие трансверсальности:
Выражаем $\cos {{\gamma }_{1}} = - x{\text{/}}{{l}_{2}}$, ${\text{tg}}{{\gamma }_{1}} = y{\text{/}}x$, $\cos \gamma _{1}^{'} = 2(3 - x{\text{)/}}{{l}_{2}}$, ${\text{tg}}\gamma _{1}^{'} = y{\text{/}}(x - 3)$ через координаты точки разделения. Здесь ${{l}_{2}} = \sqrt {{{x}^{2}} + {{y}^{2}}} $ – длина пути носителя после разделения. Подставляя значения тригонометрических функций и с учетом (4.9), получаем систему
Из первых двух уравнений находим
Подставляем эти выражения в третье уравнение в (4.9). После упрощений приходим к равенству
Для $0 \leqslant x \leqslant 4$ и $0 \leqslant y \leqslant 4$ получаем уравнение $(x - y)(x + y - 4) = 0$. Отсюда x = y или x + y = 4. Прямая x = y (см. рис. 3) не имеет общих точек с окружностью Аполлония, а прямая x + y = 4 пересекает ее в точке с координатами $x = 4 - \sqrt 2 $, $y = \sqrt 2 $. Следовательно, точка разделения будет $(4 - \sqrt 2 ,\sqrt 2 )$. Остальные неизвестные находятся без труда. Вычислим только минимальное значение функционала $\min T = 2\sqrt {{{x}^{2}} + {{y}^{2}}} {\text{/}}V = 2\sqrt {5 - 2\sqrt 2 } \approx 2.947$.
Таким образом, необходимым условиям оптимальности удовлетворяет траектория с точкой разделения $(4 - \sqrt 2 ,\sqrt 2 )$. Заметим, что эта траектория действительно оптимальная. В самом деле, из всех двухзвенных ломаных с концами (0, 0), (4, 4) и “промежуточной” вершиной (x, y), принадлежащей окружности, кратчайшей будет такая ломаная, звенья которой образуют равные углы с радиусом окружности, проведенным в вершину (x, y). Это следует из правила геометрической оптики: “угол падения равен углу отражения”.
Заключение. Предлагаемые условия оптимальности применяются для решения задач управления гибридными системами переменной размерности. Эти задачи отличаются от непрерывно-дискретных систем свободными моментами переключений, которые выбираются при оптимизации процесса управления. Именно поиск оптимальных моментов переключений является наиболее сложной частью решения. Необходимые условия обычно позволяют аналитически выразить управления непрерывным движением и переключениями через вспомогательные переменные. Получить аналитические выражения для оптимальных моментов переключений невозможно даже в простых примерах. Поэтому их приходится искать численно, а необходимые условия использовать для контроля процесса оптимизации. Следует заметить, что минимизируемый функционал как функция моментов переключений имеет овражный характер и множество локальных минимумов.
Изменение модели системы управления при переключениях, в частности ее размерности, ожидаемо усложняет условия оптимальности, так как количественно меняется набор вспомогательных функций. Гораздо сложнее учитывать мгновенные многократные переключения. В случае аналитического решения нужно рассматривать разные варианты реализации условий дополняющей нежесткости. При численном решении такие переключения требуется специальным образом предусматривать в процессе оптимизации.
Применение доказанных условий оптимальности кажется перспективным для решения задач управления группами подвижных объектов переменного состава. В частности, это задачи группового быстродействия. Такие задачи востребованы в авиации, космонавтике, робототехнике.
Список литературы
Величенко В.В. Оптимальное управление составными системами // Докл. АН СССР. 1967. Т. 176. № 4. С. 754–756.
Барсегян В.Р. Управление составных динамических систем и систем с многоточечными промежуточными условиями. М.: Наука, 2016.
Кириллов А.Н. Динамические системы с переменной структурой и размерностью // Изв. вузов. Приборостроение. 2009. Т. 52. № 3. С. 23–28.
Кириченко Н.Ф., Сопронюк Ф.А. Минимаксное управление в задачах управления и наблюдения для систем с разветвлением структур // Обозрение прикладной и промышленной математики. 1995. Т. 2. № 1.
Медведев В.А., Розова В.Н. Оптимальное управление ступенчатыми системами // АиТ. 1972. №. 3. С. 15–23.
Гурман В.И. Принцип расширения в задачах управления. М.: Наука, 1985.
Болтянский В.Г. Задача оптимизации со сменой фазового пространства // Дифференц. уравнения. 1983. Т. 19. № 3. С. 518–521.
Sussmann H.J. A Maximum Principle for Hybrid Optimal Control Problems // Proc. 38th IEEE Conf. on Decision and Control. Phoenix, 1999.
Дмитрук А.В., Каганович А.М. Принцип максимума для задач оптимального управления с промежуточными ограничениями // Нелинейная динамика и управление. Вып. 6. М.: Физматлит, 2008. С. 101–136.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Физматгиз, 1961.
Бортаковский А.С. Синтез оптимальных систем управления со сменой моделей движения // Изв. РАН. ТиСУ. 2018. № 4. С. 57–74.
Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука, 1973.
Пропой А.И. Элементы теории оптимальных дискретных систем. М.: Наука, 1973.
Бортаковский А.С. Достаточные условия оптимальности гибридных систем переменной размерности // Тр. МИАН. 2020. Т. 308. С. 88–100.
Бортаковский А.С. Необходимые условия оптимальности непрерывно-дискретных систем с мгновенными многократными переключениями дискретной части // Изв. РАН. ТиСУ. 2011. № 4. С. 73–85.
Величенко В.В. Условия оптимальности в задачах управления с промежуточными условиями // Докл. АН СССР. 1967. Т. 174. № 5. С. 1011–1913.
Емельянов С.В. Системы автоматического управления с переменной структурой. М.: Наука, 1967.
Boltyanski V.G. The Maximum Principle for Variable Structure Systems // Int. J. on Control. 2004. V. 77. № 17. P. 1445–1451.
Кротов В.Ф., Гурман В.И. Методы и задачи оптимального управления. М.: Наука, 1973.
Федоренко Р.П. Приближенное решение задач оптимального управления. М.: Наука, 1978.
Летов А.М. Динамика полета и управление. М.: Наука, 1973.
Васильев Ф.П. Методы оптимизации. М.: Факториал Пресс, 2002.
Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1974.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления