Известия РАН. Теория и системы управления, 2022, № 1, стр. 19-27

Введение. Традиционно управление ориентацией робототехнической системы осуществляют с помощью внешних движителей (колес, ног, винтов и т.д.). В случае агрессивных и ранимых сред предпочтительно использование робота с гладким и герметичным корпусом. Организовать движение такого робота можно с помощью движения внутренних масс. В [1–4] изучаются возможности управления ориентацией механической системы посредством движения одной или нескольких внутренних масс. Задача оптимального по быстродействию управления плоским поворотом тела при помощи внутренней массы поставлена и решена в публикации [5] в важном случае, когда внутренняя масса мала по сравнению с массой тела. Эта задача описана в [6]. В [7–10] результаты работы [5] развиты и обобщены для управления пространственной (трехмерной) ориентацией твердого тела при помощи подвижной внутренней массы. При рассмотрении поворота твердого тела при помощи подвижной внутренней массы в ряде случаев требуется учитывать геометрические ограничения, наложенные на ее траекторию. Как для задачи управления мобильным (капсульным) роботом, так и для управления ориентацией космического аппарата или другого подвижного объекта движение внутренней массы может быть ограничено габаритами того объема, в котором осуществляется движение внутренней массы [11].

В статье построены траектории движения внутренней массы, обеспечивающие заданный поворот твердого тела за кратчайшее время при ограничении в виде окружности. Как и в работах [5–11], предполагается, что внешними силами, действующими на систему, можно пренебречь. Это предположение справедливо для космических аппаратов, а также для случая быстрого поворота роботов, когда силы взаимодействия внутренней массы и несущего тела значительно превосходят внешние силы.

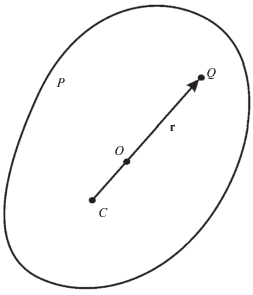
1. Описание механической системы. Рассмотрим систему, состоящую из твердого тела P массы M и подвижной материальной точки Q массы m, расположенной внутри тела (рис. 1). Посредством актюатора точка Q может перемещаться относительно тела P. Единственной силой, действующей в системе, является сила взаимодействия между телом P и материальной точкой Q. В начальный момент времени система покоится. Ограничимся рассмотрением плоскопараллельных движений указанных тел в плоскости, перпендикулярной одной из главных центральных осей инерции тела P.

Обозначим через C проекцию центра масс тела P на плоскость движения, а через О – проекцию центра масс системы P + Q на эту же плоскость. Введем векторы ${{R}_{С}} = \overline {OC} $ и $r = \overline {CQ} $. Так как внешние силы отсутствуют, то центр масс системы P + Q неподвижен. Поэтому имеем

где 0 – нулевой вектор.

Пусть ${{V}_{C}} = {{\dot {R}}_{C}}$ – абсолютная скорость центра масс C тела Р, а ω – угловая скорость тела P. Запишем условие сохранения импульса:

Здесь $\dot {r}$ – скорость тела Q относительно тела P. Обозначим через J момент инерции твердого тела P относительно оси, проходящей через точку C перпендикулярно плоскости движения тел. Как предполагается, эта ось является одной из главных центральных осей инерции тела P. Тогда из теоремы об изменении кинетического момента относительно начала координат О следует, что

Пусть $\mu = m/(M + m),$ тогда из соотношений (1.1) и (1.2) получим

Подставим (1.4) в уравнение (1.3). После преобразований получим основное уравнение

Свяжем с твердым телом P декартову систему координат CXY с началом в точке C. Обозначим через x и y координаты вектора r, через u и ${v}$ – проекции скорости точки Q на оси CX и CY соответственно, а через φ – угол поворота тела P в плоскости CXY. Тогда уравнение (1.5) примет следующую форму:

где $a = \sqrt {J{\text{/}}M} $ – радиус инерции тела P.

2. Постановки задач управления. Предполагаем, что точка Q может перемещаться с постоянной по величине скоростью V относительно тела P. Таким образом, на управляющие воздействия u и ${v}$ в системе (1.6) наложено ограничение

Кроме того, на координаты x и y точки Q наложено фазовое ограничение

где R – радиус окружности, внутри которой может осуществляться движение точки Q. Начальные состояния точки Q внутри окружности радиуса R и тела P запишем как где x₀ – заданное число, $\left| {{{x}_{0}}} \right| < R$.

Будем рассматривать две задачи управления: задачу со свободным концом траектории и двухточечную задачу.

В задаче со свободным концом зафиксируем угол поворота твердого тела при помощи условия

a конечное положение точки Q, т.е. координаты x (T) и y (T), считаем свободными.

В двухточечной задаче, помимо условия (2.4), наложены краевые условия

на конечное положение точки Q.

В обеих задачах требуется найти управления u(t), ${v}$(t) и траектории x(t), y(t) точки Q, при которых удовлетворяются уравнение (1.6), наложенные условия (2.1)–(2.5) и достигается наименьшее значение времени движения Т.

Точное решение поставленных задач оптимального быстродействия при произвольном μ приводит к операциям с эллиптическими функциями [6, 11]. Ниже предлагается более простое решение, близкое к оптимальному в важном случае малых μ.

Как показано в [5], в случае малых μ оптимальные траектории точки Q при отсутствии фазовых ограничений являются дугами окружностей. Поэтому естественно искать решение поставленных задач в виде комбинации дуг окружностей и движения по фазовому ограничению, которое является окружностью радиуса R. В точках сопряжения дуг окружностей они должны иметь общую касательную. Это вытекает из условий оптимальности [11] и представляется естественным с физической точки зрения: при негладком сопряжении дуг будут иметь место скачки скоростей тел, что нежелательно.

3. Анализ траекторий. В результате приходим к следующей структуре траекторий для поставленных задач.

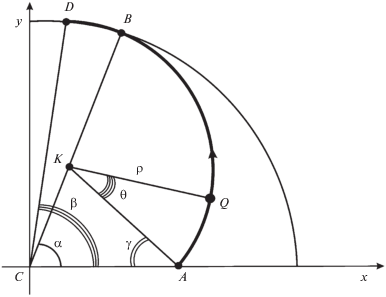
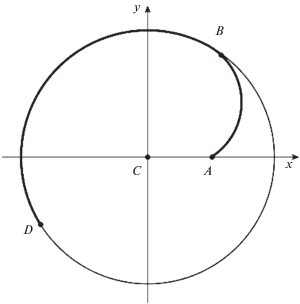
Сначала рассмотрим траектории для задачи со свободным правым концом. Такая траектория начинается в точке А с координатами $({{x}_{0}},{\text{0)}}$ из (2.3) и состоит из дуги АВ окружности некоторого радиуса ρ и дуги BD окружности радиуса R, лежащей на заданном ограничении (рис. 2). В точке В, имеющей координаты $(R{\text{cos}}\alpha ,R{\text{sin}}\alpha )$, обе окружности касаются. Траектория заканчивается в некоторой точке D с координатами $(R{\text{cos}}\beta ,R{\text{sin}}\beta )$. Данная траектория однозначно определяется параметрами α, ρ и β, которые подлежат определению.

Обозначим через К центр окружности радиуса ρ на рис. 2. Имеем равенства

Координаты точки К равны

Из треугольника СКА получим равенство

откуда находим

Обозначим через γ угол САК, а через θ – угол AKQ, определяющий положение точки Q, движущейся по окружности радиуса ρ и отсчитанный от радиуса KA (рис. 2). При движении Q от точки А до точки В этот угол изменяется от 0 до $\gamma + \alpha $. Из треугольника СКА имеем равенство

которое служит для определения угла γ через α и ρ. Координаты движущейся точки Q при этом запишутся в виде а ее скорости u, ${v}$, согласно (1.6), представим как

Подставим соотношения (3.1), (3.4) и (3.5) в последнее равенство (1.6). Получим

Для движения точки Q по дуге BD окружности радиуса R имеем соотношения

где δ – полярный угол точки Q, изменяющийся на дуге BD от α до β.

Подставляя соотношения (3.7) в последнее равенство (1.6), найдем

Суммарный угол поворота твердого тела ${{\varphi }_{Т}}$ получим, интегрируя равенство (3.6) для дуги АB и равенство (3.8) для дуги BD. Интегрирование по времени заменим интегрированием по углу θ от 0 до $\gamma + \alpha $ для равенства (3.6) и по углу δ от α до β для равенства (3.8). В результате получим равенство

где введено следующее обозначение:

Так как скорость движения точки Q постоянна и равна V, то для определения времени достаточно подсчитать полную длину траектории ABD. Имеем

Исключая β при помощи равенства (3.9), получим из (3.11)

Оптимизация траектории сводится к определению параметра α, доставляющего минимум выражению (3.12). Параметры γ и ρ, от которых зависит интеграл Δφ из (3.10) и правая часть соотношения (3.12), выражаются через α формулами (3.2) и (3.3). Поэтому вместо нахождения параметра α можно искать минимум выражения (3.12) по параметру ρ, считая, что углы α и γ выражаются через ρ посредством указанных формул. Искомый минимум можно определить численно. Заметим, что после дифференцирования выражения (3.12) по α или ρ параметр ${{\varphi }_{Т}}$ уничтожается. Следовательно, дуга AB не зависит от условия на конечный поворот твердого тела.

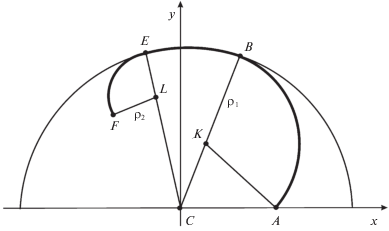
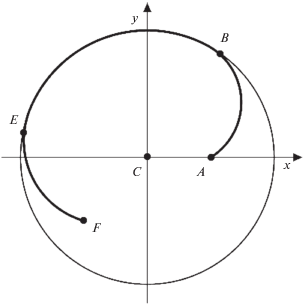
В двухточечной задаче (рис. 3) заданы начальная точка А и конечная точка F, лежащие внутри окружности радиуса R. Соответствующая траектория состоит из двух дуг АВ и EF радиусов ${{\rho }_{1}}$ и ${{\rho }_{2}}$ в начале и в конце движения и из дуги ВЕ радиуса R, лежащей на ограничении. Действуя аналогично случаю задачи со свободным правым концом, можно привести поиск оптимальной траектории к задаче минимизации времени движения по двум параметрам ${{\rho }_{1}}$ и ${{\rho }_{2}}$.

Например, можно выполнить следующие шаги. Вначале найдем параметры дуги AB из решения задачи со свободным концом и зафиксируем найденные значения $\Delta {{\varphi }_{1}},\alpha $ и ${{\rho }_{1}}$. Параметры дуги ВЕ и EF можно определить, решая задачу, похожую на задачу со свободным концом в обратном направлении. Систему координат расположим по аналогии с решенной задачей, а в начальный момент времени поместим материальную точку в ($\sqrt {x_{T}^{2} + y_{T}^{2}} ,0$), см. точку $F$ на рис. 3.

Для обратной задачи в качестве необходимого поворота твердого тела возьмем величину ${{\varphi }_{T}} - \Delta {{\varphi }_{1}}$. Она является уголом, на который должно повернуться твердое тело P после прохода точки Q по дугам FE и EB. Также добавим ограничение на конец дуги EB для сопряжения с дугой AB, найденной ранее. Будем обозначать переменные обратной задачи символом ~, тогда “новые” (для обратной задачи) и “старые” переменные связаны следующим образом:

где $\varepsilon $ – угол поворота “новой” системы координат относительно “старой”.

Обозначим через ${{T}_{1}}$, ${{T}_{2}}$, ${{T}_{3}}$ времена движения по дугам $AB$, $BE$, $EF$ соответственно. В результате решения первой задачи найдем ${{T}_{1}}$, а в результате решения второй (обратной) задачи определим ${{T}_{2}}$ и ${{T}_{3}}$.

Таким образом, путем решения двух однотипных задач минимизации по одной переменной будет найдена оптимальная траектория, доставляющая минимум суммарному времени:

5. Обсуждение результатов. Примеры траекторий при различных параметрах системы приведены на рис. 4–7. Во всех примерах 1–4 приняты следующие значения параметров:

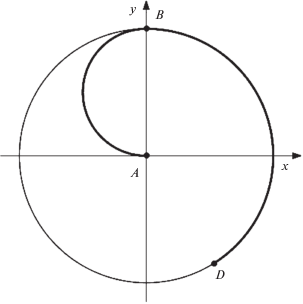
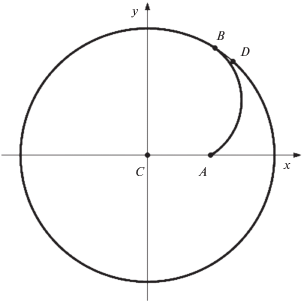
Примеры 1–3 соответствуют задаче со свободным правым концом, а пример 4 – двухточечной задаче. Для примеров 1–3 соответствующие данные представлены в таблице. В статье [11] для случая, когда в начальный момент времени точка Q находится в центре окружности радиуса R, найдена оптимальная траектория без учета ограничения на движение точки Q дугами окружностей. На рис. 4 приведены результаты численного решения с параметрами из упомянутой статьи. Траектории получились похожими, а длительности маневров почти совпали ($T = 8.35$ против $T = 8.34$). На рис. 5 описан случай, когда необходим поворот твердого тела в обратном направлении. Отметим также, что смещение начального положения материальной точки не приводит к качественному изменению траектории движения. Выше было замечено, что изменение величины необходимого поворота твердого тела P не приводит к изменению параметра α. При увеличении необходимого поворота твердого тела ${{\varphi }_{T}}$ дуга BD увеличивается, причем она может стать больше длины окружности радиуса R. На рис. 6 приведена траектория для случая, аналогичного рис. 5 с увеличенным значением ${{\varphi }_{T}}$. Как и предполагалось, дуга AB осталась неизменной, а дуга BD увеличилась.

Пример траектории для двухточечной задачи описан на рис. 7. Соответствующие значения параметров для этого примера таковы:

Условия, при которых построена траектория на рис. 7, аналогичны условиям траектории на рис. 5. Добавление краевых условий на конечное положение точки Q привело к увеличению времени маневра T. Это ожидаемо и связано с необходимостью попадания точки Q в ее конечное положение по дуге EF, что происходит с меньшей угловой скоростью твердого тела P. Изменение величины необходимого поворота, начальных или конечных условий для материальной точки не приводит к качественным изменениям траектории движения материальной точки. Длины дуг меняются по аналогии со случаем задачи со свободным концом.

Заключение. Когда внешние силы отсутствуют или очень малы, для управления ориентацией твердого тела можно использовать движение внутренней массы. Предложены решения задач о наискорейшем плоском повороте твердого тела посредством движения внутренней массы при наложенных фазовых ограничениях и различных краевых условиях. Задача сведена к поиску минимума у нелинейного выражения с одним неизвестным параметром. Анализ полученного выражения показал, что траектория выхода внутренней массы на ограничивающую окружность не зависит от величины необходимого поворота твердого тела. Построены и проанализированы оптимальные траектории движения внутренней массы. Результаты исследования могут представлять интерес при разработке мобильных роботов, которые не имеют внешних движителей, систем ориентации космических аппаратов и других движущихся объектов.