Известия РАН. Теория и системы управления, 2022, № 1, стр. 41-55
МНОГОАСПЕКТНАЯ КЛАСТЕРИЗАЦИЯ ПОДПРОСТРАНСТВ МЕТОДОМ АДАПТИВНОЙ ОПТИМИЗАЦИИ ГЛОБАЛЬНОГО ГРАФА СРОДСТВА
Л. Ванг a, b, *, Д. Жу a, b, Ю. Жу a, b, И. А. Матвеев c, **, С. Чен d
a Научный колледж Нанкинского ун-та аэронавтики и космонавтики
Нанкин, КНР
b Лаборатория математического моделирования и высокопроизводительных вычислений летательных аппаратов, Нанкинский ун-т аэронавтики и космонавтики
Нанкин, КНР
c Федеральный исследовательский центр “Информатика и управление” РАН
Москва, Россия
d Факультет экспериментального обучения, Нанкинский ун-т аэронавтики и космонавтики
Нанкин, КНР
* E-mail: wlpmath@nuaa.edu.cn
** E-mail: matveev@ccas.ru
Поступила в редакцию 11.08.2021
После доработки 15.08.2021
Принята к публикации 27.09.2021
- EDN: EHWAEA
- DOI: 10.31857/S0002338822010127
Аннотация
Рассматривается задача кластеризации объектов, каждый из которых представлен несколькими векторами данных в различных пространствах признаков – так называемая многоаспектная кластеризация. Предлагается метод решения этой задачи посредством построения графов смежности в каждом из пространств признаков и общего графа сродства объектов. Выполняется последовательность итераций, на каждой из которых уточняются графы смежности и граф сродства. Также накладывается ограничение на ранг матрицы Лапласа графа сродства, что в силу известной теоремы обеспечивает разбиение графа на несколько компонент связности, которые после завершения итераций считаются искомыми кластерами. В численных экспериментах используются несколько тестовых баз из открытых источников. Результаты сравниваются с известными методами, получено некоторое преимущество предлагаемого подхода.
0. Введение. В связи с информатизацией возрастает количество данных с многими представлениями или аспектами, в которых описания объектов взяты из нескольких различных источников или даны различными признаками [1]. Например, веб-страница может быть представлена текстом, изображениями и гиперссылками; изображение может быть описано с помощью гистограмм, спектральных или морфологических характеристик [2], наборами угловых точек и т.д. Данные с несколькими аспектами порождают новый класс методов кластеризации, многоаспектную кластеризацию (МАК) (multi-view clustering, MVC). Методы наиболее полного использования дополнительной и непротиворечивой информации из различных представлений важны во многих приложениях [3]. Разработано множество алгоритмов МАК, которые в соответствии с целью и реализуемой стратегией можно разделить на пять категорий: многоаспектная спектральная кластеризация (multi-view spectral clustering) [4], многоядерная кластеризация (multi-kernel clustering) [5], многоаспектная кластеризация неотрицательным матричным разложением (multi-view nonnegative matrix factorization clustering) [6], многоаспектная кластеризация подпространств (multi-view subspace clustering) [7] и канонический корреляционный анализ (canonical correlation analysis) [8].
В этой статье основное внимание уделяется многоаспектной кластеризации подпространств (МАКП) (multi-view subspace clustering, MVS). Этот класс методов появился при сочетании двух подходов: многоаспектности (использования данных об объектах из различных представлений) и поиска таких разбиения и признаков, что каждый кластер соответствует подпространству объединенного пространства признаков. Известные алгоритмы МАКП работают следующим образом:
1) для каждого аспекта строится матрица смежности;
2) построенные матрицы некоторым образом объединяются в матрицу сродства;
3) для полученной матрицы сродства выполняется алгоритм спектральной кластеризации, дающий окончательный результат.
Очевидно, эффективность МАКП существенно зависит от способа построения матрицы сродства. Сегментация ансамбля подпространств при блочных ограничениях (ensemble subspace segmentation under blockwise constraints, ESSB) [9] сначала строит матрицы смежности для каждого аспекта, а затем получает матрицу сродства как среднее этих матриц. Такой подход не использует взаимосвязь различных аспектов [10]. Система кластеризации на основе графов (graph-based system, GBS) [11] выделяет структуру многообразия при помощи разреженного представления различных аспектов, единая матрица сродства получается как взвешенная комбинация. Многоаспектная кластеризация обучением графа (multiview clustering by graph learning, MVGL) [12] строит начальные матрицы для отдельных аспектов, затем эти матрицы уточняются решением специальной оптимизационной задачи. Матрица сродства получается их комбинацией.
Здесь и далее для отношений смежности и сродства термины граф и матрица используются как взаимозаменяемые, поскольку существует взаимно-однозначное соответствие между полным неориентированным взвешенным графом с N пронумерованными вершинами и симметрической матрицей размером N × N, содержащей веса ребер графа. Граф с несколькими компонентами связности и вершинами, занумерованными так, что номера вершин каждой компоненты идут подряд, соответствует блочно-диагональной матрице. Для приложений смысл имеет граф и его компоненты связности, называемые кластерами, при расчетах используется матричное представление. Матрицей Лапласа (Кирхгофа) для матрицы W называется матрица
где D – диагональная матрица, диагональные элементы которой равны сумме в соответствующих строках W. Доказана следующая теорема.Теорема. Если матрица Лапласа ${{L}_{W}}$ имеет c нулевых собственных значений, то граф W содержит c компонент связности [13].
Следствие 1. Если ранг ${\text{rank}}\;{{L}_{W}} = N - c$, то граф W содержит c компонент связности.
Следствие 2. Если ранг ${\text{rank}}\;{{L}_{W}} = N - c$, то связанной перестановкой строк и столбцов можно свести матрицу W к блочно-диагональному виду.
Методы [9, 11, 12] объединяют информацию из разных аспектов для создания матрицы сродства. При этом методы GBS и MVGL используют дополнительную информацию о взаимосвязях аспектов. Однако матрицы смежности для каждого аспекта получаются отдельно и далее не меняются. Если многоаспектные данные содержат шум или пропуски, первоначально построенные матрицы смежности не могут точно выразить корреляции объектов в каждом отдельном аспекте, получаемая матрица сродства также не точна и качество кластеризации падает. Имеет смысл улучшать построенные матрицы смежности, используя матрицу сродства, объединяющую все аспекты.
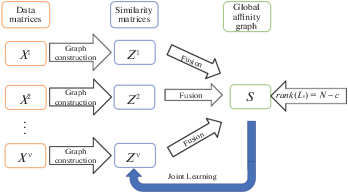
В статье предлагается новый алгоритм МАКП: адаптивное обучение глобального графа сродства (adaptive global affinity graph learning, AGAGL). На рис. 1 показана общая схема работы AGAGL, включающая начальное построение матриц смежности отдельных аспектов, сведение этих матриц к одной глобальной матрице сродства с использованием функции невязки и ограничения на ранг матрицы Лапласа. После получения матрицы сродства пересчитываются матрицы смежности. В конечном счете разбиение на кластеры получается, согласно следствию 1, непосредственно из глобальной матрицы сродства без каких-либо дополнительных алгоритмов кластеризации.
Особенности представленного метода:
1) введена функция невязки между глобальной матрицей сродства и матрицами смежности отдельных аспектов;
2) на каждом шаге итеративно пересчитываются матрица сродства и матрицы смежности;
3) окончательное разбиение на кластеры получается благодаря ограничению ранга матрицы Лапласа графа сродства.
Далее в разд. 1 дана постановка задачи и описаны некоторые применяемые методы, в разд. 2 рассмотрен предлагаемый метод и процедура оптимизации. Экспериментальные результаты и анализ приведены в разд. 3.
1. Постановка задачи и применяемые методы. Изложим чуть более подробно два подхода, из которых был развит представленный метод.
1.1. Кластеризация подпространств. Пусть в линейном пространстве размерности d задано c попарно не совпадающих подпространств. Из каждого подпространства взято несколько ненулевых объектов (векторов), их общее количество равно N, $N > d$. Эту совокупность назовем обучающей выборкой. Ее можно представить в виде матрицы $X = [{{x}_{1}}, \cdots ,{{x}_{N}}]$, составленной из столбцов-векторов ${{x}_{i}} \in {{\mathbb{R}}^{d}}$. Цель метода кластеризации подпространств – найти разбиение N объектов обучающей выборки на c кластеров, наиболее близкое к истинному, т.е. в каждом полученном кластере должны содержаться объекты одного подпространства. Предполагается, что каждый вектор обучающей выборки может быть представлен как линейная комбинация остальных:
Это можно записать в виде $X = XZ$, $X \in {{\mathbb{R}}^{{d \times N}}}$, $Z \in {{\mathbb{R}}^{{N \times N}}}$, ${\text{diag}}\;Z = 0$. Матрицу Z назовем матрицей смежности, элемент zij определяет сходство векторов xi и xj, $i \ne j$. Большую роль при обработке реальных данных играет также наличие шума измерения (относительно небольших случайных отклонений многих значений xij, как правило, описываемых нормальным распределением) и выбросов (больших отклонений некоторых векторов xi). В этом случае разложение записывается как $X = XZ + E$, где $E \in {{\mathbb{R}}^{{d \times N}}}$ – матрица невязки. Эти представления неоднозначны, поэтому на матрицы смежности и невязки можно накладывать различные ограничения (регуляризации), получая различные алгоритмы, такие, как регрессия наименьших квадратов (least squares regression, LSR) [14], разреженный граф с ограничениями на блоки (blockwise constrained sparse graph, SGB) [15], низкоранговое представление (low-rank representation, LRR) [16], разреженная кластеризация подпространств (sparse subspace clustering, SSC) [17], и т.д.
LSR минимизирует взвешенную сумму нормы Фробениуса матрицы Z и матрицы невязки $E = X - XZ$. Такой подход хорошо работает на данных с гауссовым шумом. LSR формулируется как следующая оптимизационная задача:
(1.1)
$\begin{gathered} \mathop {min}\limits_{Z,E} (\mathop {\left\| Z \right\|}\nolimits_F^2 + \lambda \mathop {\left\| E \right\|}\nolimits_F^2 ) \\ {\text{s}}.{\text{t}}.\quad X = XZ + E,\quad {\text{diag}}\;Z = 0, \\ \end{gathered} $(1.2)
$\begin{gathered} \mathop {min}\limits_{Z,E} (\mathop {\left\| Z \right\|}\nolimits_F^2 + \lambda \mathop {\left\| E \right\|}\nolimits_{2,1}^2 + \mu {\text{Tr}}(ZW{{Z}^{{\text{T}}}})) \\ {\text{s}}.{\text{t}}.\quad X = XZ + E,\quad {\text{diag}}\;Z = 0, \\ \end{gathered} $После нахождения оптимального решения Z окончательное разбиение на кластеры получается спектральной кластеризацией $Z$ [19–22].
1.2. МАКП. Набор данных с несколькими аспектами $X = \{ {{X}^{1}}, \cdots ,{{X}^{v}}\} $ представляет собой матрицу, составленную вертикально из ${v}$ матриц аспектов. Матрица i-го аспекта X i = = 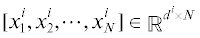 , d i – размерность аспекта, N – количество объектов выборки, $\sum {{{d}_{i}} = d} $. Есть два способа получить матрицу сродства Z для МАКП.
, d i – размерность аспекта, N – количество объектов выборки, $\sum {{{d}_{i}} = d} $. Есть два способа получить матрицу сродства Z для МАКП.
Первый способ. Сразу строить единую матрицу, общую для всех аспектов. Различные аспекты должны иметь одну и ту же матрицу смежности, поскольку данные каждого из них соответствуют одним и тем же объектам. Такой метод называется ранним слиянием (early fusion). В [23] предложена следующая модель раннего слияния:
(1.3)
$\begin{gathered} \mathop {min}\limits_{Z,{{\alpha }_{i}}} \sum\limits_{i = 1}^{v} \,({{\alpha }^{i}}\mathop {{\text{||}}{{X}^{i}} - {{X}^{i}}Z{\text{||}}}\nolimits_{2,p}^p + \mu {\text{Tr}}(ZL_{W}^{i}{{Z}^{{\text{T}}}})) \\ {\text{s}}.{\text{t}}.\quad {{\alpha }^{i}} \geqslant 0,\quad {\text{diag}}Z = 0, \\ \end{gathered} $Второй способ. Получить матрицу смежности ${{Z}^{i}}$ для каждого аспекта, объединить эти отдельные матрицы в матрицу сродства Z [9, 25, 26] и, наконец, провести кластеризацию по Z. Такой метод называется поздним слиянием (late fusion). Например, в ESSB [9] матрица смежности каждого аспекта определяется решением следующей задачи:
(1.4)
$\begin{gathered} \mathop {min}\limits_{{{Z}^{i}},{{E}^{i}}} ({\text{||}}{{Z}^{i}}{\text{||}}_{F}^{2} + \lambda {\text{||}}{{E}^{i}}{\text{|}}{{{\text{|}}}_{{2,1}}} + \mu {\text{Tr}}({{Z}^{i}}L_{W}^{i}{{Z}^{i}}^{{\text{T}}})) \hfill \\ {\text{s}}.{\text{t}}.\quad {{X}^{i}} = {{X}^{i}}{{Z}^{i}} + {{E}^{i}},\quad {\text{diag}}\;{{Z}^{i}} = 0. \hfill \\ \end{gathered} $Матрица сродства задается усреднением матриц смежности:
2. Метод AGAGL. Составим целевую функцию, сочетая кластеризацию подпространств, МАКП и вводя ограничения на ранг матрицы Лапласа.
2.1. Построение целевой функции. Аналогично регрессии наименьших квадратов (1.1) для матриц смежности ${{Z}^{i}}$ используется норма Фробениуса, для невязок ${{E}^{i}}$ берется норма ${{l}_{{2,1}}}$, порождающая матрицы с немногими ненулевыми столбцами, соответствующими выбросам данных [15]. Чтобы раскрыть внутреннюю локальную структуру данных, добавим к (1.1) слагаемое лапласовской регуляризации, которое обеспечивает то, что два похожих объекта в исходном пространстве близки и в новом пространстве [26]. Регуляризация лапласианом выражается как
(2.1)
$\begin{gathered} \mathop {min}\limits_{{{Z}^{i}},{{E}^{i}}} \left( {\sum\limits_{i = 1}^{v} {\text{||}}{{Z}^{i}}{\text{||}}_{F}^{2} + \lambda \sum\limits_{i = 1}^{v} \,{\text{||}}{{E}^{i}}{\text{|}}{{{\text{|}}}_{{2,1}}} + \mu \sum\limits_{i = 1}^{v} \,{\text{Tr}}({{Z}^{i}}L_{W}^{i}{{Z}^{i}}^{{\text{T}}})} \right) \\ {\text{s}}.{\text{t}}.\quad {{X}^{i}} = {{X}^{i}}{{Z}^{i}} + {{E}^{i}},\quad {\text{diag}}\;{{Z}^{i}} = 0, \\ \end{gathered} $В связи с тем, что данные различных аспектов поступают от одних и тех же исходных объектов, существует общая структура кластера для всех аспектов. Следует найти глобальный граф сродства $S$ для описания общей структуры. Чтобы в полной мере использовать информацию о согласованности, скрытую в нескольких аспектах, определяется функция стоимости несогласия для измерения разницы между матрицей смежности ${{Z}^{i}}$ и общей матрицей сродства $S$:
Объединяя (2.1) и (2.2), можно записать задачу:
(2.3)
$\begin{gathered} \mathop {min}\limits_{{{Z}^{i}},{{E}^{i}},{{L}^{i}},S} \left( {\sum\limits_{i = 1}^{v} {\text{||}}{{Z}^{i}}{\text{||}}_{F}^{2} + \lambda \sum\limits_{i = 1}^{v} {\text{||}}{{E}^{i}}{\text{|}}{{{\text{|}}}_{{2,1}}}} \right. + \left. {\mu \sum\limits_{i = 1}^{v} \,{\text{Tr}}({{Z}^{i}}L_{W}^{i}{{Z}^{i}}^{{\text{T}}}) + \alpha \sum\limits_{i = 1}^{v} {\text{||}}S - {{Z}^{i}}{\text{||}}_{F}^{2}} \right) \\ {\text{s}}.{\text{t}}.\quad {{X}^{i}} = {{X}^{i}}{{Z}^{i}} + {{E}^{i}},\quad {\text{diag}}\;{{Z}^{i}} = 0,\quad {\text{rank}}\;{{L}_{S}} = N - c. \\ \end{gathered} $В известных из литературы методах МАК после получения матрицы сродства необходимо выполнить окончательную кластеризацию, например, методом k-средних или N-разреза. С ограничением ранга ${\text{rank}}\;{{L}_{S}} = N - c$ можно напрямую получить результат кластеризации из графа сродства S без каких-либо дополнительных шагов кластеризации. Поскольку ${{L}_{S}}$ является полуположительно определенной матрицей [27], все ее собственные значения неотрицательны. Предположим, что $N$ собственных значений ${{L}_{S}}$ упорядочены по возрастанию: $0 \leqslant {{\sigma }_{1}} \leqslant \cdots \leqslant {{\sigma }_{N}}$. Если выполняется rank${{L}_{S}} = N - c$, это означает, что сумма c наименьших собственных значений ${{L}_{S}}$ равна 0, т.е.
Согласно теореме, можно получить [28], что
(2.5)
$\sum\limits_{i = 1}^c \,{{\sigma }_{i}} = \mathop {min}\limits_{{{Q}^{{\text{T}}}}Q = I} {\text{Tr}}({{Q}^{{\text{T}}}}{{L}_{S}}Q),\quad Q \in {{\mathbb{R}}^{{c \times N}}}.$Когда все элементы S нулевые, для (2.5) существует тривиальное решение. Чтобы избежать тривиального решения, добавляется ограничение $1 \cdot {{s}_{j}} = 1$, где ${{s}_{j}}$ представляет каждый столбец матрицы S, $1 = [1, \ldots ,1]$, точка обозначает операцию скалярного умножения векторов. Тогда (2.5) преобразуется в
(2.6)
$\begin{gathered} \mathop {min}\limits_Q {\text{Tr}}({{Q}^{{\text{T}}}}{{L}_{S}}Q) \\ {\text{s}}.{\text{t}}.\quad {{Q}^{{\text{T}}}}Q = I,\quad 1 \cdot {{s}_{j}} = 1,\quad {{s}_{j}} \geqslant 0,\quad Q \in {{\mathbb{R}}^{{c \times N}}}. \\ \end{gathered} $Оптимизационную задачу AGAGL можно окончательно записать в виде
(2.7)
$\begin{gathered} \mathop {min}\limits_{{{Z}^{i}},{{E}^{i}},{{L}^{i}},S,Q} \left( {\sum\limits_{i = 1}^{v} {\text{||}}{{Z}^{i}}{\text{||}}_{F}^{2} + \lambda \sum\limits_{i = 1}^{v} {\text{||}}{{E}^{i}}{\text{|}}{{{\text{|}}}_{{2,1}}} + \mu \sum\limits_{i = 1}^{v} \,{\text{Tr}}({{Z}^{i}}{{L}^{i}}{{Z}^{i}}^{{\text{T}}}) + } \right.\left. {\alpha \sum\limits_{i = 1}^{v} {\text{||}}S - {{Z}^{i}}{\text{||}}_{F}^{2} + \beta {\text{Tr}}({{Q}^{T}}{{L}_{S}}Q)} \right) \\ {\text{s}}.{\text{t}}.\quad {{X}^{i}} = {{X}^{i}}{{Z}^{i}} + {{E}^{i}},\quad {\text{diag}}\;{{Z}^{i}} = 0,\quad {{Q}^{{\text{T}}}}Q = I,\quad 1 \cdot {{s}_{j}} = 1,\quad {{s}_{j}} \geqslant 0, \\ \end{gathered} $2.2. Процедура оптимизации. Для решения задачи (2.7) применяется расширенный метод множителей Лагранжа. Расширенное уравнение Лагранжа может быть записано как
(2.8)
$\begin{gathered} \mathop {min}\limits_{{{Z}^{i}},{{E}^{i}},{{L}^{i}},S,Q} L = \sum\limits_{i = 1}^{v} \,[{\text{Tr}}\{ {{Z}^{i}}^{{\text{T}}}((1 + \alpha )I + \mu {{L}^{i}}){{Z}^{i}}\} - 2\alpha {\text{Tr}}({{Z}^{i}}^{{\text{T}}}S)] + \\ \, + \alpha \sum\limits_{i = 1}^{v} \,\mathop {\left\| S \right\|}\nolimits_F^2 + \lambda \sum\limits_{i = 1}^{v} {\text{||}}{{E}^{i}}{\text{|}}{{{\text{|}}}_{{2,1}}}\beta {\text{Tr}}({{Q}^{{\text{T}}}}{{L}_{s}}Q) + \sum\limits_{i = 1}^{v} \,\langle {{Y}^{i}},{{X}^{i}} - {{X}^{i}}{{Z}^{i}} - {{E}^{i}}\rangle + \frac{\varepsilon }{2}\sum\limits_{i = 1}^{v} {\text{||}}{{X}^{i}} - {{X}^{i}}{{Z}^{i}} - {{E}^{i}}{\text{||}}_{F}^{2} \\ {\text{s}}.{\text{t}}.\quad {{Q}^{{\text{T}}}}Q = I, \\ \end{gathered} $Итеративно решаются несколько подзадач.
Подзадача ${{Z}^{i}}$. Пересчитаем ${{Z}^{i}}$, фиксируя остальные переменные. Взяв частную производную лагранжиана по ${{Z}^{i}}$ и приравнивая ее к нулю, имеем
(2.9)
${{Z}^{i}} = \frac{{2\alpha S + {{X}^{i}}^{{\text{T}}}{{Y}^{i}} + \varepsilon {{X}^{i}}^{{\text{T}}}{{X}^{i}} - \varepsilon {{X}^{i}}^{{\text{T}}}{{E}^{i}}}}{{2\left( {1 + \alpha } \right)I + 2\mu {{L}^{i}} + \varepsilon {{X}^{i}}^{{\text{T}}}{{X}^{i}}}}.$Подзадача ${{L}^{i}}$. Поскольку исходная выборка содержит шум и выбросы, ${{Z}^{i}}$ можно использовать для получения набора данных с уменьшенным шумом, обозначим его ${{\tilde {X}}^{i}} = {{X}^{i}}{{Z}^{i}}$. В отличие от большинства предыдущих работ, где строится граф k-ближайших соседей на исходном наборе данных, здесь можно построить матрицу весов ${{W}^{i}}$ на наборе данных ${{\tilde {X}}^{i}}$ и вычислить матрицу Лапласа, согласно (0.1).
Подзадача ${{E}^{i}}$. Для каждого ${{E}^{i}}$ отбрасываем другие несвязанные члены и получаем функцию как
(2.10)
${{E}^{i}} = arg\mathop {min}\limits_{{{E}^{i}}} \left( {\frac{\lambda }{\varepsilon }{\text{||}}{{E}^{i}}{\text{|}}{{{\text{|}}}_{{2,1}}} + \frac{1}{2}{\text{||}}{{E}^{i}} - ({{X}^{i}} - {{X}^{i}}{{Z}^{i}} + {{Y}^{i}}{\text{/}}\varepsilon ){\text{||}}_{F}^{2}} \right).$Дальнейшее решение осуществляется с помощью оператора сжатия [29].
Подзадача S. Чтобы обновить S, другие переменные фиксируются. Целевая функция (2.7) может быть переформулирована как
(2.11)
$\begin{gathered} \mathop {min}\limits_S \left( {\alpha \mathop {\left\| S \right\|}\nolimits_F^2 - 2\alpha \sum\limits_{i = 1}^{v} \,{\text{Tr}}({{Z}^{i}}^{{\text{T}}}S) + \beta {\text{Tr}}({{Q}^{{\text{T}}}}{{L}_{S}}Q)} \right) \\ {\text{s}}.{\text{t}}.\quad 1 \cdot {{s}_{j}} = 1,\quad {{s}_{j}} \geqslant 0. \\ \end{gathered} $Обозначая
получаем(2.12)
$\begin{gathered} \mathop {min}\limits_S (\alpha \mathop {\left\| S \right\|}\nolimits_F^2 - {\text{Tr}}\left( {MS} \right) + \beta {\text{Tr}}({{Q}^{{\text{T}}}}{{L}_{S}}Q)) \\ {\text{s}}.{\text{t}}.\quad 1 \cdot {{s}_{j}} = 1,\quad {{s}_{j}} \geqslant 0. \\ \end{gathered} $Поскольку векторы sj не зависят друг от друга при различных j, оптимизация проводится отдельно по каждому j. Слагаемое, ограничивающее ранг, равно
(2.13)
$\begin{gathered} \mathop {min}\limits_{{{s}_{j}}} \left( {\alpha s_{j}^{{\text{T}}}{{s}_{j}} - \sum\limits_{i = 1}^N \,{{m}_{{ij}}}{{s}_{{ij}}} + \sum\limits_{i = 1}^N \,\beta \mathop {\left\| {{{q}_{i}} - {{q}_{j}}} \right\|}\nolimits_2^2 {{s}_{{ij}}}} \right) = \mathop {min}\limits_{{{s}_{j}}} \left( {\alpha s_{j}^{{\text{T}}}{{s}_{j}} + \sum\limits_{i = 1}^N \,[\beta \mathop {\left\| {{{q}_{i}} - {{q}_{j}}} \right\|}\nolimits_2^2 - {{m}_{{ij}}}]{{s}_{{ij}}}} \right) \\ {\text{s}}.{\text{t}}.\quad 1\; \cdot \;{{s}_{j}} = 1,\quad {{s}_{j}} \geqslant 0. \\ \end{gathered} $Обозначим i-й элемент вектора pj как ${{p}_{{ij}}} = \beta \mathop {\left\| {{{q}_{i}} - {{q}_{j}}} \right\|}\nolimits_2^2 - {{m}_{{ij}}}$. Тогда целевая функция (2.13) записывается следующим образом:
(2.14)
$\begin{gathered} \mathop {min}\limits_{{{s}_{j}}} \mathop {\left\| {{{s}_{j}} + \frac{{{{p}_{j}}}}{{2\alpha }}} \right\|}\nolimits_2^2 \\ {\text{s}}.{\text{t}}.\quad 1 \cdot {{s}_{j}} = 1,\quad {{s}_{j}} \geqslant 0. \\ \end{gathered} $Лагранжиан (2.14)
(2.15)
$L({{s}_{j}},\eta ,\rho ) = \mathop {\left\| {{{s}_{j}} + \frac{{{{p}_{j}}}}{{2\alpha }}} \right\|}\nolimits_2^2 - \eta (1 \cdot {{s}_{j}} - 1) - {{\rho }^{{\text{T}}}}{{s}_{j}},$Подзадача Q. Фиксируя S, пересчитываем Q:
(2.17)
$\begin{gathered} \mathop {min}\limits_Q {\text{Tr}}({{Q}^{{\text{T}}}}{{L}_{S}}Q) \\ {\text{s}}.{\text{t}}.\quad {{Q}^{{\text{T}}}}Q = I,\quad Q \in {{\mathbb{R}}^{{N \times c}}}. \\ \end{gathered} $В (2.17) оптимальное решение Q составлено из собственных векторов, соответствующих c наименьшим собственным значениям матрицы Лапласа графа ${{L}_{S}}$.
Шаги предлагаемого алгоритма AGAGL даны ниже. Согласно следствию 1, если ${\text{rank}}\,{{L}_{S}}$ = N – c, то выборку можно напрямую разделить на c кластеров – компонент связности глобального графа сродства. Следовательно, условием остановки алгоритма является то, что сумма c наименьших собственных значений ${{L}_{S}}$ равна нулю, т.е. выполняется (2.4).
Алгоритм AGAGL.
Вход: многоаспектный набор данных X, параметры $\lambda $, $\mu $, $\alpha $, $\beta $, количество кластеров $c$, число ближайших соседей $k$ (для вспомогательного метода).
Выход: матрица $S$, содержащая $c$ компонент связности.
Шаг 1. Для каждого ${{X}^{i}}$ построить ${{L}^{i}}$ методом $k$ ближайших соседей.
Шаг 2. Рассчитать ${{Z}^{i}}$, согласно (2.9), при $S = 0$.
Шаг 3. Вычислить $S = \sum\limits_{i = 1}^v \,{{Z}^{i}}$.
Шаг 4. Определить $Q$, согласно (2.17).
Шаг 5. Присвоить ${{\varepsilon }_{0}} = {{10}^{{ - 6}}}$, ${{\varepsilon }_{{max}}} = {{10}^{6}}$, ${{E}^{i}} = 0$, ${{Y}^{i}} = 0$, $p = 1$.
Шаг 6. Для $i = 1,2, \ldots ,{v}$.
Шаг 7. Пересчитать ${{Z}^{i}}$, согласно (2.9).
Шаг 8. Составить матрицу Лапласа набора ${{\tilde {X}}^{i}} = {{X}^{i}}{{Z}^{i}}$.
Шаг 9. Пересчитать ${{E}^{i}}$, согласно (2.10).
Шаг 10. Пересчитать множители Лагранжа: ${{Y}^{i}} = {{Y}^{i}} + \varepsilon ({{X}^{i}} - {{X}^{i}}{{Z}^{i}} - {{E}^{i}})$.
Шаг 11. Пересчитать $\varepsilon = min(p\varepsilon ,{{\varepsilon }_{{max}}})$.
Шаг 12. Конец цикла по i.
Шаг 13. Для $j = 1,2, \ldots ,N$.
Шаг 14. Пересчитать $j$-й столбец $S$, согласно (2.16);
Шаг 15. Конец цикла по $j$.
Шаг 16. Вычислить матрицу сродства $S = \tfrac{1}{2}(S + {{S}^{{\text{T}}}})$.
Шаг 17. Сформировать $Q$ по c наименьшим собственным значениям ${{L}_{S}}$.
Шаг 18. Если $S$ содержит c связных компонент – завершить, иначе перейти к шагу 6.
2.3. Вычислительная сложность. В алгоритме есть пять неизвестных переменных, а именно ${{Z}^{i}}$, ${{L}^{i}}$, ${{E}^{i}}$, $S$ и $Q$. Каждая из них пересчитывается итеративно в указанном порядке. Основная вычислительная сложность складывается из четырех подзадач. При обновлении ${{Z}^{i}}$ сложность в основном связана с обращением и умножением матрицы и составляет $O({v}{{N}^{3}} + d{{N}^{2}})$, где $d = \sum {{{d}_{{v}}}} $ – общая размерность данных всех аспектов. Для пересчета $S$ необходимо рассмотреть каждый столбец ${{s}_{j}}$. Стоимость рассмотрения каждого столбца равна $O(N)$. Таким образом стоимость пересчета $S$ составляет $O({{N}^{2}})$. Чтобы решить $Q$, вычисляются $c$ собственных векторов матрицы Лапласа ${{L}_{S}}$, а сложность составляет $O(c{{N}^{2}})$. Итак, общая вычислительная сложность есть $O({v}{{N}^{3}}$ + dN2 + cN2).
3. Эксперименты. В этом разделе описано проведение вычислительных экспериментов: наборы данных, меры, оценка качества, алгоритмы, с которыми сравнивается представленный метод, результаты сравнения. Представлено влияние параметров метода на качество кластеризации, исследована сходимость.
3.1. Наборы данных. Для экспериментов было выбрано пять наборов данных.
Набор BBC [31] содержит тексты 145 документов. Каждый документ разделен на четыре части, поэтому набор данных содержит четыре разных аспекта.
Набор Caltech-101 [32] содержит 8677 изображений из 101 категории. Для экспериментов выбраны наиболее широко представленные семь классов, включая лица, мотоциклы, купюры, Гарфилд, знак “стоп”, кресло; общее количество изображений составляет 1474. Каждое изображение описывается шестью аспектами, такими, как 40-мерные моменты вейвлетов, 48-мерное преобразование Габора, 254-мерные признаки CENTRIST [33], 1984-мерная гистограмма ориентированных градиентов (HOG), 512-мерный GIST [34] и 928-мерные локальные бинарные шаблоны (LBP).
Набор MFD [35] содержит образцы рукописных цифр – 10 классов от 0 до 9, всего 2000 образцов. Образцы представлены шестью различными способами, включая 76-мерные коэффициенты Фурье форм символов, 216-мерные профильные корреляции, 64-мерные коэффициенты Карунена–Лоэва, 240 средних значений пикселей в окнах 2 × 3, 47-мерный момент Цернике и 6-мерный морфологический.
Набор HW2sources также содержит рукописные цифры от 0 до 9. Случайным образом выбрано 2000 образцов из баз MNIST [36] и USPS [37] по 200 каждого класса. Поскольку образцы классов получены из двух разных источников, то набор HW2sources имеет два аспекта.
Набор 3sources содержит 169 текстов новостей, разделенных на шесть классов. Новости взяты из трех источников: BBC, Reuters и Guardian.
В табл. 1 даны характеристики этих наборов.
Таблица 1.
Описание баз данных
| База данных | Количество объектов | Тип данных | ||
|---|---|---|---|---|
| объектов | кластеров | аспектов | ||
| BBC | 145 | 2 | 4 | Текст |
| Caltech-101 | 1474 | 7 | 6 | Изображение |
| MFD | 2000 | 10 | 6 | ’’ |
| HW2sources | 2000 | 10 | 2 | ’’ |
| 3sources | 169 | 6 | 3 | Текст |
3.2. Меры качества. Чтобы сравнить предложенный алгоритм с другими, используются три показателя оценки качества кластеризации: точность, нормализованная взаимная информация, чистота.
Точность. Обозначим через ${{U}_{i}}$ истинный номер кластера, куда входит объект ${{x}_{i}}$, ${{V}_{i}}$ – номер кластера, куда попал этот объект при кластеризации, $\nu (x)$ – перенумерация, обладающая свойством $a = b \Leftrightarrow \nu (a) = \nu (b)$, $\delta $ – символ Кронекера. Точность кластеризации ${{Q}_{{Acc}}}$ – доля объектов, правильно отнесенных к кластерам при оптимальной перенумерации (используется венгерский алгоритм [38]):
(3.1)
${{Q}_{{Acc}}} = \frac{1}{N}\mathop {max}\limits_\nu \sum\limits_{i = 1}^N \,\delta \left( {{{U}_{i}},\nu ({{V}_{i}})} \right).$Нормализованная взаимная информация. Даны два набора кластеров $U$ и $V$, которые обозначаются как $U = \{ {{U}_{1}}, \cdots ,{{U}_{k}}\} $ и $V = \{ {{V}_{1}}, \cdots ,{{V}_{m}}\} $. Если взять в качестве $U$ истинное разбиение, известное из обучающей выборки, то качество кластеризации разбиения $V$ можно определить как нормализованную взаимную информацию наборов кластеров $U$ и $V$:
(3.2)
${{Q}_{{NMI}}} = \frac{{\sum\limits_{{{U}_{i}} \in U,{{V}_{j}} \in V} \,P({{U}_{i}},{{V}_{j}})lo{{g}_{2}}\frac{{P({{U}_{i}},{{V}_{j}})}}{{P({{U}_{i}})P({{V}_{j}})}}}}{{max\left\{ {H(U),H(V)} \right\}}},$Чистота. Пусть задан набор $c$ кластеров $\left\{ {{{C}_{1}}, \cdots ,{{C}_{c}}} \right\}$, ${{m}_{i}} = {\text{|}}{{C}_{i}}{\text{|}}$ – число объектов в ${{C}_{i}}$, ${{m}_{{ij}}}$ – число объектов истинного класса j, попавших в кластер ${{C}_{i}}$, ${{P}_{{ij}}} = {{m}_{i}}{\text{/}}{{m}_{{ij}}}$ – вероятность того, что объект из кластера ${{C}_{i}}$ принадлежит классу j. Чистотой кластера ${{C}_{i}}$ назовем величину $P({{C}_{i}}) = \mathop {max}\limits_j {{P}_{{ij}}}$, чистотой всего разбиения – величину
где N – общее число объектов выборки.3.3. Алгоритмы сравнения. Метода сравнивается с шестью классическими алгоритмами:
k-средних: базовый алгоритм кластеризации, применяется к наборам данных с одним аспектом, исполняется для каждого аспекта, в качестве результата берется среднее (1.5);
ESSB [9]: сегментация ансамбля подпространств при блочных ограничениях;
AMGL [39]: взвешенное обучение системы графов (auto-weighted multiple graph learning, AMGL) – алгоритм, автоматически определяющий оптимальный вес для графа каждого аспекта;
GBS [11]: система кластеризации на основе графов;
MVGL [12]: многоаспектная кластеризация обучением графа;
DSS-MSC [40]: многоаспектная кластеризация подпространств с двойным разделением (dual shared-specific multi-view subspace clustering) одновременно извлекает информацию общую для нескольких аспектов и выделяет в каждом из аспектов специфический остаток.
3.4. Результаты эксперимента. Каждый из алгоритмов 30 раз выполнен для каждого набора данных. В табл. 2–4 приведены средние значения и среднеквадратичные отклонения для ${{Q}_{{Acc}}}$, ${{Q}_{{NMI}}}$ и ${{Q}_{{Pur}}}$.
Таблица 2.
Величины QAcc на базах данных
| Метод | База данных | ||||
|---|---|---|---|---|---|
| MFD | Caltech-101 | BBC | HW2sources | 3sources | |
| K-means | 58.84 ± 2.63 | 44.94 ± 1.55 | 88.44 ± 4.41 | 45.53 ± 2.01 | 54.17 ± 5.12 |
| ESSB | 84.48 ± 2.66 | 55.09 ± 0.06 | 89.48 ± 2.42 | 79.52 ± 0.05 | 66.98 ± 3.76 |
| AMGL | 80.60 ± 5.99 | 62.69 ± 5.58 | 63.22 ± 8.14 | 91.91 ± 7.39 | 60.95 ± 6.93 |
| MVGL | 94.20 ± 0 | 57.06 ± 0 | 95.50 ± 0 | 95.50 ± 0 | 77.51 ± 0 |
| GBS | 88.10 ± 0 | 69.20 ± 0 | 95.85 ± 0 | 95.85 ± 0 | 69.23 ± 0 |
| DSS-MSC | 94.54 ± 0.21 | 63.24 ± 0.42 | 89.73 ± 5.70 | 89.73 ± 5.70 | 71.76 ± 1.61 |
| ACAGL | 97.40 ± 0 | 83.65 ± 0 | 95.90 ± 0 | 95.90 ± 0 | 78.11 ± 0 |
Таблица 3.
Величины QNMI на базах данных
| Метод | База данных | ||||
|---|---|---|---|---|---|
| MFD | Caltech-101 | BBC | HW2sources | 3sources | |
| K-means | 59.92 ± 1.17 | 33.24 ± 1.02 | 2.03 ± 2.53 | 42.39 ± 1.10 | 43.11 ± 3.98 |
| ESSB | 88.14 ± 0.06 | 50.81 ± 0.06 | 20.76 ± 3.04 | 80.84 ± 0.08 | 63.92 ± 3.05 |
| AMGL | 84.64 ± 3.70 | 53.00 ± 7.49 | 6.04 ± 1.70 | 90.20 ± 3.84 | 56.08 ± 3.06 |
| MVGL | 89.05 ± 0 | 53.17 ± 0 | 53.50 ± 0 | 90.78 ± 0 | 62.84 ± 0 |
| GBS | 89.23 ± 0 | 60.56 ± 0 | 53.50 ± 0 | 90.92 ± 0 | 54.80 ± 0 |
| DSS-MSC | 89.48 ± 0.38 | 55.20 ± 0.47 | 56.27 ± 3.03 | 84.32 ± 2.90 | 59.11 ± 2.10 |
| ACAGL | 94.18 ± 0 | 55.15 ± 0 | 85.76 ± 0 | 91.17 ± 0 | 69.90 ± 0 |
Таблица 4.
Величины QOur на базах данных
| Метод | База данных | ||||
|---|---|---|---|---|---|
| MFD | Caltech-101 | BBC | HW2sources | 3sources | |
| K-means | 62.74 ± 1.91 | 79.53 ± 053 | 92.54 ± 0.25 | 49.59 ± 1.59 | 66.81 ± 2.91 |
| ESSB | 88.32 ± 1.31 | 87.64 ± 0.03 | 92.41 ± 0 | 84.22 ± 0.05 | 78.34 ± 2.42 |
| AMGL | 83.35 ± 5.04 | 83.77 ± 5.28 | 94.34 ± 0.98 | 92.90 ± 5.62 | 80.00 ± 3.99 |
| MVGL | 94.20 ± 0 | 87.04 ± 0 | 97.24 ± 0 | 95.50 ± 0 | 81.07 ± 0 |
| GBS | 88.10 ± 0 | 88.47 ± 0 | 97.24 ± 0 | 95.85 ± 0 | 75.56 ± 0 |
| DSS-MSC | 94.54 ± 0.21 | 88.37 ± 0.21 | 97.36 ± 0.26 | 90.67 ± 3.86 | 77.06 ± 1.47 |
| ACAGL | 97.40 ± 0 | 87.18 ± 0 | 99.31 ± 0 | 95.90 ± 0 | 82.25 ± 0 |
Из таблиц видно, что предлагаемый метод в целом лучше известных из литературы. AGAGL получает лучшие результаты по всем наборам данных, кроме набора данных Caltech-101 с точки зрения ${{Q}_{{NMI}}}$ и ${{Q}_{{Pur}}}$. По сравнению с некоторыми алгоритмами, такими, как ESSB, DSS-MSC и AMGL, предложенный метод не требует дополнительного шага кластеризации на изученном графе.
3.5. Анализ чувствительности параметров. В статье в основном используются четыре параметра: $\lambda $, $\mu $, $\alpha $, $\beta $. Их влияние на показатели кластеризации изучалось на наборе данных MFD.
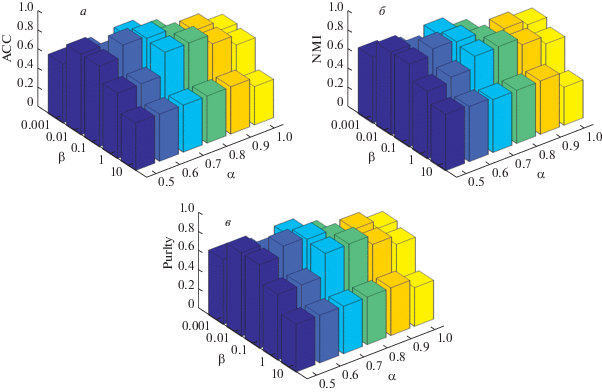
Влияние $\alpha $, $\beta $ на качество кластеризации. Для фиксированных значений $\lambda = 1$ и $\mu = 1$ проверены значения $\alpha = $ $\{ 0.5,0.6,0.7,0.8,0.9,1.0\} $ и $\beta = $ $\{ 0.001,0.01,0.1,1,10\} $, произведено 15 прогонов. На рис. 2 показаны величины ACC, NMI и Purity.
Как видно из рисунков, значения ${{Q}_{{Acc}}}$, ${{Q}_{{NMI}}}$ и ${{Q}_{{Pur}}}$ максимальны при значении веса рангового ограничения $\beta = 0.1$ и веса невязки $\alpha = 0.7$.
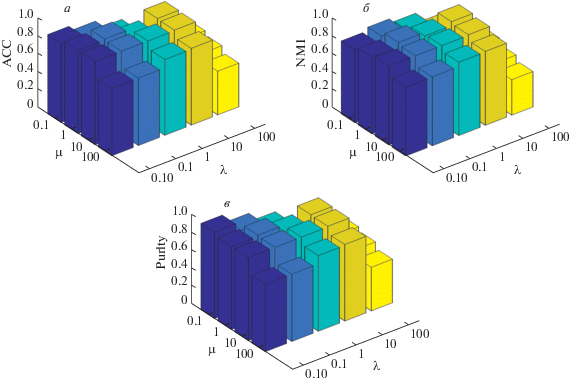
Влияние $\lambda $, $\mu $ на качество кластеризации. При фиксированных значениях $\alpha = 0.5$ и $\beta = 0.1$ значения параметров $\lambda $ и $\mu $ перебираются на множестве $\{ 0.01,\;0.1,\;1,\;10,\;100\} $, производено 15 прогонов. На рис. 3 даны величины ${{Q}_{{Acc}}}$, ${{Q}_{{NMI}}}$ и ${{Q}_{{Pur}}}$.
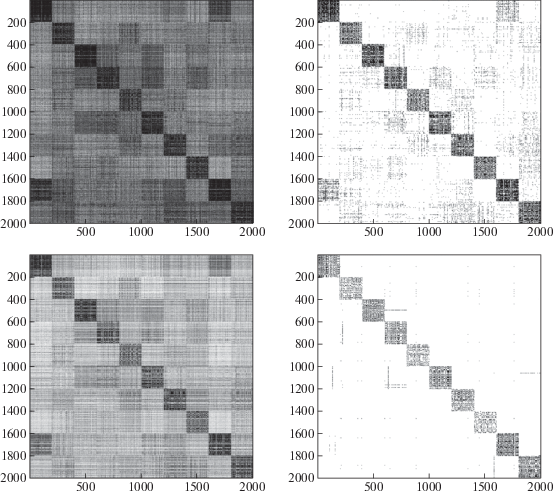
3.6. Обученный граф сродства. Чтобы отразить качество глобального графа сродства предложенного метода, проведены эксперименты с набором данных MFD и получен глобальный граф сродства с блочно-диагональной структурой. На рис. 4 показаны сгенерированные на разных итерациях граф смежности Z, рассчитанный как среднее значение суммы матриц смежности различных представлений (1.5) (в левой колонке) и глобальный граф сродства S (в правой колонке). Верхний ряд соответствует четвeртой итерации, нижний – десятой. Как видно из рисунка, глобальный граф сродства, построенный предложенным методом, лучше кластеризует данные, чем Z.
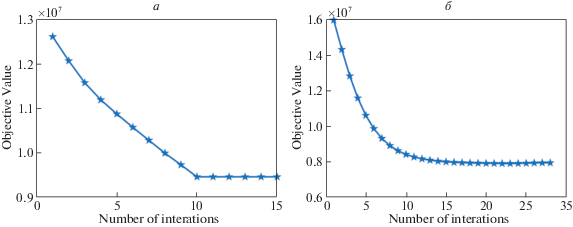
3.7. Исследование сходимости. Проверка сходимости метода сделана на наборах MFD и HW2sources, которые содержат большое количество выборок. На рис. 5 приведены графики значения целевой функции по итерациям. Видно, что для обоих наборов данных постоянное значение целевой функции достигается уже в районе 10-й итерации, т.е. граф сродства, содержащий искомые $c$ компонент связности, получается за 10 итераций.
Заключение. Представлен новый метод многоаспектной кластеризации подпространств, использующий оптимизацию глобального графа сродства. Метод итеративный, на каждой итерации глобальный граф сродства строится на основании матриц смежности, полученных для отдельных аспектов, а эти матрицы далее уточняются с помощью графа сродства. Компоненты связности глобального графа сродства задают разбиение выборки на кластеры без каких-либо дополнительных шагов. Экспериментальные результаты на нескольких наборах данных показывают эффективность метода.
Список литературы
Li Y., Yang M., Zhang Z. Multi-View Representation Learning: A Survey from Shallow Methods to Deep Methods // IEEE Trans. Knowledge and Data Engineering. 2019. V. 31. № 10. P. 1863–1883.
Vizilter Y.V., Vygolov O.V., Zheltov S.Y. Comparison of Statistical Properties for Various Morphological Filters Based on Mosaic Image Shape Models // J. Computer Optics. 2021. V. 45. № 3. P. 449–460.
Li Y., Liao H. Multi-view Clustering via Adversarial View Embedding and Adaptive View Fusion // Applied Intelligence. 2021. V. 51. P. 1201–1212.
Kumar A., Rai P., Daume H. Co-regularized Multi-view Spectral Clustering // Proc. 24th Intern. Conf. Neural Information Processing Systems / Eds J. Shawe-Taylor, R.S. Zemel, P.L. Bartlett, F. Pereira, K.Q. Weinberger. N.Y., USA: Curran Associates, 2011. P. 1413–1421.
Zhao B., Kwok J.T., Zhang C. Multiple Kernel Clustering // Proc. SIAM Intern. Conf. Data Mining. Sparks, Nevada, USA, 2009. P. 638–649.
Liu J., Wang C., Gao J., Han J. Multi-view Clustering via Joint Nonnegative Matrix Factorization // Proc. SIAM Intern. Conf. Data Mining / Eds J. Ghosh, Z. Obradovic, J. Dy, Z.-H. Zhou, C. Kamath, S. Parthasarathy. Austin, TX, USA, 2013. P. 252–260.
Gao H., Nie F., Li X., Huang H. Multi-view Subspace Clustering // Proc. IEEE Intern. Conf. Computer Vision. Santiago, Chile, 2015. P. 4238–4246.
Chaudhuri K., Kakade S.M., Livescu K., Sridharan K. Multi-view Clustering via Canonical Correlation Analysis // Proc. 26th Annual Intern. Conf. Machine Learning. Montreal, Canada, 2009. P. 129–136.
Zhao H., Ding Z., Yun F. Ensemble Subspace Segmentation Under Block-wise Constraints // IEEE Trans. Circuits and Systems for Video Technology. 2018. V. 28. № 7. P. 1526–1539.
Zhao K., Zhao X., Peng C. et al. Partition Level Multiview Subspace Clustering // Neural Networks. 2020. V. 122. P. 279–288.
Wang H., Yang Y., Liu B., Fujita H. A Study of Graph-based System for Multi-view Clustering // Knowledge-Based Systems. 2019. V. 163. P. 1009–1019.
Zhan K., Zhang C., Guan J., Wang J. Graph Learning for Multiview Clustering // IEEE Trans. Cybernetics. 2018. V. 48. № 10. P. 2887–2895.
Mohar B., Alavi Y., Chartrand G. et al. The Laplacian Spectrum of Graphs // Graph Theory, Combinatorics, and Applications. 1991. V. 2. P. 871–898.
Lu C.-Y., Min H., Zhao Z.-Q. et al. Robust and Efficient Subspace Segmentation via Least Squares Regression // Proc. 12th Europ. Conf. Computer Vision. Florence, Italy, 2012. P. 347–360.
Zhao H., Zheng M., Fu Y. Block-wise Constrained Sparse Graph for Face Image Representation // Proc. 11th IEEE Intern. Conf. and Workshops on Automatic Face and Gesture Recognition. Ljubljana, Slovenia, 2015. P. 1–6.
Liu G., Lin Z., Yu Y. Robust Subspace Segmentation by Low-rank Representation // Proc. Intern. Conf. Machine Learning / Eds J. Furnkranz, T. Joachims. Madison, WI, USA: Omnipress, 2010. P. 663–670.
Elhamifar E., Vidal R. Sparse Subspace Clustering // IEEE Conf. Computer Vision and Pattern Recognition. Miami, FL, USA, 2009. P. 2790–2797.
Zhang C., Fu H., Liu S. et al. Low-rank Tensor Constrained Multi-view Subspace Clustering // Proc. IEEE Intern. Conf. Computer Vision. Santiago, Chile, 2015. P. 1582–1590.
Xia R., Pan Y., Du L., Yin J. Robust Multi-view Spectral Clustering via Low-rank and Sparse Decomposition // Proc. 28 AAAI Conf. Artificial Intelligence. Quebec, Canada, 2014. P. 2149–2155.
Ng A.Y., Jordan M.I., Weiss Y. On Spectral Clustering: Analysis and an Algorithm // Proc. Intern. Conf. Neural Information Processing System / Eds T.G. Dietterich, S. Becker, Z. Ghahramani. Cambridge, MA, USA: MIT Press, 2001. P. 849–856.
Wang Y., Wu L., Lin X., Gao J. Multiview Spectral Clustering via Structured Low-rank Matrix Factorization // IEEE Trans. Neural Networks and Learning Systems. 2018. V. 29. № 10. P. 4833–4843.
Brbic M., Kopriva I. Multi-view Low-rank Sparse Subspace Clustering // Pattern Recognition. 2018. V. 73. P. 247–258.
Abavisani M., Patel V.M. Multimodal Sparse and Low-rank Subspace Clustering // Information Fusion. 2018. V. 39. P. 168–177.
Wang Y., Zhang W., Wu L., Lin X. et al. Iterative Views Agreement: An Iterative Low-rank Based Structured Optimization Method to Multi-view Spectral Clustering // Proc. 25th Intern. Joint Conf. Artificial Intelligence. N.Y., USA, 2016. P. 2153–2159.
Xie D., Zhang X., Gao Q. et al. Multiview Clustering by Joint Latent Representation and Similarity Learning // IEEE Trans. Cybernetics. 2020. V. 50. № 11. P. 4848–4854.
Cao X., Zhang C., Fu H. et al. Diversity-induced Multi-view Subspace Clustering // Proc. IEEE Conf. Computer Vision and Pattern Recognition. Boston, MA, USA, 2015. P. 586–594.
von Luxburg U. A Tutorial on Spectral Clustering // Statistics and Computing. 2007. V. 17. P. 395–416.
Fan K. On a Theorem of Weyl Concerning Eigenvalues of Linear Transformations. I // Proc. National Academy of Sciences. 1949. V. 35. № 11. P. 652–655.
Yang J., Yin W., Zhang Y. et al. A Fast Algorithm for Edge-Preserving Variational Multichannel Image Restoration // SIAM J. Imaging Sciences. 2009. V. 2. № 2. P. 569–592.
Boyd S., Vandenberghe L. Convex Optimization. Cambridge University Press, 2004.
Green D., Cunningham P. Practical Solutions to the Problem of Diagonal Dominance in Kernel Document Clustering // Proc. Intern. Conf. Machine Learning. Pittsburgh, USA, 2006. P. 377–384.
Li F.-F., Fergus R., Perona P. Learning Generative Visual Models from Few Training Examples: An incremental Bayesian Approach Tested on 101 Object Categories // Computer Vision and Image Understanding. 2007. V. 106. № 1. P. 59–70.
Wu J., Rehg J.M. CENTRIST: A Visual Descriptor for Scene Categorization // IEEE Trans. Pattern Analysis and Machine Intelligence. 2011. V. 33. № 8. P. 1489–1501.
Oliva A., Torralba A. Modeling the Shape of the Scene: A Holistic Representation of the Spatial Envelope // Intern. J. Computer Vision. 2001. V. 42. № 3. P. 145–175.
Dua D., Graff C. UCI Machine Learning Repository // Center for Machine Learning and Intelligent Systems. Irvine, CA, USA, 2019.
LeCun Y., Bottou L., Bengio Y., Haffner P. Gradient-based Learning Applied to Document Recognition // Proc. IEEE. 1998. V. 86. № 11. P. 2278–2324.
Hull J.J. A Database for Handwritten Text Recognition Research // IEEE Trans. Pattern Analysis and Machine Intelligence. 1994. V. 16. № 5. P. 550–554.
Chen S., Donoho D.L., Saunders M.A. Atomic Decomposition by Basis Pursuit // SIAM Review. 2001. V. 43. № 1. P. 129–159.
Nie F., Li J., Li X. Parameter-free Auto-weighted Multiple Graph Learning: A Framework for Multiview Clustering and Semi-supervised Classification // Intern. Joint Conf. Artificial Intelligence. Palo Alto, CA, USA, 2016. P. 1881–1887.
Zhou T., Zhang C.-Q., Peng X. et al. Dual Shared-specific Multi-view Subspace Clustering // IEEE Tran. Cybernetics. 2019. V. 50. № 8. P. 3517–3530.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления