Известия РАН. Теория и системы управления, 2022, № 1, стр. 3-10

0. Введение. Рассмотрим проблему анализа устойчивости линейных динамических систем. Полином

с действительными коэффициентами называют устойчивым, если действительные части всех корней характеристического уравнения ${{P}_{n}}(y) = 0$ отрицательны.

Согласно основной теореме алгебры, этот полином может быть представлен в форме произведений элементарных полиномов вида ${{P}_{{1i}}}(y) = y + {{r}_{i}}$ и P_2i(y) = ${{y}^{2}} + 2{{r}_{i}}y + (\omega _{i}^{2} + r_{i}^{2})$, где $ - {{r}_{i}}$ и ${{\omega }_{i}}$ – действительная и мнимая части комплексно-сопряженных корней характеристического уравнения. Полином ${{P}_{n}}(y)$ устойчив тогда и только тогда, когда устойчив каждый из элементарных полиномов.

В свою очередь для устойчивости каждого из элементарных полиномов необходимо и достаточно, чтобы их коэффициенты были положительны. Коэффициенты полинома ${{P}_{n}}(y)$ представляют собой свертку коэффициентов элементарных полиномов, так что у устойчивого полинома они заведомо положительны. Это свойство легко проверяется, но оно не достаточно. Полином с положительными коэффициентами может быть и неустойчивым. Необходимые и достаточные условия устойчивости дают алгебраические критерии Рауса, Гурвица, частотные критерии Михайлова–Найквиста [1]. Использование этих критериев при большом значении n достаточно трудоемко.

Ниже сделана попытка найти дополнительные признаки, которые характерны для последовательности коэффициентов устойчивых полиномов. Эти признаки вытекают из свойств операции свертки.

Операция свертки функций действительного переменного – одна из самых распространенных в прикладной математике [2–7]. Она имеет форму

в непрерывном и в дискретном случаях.

Приведем два примера.

Плотность распределения суммы z независимых случайных величин x и y представляет собой свертку плотностей распределения каждой из них. Так что

Коэффициенты c_j произведения ${{P}_{{n + m}}}(x)$ двух полиномов вида

и равны свертке последовательностей их коэффициентов

Коэффициенты b_{i – j}= 0 при i – j < 0 и i – j > m.

Некоторые теоремы теории вероятностей, по существу, определяют свойства операции свертки и полностью справедливы применительно к последовательностям коэффициентов полиномов [3].

Приведем некоторые свойства операции свертки [4].

1. Свертка коммутативна, так что

2. Свертка ассоциативна:

3. Свертка дистрибутивна относительно сложения:

4. Площадь под кривой z(t), если она ограничена, равна произведению площадей под кривыми x(t) и y(t). Как следствие, если x(t) и y(t) неотрицательны и их площадь равна единице, то их свертка z(t) также имеет единичную площадь.

5. Ее первый момент

а второй центральный момент

В теории вероятностей первый момент – математическое ожидание, а второй центральный – дисперсия случайной величины.

1. Предельные теоремы теории вероятностей. 1.1. Теорема Муавра–Лапласа. Согласно предельной теореме Муавра–Лапласа, при стремлении числа опытов $n$ к бесконечности вероятность того, что случайная величина, принимающая с вероятностью p значение единица и с вероятностью $q = 1 - p$ значение ноль, в $i$-опытах окажется равной единице:

В этом выражении

где ${{M}_{n}}$ и ${{D}_{n}}$ – математическое ожидание и дисперсия суммы $n$ одинаково распределенных случайных величин, принимающих значения единица и ноль. В данном случае они равны np и npq соответственно. Зависимость $x(i,n)$ равномерно по i, n ограничена, т.е. существуют такие значения $A$ и $B$, что $ - \infty < A \leqslant x(i,n) \leqslant B < \infty $.

Величина ${{\delta }_{n}}$, определяющая различие между последовательностью ${{b}_{{ni}}}$ и нормальным дискретным распределением $N(i,n)$, стремится к нулю с ростом $n$ так, что равномерно по i

где C – положительная константа, не зависящая от n, i. Свойство (1.1) называют свойством асимптотической нормальности.

1.2. Формулировка Ляпунова центральной предельной теоремы. В этой формулировке центральной предельной теоремы (ЦПТ) не требуется, чтобы сворачиваемые дискретные плотности распределения были одинаковы. Она утверждает, что при некотором доказанном Ляпуновым условии результат свертки неотрицательных функций, сумма ординат которых равна единице, имеющих первый и второй центральный моменты (см. (0.7), (0.8)), а также абсолютный центральный момент степени, большей двух, для достаточно большого значения $n$ приближается к нормальному распределению $N(i,n)$, фигурирующему в (1.1).

Через ${{c}_{i}}$ обозначим абсолютный центральный момент степени, большей двух, для k-го элементарного полинома ${{P}_{i}}(y)$, имеющего нормированные коэффициенты ${{b}_{{jk}}}$, т.е.

где $\epsilon > 0$. Обозначим через где n – число элементарных полиномов.

Формулировка Ляпунова ЦПТ состоит в следующем.

Теорема [8, 9]. Для того, чтобы плотность распределения свертки положительных нормированных дискретных функций была асимптотически нормальной, достаточно существования такого значения ${{\epsilon }_{0}} > 0$, чтобы для всех $0 < \epsilon < {{\epsilon }_{0}}$

Дробь ${{L}_{n}}(\epsilon )$ в левой части этого выражения называют дробью Ляпунова.

Процитируем оценку этой теоремы из посвященной ей статьи в Википедии: “Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный”.

2. Преобразования полиномов. Рассмотрим линейную динамическую систему, характеристическое уравнение которой имеет форму

где ${{a}_{i}}$ – действительные коэффициенты.

Будем предполагать, что действительные части корней характеристического уравнения устойчивого полинома отделены от нуля, т.е. найдется такое не зависящее от $n$ значение $\rho > 0$, что расстояния всех корней уравнения (2.1) от мнимой оси ${{r}_{i}} \geqslant \rho $. Для устойчивого полинома коэффициенты каждого из элементарных полиномов также отделены от нуля.

Элементарный полином первой степени ${{P}_{{1i}}}(y) = y + {{r}_{i}}$ соответствует действительному отрицательному корню, расположенному на расстоянии ${{r}_{i}}$ от мнимой оси. Элементарный полином второй степени

соответствует паре комплексно-сопряженных корней с действительной частью $ - {{r}_{i}}$ и мнимой частью $ \pm {{\omega }_{i}}$.

Далее будем нормировать коэффициенты полинома, разделив каждый коэффициент на их сумму, так что для полинома ${{P}_{{1i}}}(y)$ коэффициенты после нормировки равны

при $y$ в первой и в нулевой степенях соответственно. Первый и второй центральный моменты для такого полинома:

Для элементарного полинома второй степени (2.2) после нормирования коэффициенты при y – в квадрате, в первой и нулевой степени

Здесь через ${{\sigma }_{i}}$ обозначена сумма коэффициентов полинома второй степени:

Первый и второй центральный моменты последовательности коэффициентов устойчивого полинома второй степени равны

Нормированная последовательность коэффициентов

полинома ${{P}_{n}}(y)$ (см. (2.1)) равна свертке нормированных последовательностей коэффициентов элементарных полиномов, а ее первый и второй центральный моменты, равные сумме соответствующих моментов элементарных полиномов (см. свойство 5 свертки), могут быть подсчитаны непосредственно через ${{b}_{i}}$:

Первоначально рассмотрим случай, когда все корни полинома ${{P}_{n}}(y)$ действительные и кратные, т.е. он равен с учетом нормировки

Коэффициенты этого полинома образуют последовательность биномиальных коэффициентов [8, 10]:

По теореме Муавра–Лапласа эта последовательность асимптотически нормальна.

Теорему Муавра–Лапласа обычно относят к теории вероятностей. Но, по существу, она посвящена свойству последовательных сверток положительных нормированных дискретных функций. В случае биномиальных коэффициентов эти дискретные функции одинаковы. Поэтому свертка коэффициентов элементарных полиномов с одинаковыми действительными корнями асимптотически нормальна.

То же относится и к теореме Ляпунова. Распределения случайных величин лишь одно из ее приложений. Как и классическая формулировка ЦПТ, теорема Ляпунова определяет свойство свертки детерминированных положительных функций, для каждой из которых существуют ${{m}_{i}},\;{{d}_{i}},\;{{c}_{i}}$. Эти функции могут быть разными. Для асимптотической нормальности их свертки достаточно выполнения условия (1.4). В качестве меры погрешности приближения ${{\delta }_{n}}$ используется дробь Ляпунова или функция от нее, стремящаяся к нулю при ${{L}_{n}} \to 0$. Далее рассмотрены следствия из этой теоремы применительно к устойчивым полиномам.

3. Условие асимптотической нормальности последовательности коэффициентов устойчивых полиномов. Нормированная последовательность ${{b}_{i}}$ коэффициентов полинома P_n$(y)$ представляет собой свертку нормированных последовательностей коэффициентов элементарных полиномов.

Роль плотностей распределения играют нормированные последовательности положительных коэффициентов элементарных полиномов.

Эти коэффициенты меньше единицы и равны нулю при $i > 2$ и $i < 0$, так что для них все перечисленные в теореме Ляпунова моменты существуют. Они определены значениями корней характеристического уравнения.

Таким образом, из теоремы Ляпунова вытекает следствие.

Следствие. Для того, чтобы последовательность коэффициентов устойчивого полинома ${{P}_{n}}(y)$ обладала свойством асимптотической нормальности, достаточно, чтобы характеристики элементарных полиномов ${{m}_{i}},{{d}_{i}},{{c}_{i}}(\epsilon )$ удовлетворяли условию (1.4) при $\epsilon > 0$.

Конкретизируем это утверждение для нашей задачи.

1. Так как коэффициенты элементарных полиномов отделены от нуля, то второй центральный момент каждого из них ${{d}_{i}} \geqslant \delta > 0$. В силу этого с ростом $n$ второй центральный момент ${{D}_{n}}$ полинома ${{P}_{n}}$ неограниченно возрастает.

2. В силу малости $\epsilon $ и гладкости зависимостей ${{c}_{i}}(\epsilon )$ числитель дроби Ляпунова может быть представлен в форме ${{C}_{n}} = {{D}_{n}} + \epsilon {{S}_{n}} + o(\epsilon )$, где

а остаточный член $\frac{{o(\epsilon )}}{\epsilon } \to 0$ при $\epsilon \to 0$.

Покажем, что для справедливости условия Ляпунова достаточно выполнения неравенства:

Здесь, как и выше, строгое неравенство соответствует тому, что найдется такое значение $\eta < 0$, что для всех значений i производная, фигурирующая в условии (3.1), не превосходит $\eta $.

Если неравенство (3.1) выполнено, то для каждого из элементарных полиномов ${{d}_{i}} > {{c}_{i}}(\epsilon )$. В этом случае ${{C}_{n}}(\epsilon ) < {{C}_{n}}(0) = {{D}_{n}}$ и справедливо неравенство

С ростом D_n правая, а значит, и левая части неравенства стремятся к нулю.

3.1. Полином с действительными корнями. Покажем, что условию (3.1) удовлетворяет полином с отрицательными действительными корнями, находящимися от мнимой оси на расстояниях ${{r}_{i}}$. Выражения для моментов такого полинома записаны в (2.6).

Центральный момент ${{c}_{i}}(\epsilon )$ для такой последовательности коэффициентов равен:

Производная

Здесь учтено, что сумма коэффициентов $p + q = 1$ и они строго положительные. При этих условиях функция Гиббса, стоящая в неравенстве (3.4) в квадратных скобках, отрицательная для $0 < p < 1$.

Таким образом условие (3.1) выполнено, и для любого устойчивого полинома с действительными корнями последовательность его коэффициентов асимптотически нормальна.

3.2. Полином с комплексными корнями. Значения ${{m}_{i}},{{d}_{i}},{{c}_{i}}(\epsilon )$ могут быть подсчитаны для элементарного полинома второй степени, соответствующего паре комплексно-сопряженных корней ${{P}_{i}}(y) = {{y}^{2}} + 2{{r}_{i}}y + r_{i}^{2} + \omega _{i}^{2}$, по формулам (2.5)–(2.6).

Абсолютный момент степени, большей двух, для элементарного квадратного полинома

Каждый из этих моментов зависит от действительной и мнимой частей корней ${{r}_{i}},{{\omega }_{i}}$ в соответствии с (2.5)–(2.6).

Для выполнения условия Ляпунова достаточно, чтобы для любого $i$, выполнялось условие (3.1). Учитывая, что производная A^ε по ε равна A^εlnA, и устремляя ε к нулю, получим требование неположительности производной:

При стремлении ${{m}_{i}}$ к нулю, к единице и к двум левая часть неравенства (3.6) стремится к $ - \infty $.

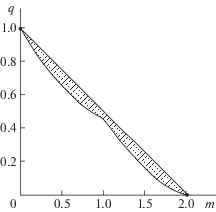
На pис. 1 заштрихована область, в которой полином второй степени устойчив, но неравенство (3.6) нарушено и выполнение условий Ляпунова не гарантировано. Здесь q и m представляют собой коэффициент при y в нулевой степени и первый момент последовательности коэффициентов и вычисляются по формулам (2.5), (2.6).

Верхней границе заштрихованной области (прямой на рисунке) соответствуют мнимые корни полинома. Для всех коэффициентов полинома, которым соответствует точка, лежащая ниже заштрихованной области, асимптотическая нормальность гарантирована.

Если устойчивый полином ${{P}_{n}}(y)$ имеет несколько комплексных корней, то условие асимптотической нормальности может быть нарушено, если в заштрихованной области окажутся все комплексные корни.

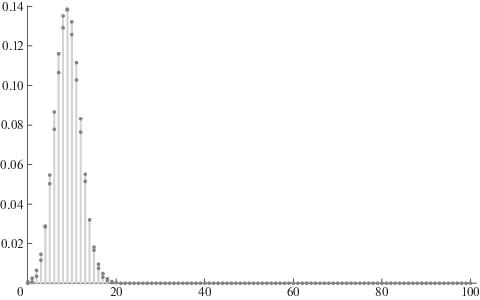
На pис. 2 показан вид последовательности коэффициентов устойчивого полинома.

Для того, чтобы проверить, является ли полином достаточно большой степени устойчивым, нужно найти M_n и D_n по приведенным выше формулам (2.8). Последовательность коэффициентов ${{a}_{i}}$ устойчивого полинома должна быть унимодальной, причем максимум ее достигается в точке $i*$, ближайшей слева или справа к величине M_n, а максимальное значение коэффициента должно быть приближенно равно

4. Примеры. 4.1. Устойчивый полином. Рассмотрим полином пятой степени

Его коэффициенты положительны, их последовательность имеет единственный максимум при i = 2, а значение максимального коэффициента равно 20. Сумма коэффициентов полинома R_n = 60.

Сравним эти значения с величинами, соответствующими асимптотической нормальности последовательности коэффициентов. После деления каждого из коэффициентов на их сумму и вычисления моментов по формуле (2.8) получим M_n = 2.13, D_n = 1.28. Величина максимального коэффициента, вычисленная по формуле (3.7), равна 21.14. Таким образом, уже для n = 5 фактический номер максимального коэффициента и его величина близки к их значениям, соответствующим нормальному распределению, что позволяет сделать вывод об устойчивости полинома.

Полином (4.1) устойчив, имеет действительные корни в точках –1 (кратности 2) и –2 и комплексно-сопряженные с действительной частью –1 и мнимой ±1.

4.2. Неустойчивый полином. Рассмотрим полином пятой степени

Все его коэффициенты положительны, их последовательность унимодальна, а их сумма равна R_n = 48. Те же расчеты, что и для полинома (4.1), приводят к значениям M_n = 1.33, D_n = 1.22. Расчетная величина максимального коэффициента, найденная по формуле (3.7), равна 17.32, что существенно меньше его реального значения.

Полином (4.2) неустойчив, имеет действительные корни в точках –1 (кратности 2) и –2 и два комплексно-сопряженных с действительной частью +1 и мнимой ±2.

Заключение. Доказано, что коэффициенты устойчивых полиномов не только положительны, но и их последовательность асимптотически нормальна, а значит, имеет единственный максимум. Получены формулы для оценки номера и величины максимального коэффициента. Близость этих оценок к реальным значениям номера и величины этого коэффициента является дополнительным признаком устойчивости и освобождает от необходимости использования частотных или алгебраических критериев.