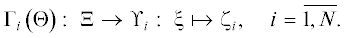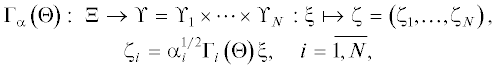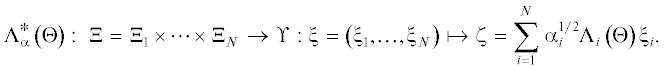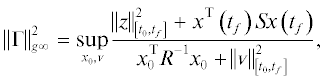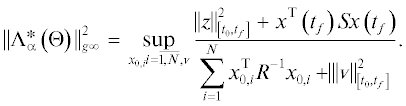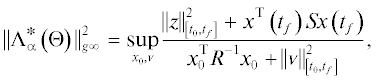Известия РАН. Теория и системы управления, 2022, № 2, стр. 43-57
МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ ИНДУЦИРОВАННЫХ НОРМ ЛИНЕЙНЫХ ОПЕРАТОРОВ: ПРЯМАЯ И ДВОЙСТВЕННАЯ ЗАДАЧИ УПРАВЛЕНИЯ И ФИЛЬТРАЦИИ
Д. В. Баландин a, *, Р. С. Бирюков a, b, М. М. Коган b
a Нижегородский государственный ун-т им. Н.И. Лобачевского
Нижний Новгород, Россия
b Нижегородский государственный архитектурно-строительный ун-т
Нижний Новгород, Россия
* E-mail: dbalandin@yandex.ru
Поступила в редакцию 02.04.2021
После доработки 25.10.2021
Принята к публикации 29.11.2021
- EDN: NLIICI
- DOI: 10.31857/S0002338822020044
Аннотация
Рассматриваются задачи многокритериальной оптимизации индуцированных норм линейных операторов, зависящих от параметров и отображающих одно линейное пространство в несколько или несколько линейных пространств в одно. В обоих случаях непосредственная минимизация оптимальной целевой функции в виде линейной свертки отдельных критериев является затруднительной. Показано, что для задач каждого из этих типов можно указать субоптимальную целевую функцию в виде индуцированной нормы вспомогательного линейного оператора, минимизация которой приводит к субоптимальным по Парето решениям. При этом устанавливается возможность локализовать в критериальном пространстве множество Парето и тем самым оценить степень субоптимальности получаемых решений. В качестве приложения рассматриваются многокритериальные задачи оптимального управления и фильтрации с критериями вида обобщенных ${{H}_{\infty }}$-норм.
Введение. В математических постановках задач управления или фильтрации оптимизируемыми критериями часто являются индуцированные нормы линейных операторов, отображающих в силу уравнений системы ее начальное состояние и/или внешнее возмущение в терминальное состояние и/или целевой выход. В результате находятся минимаксные регуляторы или фильтры, наилучшие в наихудшей ситуации. Так, для интегрируемых с квадратом возмущений из пространства L2 к таким критериям относится обобщенная ${{H}_{\infty }}$-норма, которая в общем случае соответствует уровню гашения начального и внешнего возмущений, а в частном случае при нулевом начальном состоянии системы превращается в стандартную ${{H}_{\infty }}$-норму. Если целевой выход не учитывается, то обобщенная ${{H}_{\infty }}$-норма характеризует максимальное значение евклидовой нормы терминального состояния относительно всех начальных и внешних возмущений с ограниченной нормой. Когда внешнее возмущение не учитывается, индуцированная норма оператора, отображающего начальное состояние в целевой выход, называемая также ${{\gamma }_{0}}$-нормой, показывает максимально возможное значение L2-нормы целевого выхода относительно евклидовой нормы начального состояния, а оптимальное управление по этому критерию – это линейно-квадратичное управление при неопределенных начальных условиях.
Для каждого из этих критериев уже разработаны методы, позволяющие синтезировать оптимальные регуляторы и фильтры (см., например, [1, 2] и ссылки в них). Вместе с тем реальные задачи управления и фильтрации, как известно, всегда являются многокритериальными. В связи с этим представляет интерес синтез регуляторов, обеспечивающих минимальный уровень гашения начального и внешнего возмущений не для одного целевого выхода системы, а для нескольких. Кроме того, в реальных системах, как правило, имеются несколько входов для потенциально возможных возмущений и заранее неясно, на каком из этих входов действительно возникнет возмущение. В таком случае требуется синтезировать регулятор, обеспечивающий оптимальное гашение возмущений, возникающих на любом из возможных входов.
Здесь нужно отметить, что нахождение оптимальных по Парето, т.е. неулучшаемых по совокупности критериев, решений, обеспечивающих определенный компромисс между конкурирующими критериями, представляет собой трудную задачу [3, 4]. В теории управления можно указать только отдельные случаи, в которых удается ее решить до конца. Это линейно-квадратичные гауссовские управления [5] и H2-оптимальные управления [6] на основе $Q$-параметризации стабилизирующих регуляторов для линейных стационарных систем на бесконечном интервале времени, а также обобщенные H2 оптимальные управления [7–10] для линейных нестационарных систем на конечном горизонте и стационарных систем на бесконечном горизонте. В задачах управления с критериями, включающими ${{H}_{\infty }}$-норму, удавалось синтезировать многокритериальные управления, как правило, только при дополнительных ограничениях типа равенства матриц функций Ляпунова [11] или типа равенства вспомогательных матричных переменных [12, 13], налагаемых на матричные уравнения или линейные матричные неравенства, характеризующие каждый из критериев. Такое же ограничение неявно присутствует и в концепции так называемого смешанного ${{H}_{2}}{\text{/}}{{H}_{\infty }}$-управления [14–18]. В [19] для синтеза двукритериального управления применялся подход, состоящий в получении конечномерных $Q$-аппроксимаций оптимальных по Парето регуляторов. В [20–22] для задач многокритериальной оптимизации с критериями в виде ${{H}_{\infty }}$- и ${{\gamma }_{0}}$-норм в детерминированной и стохастической постановках были найдены субоптимальные по Парето законы управления, относительные потери которых по сравнению с оптимальными по Парето не превышают $1 - \sqrt N {\text{/}}N$, где N – число критериев.
Статья посвящена разработке некоторого общего подхода к многокритериальной минимаксной оптимизации применительно к линейным задачам управления и фильтрации. В ней установлено, что при многокритериальной оптимизации индуцированных норм $N$ линейных операторов, зависящих от параметров и отображающих одно линейное пространство в $N$ образов, можно указать область в N-мерном критериальном пространстве, содержащую точки множества Парето, которые являются оптимальными по отношению к линейной свертке критериев. Одна граница этой области соответствует субоптимальным по Парето решениям, которые оптимизируют индуцированную норму вспомогательного линейного оператора, отображающего исходное линейное пространство в прямую сумму образов исходных операторов. Знание другой границы этой области позволяет оценить, в какой мере значения критериев при найденных решениях отличаются от оптимальных по Парето. Далее показано, что для задачи многокритериальной оптимизации индуцированных норм N линейных операторов, отображающих N линейных пространств в одно линейное пространство, можно применить принцип двойственности и также указать единый критерий в виде индуцированной нормы некоторого вспомогательного линейного оператора, оптимизация которого позволяет находить субоптимальные по Парето решения. Все эти результаты применяются для синтеза субоптимальных по Парето регуляторов и фильтров в линейных нестационарных системах на конечном горизонте и в стационарных системах на бесконечном горизонте в многокритериальных задачах с обобщенными ${{H}_{\infty }}$-нормами в качестве критериев. Для этого дается новая характеризация обобщенной ${{H}_{\infty }}$-нормы в терминах дифференциальных линейных матричных неравенств. Приводятся иллюстрирующие примеры.
1. Локализация подмножества Парето-фронта в прямой и двойственной многокритериальных задачах. 1.1. Прямая многокритериальная задача. Пусть имеются N линейных ограниченных операторов, зависящих от параметров ${{\Theta }}$ и отображающих линейное пространство Ξ со скалярным произведением ${{\langle \cdot , \cdot \rangle }_{{{\Xi }}}}$ в линейные пространства ${{\Upsilon }_{i}}$ со скалярными произведениями ${{\langle \cdot , \cdot \rangle }_{{{{\Upsilon }_{i}}}}}$, т.е.
Задача состоит в нахождении оптимальных по Парето решений в многокритериальной задаче минимизации с критериями ${{J}_{i}}\left( {{\Theta }} \right)$, $i = 1, \ldots ,N$, которые являются квадратами индуцированных норм этих операторов:
Напомним, что решение ${{{{\Theta }}}_{P}}$ называется оптимальным по Парето, если не существует такого решения ${{\Theta }}$, что выполняются неравенства ${{J}_{i}}\left( {{\Theta }} \right) \leqslant {{J}_{i}}\left( {{{{{\Theta }}}_{P}}} \right)$, $i = \overline {1,N} $, в которых, по меньшей мере, одно является строгим. Множество точек $\left( {{{J}_{1}}, \ldots ,{{J}_{N}}} \right)$ в N-мерном критериальном пространстве, соответствующих всем таким решениям, называется множеством Парето:
Оптимальные по Парето решения – это множество неулучшаемых решений в том смысле, что для каждого из них не существует решения, при котором значения всех критериев были бы не больше, чем при данном, а значение хотя бы одного критерия было бы строго меньше.
Самым распространенным методом нахождения оптимальных по Парето решений многокритериальной задачи является метод скаляризации, т.е. выбора одного критерия в виде, например, линейной свертки этих критериев:
Назовем линейную свертку ${{J}_{\alpha }}\left( {{\Theta }} \right)$ оптимальной целевой функцией. Как известно [3], параметры ${{{{\Theta }}}_{\alpha }}$, для которых выполняется
В общем случае ими может не исчерпываться все множество Парето, т.е. ${{\mathcal{P}}_{\mathcal{L}}} \subseteq \mathcal{P}$.
Непосредственное нахождение параметров ${{{{\Theta }}}_{\alpha }}$ для многокритериальной оптимизации квадратов индуцированных норм линейных операторов представляется затруднительным, так как оптимальная целевая функция для этой задачи оказывается линейной комбинацией максимумов разных функционалов. В связи с этим оценим ее снизу, заменяя сумму максимумов на максимум суммы:
где линейный оператор ${{{{\Gamma }}}_{\alpha }}\left( {{\Theta }} \right)$ определяется как а скалярное произведение в $\Upsilon $ – какНазовем ${{\hat {J}}_{\alpha }}\left( {{\Theta }} \right) = {\text{||}}{{{{\Gamma }}}_{\alpha }}\left( {{\Theta }} \right){\text{|}}{{{\text{|}}}^{2}}$ субоптимальной целевой функцией, а параметры ${{{{\hat {\Theta }}}}_{\alpha }}$, оптимальные по отношению к ${{\hat {J}}_{\alpha }}\left( {{\Theta }} \right)$, при которых
Равенство
(1.4)
${{\mu }_{ + }}\left( \alpha \right) = \mathop \sum \limits_{i = 1}^N {{\alpha }_{i}}{{J}_{i}}({{{{\hat {\Theta }}}}_{\alpha }}) \geqslant \mathop \sum \limits_{i = 1}^N {{\alpha }_{i}}{{J}_{i}}\left( {{{{{\Theta }}}_{\alpha }}} \right) = \mu \left( \alpha \right),$Из справедливости неравенств
(1.5)
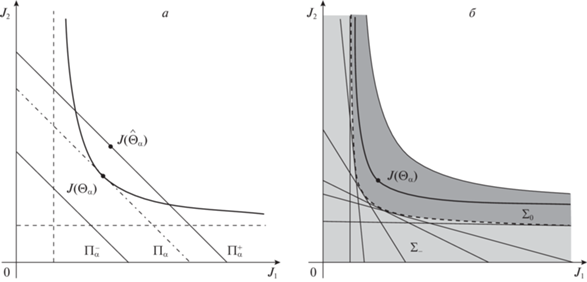
$\mu \left( \alpha \right) = \mathop \sum \limits_{i = 1}^N {{\alpha }_{i}}{{J}_{i}}\left( {{{{{\Theta }}}_{\alpha }}} \right) = {{J}_{\alpha }}\left( {{{{{\Theta }}}_{\alpha }}} \right) \geqslant {{\hat {J}}_{\alpha }}\left( {{{{{\Theta }}}_{\alpha }}} \right) \geqslant {{\hat {J}}_{\alpha }}\left( {{{{{{\hat {\Theta }}}}}_{\alpha }}} \right) = {{\mu }_{ - }}\left( \alpha \right)$Заметим, что гиперплоскость ${{\Pi }}_{\alpha }^{0}$, параллельная гиперплоскостям ${{\Pi }}_{\alpha }^{ - }$ и ${{\Pi }}_{\alpha }^{ + }$ и проходящая через точку $\left( {{\text{mi}}{{{\text{n}}}_{{{\Theta }}}}{{J}_{1}}\left( {{\Theta }} \right), \ldots ,{\text{mi}}{{{\text{n}}}_{{{\Theta }}}}{{J}_{N}}\left( {{\Theta }} \right)} \right)$, описывается уравнением
Следовательно, гиперплоскость ${{\Pi }}_{\alpha }^{ - }$ находится на большем расстоянии от начала координат, чем ${{\Pi }}_{\alpha }^{0}$, при выполнении условия
Определим в пространстве критериев для любого набора $\alpha \in \mathcal{S}$ следующие множества:
(1.6)
$\begin{array}{*{20}{c}} {{{\Sigma }}_{\alpha }^{ - } = \left\{ {\left( {{{J}_{1}}, \ldots ,{{J}_{N}}} \right):\mathop \sum \limits_{i = 1}^N {{\alpha }_{i}}{{J}_{i}} < {{{\hat {J}}}_{\alpha }}\left( {{{{{{\hat {\Theta }}}}}_{\alpha }}} \right),{\text{\;\;\;\;}}{{J}_{i}} \geqslant 0,{\text{\;\;\;\;}}i = \overline {1,N} } \right\},} \\ {{{\Sigma }}_{\alpha }^{ + } = \left\{ {\left( {{{J}_{1}}, \ldots ,{{J}_{N}}} \right):\mathop \sum \limits_{i = 1}^N {{\alpha }_{i}}{{J}_{i}} \leqslant \mathop \sum \limits_{i = 1}^N {{\alpha }_{i}}{{J}_{i}}\left( {{{{{{\hat {\Theta }}}}}_{\alpha }}} \right),{\text{\;\;\;\;}}{{J}_{i}} \geqslant 0,{\text{\;\;\;\;}}i = \overline {1,N} } \right\},} \\ {{{{{\Sigma }}}_{ - }} = \bigcup\limits_{\alpha \in S}^{} {{{\Sigma }}_{\alpha }^{ - }} ,{\text{\;\;\;\;}}{{{{\Sigma }}}_{ + }} = \bigcup\limits_{\alpha \in S}^{} {{{\Sigma }}_{\alpha }^{ + }} ,{\text{\;\;\;\;}}{{{{\Sigma }}}_{0}} = {{{{\Sigma }}}_{ + }}{{\backslash }}{{{{\Sigma }}}_{ - }}.} \end{array}$Докажем, что точки $J\left( {{{{{\Theta }}}_{\alpha }}} \right) \in {{\mathcal{P}}_{\mathcal{L}}} \subseteq \mathcal{P}$ принадлежат множеству Σ0 (см. рис. 1,б).
Действительно, так как
Так как
Теорема 1. В задаче многокритериальной оптимизации квадратов индуцированных норм (1.1) линейных операторов ${{{{\Gamma }}}_{i}}\left( {{\Theta }} \right)$, $i = \overline {1,N} $, множество точек ${{\mathcal{P}}_{\mathcal{L}}} \subseteq \mathcal{P}$ критериального пространства, которые соответствуют оптимальным по Парето параметрам ${{{{\Theta }}}_{\alpha }}$, минимизирующим оптимальную целевую функцию ${{J}_{\alpha }}\left( {{\Theta }} \right)$ в виде линейной свертки (1.2), принадлежит множеству ${{{{\Sigma }}}_{0}}$, определенному в (1.6) в терминах субоптимальной целевой функции ${{\hat {J}}_{\alpha }}\left( {{\Theta }} \right)$ в виде квадрата индуцированной нормы оператора ${{{{\Gamma }}}_{\alpha }}\left( {{\Theta }} \right)$, определенного в (1.3).
В двукритериальных задачах нижней и верхней границами области, которой принадлежит множество ${{\mathcal{P}}_{\mathcal{L}}}$ в пространстве критериев $\left( {{{J}_{1}},{{J}_{2}}} \right)$, являются “огибающие” семейства прямых:
Заметим, что значениям α = 1 и α = 0 отвечают прямые ${{J}_{1}} = {\text{mi}}{{{\text{n}}}_{{{\Theta }}}}{{J}_{1}}\left( {{\Theta }} \right)$ и ${{J}_{2}} = {\text{mi}}{{{\text{n}}}_{{{\Theta }}}}{{J}_{2}}\left( {{\Theta }} \right)$ соответственно.
Для количественной оценки близости значений функционалов при найденных субоптимальных решениях ${{{{\hat {\Theta }}}}_{\alpha }}$ и неизвестных оптимальных решениях Θα введем показатель субоптимальности
1.2. Двойственная многокритериальная задача. Пусть теперь имеются N линейных ограниченных операторов, зависящих от параметров ${{\Theta }}$ и отображающих линейные пространства ${{{{\Xi }}}_{i}}$ со скалярными произведениями ${{\langle \cdot , \cdot \rangle }_{{{{{{\Xi }}}_{i}}}}}$ в линейное пространство $\Upsilon $ со скалярным произведением ${{\langle \cdot , \cdot \rangle }_{\Upsilon }}$, т.е.
Рассмотрим многокритериальную задачу минимизации квадратов индуцированных норм этих операторов:
(1.7)
${{J}_{i}}\left( {{\Theta }} \right) = {\text{||}}{{{{\Lambda }}}_{i}}\left( {{\Theta }} \right){\text{|}}{{{\text{|}}}^{2}} = \mathop {{\text{sup}}}\limits_{{{\xi }_{i}} \in {\text{\;}}{{{{\Xi }}}_{i}}} \frac{{{\text{||}}\zeta {\text{|}}{{{\text{|}}}^{2}}}}{{{\text{||}}{{\xi }_{i}}{\text{|}}{{{\text{|}}}^{2}}}},\quad i = \overline {1,N} .$Для нахождения субоптимальной целевой функции, позволяющей определить субоптимальные решения и локализовать множество Парето в этой задаче, применим теорию двойственности. А именно определим сопряженные линейные операторы
Поскольку нормы взаимно сопряженных линейных ограниченных операторов равны, запишем
критерии рассматриваемой задачи как 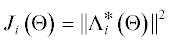 , $i = \overline {1,N} $. Согласно изложенному в предыдущем разделе, выберем субоптимальную целевую функцию
в виде ${{\hat {J}}_{\alpha }}\left( {{\Theta }} \right) = {\text{||}}{{{{\Lambda }}}_{\alpha }}\left( {{\Theta }} \right){\text{|}}{{{\text{|}}}^{2}}$, где
, $i = \overline {1,N} $. Согласно изложенному в предыдущем разделе, выберем субоптимальную целевую функцию
в виде ${{\hat {J}}_{\alpha }}\left( {{\Theta }} \right) = {\text{||}}{{{{\Lambda }}}_{\alpha }}\left( {{\Theta }} \right){\text{|}}{{{\text{|}}}^{2}}$, где
Мы получили субоптимальную целевую функцию, выраженную в терминах линейных операторов, сопряженных к заданным. Сделаем еще один шаг и найдем сопряженный оператор к ${{{{\Lambda }}}_{\alpha }}\left( {{\Theta }} \right)$, имеющий такую же индуцированную норму. Так как
Таким образом, для рассматриваемой многокритериальной задачи с критериями (1.7) верно
утверждение теоремы 1, где в качестве субоптимальной целевой функции выступает 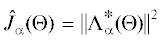 .
.
2. Применение к многокритериальным задачам оптимального управления и фильтрации. 2.1. Обобщенная ${{H}_{\infty }}$-норма. Применим изложенные выше результаты к синтезу субоптимальных по Парето регуляторов и фильтров для линейных динамических систем вида
(2.1)
$\begin{array}{*{20}{l}} {\dot {x} = A\left( t \right)x + B\left( t \right){v},\quad x\left( {{{t}_{0}}} \right) = {{x}_{0}},} \\ {z = C\left( t \right)x + D\left( t \right){v},\quad t \in \left[ {{{t}_{0}},{\text{\;}}{{t}_{f}}} \right].} \end{array}$В качестве линейного оператора в этих задачах выберем отображение пары (x(t0), ${v}(t)) \in {{{\text{R}}}^{n}} \times {{L}_{2}}$ = Ξ0, состоящей из начального состояния системы и возмущения на входе, в пару $(x({{t}_{f}}),z(t)) \in {{{\text{R}}}^{n}} \times {{L}_{2}} = {{\Upsilon }_{0}}$, состоящую из терминального состояния и целевого выхода системы. Скалярные произведения в соответствующих пространствах определим как
В следующей теореме сформулированы условия, при которых обобщенная ${{H}_{\infty }}$-норма на конечном горизонте ограничена сверху заданным значением параметра $\gamma > 0$.
Теорема 2. Пусть выполняется неравенство
(2.3)
${{\gamma }^{2}}I - {{D}^{{\text{T}}}}\left( t \right)D\left( t \right) > 0\quad \forall t \in \left[ {{{t}_{0}},{{t}_{f}}} \right].$i) обобщенная ${{H}_{\infty }}$-норма системы (2.1) удовлетворяет неравенству 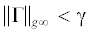 ;
;
ii) дифференциальные линейные матричные неравенства
(2.4)
$\left( {\begin{array}{*{20}{c}} { - \dot {Y}\left( t \right) + Y\left( t \right){{A}^{{\text{T}}}}\left( t \right) + A\left( t \right)Y\left( t \right)}&{B\left( t \right)}&{Y\left( t \right){{C}^{{\text{T}}}}\left( t \right)} \\ {{{B}^{{\text{T}}}}\left( t \right)}&{ - I}&{{{D}^{{\text{T}}}}\left( t \right)} \\ {C\left( t \right)Y\left( t \right)}&{D\left( t \right)}&{ - {{\gamma }^{2}}I} \end{array}} \right) \leqslant 0,{\text{\;\;\;\;}}t \in \left[ {{{t}_{0}},{\text{\;}}{{t}_{f}}} \right],$(2.5)
$\left( {\begin{array}{*{20}{c}} {Y\left( {{{t}_{f}}} \right)}&{Y\left( {{{t}_{f}}} \right){{S}^{{1/2}}}} \\ {{{S}^{{1/2}}}Y\left( {{{t}_{f}}} \right)}&{{{\gamma }^{2}}I} \end{array}} \right) > 0$iii) дифференциальные линейные матричные неравенства
(2.6)
$\left( {\begin{array}{*{20}{c}} {\dot {X}\left( t \right) + {{A}^{{\text{T}}}}\left( t \right)X\left( t \right) + X\left( t \right)A\left( t \right)}&{X\left( t \right)B\left( t \right)}&{{{C}^{{\text{T}}}}\left( t \right)} \\ {{{B}^{{\text{T}}}}\left( t \right)X\left( t \right)}&{ - {{\gamma }^{2}}I}&{{{D}^{{\text{T}}}}\left( t \right)} \\ {C\left( t \right)}&{D\left( t \right)}&{ - I} \end{array}} \right) \leqslant 0,\quad t \in \left[ {{{t}_{0}},{\text{\;}}{{t}_{f}}} \right],$Доказательство. Покажем сначала эквивалентность условий i) и ii). Пусть выполнено неравенствo ${{\left\| {{\kern 1pt} {{\Gamma }}{\kern 1pt} } \right\|}_{{g\infty }}} < \gamma $, покажем, что это влечет выполнение неравенств (2.4) и (2.5). На траекториях системы (2.1) определим функционал
(2.8)
$\bar {J}\left( {v} \right) = {{\gamma }^{2}}[{\text{||}}{v}{\text{||}}_{{\left[ {{{t}_{0}},{{t}_{f}}} \right]}}^{2} + x_{0}^{{\text{T}}}{{R}^{{ - 1}}}{{x}_{0}}] - \,{\text{||}}z{\text{||}}_{{\left[ {{{t}_{0}},{\text{\;}}{{t}_{f}}} \right]}}^{2}.$С учетом (2.2) неравенство  эквивалентно неравенству
эквивалентно неравенству
(2.9)
$\bar {J}\left( {v} \right) > {{x}^{{\text{T}}}}\left( {{{t}_{f}}} \right)Sx\left( {{{t}_{f}}} \right)\quad \forall {{x}_{0}} \in {{{\text{R}}}^{{{{n}_{x}}}}},\quad \forall {v} \in {{L}_{2}}:{\text{\;}}x_{0}^{{\text{T}}}{{R}^{{ - 1}}}{{x}_{0}} + \,{\text{||}}{v}{\text{||}}_{{\left[ {{{t}_{0}},{{t}_{f}}} \right]}}^{2} \ne 0.$Поставим задачу минимизации этого функционала относительно ${v}$, которую будем решать методом динамического программирования.
С этой целью введем вдоль траектории системы функцию Беллмана
(2.10)
$V\left( {t,x} \right) = \mathop {{\text{min}}}\limits_{{v}\left( \tau \right),\tau \in \left[ {{{t}_{0}},t} \right]} \{ {{\gamma }^{2}}[{\text{||}}{v}{\text{||}}_{{\left[ {{{t}_{0}},t} \right]}}^{2} + x_{0}^{{\text{T}}}{{R}^{{ - 1}}}{{x}_{0}}] - \,{\text{||}}z{\text{||}}_{{\left[ {{{t}_{0}},t} \right]}}^{2}\} ,$(2.11)
$\mathop {\min }\limits_{{v}(t)} ( - \dot {V}\, - \,{\text{|}}z{{{\text{|}}}^{2}} + {{\gamma }^{2}}{\text{|}}{v}{{{\text{|}}}^{2}}) = 0,\quad V\left( {{{t}_{0}},x} \right) = {{\gamma }^{2}}{{x}^{{\text{T}}}}{{R}^{{ - 1}}}x,$(2.12)
$\begin{array}{*{20}{c}} {\dot {Q} = AQ + Q{{A}^{{\text{T}}}} + Q{{C}^{{\text{T}}}}CQ + {{{({{B}^{{\text{T}}}} + {{D}^{{\text{T}}}}CQ)}}^{{\text{T}}}}{{{({{\gamma }^{2}}I - {{D}^{{\text{T}}}}D)}}^{{ - 1}}}({{B}^{{\text{T}}}} + {{D}^{{\text{T}}}}CQ),} \\ {Q\left( {{{t}_{0}}} \right) = {{\gamma }^{{ - 2}}}R.} \end{array}$Здесь для сокращения записи опущен аргумент t у матриц, фигурирующих в матричном дифференциальном уравнении. Заметим, что из положительной полуопределенности квадратичных слагаемых в правой части дифференциального уравнения (2.12) и положительной определенности матрицы $Q\left( {{{t}_{0}}} \right)$ следует положительная определенность решения, т.е. $Q(t) > 0,t \in [{{t}_{0}},{{t}_{f}}]$, и, следовательно, матрица $Q\left( t \right)$ обратима на всем рассматриваемом отрезке.
Обратимся опять к уравнению Беллмана (2.11), из которого следует что вдоль траектории системы (2.1) при любых возмущениях ${v}\left( t \right)$ для найденной функции Беллмана $V\left( {t,x} \right) = {{x}^{{\text{T}}}}{{Q}^{{ - 1}}}\left( t \right)x$ выполняется неравенство
которое принимает вид квадратичного неравенства ${{\xi }^{{\text{T}}}}M\xi \leqslant 0$, ${{\xi }^{{\text{T}}}} = ({{x}^{{\text{T}}}}{\text{\;\;}}{{{v}}^{{\text{T}}}})$ с отрицательно полуопределенной матрицейУмножая матрицу M слева и справа на положительно определенную матрицу $L = {\text{diag}}\left( {Q{\text{\;\;}}I} \right)$, получим
Применяя к последнему неравенству лемму Шура [26] и делая замену $Q = {{\gamma }^{{ - 2}}}Y$, получаем матричное неравенство
(2.14)
$\begin{array}{*{20}{c}} { - \dot {Y} + AY + Y{{A}^{{\text{T}}}} + {{\gamma }^{{ - 2}}}Y{{C}^{{\text{T}}}}CY + } \\ { + \,{{{({{B}^{{\text{T}}}} + {{\gamma }^{{ - 2}}}{{D}^{{\text{T}}}}CY)}}^{{\text{T}}}}{{{(I - {{\gamma }^{{ - 2}}}{{D}^{{\text{T}}}}D)}}^{{ - 1}}}({{B}^{{\text{T}}}} + {{\gamma }^{{ - 2}}}{{D}^{{\text{T}}}}CY) \leqslant 0,} \end{array}$Докажем теперь, что из ii) следует i). Пусть линейные матричные неравенства (2.4) и (2.5) разрешимы относительно $Y\left( t \right) > 0$ при $t \in \left[ {{{t}_{0}},{\text{\;}}{{t}_{f}}} \right]$ и ${{\gamma }^{2}} > 0$. Тогда непосредственно проверяется, что для квадратичной формы $V = {{\gamma }^{2}}{{x}^{{\text{T}}}}{{Y}^{{ - 1}}}\left( t \right)x$ на траекториях системы (2.1) выполняется
(2.16)
$\dot {V} + \,{\text{|}}z{{|}^{2}} - \,{{\gamma }^{2}}{\text{|}}{v}{{{\text{|}}}^{2}} \leqslant 0.$Интегрируя неравенства (2.16) на отрезке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ и учитывая (2.15), получаем
(2.17)
${\text{||}}z{\text{||}}_{{\left[ {{{t}_{0}},{{t}_{f}}} \right]}}^{2} + {{x}^{{\text{T}}}}\left( {{{t}_{f}}} \right)Sx\left( {{{t}_{f}}} \right) < {{\gamma }^{2}}[{\text{||}}{v}{\text{||}}_{{\left[ {{{t}_{0}},{{t}_{f}}} \right]}}^{2} + x_{0}^{{\text{T}}}{{R}^{{ - 1}}}{{x}_{0}}]$Покажем далее эквивалентность условий i) и iii). На траекториях системы (2.1) определим функционал
(2.18)
$\hat {J}\left( {v} \right) = {\text{||}}z{\text{||}}_{{\left[ {{{t}_{0}},{{t}_{f}}} \right]}}^{2} + {{x}^{{\text{T}}}}\left( {{{t}_{f}}} \right)Sx\left( {{{t}_{f}}} \right) - {{\gamma }^{2}}{\text{||}}{v}{\text{||}}_{{\left[ {{{t}_{0}},{{t}_{f}}} \right]}}^{2}.$С учетом (2.2) неравенство 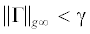 эквивалентно неравенству
эквивалентно неравенству
(2.19)
$\hat {J}\left( {v} \right) < {{\gamma }^{2}}x_{0}^{{\text{T}}}{{R}^{{ - 1}}}{{x}_{0}}{\text{\;}}\,\,\forall {{x}_{0}} \in {{{\text{R}}}^{{{{n}_{x}}}}},\quad \forall {v} \in {{L}_{2}}:{\text{\;}}x_{0}^{{\text{T}}}{{R}^{{ - 1}}}{{x}_{0}} + \,{\text{||}}{v}{\text{||}}_{{\left[ {{{t}_{0}},{{t}_{f}}} \right]}}^{2} \ne 0.$Поставим задачу максимизации этого функционала относительно ${v}$, которую будем решать методом динамического программирования. Вдоль траектории системы введем функцию Беллмана
(2.20)
$V\left( {t,x} \right) = \mathop {{\text{max}}}\limits_{{v}\left( \tau \right),{\text{\;}}\tau \in \left[ {t,{{t}_{f}}} \right]} \left\{ {{\text{||}}z{\text{||}}_{{\left[ {t,{{t}_{f}}} \right]}}^{2} + {{x}^{{\text{T}}}}\left( {{{t}_{f}}} \right)Sx\left( {{{t}_{f}}} \right) - {{\gamma }^{2}}{\text{||}}{v}{\text{||}}_{{\left[ {t,{{t}_{f}}} \right]}}^{2}} \right\},$(2.21)
$\mathop {\max }\limits_{{v}\left( t \right)} (\dot {V} + \,{\text{|}}z{{{\text{|}}}^{2}} - {{\gamma }^{2}}{\text{|}}{v}{{{\text{|}}}^{2}}) = 0,\quad V\left( {{{t}_{f}},x} \right) = {{x}^{{\text{T}}}}Sx.$Решая задачу на экстремум и полагая в качестве функции Беллмана квадратичную форму ${{x}^{{\text{T}}}}X\left( t \right)x$, находим матрицу X, удовлетворяющую уравнению Риккати:
(2.22)
$\begin{array}{*{20}{c}} {\dot {X} + {{A}^{{\text{T}}}}X + XA + {{C}^{{\text{T}}}}C + {{{({{B}^{{\text{T}}}}X + {{D}^{{\text{T}}}}C)}}^{{\text{T}}}}{{{({{\gamma }^{2}}I - {{D}^{{\text{T}}}}D)}}^{{ - 1}}}({{B}^{{\text{T}}}}X + {{D}^{{\text{T}}}}C) = 0,} \\ {X\left( {{{t}_{f}}} \right) = S.} \end{array}$Из уравнения Беллмана (2.21) следует, что вдоль траектории системы (2.1) при любых возмущениях ${v}\left( t \right)$ для найденной функции Беллмана $V\left( {t,x} \right) = {{x}^{{\text{T}}}}X\left( t \right)x$ выполняется неравенство
(2.23)
$\dot {V} + \,{\text{|}}z{{{\text{|}}}^{2}} - {{\gamma }^{2}}{\text{|}}{v}{{{\text{|}}}^{2}} \leqslant 0,$Применение к этому неравенству леммы Шура приводит к дифференциальному линейному матричному неравенству (2.6). С учетом неравенства (2.19) получаем квадратичное неравенство
Доказательство того, что из iii) следует i), проводится аналогично факту, что из ii) следует i). Таким образом, показана эквивалентность i) и iii). Теорема полностью доказана.
Для вычисления обобщенной ${{H}_{\infty }}$-нормы предлагается следующая процедура. Введем на отрезке $\left[ {{{t}_{0}},{{t}_{f}}} \right]$ равномерную сетку ${{t}_{k}} = {{t}_{{k - 1}}} + h$, $k = \overline {1,N} $, где $h = \left( {{{t}_{f}} - {{t}_{0}}} \right){\text{/}}N$, и проведем дискретизацию неравенства (2.4). В результате получаем следующую стандартную задачу полуопределенного программирования, решаемую средствами пакета Matlab (см., например, [2]): найти минимальное значение γ2 при ограничениях
(2.24)
$\left( {\begin{array}{*{20}{c}} { - \left( {{{Y}_{{k + 1}}} - {{Y}_{k}}} \right){\text{/}}h + {{Y}_{k}}A_{k}^{{\text{T}}} + {{A}_{k}}{{Y}_{k}}}&{{{B}_{k}}}&{{{Y}_{k}}C_{k}^{{\text{T}}}} \\ {B_{k}^{{\text{T}}}}&{ - I}&{D_{k}^{{\text{T}}}} \\ {{{C}_{k}}{{Y}_{k}}}&{{{D}_{k}}}&{ - {{\gamma }^{2}}I} \end{array}} \right) \leqslant 0,\quad {{Y}_{k}} > 0,\quad k = \overline {0,N - 1} ,$(2.25)
${{Y}_{0}} = R,\quad \left( {\begin{array}{*{20}{c}} {{{Y}_{N}}}&{{{Y}_{N}}{{S}^{{1/2}}}} \\ {{{S}^{{1/2}}}{{Y}_{N}}}&{{{\gamma }^{2}}I} \end{array}} \right) > 0.$Аналогичным образом обобщенная ${{H}_{\infty }}$-норма вычисляется на основе неравенства (2.6).
Для стационарных систем вида (2.1) на бесконечном горизонте обобщенная ${{H}_{\infty }}$-норма определяется как в (2.2) при S = 0, ${{t}_{f}} = \infty $ и характеризуется строгими линейными матричными неравенствами (2.4) при $Y\left( t \right) \equiv Y$, $\dot {Y} \equiv 0$ или (2.6), (2.7) при $X\left( t \right) \equiv X$, $\dot {X} \equiv 0$ [27, 28].
2.2. Синтез субоптимальных по Парето регуляторов и фильтров. Для того, чтобы компактно и единообразно изложить синтез субоптимальных по Парето регуляторов и фильтров, будем записывать уравнения системы
(2.26)
$\begin{gathered} \dot {x} = A\left( t \right)x + B\left( t \right){v}, \\ y = {{C}_{y}}\left( t \right)x + {{D}_{y}}\left( t \right){v}, \\ z = {{C}_{z}}\left( t \right)x + {{D}_{z}}\left( t \right){v} \\ \end{gathered} $Здесь для задачи управления
(2.27)
$\begin{array}{*{20}{l}} {{{A}_{{{\Theta }}}}\left( t \right) = A\left( t \right) + {{B}_{u}}\left( t \right){{\Theta }}\left( t \right),\quad {{B}_{{{\Theta }}}}\left( t \right) = B\left( t \right),} \\ {{{C}_{{{\Theta }}}}\left( t \right) = C\left( t \right) + {{D}_{u}}\left( t \right){{\Theta }}\left( t \right),\quad {{D}_{{{\Theta }}}}\left( t \right) = D\left( t \right)} \end{array}$(2.28)
$\begin{gathered} {{A}_{{{\Theta }}}}\left( t \right) = A\left( t \right) - {{\Theta }}\left( t \right){{C}_{y}}\left( t \right),\quad {{B}_{{{\Theta }}}}\left( t \right) = B\left( t \right) - {{\Theta }}\left( t \right){{D}_{y}}\left( t \right), \\ {{C}_{{{\Theta }}}}\left( t \right) = {{C}_{z}}\left( t \right),\quad {{D}_{{{\Theta }}}}\left( t \right) = {{D}_{z}}\left( t \right). \\ \end{gathered} $Заметим, что при различных возмущениях в системе и измерениях уравнения системы
Рассмотрим сначала многокритериальную задачу для системы c одним входом для возмущения и N целевыми выходами:
(2.29)
$\begin{gathered} \dot {x} = {{A}_{{{\Theta }}}}\left( t \right)x + {{B}_{{{\Theta }}}}\left( t \right){v},\quad x\left( {{{t}_{0}}} \right) = {{x}_{0}}, \\ {{z}_{i}} = {{C}_{{{{\Theta }},{\text{\;}}i}}}\left( t \right)x + {{D}_{{{{\Theta }},{\text{\;}}i}}}\left( t \right){v},\quad i = \overline {1,N} \\ \end{gathered} $(2.30)
${{J}_{i}}\left[ {{{\Theta }}\left( t \right)} \right] = \mathop {{\text{sup}}}\limits_{{{x}_{0}},{v}} \frac{{{\text{||}}{{z}_{i}}{\text{||}}_{{\left[ {{{t}_{0}},{\text{\;}}{{t}_{f}}} \right]}}^{2} + {{x}^{{\text{T}}}}\left( {{{t}_{f}}} \right){{S}_{i}}x\left( {{{t}_{f}}} \right)}}{{x_{0}^{{\text{T}}}{{R}^{{ - 1}}}{{x}_{0}} + \,{\text{||}}{v}{\text{||}}_{{\left[ {{{t}_{0}},{\text{\;}}{{t}_{f}}} \right]}}^{2}}},\quad i = \overline {1,N} .$В данном случае оператор ${{{{\Gamma }}}_{\alpha }}\left( {{\Theta }} \right)$, определенный в (1.3), отображает пару $\left( {x\left( {{{t}_{0}}} \right),v\left( t \right)} \right)$ в набор пар $((\alpha _{1}^{{1/2}}x\left( {{{t}_{f}}} \right),\alpha _{1}^{{1/2}}{{z}_{1}}\left( t \right)); \ldots ;(\alpha _{N}^{{1/2}}x\left( {{{t}_{f}}} \right),\alpha _{N}^{{1/2}}{{z}_{N}}\left( t \right)))$, где $x\left( {{{t}_{f}}} \right)$ и ${{z}_{i}}\left( t \right)$ удовлетворяют уравнениям (2.29) с начальными условиями $x\left( {{{t}_{0}}} \right)$ и возмущением ${v}\left( t \right)$, а квадрат его индуцированной нормы равен
(2.31)
$\begin{array}{*{20}{c}} {{{z}_{\alpha }}\left( t \right) = {{C}_{{{{\Theta }},\alpha }}}\left( t \right)x + {{D}_{{{{\Theta }},\alpha }}}\left( t \right){v},} \\ {{{C}_{{{{\Theta }},\alpha }}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {\alpha _{1}^{{1/2}}{{C}_{{{{\Theta }},{\text{\;}}1}}}\left( t \right)} \\ \cdots \\ {\alpha _{N}^{{1/2}}{{C}_{{{{\Theta }},N}}}\left( t \right)} \end{array}} \right),\quad {{D}_{{{{\Theta }},{\text{\;}}\alpha }}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {\alpha _{1}^{{1/2}}{{D}_{{{{\Theta }},{\text{\;}}1}}}\left( t \right)} \\ \cdots \\ {\alpha _{N}^{{1/2}}{{D}_{{{{\Theta }},{\text{\;}}N}}}\left( t \right)} \end{array}} \right).} \end{array}$Таким образом, субоптимальная целевая функция для этой задачи, совпадающая с квадратом нормы оператора ${{{{\Gamma }}}_{\alpha }}\left( {{\Theta }} \right)$, является квадратом обобщенной ${{H}_{\infty }}$-нормы комбинированного выхода ${{z}_{\alpha }}$ системы (2.29) с матрицей терминального состояния ${{S}_{\alpha }}$.
Субоптимальными по Парето регуляторами или фильтрами являются обобщенные ${{H}_{\infty }}$-оптимальные решения по отношению к этой норме для всех $\alpha \in S$, которые находятся на основе теоремы 2. А именно для задачи управления подставим в неравенства (2.4), (2.5) соответствующие матрицы (2.27) и обозначим ${{Z}_{1}}\left( t \right) = {{\Theta }}\left( t \right)Y\left( t \right)$. Применяя вычислительную процедуру, описанную в разд. 2.1, находим параметры регулятора ${{\Theta }}\left( {{{t}_{k}}} \right) = {{Z}_{1}}\left( {{{t}_{k}}} \right){{Y}^{{ - 1}}}\left( {{{t}_{k}}} \right)$. Для задачи фильтрации подставим в неравенства (2.6), (2.7) соответствующие матрицы (2.28), обозначим ${{Z}_{2}}(t) = X(t){{\Theta }}(t)$ и найдем параметры фильтра как ${{\Theta }}\left( {{{t}_{k}}} \right) = {{X}^{{ - 1}}}\left( {{{t}_{k}}} \right){{Z}_{2}}\left( {{{t}_{k}}} \right)$.
Заметим, что при выборе в одном из критериев в (2.30) ${{z}_{1}} \equiv 0$ и ${{S}_{1}} = I$, а в другом − ${{z}_{2}} \not\equiv 0$ и ${{S}_{2}} = 0$ находятся управления, обеспечивающие компромисс между величинами евклидовой нормы терминального состояния и интеграла от квадрата евклидовой нормы целевого выхода ${{z}_{2}}$, характеризующего переходный процесс в системе.
Рассмотрим теперь двойственную многокритериальную задачу для системы c N входами ${{{v}}_{i}}\left( t \right)$ и одним целевым выходом z, когда возмущение поступает только на один из входов. В этой задаче критериями являются квадраты обобщенных ${{H}_{\infty }}$-норм от входа ${{{v}}_{i}}$ к выходу z:
Согласно (1.8), оператор ${{\Lambda }}_{\alpha }^{{\text{*}}}\left( {{\Theta }} \right)$ для этой задачи отображает набор пар $(({{x}_{{0,1}}},{{{v}}_{1}}(t))$; ...; $({{x}_{{0,N}}},{{{v}}_{N}}(t)))$ в пару $\left( {x\left( {{{t}_{f}}} \right),z\left( t \right)} \right)$, где z(t) − выход системы:
(2.32)
$\begin{array}{*{20}{l}} {\dot {x} = {{A}_{{{\Theta }}}}\left( t \right)x + (\alpha _{1}^{{1/2}}{{B}_{{{{\Theta }},{\text{\;}}1}}}\left( t \right) \ldots \alpha _{N}^{{1/2}}{{B}_{{{{\Theta }},{\text{\;}}N}}}\left( t \right)){v},} \\ {z = {{C}_{{{\Theta }}}}\left( t \right)x + (\alpha _{1}^{{1/2}}{{D}_{{{{\Theta }},{\text{\;}}1}}}\left( t \right) \ldots \alpha _{N}^{{1/2}}{{D}_{{{{\Theta }},{\text{\;}}N}}}\left( t \right)){v}} \end{array}$Квадрат индуцированной нормы этого оператора равен
Так как отношение в правой части этого равенства принимает максимальное значение при ${{x}_{{0,i}}} = \alpha _{i}^{{1/2}}{{x}_{0}}$ и при этом
то субоптимальная целевая функция является обобщенной ${{H}_{\infty }}$-нормой системы (2.32) с входом ${v}(t)$ и выходом $z\left( t \right)$, а субоптимальные по Парето регуляторы и фильтры находятся аналогично тому, как описано выше для прямой многокритериальной задачи.Изложенные соображения относительно решений прямой и двойственной многокритериальных задач могут быть применены к системам с M входами для возмущений и N целевыми выходами следующего вида:
Обозначая комбинированное возмущение ${v} = {\text{col}}\left( {{{{v}}_{1}}, \ldots ,{{{v}}_{M}}} \right)$ и выбирая в качестве критериев обобщенные ${{H}_{\infty }}$-нормы системы от ${v}$ к ${{z}_{i}}$, приведенные в (2.30), приходим к прямой многокритериальной задаче минимизации влияния возмущений на N целевых выходов. В другом случае, обозначая комбинированный целевой выход $z = {\text{col}}\left( {{{z}_{1}}, \ldots ,{{z}_{N}}} \right)$ и выбирая в качестве критериев обобщенные ${{H}_{\infty }}$-нормы системы от ${{{v}}_{i}}$ к $z$, приведенные в (1.7) при N = M, приходим к двойственной многокритериальной задаче минимизации влияния возмущения в каждом из потенциально возможных входов на комбинированный целевой выход.
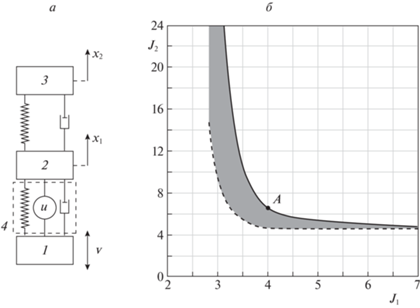
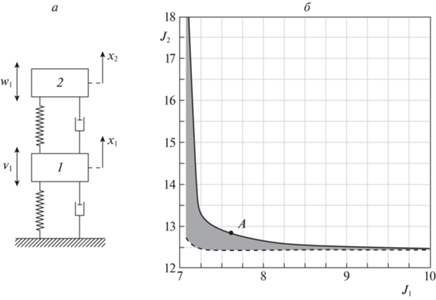
3. Результаты математического моделирования. Рассмотрим в качестве примера механическую систему с двумя степенями свободы, показанную на рис. 2, а и представляющую собой упругий объект, который моделируется двумя материальными точками 2 и 3, связанными между собой линейными упругим и диссипативным элементами. Этот объект связан упругим и диссипативным элементами и управляемым элементом (называемым далее виброизолятором) с другим телом 1, которое является подвижным основанием. Динамика данной механической системы (в безразмерных переменных и параметрах) описывается дифференциальными уравнениями
(3.1)
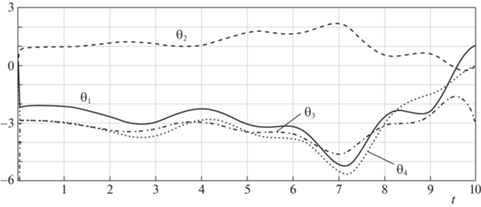
$\begin{gathered} {{{\ddot {x}}}_{1}} = - 2\beta {{{\dot {x}}}_{1}} + \beta {{{\dot {x}}}_{2}} - 2{{x}_{1}} + {{x}_{2}} + {v} + u, \\ {{{\ddot {x}}}_{2}} = - \beta \left( {{{{\dot {x}}}_{2}} - {{{\dot {x}}}_{1}}} \right) - {{x}_{2}} + {{x}_{1}} + {v}, \\ \end{gathered} $Зададим на интервале времени длительностью $T = 10$ равномерную сетку с шагом $h = 0.05$. Положим $R = I$ и ${{S}_{1}} = {{S}_{2}} = I$. Используя вычислительную процедуру, приведенную после доказательства теоремы 2, найдем множество ${{{{\Sigma }}}_{0}}$ (см. рис. 2, б). Отметим, что точки верхней границы множества ${{{{\Sigma }}}_{0}}$ соответствуют субоптимальным по Парето регуляторам с показателем субоптимальности $\eta = 0.2303$. Точка A на верхней границе множества ${{{{\Sigma }}}_{0}}$ имеет координаты (4.006; 6.536) и соответствует свертке с ${{\alpha }_{1}} = 0.7$ и ${{\alpha }_{2}} = 0.3$. На рис. 3 приведены графики зависимости от времени оптимальных коэффициентов обратной связи, отвечающих точке A: сплошная кривая соответствует коэффициенту ${{\theta }_{1}}\left( t \right)$, пунктирная − ${{\theta }_{2}}\left( t \right)$, штрихпунктирная − ${{\theta }_{3}}\left( t \right)$ и точечная − ${{\theta }_{4}}\left( t \right)$.
В качестве следующего примера рассмотрим задачу фильтрации на бесконечном горизонте для механической системы с двумя степенями свободы, схема которой показана на рис. 4, а. Она представляет собой упругий объект, который моделируется двумя материальными точками 1 и 2, связанными между собой и основанием линейными упругим и диссипативным элементами. Динамика данной механической системы (в безразмерных переменных и параметрах) описывается дифференциальными уравнениями
В численных расчетах использовались неравенства (2.6) и (2.7) теоремы 2 при R = = ${\text{diag}}(0.1I;0.5I)$. Найденное множество ${{{{\Sigma }}}_{0}}$ изображено на рис. 4, б серым цветом. Точки верхней границы множества ${{{{\Sigma }}}_{0}}$ соответствуют субоптимальным по Парето фильтрам со значением показателя субоптимальности $\eta = 0.054$. Это свидетельствует о том, что качество фильтрации при полученных фильтрах и оптимальных по Парето отличается незначительно. На верхней границе множества ${{{{\Sigma }}}_{0}}$ указана точка A c координатами (7.611; 12.812), отвечающая значению $\alpha = 0.65$, в этом случае матрица коэффициентов субоптимального по Парето фильтра равна ${{{{\hat {\Theta }}}}_{\alpha }} = (26.488$; 42.519; –9.934; 2.450)T. Для сравнения приведем матрицы коэффициентов фильтров при α = 0 и α = 1, оптимальных по каждому из критериев:
Заключение. Показано, что при многокритериальной оптимизации индуцированных норм линейных операторов можно указать единый критерий в виде индуцированной нормы некоторого вспомогательного линейного оператора, оптимизация которого позволяет найти субоптимальные по Парето решения и локализовать в критериальном пространстве множество Парето. Применение этого результата в многокритериальных задачах управления и фильтрации на конечном и бесконечном горизонтах с обобщенными ${{H}_{\infty }}$-нормами в качестве критериев позволяет характеризовать в терминах линейных матричных неравенств субоптимальные по Парето регуляторы и фильтры и оценить степень их субоптимальности.
Список литературы
Boyd S., El Ghaoui L., Feron E., Balakrishnan V. Linear Matrix Inequalities in Systems and Control Theory. Philadelphia: SIAM, 1994.
Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных матричных неравенств. М.: Физматлит, 2007.
Гермейер Ю.Б. Введение в теорию исследования операций. М.: Наука, 1971.
Ehrgott M. Multicriteria Optimization. Berlin - Heidelberg: Springer, 2005.
Mäkilä P.M. On Muptiple Criteria Stationary Linear Quadratic Control // IEEE Trans. Autom. Control. 1989. V. 34. № 12. P. 1311–1313.
Khargonekar P.P., Rotea M.A. Muptiple Objective Optimal Control of Linear Systems: the Quadratic Norm Case // IEEE Trans. Autom. Control. 1991. V. 36. № 1. P. 14–24.
Баландин Д.В., Бирюков Р.С., Коган М.М. Оптимальное управление максимальными уклонениями выходов линейной нестационарной системы на конечном интервале времени // АиТ. 2019. № 10. С. 37–61.
Баландин Д.В., Бирюков Р.С., Коган М.М. Минимаксное управление уклонениями выходов линейной дискретной нестационарной системы // АиТ. 2019. № 12. С. 3–24.
Balandin D.V., Kogan M.M. Multi-Objective Generalized ${{H}_{2}}$ Control // Automatica. 2019. V. 99. № 1. P. 317–322.
Balandin D.V., Biryukov R.S., Kogan M.M. Finite-Horizon Multi-Objective Generalized ${{H}_{2}}$ Control with Transients // Automatica. 2019. V. 106. № 8. P. 27–34.
Scherer C., Gahinet P., Chilali M. Multiobjective Output-Feedback Control via LMI Optimization // IEEE Trans. Autom. Control. 1997. V. 42. № 7. P. 896–911.
Oliveira M. C., Bernussou J., Geromel J.C. A New Discrete-time Robust Stability Condition // System Control Letters. 1999. V. 37. P. 261–265.
Ebihara Y., Hagiwara T. New Dilated LMI Characterisations for Continuous-time Control Multi-objective Controller Synthesis // Automatica. 2004. V. 40. P. 2003–2009.
Bernstein D.S., Haddad W.M. LQG Control with an ${{H}_{\infty }}$ Performance Bound: a Riccati Equation Approach // IEEE Trans. Autom. Control. 1989. V. 34. № 3. P. 293–305.
Khargonekar P.P., Rotea M.A. Mixed ${{H}_{2}}{\text{/}}{{H}_{\infty }}$ Control: a Convex Optimization Approach // IEEE Trans. Autom. Control. 1991. V. 36. № 7. P. 824–831.
Zhou K., Glover K., Bodenheimer B., Doyle J. Mixed ${{H}_{2}}$ and ${{H}_{\infty }}$ Performance Objectives I: Robust Performance Analysis // IEEE Trans. Autom. Control. 1994. V. 39. № 8. P. 1564–1574.
Doyle J., Zhou K., Glover K., Bodenheimer B. Mixed ${{H}_{2}}$ and ${{H}_{\infty }}$ Performance Objectives II: Optimal Control // IEEE Trans. Autom. Control. 1994. V. 39. № 8. P. 1575–1587.
Chen X., Zhou K. Multiobjective ${{H}_{2}}{\text{/}}{{H}_{\infty }}$ Control Design // SIAM J. Control Optim. 2001. V. 40. № 2. P. 628–660.
Hindi H.A., Hassibi B., Boyd S.P. Multi-objective ${{H}_{2}}{\text{/}}{{H}_{\infty }}$ Optimal Control via Finite Dimensional $Q$-Parametrization and Linear Matrix Inequalities // Proc. Amer. Control Conf. Philadelphia, USA, 1998. P. 3244–3249.
Баландин Д.В., Коган М.М. О множестве Парето в задачах управления и фильтрации при детерминированных и стохастических возмущениях // АиТ. 2017. № 1. С. 35–58.
Баландин Д.В., Коган М.М. Субоптимальные по Парето регуляторы против коалиций возмущений // АиТ. 2017. № 2. С. 3–26.
Balandin D.V., Kogan M.M. Pareto Suboptimal Controllers in Multi-objective Disturbance Attenuation Problems // Automatica. 2017. V. 84. № 10. P. 56–61.
Khargonekar P.P., Nagpal K.M., Poolla K.R. ${{H}_{\infty }}$ Control with Transients // SIAM J. Control Optim. 1991. V. 29. № 6. P. 1373–1393.
Баландин Д.В., Коган М.М. Минимаксный подход к синтезу оптимального управления при неопределенных начальных условиях // АиТ. 2009. № 11. С. 3–12.
Balandin D.V., Kogan M.M. Revisited LQ Output-feedback Control: Minimax Controller for a Set of Initial States // Intern. J. Control. 2009. V. 82. № 11. P. 2051–2058.
Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.
Баландин Д.В., Коган М.М. Обобщенное ${{H}_{\infty }}$-оптимальное управление как компромисс между ${{H}_{\infty }}$-оптимальным и $\gamma $-оптимальным управлениями // АиТ. 2010. № 6. С. 20–38.
Balandin D.V., Kogan M.M. LMI Based ${{H}_{\infty }}$-optimal Control with Transients // Intern. J. Control. 2010. V. 83. № 8. P. 1664–1673.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления