Известия РАН. Теория и системы управления, 2022, № 2, стр. 29-42

Введение. На борту летательного аппарата (ЛА) при наличии аппаратуры радиотехнической разведки (РТР), постов обнаружения теплового излучения оптиколокационной станции (ОЛС), бортовой радиолокационной станции (БРЛС), пеленгующей источники активных помех, “скрытно” имеем следующую измеренную информацию по радио- и теплоизлучающим воздушным и наземным объектам:

идентификатор РТР радиоэлектронной системы объекта, время измерения параметров сигнала, пеленг измерения в плоскости XOZ связанной системы координат (ССК), крен, тангаж, курс ЛА в момент измерения;

идентификатор ОЛС теплового излучения объекта, время измерения, пеленги измерения в ССК, крен, тангаж и курс ЛА в момент измерения;

идентификатор БРЛС постановщика активных помех (ПАП), время измерения, измеренные азимут и угол места ПАП.

Информация по координатам излучающих воздушных (ВО) и наземных (НО) объектов является неполной (неполное приборное обеспечение (НПО)). Не измеряется дальность, а в случае РТР не измеряется и второй пеленг в ССК. Комплексное гипотезное сопровождение [1, 2] излучающих ВО и НО на борту каждого ЛА группы формирует трассы этих объектов в двух системах координат ЛА: нормальной подвижной системе координат (НПСК), связанной с центром масс ЛА и стабилизированной по крену, и наземной системе координат (НСК) с началом в выбранной на ЛА “условной точке” с географическими координатами (λ_ut, φ_ut) [2].

Все основные процессы сопровождения (захват по первому измерению, ассоциация и фильтрация всех измерений, неоднозначная экстраполяция оценок фазовых координат) выполняются с помощью гипотезных трасс. Гипотезные трассы обеспечивают трассовое сопровождение ВО и НО при НПО.

По излучающим ВО на индикатор выдается (рис. 1):

нумерованный укороченный пеленг и наиболее вероятное местоположение на нем ВО, когда стандартная ошибка ϭ_D текущей дальности D больше 5%D (ϭ_D > 5%D ) и полусфера еще не определена (НПО3) (рис. 1, а);

укороченный пеленг, наиболее вероятное местоположение на нем ВО с указанием полусферы, когда ϭ_D > 5%D и определена полусфера, но точность оценки вектора скорости ϭ_ψ > 5° (НРО2 с признаком формирования курса PR_FK = 0) (рис. 1, б);

укороченный пеленг, наиболее вероятное местоположение на нем сопровождаемого объекта с вектором скорости, когда ϭ_D > 5%D и ϭ_ψ ≤ 5° (НРО2 с признаком формирования курса PR_FK = 1) (рис. 1, в);

местоположение ВО с вектором скорости, когда ϭ_D ≤ 5%D и ϭ_ψ ≤ 5° (НПО1) или полное приборное обеспечении (ППО с PR_FK = 1) (рис. 1, д);

местоположение ВО, когда при первом замере дальности PR_FK = 0 (рис. 1, г).

Признак приборного обеспечения PR_PO характеризует тип НПО: PR_PO = 1 при НПО1, PR_PO = 2 при НПО2, PR_PO = 3 при НПО3. При ППО PR_PO = 0.

Местоположение сопровождаемого объекта обозначается небольшим кругом с указанием всех текущих источников информации по этому объекту – БРЛС, ОЛС, РТР, КСС (комплекс средств связи) (рис. 2).

Для индикации высоты и вертикальной скорости сопровождаемых ВО целесообразно ввести на пульте кнопку “ФОРМУЛЯР”, при нажатии которой дополнительно к номеру сопровождаемого объекта выдается высота в сотнях метров (абсолютная или относительная) и стрелкой (вверх или вниз) указывается направление вертикальной скорости (рис. 3).

По излучающим НО на индикатор выдается (рис. 1, а, г):

нумерованный укороченный пеленг и наиболее вероятное местоположение на нем сопровождаемого объекта, когда точность оценки дальности σ_D > 5%D (НПО2);

местоположение сопровождаемого объекта, когда σ_D ≤ 5%D (НПО1) или ППО.

Точность трассового сопровождения излучающих ВО и НО на борту одиночного ЛА зависит от диапазонов [D_min, D_max], [V_min, V_max] возможных значений начальной дальности и скорости и траектории движения самого ЛА. В случае одиночного ЛА для повышения точности сопровождения объектов НПО2 (НПО3) (перевода их в объекты НПО1) применяется информационный маневр и введение гипотезной трассы НПО1 (трассы с начальной “пробной” дальностью D и стандартной ошибкой σ_D ≤ 5%D). Возможность выделения гипотезной трассы НПО1 зависит от близости “пробной” дальности к истинной дальности, а время выделения зависит от траектории движения ЛА (информационного маневра). Время достижения точности НПО1 для одиночного ЛА исчисляется несколькими десятками секунд.

В группе ЛА можно значительно сократить время гарантированного достижения НПО1, выполняя гипотезную триангуляцию. Для гипотезной триангуляции по каналам комплекса средств связи между ЛА группы производится обмен следующей информацией:

географическими координатами “условных точек” λ_ut , φ_ut ЛА группы,

координатами и скоростями ЛА в НСК,

трассами сопровождаемых ВО и НО в НСК (трассовыми поддержками),

измеренной информацией по излучающим ВО и НО и географическими координатами ЛА в момент измерения (измерениями).

1. Постановка задачи. В НПСК излучающий ВО определяется семью фазовыми координатами: азимут β, дальность D, радиальная скорость ${{{v}}_{r}}$ и тангенциальная скорость ${{{v}}_{t}}$, угловая скорость разворота по курсу ω_ψ , угол места ε и вертикальная скорость ${{{v}}_{h}}$, а излучающий НО – тремя координатами: β, D, ε. Обозначим фазовые координаты p-го ВО: Θ$_{1}^{{(p)}}$ = β^(p), Θ$_{2}^{{(p)}}$ = 1/(D^(p)cosε^(p)), Θ$_{3}^{{(p)}}$ = ${v}_{r}^{{(p)}}$, Θ$_{4}^{{(p)}}$ = ${v}_{t}^{{(p)}}$, Θ$_{5}^{{(p)}}$ = |ω$_{\psi }^{{(p)}}$|, Θ$_{6}^{{(p)}}$ = ε^(p), Θ$_{7}^{{(p)}}$ = |${v}_{h}^{{(p)}}$|, а координаты q-го НО: Θ$_{1}^{{(q)}}$ = β^(q), Θ$_{2}^{{(q)}}$ = = 1/(D^(q)cosε^(q)), Θ$_{6}^{{(p)}}$ = ε^(q).

Уравнения для p-го ВО имеют вид [2]

где V_x, V_y, V_z – проекции вектора скорости ЛА в НПСК, H, φ – высота и географическая широта местоположения ЛА, N(φ) – длина нормали к точке поверхности земного эллипсоида на широте φ от оси OX.

Маневр p-го ВО по курсу и высоте представлен произведениями  j_ψΘ$_{5}^{{(p)}}$ и  j_hΘ$_{7}^{{(p)}}$, где

Уравнения для q-го НО имеют вид

На борту n-го ЛА группы аппаратурой РТР, ОЛС и БРЛС обнаружено p_n ВО и q_n НО, причем каждый из этих объектов может быть обнаружен разными источниками информации:

одним – РТР, ОЛС или БРЛС,

двумя – РТР и БРЛС, РТР и ОЛС, БРЛС и ОЛС,

тремя – РТР, БРЛС и ОЛС.

При описании канала измерения РТР используется формула расчета измеренного азимута $x_{{1,R}}^{{(p,q)}}$ по пеленгу $\varphi _{y}^{{(p,q)}}$ в ССК и углу места ε^j j-й гипотезной трассы, крену γ, тангажу υ и курсу ψ ЛА:

где φ$_{z}^{j}$= 2arctg[(B –$\sqrt {{{A}^{2}} + {{B}^{2}} - \sin {}^{2}{{\varepsilon }^{j}}} $)/(A + sin${{\varepsilon }^{j}}$)], A = cosφ$_{y}^{{(p,q)}}$sinυ + sinφ$_{y}^{{(p,q)}}$sinγcosυ, B = cosγcosυ.

Канал измерения РТР:

идентификатор РТР N_R,

признак объекта (ВО или НО),

время измерения t_z и измеренный азимут:

где ошибка расчета измерения $\xi _{{\beta ,R}}^{{(n)}}\left( {{{t}_{z}}} \right)$ – независимая гауссовская последовательность с нулевым математическим ожиданием и дисперсией $\sigma _{{\beta ,R}}^{2}$(t_z).

При описании канала измерения ОЛС используются формулы расчета измеренных азимута $x_{{1,O}}^{{(p,q)}}$ и угла места $x_{{6,O}}^{{(p,q)}}$ по пеленгам $\varphi _{y}^{{(p,q)}}$ и φ$_{z}^{{(p,q)}}$, крену γ, тангажу υ и курсу ψ ЛА:

Канал измерения ОЛС:

идентификатор ОЛС N_O,

признак объекта,

время измерения t_z и измеренные азимут и угол места:

где вектор ошибок расчета измерений {ξ$_{{\beta ,O}}^{{(n)}}$(t_z), ξ$_{{\varepsilon ,O}}^{{(n)}}$(t_z)} – независимая гауссовская последовательность с нулевым математическим ожиданием и корреляционной матрицей ${{R}_{O}}$(t_z).

Канал измерения БРЛС по ПАП:

идентификатор БРЛС N_L,

признак объекта,

время измерения t_z и измеренные азимут и угол места:

где вектор ошибок измерений {ξ$_{{\beta ,L}}^{{(n)}}$(t_z), ξ$_{{\varepsilon ,L}}^{{(n)}}$(t_z)} – независимая гауссовская последовательность с нулевым математическим ожиданием и корреляционной матрицей ${{R}_{L}}$(t_z).

Решение задачи комплексного гипотезного сопровождения p_n ВО и q_n НО при таких измерителях на борту n-го ЛА приведено в работе [2]. Оно выполняется алгоритмами захвата, отбора, ассоциации, фильтрации, управления гипотезами, экстраполяции и формирования выходных трасс.

В алгоритме захвата по измерению РТР формируется 24 гипотезные трассы по скорости

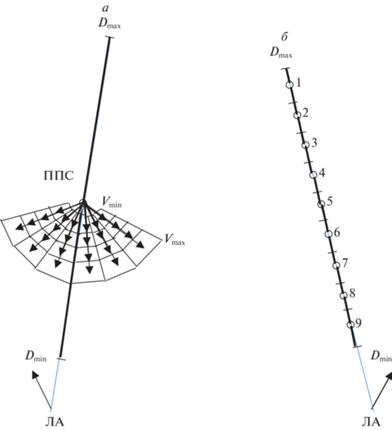
для ВО (рис. 4, а) и 9 гипотезных трасс по дальности для НО (рис. 4, б).

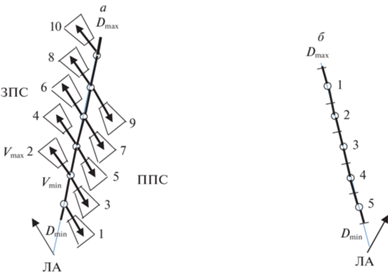
В алгоритме захвата по измерению ОЛС формируется 10 гипотезных трасс по скорости

для ВО (рис. 5, а) и 5 гипотезных трасс по дальности для НО (рис. 5, б).

В алгоритме захвата по измерению БРЛС формируется 24 гипотезные трассы по скорости для ВО (рис. 4, а) и 5 гипотезных трасс по дальности для НО (рис. 5, б).

В качестве алгоритма фильтрации для измерений ОЛС и БРЛС используется азимутально-угломестный фильтр Ф_βε [2], а для измерения РТР его частный случай – азимутальный фильтр Ф_β.

В рассматриваемой задаче гипотезной триангуляции предполагается наличие системы единого времени в группе ЛА и надо выполнить следующие действия.

1. Определить состав трассовой поддержки передаваемой ЛА по КСС, который

необходим для решения задачи гипотезной триангуляции.

2. Определить состав измеренной информации, передаваемый ЛА по КСС, который

необходим для решения задачи гипотезной триангуляции.

3. Произвести пересчет трассовых поддержек, полученных с бортов ЛА группы, в свою систему координат НПСК.

4. Выполнить однозначное отождествление по идентификаторам и координатам всех пересчитанных трассовых поддержек, полученных с бортов ЛА группы объектов НПО, с внутренними трассами своих сопровождаемых объектов.

5. Для каждого своего отождествленного p-го (q-го) объекта определить три гипотезные трассы  j₁,  j₂,  j₃ по критерию минимальной приведенной невязки – невязки, деленной на число измеряемых координат:

пять – азимут, обратная дальность, радиальная и тангенциальная скорости, угол места для ВО с PR_FK = 1,

три – азимут, обратная дальность, угол места для НО и ВО с PR_FK = 0:

и записать в них полученные измерения.

6. Вычислить триангуляционную дальность ${{D}^{j}}$ и ее дисперсию $d_{{DD}}^{j}$ для каждой  j-й гипотезной трассы с измерением по критерию: $\mathop {\min }\limits_{\mathop {{{D}^{j}}}\limits_{} } $${{\Delta }^{j}}$ (или $\mathop {\max }\limits_{\mathop {{{D}^{j}}}\limits_{} } $cos²${{\Delta }^{j}}$), где ${{\Delta }^{j}}$ – угол между вектором измеренных пеленгов {y₀, y₂, y₄} и вектором пеленгов {${{D}^{j}}{{a}^{j}}$ + ${{m}_{{x0}}}$, ${{D}^{j}}{{b}^{j}}$ + ${{m}_{{y0}}}$, ${{D}^{j}}{{c}^{j}}$ + ${{m}_{{z0}}}$}  j-й гипотезной трассы на передающем ЛА в момент замера, расcчитаный по азимуту ${{\beta }^{j}}$, углу места ${{\varepsilon }^{j}}$ и дальности ${{D}^{j}}$этой гипотезной трассы на принимающем ЛА:

где ${{A}^{j}}$ = ${{a}^{j}}$y₀ + ${{b}^{j}}$y₂ + ${{c}^{j}}$y₄, B = $m_{{x0}}^{s}$y₀ + $m_{{y0}}^{s}$y₂ + $m_{{z0}}^{s}$y₄, ${{E}^{j}}$ = (${{a}^{j}}$)² + (${{b}^{j}}$)² + (${{c}^{j}}$)², $m_{{xx}}^{s}$, … , $m_{{zz}}^{s}$, $m_{{x0}}^{s}$, $m_{{y0}}^{s}$, $m_{{y0}}^{s}$ – коэффициенты перехода от НПСК своего ЛА к НПСК передающего ЛА в момент замера.

7. Для субоптимальной оценки фазовых координат сопровождаемого объекта вывести многомерный нелинейный гипотезный фильтр, на вход которого подается вычисленная триангуляционная дальность.

2. Решение задачи. Рассмотрим выполнение перечисленных требований.

2.1. Состав трассовой поддержки, передаваемой ЛА по КСС: Nf  – номер формуляра трассы объекта, О – признак объекта, ListI – список источников информации, PR_PO – признак приборного обеспечения, t_z – время последнего замера, x(t_z), y(t_z), z(t_z) – неэкстраполированные декартовые координаты объекта в НСК, ${{{v}}_{x}}$(t_z), ${{{v}}_{y}}$(t_z), ${{{v}}_{z}}$(t_z) – неэкстраполированные проекции скорости объекта в НСК, β(t_z) – неэкстраполированный азимут объекта, s_D(t_z), s_L(t_z), s_h(t_z), ${{s}_{{v}}}$(t_z), s_ψ(t_z) и ${{k}_{{{v}\psi }}}$(t_z) – стандартные ошибки по D, L (нормали к визирному лучу), h (высоте), ${v}$, ψ и коэффициент корреляции ${v}$ и ψ, рассчитываемые по вероятностям ${{\pi }_{j}}$(t_z), оценкам m$_{k}^{j}$(t_z) и корреляционным моментам d$_{{kl}}^{j}$(t_z) гипотезных трасс сопровождаемого объекта, PR_UM, PR_FK – признаки измерения угла места и формирования курса.

2.2. Состав измеренной информации, передаваемый ЛА по КСС:   Nf  – номер формуляра трассы объекта, ${{\beta }^{s}}$(t_z) – измеренный азимут объекта, ${{\varepsilon }^{s}}$(t_z) – измеренный угол места объекта, $s_{\beta }^{s}$(t_z), $s_{\varepsilon }^{s}$(t_z) – стандартные ошибки по β^S, ε^S, PR_UM – признак измерения угла места, ${{\lambda }^{s}}$(t_z), ${{\varphi }^{s}}$(t_z), ${{H}^{s}}$(t_z) – географические координаты ЛА в момент замера t_z.

2.3. Формирование отметки измерения по трассовой поддержке, полученной с борта ЛА группы. Для отождествления трассовых поддержек с внутренними трассами своих сопровождаемых объектов формируются отметки измерения, которые формируются в три этапа:

запись в отметку измерения идентификаторов объекта N_R, N_O, N_L и признаков PR_PO, PR_UM, PR_FK,

пересчет трассовых поддержек в систему координат НПСК своего ЛА,

определение сферических координат переданного объекта.

Пересчет выполняется по формулам

Для ВО при PR_FK = 1 вычисляются еще проекции вектора скорости:

где приведены коэффициенты перехода:

Здесь λ(t_z), φ(t_z), Н(t_z) – географические координаты своего ЛА в момент замера t_z:

где t – текущее время.

Сферические координаты определяются по формулам

При PR_UM = 1 имеем ${{x}_{6}}$(t_z) = arcsin(y₀/D(t_z)).

Далее вычисляются корреляционные моменты s₁₁, s_1D, s_DD, s₆₆ сферических координат ${{x}_{1}}$ , D, ${{x}_{6}}$ объекта:

где $\sigma _{{XZ}}^{2}$, $\sigma _{H}^{2}$ – дисперсии декартовых координат и высоты полета передающего ЛА, рассчитанные по паспортным данным его навигационной системы.

При PR_FK = 1 определяются проекции скорости объекта и их корреляционные моменты:

2.4. Ассоциация сформированных отметок измерения с внутренними трассами своих сопровождаемых объектов. Необходимо установить однозначное соответствие: каждой отметке измерения одного ЛА группы соответствует одна внутренняя трасса, а каждая внутренняя трасса содержит не более одной отметки измерения этого ЛА. Для каждой внутренней трассы с отметками этого ЛА производится ранжирование этих отметок по средней приведенной невязке $s_{\chi }^{2}$, вычисленной по гипотезным трассам. Внутренняя трасса ВО содержит неманеврирующие и маневрирующие гипотезные трассы, а внутренняя трасса НО – только неманеврирующие гипотезные трассы движения объекта в НПСК.

Сначала вычисляется $s_{\chi }^{2}$ по неманеврирующим гипотезным трассам  j = 0 с вероятностями π_j

При наличии маневрирующих гипотезных трасс возможна ее корректировка. Для каждой маневрирующей гипотезной трассы (j $ \ne $ 0) в цикле по интенсивности маневра прострелом определяется минимальная приведенная невязка $\overline {\chi _{j}^{2}} $. При $\overline {\chi _{j}^{2}} $ < $s_{\chi }^{2}$ производится корректировка $s_{\chi }^{2}$ = $\overline {\chi _{j}^{2}} $. Если для отметки ЛА группы в ближайшей (по невязке $s_{\chi }^{2}$) внутренней трассе эта отметка также является ближайшей из отметок этого ЛА (однозначная ассоциация), то она одна остается в этой внутренней трассе и вычеркивается из остальных внутренних трасс. В противном случае, из возможных вариантов ассоциации выбирается тот, при котором минимальна сумма средних приведенных невязок.

Для трассовых поддержек с признаком PR_PO >1, отождествленных с внутренними трассами без измерения дальности, назначается режим гипотезной триангуляции и корректируется состав измерения – остается только дальность. Вычисляются коэффициенты перехода от НПСК своего ЛА в момент замера с центром λ(t_z), φ(t_z), Н(t_z) к НПСК ЛА группы с центром λ^s(t_z), φ^s (t_z), Н ^s(t_z):

2.5. Определение трех ближайших по невязке гипотезных трасс и запись в них адресов отметок измерения. В процессе вычисления для внутренней трассы средней приведенной невязки $s_{\chi }^{2}$ по каждой ее j-й гипотезной трассе вычисляется приведенная невязка $\overline {\chi _{j}^{2}} $ и по ней производится ранжирование гипотезных трасс, которое записывается в отметку измерения. В результате ассоциации во внутренней трассе остается одна отметка измерения. Выбираем в этой отметке измерения три первые гипотезные трассы и в остальных гипотезных трассах исключаем эту отметку измерения.

2.6. Вычисление триангуляционной дальности и ее дисперсии. Триангуляционная дальность D^j рассчитывается для каждой из трех выбранных гипотезных трасс объекта как точка минимума функции (1.7):

Для трех выбранных гипотезных трасс объекта ОЛС и БРЛС

где A^j, B, E^j, F^j, H вычисляются по формулам (1.8).

Для трех выбранных гипотезных трасс объекта РТР

где E^j, F^j, H вычисляются по формулам (1.8), ${{A}^{j}}$ = ${{a}^{j}}$y₀ + ${{c}^{j}}$y₄, B = ${{m}_{{x0}}}$y₀ + ${{m}_{{z0}}}$y₄,

Поскольку углы ${{\beta }^{s}}$(t_z), ${{\varepsilon }^{s}}$(t_z), m$_{1}^{j}$(t_z), m$_{6}^{j}$(t_z) определяются со стандартными ошибками $s_{\beta }^{s}$(t_z), $s_{\varepsilon }^{s}$(t_z), s$_{1}^{j}$(t_z) = $\sqrt {d_{{11}}^{j}({{t}_{z}})} $, s$_{6}^{j}$(t_z) = $\sqrt {d_{{66}}^{j}({{t}_{z}})} $, где $d_{{11}}^{j}({{t}_{z}})$, $d_{{66}}^{j}({{t}_{z}})$ – дисперсии азимута и угла места в  j-й гипотезной трассе, и коэффициенты перехода – нелинейные функции, то для вычисления несмещенной триангуляционной дальности и ее дисперсии методом статистического моделирования заменим непрерывное распределение ошибок вычисления  ${{\beta }^{s}}$(t_z), ${{\varepsilon }^{s}}$(t_z), m$_{1}^{j}$(t_z), m$_{6}^{j}$(t_z) для объектов ОЛС и БРЛС дискретным с равными вероятностями в девяти точках:

а непрерывное распределение ошибок вычисления β^s(t_z), m$_{1}^{j}$(t_z) для объектов РТР – дискретным с равными вероятностями в пяти точках:

Для трех гипотезных трасс объекта ОЛС и БРЛС триангуляционная дальность

Ее дисперсия

Для трех гипотезных трасс объекта РТР триангуляционная горизонтальная дальность

Ее дисперсия

2.7. Многомерный нелинейный гипотезный фильтр триангуляционной дальности. Фильтр для триангуляционной дальности выводится из дальностного фильтра Ф_D [2] и имеет вид

Апостериорные вероятности гипотезных трасс пересчитываются по формулам

где Н₁, Н₂ – нормирующие множители. Здесь π_j(t_z – 0), m$_{k}^{j}$(t_z – 0), d$_{{kl}}^{j}$(t_z – 0) – значения параметров π_j, m$_{k}^{j}$, d$_{{kl}}^{j}$ в точке t_z слева до фильтрации, т.е. экстраполированных ко времени t_z.

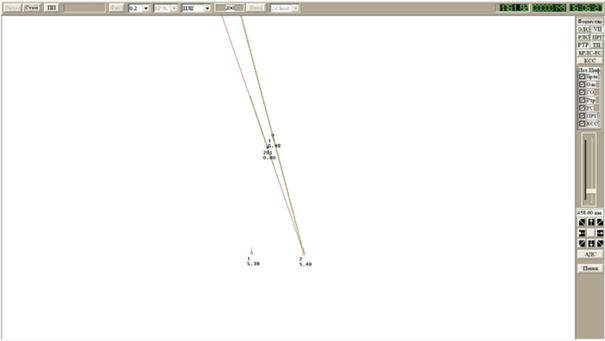
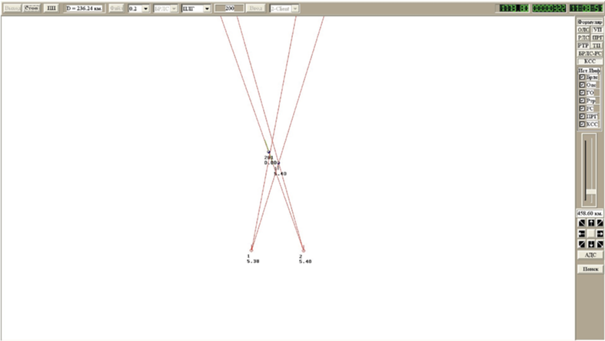
3. Пример. Гипотезная триангуляция ВО и НО РТР парой ЛА. РТР измеряет пеленг φ_y в плоскости XOZ ССК. Обмен информацией по КСС производится после завязки трасс и проверки их на истинность (рис. 6). Поэтому в первом обмене приходит информация только по НО. Между поступлениями информации по КСС на борту каждого ЛА обрабатываются замеры своего РТР.

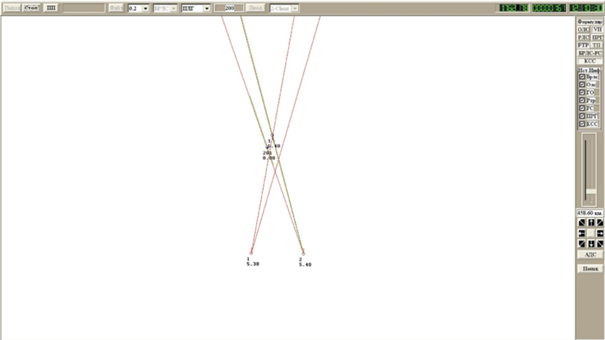
На рис. 6–11 – вид тактического индикатора ведомого ЛА в характерные моменты времени: первая выдача выходной трассы по информации РТР (рис. 7), выделение гипотезной трассы, определение вектора скорости ВО, достижение НПО1. Красные линии показывают замеры пеленгов на каждом ЛА, укороченный пеленг зеленого цвета – текущий диапазон по дальности при НПО2.

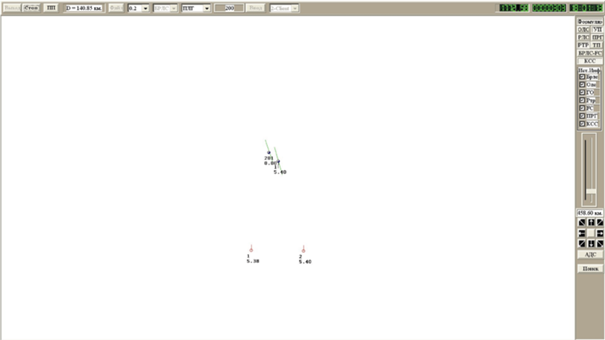
Выделение гипотезной трассы НО происходит после второго обмена по КСС (рис. 8) .Стандартная ошибка оценки дальности превышает необходимые для НПО1 5%D (рис. 9). Для НО вводится дополнительная гипотезная трасса с парамерами НПО1 и на следующем третьем обмене достигается σ_D < 5%D (рис. 10).

Информация по ВО поступает начиная со второго обмена по КСС. При первом же поступлении информации по ВО формируется признак PR_FK = 1, т.е. стандартная ошибка оценки вектора скорости по курсу не превышает 5°.

Выделение гипотезной трассы ВО происходит после третьего обмена по КСС (информация по ВО поступает второй раз по КСС). Стандартная ошибка оценки дальности при этом σ_D = = 6.21%D (рис. 9). Так как σ_ψ < 5° , то для достижения НПО1 необходимо снизить ошибку по дальности. Вводится дополнительная гипотезная трасса НПО1 и на следующем четвертом обмене (третье поступление информации о ВО по КСС) достигается σ_D <5%D (рис. 11). Таким образом, для достижения НПО1 как для НО, так и ВО достаточно трех циклов триангуляции.

Заключение. Решена задача повышения точности “скрытного” трассового сопровождения радио- и теплоизлучающих ВО и НО на борту ЛА за счет гипотезной триангуляции:

сброс неотождествленных гипотезных трасс (уменьшается диапазон значений дальности, а для ВО и скорости),

фильтрация в отождествленных гипотезных трассах многомерным нелинейным гипотезным фильтром Ф_D триангуляционных дальностей, вычисленных по критерию минимальной невязки измеренных пеленгов и их расчетных значений для этих гипотезных трасс,

ввод для ускорения достижения НПО1 дополнительной гипотезной трассы с пробной дальностью и точностью НПО1.

Гипотезная триангуляция позволяет достигать точности НПО1 (σ_D ≤ 5%D для НО, σ_D ≤ 5%D и σ_ψ ≤ 5° для ВО) после трех обменов информацией по КСС.