Известия РАН. Теория и системы управления, 2022, № 3, стр. 41-56
КВАЗИОПТИМАЛЬНАЯ СТАБИЛИЗАЦИЯ КОЛЕБАТЕЛЬНЫХ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
П. С. Воеводин a, *, Ю. М. Заболотнов a, **
a Самарский национальный исследовательский ун-т
Самара, Россия
* E-mail: p.voevodin@inbox.ru
** E-mail: yumz@yandex.ru
Поступила в редакцию 11.02.2021
После доработки 28.06.2021
Принята к публикации 29.11.2021
- EDN: FVMHEY
- DOI: 10.31857/S0002338822020159
Аннотация
Рассматривается задача квазиоптимальной стабилизации малых колебаний механических систем со многими степенями свободы с медленно изменяющимися параметрами и малыми возмущениями. Для синтеза приближенно оптимальных регуляторов используется принцип динамического программирования Беллмана в сочетании с методом усреднения. Метод усреднения применяется для получения асимптотического решения уравнений Гамильтона–Якоби–Беллмана. Предлагаемый алгоритм синтеза позволяет существенно упростить задачу конструирования приближенно оптимальных регуляторов, а для рассматриваемых частных случаев получить аналитическое решение. В качестве примера рассматривается задача стабилизации движения малого космического аппарата относительно направления троса при развертывании космической тросовой системы.
Введение. Применение метода усреднения для решения разнообразных задач оптимального управления рассматривалось во многих работах, например [1–5]. Систематическое изложение вопросов, связанных с применением асимптотических методов, в частности метода усреднения, для синтеза управлений представлено в монографиях [2, 4], где особое внимание уделено вопросам стабилизации движений колебательных систем. В этих публикациях разработаны общие алгоритмы применения принципов максимума Понтрягина и динамического программирования Беллмана для синтеза управлений в задачах стабилизации движений колебательных систем. Подробно рассмотрены оптимизация по критериям быстродействия и минимальным затратам на управление [2, 4].
В статье рассматривается задача стабилизации движения колебательной системы со многими степенями свободы при действии малых возмущений. Предлагается процедура расчета оптимального регулятора, основанная на совместном применении принципа динамического программирования Беллмана и метода усреднения. Синтез регулятора осуществляется с помощью квадратичного критерия оптимальности, зависящего от амплитуд колебаний в системе и управления, т.е. используется свертка критериев оптимальности. Метод усреднения применяется для приближенного решения уравнения Гамильтона–Якоби–Беллмана, что позволяет в некоторых случаях получить достаточно простое аналитическое решение задачи. В частности, это относится к случаю медленного изменения параметров системы. Рассматривается пример применения предлагаемой методики для стабилизации угловых колебаний малого космического аппарата (КА) относительно направления троса при развертывании космической тросовой системы. Показано, что, изменяя весовые коэффициенты в критерии оптимальности, характеризующие определенные моды колебаний в системе, можно формировать вид прецессии КА относительно направления троса.
1. Уравнения движения и постановка задачи. Рассматриваются движения колебательной системы с малыми возмущениями и управлением вида
(1.1)
$\ddot {y} + C\left( {{\tau }} \right)y = {{\varepsilon }}f\left( {y,\dot {y},{{\tau }}} \right) + {{\varepsilon }}Nu\left( t \right),$Предполагается, что система (1.1) удовлетворяет условиям управляемости и наблюдаемости [6].
Невозмущенное решение ε = 0 систем (1.1), (1.2) характеризуется частотами ${{{{\omega }}}_{k}}\left( {{\tau }} \right)$ и собственными векторами ${{{{\gamma }}}^{{(k)}}}\left( {{\tau }} \right)$, где $k = \overline {1,n} $, которые определяются из следующих соотношений:
(1.2)
${\text{|}}C\left( {{\tau }} \right) - {{{{\omega }}}^{2}}\left( {{\tau }} \right)E{\text{|}} = 0,\quad (C\left( {{\tau }} \right) - {{\omega }}_{k}^{2}\left( {{\tau }} \right)E){{{{\gamma }}}^{{(k)}}}\left( {{\tau }} \right) = 0,$Тогда, переходя в системе (1.1) к нормальным координатам $x(t) = {{\Gamma }^{{ - 1}}}({{\varepsilon }}t)y(t)$, где $\Gamma \left( {{{\varepsilon }}t} \right)$ – матрица собственных векторов (далее просто $\Gamma $), получим
(1.3)
$\ddot {x} + {{\Omega }^{2}}\left( {{\tau }} \right)x = {{\varepsilon }}F\left( {x,\dot {x},{{\tau ,\varepsilon }}} \right) + {{\varepsilon }}Mu,$Невозмущенное решение в нормальных координатах имеет вид
(1.4)
${{x}_{k}} = {{A}_{k}}\cos {{{{\varphi }}}_{k}}(t),\quad {{\dot {x}}_{k}} = - {{{{\omega }}}_{k}}\left( {{\tau }} \right){{A}_{k}}\sin {{{{\varphi }}}_{k}}(t),\quad k = \overline {1,n} ,$Основываясь на виде невозмущенного решения (1.4) и имея в виду использование метода усреднения для построения приближенно оптимального управления, применяется стандартная замена переменных вида $\left( {x,\dot {x}} \right) \Rightarrow \left( {A,{{\varphi }}} \right)$ в системе (1.3), где $A,{{\varphi }}$ – вектора амплитуд и фаз колебаний. Тогда, применяя метод вариации произвольных постоянных (метод медленно меняющихся амплитуд [7]) и рассматривая соотношения (1.4) как замену переменных, получим
(1.5)
${{\dot {A}}_{k}} = - \frac{{{\varepsilon }}}{{{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}\left[ {{{\Phi }_{k}}\left( {A,{{\varphi }},{{\tau ,\varepsilon }}} \right) + {{U}_{k}}} \right]\sin {{{{\varphi }}}_{k}},$(1.6)
${{{{\dot {\varphi }}}}_{k}} = {{{{\omega }}}_{k}}\left( {{\tau }} \right) - \frac{{{\varepsilon }}}{{{{A}_{k}}{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}\left[ {{{\Phi }_{k}}\left( {A,{{\varphi }},{{\tau ,\varepsilon }}} \right) + {{U}_{k}}} \right]\cos {{{{\varphi }}}_{k}},$Рассматривается задача о стабилизации движения колебательной системы, обеспечивающая ее динамическую устойчивость (уменьшение амплитуд колебаний) исходя из минимума квадратичного критерия оптимальности:
где ${{a}_{k}},c > 0$ – весовые коэффициенты, причем обычно полагаютДвижение систем (1.5), (1.6) рассматривается на асимптотически большом интервале времени
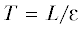 , где $L < \infty $ – некоторая константа, следовательно, функционал (1.7) изменяется на величину порядка
O(1).
, где $L < \infty $ – некоторая константа, следовательно, функционал (1.7) изменяется на величину порядка
O(1).
2. Определение приближенно оптимального управления. В соответствии с принципом динамического программирования Беллмана оптимальное управление находится из условия
где $V\left( {A,{{\varphi }},{{\tau }}} \right)$ – функция Беллмана, полная производная которой определяется в силу систем (1.5), (1.6).Выделяя в условии (2.1) функцию, зависящую от управления, и учитывая выражение для производной функции $V\left( {A,{{\varphi }},{{\tau }}} \right)$, получим
(2.2)
$\mathop {\min }\limits_{{{U}_{k}}} \sum\limits_{k = 1}^n {\left[ {cU_{k}^{2} - \frac{{{{U}_{k}}}}{{{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}{{P}_{k}}\left( {V,{{A}_{k}},{{\varphi }_{k}}} \right)} \right]} = 0,$Тогда из необходимого условия минимума (2.2) нетрудно найти выражение для оптимального управления:
(2.3)
$U_{k}^{o} = \frac{1}{{2c{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}{{P}_{k}}\left( {V,{{A}_{k}},{{{{\varphi }}}_{k}}} \right).$Подставляя выражение (2.3) в соотношение (2.1), приходим к уравнению в частных производных Гамильтона–Якоби–Беллмана:
(2.4)
$\begin{gathered} {{\varepsilon }}\frac{{\partial V}}{{\partial {{\tau }}}} + \sum\limits_{k = 1}^n {\left[ {{{\varepsilon }}{{a}_{k}}A_{k}^{2} - {{\varepsilon }}\frac{{{{\Phi }_{k}}\left( {A,{{\varphi }},{{\tau ,\varepsilon }}} \right){{P}_{k}}\left( {V,{{A}_{k}},{{{{\varphi }}}_{k}}} \right)}}{{{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}{\text{ + }}} \right.} \\ \,\left. { + \frac{{\partial V}}{{\partial {{{{\varphi }}}_{k}}}}{{{{\omega }}}_{k}}\left( {{\tau }} \right) - {{\varepsilon }}\frac{{{{P}_{k}}{{{\left( {V,{{A}_{k}},{{{{\varphi }}}_{k}}} \right)}}^{2}}}}{{4c{{\omega }}_{k}^{2}\left( {{\tau }} \right)}}} \right] = 0. \\ \end{gathered} $Для определения приближенного решения уравнения (2.4) применяется метод усреднения. В этом случае используется почти тождественная замена переменных [3]
(2.5)
$A = {{A}^{o}} + {{\varepsilon }}{{{{\nu }}}_{1}}({{A}^{o}},{{{{\varphi }}}^{o}},{{\tau }}) + {{{{\varepsilon }}}^{2}}...,\quad {{\varphi }} = {{{{\varphi }}}^{o}} + {{\varepsilon }}{{{{\mu }}}_{1}}({{A}^{o}},{{{{\varphi }}}^{o}},{{\tau }}) + {{{{\varepsilon }}}^{2}}...,$Приближенные решения уравнения (2.4) также предлагается определять в виде асимптотического ряда
(2.6)
$V({{A}^{o}},{{{{\varphi }}}^{o}},{{\tau }}) = {{V}^{o}}({{A}^{o}},{{\tau }}) + {{\varepsilon }}{{V}_{1}}({{A}^{o}},{{{{\varphi }}}^{o}},{{\tau }}) + {{{{\varepsilon }}}^{2}}...,$Здесь рассматривается нерезонансный случай, т.е. предполагается, что для ${{\tau }} \in \left[ {0,T} \right]$ поправки к первому приближению метода усреднения ${{{{\nu }}}_{1}}({{A}^{o}},{{{{\varphi }}}^{o}},{{\tau }}),{{{{\mu }}}_{1}}({{A}^{o}},{{{{\varphi }}}^{o}},{{\tau }})$ ограничены.
Подставляя ряды (2.5), (2.6) в уравнение (2.4), получим в первом приближении
(2.7)
$\frac{{\partial {{V}^{o}}}}{{\partial {{\tau }}}} + \sum\limits_{k = 1}^n {\left[ {{{a}_{k}}{{{(A_{k}^{o})}}^{2}} - \frac{{{{\Phi }_{k}}({{A}^{o}},{{{{\varphi }}}^{o}},{{\tau ,0}})P_{k}^{o}}}{{{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}{\text{ + }}\frac{{\partial {{V}_{1}}}}{{\partial {{\varphi }}_{k}^{o}}}{{{{\omega }}}_{k}}\left( {{\tau }} \right) - \frac{{{{{(P_{k}^{o})}}^{2}}}}{{4c{{\omega }}_{k}^{2}\left( {{\tau }} \right)}}} \right]} = 0.$Здесь сохранены только члены порядка $O\left( {{\varepsilon }} \right)$, а члены более высокого порядка по малому параметру ε опущены. При этом функция ${{P}_{k}}\left( {V,{{A}_{k}},{{{{\varphi }}}_{k}}} \right)$ представляется в виде ${{P}_{k}}\left( {V,{{A}_{k}},{{{{\varphi }}}_{k}}} \right) = P_{k}^{o} + {{\varepsilon }}...$, где $P_{k}^{o} = \sin {{\varphi }}_{k}^{o}\partial {{V}^{o}}{\text{/}}\partial A_{k}^{o}$.
Проводя процедуру усреднения по фазам уравнения (2.7), получим
(2.8)
$\frac{{\partial {{V}^{o}}}}{{\partial {{\tau }}}} + \sum\limits_{k = 1}^n {\left[ {{{a}_{k}}{{{(A_{k}^{o})}}^{2}} - \frac{{\langle {{\Phi }_{k}}P_{k}^{o}\rangle }}{{{{{{\omega }}}_{k}}\left( {{\tau }} \right)}} - \langle {{{(P_{k}^{o})}}^{2}}\rangle {\text{/}}4c{{\omega }}_{k}^{2}\left( {{\tau }} \right)} \right]} = 0,$Проведение усреднения позволило упростить уравнение Гамильтона–Якоби–Беллмана (2.8), так как в этом случае количество независимых переменных уравнения в частных производных уменьшилось в 2 раза, так как ${{V}^{o}}({{A}^{o}},{{\tau }})$. Если из уравнения (2.8) удастся найти положительно определенную функцию ${{V}^{o}}({{A}^{o}},{{\tau }}) \geqslant 0$, когда ${{\tau }} \in \left[ {0,L} \right]$, то приближенно оптимальное управление найдется из выражения
(2.9)
${{\varepsilon }}U_{k}^{o} = \frac{{{\varepsilon }}}{{2c{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}\sin {{\varphi }}_{k}^{o} + {{{{\varepsilon }}}^{2}}...,\quad k = \overline {1,n} .$Имея в виду соотношение $U = {{\Gamma }^{{ - 1}}}Nu$, управление в исходных координатах будет иметь вид
Тогда из условия (2.1) следуетВ силу вида функции $W\left( {A,U} \right)$ (1.7) ее усредненный аналог $W({{A}^{o}},{{U}^{o}})$ есть знакоопределенная по $A_{k}^{o}$ и положительная функция. В этом случае $d{{V}^{o}}{\text{/}}dt \leqslant 0$ – знакоопределенная и отрицательная функция, что приводит к монотонному убыванию
${{V}^{o}}({{A}^{o}},{{\tau }})$. А это в свою очередь ведет к монотонному убыванию нормы вектора амплитуд $\left\| {{{A}^{o}}} \right\|$, когда 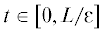 .
.
Соответствие свойств устойчивости усредненной и исходной систем уравнений подробно рассмотрено, например, в монографии [8] и следует из общих теорем метода усреднения.
В прикладных задачах после определения приближенно оптимального управления (2.9) можно провести усреднение системы (1.5), (1.6) с учетом найденного управления и исследовать движение системы, например, методами качественной теории дифференциальных уравнений в пространстве переменных $(A_{1}^{0},...,A_{n}^{0})$. В частности, когда $n = 2$, можно использовать метод фазовой плоскости [9].
3. Случай отсутствия возмущений в усредненной системе. Если матрица $C\left( {{\tau }} \right)$ не зависит от времени ${{\tau }}$, т.е. ${{\omega }}_{k}^{'}\left( {{\tau }} \right) = 0$, $\Gamma {\kern 1pt} '\left( {{\tau }} \right) = 0$ и выполняется условие ортогональности
то усреднение уравнений (1.5), (1.6) дает $\dot {A}_{k}^{o} = 0$, ${{\dot {\varphi }}}_{k}^{o} = {{{{\omega }}}_{k}}$.В этом случае уравнение (2.8) упрощается:
(3.1)
$\sum\limits_{k = 1}^n {\left[ {{{a}_{k}}{{{(A_{k}^{o})}}^{2}} - {{{\left( {\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}} \right)}}^{2}}{\text{/}}8c{{\omega }}_{k}^{2}} \right]} = 0.$Тогда решение уравнения (2.8) можно искать в виде
где bk – определяемые коэффициенты.Подставляя (3.2) в уравнение (3.1) и приравнивая к нулю множители при ${{(A_{k}^{o})}^{2}}$, получим систему алгебраических уравнений для определения коэффициентов ${{b}_{k}}$: $ - {{a}_{k}} + b_{k}^{2}{\text{/}}2c{{\omega }}_{k}^{2} = 0$, $k = \overline {1,n} $, откуда
С учетом (3.3) приближенно оптимальное управление примет вид
(3.4)
${{\varepsilon }}U_{k}^{o} = {{\varepsilon }}\sqrt {2{{a}_{k}}/c} A_{k}^{o}\sin {{\varphi }}_{k}^{o} + {{{{\varepsilon }}}^{2}}...$(3.5)
${{\varepsilon }}U_{k}^{o} = - \frac{{{\varepsilon }}}{{{{{{\omega }}}_{k}}}}{{\dot {x}}_{k}}\sqrt {2{{a}_{k}}{\text{/}}c} + {{{{\varepsilon }}}^{2}}...,\quad k = \overline {1,n} .$Для получения управления в исходных координатах необходимо учесть, что $\dot {x} = {{\Gamma }^{{ - 1}}}\dot {y} + {{\varepsilon }}...$ и использовать соотношение (2.10).
Подставив управление (3.5) в системы (1.5), (1.6) и проводя стандартную процедуру усреднения, получим уравнения для амплитуд
(3.6)
$\dot {A}_{k}^{o} = - \frac{{{\varepsilon }}}{{{\text{2}}{{{{\omega }}}_{k}}}}A_{k}^{o}\sqrt {2{{a}_{k}}{\text{/}}c} ,$4. Случай медленного изменения частот системы. Если выполняется условие ортогональности
(или когда возмущения $f\left( {y,\dot {y},{{\tau }}} \right) = 0$), то усреднение уравнений (1.5), (1.6) при отсутствии управления дает(4.1)
$\dot {A}_{k}^{o} = - {{\varepsilon }}{{B}_{k}}\left( {{\tau }} \right)A_{k}^{o},\quad {{{{\dot {\varphi }}}}_{k}} = {{{{\omega }}}_{k}}\left( {{\tau }} \right),$В этом случае уравнение (2.8) принимает вид
(4.2)
$\frac{{\partial {{V}^{o}}}}{{\partial {{\tau }}}} = - \sum\limits_{k = 1}^n {\left[ {{{a}_{k}}{{{(A_{k}^{o})}}^{2}} - {{B}_{k}}\left( {{\tau }} \right)A_{k}^{o}\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}} - {{{\left( {\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}} \right)}}^{2}}{\text{/}}8c{{\omega }}_{k}^{2}\left( {{\tau }} \right)} \right]} .$Решение уравнения (2.8) ищется как
(4.3)
${{V}^{o}}({{A}^{o}},{{\tau }}) = \sum\limits_{k = 1}^n {{{b}_{k}}\left( {{\tau }} \right){{{(A_{k}^{o})}}^{2}}} .$Подставляя (4.3) в уравнение (4.2) и приравнивая к нулю коэффициенты при ${{(A_{k}^{o})}^{2}}$, получим систему обыкновенных дифференциальных уравнений для определения функций ${{b}_{k}}\left( {{\tau }} \right)$:
(4.4)
$d{{b}_{k}}{\text{/}}d{{\tau }} = - {{a}_{k}} + 2{{B}_{k}}\left( {{\tau }} \right){{b}_{k}} + b_{k}^{2}{\text{/}}2c{{\omega }}_{k}^{2}\left( {{\tau }} \right),\quad k = \overline {1,n} .$Во многих аналогичных задачах при аналитическом конструировании оптимальных регуляторов (АКОР), например [10, 11], часто используется установившееся или квазистатическое решение матричного уравнения Риккати. Аналогично можно рассмотреть квазистатическое решение системы (4.4). Тогда, приравнивая правые части (4.4) к нулю, получим
(4.5)
$ - {{a}_{k}} + 2{{B}_{k}}\left( {{\tau }} \right){{b}_{k}} + b_{k}^{2}{\text{/}}2c{{\omega }}_{k}^{2}\left( {{\tau }} \right) = 0.$Положительное решение квадратного уравнения (4.4) имеет вид
(4.6)
${{b}_{k}} = c{{{{\omega }}}_{k}}\left( {{\tau }} \right)( - 2{{B}_{k}}\left( {{\tau }} \right){{{{\omega }}}_{k}}\left( {{\tau }} \right) + \sqrt {{\text{4}}B_{k}^{2}\left( {{\tau }} \right){{\omega }}_{k}^{2}\left( {{\tau }} \right) + 2{{a}_{k}}{\text{/}}c} ).$Тогда приближенно оптимальное управление (2.8), учитывая (4.6), запишем как
(4.7)
$U_{k}^{o} = ( - 2{{B}_{k}}\left( {{\tau }} \right){{{{\omega }}}_{k}}\left( {{\tau }} \right) + \sqrt {{\text{4}}B_{k}^{2}\left( {{\tau }} \right){{\omega }}_{k}^{2}\left( {{\tau }} \right) + 2{{a}_{k}}{\text{/}}c} )A_{k}^{o}\sin {{\varphi }}_{k}^{o} + {{\varepsilon }}...$Аналогично предыдущему случаю управление (4.7) может быть выражено через исходные координаты системы (1.1), используя $\dot {x} = {{\Gamma }^{{ - 1}}}\dot {y} + {{\varepsilon }}...$ и выражения (1.4), (2.10).
Подставляя управление (4.7) в уравнения (1.5) и усредняя по фазам, получим в первом приближении для амплитуд колебаний
(4.8)
$\dot {A}_{k}^{o} = - {{\varepsilon }}\frac{{A_{k}^{o}}}{{{{{{\omega }}}_{k}}\left( {{\tau }} \right)}}\sqrt {B_{k}^{2}\left( {{\tau }} \right){{\omega }}_{k}^{2}\left( {{\tau }} \right) + {{a}_{k}}{\text{/}}2c} .$Систему (4.4) можно приближенно решить, используя прием обратного интегрирования, предложенный в [10]. В прикладных задачах во многих случаях можно конкретно указать отрезок ${{\tau }} \in \left[ {0,T} \right]$, на котором рассматривается движение системы. Тогда, задавая граничное условие на коэффициенты в виде ${{b}_{k}}\left( T \right) = 0$ и численно интегрируя систему (4.4) с отрицательным шагом от $T$ до нуля, получим зависимость ${{b}_{k}}\left( {{\tau }} \right)$.
Здесь необходимо отметить, что при интегрировании системы (3.3) в этом случае имеем ${{b}_{k}}\left( {{\tau }} \right) > 0$, когда ${{\tau }} \in \left[ {0,T} \right)$. Интегрирование с отрицательным шагом означает формальное изменение знака правых частей уравнений (3.3), которые становятся положительными, так как ${{a}_{k}} > 0$. Тогда функция (3.2) является положительно-определенной для каждого ${{\tau }} \in \left[ {0,T} \right)$, что приводит к динамической устойчивости колебательной системы.
Данный прием имеет обоснование и в общем случае, так как известно, что решение матричного уравнения Риккати (уравнение (4.4) есть частный случай матричного уравнения) равномерно стремится к положительно-определенной матрице [11] при соответствующем задании начальных условий, если ${{t}_{0}} = - \infty \,,$ где t0 – начальное время.
5. Учет линейных возмущений. Рассматриваются линейные возмущения вида
(5.1)
$f\left( {y,\dot {y},{{\tau }}} \right) = {{R}_{1}}\left( {{\tau }} \right)y + {{R}_{2}}\left( {{\tau }} \right)\dot {y},$Для простоты возмущения, связанные с медленным изменением частот системы, в этом разделе сначала не будут записываться, так как рассматриваемые оба типа возмущений с точки зрения применения метода усреднения аддитивны и, следовательно, в усредненных уравнениях соответствующие члены просто суммируются.
После перехода к нормальным координатам в уравнении (1.3) имеем
(5.2)
$F\left( {x,\dot {x},{{\tau }}} \right) = {{\Gamma }^{{ - 1}}}[{{R}^{{\left( 1 \right)}}}\left( {{\tau }} \right)\Gamma x + {{R}^{{\left( 2 \right)}}}\left( {{\tau }} \right)\left( {\Gamma \dot {x} + {{\varepsilon }}\Gamma {\kern 1pt} 'x} \right)].$Тогда в уравнении (2.8) выражения $\left\langle {{{\Phi }_{k}}P_{k}^{o}} \right\rangle $, учитывающие возмущения в усредненной системе, примут вид
(5.3)
$\left\langle {{{\Phi }_{k}}P_{k}^{o}} \right\rangle = \frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}\left\langle {{{F}_{k}}\sin {{{{\varphi }}}_{k}}} \right\rangle ,$Учитывая замену переменных (1.4) и свойство ортогональности тригонометрических функций, получим
(5.4)
$\left\langle {{{\Phi }_{k}}P_{k}^{o}} \right\rangle = - \frac{1}{2}A_{k}^{o}{{{{\omega }}}_{k}}\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}{{r}_{k}}.$Тогда уравнение (2.8) принимает вид
(5.5)
$\frac{{\partial {{V}^{o}}}}{{\partial {{\tau }}}} = - \sum\limits_{k = 1}^n {\left[ {{{a}_{k}}{{{(A_{k}^{o})}}^{2}} + {{r}_{k}}\left( {{\tau }} \right)A_{k}^{o}\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}{\text{/}}2 - {{{\left( {\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}} \right)}}^{2}}{\text{/}}8c{{\omega }}_{k}^{2}} \right]} ,$Уравнение (5.5) отличается от уравнения для предыдущего случая формальной заменой ${{B}_{k}}{\text{(}}\tau {\text{)}} \Rightarrow - {{r}_{k}}{\text{(}}\tau {\text{)/}}2$. Поэтому, повторяя выкладки предыдущего случая, для решения (4.3) получим
(5.6)
$d{{b}_{k}}{\text{/}}d{{\tau }} = - {{a}_{k}} - {{r}_{k}}\left( {{\tau }} \right){{b}_{k}} + b_{k}^{2}{\text{/}}2c{{\omega }}_{k}^{2}.$Для квазистатического решения уравнения (5.6) квазиоптимальное управление принимает вид
(5.7)
${{\varepsilon }}U_{k}^{o} = {{\varepsilon }}({{r}_{k}}\left( {{\tau }} \right) + \sqrt {{{r}_{k}}{{{\left( {{\tau }} \right)}}^{2}} + 2{{a}_{k}}{\text{/}}c{{\omega }}_{k}^{2}} ){{{{\omega }}}_{k}}A_{k}^{o}\sin {{\varphi }}_{k}^{o} + {{{{\varepsilon }}}^{2}}...,$(5.8)
$\dot {A}_{k}^{o} = - \frac{{{\varepsilon }}}{{\text{2}}}A_{k}^{o}\sqrt {{{r}_{k}}{{{\left( {{\tau }} \right)}}^{2}} + 2{{a}_{k}}{\text{/}}c{{\omega }}_{k}^{2}} ,\quad k = \overline {1,n} .$Так как рассматриваемые возмущения аддитивны, то общее решение для приближенно оптимального управления запишем как
(5.9)
${{\varepsilon }}U_{k}^{o} = {{\varepsilon }}({{{{\delta }}}_{k}}\left( {{\tau }} \right) + \sqrt {{{{{\delta }}}_{k}}{{{\left( {{\tau }} \right)}}^{2}} + 2{{a}_{k}}{\text{/}}c{{{{\omega }}}_{k}}{{{\left( {{\tau }} \right)}}^{2}}} ){{{{\omega }}}_{k}}\left( {{\tau }} \right)A_{k}^{o}\sin {{\varphi }}_{k}^{o} + {{{{\varepsilon }}}^{2}}...,$Подставляя управление (5.9) в уравнение и проводя процедуру усреднения, получим для амплитуд колебаний
(5.10)
$\dot {A}_{k}^{o} = - \frac{{{\varepsilon }}}{{\text{2}}}A_{k}^{o}\sqrt {{{{{\delta }}}_{k}}{{{\left( {{\tau }} \right)}}^{2}} + 2{{a}_{k}}{\text{/}}c{{\omega }_{k}}{{{\left( {{\tau }} \right)}}^{2}}} .$Из (5.10) следует монотонное убывание амплитуд колебаний для усредненной системы для рассматриваемых возмущений.
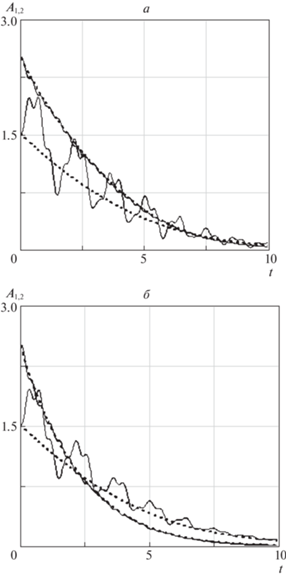
6. Пример определения квазиоптимального управления для системы с двумя степенями свободы. Для иллюстрации применения описанного подхода к определению приближенно оптимального управления рассматривается колебательная система с двумя степенями свободы (n = 2) и с медленными изменяющимися параметрами. Все элементы матриц колебательной системы C(τ), ${{R}_{{1,2}}}{\text{(}}\tau {\text{)}}$ медленно изменяются. Для оценки “медленности” изменения некоторого параметра p можно использовать величину $\dot {p}{\text{/}}p$ [12] (размерность c–1), которая сравнивается к частотами системы ${{{{\omega }}}_{{1,2}}}$, т.е. за характерные величины принимаются безразмерные параметры μ1, 2 = $\left| {\dot {p}{\text{/}}p{{{{\omega }}}_{{1,2}}}} \right|$. Неустойчивость колебаний в системе в примере обусловлена в основном соответствующим заданием матрицы возмущений ${{R}^{{\left( 2 \right)}}}\left( {{\tau }} \right)$, для элементов которой максимальное значение ${{{{\mu }}}_{{1,2}}}$ приблизительно равно 0.15. Изменение элементов матриц $C\left( {{\tau }} \right),\,\,{{R}^{{\left( 2 \right)}}}\left( {{\tau }} \right)$ показано на рис. 1. Матрица возмущений ${{R}^{{\left( 2 \right)}}}\left( {{\tau }} \right)$ взята кососимметричной, что характерно для гироскопических систем. Последнее обстоятельство связано с тем, что (как показали численные расчеты) это приводит к наибольшим колебаниям переменных исходной системы относительно своих средних значений. Изменение нормальных координат для исходной системы в случае отсутствия управления приведено на рис. 2. Там же штриховыми линиями показано изменение амплитудных характеристик, определенных в силу усредненной системы. При введении управления в соответствии с критерием (1.7) с равными весами ${{a}_{1}} = {{a}_{2}} = c$ получаем зависимости для амплитуд колебаний с приблизительно равными временами переходных процессов (рис. 3, а, где штриховые линии соответствуют усредненной системе). Изменяя вес c перед управлением, нетрудно обеспечить заданное время переходных процессов в системе естественно с учетом ограничений на управление, если они известны. Изменяя соотношения весов ${{a}_{{1,2}}}$, можно вводить управление с приоритетным гашением колебаний, соответствующим определенной частоте. В качестве примера на рис. 3, б показаны переходные процессы в случае, когда отношение весов ${{a}_{1}}{\text{/}}{{a}_{2}} = 20$. Во всех случаях, что соответствует аналитическим выражениям для управления, например (5.9), управляемые движения системы определяются только величинами отношений ${{a}_{{1,2}}}{\text{/}}с$ и не зависят от абсолютных величин весовых коэффициентов.
Рис. 1.
Изменение элементов матриц $C\left( {{\tau }} \right),\,\,{{R}^{{\left( 2 \right)}}}\left( {{\tau }} \right)$ в системе с двумя степенями свободы (модельный пример)

Рис. 2.
Изменение нормальных координат в системе с двумя степенями свободы при отсутствии управления (модельный пример)
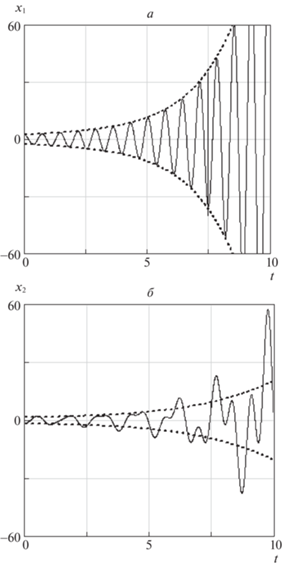
Рис. 3.
Переходные процессы в системе с двумя степенями свободы при наличии управления: a – равные весовые коэффициенты в критерии оптимальности ${{a}_{1}} = {{a}_{2}} = c\,;$ б – приоритетное гашение колебаний по нормальной координате ${{x}_{1}}$ (амплитуда ${{A}_{1}}$, ${{a}_{1}}{\text{/}}{{a}_{2}} = 20$)
7. Пример определения квазиоптимального управления в одной прикладной задаче. Рассматривается стабилизация углового движения малого КА на тросе при развертывании тросовой системы (ТС) на околоземной орбите. Особенностью данной задачи является то, что слагаемые, характеризующие гироскопические эффекты, включаются в невозмущенную систему, что не ограничивает их величину при определении приближенно оптимального управления. В этом случае система дифференциальных уравнений, описывающая угловое движение КА относительно направления троса, близка к системе уравнений классической задачи движения волчка Лагранжа вокруг неподвижной точки [13].
Стабилизация осуществляется относительно направления троса и характеризуется углом нутации ${{\theta }}$. Уравнения для малых углов нутации в этом случае в комплексной форме имеют вид [14]
(6.1)
$\frac{{{{d}^{2}}{{\xi }}}}{{d{{t}^{2}}}} - i{{\bar {J}}_{x}}{{{{\omega }}}_{x}}\frac{{d{{\xi }}}}{{dt}} + {{\omega }}_{p}^{2}{{\xi }} = 0,$Для иллюстрации методики рассматривается простой случай статически и динамически симметричного КА, когда точка крепления троса и центр масс КА лежат на его оси динамической симметрии Ox, а система координат $Oxyz$ является главной и центральной. В этом случае угловая скорость ωx = const и определяется начальными условиями при отделении малого КА от базового КА. Если ωx = 0, то уравнение (6.1) описывает плоские колебания КА относительно направления троса с частотой ωp. Если ωx ≠ 0, то имеем пространственное движение твердого тела относительно точки крепления троса, близкое к случаю Лагранжа, при действии момента от силы натяжения троса. В этом случае предполагается, что для исключения кручения троса используются специальные шарниры.
Возмущение, действующее на КА, связанно с медленным изменением силы натяжения троса ${{F}_{t}}$, которое изменяется в силу заданной программы развертывания системы (номинальный закон управления) и является фактически медленно изменяющимся параметром системы.
Тогда, вводя управление в уравнение (6.1), получим
(6.2)
$\frac{{{{d}^{2}}{{\xi }}}}{{d{{t}^{2}}}} - i{{\bar {J}}_{x}}{{{{\omega }}}_{x}}\frac{{d{{\xi }}}}{{dt}} + {{\omega }}_{p}^{2}{{\xi }} = \varepsilon u,$Невозмущенное уравнение, соответствующее (6.2), имеет вид (6.1) при условии ${{{{\omega }}}_{p}} = {\text{const}}$. Решение невозмущенного уравнения записывается в виде [14]
(6.3)
${{\xi }} = {{A}_{1}}\exp \left( {i{{{{\varphi }}}_{1}}} \right) + {{A}_{2}}\exp \left( {i{{{{\varphi }}}_{2}}} \right),\quad {{\dot {\xi }}} = i{{A}_{1}}{{{{\omega }}}_{1}}\exp \left( {i{{{{\varphi }}}_{1}}} \right) + i{{A}_{2}}{{{{\omega }}}_{2}}\exp \left( {i{{{{\varphi }}}_{2}}} \right),$При определении решения (6.3) частоты системы находятся из уравнения
(6.4)
${{{{\omega }}}^{2}} - {{\bar {J}}_{x}}{{{{\omega }}}_{x}}{{\omega }} - {{\omega }}_{p}^{2} = 0.$Рассматривая соотношения (6.3) как замену переменных $\left( {{{\xi ,\dot {\xi }}}} \right) \Rightarrow \left( {{{A}_{{1,2}}},{{{{\varphi }}}_{{1,2}}}} \right)$ и применяя метод вариации произвольных постоянных для уравнения (6.2), получим дифференциальные уравнения для новых переменных:
(6.5)
${{\dot {A}}_{{1,2}}} = \mp \left[ {{{A}_{{1,2}}}{{{{{\dot {\omega }}}}}_{{1,2}}} + {{A}_{{2,1}}}{{{{{\dot {\omega }}}}}_{{2,1}}}\cos \left( {{{{{\varphi }}}_{1}} - {{{{\varphi }}}_{2}}} \right) + {{u}_{{{\beta }}}}\sin {{{{\varphi }}}_{{1,2}}} - {{u}_{{{\alpha }}}}{\text{cos}}{{{{\varphi }}}_{{1,2}}}} \right]{\text{/}}2{{{{\omega }}}_{a}},$(6.6)
${{{{\dot {\varphi }}}}_{{1,2}}} = {{{{\omega }}}_{{1,2}}} + \left[ {{{A}_{{2,1}}}{{{{{\dot {\omega }}}}}_{{2,1}}}\sin \left( {{{{{\varphi }}}_{1}} - {{{{\varphi }}}_{2}}} \right) \mp {{u}_{{{\beta }}}}{\text{cos}}{{{{\varphi }}}_{{1,2}}} \mp {{u}_{{{\alpha }}}}{\text{sin}}{{{{\varphi }}}_{{1,2}}}} \right]{\text{/}}2{{A}_{{1,2}}}{{{{\omega }}}_{a}}.$В этом случае усредненное уравнение Гамильтона–Якоби–Беллмана (4.2) принимает вид
(6.7)
$\frac{{\partial {{V}^{o}}}}{{\partial {{\tau }}}} = - \sum\limits_{k = 1}^2 {\left[ {{{a}_{k}}{{{(A_{k}^{o})}}^{2}} - {{\omega }}_{k}^{'}\left( {{\tau }} \right)A_{k}^{o}\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}{\text{/}}2{{{{\omega }}}_{a}}\left( {{\tau }} \right) - {{{\left( {\frac{{\partial {{V}^{o}}}}{{\partial A_{k}^{o}}}} \right)}}^{2}}{\text{/}}16c{{\omega }}_{a}^{2}\left( {{\tau }} \right)} \right]} ,$Тогда, определяя решение уравнения (6.7) в виде (4.3), получаем уравнения для коэффициентов ${{b}_{k}}\left( {{\tau }} \right)$:
(6.8)
$d{{b}_{k}}{\text{/}}d{{\tau }} = - {{a}_{k}} + {{\left( { - 1} \right)}^{k}}{{\omega }}_{k}^{'}\left( {{\tau }} \right){{b}_{k}}{\text{/}}{{{{\omega }}}_{a}}\left( {{\tau }} \right) + b_{k}^{2}{\text{/}}4c{{{{\omega }}}_{a}}{{\left( {{\tau }} \right)}^{2}},\quad k = 1,2.$Квазистатические решения уравнений (6.8) записывается как
(6.9)
${{b}_{k}} = 2c{{{{\omega }}}_{a}}\left( {{\tau }} \right)[{{\left( { - 1} \right)}^{k}}{{\omega }}_{k}^{'}\left( {{\tau }} \right) + \sqrt {{{\omega }}_{k}^{'}{{{\left( {{\tau }} \right)}}^{2}} + {{a}_{k}}{\text{/}}c} ],\quad k = 1,2.$Решениям (6.9) соответствуют управления
(6.10)
${{u}_{{{\beta }}}} = ({{b}_{1}}A_{1}^{o}\sin {{{{\varphi }}}_{1}} - {{b}_{2}}A_{2}^{o}\sin {{{{\varphi }}}_{2}}){\text{/}}2c{{{{\omega }}}_{a}},$(6.11)
${{u}_{{{\alpha }}}} = ({{b}_{2}}A_{2}^{o}{\text{cos}}{{{{\varphi }}}_{2}} - {{b}_{1}}A_{1}^{o}{\text{cos}}{{{{\varphi }}}_{1}}){\text{/}}2c{{{{\omega }}}_{a}}.$Управления (6.10), (6.11) в переменных (β, α) примут вид
(6.12)
${{u}_{{{\beta }}}} = {{p}_{{{\alpha }}}}{{\alpha }} + {{p}_{{{{\beta }}{\kern 1pt} '}}}{{\beta }}{\kern 1pt} '{\text{,}}\quad {{u}_{{{\alpha }}}} = {{p}_{{{\beta }}}}{{\beta }} + {{p}_{{{{\alpha }}{\kern 1pt} '}}}{{\alpha }}{\kern 1pt} ',$Усредненные уравнения для амплитуд колебаний $A_{{1,2}}^{o}$ с учетом полученных управлений (6.12) запишем как
(6.13)
$\frac{{dA_{{1,2}}^{o}}}{{d{{\tau }}}} = - \frac{{A_{{1,2}}^{o}}}{{2{{{{\omega }}}_{a}}}}\sqrt {{{\omega }}_{{1,2}}^{'}{{{\left( {{\tau }} \right)}}^{2}} + {{a}_{{1,2}}}{\text{/}}c} .$В качестве примера стабилизации движения малого КА в составе космической ТС рассматривается процесс формирования ТС, предназначенной для возвращения малогабаритной спускаемой капсулы (СК) на Землю. Используемый при этом закон изменения силы натяжения троса близок к зависимости, которая использовалась в реальном тросовом эксперименте YES2 [15]. Процесс формирования ТС имеет два этапа: “медленное” и “быстрое” развертывание троса. Система состоит из базового КА, на котором расположен механизм для управления развертыванием ТС, и троса с концевой массой (капсулой). На первом этапе используется программа “медленного” развертывания и трос с капсулой по окончании этапа приводится в положение, близкое к местной вертикали (длина троса около 3 км). На втором этапе полная длина троса по окончанию развертывания ТС будет около 30 км, причем в конечном положении трос с капсулой составляет с вертикалью некоторый заданный угол. На этом этапе используется близкая к релейной программа, которая состоит из участков разгона и торможения троса с капсулой. Конечное отклоненное положение троса с капсулой позволяет обеспечить дополнительный импульс торможения капсулы при ее отделении от троса вблизи вертикали за счет относительной скорости колебательного движения ТС вокруг своего центра масс.
Номинальная программа развертывания ТС обеспечивается механизмом управления выпуском троса [15], который работает в соответствии с принципом обратной связи по измерениям длины и скорости выпуска троса. Для вычисления номинальных зависимостей длины и скорости троса используется простая модель развертывания ТС [16]:
(6.14)
$\frac{{{{d}^{2}}{{\psi }}}}{{d{{{{\tau }}}^{2}}}} = - 2\frac{{l{\kern 1pt} '}}{l}({{\psi }}{\kern 1pt} '\; + 1) - \frac{3}{2}\sin 2{{\psi ,}}$(6.15)
$\frac{{{{d}^{2}}l}}{{d{{{{\tau }}}^{2}}}} = l[{{({{\psi }}{\kern 1pt} '\; + 1)}^{2}} + 3{{\cos }^{2}}{{\psi }} - 1] - {{F}_{t}}{\text{/}}{{m}_{c}}\Omega _{o}^{2},$Уравнения (6.14), (6.15) записаны в предположении, что масса базового КА много больше массы капсулы, а трос невесом.
Номинальная зависимость силы натяжения троса от времени задается следующей программой [14]:
(6.16)
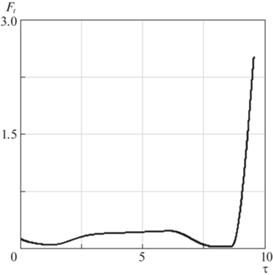
${{F}_{t}}\left( {{{\tau }},l,\dot {l}} \right) = \left\{ {\begin{array}{*{20}{l}} {{{m}_{c}}\Omega _{o}^{2}\left[ {{{{{\eta }}}_{1}}\left( {l - {{l}_{1}}} \right) + {{{{\eta }}}_{2}}l' + 3{{l}_{1}}} \right]\quad {\text{if}}\quad 0 \leqslant {{\tau }} \leqslant {{{{\tau }}}_{1}},} \\ {{{F}_{1}} + \left( {{{F}_{{\min }}} - {{F}_{1}}} \right){\text{si}}{{{\text{n}}}^{2}}\left( {{{\tau }} - {{{{\tau }}}_{1}}} \right)\quad {\text{if}}\quad {{{{\tau }}}_{1}} < {{\tau }} \leqslant {{{{\tau }}}_{2}},} \\ {{{F}_{{\min }}}\quad {\text{if}}\quad {{{{\tau }}}_{2}} < {{\tau }} \leqslant {{{{\tau }}}_{3}},} \\ {{{F}_{{\min }}} + \left( {{{F}_{{\max }}} - {{F}_{{\min }}}} \right){\text{si}}{{{\text{n}}}^{2}}\left( {{{\tau }} - {{{{\tau }}}_{3}}} \right)\quad {\text{if}}\quad {{{{\tau }}}_{3}} < {{\tau }} \leqslant {{{{\tau }}}_{4}},} \\ {{{F}_{{\max }}}\quad {\text{if}}\quad {{{{\tau }}}_{4}} < {{\tau }} \leqslant {{{{\tau }}}_{k}},} \end{array}} \right.$Пример изменения номинальной силы натяжения троса от времени приводится на рис. 4. Используются следующие исходные данные: высота круговой орбиты 270 км, ${{l}_{1}} = 3000$ м, ${{{{\eta }}}_{1}} = 4$, ${{{{\eta }}}_{2}} = 3.5$, ${{F}_{1}} = 0.224$ Н, ${{F}_{{\min }}} = 0.02$ Н, ${{F}_{{\max }}} = 2.1$ Н, ${{{{\tau }}}_{k}} = 9.55$, ${{{{\tau }}}_{{k1}}} = 7$, ${{{{\tau }}}_{r}} = 9.13$, ${{\chi }_{{1,2}}} = 0.004$. Начальные условия при отделении капсулы от базового КА ${{\psi }} = {{\psi }}{\kern 1pt} ' = 0,$ $l = 1$ м, $l{\kern 1pt} '{{\Omega }_{o}} = 2.5$ м/с.
Выбором параметров ${{{{\eta }}}_{{1,2}}}$ обеспечивается асимптотическая устойчивость вертикального конечного положения равновесия на первом этапе развертывания ТС [17] в силу уравнений (6.14), (6.15) для $l = {{l}_{1}}$. А параметры ${{F}_{{\min }}},\;{{F}_{{\max }}}{\text{,}}\;{{{{\tau }}}_{k}},\;{{{{\tau }}}_{r}}{\text{ }}$ подбираются исходя из заданных конечных краевых условий движения ТС: $l{\kern 1pt} ' = {{\psi }}{\kern 1pt} ' = 0,$ $l = 3 \times {{10}^{4}}$ м, ${{\psi }} = 56^\circ $.
Капсула здесь представляет собой сферу радиусом 0.2 м массой ${{m}_{c}} = 20$ кг.
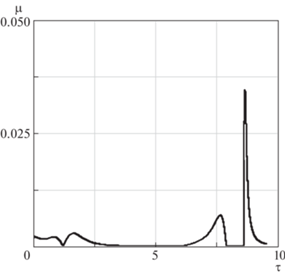
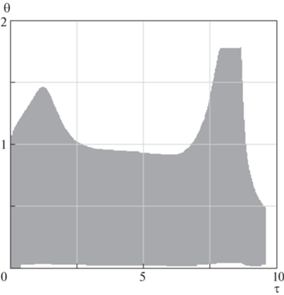
Решения уравнений (6.14), (6.15) в данной постановке не зависят от углового движения капсулы относительно направления троса. Поэтому силу натяжения троса в данной задаче можно рассматривать как медленно изменяющийся параметр. Для оценки скорости изменения медленно изменяющего параметра рассматривается величина $F_{t}^{'}{\text{/}}{{F}_{t}}$, которая сравнивается с характерными частотами колебательной системы. В качестве характерной частоты колебаний в данной задаче (при малых угловых скоростях ${{{{\omega }}}_{x}}$) можно рассматривать частоту ${{{{\omega }}}_{p}}$. Тогда безразмерный параметр ${{\mu }} = {\text{|}}F_{t}^{'}{\text{/}}{{F}_{t}}{{{{\omega }}}_{p}}{\text{|}}$ будет характеризовать относительную скорость изменения силы натяжения троса, т.е. будет пропорционален малому параметру задачи ${{\varepsilon }}$. На рис. 5 приводится зависимость параметра ${{\mu }}$ от безразмерного времени ${{\tau }}$ для исходных данных, представленных выше. Наибольшие значения параметр ${{\mu }}$ принимает при переходе на второй этап развертывания ТС ${{{{\tau }}}_{{k1}}} \approx 7.7$ и в момент ${{{{\tau }}}_{r}} \approx 8.7$, когда имеет место переход от участка ускоренного движения троса к участку его торможения.
Отделение СК от базового КА имеет случайный характер. Так, например, угловые скорости капсулы ${{{{\omega }}}_{{x,y,z}}}$ в связанной с ней системе координат $Oxyz$ при отделении обычно распределены по нормальному закону [18]. Тогда возможна реализация неблагоприятных случаев движения СК относительно троса, когда угол нутации капсулы будет превышать π/2. Это может привести к запутыванию и ослаблению троса и, как следствие, к потере управляемости при работе системы регулирования развертыванием ТС.
На рис. 6 приводится пример, когда угол нутации капсулы на некоторых участках движения превышает π/2. Вычисления проведены при следующих начальных условиях отделения: ${{{{\omega }}}_{x}} = 0.01$ c–1, ${{{{\omega }}}_{y}} = 0$, ${{{{\omega }}}_{z}} = 0.13$ c–1, ${{\theta }} = {{\pi /}}3.$
Рис. 6.
Изменение угла нутации капсулы, определенного относительно направления троса, при отсутствии управления
Здесь также необходимо отметить, что в данном примере рассматривается идеальный вариант статически и динамически симметричного твердого тела (капсулы). Влияние малой асимметрии капсулы может привести к возникновению резонансных режимов ее движения [14], что создает еще большие возмущения при движении капсулы вокруг своего центра масс.
На рис. 7 показаны зависимости, которые характеризуют переходный процесс в системе при использовании приближенно оптимального управления (6.12) с критерием оптимальности (1.7) и с весовыми коэффициентами ${{a}_{{1,2}}} = с = 1{\text{/}}3$. На рис. 7 штриховой линией показана огибающая ${{{{\theta }}}_{{\max }}}\left( {{\tau }} \right)$ зависимости θ(τ), определенная в соответствии с усредненными уравнениями (6.13): ${{{{\theta }}}_{{\max }}}\left( {{\tau }} \right) = A_{1}^{o}\left( {{\tau }} \right) + A_{2}^{o}\left( {{\tau }} \right)$.
Рис. 7.
Переходный процесс по углу нутации капсулы при наличии управления: равные весовые коэффициенты ${{a}_{1}} = {{a}_{2}} = c$ в критерии оптимальности
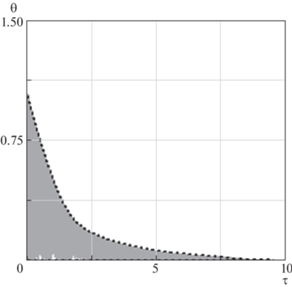
Увеличение весового коэффициента $c$ позволяет обеспечить управление с уменьшенными затратами (в данном случае модуль управляющего воздействия не превышает $3.6 \times {{10}^{{ - 3}}}$ c–2), однако, с другой стороны, увеличивает время переходного процесса.
Изменяя соотношение между весовыми коэффициентами ${{a}_{{1,2}}}$, которые определяют уровень ошибок управления по амплитудам $A_{1}^{o},\;A_{2}^{o}$, можно сформировать заданный вид прецессии СК относительно направления троса. Формируя заданный вид прецессии, можно избежать реализации длительных резонансных режимов движения, которые могут привести к потере устойчивости углового движения СК при наличии у нее малой асимметрии. Так, например, если известно направление угловой скорости вращения капсулы относительно продольной оси ${{\omega }_{x}} > 0$ после отделения от базового КА, то определяющую роль в возрастании амплитуд колебаний по углу нутации при проходе через резонанс играет амплитуда $A_{1}^{o}$ [19], которая соответствует “прямой” прецессии СК. При реализации “прямой” прецессии направление прецессии тела относительно направления троса совпадает с направлением его вращения вокруг своей продольной оси x. Поэтому гашение колебаний по этой амплитуде приведет к меньшим возмущениям в угловом движении СК при проходе через резонанс. Возможность смены вида прецессии иллюстрируется рис. 8, где момент изменения вида прецессии соответствует условию $A_{1}^{o} = A_{2}^{o}$ (рис. 8, а, где $A_{1}^{o}$ – сплошная линия). На рис. 8, б показано, как изменяется производная угла прецессии $\dot {\Psi }$, вычисленная по исходным уравнениям углового движения СК (6.2). В данном случае при отделении от базового КА имеет место “прямая” прецессия $\dot {\Psi } > 0$ СК (рис. 8, а), при выполнении условия $A_{1}^{o} = A_{2}^{o}$ происходит переход на “обратную” прецессию ($\dot {\Psi } < 0$, ${{{{\omega }}}_{x}} > 0$). Для изменения вида прецессии в критерии оптимальности (1.7) были использовано отношение весовых коэффициентов ${{a}_{1}}{\text{/}}{{a}_{2}} = 20$.
Рис. 8.
Пример изменения вида прецессии капсулы относительно направления троса с помощью изменения весовых коэффициентов в критерии оптимальности $\left( {{{a}_{1}}{\text{/}}{{a}_{2}} = 20} \right)$

Заключение. Разработана методика синтеза приближенно оптимального регулятора для стабилизации движения колебательных систем со многими степенями свободы. Рассматриваемый подход позволяет определить уравнения для регуляторов в аналитическом виде. Методика основана на приближенном методе решения уравнения Гамильтона–Якоби–Беллмана, основанном на представлении функции Беллмана в виде ряда по малому параметру задачи. Ряд представляет собой сумму непериодического слагаемого, зависящего от медленной переменной системы, и поправок, имеющих нулевое среднее. Существование положительно-определенной в силу усредненной системы функции Беллмана–Ляпунова обеспечивает динамическую устойчивость колебательной системы на асимптотически большом интервале времени. Эффективность методики подтверждается двумя примерами: иллюстративным для стандартной системы с двумя степенями свободы и для прикладной задачи стабилизации углового движения малого КА относительно направления троса при развертывании протяженной космической системы (длина троса 30 км). Использование данного подхода к более сложным случаям нелинейных возмущений требует дополнительных исследований и связано с возможностью определения приближенных решений уравнения Гамильтона–Якоби–Беллмана.
Список литературы
Лебедев В.Н. Расчет движения космического аппарата с малой тягой. М.: ВЦ АН СССР, 1967. 108 с.
Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980. 384 с.
Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1986. 378 с.
Акуленко Л.Д. Асимптотические методы оптимального управления. М.: Наука, 1987. 368 с.
Салмин В.В., Ишков С.А., Старинова О.Л. Методы решения вариационных задач механики космического полета с малой тягой. Самара: Изд-во СНЦ РАН, 2006. 162 с.
Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем. М.: Едиториал УРСС, 2004. 400 с.
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974. 410 с.
Хапаев М.М. Усреднение в теории устойчивости. М.: Наука, 1986. 192 с.
Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1981. 918 с.
Летов А.М. Динамика полета и управление. М.: Наука, 1969. 360 с.
Дмитриевский А.А., Иванов Н.М., Лысенко Л.Н., Богодистов С.С. Баллистика и навигация ракет. М.: Машиностроение, 1985. 310 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 1. Механика. М.: Наука, 1988. 216 с.
Заболотнов Ю.М., Лобанков А.А. Синтез регулятора для стабилизации движения твердого тела вокруг неподвижной точки // Изв. РАН. МТТ. 2017. № 3. С. 59–71.
Заболотнов Ю.М., Наумов О.Н. Движение спускаемой капсулы относительно центра масс при развертывании орбитальной тросовой системы // Космич. исслед. 2012. Т. 50. № 2. С. 183–193.
Kruijff, M. Tethers in Space. Oisterwijk: Uitgeverij BOX Press, 2011. 423 p.
Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990. 336 с.
Заболотнов Ю.М. Управление развертыванием орбитальной тросовой системы в вертикальное положение с малым грузом // ПММ. 2015. Т. 79. № 1. С. 37–47.
Заболотнов Ю.М. Статистический анализ движения относительно центра масс легкой капсулы при входе в атмосферу // Космич. исслед. 2013. Т. 51. № 3. С. 228–239.
Ярошевский В.А. Движение неуправляемого тела в атмосфере. М.: Машиностроение, 1978. 167 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления