1. На главную
  2. Электронные версии
  3. Известия РАН. Теория и системы управления
  4. № 3, 2022

Известия РАН. Теория и системы управления, 2022, № 3, стр. 57-68

ОБ ОДНОМ ПОДХОДЕ К АНАЛИЗУ УСТОЙЧИВОСТИ “ЧАСТИЧНЫХ” ПОЛОЖЕНИЙ РАВНОВЕСИЯ НЕЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ

В. И. Воротников a, *, Ю. Г. Мартышенко b, **

a Сочинский институт РУДН
Сочи, Россия

b Российский государственный университет нефти и газа
Москва, Россия

* E-mail: vorotnikov-vi@rambler.ru
** E-mail: j-mart@mail.ru

Поступила в редакцию 10.09.2021
После доработки 07.01.2022
Принята к публикации 31.01.2022

Полный текст (PDF)

Аннотация

Рассматривается нелинейная система конечно-разностных уравнений общего вида, допускающая “частичное” (по части переменных) нулевое положение равновесия. Описывается подход к изучению устойчивости этого положения равновесия, основанный на предварительном изучении устойчивости по части определяющих его переменных на базе метода функций Ляпунова, с последующим анализом структурной формы системы. Для расширения возможностей данного подхода предлагается проводить корректировку области, в которой строится функция Ляпунова; это достигается введением второй (векторной, вообще говоря) вспомогательной функции. Приводятся примеры, показывающие особенности данного подхода.

Введение. Дискретные (конечно-разностные) системы широко используются в теории процессов управления, вычислительной математике и ее приложениях, а также при моделировании дискретных во времени процессов. При этом в сравнении с моделями с непрерывной динамикой дискретные модели в ряде случаев могут более точно отражать моделируемые процессы. С другой стороны, дискретные системы являются дискретными приближениями или разностными схемами для систем дифференциальных уравнений с непрерывной динамикой, а также составной частью гибридных (с импульсным эффектом) систем, эволюция которых происходит в непрерывно-дискретном времени. Теории и методам качественного исследования нелинейных дискретных по времени систем, включая исследования устойчивости дискретных по времени процессов, посвящена обширная литература, в том числе ряд монографий [1–6].

Одно из активно развивающихся направлений исследований связано с изучением задач частичной устойчивости дискретных процессов. Такие задачи естественным образом возникают в приложениях и часто сводятся к обладающей большой общностью задаче устойчивости по части переменных (а не по всем переменным) нулевого положения равновесия нелинейной системы конечно-разностных уравнений при общих допущениях относительно ее правой части [6–11]; рассматривается также устойчивость по заданным функциям фазовых переменных (по выходу) [2]. Приложения связаны, в частности, с задачами: вычислительной математики и оптимизации [2, 10, 11]; балансировки загрузки компьютерных сетей [7]; адаптивного управления [8]; оценки устойчивости фильтров Калмана [9]; моделирования эпидемических ситуаций [10, 11]; построения законов наведения на маневрирующую цель [12]. Отметим, что систематические исследования задач частичной устойчивости в значительной степени инициированы работой [13] (см. также обзор [14]).

В статье рассматривается нелинейная система конечно-разностных уравнений общего вида, для которой существует “частичное” (по некоторой части переменных) нулевое положение равновесия. Сначала устойчивость и асимптотическая устойчивость данного положения равновесия анализируются по отношению не ко всем определяющим его переменным, а только по их части. При этом делается допущение о том, что начальные возмущения переменных, не определяющих “частичное” положение равновесия, могут быть большими (ограниченными по норме произвольным наперед заданным числом) по одной части и произвольными по оставшейся части этих переменных. Для случая нелинейных систем с непрерывной динамикой такие задачи изучались ранее в [15, 16]. Отметим, что предположение о существовании “полного” (по всем переменным) нулевого положения равновесия у рассматриваемых классов систем часто не является необходимым и даже может противоречить смыслу решаемых задач.

Для анализа поставленных задач частичной устойчивости применяется дискретный вариант метода функций Ляпунова [1] в соответствующей модификации. Получены условия частичной устойчивости указанного вида, обобщающие ряд известных результатов по частичной устойчивости дискретных систем. С целью расширения возможностей используемого метода предлагается проводить корректировку области, в которой строится вспомогательная функция Ляпунова. Это достигается посредством введения дополнительной (векторной, вообще говоря) вспомогательной функции. В результате основная функция Ляпунова, а также ее приращение в силу изучаемой системы, могут быть знакопеременными и не удовлетворять используемым разностным неравенствам в обычно рассматриваемой при изучении частичной устойчивости области фазового пространства системы.

Затем указываются условия на структурную форму нелинейной системы, при которых устойчивость (асимптотическая устойчивость) по отношению к части переменных “частичного” нулевого положения равновесия означает устойчивость (асимптотическую устойчивость) этого положения равновесия по всем определяющим его переменным. При соответствующем уточнении такие условия определяют свойство частичной детектируемости (partial detectability) данной системы [17–21].

Полученные результаты позволяют сформулировать подход к изучению устойчивости “частичного” положения равновесия нелинейной конечно-разностной системы, включающий два этапа: 1) предварительный анализ устойчивости по части определяющих это положение равновесия переменных на основе метода функций Ляпунова; 2) последующий анализ частичной детектируемости системы. Предложенный подход может использоваться также при решении соответствующих задач частичной стабилизации нелинейных дискретных управляемых систем посредством управлений, дискретно формируемых по принципу обратной связи.

Для линейных конечно-разностных систем указаны достаточные условия на коэффициенты, при выполнении которых асимптотическая устойчивость системы по отношению к части переменных означает еe асимптотическую устойчивость по отношению к бóльшей части переменных.

1. Постановка задачи. Рассмотрим линейное конечномерное пространство Rn векторов x с евклидовой нормой ||x|| = $\sqrt {x_{1}^{2} + x_{2}^{2} + ... + x_{n}^{2}} $ (xi – i-я компонента вектора x). Введем разбиение x = = (yT, zT)T (T – транспонирование). Обозначим через  ${{\mathbb{Z}}_{ + }}$ = {k = 0, 1, 2, …} множество целых неотрицательных чисел.

Пусть дана нелинейная система конечно-разностных уравнений [1–6]

${\mathbf{x}}(k + 1) = {\mathbf{X}}(k,{\mathbf{x}}(k)),$
которую, с учетом разбиения x = (yT, zT)T, представим в виде двух групп уравнений:

(1.1)
${\mathbf{y}}(k + 1) = {\mathbf{Y}}(k,{\mathbf{y}}(k),{\mathbf{z}}(k)),~\quad {\mathbf{z}}(k + 1) = {\mathbf{Z}}(k,{\mathbf{y}}(k),{\mathbf{z}}(k)).$

В системе (1.1) k ∈ ${{\mathbb{Z}}_{ + }}$– дискретное время, x = (yT, zT)T – фазовый вектор. Вектор-функция X = = (YT, Z T)T, определяющая правые части системы (1.1), при каждом k ∈${{\mathbb{Z}}_{ + }}$ непрерывна по x в области ||x|| < ∞. В этом случае для всех k0, x0 существует единственное решение x(k) = x(k; k0, x0) системы (1.1), удовлетворяющее начальному условию x(k0) = x0, которое определено для всех k ≥ k0. При выполнении условия Y(k, 0, z(k)) ≡ 0 множество М = {x(k): y(k) = 0} является “частичным” положением равновесия (инвариантным множеством) системы (1.1).

Далее будет рассматриваться устойчивость по части переменных (разд. 2) и по всем переменным (разд. 3, 4) “частичного” положения равновесия y(k) = 0 системы (1.1). При этом помимо самостоятельного интереса задача устойчивости по части переменных используется как вспомогательная на первом этапе анализа устойчивости по всем переменным.

Имея в виду анализ устойчивости “частичного” положения равновесия y(k) = 0 по отношению не ко всем определяющим его переменным, а только по их некоторой заданной части, предположим, что y = (${\mathbf{y}}_{1}^{{\text{T}}}$, ${\mathbf{y}}_{2}^{{\text{T}}}$)T. Вектор y1 включает те компоненты вектора y, устойчивость по отношению к которым рассматривается. Кроме того, чтобы расширить потенциальные возможности понятий устойчивости, представим также компоненту z вектора x в виде z = (${\mathbf{z}}_{1}^{{\text{T}}}$, ${\mathbf{z}}_{2}^{{\text{T}}}$).

Обозначим через Dδ область значений x0, таких, что ||y0|| < δ, ||z10|| ≤ L, ||z20|| < ∞; область D∆ получается заменой δ на ∆.

Определение 1.“Частичное” положение равновесия y(k) = 0 системы (1.1) при больших значениях z10в целом по z20 (for a large values of z10 and on the whole with respect to z20):

1) y1-устойчиво, если для каждого k0 ∈ ${{\mathbb{Z}}_{ + }}$, а также для произвольного числа ε > 0, как бы мало оно не было, и для любого наперед заданного числа L > 0 найдется δ(ε, k0, L) > 0, такое, что неравенство ||y1(k, k0, x0)|| < ε имеет место для всех k ≥ k0 и x0 ∈ Dδ ;

2) равномерно y1-устойчиво, если δ = δ(ε, L);

3) равномерно асимптотически y1-устойчиво, если оно равномерно y1-устойчиво и существует ∆(L) > 0, такое, что для произвольного решения x(k; k0, x0) системы (1.1), для которого x0 ∈ D∆, предельное соотношение ||y1(k; k0, x0)|| = 0, k → ∞ выполняется равномерно по k0, x0 из области k0 ≥ 0, x0 ∈ D∆ (для любых η > 0, k0 ∈ ${{\mathbb{Z}}_{ + }}$ и любого наперед заданного числа L > 0 найдется целое число T(η, L) > 0, такое, что ||y1(k; k0, x0)|| < η при всех k ≥ k0 + T(η, L), x0 ∈ D∆).

Соответствующие понятия устойчивости по всем переменным “частичного” положения равновесия y(k) = 0 системы (1.1) при больших значениях z10 в целом по z20 получаются из введенных понятий заменой y1(k, k0, x0) на y(k, k0, x0).

Замечание 1. Определение 1 содержит дискретные аналоги понятий частичной устойчивости, введенных для систем с непрерывной динамикой [16]. Наиболее близкими к ним являются понятия устойчивости по всем переменным “частичного” положения равновесия y(k) = 0 системы (1.1), предполагающие [4], что ||y0|| < δ, ||z0|| < ∞, где δ может зависеть не только от ε, k0, но и от z0 (это условие эквивалентно условиям ||y0|| < δ, ||z0|| ≤ L, где L > 0 – любое наперед заданное число и δ зависит не только от ε, k0, но и от L). В определении 1 имеет место включение x0 ∈ Dδ и, кроме того, рассматривается устойчивость по части переменных; поэтому данное понятие устойчивости более общее. Мотивацией к разделению вектора z0 на две части является возможность поиска компромисса между содержательным смыслом понятия частичной устойчивости и соответствующими требованиями к функциям Ляпунова. Действительно, введенные определения 1)–3) являются “промежуточными” между обычно используемыми понятиями устойчивости (как по всем, так и по части переменных) при больших значениях z0 или в целом по z0 “частичного” положения равновесия y(k) = 0 системы (1.1), которые приводят к различным требованиям к функциям Ляпунова.

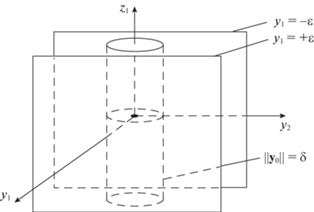
Замечание 2. В случае dim y1 = dim y2 = dim z1 = 1 введенному понятию частичной устойчивости можно дать наглядную геометрическую интерпретацию в трехмерном пространстве Oy1y2z1. Для каждого k0 ∈ ${{\mathbb{Z}}_{ + }}$ и для любого сколь угодно малого числа ε > 0, а также для любого наперед заданного числа L > 0 граница допустимой области x0 ∈ Dδ начальных возмущений является цилиндром ||y0|| = δ высоты 2L, расположенном между двумя плоскостями y1= ±ε (см. рисунок). Если решения системы (1.1) начинаются при k = k0 внутри этого δ-цилиндра (при произвольном значении z20), то соответствующие этим решениям траектории будут оставаться при всех k ≥ k0 между указанными двумя ε-плоскостями.

Замечание 3. Введенные понятия устойчивости возникают, в частности, при переходе (посредством обозначений x(r) = x(k), xn + 1(r) = k, r = k − k0) от системы (1.1) с начальным условием x(k0) = x0 к стационарной дискретной системе

${\mathbf{x}}(r + 1) = {\mathbf{X}}({\mathbf{x}}(r),{{x}_{n}}_{{ + {\text{ }}1}}(r)),\quad {{x}_{n}}_{{ + {\text{ }}1}}(r + 1) = {{x}_{n}}_{{ + {\text{ }}1}}(r) + 1,$
$({\mathbf{x}}(0) = {{{\mathbf{x}}}_{0}},~{{x}_{n}}_{{ + {\text{ }}1}}(0) = {{k}_{0}}),$
когда требования равномерности (неравномерности) по k0 в задачах y1-устойчивости при больших значениях z0 или в целом по z0 “частичного” положения равновесия y(k) = 0 заменяются требованиями “в целом по xn + 1(0)” (“при больших значениях xn + 1(0)”).

Для решения поставленных задач частичной устойчивости будут использоваться однозначные непрерывные по x при каждом k ∈ ${{\mathbb{Z}}_{ + }}$скалярные функции V = V(k, x), V(k, 0) ≡ 0, определенные в области

(1.2)
${\text{||}}{{{\mathbf{y}}}_{1}}{\text{||}} < h,\quad {\text{||}}{{{\mathbf{y}}}_{2}}{\text{||}} + \,{\text{||}}{\mathbf{z}}{\text{||}} < \infty ,~$
а также соответствующие приращения этих функций в силу системы (1.1), вычисляемые по формуле ∆V(k, x(k))) = V(k + 1, X(k, x(k))) – V(k, x(k)).

Также будут рассматриваться: 1) вспомогательные скалярные функции V*(k, y, z1), V*(y, z1) и вектор-функция μ(k, x), μ(k, 0) ≡ 0, при каждом k ∈ ${{\mathbb{Z}}_{ + }}$ непрерывные по x в области (1.2); 2) непрерывные монотонно возрастающие по r > 0 скалярные функции ai(r), ai(0) = 0 (i = 1, 2, 3) (функции типа Хана).

2. Условия частичной устойчивости. Пусть можно указать векторную функцию μ(k, x), μ(k, 0) ≡ 0, такую, что при каждом k ∈ ${{\mathbb{Z}}_{ + }}$в области

(2.1)
${\text{||}}{{{\mathbf{y}}}_{1}}{\text{||}} + \,{\text{||}}{\mathbf{\mu }}(k,{\mathbf{x}}){\text{||}} < {{h}_{1}} < h,\quad ~{\text{||}}{{{\mathbf{y}}}_{2}}{\text{|| }} + \,{\text{||}}{\mathbf{z}}{\text{||}} < \infty ~$
вспомогательная V-функция в силу исходной системы (1.1) удовлетворяет разностному неравенству [22]
(2.2)
$\Delta V \leqslant \omega (k,V(k,{\mathbf{x}}(k)));~$
ω(k, ${v}$(k)) – непрерывная при k ∈ ${{\mathbb{Z}}_{ + }}$, ${v}$(k) ≥ 0 функция, такая, что для уравнения
(2.3)
${v}(k + 1) = w(k,v(k)),~w(k,0) \equiv 0$
выполнены условия существования и единственности решений для всех k0, ${{{v}}_{0}}$ ≥ 0.

Теорема 1. Пусть для системы (1.1), наряду с основной скалярной V-функцией, можно указать дополнительную векторную функцию μ(k, x), μ(k, 0) ≡ 0, для которых при каждом k ∈ ${{\mathbb{Z}}_{ + }}$ в области (2.1) выполняется условие

(2.4)
$~V(k,{\mathbf{x}}) \geqslant {{a}_{1}}({\text{||}}{{{\mathbf{y}}}_{1}}{\text{||}} + \,{\text{||}}{\mathbf{\mu }}(k,{\mathbf{x}}){\text{||}}),~~$
а также имеет место разностное неравенство (2.2).

Тогда при больших значениях z10 в целом по z20 “частичное” положение равновесия y(k) = 0:

1) y1-устойчиво, если выполнены условия

(2.5)
$~V(k,{\mathbf{x}}) \leqslant V{\text{*}}(k,{\mathbf{y}},{{{\mathbf{z}}}_{1}}),\quad ~V{\text{*}}(k,{\mathbf{0}},{{{\mathbf{z}}}_{1}}) \equiv 0,~$
и решение ${v}$(k) = 0 уравнения (2.3) устойчиво;

2) равномерно y1-устойчиво (равномерно асимптотически y1-устойчиво), если выполнены условия

(2.6)
$V(k,{\mathbf{x}}) \leqslant V{\text{*}}({\mathbf{y}},{{{\mathbf{z}}}_{1}}),~\quad V{\text{*}}({\mathbf{0}},{{{\mathbf{z}}}_{1}}) \equiv 0~$
и решение ${v}$(k) = 0 уравнения (2.3) равномерно устойчиво (равномерно асимптотически устойчиво).

Доказательство приведено в Приложении.

Полученные условия частичной устойчивости опираются на дискретный вариант [22] принципа сравнения с функцией Ляпунова [23, 24] для анализа устойчивости нелинейных динамических систем. Однако при этом, в отличие от [22], изучаются более общие свойства системы (1.1), а для расширения возможностей указанного подхода наряду с основной вспомогательной функцией Ляпунова рассматривается дополнительная (векторная, вообще говоря) вспомогательная функция для корректировки области, в которой строится основная функция Ляпунова. В результате V-функция и ее приращение ∆V  в силу системы (1.1) в теореме 1 при каждом k ∈ ${{\mathbb{Z}}_{ + }}$ являются, вообще говоря, знакопеременными функциями в области

(2.7)
${\text{||}}{{{\mathbf{y}}}_{1}}{\text{||}} < {{h}_{1}} < h,\quad ~{\text{||}}{{{\mathbf{y}}}_{2}}{\text{||}} + \,{\text{||}}{\mathbf{z}}{\text{||}} < \infty ,~~$
которая обычно рассматривается при анализе y1-устойчивости, и могут не удовлетворять в этой области разностному неравенству (2.2).

В рамках предложенного подхода используемые нелинейные V-функции Ляпунова могут быть построены как знакоопределенные квадратичные формы V(k, x) ≡ V*(k, y1, μ(k, x)) переменных y1, μ, что расширяет возможности конструктивного построения таких функций.

Замечание 4. Теорема 1 дополняет результаты по частичной устойчивости дискретных систем: у-устойчивости положения равновесия x(k) = 0 (при условии ||x0|| < δ) [2, 6–11] и устойчивости “частичного” положения равновесия y(k) = 0 [4]. Введение дополнительной μ-функции позволяет расширить класс используемых V-функций Ляпунова. Условия (2.5) являются “промежуточными” между менее ограничительным условием V(k, 0, z) ≡ 0 и более ограничительными условиями V(k, x) ≤ V*(k, y), V*(k, 0) ≡ 0, при выполнении которых “частичное” положение равновесия y(k) = 0 системы (1.1) соответственно y1-устойчиво при больших значениях z0 или y1‑устойчиво в целом по z0. Аналогично условию (2.6) являются “промежуточными” между условиями V(k, x) ≤ V*(y, z), V*(0, z) ≡ 0 и условием V(k, x) ≤ a2(||y||), при выполнении которых “частичное” положение равновесия y(k) = 0 системы (1.1) соответственно равномерно y1-устойчиво при больших значениях z0 или равномерно y1-устойчиво в целом по z0.

Замечание 5. Требования к основной функции Ляпунова в теореме 1 можно ослабить, если вместо нее использовать классическую вектор-функцию Ляпунова [24], область построения которой корректируется посредством вспомогательной вектор-функции μ(k, x).

Пример 1. Пусть система (1.1) состоит из уравнений

${{y}_{1}}\left( {k + 1} \right) = \left[ {a + l{{y}_{2}}\left( k \right){{z}_{1}}\left( k \right)} \right]{{y}_{1}}\left( k \right),$
(2.8)
${{y}_{2}}\left( {k + 1} \right) = \left[ {b + d{{y}_{1}}\left( k \right)} \right]{{y}_{2}}\left( k \right),$
${{z}_{1}}\left( {k + 1} \right) = \left[ {c + e{{y}_{1}}\left( k \right)} \right]{{z}_{1}}\left( k \right),\quad ~{{z}_{2}}\left( {k + 1} \right) = {{Z}_{2}}(k,{\mathbf{x}}\left( k \right)),$
где a, b, c, d, e, l – постоянные параметры, а функция Z2  удовлетворяет только общим требованиям к системе (1.1).

Наряду с основной V-функцией

(2.9)
$V({\mathbf{x}}) = y_{1}^{2} + 2y_{2}^{2}z_{1}^{2}$
также рассмотрим вспомогательную функцию μ1 = y2z1. Для V-функции (2.9) в области (2.1) выполняются условия (2.4) и (2.6).

Для каждого k ∈ ${{\mathbb{Z}}_{ + }}$ в области (2.1) приращение ∆V  выбранной V-функции (2.9) в силу системы (2.8) определяется следующим образом:

$\Delta V = {\text{ }}{{[a + l{{y}_{2}}(k){{z}_{1}}(k)]}^{2}}y_{1}^{2}(k){\text{ }} + $
$ + {\text{ }}2y_{2}^{2}(k)z_{1}^{2}(k){\text{ }}{{[b + d{{y}_{1}}(k)]}^{2}}{{[c + e{{y}_{1}}(k)]}^{2}} - y_{1}^{2}(k) - {\text{ }}2y_{2}^{2}(k)z_{1}^{2}(k){\text{ }} = $
$ = {{a}^{2}}y_{1}^{2}\left( k \right) + 2aly_{1}^{2}\left( k \right){{y}_{2}}\left( k \right){{z}_{1}}\left( k \right) + {{l}^{2}}y_{1}^{2}\left( k \right)y_{2}^{2}\left( k \right)z_{1}^{2}\left( k \right) + 2{{b}^{2}}{{c}^{2}}y_{2}^{2}\left( k \right)z_{1}^{2}\left( k \right) + $
$ + \,{{r}_{1}}{{y}_{1}}\left( k \right)y_{2}^{2}\left( k \right)z_{1}^{2}\left( k \right) + {{r}_{2}}y_{1}^{2}\left( k \right)y_{2}^{2}\left( k \right)z_{1}^{2}\left( k \right) + {{r}_{3}}y_{1}^{3}\left( k \right)y_{2}^{2}\left( k \right)z_{1}^{2}\left( k \right) + $
$ + {\text{ }}2{{d}^{2}}{{e}^{2}}y_{1}^{4}\left( k \right)y_{2}^{2}\left( k \right)z_{1}^{2}\left( k \right) - y_{1}^{2}\left( k \right) - 2y_{2}^{2}\left( k \right)z_{1}^{2}{{\left( k \right)}^{~}} = $
$ = ({{a}^{2}} - 1)y_{1}^{2}\left( k \right) + 2({{b}^{2}}{{c}^{2}}--1)\mu _{1}^{2}\left( k \right) + {{r}_{1}}{{y}_{1}}\left( k \right)\mu _{1}^{2}\left( k \right) + 2aly_{1}^{2}\left( k \right){{\mu }_{1}}\left( k \right) + $
$ + \,{{r}_{2}}y_{1}^{2}\left( k \right)\mu _{1}^{2}\left( k \right) + {{r}_{3}}y_{1}^{3}\left( k \right)\mu _{1}^{2}\left( k \right) + 2{{d}^{2}}{{e}^{2}}y_{1}^{4}\left( k \right)\mu _{1}^{2}\left( k \right),$
${{r}_{0}} = 4\left( {be + cd} \right),\quad {{r}_{1}} = bc{{r}_{0}},\quad ~{{r}_{2}} = 2({{b}^{2}}{{e}^{2}} + 4bcde + {{c}^{2}}{{d}^{2}}) + {{l}^{2}},\quad ~{{r}_{3}} = de{{r}_{0}}.$

При выполнении условий

(2.10)
${{a}^{2}} < 1,~\quad {{b}^{2}}{{c}^{2}} < 1~~$
для каждого k ∈ ${{\mathbb{Z}}_{ + }}$ квадратичная часть (∆V)* полученного выражения для ∆V является определенно отрицательной по y1(k), μ1(k) функцией:
$(\Delta V){\text{*}} \leqslant - \gamma {\text{*}}[y_{1}^{2}\left( k \right) + \mu _{1}^{2}\left( k \right)],\quad \gamma {\text{*}} = {\text{min}}[(1 - {{a}^{2}}),2(1 - {{b}^{2}}{{c}^{2}})],$
причем γ* ∈ (0, 1). Поэтому для каждого k ∈ ${{\mathbb{Z}}_{ + }}$ при достаточно малом h1 > 0 в области (2.1) (но не в области (2.7)) для значений параметров a, b, c, удовлетворяющих условиям (2.10), и при любых значениях параметров d, e, l для функции Ляпунова (2.9) в силу системы (2.8) имеет место неравенство ∆V ≤ − γV(x(k)), в котором γ = min [(1 – a2), (1 – b2c2)].

На основании второй части теоремы 1 заключаем, что при условиях (2.10) “частичное” положение равновесия y1(k) = y2(k) = 0 системы (2.8) равномерно асимптотически y1-устойчиво при больших значениях z10 в целом по z20.

Для численной характеристики рассматриваемой системы и применяемого метода исследования устойчивости допустим, что a = b = 1/2, c = 1. В этом случае вытекающая из условия ∆V ≤ ≤ −γV(x(k)) оценка $y_{1}^{2}$(k) ≤ (1 − γ)kV(x0) (при k0 = 0, x0 ∈ Dδ) решений системы (2.8) по переменной y1 имеет место при γ = 0.25 и не зависит от значений d, e, l. Для сравнения при начальных данных y1(0) = y2(0) = 0.1 и z1(0) = 1 в таблице наряду с указанными “оценочными” значениями y1(k) (верхняя строка) также приводятся точные значения y1(k) (нижняя строка), вычисленные при l = − d = 1, e = 2.

3. Условия частичной детектируемости. Выделим структурную форму системы (1.1), для которой y1-устойчивость (асимптотическая y1-устойчивость) “частичного” положения равновесия y(k) = 0 означает его устойчивость (асимптотическую устойчивость) по всем переменным.

В соответствии с разбиением x = (${\mathbf{y}}_{1}^{{\text{T}}}$, ${\mathbf{y}}_{2}^{{\text{T}}}$, zT)T представим первую группу уравнений системы (1.1) в виде двух групп уравнений:

${{{\mathbf{y}}}_{1}}(k + 1) = {{{\mathbf{Y}}}_{1}}(k,{{{\mathbf{y}}}_{1}}(k),{{{\mathbf{y}}}_{2}}(k),{\mathbf{z}}(k)),\quad ~{{{\mathbf{y}}}_{2}}(k + 1) = {{{\mathbf{Y}}}_{2}}(k,{{{\mathbf{y}}}_{1}}(k),{{{\mathbf{y}}}_{2}}(k),{\mathbf{z}}(k)),$
а вектор-функцию Y2(k, x(k)) разделим на две части следующим образом:

${{{\mathbf{Y}}}_{2}}(k,{\mathbf{x}}\left( k \right)) = {\mathbf{Y}}_{2}^{0}(k,{{{\mathbf{y}}}_{2}}\left( k \right)) + {\mathbf{R}}(k,{{{\mathbf{y}}}_{1}}\left( k \right),{{{\mathbf{y}}}_{2}}\left( k \right),{\mathbf{z}}\left( k \right))$
$({\mathbf{R}}(k,{\mathbf{x}}\left( k \right)) = {{{\mathbf{Y}}}_{2}}(k,{\mathbf{x}}\left( k \right)) - {\mathbf{Y}}_{2}^{0}(k,{{{\mathbf{y}}}_{2}}\left( k \right)),~\quad {\mathbf{R}}(k,{\mathbf{0}},{{{\mathbf{y}}}_{2}}\left( k \right),{\mathbf{0}}) \equiv {\mathbf{R}}(k,{\mathbf{0}},{\mathbf{0}},{\mathbf{z}}\left( k \right)) \equiv {\mathbf{0}}).$

Дискретная (конечно-разностная) система уравнений

(3.1)
${{{\mathbf{y}}}_{2}}(k + {\text{ }}1) = {\mathbf{Y}}_{2}^{0}(k,{{{\mathbf{y}}}_{2}}(k))~$
будет “приведенной” (по переменным y2) подсистемой системы (1.1).

Допустим, что вектор-функция ${\mathbf{Y}}_{2}^{0}$ для каждого k ∈ ${{\mathbb{Z}}_{ + }}$ непрерывна по y2 в области ||y2|| < ∞ и равномерно по k ∈ ${{\mathbb{Z}}_{ + }}$ на каждом компактном подмножестве из этой области удовлетворяет условию Коши–Липшица по y2.

Теорема 2. Пусть выполняются условия:

1) найдется непрерывная для каждого k ∈${{\mathbb{Z}}_{ + }}$ вектор-функция ${\mathbf{Y}}_{2}^{*}$(y1(k), y2(k)), ${\mathbf{Y}}_{2}^{*}$(0, 0) ≡ 0, такая, что для каждого k ∈${{\mathbb{Z}}_{ + }}$ в области

(3.2)
${\text{||}}{\mathbf{y}}{\text{||}} < h,\quad {\text{||}}{\mathbf{z}}{\text{||}} < \infty $
имеет место неравенство

(3.3)
${\text{||}}{\mathbf{R}}(k,{{{\mathbf{y}}}_{1}}(k),{{{\mathbf{y}}}_{2}}(k),{\mathbf{z}}(k)){\text{||}} \leqslant {\text{||}}{\mathbf{Y}}_{2}^{*}({{{\mathbf{y}}}_{1}}(k),{{{\mathbf{y}}}_{2}}(k)){\text{||}};$

2) положение равновесия y2(k) = 0 “приведенной” подсистемы (3.1) равномерно асимптотически устойчиво по всем переменным;

3) “частичное” положение равновесия y(k) = 0 системы (1.1) равномерно y1-устойчиво (равномерно асимптотически y1-устойчиво) при больших значениях z10 в целом по z20.

Тогда “частичное” положение равновесия y(k) = 0 системы (1.1) равномерно устойчиво (равномерно асимптотически устойчиво) по всем переменным при больших значениях z10 в целом по z20.

Доказательство приведено в Приложении.

Условие 1) теоремы 2 можно ослабить, если учесть то обстоятельство, что y1-устойчивость “частичного” положения равновесия y(k) = 0 системы (1.1) фактически является некоторой “расширенной” (y1, μ)-устойчивостью, “промежуточной” между y1-устойчивостью и устойчивостью по всем переменным. Наличие такой устойчивости позволяет использовать вместо неравенства (3.2) менее ограничительное неравенство

(3.4)
${\text{||}}{\mathbf{R}}(k,{{{\mathbf{y}}}_{1}}(k),{{{\mathbf{y}}}_{2}}(k),{\mathbf{z}}(k)){\text{||}} \leqslant {\text{||}}{\mathbf{Y}}_{2}^{{**}}({{{\mathbf{y}}}_{1}}(k),{\mathbf{\mu }}(k,{\mathbf{x}}),{{{\mathbf{y}}}_{2}}(k)){\text{||}},$
выполняющееся для каждого k ∈${{\mathbb{Z}}_{ + }}$ в области ||y|| + ||μ(k, x)|| < h, ||z|| < ∞.

Замечание 6. Теорема 2 является развитием соответствующих результатов из [25, 26]. В отличие от [25], где указаны условия, при которых из устойчивости по части переменных нулевого положения равновесия системы (1.1) следует устойчивость по всем переменным, изучаются более общие задачи частичной устойчивости. Такие задачи рассмотрены ранее в [26] для систем с непрерывной динамикой. Кроме того, в отличие от [26] ограничение на связь “приведенной” подсистемы с другими частями системы анализируется на основе понятий (y1, μ)-устойчивости.

Замечание 7. При выполнении условия (3.3) динамика системы (1.1) в случае y1(k; k0, х0) ≡ 0 (нуль-динамика по отношению к “измеримому выходу” y1, следуя терминологии [17]) определяется подсистемой

${{{\mathbf{y}}}_{2}}\left( {k + 1} \right) = {\mathbf{Y}}_{2}^{0}(k,{{{\mathbf{y}}}_{2}}\left( k \right)),\quad {\mathbf{z}}\left( {k + 1} \right) = {\mathbf{Z}}(k,{\mathbf{0}},{{{\mathbf{y}}}_{2}}\left( k \right),{\mathbf{z}}\left( k \right)),$
которая включает “приведенную” подсистему (3.1). При этом “приведенная” подсистема (3.1) определяет частичную нуль-динамику системы (1.1) по отношению к “измеримым” переменным y1: динамику y-компоненты решений x(k; k0, х0), для которых y1(k; k0, х0) ≡ 0.

Поэтому при выполнении условий 1), 2) теоремы 2 система (1.1) обладает следующим свойством частичной детектируемости (zero – partial state – detectability): если y1(k; k0, х0) ≡ 0, то для каждого k0 ∈${{\mathbb{Z}}_{ + }}$ и для любого заданного числа L > 0 найдется δ(ε, L) > 0, такое, что имеет место предельное соотношение ||y(k; k0, х0)|| = 0, k → ∞ при x0 ∈ Dδ. При этом условие 3) теоремы 2 рассматривается как предположение.

Замечание 8. Предложенный подход может использоваться при решении задачи стабилизации “частичного” положения равновесия y(k) = 0 системы (1.1) при добавлении к этой системе дополнительных управляющих воздействий, дискретно формируемых по принципу обратной связи. В данном случае стабилизация проводится только по части определяющих это положение равновесия переменных (по переменным, входящим в вектор y1), а устойчивость по другой части переменных (по переменным, входящим в вектор y2) определяется полученными условиями на структуру системы. В рамках данной схемы решения допускается ситуация, когда входящие в вектор y2 переменные не измеряются и не входят в управляющие воздействия.

Пример 2. Рассмотрим управляемую систему

${{y}_{1}}(k + 1) = [a + l{{y}_{2}}(k){{z}_{1}}(k)]{{y}_{1}}(k) + {{u}_{1}},$
(3.5)
${{y}_{2}}\left( {k + 1} \right) = \left[ {b + d{{y}_{1}}\left( k \right)} \right]{{y}_{2}}\left( k \right) + {{{v}}_{1}}(k,{\mathbf{x}}\left( k \right)),$
${{z}_{1}}\left( {k + 1} \right) = \left[ {c + e{{y}_{1}}\left( k \right)} \right]{{z}_{1}}\left( k \right),\quad {{z}_{2}}\left( {k + 1} \right) = {{Z}_{2}}(k,{\mathbf{x}}\left( k \right)),$
полученную из системы (2.8) добавлением управляющего воздействия u1 вида u1 = αy1(k) (α – const) и нелинейного возмущающего воздействия ${{{v}}_{1}}$(k, x(k)).

1. Допустим сначала, что ${{{v}}_{1}}$(k, x(k)) ≡ 0. Используя наряду с функцией Ляпунова (2.9) дополнительную вспомогательную функцию μ1 = y2z1, аналогично анализу системы (2.8) можно показать, что при выполнении условий

(3.6)
${{(a + \alpha )}^{2}} < 1,\quad ~{{b}^{2}}{{c}^{2}} < 1~$
“частичное” положение равновесия y1(k) = y2(k) = 0 системы (3.5) равномерно асимптотически y1-устойчиво при больших значениях z10 в целом по z20.

“Приведенная” подсистема (3.1) в данном случае имеет вид

(3.7)
${{y}_{2}}(k + 1) = b{{y}_{2}}(k),$
и при выполнении условия b2 < 1 ее нулевое положение равновесия y2(k) = 0 равномерно асимптотически устойчиво. Кроме того, верно неравенство типа (3.3), в котором $Y_{2}^{*}$ = dy1(k)y2(k).

На основании теоремы 2 заключаем, что при условиях (3.6) и условии b2 < 1 “частичное” положение равновесия y1(k) = y2(k) = 0 системы (3.5) равномерно асимптотически устойчиво для больших значений z10 в целом по z20.

2. Допустим теперь, что возмущающее воздействие ${{{v}}_{1}}$ удовлетворяет условию |${{{v}}_{1}}$(k, x(k))| ≤ ≤ |$Y_{2}^{{**}}$(y(k), μ1)| типа (3.4), не нарушающему “частичное” положение равновесия системы (3.5), причем ${{{v}}_{1}}$(k, y1(k), 0, z1(k)) ≡ 0. В этом случае для проверки выполнимости условий частичной детектируемости важно, что “частичное” положение равновесия y1(k) = y2(k) = 0 системы (3.5) не только равномерно асимптотически y1-устойчиво, но и равномерно асимптотически (y1, μ1)-устойчиво при больших значениях z10 в целом по z20.

“Приведенная” подсистема (3.1) по-прежнему имеет вид (3.7). Поэтому при выполнении условий (3.6) и условия b2 < 1 “частичное” положение равновесия y1(k) = y2(k) = 0 системы (3.5) также равномерно асимптотически устойчиво при больших значениях z10 в целом по z20 на основании теоремы 2.

4. Условия частичной детектируемости линейных стационарных дискретных систем. Рассмотрим линейную конечно-разностную систему

${{{\mathbf{y}}}_{1}}(k + 1) = {{A}_{1}}{{{\mathbf{y}}}_{1}}(k) + {{B}_{1}}{{{\mathbf{y}}}_{2}}(k) + {{C}_{1}}{\mathbf{z}}(k),$
(4.1)
${{{\mathbf{y}}}_{2}}\left( {k + 1} \right) = {{A}_{2}}{{{\mathbf{y}}}_{1}}\left( k \right) + {{B}_{2}}{{{\mathbf{y}}}_{2}}\left( k \right) + {{C}_{2}}{\mathbf{z}}\left( k \right),$
${\mathbf{z}}\left( {k + 1} \right) = {{A}_{3}}{{{\mathbf{y}}}_{1}}\left( k \right) + {{B}_{3}}{{{\mathbf{y}}}_{2}}\left( k \right) + {{C}_{3}}{\mathbf{z}}\left( k \right),$
где Ai, Bi, Ci, i = 1, 2, 3, – постоянные матрицы соответствующих размеров.

Определение 2. Линейная система (4.1) частично детектируема (y1/y-детектируема), если асимптотическая y1-устойчивость этой системы означает асимптотическую y-устойчивость.

Для анализа y1/y-детектируемости системы (4.1) введем матрицы

${{K}_{1}} = ({{D}^{т}},{{G}^{т}}{{D}^{т}}, \ldots ,{{({{G}^{т}})}^{{r + p - 1}}}{{D}^{т}}),\quad {{K}_{2}} = ({{L}^{т}},C_{3}^{т}{{L}^{т}}, \ldots ,{{(C_{3}^{т})}^{{p - 1}}}{{L}^{т}}),$
$D = \left( {{{B}_{1}},{{C}_{1}}} \right)\,,\quad G = \left( {\begin{array}{*{20}{c}} {{{B}_{2}}}&{{{C}_{2}}} \\ {{{B}_{3}}}&{{{C}_{3}}} \end{array}} \right)\,,\quad L = \left( {\begin{array}{*{20}{c}} {{{C}_{1}}} \\ {{{C}_{2}}} \end{array}} \right)\,,$
$r = {\text{dim}}({{{\mathbf{y}}}_{2}}),\quad p = {\text{dim}}\left( {\mathbf{z}} \right).$

Теорема 3. Если выполняется условие

(4.2)
${\text{rank}}{{K}_{1}} = r + {\text{rank}}{{K}_{2}},$
то линейная дискретная система (4.1) y1/y-детектируема.

Доказательство приведено в Приложении.

Условие (4.2) предполагает анализ только структурной формы (4.1) без анализа ее асимптотической устойчивости по соответствующим группам переменных. Это условие, однако, не охватывает случай нулевых матриц B1, C1, когда первая группа уравнений системы (4.1) имеет вид

(4.3)
${{{\mathbf{y}}}_{1}}(k + 1) = {{A}_{1}}{{{\mathbf{y}}}_{1}}(k).$

Если подсистема (4.3) асимптотически устойчива, то y1/y-детектируемость системы (4.1) зависит от наличия свойства y2-устойчивости подсистемы

(4.4)
${{{\mathbf{y}}}_{2}}\left( {k + 1} \right) = {{B}_{2}}{{{\mathbf{y}}}_{2}}\left( k \right) + {{C}_{2}}{\mathbf{z}}\left( k \right),\quad {\mathbf{z}}\left( {k + 1} \right) = {{B}_{3}}{{{\mathbf{y}}}_{2}}\left( k \right) + {{C}_{3}}{\mathbf{z}}\left( k \right).$

Замечание 9. Из условия (4.2), как частный случай, следует условие rank K1 = r + p “полной” детектируемости (y1/x-детектируемости) линейной дискретной системы (4.1).

Пример 3. Пусть система (4.1) состоит из уравнений (a – некоторая постоянная)

${{y}_{1}}\left( {k + 1} \right) = 1{\text{/}}2{{y}_{1}}\left( k \right) + {{y}_{2}}\left( k \right) + {{z}_{1}}\left( k \right)--2{{z}_{2}}\left( k \right),$
(4.5)
${{y}_{2}}\left( {k + 1} \right) = 3{\text{/}}4{{y}_{2}}\left( k \right) - a[{{z}_{1}}\left( k \right)--2{{z}_{2}}\left( k \right)],$
${{z}_{1}}\left( {k + 1} \right) = - {\text{ }}2{{y}_{1}}\left( k \right) + 2{{y}_{2}}\left( k \right) + 3{\text{/}}4{{z}_{1}}\left( k \right),\quad {{z}_{2}}\left( {k + 1} \right) = - {{y}_{1}}\left( k \right) + {{y}_{2}}\left( k \right) + 3{\text{/}}4{{z}_{2}}\left( k \right).$

В данном случае r = 1, p = 2 и матрицы K1 и K2 определяются следующим образом:

${{K}_{1}} = \left( {\begin{array}{*{20}{c}} 1&{3{\text{/}}4}&{9{\text{/}}16} \\ 1&{ - a + 3{\text{/}}4}&{ - 3a{\text{/}}2 + 9{\text{/}}16} \\ { - 2}&{2a - 3{\text{/}}2}&{3a - 9{\text{/}}8} \end{array}} \right),\quad {{K}_{2}} = \left( {\begin{array}{*{20}{c}} 1&{ - a}&{3{\text{/}}4}&{ - 3a{\text{/}}4} \\ { - 2}&{2a}&{ - 3{\text{/}}2}&{3a{\text{/}}2} \end{array}} \right).$

В результате имеем

${\text{rank}}{{K}_{1}} = r + {\text{rank}}{{K}_{2}} = {\text{ }}2{\text{ }} < r + p = 3\quad {\text{при}}\quad a \ne 0,$
${\text{rank}}{{K}_{1}} = 1 < r + {\text{rank}}{{K}_{2}} = 2 < r + p = 3\quad {\text{при}}\quad a = 0,$
и условие (4.2) выполняется при всех a ≠ 0.

На основании теоремы 3 система (4.5) y1/y-детектируема при всех a ≠ 0.

Заключение. Предложен подход к изучению устойчивости “частичного” положения равновесия нелинейной дискретной (конечно-разностной) системы. Подход основан на предварительном анализе устойчивости по части определяющих данное положение равновесия переменных на базе метода функций Ляпунова с последующим анализом структурной формы системы для выявления условий ее частичной детектируемости. Эти условия включают требование равномерной асимптотической устойчивости нулевого положения равновесия подсистемы, “приведенной” по переменным, устойчивость “частичного” положения равновесия по которым изначально не известна, а также ограничение на связь “приведенной” подсистемы с другими частями системы.

Полученные результаты дополняют ранее выполненные исследования по частичной устойчивости дискретных систем [2, 4, 6–11, 25], устойчивости инвариантных множеств динамических систем с непрерывной и дискретной динамикой [27–32] на основе метода функций Ляпунова, а также исследования задач стабилизации связей динамических систем [33, 34], в которых устойчивость инвариантных множеств является необходимым условием. При этом в рамках разработанного подхода требования к функциям Ляпунова ослабляются за счет сужения области фазового пространства, в которой происходит их построение; фактически можно использовать даже знакопеременные функции Ляпунова, приращения которых в силу изучаемой системы могут быть также знакопеременными. Кроме того, ослабления требований к основной V-функции Ляпунова можно добиться путем согласования постановки рассматриваемой задачи частичной устойчивости с предложенным разбиением на две части “неконтролируемых” фазовых переменных изучаемой дискретной системы.

Таблица 1.

Оценки и точные значения переменной y1(k) системы (2.8)

y1(k) k = 0 k = 5 k = 10 k = 15 k = 20 k = 25
Оценка 0.1414 0.0844 0.0411 0.0200 0.0098 0.0048
Точное значение 0.1 0.0049 0.00016 5.1 × 10–6 1.6 × 10–7 5.04 × 10–9
Рис. 1.

Области допустимых начальных и текущих отклонений от инвариантного множества y1(k) = y2(k) = 0.

Список литературы

  1. Халанай А., Векслер Д. Качественная теория импульсных систем. М.: Мир, 1971. 309 с.

  2. Фурасов В.Д. Устойчивость и стабилизация дискретных процессов. М.: Наука, 1982. 192 с.

  3. Agarwal R.P. Difference Equations and Inequalities: Theory, Methods and Applications. 2 ed. N.Y.: Marcel Dekker, 2000. 971 p.

  4. Haddad W.M., Chellaboina V. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach. Princeton: Princeton Univ. Press, 2008. 976 p.

  5. Зуев А.Л., Игнатьев А.О., Ковалев А.М. Устойчивость и стабилизация нелинейных систем. Киев: Наук. думка, 2013. 430 с.

  6. Александров А.Ю., Жабко А.П., Платонов А.В. Устойчивость движений дискретных динамических систем. СПб.: Изд. Дом Федоровой Г.В., 2015. 154 с.

  7. Michel A.N., Molchanov A.P., Sun Y. Partial Stability and Boundedness of General Dynami-cal Systems on Metric Spaces // Nonlinear Analysis: TMA. 2003. V. 52. № 4. P. 1295−1316.

  8. Fu S.H.S., Cheng C.C. On Direct Adaptive Control Design for Nonlinear Discrete-Time Uncertain Systems // J. Franklin Institute. 2008. V. 345. № 2. P. 119−135.

  9. Costa E.F., Astolfi A. Partial Stability for a Class of Nonlinear Systems // SIAM J. Control Optim. 2009. V. 47. № 6. P. 3203−3219.

  10. Ramírez-Llanos E., Martínez S. Distributed and Robust Fair Optimization Applied to Virus Diffusion Control // IEEE Trans. Network Sci. Engineering. 2017. V. 4. № 1. P. 41–54.

  11. Ramírez-Llanos E., Martínez S. Distributed Discrete-Time Optimization Algorithms with Applications to Resource Allocation in Epidemics Control // Optimal Control Appl. Meth. 2018. V. 39. № 1. P. 160−180.

  12. Shafiei M.H., Vazirpour N. The Approach of Partial Stabilization in Design of Discrete-Time Robust Guidance Laws Against Maneuvering Targets // Aeronautical J. 2020. V. 124. № 1277. P. 1114−1127.

  13. Румянцев В.В. Об устойчивости движения по отношению к части переменных // Вестн. МГУ. Сер. Матем., Механика, Физика, Астрономия, Химия. 1957. № 4. С. 9–16.

  14. Воротников В.И. Частичная устойчивость и управление: состояние проблемы и перспективы развития // АиТ. 2005. № 4. С. 3−59.

  15. Воротников В.И., Мартышенко Ю.Г. К теории частичной устойчивости нелинейных динамических систем // Изв. РАН. ТиСУ. 2010. Т. 51. Вып. 5. С. 23−31.

  16. Воротников В.И. К частичной устойчивости и детектируемости функционально-дифференциальных систем с последействием // АиТ. 2020. № 2. С. 3–17.

  17. Byrnes C.I., Isidori A., Willems J.C. Passivity, Feedback Equivalence, and the Global Stabilization of Minimum Phase Nonlinear Systems // IEEE Trans. Autom. Control. 1991. V. 36. № 11. P. 1228–1240.

  18. Sontag E.D., Wang Y. Output-to-State Stability and Detectability of Nonlinear Systems // Syst. & Control Letters. 1997. V. 29. № 5. P. 279–290.

  19. Мирошник И.В., Никифоров В.O., Фрадков А.Л. Нелинейное и адаптивное управление сложными динамическими системами. СПб.: Наука, 2000. 549 с.

  20. Ingalls B.P., Sontag E.D., Wang Y. Measurement to Error Stability: a Notion of Partial Detectability for Nonlinear Systems // Proc. 41th IEEE Conf. on Decision and Control. Las Vegas, Nevada, 2002. P. 3946−3951.

  21. Дашковский С.Н., Ефимов Д.В., Cонтаг Э.Д. Устойчивость от входа к состоянию и смежные свойства систем // АиТ. 2011. № 8. С. 3–40.

  22. Heinen J.A. Difference Inequalities and Comparison Theorems for Stability of Discrete Systems // Int. J. Syst. Sci. 1979. V. 10. № 6. C. 711–718.

  23. Corduneanu C. Применение дифференциальных неравенств к теории устойчивости // Ann. Stiintifice Univ. A.I. Cusa din Iasi. Ser.1. 1960. V. 6. № 1. С. 47–58.

  24. Матросов В.М., Aнапольский Л.Ю., Васильев С.Н. Метод сравнения в математической теории систем. Новосибирск: Наука, 1980. 480 с.

  25. Halanay A. Differential Equations: Stability, Oscillations, Time Lags. N.Y.: Acad. Press, 1966. 528 p.

  26. Воротников В.И., Мартышенко Ю.Г. К задаче частичной детектируемости нелинейных динамических систем // АиТ. 2009. № 1. С. 25–38.

  27. Зубов В.И. Проблема устойчивости процессов управления. Л.: Судостроение, 1980. 256 с.

  28. Галиуллин А.С., Мухаметзянов И.А., Мухарлямов Р.Г. и др. Построение систем программного движения. М.: Наука, 1971. 352 с.

  29. Самойленко А.М. Элементы математической теории многочастотных колебаний. Инвариантные торы. М.: Наука, 1987. 304 с.

  30. Teel A.R., Praly L. A Smooth Lyapunov Function from a Class KL-Estimate Involving Two Positive Semidefinite Functions // ESAIM: Control, Optim. Calc. Var. 2000. V. 5. № 2. P. 313−367.

  31. Ефимов Д.В. Робастное и адаптивное управление нелинейными колебаниями. СПб.: Наука, 2005. 314 с.

  32. Kellett C.M., Teel A.R. On the Robustness of KL-stability for Difference Inclusions: Smooth Discrete-Time Lyapunov Functions // SIAM J. Control Optim. 2005. V. 44. № 3. P. 777−800.

  33. Мухарлямов Р.Г. Моделирование процессов управления, устойчивость и стабилизация систем с программными связями // Изв. РАН. ТиСУ. 2015. Т. 56. Вып. 1. С. 15−28.

  34. Мухарлямов Р.Г. Управление динамикой системы с дифференциальными связями // Изв. РАН. ТиСУ. 2019. Т. 60. Вып. 4. С. 16−28.

  35. Воротников В.И. Устойчивость динамических систем по отношению к части переменных. М.: Наука, 1991. 288 с.

  36. Vorotnikov V.I. Partial Stability and Control. Boston: Birkhauser, 1998. 448 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал