Известия РАН. Теория и системы управления, 2022, № 4, стр. 49-65

Введение. Одной из наиболее существенных особенностей систем с распределенными параметрами (СРП) по сравнению с сосредоточенными системами (ССП) является расширение класса допустимых управляющих воздействий за счет включения в их число пространственно-временных управлений (ПВУВ), описываемых подобно состоянию СРП функциями векторного аргумента – времени и пространственных координат [1–8]. Применение ПВУВ открывает принципиально новые возможности управления СРП, недостижимые в классе свойственных ССП сосредоточенных управлений, которые не зависят от пространственных переменных. В частности, именно использование ПВУВ специального вида привело к созданию нового перспективного класса СРП с подвижным воздействием, охватывающего широкий круг актуальных прикладных задач самого различного физического содержания [6–8].

В работе рассматривается задача оптимального по квадратичному критерию качества управления СРП, описываемой линейным пространственно-одномерным уравнением второго порядка в частных производных параболического типа с внутренним ПВУВ при заведомо неизвестном характере его зависимости как от времени, так и от пространственной координаты. Задача исследуется в специфических и типичных для приложений условиях оценки в равномерной метрике целевых множеств с негладкой границей в конечной точке оптимального процесса в бесконечномерном фазовом пространстве СРП, исключающих применение классических условий трансверсальности при аналитическом синтезе оптимальных регуляторов [5, 9–11].

Для частного случая использования скалярных сосредоточенных управлений с априори заданным характером пространственного распределения внутренних управляющих воздействий описываемая задача изучалась в [11] для детерминированных и не полностью определенных моделей объекта. В [12] были найдены оптимальные по критерию энергосбережения программные пространственно-временные управляющие воздействия для различных возможных вариантов их фактического представления.

1. Постановка задачи. Пусть управляемая величина $Q(x,t)$ объекта с распределенными параметрами описывается в зависимости от пространственной координаты $x \in [{{x}_{0}},{{x}_{1}}]$ и времени $t \in \left[ {0,{{t}_{1}}} \right]$ одномерным линейным уравнением второго порядка в частных производных параболического типа с самосопряженным дифференциальным оператором в его правой части:

с начальными и граничными условиями при кусочно-непрерывном [2] пространственно-временном внутреннем управлении $u\left( {x,t} \right)$; заданных достаточно гладких функциях b(x), c(x), c₁(x) и постоянных коэффициентах ${{\alpha }_{0}}$, ${{\alpha }_{1}} \geqslant 0$; ${{\beta }_{0}}$, ${{\beta }_{1}} > 0$. Управляющее воздействие $u\left( {x,t} \right)$ не стесняется никакими дополнительными ограничениями.

Допустим, что необходимо обеспечить за фиксируемое априори конечное время ${{t}_{1}}$ заданную точность $\varepsilon $ равномерного приближения результирующего пространственного распределения управляемой величины $Q\left( {x,{{t}_{1}}} \right)$ к требуемому $Q{\text{**}}\left( x \right) > {{Q}_{0}}\forall x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$, согласно соотношению

определяющему оцениваемое в равномерной метрике целевое множество конечных состояний СРП [5, 9].

Пусть далее эффективность процесса управления объектом (1.1)–(1.4) оценивается типичным квадратичным функционалом качества, определяемым для простоты и наглядности без потери общности основных результатов в следующей типичной частной форме:

с постоянным весовым коэффициентом ${{\rho }_{Q}} > 0$.

Подобно тому, как применение преобразования Лапласа к обыкновенным линейным дифференциальным уравнениям модели объекта с сосредоточенными параметрами приводит к алгебраическим уравнениям относительно изображений управляемой величины, не содержащим ее производных по времени, известный аппарат конечных интегральных преобразований позволяет перейти от дифференциальных уравнений в частных производных (1.1)–(1.3) к бесконечной системе обыкновенных дифференциальных уравнений первого порядка, не содержащих производных управляемой величины по пространственной координате [13]:

относительно коэффициентов (временных мод) ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},t} \right)$ разложения Q(x, t) в сходящийся в среднем ряд по ортонормированной системе собственных функций ${{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right)$, $n = 1,2,...$, определяемых вместе с собственными числами $\mu _{n}^{2}$ известными способами [13]. Здесь ${{\bar {u}}_{n}}\left( {{{\mu }_{n}},t} \right)$ – временные моды разложения u(x, t) в ряд вида (1.7): рассматриваемые далее в качестве бесконечного числа автономных, независимых друг от друга сосредоточенных управляющих воздействий, и ${{\bar {Q}}^{{\left( 0 \right)}}}\left( {{{\mu }_{n}}} \right)$ – моды ${{Q}_{0}}\left( x \right)$.

При этом поведение каждой из модальных составляющих ${{\bar {Q}}_{n}}$ управляемой величины Q(x, t) определяется только “своим” управляющим воздействием ${{\bar {u}}_{n}}$, согласно решению каждого из уравнений (1.6) в отдельности независимо от других, обеспечивая в итоге требуемое пространственно-временное состояние Q(x, t), описываемое рядом (1.7).

Подобно [11], здесь и всюду далее в условиях выполнения усиленных условий Коши–Липшица [14] будем учитывать N₁ слагаемых в суммах (1.7), (1.8). Здесь ${{N}_{1}} = \infty $ или ${{N}_{1}} = N < \infty $ в зависимости от используемой схемы анализа и возможностей практической реализации исследуемых алгоритмов управления, ограничиваясь в случае ${{N}_{1}} = N$ с любой требуемой точностью решением “укороченной” системы N первых уравнений (1.6) при достаточно большой величине $N$ и полагая при этом ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},t} \right) = 0$, $n > N$ [14].

Переход к описанию СРП в (1.6), (1.7) в терминах модальных переменных приводит в силу ортонормированности семейства собственных функций к представлению критерия оптимальности (1.5) в следующем виде:

а требования (1.4) к конечному состоянию объекта представляются условием

Рассматриваемая задача оптимизации сводится к определению программного оптимального управления $u{\text{*}}\left( {x,t} \right)$ и алгоритма обратной связи $u{\text{*}}\left( {\bar {Q},x,t} \right)$, $\bar {Q} = \left( {{{{\bar {Q}}}_{n}}} \right)$, $n = \overline {1,{{N}_{1}}} $, обеспечивающих при ${{N}_{1}} = \infty $ перевод объекта (1.6)–(1.8) за заданное время t₁ в требуемое конечное состояние, удовлетворяющее (1.10) при минимально возможном значении критерия оптимальности (1.9).

При использовании усеченной модели объекта с ${{N}_{1}} = N < \infty $ все полученные далее результаты следует считать субоптимальными.

2. Программное оптимальное пространственно-временное управление. Структура модального управляющего воздействия. На сформулированную бесконечномерную задачу оптимального управления распространяется принцип максимума Понтрягина [5, 15]. Базовое условие

достижения на соответствующих оптимальному процессу величинах $\bar {Q}{\text{*}}\left( t \right)$, $\bar {u}{\text{*}}\left( t \right)$, $\psi {\text{*}}\left( t \right)$ максимума функции Понтрягина Н по векторному аргументу $\bar {u}\left( t \right) = \left( {{{{\bar {u}}}_{n}}\left( {{{\mu }_{n}},t} \right)} \right)$ для рассматриваемой задачи оптимизации (1.6)–(1.10): где $\bar {Q}\left( t \right) = \left( {{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right)} \right)$, $n = \overline {1,{{N}_{1}}} $, и вектор сопряженных переменных $\psi \left( t \right) = \left( {{{\psi }_{n}}\left( t \right)} \right)$, $n = \overline {1,{{N}_{1}}} $, описывается системой уравнений определяет в открытой области изменения управляющих воздействий каждое из автономных программных управлений $\bar {u}_{n}^{*}\left( {{{\mu }_{n}},t} \right)$ в форме явной функции от соответствующей сопряженной переменной $\psi _{n}^{*}\left( t \right)$ независимо от других составляющих $\bar {u}{\text{*}}\left( t \right)$:

Краевая задача принципа максимума для модальных управляющих воздействий. Каждое из уравнений (1.6) после подстановки модального управления в виде (2.4) образует совместно с соответствующим уравнением (2.3) линейную программно-управляемую систему второго порядка относительно двух переменных ${{\bar {Q}}_{n}}$, ${{\psi }_{n}}$ для каждого $n = \overline {1,{{N}_{1}}} $:

Система (2.5) в отличие от подобной системы порядка 2N₁ для всей совокупности составляющих $\bar {Q}\left( t \right)$, $\psi \left( t \right)$ в задаче с сосредоточенным внутренним управлением [11] замыкается требованиями к ее конечному состоянию, которые считаются определенными, исходя из общего для всех $n = \overline {1,{{N}_{1}}} $ условия (1.10).

Решение этой системы может быть представлено, подобно [11], в векторно-матричной форме

где ${{A}_{n}}$ – 2 × 2-матрица коэффициентов системы (2.5), ${{e}^{{{{A}_{n}}t}}}$ – 2 × 2-матрица (матричная экспонента) где ${{A}_{{nks}}}$, $k$, $s = 1,2$, – заданные в соответствии со структурой уравнений (2.5) элементы ${{e}^{{{{A}_{n}}t}}}$.

Параметризация пространственно-временных управлений. Согласно (2.6), $\psi _{n}^{*}\left( t \right)$, а следовательно, и программное управление $\bar {u}_{n}^{*}\left( {{{\mu }_{n}},t} \right)$ в (2.4) определяются с точностью до начальных значений $\psi _{n}^{*}\left( 0 \right)$, совокупность которых для всех $n = \overline {1,{{N}_{1}}} $ выступает, таким образом, в качестве естественного параметрического представления $u{\text{*}}\left( {x,t} \right)$, согласно (1.8), (2.4), (2.6). Однако подобный подход для СРП оказывается неконструктивным, прежде всего в силу бесконечной размерности вектора $\psi {\text{*}}\left( 0 \right)$ при ${{N}_{1}} = \infty $.

В работе [16] применительно к требованиям (1.10), предъявляемым к $\bar {Q}{\text{*}}\left( {{{t}_{1}}} \right)$, предложен конструктивный способ последовательной конечномерной параметризации управляющих воздействий (“$\psi $-параметризация”) на множестве M-мерных векторов ${{\psi }^{{\left( M \right)}}} = \left( {{{{\tilde {\psi }}}_{i}}} \right)$, $i = \overline {1,M} $; ${{\tilde {\psi }}_{i}} = {{\psi }_{i}}\left( {{{t}_{1}}} \right)$, $M < {{N}_{1}}$, конечных значений первых M сопряженных функций в (2.3) при равных нулю всех остальных значениях ${{\psi }_{i}}\left( {{{t}_{1}}} \right)$:

С возрастанием $M$ обеспечивается попадание под действием параметризуемых на множестве параметров (2.8) управляющих воздействий в сужающееся к заданному состоянию $Q{\text{**}}\left( x \right)$ в пространстве $\left( {{{{\bar {Q}}}_{n}}} \right)$ целевое множество, гарантируя выполнение условий (1.10) для допустимых значений $\varepsilon $ при некотором конечном значении $M \geqslant 1$ [16].

В целях определения в явной форме $\psi $-параметризованного модального управления получим по указанной в [11] схеме путем переноса (прогонки) начальных условий в (2.6) в конечный момент времени ${{t}_{1}}$ следующее выражение в отдельности для каждой из сопряженных функций $\psi _{n}^{*}\left( t \right)$, $n = \overline {1,{{N}_{1}}} $, в оптимальном процессе в зависимости от их конечных значений $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$ и начального состояния объекта ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},0} \right)$:

где

Здесь ${{\hat {A}}_{{nks}}}$, $k$, $s = 1,2$ – подобные (2.7) элементы обратной матрицы ${{e}^{{ - {{A}_{n}}t}}}$ и

При определении $\psi {\text{*}}\left( {{{t}_{1}}} \right)$ в форме (2.8) будем иметь, согласно (2.9),

где $\tilde {\psi }_{n}^{*}$ – значения ${{\tilde {\psi }}_{n}}$ в (2.8), соответствующие оптимальному процессу.

Подстановка (2.12) в (2.4) определяет ψ-параметризованные модальные управления в форме линейной зависимости от $\tilde {\psi }_{n}^{*}$:

Отсюда, в частности, следует, что $\bar {u}_{n}^{*}\left( {{{\mu }_{n}},t} \right)$ при $n > M$ определяются только начальным значением ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},0} \right)$.

Последующая подстановка (2.13) в (1.8), где следует учесть ${{N}_{1}} \leqslant \infty $ слагаемых бесконечной суммы, приводит к ψ-параметризованной форме оптимального пространственно-временного управления:

Таким образом, искомое программное управление находится, согласно (2.13), (2.14), с точностью до выбора оптимального вектора параметров $\psi _{*}^{{\left( M \right)}} = (\tilde {\psi }_{i}^{*})$, $i = \overline {1,M} $, в (2.8). К его определению и сводится последующая задача, которая может быть решена специальным методом параметрической оптимизации [5, 9, 16].

Переход к задаче полубесконечной оптимизации и метод ее решения. Интегрирование системы уравнений (2.5) с ψ-параметризованным модальным управлением вида (2.8), (2.13) позволяет получить зависимости $Q(x,{{\psi }^{{\left( M \right)}}})$ управляемой величины в конце процесса управления и критерия оптимальности ${{I}_{1}}({{\psi }^{{\left( M \right)}}})$ в (1.7), (1.9) для каждого значения $\bar {Q}\left( 0 \right)$ в форме явных функций только своих аргументов. В результате осуществляется точная редукция исходной задачи оптимального управления к задаче полубесконечной оптимизации (ЗПО) [5, 9, 16]:

на минимум функции ${{I}_{1}}({{\psi }^{{\left( M \right)}}})$ конечного числа M переменных ${{\tilde {\psi }}_{i}}$, $i = \overline {1,M} $, в (2.8) с бесконечным числом ограничений для всех $x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]$, заменяемых одним эквивалентным ограничением (2.16) на максимум ошибки равномерного приближения $Q(x,{{\psi }^{{\left( M \right)}}})$ к $Q{\text{**}}\left( x \right)$ в пределах всего отрезка $\left[ {{{x}_{0}},{{x}_{1}}} \right]$.

Для заданной величины $\varepsilon $ в (2.16) размерность M вектора ${{\psi }^{{\left( M \right)}}} = \left( {{{{\tilde {\psi }}}_{i}}} \right)$, $i = \overline {1,M} $, однозначно определяется соотношением [16]

где и значения минимакса $\varepsilon _{{\min }}^{{\left( \omega \right)}}$ образуют, как правило, убывающую цепочку неравенств с возрастанием $\omega $ [5, 9, 16].

Задача (2.15), (2.16) оказывается разрешимой, если $\varepsilon \geqslant {{\varepsilon }_{{\inf }}}$. Здесь точная нижняя грань ${{\varepsilon }_{{\inf }}}$ достижимых значений $\varepsilon $ оказывается равной минимаксу $\varepsilon _{{\min }}^{{\left( \rho \right)}}$, где $\rho = \infty $ при ${{\varepsilon }_{{\inf }}} = 0$ и $\rho < \infty $ при ${{\varepsilon }_{{\inf }}} > 0$ соответственно для управляемых и неуправляемых объектов относительно заданного конечного состояния $Q{\text{**}}(x)$ [9].

Решение ЗПО (2.15), (2.16) относительно вектора параметров ${{\psi }^{{\left( M \right)}}}$, а также априори неизвестной величины минимакса $\varepsilon _{{\min }}^{{\left( M \right)}}$ в случае, когда в (2.16) $\varepsilon = \varepsilon _{{\min }}^{{\left( M \right)}}$, может быть получено альтернансным методом [5, 9, 16] в условиях малостеснительных допущений, которые всюду далее считаются выполненными.

Метод базируется на специальных альтернансных свойствах искомого вектора $\psi _{*}^{{\left( M \right)}}$, являющихся аналогом условий экстремума в теории чебышевских приближений, и дополнительной информации о форме кривой пространственного распределения оптимального результирующего состояния $Q(x,\psi _{*}^{{\left( M \right)}}) - Q{\text{**}}\left( x \right)$ управляемой величины, диктуемой закономерностями предметной области рассматриваемой задачи.

Согласно альтернансным свойствам, равные допустимой величине $\varepsilon $ одинаковые значения максимальных отклонений $\mathop {\max }\limits_{x \in \left[ {{{x}_{0}},{{x}_{1}}} \right]} {\text{|}}Q(x,\psi _{*}^{{\left( M \right)}}) - Q{\text{**}}\left( x \right){\text{|}}$ достигаются в некоторых точках $x_{j}^{0}$, $j = \overline {1,R} $, на отрезке $\left[ {{{x}_{0}},{{x}_{1}}} \right]$. Общее число R этих точек, удовлетворяющее базовым соотношениям

оказывается равным числу всех искомых неизвестных в ЗПО (2.15), (2.16), порождая тем самым замкнутую относительно этих неизвестных систему соотношений

При наличии дополнительной информации из предметной области о форме кривой $Q(x,\psi _{*}^{{\left( M \right)}})$ на отрезке $\left[ {{{x}_{0}},{{x}_{1}}} \right] \ni x$, позволяющей идентифицировать координаты $x_{j}^{0}$ и знаки $Q(x_{j}^{0},\psi _{*}^{{\left( M \right)}})$, равенства (2.20), дополненные условиями существования экстремума функции $Q(x,\psi _{*}^{{\left( M \right)}})$ – $Q{\text{**}}(x)$ в точках $x_{{{{j}_{g}}}}^{0} \in \operatorname{int} \left[ {{{x}_{0}},{{x}_{1}}} \right]$, $g = \overline {1,{{R}_{1}}} $, где ${{R}_{1}} \leqslant R$ и $x_{{{{j}_{g}}}}^{0} \in \{ x_{j}^{0}\} $, переводятся в систему уравнений:

с однозначно определяемым знаком $\varepsilon $ в каждой точке $x_{j}^{0}$, которая разрешается в условиях (2.19) относительно $\tilde {\psi }_{i}^{*}$, $i = \overline {1,M} $, значений $x_{{{{j}_{g}}}}^{0}$, $g = \overline {1,{{R}_{1}}} $, а также $\varepsilon _{{\min }}^{{\left( M \right)}}$, если в (2.17), (2.19) $\varepsilon = \varepsilon _{{\min }}^{{\left( M \right)}}$.

Явное выражение для зависимости $Q(x_{j}^{0},\psi _{*}^{{\left( M \right)}})$ от своих аргументов в системе уравнений (2.21) представляется в форме бесконечной или укороченной суммы вида (1.10) разложения в ряд (1.7):

где значения модальных переменных ${{\bar {Q}}_{n}}({{\mu }_{n}},\psi _{*}^{{\left( M \right)}})$ в конце оптимального процесса находятся, согласно (2.6), в подобном (2.9) виде [11]:

В итоге решение системы уравнений (2.21) с подстановкой (2.22), (2.23) полностью определяет искомый алгоритм программного пространственно-распределенного управления в форме (2.14).

3. Программное управление с ограничениями на характер его пространственно-временного распределения. Техническая реализация алгоритма управления (2.14), не стесняемого дополнительными условиями, накладываемыми на форму его пространственно-временного распределения, может оказаться затруднительной, прежде всего, в виду сложной зависимости $u{\text{*}}\left( {x,t} \right)$ от пространственной координаты. В такой ситуации часто используются отвечающие подобным условиям различные частные варианты представления ПВУВ, заведомо обеспечивающие их осуществимость стандартными техническими средствами [5, 12, 17].

3.1. Редукция к задаче многоканального сосредоточенного управления. Во многих типичных случаях $u\left( {x,t} \right)$ в (1.1) ищется в форме взвешенной суммы заранее фиксируемых проектными решениями объекта и заведомо технически реализуемых (чаще всего кусочно-постоянных) зависимостей ${{F}_{m}}\left( x \right)$, $m = \overline {1,s} $; $s \geqslant 1$, от пространственной координаты с весовыми коэффициентами, в роли которых выступают искомые сосредоточенные управляющие воздействия ${{\upsilon }_{m}}\left( t \right)$ [5, 12, 17]:

Исследуемая задача оптимизации (1.1)–(1.5) с подстановкой (3.1) в (1.1) при s = 1 сводится к рассмотренной в [11] и является ее обобщением на случай многоканального управления при s > 1 в (3.1). Конечное интегральное преобразование равенства (3.1) приводит к следующему выражению для модальных управляющих воздействий ${{\bar {u}}_{n}}\left( {{{\mu }_{n}},t} \right)$ в (1.6) [5, 13, 17]:

где ${{\bar {F}}_{{mn}}}$ – n-я мода разложения ${{F}_{m}}\left( x \right)$ в ряд вида (1.7) по собственным функциям начально-краевой задачи (1.1)–(1.3).

При этом критерий оптимальности принимает вместо (1.9) следующий вид с учетом суммирования в подынтегральной функции квадратичного функционала качества эффекта многоканального управления:

Рассматриваемая задача оптимального программного управления сводится к определению s сосредоточенных управлений $\upsilon {\text{*}}\left( t \right) = (\upsilon _{m}^{*}\left( t \right))$, $m = \overline {1,s} $, переводящих объект управления (1.6)–(1.8), (3.2) в конечное состояние (1.10) при минимально возможном значении критерия оптимальности (3.3).

Структура оптимальных управлений $\upsilon _{m}^{*}\left( t \right)$ устанавливается с использованием аппарата принципа максимума Понтрягина по аналогичной разд. 2 схеме на основании базового условия вида (2.1), где теперь функция Понтрягина представляется вместо (2.2) в следующем виде:

Отсюда, получаем оптимальные программные управления

теперь уже в форме взвешенной суммы всех ${{N}_{1}}$ сопряженных переменных в отличие от (2.4), где автономные модальные управляющие воздействия зависят только от одной сопряженной функции. Здесь ${{\bar {F}}_{m}}$ – матрица-строка, $\psi {\text{*}}\left( t \right)$ – матрица-столбец.

Уравнения (1.6) с подстановкой управляющих воздействий в форме (3.2), (3.5) образуют совместно с уравнениями для сопряженных переменных (2.3) краевую задачу принципа максимума относительно $2{{N}_{1}}$ переменных ${{\bar {Q}}_{n}}$, ${{\psi }_{n}}$; $n = \overline {1,{{N}_{1}}} $ в отличие от (2.5):

решение которой определяется в виде, подобном (2.6): с блочным представлением матричной экспоненты

Здесь A_ij, i, $j = 1,2$, – известные матрицы размерности ${{N}_{1}} \times {{N}_{1}}$ в соответствии со структурой системы уравнений (3.6) [11].

Дальнейшее решение рассматриваемой задачи программного управления проводится по предложенной в [11] схеме, обобщающей результаты (2.8)–(2.23) на исследуемый случай многоканального управления.

На первом этапе осуществляется ψ-параметризация управлений (3.5) на конечномерном подмножестве значений ${{\psi }_{n}}\left( {{{t}_{1}}} \right)$, $n = \overline {1,M} $, согласно соотношениям (2.8). Затем путем, указанным в [11], находится вместо (2.9), (2.10) линейная зависимость вектора ψ*(t) в оптимальном процессе от его параметризуемой, согласно (2.8), конечной величины ψ*(t₁) и начального состояния объекта $\bar {Q}\left( 0 \right)$:

где и ${{\hat {A}}_{{ij}}}$, i, $j = 1,2$, – подобные (3.8) блоки обратной матрицы ${{e}^{{ - At}}}$.

Искомое программное управление (3.5) находится в ψ-параметризуемой форме после подстановки в (3.5) выражения (3.9):

Дальнейшая проблема сводится к определению оптимального вектора параметров $\psi _{*}^{{\left( M \right)}}$ в составе вектора $\psi {\text{*}}\left( {{{t}_{1}}} \right)$ в (2.8) путем редукции к задаче полубесконечной оптимизации (2.15), (2.16). Альтернансные свойства (2.17)–(2.19) ее решений опять порождают замкнутую систему равенств (2.20), где в отличие от случая автономного модального управления по всем ${{\bar {u}}_{n}}$, $n = \overline {1,{{N}_{1}}} $, зависимость $Q(x,\psi _{*}^{{\left( M \right)}})$ в виде явной функции своих аргументов определяется для вектора $\bar {Q}\left( {{{t}_{1}}} \right) = \bar {Q}(\psi _{*}^{{\left( M \right)}})$ в (1.7) интегрированием системы уравнений (3.6) с подстановкой $\psi {\text{*}}\left( t \right)$ в параметризованной форме (3.9). При этом покоординатное представление ${{\bar {Q}}_{n}}({{\mu }_{n}},\psi _{*}^{{\left( M \right)}})$ в (2.23) заменяется векторным равенством [11]

и, согласно (1.7),

Система равенств (2.20) опять сводится к однозначно формулируемой системе уравнений вида (2.21), решение которой относительно всех искомых неизвестных известными численными методами исчерпывает решение исходной задачи программного управления (1.6)–(1.8), (1.10), (3.2), (3.3).

Если можно ограничиться учетом только ${{N}_{1}} = N$ мод ${{\bar {Q}}_{n}}$ при $n = \overline {1,N} $ в (1.6) и если возможен выбор s = N в (3.1), то равенства (3.2) при $n = \overline {1,N} $, N = s образуют линейную систему уравнений относительно $\upsilon _{m}^{*}\left( t \right)$, $m = \overline {1,s} $, для заданных значений $\bar {u}_{n}^{*}\left( {{{\mu }_{n}},t} \right)$ в (2.13), решение которой определяется формулами Крамера непосредственно по решению задачи с автономными модальными управлениями:

Здесь $D = \det \left[ {{{{\bar {F}}}_{{mn}}}} \right]$, $m$, $n = \overline {1,s} $; D_mn – алгебраическое дополнение n-го элемента m-го столбца D, и $D \ne 0$ при линейно независимых функциях ${{F}_{m}}\left( x \right)$.

3.2. Оптимизация проектных решений. В частном варианте

c заданной функцией $F\left( t \right)$ и неизменяемым во времени пространственным управляющим воздействием $\upsilon \left( x \right)$, в роли которого рассматриваются искомые проектные решения объекта, следует принять в (1.6):

Здесь ${{\bar {\upsilon }}_{n}}$ – постоянные во времени моды управления $\upsilon \left( x \right)$, восстанавливаемого по значениям ${{\bar {\upsilon }}_{n}}$ подобно (1.8):

Величины ${{\bar {\upsilon }}_{n}}$ следует рассматривать далее в качестве автономных модальных управлений вместо ${{\bar {u}}_{n}}$ в (1.6). Критерий оптимизации принимает в данном случае вместо (3.3) следующий вид:

и требуется найти оптимальную величину $\bar {\upsilon }{\text{*}}$ и соответствующее ему, согласно (3.17), оптимальное проектное решение $\upsilon {\text{*}}\left( x \right)$, обеспечивающие перевод объекта управления (1.6), (1.7), (3.16) в требуемое конечное состояние (1.10) при минимальной величине критерия оптимальности (3.18). Здесь вектор $\bar {\upsilon }$ уже представляет собой неизменное во времени параметрическое представление искомого пространственного управления $\upsilon \left( x \right)$.

Действительно, для одинаковых конечных значений ${{\bar {u}}_{n}}\left( {{{\mu }_{n}},{{t}_{1}}} \right)$ в (2.4) и (3.16) получаем равенство

позволяющее рассматривать $\bar {\upsilon }$ в роли вектора $\psi \left( {{{t}_{1}}} \right)$ финишных значений сопряженных переменных.

Последующее представление $\bar {\upsilon }$ по правилу (2.8) приводит к описанию $\upsilon \left( x \right)$ в виде укороченной суммы M первых слагаемых в (3.17):

являющейся параметризуемым на конечномерном подмножестве векторов ${{\bar {\upsilon }}^{{\left( M \right)}}} = \left( {{{{\bar {\upsilon }}}_{n}}} \right)$, $n = \overline {1,M} $, распределенным управлением, где аналогично (2.8)

В таком случае рассматриваемая задача оптимального управления непосредственно редуцируется к задаче полубесконечной оптимизации вида (2.15), (2.16):

относительно искомой величины $\bar {\upsilon }_{*}^{{\left( M \right)}}$. Здесь размерность M вектора ${{\bar {\upsilon }}^{{\left( M \right)}}}$ определяется по правилу (2.17), где подобно (2.18) следует принять

Явная форма зависимости $Q(x,{{\bar {\upsilon }}^{{\left( M \right)}}})$ от своих аргументов в (3.21) определяется в форме ряда (1.7) при значениях ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},{{t}_{1}}} \right)$, которые находятся интегрированием уравнений объекта (1.6) в условиях (3.16), (3.20):

Решение ЗПО (3.21) по схеме альтернансного метода с последующей подстановкой результатов в (3.19) определяет искомую зависимость $\upsilon {\text{*}}\left( x \right)$. Если, подобно (2.14), техническая реализация проектного решения в форме (3.17), (3.19) оказывается затруднительной, то подобно (3.1) поиск $\upsilon \left( x \right)$ производится в классе заведомо реализуемых функций ${{F}_{m}}\left( x \right)$, суммируемых с весовыми коэффициентами h_m:

Тогда в (3.16) следует принять аналогично (3.2)

Критерий оптимальности представляется в отличной от (3.18) форме

и опять осуществляется прямая редукция задачи оптимизации проектных решений к ЗПО вида (2.15), (2.16) теперь уже при заведомо фиксируемой размерности s вектора h в (3.24): где $Q\left( {x,h} \right)$ вычисляется в форме (1.7), (3.23) с подстановкой (3.25) для всех значений ${{\bar {\upsilon }}_{n}}$, $n = \overline {1,{{N}_{1}}} $. Решение задачи (3.27) относительно оптимальной величины h* альтернансным методом определяет искомое распределенное управление в форме (3.24).

Если требуется выбрать значения h_m в (3.24) из условий достижения величины $\bar {\upsilon }_{*}^{{\left( M \right)}}$ в задаче (3.21), то такой выбор реализуется только в условиях ${{N}_{1}} = M \leqslant s$ путем определения искомых коэффициентов $h_{m}^{*}$ в подобной (3.14) форме решения относительно $h_{m}^{*}$ линейной системы уравнений, образуемой равенствами (3.25) при ${{N}_{1}} = M = s$ для заданных величин $\bar {\upsilon }_{n}^{*}$, $n = \overline {1,s} $. Следовательно, достижимые значения $\varepsilon $ в (3.27) ограничиваются в таком случае реализуемым числом s в (3.24).

4. Синтез оптимального управления. Рассмотрим далее задачу синтеза пространственно-временного оптимального управления $u{\text{*}}\left( {\bar {Q},x,t} \right)$ с обратными связями по состоянию объекта при известных алгоритмах программных управляющих воздействий.

4.1. Синтез оптимального регулятора с модальными управляющими воздействиями. Перенос граничных условий при $t = {{t}_{1}}$ в произвольный момент времени $t \in \left[ {0,{{t}_{1}}} \right)$ определяет, подобно [11], в краевой задаче (2.5) следующие зависимости конечных значений сопряженных переменных $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$ и временных мод $\bar {Q}_{n}^{*}\left( {{{\mu }_{n}},{{t}_{1}}} \right)$ от их текущих значений в оптимальном процессе $(\bar {Q}_{n}^{*}({{\mu }_{n}},t),\psi _{n}^{*}(t))$ для всех $n = \overline {1,{{N}_{1}}} $:

где ${{A}_{{nks}}}$, $k$, $s = 1,2$ – элементы 2 × 2-матрицы (2.7).

После умножения равенств (4.1), (4.2) соответственно на известные, согласно результатам расчета программного управления значения $\bar {Q}_{n}^{*}\left( {{{\mu }_{n}},{{t}_{1}}} \right) = \bar {Q}_{n}^{*}({{\mu }_{n}},\psi _{*}^{{\left( M \right)}})$ и $\psi _{n}^{*}\left( {{{t}_{1}}} \right)$ в (2.8), (2.23), левые части соотношений (4.1), (4.2) становятся одинаковыми. Последующее вычитание этих уравнений приводит к следующему результату:

однозначным образом определяющему зависимость $\psi _{n}^{*}(t,\psi _{n}^{*}\left( {{{t}_{1}}} \right),\bar {Q}_{n}^{{}}\left( {{{\mu }_{n}},0} \right),\bar {Q}_{n}^{*}\left( {{{\mu }_{n}},t} \right))$ от своих аргументов. Здесь зависимость $\psi _{n}^{*}$ от $\bar {Q}_{n}^{{}}\left( {{{\mu }_{n}},0} \right)$ в (4.3) характеризуется представлением $\bar {Q}_{n}^{*}\left( {{{\mu }_{n}},{{t}_{1}}} \right)$ в (4.4), (4.5) в виде (2.23).

Подстановка (4.3) в выражение (2.4) для автономного программного управления приводит к линейному закону синтеза оптимального пространственно-временного управляющего воздействия в форме (1.8) с нестационарными коэффициентами обратных связей по измеряемому состоянию $\bar {Q}\left( t \right) = \left( {{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right)} \right)$, $n = \overline {1,{{N}_{1}}} $:

Значения ${{T}_{{n1}}}$ и ${{T}_{{n2}}}$ представляются, согласно (4.4), (4.5), известными функциями времени с фиксируемыми на протяжении процесса управления величинами ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},0} \right)$ в (2.23), которые находятся по результатам наблюдения $\bar {Q}\left( t \right)$ в момент t = 0.

Переход в (4.6) от $\bar {Q}\left( t \right)$ к измеряемому выходу объекта ${{Q}_{u}}({{x}_{u}},t)\, = \,(Q({{x}_{{uj}}},t))$ в r  точках ${{x}_{{uj}}} \in [{{x}_{0}},{{x}_{1}}]$, $j = \overline {1,r} $, определяется, согласно (1.7), векторно-матричным уравнением наблюдения

В условиях $r < {{N}_{1}}$ неполного измерения состояния для восстановления вектора $\bar {Q}\left( t \right)$ по значениям ${{Q}_{u}}\left( {{{x}_{u}},t} \right)$ требуется построение наблюдателя полного или пониженного порядка [17].

Если по условиям требуемой точности моделирования объекта (1.6) можно ограничиться учетом только M первых составляющих $\bar {Q}\left( t \right) = \left( {{{{\bar {Q}}}_{n}}\left( {{{\mu }_{n}},t} \right)} \right)$, $n = \overline {1,M} $, с минимальным их числом $M < {{N}_{1}}$, необходимым для решения системы уравнений (2.21) относительно вектора $\psi _{*}^{{\left( M \right)}}$, то $\bar {Q}\left( t \right)$ непосредственно определяется решением уравнения (4.7) относительно $\bar {Q}\left( t \right)$ при $r = M$, ${{N}_{1}} = N = M$:

Подстановка (4.8) в (4.6) приводит к линейному алгоритму синтеза по измеряемому выходу объекта:

где $\Phi _{u}^{{ - 1}}{{Q}_{u}}\left( {{{x}_{u}},t} \right)$ – матрица-строка; $\varphi \left( {x,t} \right)$ – матрица-столбец.

4.2. Синтез оптимального регулятора с многоканальным сосредоточенным управлением. При затруднениях в решении задачи синтеза алгоритмов оптимального управления (4.6), (4.9), связанных со сложным характером зависимости u* от x и использованием в связи с этим заведомо реализуемых управляющих воздействий вида (3.1), возникает задача аналитического конструирования оптимальных регуляторов для многоканальных сосредоточенных управлений ${{\upsilon }_{m}}\left( t \right)$ при $s > 1$.

Обобщение зависимостей (4.1)–(4.5) на этот случай приводит к соответствующим векторно-матричным равенствам, базирующимся на описании оптимального процесса решениями (3.7), (3.8) краевой задачи (3.6) [11]:

Умножение слева равенств (4.10) и (4.11) соответственно на известные по решениям задачи многоканального программного управления ${{N}_{1}} \times {{N}_{1}}$-матрицы ${\text{diag}}{\kern 1pt} {\kern 1pt} [\bar {Q}_{j}^{*}({{\mu }_{j}},{{t}_{1}})]$, $\bar {Q}{\text{*}}\left( {{{t}_{1}}} \right) = (\bar {Q}_{j}^{*}\left( {{{\mu }_{j}},{{t}_{1}}} \right))$, $j = \overline {1,{{N}_{1}}} $, и ${\text{diag}}[\psi _{j}^{*}\left( {{{t}_{1}}} \right)]$, $\psi {\text{*}}\left( {{{t}_{1}}} \right) = (\psi _{j}^{*}\left( {{{t}_{1}}} \right))$, $j = \overline {1,{{N}_{1}}} $, и последующее вычитание результатов приводит вместо (4.3) к базовому векторному соотношению

где и согласно (3.12).

Подстановка (4.12) в (3.5) определяет линейный с нестационарными коэффициентами алгоритм синтеза для сосредоточенных управлений с обратными связями по $\bar {Q}\left( t \right)$

и уравнение оптимального регулятора для пространственно-временного управляющего воздействия в (3.1):

В условиях ${{N}_{1}} = N = M = r$ в (4.7) вектор $\bar {Q}{\text{*}}\left( t \right)$ в (4.18) находится непосредственно по измеряемому выходу объекта, согласно (4.8). После подстановки (4.8) в (4.18) получаем оптимальное управление с линейной обратной связью по управляемой величине:

Здесь в (4.19) аналогично (4.6) матрицы ${{T}_{1}}$, ${{T}_{2}}$ вычисляются с фиксируемыми на протяжении процесса управления значениями $\bar {Q}\left( 0 \right)$ в (4.16), которые задаются по измерениям начального состояния объекта при $t = 0$.

5. Пространственно-временное управление нестационарным процессом теплопроводности. В качестве примера, представляющего самостоятельный интерес, рассмотрим задачу аналитического конструирования оптимального регулятора для пространственно-временного управления процессом нагрева неограниченной пластины.

Пусть температурное поле Q(x, t) пластины в процессе ее нагрева описывается линейным неоднородным уравнением теплопроводности вида (1.1)–(1.3) в относительных единицах [10, 13]:

с заданными начальными и граничными условиями учитывающими тепловые потери в окружающую среду с нулевой температурой на границе пластины x = 1 по закону конвективной теплопередачи с заданным значением $\alpha $ критерия Био. Здесь u(x, t) – нестесняемое дополнительными ограничениями кусочно-непрерывное пространственно-временное управляющее воздействие по мощности внутреннего тепловыделения.

В пространстве модальных переменных ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},t} \right)$, $n = 1,2,...$, объект управления (5.1)–(5.3) описывается бесконечной системой уравнений (1.6) с автономными управлениями ${{\bar {u}}_{n}}\left( {{{\mu }_{n}},t} \right)$. Температурное поле Q(x, t) представляется его разложением в ряд вида (1.7) по собственным функциям ${{\varphi }_{n}}\left( {{{\mu }_{n}},x} \right) = \cos \left( {{{\mu }_{n}}x} \right)$ [10, 13]:

где ${{\mu }_{n}}$, $n = 1,2,...$, – бесконечно возрастающая последовательность корней трансцендентного уравнения

Задача заключается в определении алгоритма обратной связи $u{\text{*}}\left( {Q,x,t} \right)$, обеспечивающего перевод объекта (1.6), (5.4) за заданное время ${{t}_{1}}$ в требуемое конечное состояние $Q{\text{**}}(x) = Q{\text{**}}$ = = const > Q₀ с заданной точностью равномерного приближения ε, согласно (1.10), при минимальном значении квадратичного критерия качества (1.9), где примем ${{\rho }_{Q}} = 1$.

Аналитический синтез оптимального регулятора сводится на первом этапе к вычислению программного управления u*(x, t) описанным в разд. 2 способом с последующим определением $u{\text{*}}\left( {Q,x,t} \right)$ при найденном управлении путем, указанным в разд. 4.1.

Определение программного управления. Решение краевой задачи (2.5) в форме (2.6) полностью определяется значениями элементов ${{A}_{{nks}}}$, k, $s = 1,2$, 2 × 2-матрицы ${{e}^{{{{A}_{n}}t}}}$ в (2.7). Используя технологию вычисления матричной экспоненты, описанную в [11], получаем следующие выражения для ${{A}_{{nks}}}$ в (2.7):

Здесь

${{G}_{{is}}}$ – алгебраическое дополнение s-го элемента $i$-го столбца $G$ и – корни характеристического уравнения системы (2.5).

Явная форма параметрического представления модальных управляющих воздействий  ${{\bar {u}}_{n}}({{\mu }_{n}},t)$ и искомого программного управления $u{\text{*}}\left( {x,t} \right)$ на подмножестве M-мерных векторов ${{\psi }^{{\left( M \right)}}}$ в (2.8) описывается выражениями (2.13) и (2.14) соответственно, где ${{K}_{n}}\left( {t,{{t}_{1}}} \right)$, ${{K}_{{1n}}}\left( {t,{{t}_{1}}} \right)$ вычисляются по формулам (2.10) при значениях ${{A}_{{nks}}}$, определяемых, согласно (5.6)–(5.9).

Последующий переход к задаче полубесконечной оптимизации (2.15), (2.16) приводит в силу альтернансных свойств (2.19) к замкнутой системе равенств (2.20) относительно оптимальной величины $\psi _{*}^{{\left( M \right)}}$ вектора ${{\psi }^{{\left( M \right)}}}$, где $Q(x_{j}^{0},\psi _{*}^{{\left( M \right)}})$ описывается разложением в ряд (2.22), (2.23). Последний представляется в форме (5.4) с учетом соотношений (2.11) для коэффициентов ${{B}_{n}}\left( {{{t}_{1}}} \right)$, ${{B}_{{1n}}}\left( {{{t}_{1}}} \right)$, которые вычисляются опять по значениям ${{A}_{{nks}}}$ в (5.6)–(5.9).

Ограничимся далее типичным в приложениях случаем $\varepsilon = \varepsilon _{{\min }}^{{\left( 2 \right)}}$ в (2.16), (2.20), для которого, согласно (2.17), (2.19), следует принять $M = 2$, $R = 3$ в (2.14), (2.20)–(2.23).

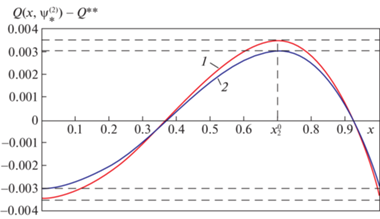
Физические закономерности поведения нестационарных температурных полей в оптимальном процессе управления нагревом пластины и альтернансные свойства $Q(x,\psi _{*}^{{\left( 2 \right)}})$, требующие выполнения строгих равенств в (2.20) в трех точках $x_{j}^{0} \in [0,\,1],\,j = 1,\,2,\,3$, при R = 3, определяют в таком случае при ${{Q}_{0}} = {\text{const}}$ в (1.2), подобно [5, 9, 10, 12], форму кривой $Q(x,\psi _{*}^{{\left( 2 \right)}}) - Q{\text{**}}$ результирующего распределения температуры по пространственной координате (см. далее рис. 1). Это позволяет перевести равенства (2.20) в систему уравнений (2.21) с заведомо идентифицируемыми точками $x_{1}^{0} = 0$; $x_{2}^{0} \in \left( {0,1} \right)$; $x_{3}^{0} = 1$ и знаками $Q(x_{j}^{0},\psi _{*}^{{\left( 2 \right)}}) - Q{\text{**}}$:

разрешаемую стандартными численными методами поиска корней нелинейных систем трансцендентных уравнений относительно неизвестных $\psi _{*}^{{\left( 2 \right)}} = (\tilde {\psi }_{1}^{*},\tilde {\psi }_{2}^{*})$, $x_{2}^{0}$ и $\varepsilon _{{\min }}^{{\left( 2 \right)}}$.

Последующая подстановка $\psi _{*}^{{\left( M \right)}} = \psi _{*}^{{\left( 2 \right)}}$ в (2.13), (2.14) окончательно определяет искомое программное управление в рассматриваемой задаче оптимизации.

Синтез оптимального регулятора. Искомый алгоритм $u{\text{*}}\left( {\bar {Q}\left( t \right),x,t} \right)$ обратной связи определяется по найденному программному управлению уравнением регулятора (4.6) в условиях $M = 2$ в (2.8), (2.23). Если в первом приближении достаточно учесть только две моды ${{\bar {Q}}_{n}}\left( {{{\mu }_{n}},t} \right)$, $n = 1,2$, в выражении (5.4) при ${{N}_{1}} = N = M = 2$, то при наличии двух измерителей состояния $Q({{x}_{u}},t)\, = \,(Q({{x}_{{uj}}},t))$, $j = 1,2$, где, в соответствии с (4.7)

и, согласно (5.4), значения ${{\bar {Q}}_{1}}$ и ${{\bar {Q}}_{2}}$ находятся по результатам измерения $Q\left( {{{x}_{{uj}}},t} \right)$ решением системы уравнений (5.11) в форме (4.8). Здесь

В итоге оптимальное управление $u{\text{*}}\left( {{{Q}_{u}},x,t} \right)$ с обратной связью по неполному измерению управляемой величины находится в форме (4.9) после подстановки (4.8), (5.13) в (4.6) при ${{N}_{1}} = M = 2$. В частности, если ${{x}_{{u1}}} = 1$, ${{x}_{{u2}}} = 0$, то в (5.12), (5.13) будем иметь

На рис. 1, 2 представлены некоторые расчетные результаты, полученные при $Q{\text{**}} = 0.5$; $\alpha = 0.5$; ${{t}_{1}} = 0.2$. На рис. 1 показаны распределения температуры по толщине пластины в конце оптимального процесса нагрева для двух различных значений ${{Q}_{0}}$ (кривая 1 – ${{Q}_{0}} = 0.15$; $\tilde {\psi }_{1}^{*} = 4.58$; $\tilde {\psi }_{2}^{*} = - 13.71$; $\varepsilon _{{\min }}^{{\left( 2 \right)}} = 0.0035$; кривая 2 – ${{Q}_{0}} = 0$; $\tilde {\psi }_{1}^{*} = 5.99$; $\tilde {\psi }_{2}^{*} = - 13.15$; $\varepsilon _{{\min }}^{{\left( 2 \right)}} = 0.003$) при выборе двух измерителей выхода объекта в точках ${{x}_{{u1}}} = 1$, ${{x}_{{u2}}} = 0$. Рисунок 2 иллюстрирует для случая ${{Q}_{0}} = 0$ поведение в процессе нагрева на пространственно-временной плоскости оптимальных управляющих воздействий, изменяющихся во времени по алгоритму (4.9) в зависимости от текущих значений измеряемых сигналов обратной связи с нестационарными коэффициентами передачи.

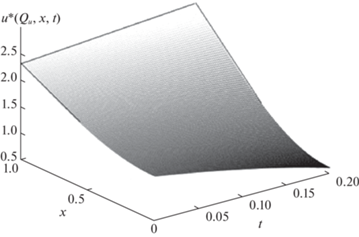
Как следует из приведенных данных, алгоритм (4.9) оптимального управления обеспечивает при различных начальных условиях заданную точность равномерного приближения к требуемому конечному состоянию объекта.

Заключение. Предлагаемые методы решения линейно-квадратичных задач пространственно-временного управления системами с распределенными параметрами параболического типа разработаны применительно к характерным для приложений оценкам целевых множеств конечных состояний объекта в равномерной метрике. Полученные уравнения регуляторов с автономными модальными управлениями, не стесняемыми дополнительными ограничениями и с учетом ограничений по условиям технической реализуемости пространственного распределения управляющих воздействий, сводятся к линейным алгоритмам обратной связи по наблюдаемым переменным с фиксируемыми предварительным расчетом нестационарными коэффициентами передачи и заданными зависимостями от пространственных аргументов.

Допустимые погрешности реализации предлагаемых алгоритмов обратной связи непосредственно по неполному измерению состояния объекта определяются требованиями к точности описания его модели укороченной системой уравнений для модальных составляющих управляемой величины.

Развиваемый подход к описанию оптимальных программных управлений распространен на задачи неизменяемого во времени пространственного управления, рассматриваемого в качестве искомого проектного решения объекта.