Известия РАН. Теория и системы управления, 2022, № 4, стр. 38-48

Введение. Первые задачи поиска кратчайшего пути с ограниченной кривизной, связанные с проектированием железных дорог, были поставлены и решены Марковым А.А. [1]. Детальное исследование кратчайших кривых с ограниченной кривизной и заданными на концах касательными было проведено Дубинсом [2]. Эти задачи приобрели особый интерес после публикации работы Айзекса [3], поскольку кратчайшие кривые стали рассматриваться как оптимальные по быстродействию траектории движения управляемого объекта – машины (автомобиля) или летательного аппарата. Простота и адекватность модели Дубинса обуславливает широкое ее использование в различных задачах планирования маршрутов автомобилей, самолетов, морского транспорта, в задачах группового управления [4], в задачах перехвата подвижной цели [5] и др.

Практический интерес представляют обобщения машины Дубинса. Модель Ридса–Шеппа [6] допускает движение автомобиля задним ходом. В модели Бердышева [7] движение происходит с изменением линейной скорости при ограниченном ускорении. В перечисленных моделях допускаются скачки угловой скорости, которые соответствуют импульсным воздействиям (ударам), при этом кривизна траектории имеет разрывы. Такое движение не соответствует обычному (штатному) поведению объектов управления в технических приложениях. Заметим, что даже железнодорожные пути, на что обращал внимание Марков А.А., имеют промежуточные участки в местах сопряжения прямолинейного пути и дуги окружности [1], которые обеспечивают непрерывное изменение кривизны пути. Управление в модели Зеликина–Борисова [8] осуществляется угловым ускорением, а не угловой скоростью. Поскольку линейная скорость постоянна, кривизна траектории меняется линейно.

Во всех перечисленных моделях линейная скорость отлична от нуля, т.е. исключаются повороты на месте. Однако для некоторых типов машин (автопогрузчики, машины на гусеничной тяге, роботы), а также летательных аппаратов (вертолеты, квадрокоптеры) повороты на месте являются допустимыми. Более того, они могут быть составной частью оптимальной траектории.

В предлагаемой модели движения угловая и линейная скорости непрерывны и меняются с ограниченными ускорениями. При этом допускаются повороты на месте (движение с нулевой линейной скоростью), а также движение задним ходом. Возможны дополнительные ограничения на величину линейной и угловой скоростей. Практический интерес представляет также модель, в которой изменение линейной скорости допускается только на прямолинейных участках движения, а повороты выполняются с постоянной линейной скоростью. В этом случае траектория представляет собой клотоиду (спираль Эйлера, спираль Корню) [9], кривизна которой изменяется линейно. Такие кривые, в частности, используются в дорожном строительстве, поскольку управление автомобилем на такой дороге достигается плавным поворотом руля.

На основе принципа максимума показано, что при оптимальном управлении линейное и угловое ускорения кусочно-постоянны [10]. Поэтому оптимальная траектория представляет собой непрерывное соединение конечного числа частей – гладких участков движения с постоянными ускорениями. Количество участков определяется терминальными условиями и ограничениями на линейную и угловую скорости движения. Для постоянных ускорений система уравнений движения интегрируется аналитически. В случае ненулевых ускорений решение выражается через интегралы Френеля [9]. Таким образом, оптимальная траектория составляется из частичных участков, аналитическое представление которых известно. Поэтому остается найти только моменты переключения с одного участка на другой. Иначе говоря, задача сводится к конечномерной минимизации по моментам переключений, причем количество таких участков небольшое. Для задачи попадания в цель, т.е. заданное терминальное положение на плоскости, – не более трех, в общем случае, видимо, – не более шести. Такая минимизация выполняется без особого труда любым подходящим численным методом. Приводятся примеры оптимальных траекторий, попадающих в заданную цель. Показано, что оптимальные траектории имеют разное количество гладких участков для так называемых “дальних” и “ближних” целей. Получена граница, разделяющая множество этих целей.

1. Постановка задачи. Пусть на промежутке времени $[0,T]$ движение системы управления описывается уравнениями

где $x$, $y$ – координаты положения на плоскости, $\gamma $ – угол направления движения (вперед), отсчитываемый от положительного направления оси абсцисс, $v$, $u$ – линейные скорость и ускорение, а $\omega $, $\varepsilon $ – угловые скорость и ускорение соответственно. Управление осуществляется выбором ускорений $u$ и $\varepsilon $, удовлетворяющих ограничениям ${\text{|}}u(t){\text{|}} \leqslant U$, ${\text{|}}\varepsilon (t){\text{|}} \leqslant \mathcal{E}$, где $U$ и $\mathcal{E}$ – заданные максимальные значения ускорений.

Начальное состояние системы задано

Конечное состояние может задаваться по-разному, в зависимости от постановки задачи. Для задачи попадания в точечную цель фиксировано только конечное положение $({{x}_{T}},{{y}_{T}})$ объекта управления:

Для задачи попадания в цель с заданным конечным направлением движения ${{\gamma }_{T}}$ к равенствам (1.3) добавляется условие $\gamma (T) = {{\gamma }_{T}}$ и, быть может, еще условие $\omega (T) = 0$; для задачи остановки объекта в заданном положении к равенствам (1.3) добавляется требование $v(T) = 0$. Возможны и другие комбинации конечных условий [8], в частности, когда задано конечное состояние $({{x}_{T}},{{y}_{T}},{{\gamma }_{T}},{{v}_{T}},{{\omega }_{T}})$ системы

Допустимыми процессами считаем траектории $x( \cdot )$, $y( \cdot )$, $\gamma ( \cdot )$, $v( \cdot )$, $\omega ( \cdot )$ – непрерывные и кусочно-гладкие на [0, T] функции и управления $u( \cdot )$, $\varepsilon ( \cdot )$ – кусочно-непрерывные на $[0,T]$ функции, удовлетворяющие уравнениям движения (1.3), терминальным условиям и ограничениям. Требуется найти наименьшее время $\min T$ и оптимальный процесс, на котором это время достигается, т.е. решить задачу быстродействия.

В постановке задачи возможны дополнительные условия, отражающие особенности прикладных задач. В первую очередь это естественное ограничение линейной скорости: $v(t) \in [0,V]$ при $t \in [0,T]$, где V – заданная величина максимальной линейной скорости. Менее естественно выглядят ограничения ${\text{|}}v(t){\text{|}} \leqslant V$ или ${{V}_{ - }} \leqslant v(t) \leqslant {{V}_{ + }}$, где ${{V}_{ - }} < 0$, ${{V}_{ + }} > 0$, допускающие отрицательные значения линейной скорости. Такие значения скорости формально следует понимать как движение назад (задний ход). В этом случае, в отличие от модели Ридса–Шеппа [6], не требуется вводить дополнительный управляющий параметр, определяющий направление движения – вперед или назад.

Во-вторых, возможно дополнительное ограничение угловой скорости ${\text{|}}\omega (t){\text{|}} \leqslant \Omega $, где $\Omega $ – заданная величина максимальной по модулю допустимой скорости. Это ограничение менее “значимо”, чем ограничение линейной скорости. Действительно, рост угловой скорости не может быть продолжительным, так как полный поворот на угол, превосходящий 2π, вряд ли возможен на оптимальной траектории [11]. Заметим, что ограничения скоростей относятся к фазовым ограничениям в задаче оптимального управления.

Представляет интерес модель гибридного движения, когда повороты выполняются с постоянной линейной скоростью, а изменение линейной скорости допустимо только при прямолинейном движении. Такое движение получается, если в (1.1) дополнительно потребовать $u(t)\omega (t)$ = 0 при $t \in [0,T]$. Однако это смешанное ограничение (на управление и фазовую переменную) трудно учитывать. Поэтому проще записать гибридную (переключаемую) систему, прямолинейное движение которой чередуется с поворотами. Прямолинейное движение описывается уравнениями

а повороты –

В моменты переключений координаты x, y, $\gamma $, ${v}$ – непрерывны, а $\omega = 0$. Заметим, что модель (1.5), (1.6) относится к гибридным системам переменной размерности [12], так как количество координат вектора состояния в (1.5) и (1.6) разное.

Поставленная задача быстродействия является естественным обобщением задачи Маркова–Дубинса и вместе с дополнительными условиями относится к задачам оптимального управления с фазовыми ограничениями. Полный анализ всех типов оптимальных траекторий затруднителен из-за большого разнообразия терминальных и дополнительных условий. Однако практическое нахождение оптимальных траекторий для конкретных ограничений достаточно просто, так как задача сводится к конечномерной минимизации с небольшим числом параметров.

2. Состав оптимальных траекторий. Для задачи быстродействия системы (1.1) применяем принцип максимума. Функция Гамильтона–Понтрягина имеет вид

где ${{\psi }_{x}}$, ${{\psi }_{y}}$, ${{\psi }_{\gamma }}$, ${{\psi }_{v}}$, ${{\psi }_{\omega }}$ – вспомогательные переменные. Записываем сопряженную систему

Условие максимума функции Гамильтона–Понтрягина по управлению приводит к равенствам

при ${{\psi }_{v}} \ne 0$ или ${{\psi }_{\omega }} \ne 0$. Если вспомогательные переменные ${{\psi }_{v}}(t) = 0$ или ${{\psi }_{\omega }}(t) = 0$ на некотором интервале, то условие максимума не позволяет однозначно найти оптимальное управление u или $\varepsilon $ соответственно. На этом интервале возникает особое управление [8, 11].

Рассмотрим сначала неособые режимы. Если ограничений на скорости $v$ и $\omega $ нет, то ускорения u и $\varepsilon $ – кусочно-постоянные, принимающие максимальные по модулю значения $u \in \{ \pm U\} $, $\varepsilon = \{ \pm \mathcal{E}\} $. Иначе говоря, оптимальные управления – релейные. Если имеется ограничение на скорость (линейную или угловую), то при достижении граничного значения соответствующее ускорениe становится нулевым. Поэтому в задачах с ограничениями на скорости ускорения u и $\varepsilon $ – кусочно-постоянные, принимающие либо нулевое, либо максимальные по модулю значения $u \in \{ 0; \pm U\} $, $\varepsilon \in \{ 0; \pm \mathcal{E}\} $. Таким образом, оптимальное неособое управление (пара функций $(u( \cdot ),\varepsilon ( \cdot ))$ – кусочно-постоянное, принимающее девять возможных значений.

Исследуем особые управления в задаче попадания в точечную цель (1.3). В этом случае из условий трансверсальности получаем

Последнее условие означает, что функция Гамильтона–Понтрягина, вычисленная на оптимальном процессе в конечный момент времени $T$, равна нулю. Отсюда следует, что

Преобразуем выражение

где ${{\psi }_{{xy}}} = \sqrt {\,\psi _{x}^{2} + \psi _{y}^{2}} $, $\sin \varphi = {{\psi }_{x}}{\text{/}}{{\psi }_{{xy}}}$, $\cos \varphi = {{\psi }_{y}}{\text{/}}{{\psi }_{{xy}}}$. При ${{\psi }_{{xy}}} = 0$ вспомогательный угол $\varphi $ не определен (можно считать его равным нулю). Используя эти обозначения, записываем уравнения для вспомогательных переменных ${{\psi }_{\gamma }}$ и ${{\psi }_{{v}}}$:

Условие (2.5) принимает вид

Поскольку на оптимальном процессе функция Гамильтона–Понтрягина постоянна, то

Если ${{\psi }_{\omega }}(t) = 0$ на некотором интервале $t \in ({{t}_{1}},{{t}_{2}})$, то ${{\psi }_{\gamma }}(t) = 0$, следовательно, ${{\dot {\psi }}_{\gamma }}(t) = 0$, значит

Согласно (2.7), ${{\psi }_{{xy}}} \ne 0$. Поэтому равенство (2.9) возможно в двух вариантах:

либо $\cos (\gamma (t) + \varphi ) \equiv {\text{0}}$, т.е. происходит прямолинейное движение $\gamma (t) \equiv {\text{const}}$, тогда $\omega (t) \equiv 0$, значит, $\varepsilon (t) \equiv 0$;

либо $v(t) \equiv 0$, т.е. происходит поворот на месте, следовательно, $u(t) = 0$, тогда, согласно (2.3), управление $u(t)$ особое, значит, ${{\psi }_{{v}}}(t) \equiv 0$. Подставляя нулевые значения ${v}$, ${{\psi }_{\omega }}$, ${{\psi }_{\gamma }}$, ${{\psi }_{{v}}}$ в (2.8), приходим к противоречию (0 = 1). Таким образом, при ${{\psi }_{\omega }}(t) \equiv 0$ особое управление $\varepsilon (t) \equiv 0$.

Пусть теперь ${{\psi }_{v}}(t) = 0$ на некотором интервале $t \in ({{t}_{1}},{{t}_{2}})$. Тогда ${{\dot {\psi }}_{{v}}}(t) = 0$, значит

Учитывая, что ${{\psi }_{{xy}}} \ne 0$, заключаем, что $\sin (\gamma (t) + \varphi ) \equiv 0$. Следовательно, это прямолинейное движение, т.е. $\omega (t) \equiv 0$ и $\varepsilon (t) \equiv 0$. Подставляя нулевые значения ${{\psi }_{{v}}}$, $\sin (\gamma + \varphi )$, $\omega $, $\varepsilon $ в (2.8), приходим к противоречию (0 = 1).

Рассмотрим особый случай – поворот на месте. Если $v(t) = 0$ на некотором интервале $t \in ({{t}_{1}},{{t}_{2}})$, то $u(t) = 0$ – особое управление. Условие (2.8) при этом будет иметь вид

Предположим, что управление $\varepsilon $ – особое. Тогда ${{\psi }_{\omega }} \equiv 0$, следовательно, ${{\psi }_{\gamma }} = - {{\dot {\psi }}_{\omega }} = 0$. Подставляя нулевые значения ${{\psi }_{\gamma }}$, ${{\psi }_{\omega }}$ в (2.11), получаем противоречие (0 = 1). Следовательно, управление $\varepsilon = \mathcal{E}{\text{sign}}\,{{\psi }_{\omega }}$ – неособое.

Таким образом, в задаче попадания в точечную цель особые управления – нулевые $u(t) = 0$, $\varepsilon (t) = 0$. Можно считать, что оптимальные управления определяются равенствами (2.3), не исключая случаев ${{\psi }_{{v}}} = 0$ или ${{\psi }_{\omega }} = 0$.

3. Траектории системы при постоянных ускорениях. Оптимальные траектории составляются из частичных траекторий – участков движения с постоянными ускорениями. Получим такие частичные траектории, интегрируя уравнения движения (1.1).

3.1. Движение с ненулевым угловым ускорением. Получим решение системы уравнений (1.1) с начальными условиями (1.2) при постоянных ускорениях $u(t) = {\text{const}}$, $\varepsilon (t) = {\text{const}} \ne {\text{0}}$. Последние три уравнения в (1.1) интегрируются элементарно:

Подставляя ${v}(t)$ и $\gamma (t)$ в первые два уравнения в (1.1), получаем

Обозначим

Тогда

Первое уравнение в (3.2) будет иметь вид

Интегрируя на промежутке [0, t], делаем замену времени t, согласно (3.4). Получаем

где

Группируя слагаемые подынтегральной функции в (3.6), находим

Первые два интеграла в (3.7) являются интегралами Френеля [9]:

а последние два – интегрируются по частям. В результате имеем

Аналогично интегрируем второе уравнение в (3.2):

Таким образом, траектория системы (1.1) при постоянных ускорениях $u(t) = {\text{const}}$, ε(t) = = ${\text{const}} \ne {\text{0}}$ определяется формулами (3.1), (3.7), (3.8). Заметим, что эти формулы годятся при движении с постоянной линейной скоростью, т.е. при $u(t) \equiv 0$, а также в случае поворота на месте, когда $u(t) \equiv 0$ и ${{v}_{0}} = 0$.

3.2. Движение с нулевым угловым ускорением. Получим решение системы уравнений (1.1) с начальными условиями (1.2) при постоянных ускорениях $u(t) = {\text{const}}$, $\varepsilon (t) = {\text{0}}$. Нужно разобрать два случая, когда начальная угловая скорость равна нулю (прямолинейное движение) или отлична от нуля (поворот с постоянной угловой скоростью).

Рассмотрим сначала случай ${{\omega }_{0}} \ne 0$. Последние три уравнения в (1.1) интегрируются элементарно:

Подставляя ${v}(t)$ и $\gamma (t)$ в первые два уравнения в (1.1), получаем

Интегрируя по частям эти уравнения, находим

Пусть теперь ${{\omega }_{0}} = 0$. Тогда последние три уравнения в (1.1) имеют решения

первые два уравнения в (1.1) принимают вид

Отсюда

Таким образом, при $u(t) = {\text{const}}$, $\varepsilon (t) = {\text{0}}$ траектория определяется формулами (3.10)–(3.12), если ${{\omega }_{0}} \ne 0$, и формулами (3.13), (3.14), если ${{\omega }_{0}} = 0$. Заметим, что случай $u(t) = 0$ не исключается. Например, при прямолинейном движении с постоянной скоростью ${{v}_{0}}$ по формулам (3.13), (3.14) для ${{\omega }_{0}} = 0$ находим

При повороте на месте с постоянной угловой скоростью ${{\omega }_{0}} \ne 0$ по формулам (3.10)–(3.12) при ${{v}_{0}} = 0$ и $u(t) = 0$ получаем

Отметим, что кривизна $\kappa (t)$ плоской траектории $(x(t),y(t))$ системы (1.1) имеет вид

т.е. является дробно-линейной функцией. Поэтому траектория представляет собой: либо дугу спирали (S), когда кривизна изменяется, либо отрезок ($L$), если кривизна нулевая, либо точку (P) в случае бесконечной кривизны, когда машина разворачивается на месте и $\omega (t) \ne 0$, $v(t) = 0$. В частности, возможно движение по окружности, когда кривизна постоянна и отлична от нуля, например при ${{\omega }_{0}} = 0$ и ${{v}_{0}} = 0$ или при $\varepsilon = 0$, $u = 0$, ${{\omega }_{0}} \ne 0$ и ${{v}_{0}} \ne 0$. Если $v(t) = {\text{const}}$, $\varepsilon \ne 0$, то кривизна линейная, а траектория является клотоидой [9].

Таким образом, оптимальные траектории составляются из типовых участков вида $S$, $L$, $P$, которые соединяются гладким образом. Комбинации участков зависят от постановки задачи, в первую очередь от конечных условий. Например, для задачи попадания в точечную цель (1.3) оптимальной может быть траектория вида $SSL$. Эта траектория составлена из трех участков: движение по спирали с $\varepsilon = \mathcal{E}$ (“закручивание” траектории), движение спирали с $\varepsilon = - \mathcal{E}$ (“раскручивание”) и движение по прямой. Для перевода системы в заданное конечное состояние (1.4) оптимальной может быть траектория вида $SSLSS$, у которой пары дуг спиралей (“закручивание” и “раскручивание”) соединены отрезком. Напомним, что оптимальные траектории машины Дубинса [2, 11], приводящие в заданное конечное состояние, представляют собой либо гладкое соединение трех дуг окружностей (тип траектории – $CCC$), либо гладкое соединение двух дуг отрезком (тип траектории – $CLC$).

Предлагаемый подход не учитывает особые режимы с неограниченным количеством переключений управлений [8, 13]. Такие теоретически возможные процессы, точнее, минимизирующие последовательности, практически нереализуемы. Их можно исключить, например, добавляя к функционалу штрафные слагаемые – временные затраты на каждое переключение управления, как это делается в задачах оптимизации переключаемых и гибридных систем.

4. Оптимальные траектории, попадающие в точечную цель. Исследуем задачу наискорейшего достижения точечной цели. Предполагаем, что начальное состояние – нулевое:

а конечное – задано условиями

В силу симметрии рассматриваем только случай ${{y}_{T}} \geqslant 0$. Пусть линейная скорость ограничена $0 \leqslant v(t) \leqslant V$, а угловая – нет ($\Omega = + \,\infty $). Согласно неравенству $v(t) \geqslant 0$, движение назад (задний ход) исключается.

Определим состав попадающих траекторий, соединяющих терминальные состояния (4.1) и (4.2). Если цель (4.2) общего положения, то для скорейшего попадания машина (1.1) должна, выполняя поворот, продвигаться к цели. В частных случаях поворот может отсутствовать. Величина поворота, разумеется, не должна превышать 2π. Будем называть цель дальней, если последний участок попадающей траектории прямолинейный. Такие траектории заведомо существуют. Действительно, если конечное положение $({{x}_{T}},{{y}_{T}})$ находится так далеко от начала координат, что машина успевает выполнить поворот, при котором угловая скорость сначала растет (“закручивание” траектории), а затем уменьшается (“раскручивание” траектории) до нулевого значения, а скорость движения после поворота будет направлена на цель. Если же последний участок оптимальной траектории криволинейный, цель будем называть ближней. Оптимальная траектория для ближних целей состоит из “закручивания” и, быть может, “раскручивания”. Кроме того, поскольку начальная скорость нулевая, попадающая траектория может начинаться с поворота на месте.

Таким образом, попадающие траектории имеют вид $PSSL$ или $PSS$ в зависимости от расположения цели. При этом не исключаются случаи, когда отсутствует тот или иной участок. Например, если цель находится прямо перед машиной (${{x}_{T}} > 0$, ${{y}_{T}} = 0$), то поворот не нужен, а оптимальная траектория – отрезок (траектория вида $L$).

Выясним параметры, задающие попадающие траектории. Траектория вида $PSSL$ состоит из четырех участков: поворот на месте ($\varepsilon = \mathcal{E}$, $u = 0$); движение по спирали – “закручивание” ($\varepsilon = \mathcal{E}$); “раскручивание” ($\varepsilon = \mathcal{E}$), прямолинейное движение ($\varepsilon = \mathcal{E}$, $\omega = 0$). Обозначим через ${{t}_{1}}$, ${{t}_{2}}$, ${{t}_{3}}$ последовательные моменты переключений: при $t \in [0,{{t}_{1}})$ поворот на месте, при $t \in [{{t}_{1}},{{t}_{2}})$ – “закручивание”, при $t \in [{{t}_{2}},{{t}_{3}})$ – “раскручивание”, при $t \in [{{t}_{3}},T]$ – прямолинейное движение. Поскольку после “раскручивания” в момент ${{t}_{3}}$ угловая скорость принимает опять нулевое значение, заключаем, что ${{t}_{3}} = 2{{t}_{2}} - {{t}_{1}}$. Кроме того, в момент ${{t}_{3}}$ скорость движения машины направлена на цель, т.е. векторы $(x({{t}_{3}}) - {{x}_{T}},y({{t}_{3}}) - {{y}_{T}}))$ и $(\dot {x}({{t}_{3}}),\dot {y}({{t}_{3}}))$ одинаково направлены:

Время $\tau = T - {{t}_{3}}$ прямолинейного движения вычисляется по следующим формулам. Обозначим через $S = \,\sqrt {\;{{{(x({{t}_{3}}) - {{x}_{T}})}}^{2}} + {{{(x({{t}_{3}}) - {{x}_{T}})}}^{2}}} $ расстояние до цели, а через ${{v}_{3}} = v({{t}_{3}})$ – линейную скорость. Тогда:

если максимально допустимая скорость уже достигнута (${{v}_{3}} = V$), полагаем $\tau = S{\text{/}}V$;

если максимально допустимая скорость еще не достигнута ($0 \leqslant {{v}_{3}} < V$), то

Первое равенство в (4.4) – для случая, когда максимальная скорость достигается на прямолинейном участке, в второе равенство – в противном случае. Отметим, что первую формулу в (4.4) можно применять при неограниченной линейной скорости, полагая $V = + \infty $.

Таким образом, траектория вида $PSSL$ определяется двумя параметрами ${{t}_{1}}$ и ${{t}_{2}}$. Минимизация времени T достижения цели выполняется с условием (4.3). Момент ${{t}_{V}}$ достижения максимальной скорости, при котором ускорение $u(t)$ принимает нулевое значение, можно вычислить заранее  ${{t}_{V}} = V{\text{/}}U - {{t}_{1}}$. После этого момента скорость не снижается, поскольку для наискорейшего достижения цели не может быть участков с торможением. В формулах (3.1), (3.8)–(3.14) при этом следует положить u = 0.

Рассмотрим теперь траекторию вида $PSS$, которая состоит из трех участков – поворота на месте и движения по спиралям с “закручиванием” и “раскручиванием” траектории. Пусть, как и ранее, ${{t}_{1}}$, ${{t}_{2}}$ – последовательные моменты переключений: при $t \in [0,{{t}_{1}})$ поворот на месте, при $t \in [{{t}_{1}},{{t}_{2}})$ – “закручивание” траектории, при $t \in [{{t}_{2}},T]$ – “раскручивание”. Как видим, эта траектория задается двумя параметрами. Минимизация времени T  достижения цели по этим параметрам выполняется с условием (4.2).

Итак, задача наискорейшего достижения точечной цели сводится к двухпараметрической условной минимизации, которая выполняется численно. Линию разделения дальних и ближних целей можно построить приближенно, что затрудняет их классификацию. В таком случае приходится решать обе задачи, считая цель дальней или ближней. После нахождения наилучшей попадающей траектории нужно проверить необходимые условия оптимальности, найти решение сопряженной системы (2.2) для вспомогательных переменных с учетом условий (2.3).

4. Примеры. Рассмотрим решение задачи попадания из нулевого начального состояния (4.1) в точечную цель (4.2). Расчеты проводились при следующих значениях параметров: $U = 1$, $\mathcal{E} = 1$, $V = 1$, $\Omega = + \infty $ в двух случаях, когда линейная скорость ограничена V = 1 или не ограничена $V = + \infty $.

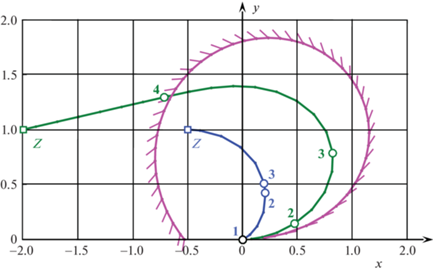
Результаты расчетов для ограниченной скорости представлены на рис. 1, где изображены граница, разделяющая дальние и ближние цели (фиолетовая линия с маленькими отрезками (“иголочками”), показывающими направление последующего прямолинейного движения), а также две оптимальные траектории (зеленая и синяя линии), попадающие в дальнюю и ближнюю цели соответственно. Цели отмечены квадратами и обозначены буквами $Z$, точки переключений управления – окружностями и цифрами. Дальняя траектория вида $PSSL$ составлена из пяти участков: вращение – поворот на месте до момента ${{t}_{1}} = 0.066$ при $u = 0$ и ε = 1, “закручивание” с разгоном – движение по спирали до момента ${{t}_{2}} = 1.066$ (достижения максимально допустимой скорости V = 1) при $u = 1$ и ε = 1, “закручивание” без разгона до момента ${{t}_{3}} = 1.835$ при $u = 0$ и $\varepsilon = 1$, “раскручивание” без разгона – движение по спирали до момента ${{t}_{4}} = 3.670$ при $u = 0$ и $\varepsilon = - 1$, равномерное прямолинейное движение до момента $T = 4.991$ (попадания в цель) при $u = 0$, ε = 0. Ближняя траектория вида $PSS$ составлена из четырех участков: вращение – поворот на месте до момента ${{t}_{1}} = 0.808$ при $u = 0$ и ε = 1, “закручивание” с разгоном – движение по спирали до момента ${{t}_{2}} = 1.808$ (достижения максимально допустимой скорости V = 1) при $u = 1$ и ε = 1, “закручивание” без разгона до момента ${{t}_{3}} = 1.898$ при $u = 0$ и ε = 1, “раскручивание” без разгона – движение по спирали до момента $T = 2.810$ (попадания в цель) при $u = 0$ и $\varepsilon = - 1$. Поворот на месте на рис. 1 не изображается, так как нет поступательного движения и объект находится в начале координат. Наличие такого участка траектории отмечено цифрой 1 около начала координат.

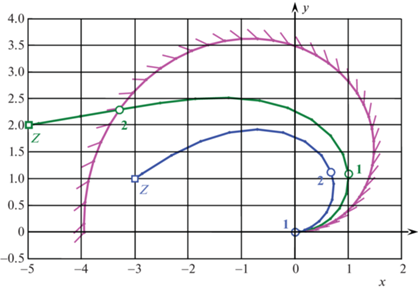
Результаты расчетов для неограниченной линейной скорости представлены на рис. 2, где изображены граница, разделяющая дальние и ближние цели (фиолетовая линия с маленькими отрезками (“иголочками”), показывающими направление последующего прямолинейного движения); а также две оптимальные траектории (зеленая и синяя линии), попадающие в дальнюю и ближнюю цели соответственно. Цели отмечены квадратами и обозначены буквами Z, точки переключений управления – окружностями и цифрами. Дальняя траектория вида $PSSL$ составлена из трех участков: “закручивание” с разгоном – движение по спирали до момента ${{t}_{1}} = 1.8196$ при u = 1 и ε = 1, “раскручивание” с разгоном – движение по спирали до момента ${{t}_{2}} = 3.6392$ при u = 1 и $\varepsilon = - 1$, прямолинейное движение с ускорением до момента $T = 4.087$ (попадания в цель) при u = 1 и ε = 0. Отметим, что у дальней траектории отсутствует участок вращения (поворота на месте). Ближняя траектория вида $PSS$ составлена из трех участков: вращение – поворот на месте до момента ${{t}_{1}} = 0.217$ при u = 0 и $\varepsilon = 1$, “закручивание” с разгоном –  движение по спирали до момента ${{t}_{2}} = 1.950$ при u  = 1 и $\varepsilon = 1$, “раскручивание” с разгоном –  движение по спирали до момента $T = 3.598$ (попадания в цель) при u = 1 и $\varepsilon = - 1$.

Покажем, что последняя траектория действительно оптимальная. Для этого нужно для найденного процесса управления получить соответствующие вспомогательные переменные и проверить выполнение соотношений (2.3) принципа максимума. Вспомогательные переменные удовлетворяют сопряженной системе

с нулевыми конечными условиями ${{\psi }_{\gamma }}(T) = 0$, ${{\psi }_{v}}(T) = 0$, ${{\psi }_{\omega }}(T) = 0$, а постоянные ${{\psi }_{{xy}}}$ и φ удовлетворяют условию (2.7), т.е.

Оптимальное управление $u(t) = {\text{sign}}\,{{\psi }_{{v}}}(t)$ имеет переключение в момент ${{t}_{1}} = 0.217$, причем $u(t) = 0$ и ${{\psi }_{{v}}}(t) = 0$ при $t < {{t}_{1}}$ (это особый участок); $u(t) = 1$ и ${{\psi }_{{v}}}(t) > 0$ при $t > {{t}_{1}}$. Оптимальное управление $\varepsilon (t) = {\text{sign}}\,{{\psi }_{\omega }}(t)$ имеет переключение в момент ${{t}_{2}} = 1.950$, т.е. $\varepsilon (t) = 1$ и ${{\psi }_{\omega }}(t) > 0$ при $t < {{t}_{2}}$, $\varepsilon (t) = - 1$ и ${{\psi }_{\omega }}(t) < 0$ при $t > {{t}_{2}}$. Поэтому нужно убедиться, что в моменты ${{t}_{1}}$ и ${{t}_{2}}$ вспомогательные переменные ${{\psi }_{{v}}}$ и ${{\psi }_{\omega }}$ равны нулю соответственно. Решения уравнений (5.1) зависят от параметра $\varphi $. Поэтому следует найти такое значение параметра $\varphi $, при котором ${{\psi }_{{v}}}({{t}_{1}}) = 0$ и ${{\psi }_{\omega }}({{t}_{2}}) = 0$. Эта задача решается численно, причем линейная скорость и угол направления для оптимальной траектории находятся аналитически:

В результате решения было получено значение $\varphi = 1.295$. Графики вспомогательных переменных представлены на рис. 3: ${{\psi }_{{v}}}(t)$ – зеленая линия, ${{\psi }_{\omega }}$ – фиолетовая линия. Окружностями обозначены моменты переключений управления. Погрешность определения моментов переключений составляет 0.022.

Таким образом, полученный процесс управления удовлетворяет принципу максимума. Погрешность можно считать незначительной, так как оптимизация моментов переключений выполнялась с точностью 0.001, а решения сопряженной системы, как известно, весьма чувствительны к погрешностям.

Заключение. Предложена модель плоского движения системы управления, обобщающая известную модель Маркова–Дубинса. Эта модель имеет более широкий набор оптимальных траекторий, в частности, траектории с участками торможения, повороты на месте, движение задним ходом. Несмотря на разнообразие поведения, решения уравнений движения найдены аналитически, что существенно упрощает построение оптимальных траекторий. Подробно исследована частная задача перехода из нулевого начального состояния в заданную точку координатной плоскости. Задачи с другими терминальными условиями хотя и поставлены, но фактически не исследованы. Предлагаемая модель может быть использована в многочисленных приложениях, в которых применяется модель Маркова–Дубинса.