Известия РАН. Теория и системы управления, 2022, № 4, стр. 3-21

О СВОЙСТВАХ ПРЕДЕЛЬНЫХ МНОЖЕСТВ УПРАВЛЯЕМОСТИ ДЛЯ КЛАССА НЕУСТОЙЧИВЫХ ЛИНЕЙНЫХ СИСТЕМ С ДИСКРЕТНЫМ ВРЕМЕНЕМ И l₁-ОГРАНИЧЕНИЯМИ

Д. Н. Ибрагимов^a, *, А. В. Осокин^a, А. Н. Сиротин^a, **, К. И. Сыпало^a

^a МАИ (национальный исследовательский ун-т), ФГУП ЦАГИ им. Н.Е. Жуковского
Москва, Россия

^* E-mail: rikk.dan@gmail.com
^** E-mail: asirotin2@yandex.ru

Поступила в редакцию 10.02.2022
После доработки 03.03.2022
Принята к публикации 28.03.2022

EDN: IADLEJ
DOI: 10.31857/S0002338822040102

Аннотация

Обсуждаются вопросы построения множеств достижимости и управляемости для линейных систем с дискретным временем и суммарным ограничением на скалярное управление в смысле l₁-нормы. Для классов не полностью управляемых и не полностью достижимых линейных систем предельные множества управляемости и достижимости соответственно построены явным образом. Приведены примеры.

Введение. При решении задач управления динамическими системами нередко приходится учитывать различные ограничения, связанные с техническими аспектами изучаемой системы. Такого рода ограничения приводят к тому, что система из заданного начального состояния может быть переведена в ограниченное множество терминальных состояний даже при бесконечном временном горизонте. Данный факт делает актуальным исследование не только вопросов достижимости и управляемости различных динамических систем, но и разработку методов построения и оценивания предельных множеств достижимости и управляемости для произвольной системы управления. Кроме того, множества управляемости и достижимости могут быть использованы в ряде задач оптимального управления для формирования позиционного управления [1, 2] для систем с дискретным временем.

В случае линейных систем с дискретным временем и скалярным управлением, не ограниченным в смысле l_p-нормы, известно, что множества достижимости и управляемости за конечное число шагов представляют собой выпуклые многогранники [1]. Однако данное свойство при переходе к бесконечному времени может не сохраняться. Более того, в [3–5] продемонстрировано, что в общем случае предельное множество управляемости и достижимости представляет собой цилиндрическое множество с выпуклым сечением. Принципиальная управляемость и достижимость такой линейной системы управления определяется структурой ее матрицы, а именно расположением ее собственных значений относительно круга единичного радиуса с центром в нуле на комплексной плоскости.

Тем не менее данные результаты относятся к линейным системам без суммарного ограничения на последовательность управляющих воздействий [1, 3, 4]. С другой стороны, зачастую ограничения на функцию управления являются гладкими [2, 6, 7], что связано с необходимыми условиями применимости классических оптимизационных методов [8, 9], хотя с точки зрения технической реализации рассматриваемой математической модели более корректно было бы использовать линейные или кусочно-линейные ограничения. Например, при описании задачи коррекции орбиты спутника [10, 11] следует учитывать два типа ограничений на управление: ограничение на силу каждого корректирующего импульса, обусловленное мощностью двигателя, и ограничение, связанное с количеством топлива. Последнее в математической модели движения спутника может быть представлено в виде ограничения на сумму модулей всех управляющих воздействий.

В статье изучаются вопросы построения предельных множеств достижимости и управляемости систем с интегральным ограничением на управление в смысле l₁-нормы. Принципиальной особенностью данной работы является то, что данные множества удается построить явным образом. В разд. 2 в виде леммы сформулированы основные свойства множеств достижимости линейных систем с дискретным временем и скалярным ограниченным управлением, в частности доказано, что каждое такое множество представляет собой выпуклый и симметричный относительно начала координат многогранник. Также в разд. 2 доказано, что аналогичные свойства справедливы и для предельных множеств управляемости не полностью достижимых систем. В разд. 3 приведены важные следствия из данных утверждений, в частности доказаны аналогичные свойства для множеств управляемости не полностью управляемых систем и представлены оценки множества вершин предельных множеств управляемости и достижимости. В разд. 4 полученные теоретические результаты продемонстрированы на примерах построения множеств управляемости и достижимости для различных систем управления.

1. Формулировка задачи. Рассматривается автономная линейная система с дискретным временем

(1.1)

$x\left( {k + 1} \right) = Ax\left( k \right) + bu\left( k \right),\quad k \in {{\mathbb{Z}}_{ + }} = \left\{ {0,1, \ldots } \right\}$

и скалярным ограниченным по импульсу управлением

(1.2)

$\sum\limits_{k = 0}^\infty {\left| {u\left( k \right)} \right| \leqslant t} ,\quad t \in \left( {0,\infty } \right).$

Это ограничение можно рассматривать как ограничение на l₁-норму последовательностей управлений ${{\left\{ {u\left( k \right)} \right\}}_{{k \in {{\mathbb{Z}}_{ + }}}}}$. Здесь $x\left( k \right) \in {{\mathbb{R}}^{n}}$ – вектор состояния; $A \in {{\mathbb{R}}^{{n \times n}}}$, $b \in {{\mathbb{R}}^{n}}$ – соответствующие матрицы системы; $u\left( k \right) \in \mathbb{R}$ – скалярное управление в момент времени $k \in {{\mathbb{Z}}_{ + }}$; $t \in \left( {0,\infty } \right)$ – произвольный параметр, характеризующий суммарные энергозатраты для управления.

Считается, что система (1.1) без ограничений на управления является управляемой, т.е. выполнено ранговое условие Калмана

(1.3)

$\operatorname{rank} (\left. b \right|\left. {Ab} \right| \cdots {\text{|}}{{A}^{{n - 1}}}b) = n.$

Пусть ${{\mathcal{Y}}_{t}}\left( k \right) \subset {{\mathbb{R}}^{n}}$ – множество достижимости системы (1.1), (1.2) за k шагов, т.е. это множество всех возможных терминальных состояний системы, в которые она может попасть из 0 за k шагов посредством использования допустимых в смысле ограничений (1.2) управлений:

${{\mathcal{Y}}_{t}}\left( k \right) = \left\{ {y \in {{\mathbb{R}}^{n}}:y = \sum\limits_{i = 0}^{k - 1} {{{A}^{i}}bu\left( {k - 1 - i} \right),\sum\limits_{i = 0}^{k - 1} {\left| {u\left( i \right)} \right| \leqslant t} } } \right\},\quad k \in \mathbb{N}: = {{\mathbb{Z}}_{ + }}{{\backslash }}\left\{ 0 \right\}.$

Через ${{\mathcal{Y}}_{t}}$ обозначается предельное множество достижимости:

${{\mathcal{Y}}_{t}} = \bigcup\limits_{k \in \mathbb{N}} {{{\mathcal{Y}}_{t}}\left( k \right)} .$

Аналогично вводится множество ${{\mathcal{X}}_{t}}\left( k \right)$ 0-управляемости за k шагов дискретной системы, определяемой соотношениями (1.1) и (1.2). Это множество всех возможных начальных состояний x(0) системы, из которых она может попасть в 0 за k шагов посредством использования допустимых в смысле ограничений (1.2) управлений:

${{\mathcal{X}}_{t}}\left( k \right) = \left\{ {x \in {{\mathbb{R}}^{n}}:0 = \sum\limits_{i = 0}^{k - 1} {{{A}^{i}}bu\left( {k - 1 - i} \right)} + {{A}^{k}}x,\sum\limits_{i = 0}^{k - 1} {\left| {u\left( i \right)} \right| \leqslant t} } \right\},\quad k \in \mathbb{N}: = {{\mathbb{Z}}_{ + }}{{\backslash }}\left\{ 0 \right\}.$

Здесь ${{\mathcal{X}}_{t}}$ – предельное множество $0$-управляемости:

${{\mathcal{X}}_{t}} = \bigcup\limits_{k \in \mathbb{N}} {{{\mathcal{X}}_{t}}\left( k \right)} .$

Обозначим через $\sigma \left( A \right) = \left\{ {{{\alpha }_{1}}, \ldots ,{{\alpha }_{n}}} \right\} \subset \mathbb{C}$ спектр матрицы A, т.е. множество всех собственных значений A с учетом кратности. Целью статьи является исчерпывающее описание множеств ${{\mathcal{X}}_{t}}$ и ${{\mathcal{Y}}_{t}}$ для одного класса систем, удовлетворяющих соотношениям (1.1)–(1.3). Более точно будут изучаться предельные множества достижимости ${{\mathcal{Y}}_{t}}$ для асимптотически устойчивых систем, т.е. тех систем, для которых справедливо условие

(1.4)

$\rho \left( A \right): = \mathop {\max }\limits_{{{\alpha }_{i}} \in \sigma \left( A \right)} \left| {{{\alpha }_{i}}} \right| < 1.$

Аналогично изучаются множества 0-управляемости ${{\mathcal{X}}_{t}}$ для неустойчивых систем с условием

(1.5)

$\mathop {\min }\limits_{{{\alpha }_{i}} \in \sigma \left( A \right)} \left| {{{\alpha }_{i}}} \right| > 1.$

Оказывается, что для выделенного класса систем (1.1)–(1.3) множества управляемости могут быть описаны явным образом, что приводит к возможности конструктивного построения допустимых управлений в задачах оптимального управления.

2. Множества достижимости. Охарактеризуем основные свойства множеств достижимости ${{\mathcal{Y}}_{t}}\left( k \right)$ системы (1.1)–(1.2). В данном случае не требуется использование условия управляемости Калмана (1.3). Здесь и везде далее через $\operatorname{conv} \left( \mathcal{Y} \right)$ обозначена выпуклая оболочка множества $\mathcal{Y} \subset {{\mathbb{R}}^{n}}$ – наименьшее по включению выпуклое множество, содержащее $\mathcal{Y}$ в качестве подмножества [9, 12].

Лемма. Для каждого натурального k справедливы утверждения:

(i) ${{\mathcal{Y}}_{t}}\left( k \right)$ – полиэдр;

(ii) множество ${{\mathcal{Y}}_{t}}\left( k \right)$ замкнуто, ограничено и симметрично относительно 0;

(iii) ${{\mathcal{Y}}_{t}}\left( k \right)$ – выпуклый многогранник, т.е.

${{\mathcal{Y}}_{t}}(k) = t\operatorname{conv} ( \pm b, \pm Ab, \ldots , \pm {{A}^{{k - 1}}}b).$

Здесь

$\operatorname{conv} ( \pm b, \pm Ab, \ldots , \pm {{A}^{{k - 1}}}b): = \operatorname{conv} (b,Ab, \ldots ,{{A}^{{k - 1}}}b, - b, - Ab, \ldots , - {{A}^{{k - 1}}}b);$

(iv) $0 \in \operatorname{int} {{\mathcal{Y}}_{t}}\left( k \right)$ при $k \geqslant n$;

(v) ${{\mathcal{Y}}_{t}}\left( k \right) \subset {{\mathcal{Y}}_{t}}\left( m \right)$ при $m \geqslant k$;

(vi) ${{\mathcal{Y}}_{t}}\left( k \right) = t{{\mathcal{Y}}_{1}}\left( k \right)$;

(vii) ${{\mathcal{Y}}_{t}}\left( k \right) \cap {{\mathcal{Y}}_{t}}\left( m \right) \ne \emptyset $ при $k,m \in \mathbb{N}$.

Доказательство леммы приведено в Приложении.

В силу определения предельное множество достижимости ${{\mathcal{Y}}_{t}}$ есть счетное объединение множеств достижимости ${{\mathcal{Y}}_{t}}\left( k \right)$ за k шагов, и поэтому некоторые перечисленные выше свойства могут перестать быть верными. Здесь будут рассмотрены особенности предельного множества достижимости ${{\mathcal{Y}}_{t}}$ для асимптотически устойчивой системы, определяемой соотношениями (1.1), (1.2) и (1.4), т.е. когда все собственные значения матрицы A лежат внутри единичного круга на комплексной плоскости. Как известно [3, 4], данная ситуация соответствует системе, которая не является полностью достижимой, т.е. вектор состояния которой может попасть за конечное число шагов из 0 не во все точки пространства ${{\mathbb{R}}^{n}}$.

Теорема. Пусть для системы (1.1)–(1.2) выполняются условия (1.3) и (1.4). Тогда существует $K \in \mathbb{N}$, такое, что

(2.1)

${{\mathcal{Y}}_{t}} = {{\mathcal{Y}}_{t}}\left( K \right).$

Доказательство теоремы приведено в Приложении.

3. Следствия теоремы. Нижним пределом последовательности множеств ${{\left\{ {{{\mathcal{Y}}_{t}}\left( k \right)} \right\}}_{{k \in \mathbb{N}}}}$ [13, Гл. 1, § 1, п. 1] называется множество $\lim \inf {{\mathcal{Y}}_{t}}\left( k \right)$, состоящее из точек, принадлежащих всем множествам ${{\left\{ {{{\mathcal{Y}}_{t}}\left( k \right)} \right\}}_{{k \in \mathbb{N}}}}$, кроме, быть может, конечного их числа.

Следствие 1. Пусть для системы (1.1)–(1.2) выполняются условия (1.3), (1.4). Тогда справедливо равенство

${{\mathcal{Y}}_{t}} = \mathop {\lim }\limits_{k \to \infty } {{\mathcal{Y}}_{t}}\left( k \right).$

Доказательство. Формализуя определение нижнего предела последовательности множеств, получаем

$\lim \inf {{\mathcal{Y}}_{t}}\left( k \right) = \left\{ {x:\exists k\;\;\forall m \geqslant k\;\;x \in {{\mathcal{Y}}_{t}}\left( m \right)} \right\} = \bigcup\limits_{k = 1}^\infty {\bigcap\limits_{m = k}^\infty {{{\mathcal{Y}}_{t}}\left( m \right)} } .$

В силу утверждения (v) леммы находим

$\bigcap\limits_{m = k}^\infty {{{\mathcal{Y}}_{t}}\left( m \right)} = {{\mathcal{Y}}_{t}}\left( k \right),$

что приводит к равенству

$\lim \inf {{\mathcal{Y}}_{t}}\left( k \right) = \bigcup\limits_{k = 1}^\infty {{{\mathcal{Y}}_{t}}\left( k \right)} .$

Аналогично верхним пределом последовательности множеств ${{\left\{ {{{\mathcal{Y}}_{t}}\left( k \right)} \right\}}_{{k \in \mathbb{N}}}}$ [13, Гл. 1] называется множество $\lim \sup {{\mathcal{Y}}_{t}}\left( k \right)$, состоящее из точек, принадлежащих бесконечному числу различных множеств ${{\left\{ {{{\mathcal{Y}}_{t}}\left( k \right)} \right\}}_{{k \in \mathbb{N}}}}$. Формализуя определение, получаем

$\lim \sup {{\mathcal{Y}}_{t}}\left( k \right) = \left\{ {x:\forall k\;\;\exists m \geqslant k\;\;x \in {{\mathcal{Y}}_{t}}\left( m \right)} \right\} = \bigcap\limits_{k = 1}^\infty {\bigcup\limits_{m = k}^\infty {{{\mathcal{Y}}_{t}}\left( m \right)} } .$

В силу утверждения (v) леммы приходим к равенствам

$\bigcup\limits_{m = k}^\infty {{{\mathcal{Y}}_{t}}\left( m \right)} = \bigcup\limits_{m = 1}^\infty {{{\mathcal{Y}}_{t}}\left( m \right)} ,$

$\lim \sup {{\mathcal{Y}}_{t}}\left( k \right) = \bigcup\limits_{k = 1}^\infty {{{\mathcal{Y}}_{t}}\left( k \right)} .$

Окончательно

$\bigcup\limits_{k = 1}^\infty {{{\mathcal{Y}}_{t}}\left( k \right)} = \lim \inf {{\mathcal{Y}}_{t}}\left( k \right) = \lim \sup {{\mathcal{Y}}_{t}}\left( k \right): = \mathop {\lim }\limits_{k \to \infty } {{\mathcal{Y}}_{t}}\left( k \right) = {{\mathcal{Y}}_{t}}.$

Следствие 2. Предельное множество достижимости ${{\mathcal{Y}}_{t}}$ обладает всеми свойствами (i), (ii), (iv), (vi) леммы множеств достижимости ${{\mathcal{Y}}_{t}}\left( k \right)$ для конечного числа шагов $k \geqslant n$.

Данное утверждение вполне объясняется использованием предельного перехода в следствии 1.

Из теоремы вытекает, что число K определяется не единственным образом. Тем не менее, выберем соответствующее минимальное число из (2.1):

(3.1)

${{K}_{{\min }}} = \min \left\{ {K:{{\mathcal{Y}}_{t}} = {{\mathcal{Y}}_{t}}\left( K \right)} \right\}.$

Число K_min из (3.1) можно эффективно оценить сверху. Действительно, поскольку в конечномерном линейном пространстве ${{\mathbb{R}}^{n}}$ нормы эквивалентны [14, Гл. 3, § 4], то имеется хотя бы одно число $\gamma \in \left( {0,\infty } \right)$, такое, что для произвольного $y = {{\left( {{{y}_{1}}, \ldots ,{{y}_{n}}} \right)}^{{\text{T}}}} \in {{\mathbb{R}}^{n}}$

(3.2)

${{\left\| y \right\|}_{{{{\mathcal{Y}}_{t}}\left( n \right)}}} \leqslant \gamma {{\left\| y \right\|}_{1}},$

где

${{\left\| y \right\|}_{1}} = \sum\limits_{i = 1}^n {\left| {{{y}_{i}}} \right|} .$

Введем в рассмотрение функционал Минковского выпуклого множества $\mathcal{A} \subset {{\mathbb{R}}^{n}}$, у которого $0 \in \operatorname{int} \mathcal{A}$, определяемый [9, 12, 14] по формуле

(3.3)

$\mu \left( {x,\mathcal{A}} \right) = \inf \left\{ {\lambda > 0:x \in \lambda \mathcal{A}} \right\},\quad x \in {{\mathbb{R}}^{n}}.$

В силу [12, теорема 15.2; 14, Гл. III, § 2, теорема 3] определения (3.3), эта формула задает некоторую норму в ${{\mathbb{R}}^{n}}$:

(3.4)

${{\left\| x \right\|}_{{{{\mathcal{Y}}_{t}}\left( k \right)}}}: = \mu \left( {x,{{\mathcal{Y}}_{t}}\left( k \right)} \right),\quad k \geqslant n,\quad x \in {{\mathbb{R}}^{n}}.$

Из (3.3) и (3.4) получаем

$\begin{gathered} {{\left\| y \right\|}_{{{{\mathcal{Y}}_{t}}\left( n \right)}}} = \min \left\{ {\lambda > 0:y \in \lambda {{\mathcal{Y}}_{t}}\left( n \right)} \right\} = \\ \, = \min \{ \lambda > 0:y \in \lambda t\operatorname{conv} ( \pm b, \pm Ab, \ldots , \pm {{A}^{{n - 1}}}b)\} = \\ \, = {{t}^{{ - 1}}}\min \{ \lambda > 0:y \in \lambda \operatorname{conv} ( \pm b, \pm Ab, \ldots , \pm {{A}^{{n - 1}}}b)\} = \\ \end{gathered} $

$\begin{gathered} \, = {{t}^{{ - 1}}}\min \left\{ {\lambda > 0:y = \lambda \sum\limits_{i = 1}^n {{{A}^{{n - i}}}b{{u}_{i}}} ,\sum\limits_{i = 1}^n {\left| {{{u}_{i}}} \right|} = 1} \right\} = \\ \, = {{t}^{{ - 1}}}\min \left\{ {\lambda > 0:y = \sum\limits_{i = 1}^n {{{A}^{{n - i}}}b{{u}_{i}}} ,\sum\limits_{i = 1}^n {\left| {{{u}_{i}}} \right|} = \lambda } \right\}. \\ \end{gathered} $

Следовательно, найдется вектор ${{u}^{n}} = {{\left( {{{u}_{1}}, \ldots ,{{u}_{n}}} \right)}^{{\text{T}}}} \in {{\mathbb{R}}^{n}}$, такой, что

${{\left\| {{{u}^{n}}} \right\|}_{1}} = \lambda ,\quad y = {{A}_{n}}{{u}^{n}}.$

По условию (1.3) матрица A_n невырождена и тогда

${{u}^{n}} = A_{n}^{{ - 1}}y.$

Теперь получаем последовательно

$\begin{gathered} {{\left\| y \right\|}_{{{{\mathcal{Y}}_{t}}\left( n \right)}}} = {{t}^{{ - 1}}}\min \left\{ {\lambda > 0:y = {{A}_{n}}{{u}^{n}},{{{\left\| {{{u}^{n}}} \right\|}}_{1}} = \lambda } \right\} = \\ \, = {{t}^{{ - 1}}}\min \left\{ {\lambda > 0:{{{\left\| {A_{n}^{{ - 1}}y} \right\|}}_{1}} = \lambda } \right\} = {{t}^{{ - 1}}}{{\left\| {A_{n}^{{ - 1}}y} \right\|}_{1}} \leqslant {{t}^{{ - 1}}}{{\left\| {A_{n}^{{ - 1}}} \right\|}_{1}}{{\left\| y \right\|}_{1}}. \\ \end{gathered} $

Таким образом, можно положить

$\gamma = {{t}^{{ - 1}}}{{\left\| {A_{n}^{{ - 1}}} \right\|}_{1}},$

и, следовательно, неравенство (3.2) установлено.

Если найдется ${{K}_{1}} \in \mathbb{N}$, такое, что

(3.5)

${{\left\| {{{A}^{k}}b} \right\|}_{{{{\mathcal{Y}}_{t}}\left( n \right)}}} \leqslant 1\quad {\text{при}}\quad k \geqslant {{K}_{1}},$

то

(3.6)

${{K}_{1}} \geqslant \max \left\{ {{{K}_{{\min }}},n} \right\}.$

Действительно, из (3.4) и (3.5) следует включение

${{A}^{k}}b \in {{\mathcal{Y}}_{t}}\left( n \right)\quad {\text{при}}\quad k \geqslant {{K}_{1}}.$

В силу п. (v) леммы верно включение

${{\mathcal{Y}}_{t}}\left( n \right) \subset {{\mathcal{Y}}_{t}}\left( {{{K}_{1}}} \right),$

и, следовательно,

${{A}^{k}}b \in {{\mathcal{Y}}_{t}}\left( {{{K}_{1}}} \right)\quad {\text{при}}\quad k \geqslant {{K}_{1}}.$

Так как

${{\mathcal{Y}}_{t}}\left( {{{K}_{1}}} \right) = t\operatorname{conv} ( \pm b, \pm Ab, \ldots , \pm {{A}^{{{{K}_{1}}}}}b),$

то

${{A}^{k}}b \in {{\mathcal{Y}}_{t}}\left( {{{K}_{1}}} \right)\quad {\text{при}}\quad k = 0, \ldots ,{{K}_{1}},$

и поэтому

${{A}^{k}}b \in {{\mathcal{Y}}_{t}}\left( {{{K}_{1}}} \right)\quad {\text{при}}\quad k \in {{\mathbb{Z}}_{ + }}.$

Таким образом,

$\operatorname{conv} ( \pm b, \pm Ab, \ldots , \pm {{A}^{k}}b) \subset \operatorname{conv} ( \pm b, \pm Ab, \ldots , \pm {{A}^{{{{K}_{1}}}}}b)\quad {\text{при}}\quad k \in {{\mathbb{Z}}_{ + }},$

${{\mathcal{Y}}_{t}}\left( k \right) \subset {{\mathcal{Y}}_{t}}\left( {{{K}_{1}}} \right),\quad k \in \mathbb{N},$

${{\mathcal{Y}}_{t}}\left( {{{K}_{{\min }}}} \right) = {{\mathcal{Y}}_{t}} = \bigcup\limits_{k = 1}^\infty {{{\mathcal{Y}}_{t}}\left( k \right)} \subset {{\mathcal{Y}}_{t}}\left( {{{K}_{1}}} \right),$

т.е. верно (3.6).

В силу теоремы Шура [15, теорема 2.3.1] об унитарности триангуляции найдутся унитарная матрица U и верхняя треугольная матрица $\Lambda $, такие, что

$A = U\Lambda {{U}^{{\text{T}}}}.$

Положим

$\Lambda = \left( {\begin{array}{*{20}{c}} {{{\lambda }_{{11}}}}&{{{\lambda }_{{12}}}}&{{{\lambda }_{{13}}}}& \cdots &{{{\lambda }_{{1,n - 1}}}}&{{{\lambda }_{{1n}}}} \\ 0&{{{\lambda }_{{22}}}}&{{{\lambda }_{{23}}}}& \cdots &{{{\lambda }_{{2,n - 1}}}}&{{{\lambda }_{{2n}}}} \\ 0&0&{{{\lambda }_{{33}}}}& \cdots &{{{\lambda }_{{3,n - 1}}}}&{{{\lambda }_{{3n}}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0&0& \cdots &{{{\lambda }_{{n - 1,n - 1}}}}&{{{\lambda }_{{n - 1,n}}}} \\ 0&0&0& \cdots &0&{{{\lambda }_{{nn}}}} \end{array}} \right).$

Выберем $\delta > 0$ и соответствующую матрицу

${{D}_{\delta }} = \operatorname{diag} \left\{ {\delta ,{{\delta }^{2}},{{\delta }^{3}}, \ldots ,{{\delta }^{n}}} \right\}.$

Затем вычислим матрицу

${{D}_{\delta }}\Lambda D_{\delta }^{{ - 1}} = {{D}_{\delta }}\left( {\begin{array}{*{20}{c}} {{{\delta }^{{ - 1}}}{{\lambda }_{{11}}}}&{{{\delta }^{{ - 2}}}{{\lambda }_{{12}}}}&{{{\delta }^{{ - 3}}}{{\lambda }_{{13}}}}& \cdots &{{{\delta }^{{ - (n - 1)}}}{{\lambda }_{{1,n - 1}}}}&{{{\delta }^{{ - n}}}{{\lambda }_{{1n}}}} \\ 0&{{{\delta }^{{ - 2}}}{{\lambda }_{{22}}}}&{{{\delta }^{{ - 3}}}{{\lambda }_{{23}}}}& \cdots &{{{\delta }^{{ - (n - 1)}}}{{\lambda }_{{2,n - 1}}}}&{{{\delta }^{{ - n}}}{{\lambda }_{{2n}}}} \\ 0&0&{{{\delta }^{{ - 3}}}{{\lambda }_{{33}}}}& \cdots &{{{\delta }^{{ - (n - 1)}}}{{\lambda }_{{3,n - 1}}}}&{{{\delta }^{{ - n}}}{{\lambda }_{{3n}}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0&0& \cdots &{{{\delta }^{{ - (n - 1)}}}{{\lambda }_{{n - 1,n - 1}}}}&{{{\delta }^{{ - n}}}{{\lambda }_{{n - 1,n}}}} \\ 0&0&0& \cdots &0&{{{\delta }^{{ - n}}}{{\lambda }_{{nn}}}} \end{array}} \right) = $

$\, = \left( {\begin{array}{*{20}{c}} {{{\lambda }_{{11}}}}&{{{\delta }^{{ - 1}}}{{\lambda }_{{12}}}}&{{{\delta }^{{ - 2}}}{{\lambda }_{{13}}}}& \cdots &{{{\delta }^{{ - n + 2}}}{{\lambda }_{{1,n - 1}}}}&{{{\delta }^{{ - n + 1}}}{{\lambda }_{{1n}}}} \\ 0&{{{\lambda }_{{22}}}}&{{{\delta }^{{ - 1}}}{{\lambda }_{{23}}}}& \cdots &{{{\delta }^{{ - n + 3}}}{{\lambda }_{{2,n - 1}}}}&{{{\delta }^{{ - n + 2}}}{{\lambda }_{{2n}}}} \\ 0&0&{{{\lambda }_{{33}}}}& \cdots &{{{\delta }^{{ - n + 4}}}{{\lambda }_{{3,n - 1}}}}&{{{\delta }^{{ - n + 3}}}{{\lambda }_{{3n}}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0&0&0& \cdots &{{{\lambda }_{{n - 1,n - 1}}}}&{{{\delta }^{{ - 1}}}{{\lambda }_{{n - 1,n}}}} \\ 0&0&0& \cdots &0&{{{\lambda }_{{nn}}}} \end{array}} \right).$

Теперь положим

${{C}_{\delta }} = {{D}_{\delta }}{{U}^{{\text{T}}}}$

и введем соответствующую векторную норму ${{\left\| {\, \cdot \,} \right\|}_{{{{C}_{\delta }}}}}:{{\mathbb{R}}^{n}} \to \left[ {0,\infty } \right),$ определяемую по формуле

${{\left\| x \right\|}_{{{{C}_{\delta }}}}}: = {{\left\| {{{C}_{\delta }}x} \right\|}_{1}}\quad {\text{для}}\quad x \in {{\mathbb{R}}^{n}}.$

Соответствующая матричная норма ${{\left\| {\, \cdot \,} \right\|}_{{{{C}_{\delta }}}}}:{{\mathbb{R}}^{{n \times n}}} \to \left[ {0,\infty } \right)$ порождается векторной нормой ${{\left\| {\, \cdot \,} \right\|}_{{{{C}_{\delta }}}}}$ и для $A \in {{\mathbb{R}}^{{n \times n}}}$ определяется формулой

$\begin{gathered} {{\left\| A \right\|}_{{{{C}_{\delta }}}}} = \mathop {\max }\limits_{x \ne 0} \frac{{{{{\left\| {Ax} \right\|}}_{{{{C}_{\delta }}}}}}}{{{{{\left\| x \right\|}}_{{{{C}_{\delta }}}}}}} = \mathop {\max }\limits_{x \ne 0} \frac{{{{{\left\| {{{C}_{\delta }}Ax} \right\|}}_{1}}}}{{{{{\left\| {{{C}_{\delta }}x} \right\|}}_{1}}}} = \mathop {\max }\limits_{x \ne 0} \frac{{{{{\left\| {{{C}_{\delta }}AC_{\delta }^{{ - 1}}{{C}_{\delta }}x} \right\|}}_{1}}}}{{{{{\left\| {{{C}_{\delta }}x} \right\|}}_{1}}}} = \\ \, = \mathop {\max }\limits_{y \ne 0} \frac{{{{{\left\| {{{C}_{\delta }}AC_{\delta }^{{ - 1}}y} \right\|}}_{1}}}}{{{{{\left\| y \right\|}}_{1}}}} = {{\left\| {{{C}_{\delta }}AC_{\delta }^{{ - 1}}} \right\|}_{1}}. \\ \end{gathered} $

Далее получаем для $k \in \mathbb{N}$

$\begin{gathered} {{\left\| {{{A}^{k}}b} \right\|}_{{{{\mathcal{Y}}_{t}}\left( n \right)}}} \leqslant \gamma {{\left\| {{{A}^{k}}b} \right\|}_{1}} = \gamma {{\left\| {C_{\delta }^{{ - 1}}{{C}_{\delta }}{{A}^{k}}b} \right\|}_{1}} \leqslant \gamma {{\left\| {C_{\delta }^{{ - 1}}} \right\|}_{1}}{{\left\| {{{C}_{\delta }}{{A}^{k}}b} \right\|}_{1}} = \\ \, = \gamma {{\left\| {C_{\delta }^{{ - 1}}} \right\|}_{1}}{{\left\| {{{A}^{k}}b} \right\|}_{{{{C}_{\delta }}}}} \leqslant \gamma {{\left\| {C_{\delta }^{{ - 1}}} \right\|}_{1}}\left\| A \right\|_{{{{C}_{\delta }}}}^{k}{{\left\| b \right\|}_{{{{C}_{\delta }}}}}. \\ \end{gathered} $

Полагая $\delta > 1,$ оценим величину

$\begin{gathered} {{\left\| A \right\|}_{{{{C}_{\delta }}}}} = {{\left\| {{{C}_{\delta }}AC_{\delta }^{{ - 1}}} \right\|}_{1}} = {{\left\| {{{D}_{\delta }}{{U}^{{\text{T}}}}U\Lambda {{U}^{{\text{T}}}}UD_{\delta }^{{ - 1}}} \right\|}_{1}} = {{\left\| {{{D}_{\delta }}\Lambda D_{\delta }^{{ - 1}}} \right\|}_{1}} = \\ \, = \max \left\{ {\left| {{{\lambda }_{{11}}}} \right|,\left| {{{\delta }^{{ - 1}}}{{\lambda }_{{12}}}} \right| + \left| {{{\lambda }_{{22}}}} \right|,\left| {{{\delta }^{{ - 2}}}{{\lambda }_{{13}}}} \right| + \left| {{{\delta }^{{ - 1}}}{{\lambda }_{{23}}}} \right| + \left| {{{\lambda }_{{33}}}} \right|, \ldots ,} \right. \\ \left. {\left| {{{\delta }^{{ - n + 1}}}{{\lambda }_{{1n}}}} \right| + \ldots + \left| {{{\delta }^{{ - 1}}}{{\lambda }_{{n - 1,n}}}} \right| + \left| {{{\lambda }_{{nn}}}} \right|} \right\} \leqslant \\ \end{gathered} $

$\begin{gathered} \, \leqslant \max \left\{ {\left| {{{\lambda }_{{11}}}} \right|,\left| {{{\lambda }_{{22}}}} \right| + {{\delta }^{{ - 1}}}\left| {{{\lambda }_{{12}}}} \right|,\left| {{{\lambda }_{{33}}}} \right| + {{\delta }^{{ - 1}}}\left( {\left| {{{\lambda }_{{13}}}} \right| + \left| {{{\lambda }_{{23}}}} \right|} \right),} \right. \ldots , \\ \, \leqslant \left. {\left| {\left| {{{\lambda }_{{nn}}}} \right| + {{\delta }^{{ - 1}}}\left( {\left| {{{\lambda }_{{1n}}}} \right| + \ldots + \left| {{{\lambda }_{{n - 1,n}}}} \right|} \right)} \right|} \right\} \leqslant \\ \, \leqslant \mathop {\max }\limits_{1 \leqslant i \leqslant n} \left| {{{\lambda }_{{ii}}}} \right| + {{\delta }^{{ - 1}}}\sum\limits_{i = 1}^n {\sum\limits_{j > i}^n {\left| {{{\lambda }_{{ij}}}} \right|} } = \rho \left( A \right) + {{\delta }^{{ - 1}}}\sum\limits_{i = 1}^n {\sum\limits_{j > i}^n {\left| {{{\lambda }_{{ij}}}} \right|} } . \\ \end{gathered} $

Выберем число $\delta $ произвольно из условия

$\delta > \max \left\{ {1,\frac{{\sum\limits_{i = 1}^n {\sum\limits_{j > i}^n {\left| {{{\lambda }_{{ij}}}} \right|} } }}{{1 - \rho \left( A \right)}}} \right\}.$

Здесь используется условие (1.4). Зафиксируем выбранную постоянную $\delta $ из этого неравенства, тогда верно неравенство

${{\left\| A \right\|}_{{{{C}_{\delta }}}}} < 1,$

$\left\| A \right\|_{{{{C}_{\delta }}}}^{k} \to 0\quad {\text{при}}\quad k \to \infty .$

Поскольку $\delta $ не зависит от параметра k, то соответствующие величины

${{\left\| {C_{\delta }^{{ - 1}}} \right\|}_{1}} \ne 0,\quad {{\left\| b \right\|}_{{{{C}_{\delta }}}}} \ne 0$

также не зависят от k. Следовательно, найдется, по крайней мере, одно число ${{K}_{2}} \in \mathbb{N}$, такое, что

(3.7)

$\gamma {{\left\| {C_{\delta }^{{ - 1}}} \right\|}_{1}}\left\| A \right\|_{{{{C}_{\delta }}}}^{{{{K}_{2}}}}{{\left\| b \right\|}_{{{{C}_{\delta }}}}} \leqslant 1$

или

$\left\| A \right\|{{_{{{{C}_{\delta }}}}^{{{{K}_{2}}}}}_{{}}} \leqslant {{\gamma }^{{ - 1}}}\left\| {C_{\delta }^{{ - 1}}} \right\|_{1}^{{ - 1}}\left\| b \right\|_{{{{C}_{\delta }}}}^{{ - 1}}.$

Таким образом,

(3.8)

${{K}_{2}} \geqslant \max \left\{ {{{K}_{{\min }}},n} \right\},$

и выполняется неравенство

(3.9)

${{\left\| {{{A}^{k}}b} \right\|}_{{{{\mathcal{Y}}_{t}}\left( n \right)}}} \leqslant 1\quad {\text{при}}\quad k \geqslant {{K}_{2}}.$

Действительно, получаем

${{\left\| {{{A}^{k}}b} \right\|}_{{{{\mathcal{Y}}_{t}}\left( n \right)}}} \leqslant \gamma {{\left\| {C_{\delta }^{{ - 1}}} \right\|}_{1}}\left\| A \right\|_{{{{C}_{\delta }}}}^{{{{K}_{2}}}}{{\left\| b \right\|}_{{{{C}_{\delta }}}}} \leqslant 1,$

что доказывает требуемое.

Сказанное представляет собой соответствующее утверждение.

Следствие 3. Для минимального числа шагов множеств достижимости из (3.1) справедливы оценки

${{K}_{{\min }}} \leqslant \max \left\{ {{{K}_{1}},{{K}_{2}}} \right\},$

определяемые соотношениями (3.5), (3.6) и (3.8), (3.9).

Представленные ранее результаты могут быть расширены на некоторый более широкий класс систем (1.1), (1.2). При этом доказательства изменяются незначительно, и поэтому они опущены.

Следствие 4. Пусть имеется последовательность вещественных чисел ${{\left\{ {{{\nu }_{k}}} \right\}}_{{k \in {{\mathbb{Z}}_{ + }}}}}$, такая, что

${{\nu }_{k}} > 0,\quad \mathop {\sup }\limits_{k \in {{\mathbb{Z}}_{ + }}} \nu _{k}^{{ - 1}} < \infty ,$

которая порождает для системы (1.1), (1.4) множества управлений:

$\sum\limits_{k = 0}^\infty {{{\nu }_{k}}\left| {u\left( k \right)} \right| \leqslant t} ,\quad t \in \left( {0,\infty } \right).$

Если $\mathcal{Y}_{t}^{\nu }\left( k \right)$ и $\mathcal{Y}_{t}^{\nu }$ – соответствующие множества достижимости, то выполняются аналогичные условия леммы и теоремы и, следовательно, $\mathcal{Y}_{t}^{\nu }$ – выпуклый многогранник.

Поскольку предельное множество достижимости есть выпуклый многогранник, то существует возможность воспользоваться классическим результатом из выпуклого анализа и оценить количество допустимых управлений, необходимых для достижения заданного терминального состояния.

Следствие 5. Для каждого $y \in {{\mathcal{Y}}_{t}}$ найдутся не более n + 1 ненулевых допустимых управлений $\left\{ {u{\kern 1pt} {\text{*}}({{k}_{1}}), \ldots ,u{\kern 1pt} {\text{*}}({{k}_{{n + 1}}})} \right\}$, таких, что

$y = \sum\limits_{i = 1}^{n + 1} {{{A}^{{{{k}_{i}}}}}bu{\kern 1pt} *\left( {{{k}_{i}}} \right)} ,\quad \sum\limits_{i = 1}^{n + 1} {\left| {u{\kern 1pt} *\left( {{{k}_{i}}} \right)} \right| \leqslant t} .$

При этом минимальное число шагов для терминального состояния $y \in {{\mathcal{Y}}_{t}}$ определяется числом K_min и оценками из следствия 3.

Доказательство. В силу теоремы для произвольного $y \in {{\mathcal{Y}}_{t}}$ верно включение

$y \in t\operatorname{conv} (b,Ab, \ldots ,{{A}^{{K - 1}}}b, - b, - Ab, \ldots , - {{A}^{{K - 1}}}b)$

для некоторого $K$. Построим множество

$\mathcal{G}: = \left\{ {{{c}_{1}}, \ldots ,{{c}_{M}}} \right\},\quad {{\mathcal{Y}}_{t}} = \operatorname{conv} \mathcal{G},\quad {{c}_{i}} \in {{\mathcal{Y}}_{t}},$

в котором расположены вершины ${{c}_{i}}$ многогранника ${{\mathcal{Y}}_{t}}$ и $M \leqslant 2K$. Воспользуемся теоремой Каратеодори [9, теорема 1.14.1; 12, теорема 17], используя ее геометрическое описание [16, теорема 2.4]: множество ${{\mathcal{Y}}_{t}}$ представляет собой выпуклую оболочку множества $\mathcal{G}$ в пространстве ${{\mathbb{R}}^{n}}$ и поэтому есть объединение всех m-симплексов в ${{\mathbb{R}}^{n}}$ с вершинами в ${{\mathcal{Y}}_{t}}$ при $m \leqslant n$. Следовательно, каждая точка $y \in {{\mathcal{Y}}_{t}}$ принадлежит хотя бы одному m-симплексу из вершин ${{c}_{i}}$ множества $\mathcal{G}$. Тогда по определению найдутся числа ${{{v}}_{1}}, \ldots ,{{{v}}_{{n + 1}}}$, такие, что

$y = \sum\limits_{i = 1}^{n + 1} {{{{v}}_{i}}{{c}_{{{{k}_{i}}}}}} ,\quad \sum\limits_{i = 1}^{n + 1} {{{{v}}_{i}}} = 1,\quad {{{v}}_{i}} \geqslant 0,\quad {{c}_{{{{k}_{i}}}}} \in \mathcal{G}.$

Положим

$u{\kern 1pt} {\text{*}}\left( {{{k}_{i}}} \right) = t\left\{ \begin{gathered} {{{v}}_{i}},\quad {{c}_{{{{k}_{i}}}}} \in t\{ b,Ab, \ldots ,{{A}^{{K - 1}}}b\} , \hfill \\ - {{{v}}_{i}},\quad {{c}_{{{{k}_{i}}}}} \in t\{ - b, - Ab, \ldots , - {{A}^{{K - 1}}}b\} . \hfill \\ \end{gathered} \right.$

Тогда получаем запись, эквивалентную утверждению следствия.

Опишем аналогичные свойства множеств 0-управляемости для рассматриваемого класса систем.

Следствие 6. Для систем (1.1)–(1.3) и (1.5) множества 0-управляемости ${{\mathcal{X}}_{t}}\left( k \right)$ за конечное число шагов обладают свойствами, аналогичными свойствам леммы.

Для предельного множества 0-управляемости ${{\mathcal{X}}_{t}}$ выполняется утверждение, аналогичное теореме.

Доказательство. Для систем (1.1), (1.2) введем обозначения

${{\mathcal{X}}_{t}}{{,}_{A}}\left( k \right): = {{\mathcal{X}}_{t}}\left( k \right),\quad {{\mathcal{X}}_{t}}{{,}_{A}}: = {{\mathcal{X}}_{t}},\quad {{\mathcal{Y}}_{t}}{{,}_{A}}\left( k \right): = {{\mathcal{Y}}_{t}}\left( k \right),\quad {{\mathcal{Y}}_{t}}{{,}_{A}}: = {{\mathcal{Y}}_{t}},$

отвечающие матрице $A$. Также для системы

$y\left( {k + 1} \right) = {{A}^{{ - 1}}}y\left( k \right) + b{v}\left( k \right),\quad \sum\limits_{k = 0}^\infty {\left| {{v}\left( k \right)} \right| \leqslant t} ,$

построим аналогичные множества управляемости ${{\mathcal{X}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right)$, ${{\mathcal{X}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}$, ${{\mathcal{Y}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right)$, ${{\mathcal{Y}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}},$ отвечающие матрице A^–1. В силу предположения (1.5) матрица A не вырождена.

Справедливо равенство

(3.10)

${{\mathcal{X}}_{t}}{{,}_{A}}\left( k \right) = {{A}^{{ - 1}}}{{\mathcal{Y}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right).$

Действительно, согласно определению $y \in {{\mathcal{Y}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right)$, если и только если

$y = {{A}^{{ - \left( {k - 1} \right)}}}b{v}\left( 0 \right) + ... + b{v}\left( {k - 1} \right),\quad \sum\limits_{i = 0}^{k - 1} {\left| {{v}\left( i \right)} \right|} \leqslant t,$

${{A}^{{k - 1}}}y = {{A}^{k}}({{A}^{{ - 1}}}y) = b{v}\left( 0 \right) + ... + {{A}^{{k - 1}}}b{v}\left( {k - 1} \right),\quad \sum\limits_{i = 0}^{k - 1} {\left| {{v}\left( i \right)} \right|} \leqslant t.$

Полагая

$u\left( 0 \right) = - {v}\left( {k - 1} \right),...,u\left( {k - 1} \right) = - {v}\left( 0 \right),$

приходим к выводу, что

${{A}^{{ - 1}}}y \in {{\mathcal{X}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right),$

т.е.

${{A}^{{ - 1}}}{{\mathcal{Y}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right) \subset {{\mathcal{X}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right).$

Обратно, если $x \in {{\mathcal{X}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right)$, то

$x = - {{A}^{{ - 1}}}bu\left( 0 \right) - ... - {{A}^{{ - k}}}bu\left( {k - 1} \right),\quad \sum\limits_{i = 0}^{k + 1} {\left| {u\left( i \right)} \right|} \leqslant t,$

$Ax = - {{A}^{{\left( {k - 1} \right)}}}bu\left( {k - 1} \right) - ... - bu\left( 0 \right),\quad \sum\limits_{i = 0}^{k + 1} {\left| {u\left( i \right)} \right|} \leqslant t.$

Снова делая замену

${v}\left( 0 \right) = - u\left( {k - 1} \right),...,{v}\left( {k - 1} \right) = - u\left( 0 \right),$

приходим к выводу, что

$Ax \in {{\mathcal{Y}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right),$

т.е.

$A{{\mathcal{X}}_{t}}{{,}_{A}}\left( k \right) \subset {{\mathcal{Y}}_{t}}{{,}_{{{{A}^{{ - 1}}}}}}\left( k \right).$

Равенство (3.10) доказано.

Ясно, что теперь следствие 6 вытекает из (3.10) и утверждений леммы и теоремы.

4. Комментарии и примеры. В данном разделе построим различные примеры, демонстрирующие основные результаты леммы и теоремы.

Пример 1. Положим размерность фазового пространства n = 2, матрицу системы определим следующим образом:

$A = \left( {\begin{array}{*{20}{c}} {\frac{1}{2}}&1 \\ 0&{\frac{1}{2}} \end{array}} \right).$

При этом для любого $b \in {{\mathbb{R}}^{2}}{{\backslash }}\left\{ 0 \right\}$ данная система удовлетворяет условиям (1.3) и (1.4).

Величина K_min, определяемая соотношениями (3.1), в действительности сильно зависит от вектора b. В общем случае справедливо равенство

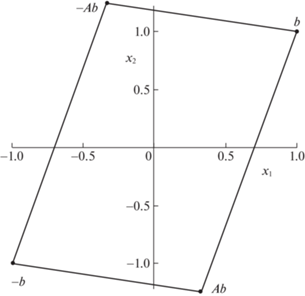
${{A}^{k}}b = \left( {\begin{array}{*{20}{c}} {\frac{1}{{{{2}^{k}}}}{{b}_{1}}}&{\frac{k}{{{{2}^{{k - 1}}}}}{{b}_{2}}} \\ 0&{\frac{1}{{{{2}^{k}}}}{{b}_{2}}} \end{array}} \right),\quad k \in {{\mathbb{Z}}_{ + }}.$

Если предположить, что ${{b}_{2}} = 0$, то с учетом п. (iii) леммы и теоремы получим, что

${{\mathcal{Y}}_{t}}(k) = t \cdot \operatorname{conv} \left\{ { \pm b} \right\} = \left[ { - t\left| {{{b}_{1}}} \right|,t\left| {{{b}_{1}}} \right|} \right] \times \left\{ 0 \right\}.$

Таким образом, ${{K}_{{\min }}} = 1$.

Если предположить, что ${{b}_{1}} = 0$, то с учетом п. (iii) леммы верно равенство

${{\mathcal{Y}}_{t}}(k) = t\left| {{{b}_{2}}} \right| \cdot \operatorname{conv} \left\{ { \pm \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right), \pm \left( {\begin{array}{*{20}{c}} 1 \\ {\frac{1}{2}} \end{array}} \right), \pm \left( {\begin{array}{*{20}{c}} 1 \\ {\frac{1}{4}} \end{array}} \right), \ldots , \pm \left( {\begin{array}{*{20}{c}} {\frac{k}{{{{2}^{{k - 1}}}}}} \\ {\frac{1}{{{{2}^{k}}}}} \end{array}} \right)} \right\}.$

Если положить

${{\lambda }_{1}} = \frac{{2k - 1}}{{{{2}^{k}}}},\quad {{\lambda }_{2}} = \frac{k}{{{{2}^{k}}}},$

то для $k \geqslant 3$ верно, что

${{\lambda }_{1}} + {{\lambda }_{2}} < 1,$

${{\lambda }_{1}}b + {{\lambda }_{2}}( - {{A}^{2}}b) = {{\lambda }_{1}}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right) + {{\lambda }_{2}}\left( {\begin{array}{*{20}{c}} { - 1} \\ { - \frac{1}{4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\frac{{ - k}}{{{{2}^{{k - 1}}}}}} \\ {\frac{{ - 1}}{{{{2}^{k}}}}} \end{array}} \right).$

Отсюда следуют включения

$ - {{A}^{k}}b \in \operatorname{conv} \{ b, - {{A}^{2}}b,0\} ,$

${{A}^{k}}b \in \operatorname{conv} \{ - b,{{A}^{2}}b,0\} .$

Тогда с учетом теоремы верно, что

${{\mathcal{Y}}_{t}}(k) = {{\mathcal{Y}}_{t}}(3),\quad k \geqslant 3,$

${{K}_{{\min }}} \leqslant 3.$

При этом следующая система несовместна:

$\left\{ {\begin{array}{*{20}{l}} {{{\lambda }_{1}}b - {{\lambda }_{2}}b + {{\lambda }_{3}}Ab - {{\lambda }_{4}}Ab = {{A}^{2}}b,} \\ {{{\lambda }_{1}} + {{\lambda }_{2}} + {{\lambda }_{3}} + {{\lambda }_{4}} = 1,} \\ {{{\lambda }_{1}},{{\lambda }_{2}},{{\lambda }_{3}},{{\lambda }_{4}} \geqslant 0.} \end{array}} \right.$

Отсюда следует, что $t{{A}^{2}}b \notin {{\mathcal{Y}}_{t}}(2)$, т.е.

${{\mathcal{Y}}_{t}}(2) \ne {{\mathcal{Y}}_{t}}(3),$

${{K}_{{\min }}} \geqslant 3.$

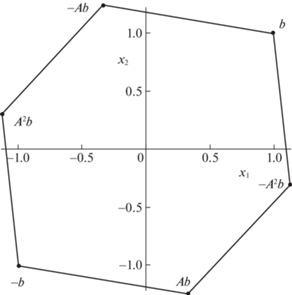
Окончательно получим равенство ${{K}_{{\min }}} = 3.$

Для случая $b = {{\left( {\begin{array}{*{20}{c}} 1&1 \end{array}} \right)}^{{\text{T}}}}$, t = 1 построим соответствующие множества достижимости графически. Результаты проиллюстрированы на рис. 1–3 .

Рис. 1.

Множество ${{\mathcal{Y}}_{t}}(2)$

Рис. 2.

Множество ${{\mathcal{Y}}_{t}}(3)$

Рис. 3.

Множества ${{\mathcal{Y}}_{t}}(4) = {{\mathcal{Y}}_{t}}(5) = {{\mathcal{Y}}_{t}}$

Пример 2. С учетом следствия 5 и равенства (3.10) построенные в примере 1 множества достижимости ${{\mathcal{Y}}_{t}}(k)$ можно преобразовать в множества 0-управляемости системы (1.1), порождаемой матрицей системы:

${{A}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} {\frac{1}{2}}&1 \\ 0&{\frac{1}{2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 2&{ - 4} \\ 0&2 \end{array}} \right).$

Согласно [12, следствие 19.5.1], для случая ${{b}_{1}} = 0$ справедливо следующее равенство:

$\begin{gathered} {{\mathcal{X}}_{{{{A}^{{ - 1}}},t}}} = {{\mathcal{X}}_{{{{A}^{{ - 1}}},t}}}(3) = A{{\mathcal{Y}}_{{A,t}}}(3) = t \cdot \operatorname{conv} \left\{ { \pm Ab, \pm {{A}^{2}}b, \pm {{A}^{3}}b} \right\} = \\ \, = t\left| {{{b}_{2}}} \right| \cdot \operatorname{conv} \left\{ { \pm \left( {\begin{array}{*{20}{c}} 1 \\ {\frac{1}{2}} \end{array}} \right), \pm \left( {\begin{array}{*{20}{c}} 1 \\ {\frac{1}{4}} \end{array}} \right), \pm \left( {\begin{array}{*{20}{c}} {\frac{3}{4}} \\ {\frac{1}{8}} \end{array}} \right)} \right\}. \\ \end{gathered} $

Пример 3. Рассмотрим случай комплексных собственных значений матрицы A, удовлетворяющих условию (1.4):

$A = \frac{1}{\alpha }\left( {\begin{array}{*{20}{c}} { - \frac{1}{2}}&{\frac{{\sqrt 3 }}{2}} \\ { - \frac{{\sqrt 3 }}{2}}&{ - \frac{1}{2}} \end{array}} \right).$

Тогда для любых $b \in {{\mathbb{R}}^{2}}$ и $k \in {{\mathbb{Z}}_{ + }}$ справедливо представление

${{A}^{k}}b = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{{\alpha }^{k}}}}Ab,\quad k = 3i + 1,} \\ {\frac{1}{{{{\alpha }^{k}}}}{{A}^{2}}b,\quad k = 3i + 2,} \\ {\frac{1}{{{{\alpha }^{k}}}}b,\quad k = 3i,} \end{array}} \right.\quad {\text{где}}\quad i \in {{\mathbb{Z}}_{ + }},$

откуда следует, что ${{K}_{{\min }}} \leqslant 3$. Также для случая $b = {{\left( {\begin{array}{*{20}{c}} 1&1 \end{array}} \right)}^{{\text{T}}}}$, t = 1, $\alpha = 1.1$ множества достижимости ${{\mathcal{Y}}_{t}}(2)$ и ${{\mathcal{Y}}_{t}}(3)$, построенные на основе п. (iii) леммы, представлены на рис. 4 и 5 соответственно. Следует также отметить, что в силу теоремы множество ${{\mathcal{Y}}_{t}}(3)$ совпадает с предельным множеством достижимости ${{\mathcal{Y}}_{t}}$.

Рис. 4.

Множество ${{\mathcal{Y}}_{t}}(2)$

Рис. 5.

Множество ${{\mathcal{Y}}_{t}}(3) = {{\mathcal{Y}}_{t}}$

Заключение. Рассмотрены методы построения предельных множеств достижимости и управляемости для линейных систем с дискретным временем и ограниченным скалярным управлением. Предполагается, что управление как функция времени является ограниченной последовательностью в смысле l₁-нормы.

Для случая, когда собственные значения матрицы системы не превосходят 1 по модулю, т.е. для не полностью достижимых систем, предельные множества достижимости удается построить явным образом: доказано, что они представляют собой выпуклый, симметричный относительно начала координат многогранник. При этом в п. (iii) леммы дано описание вершин данного многогранника. Также доказано, что последовательность множеств управляемости за конечное число шагов в этом случае представляет собой, начиная с некоторого K_min, постоянную последовательность. В следствии 3 предложена конструктивная оценка величины K_min.

Полученные результаты для множеств достижимости обобщены и для построения множеств 0-управляемости не полностью управляемых систем, т.е. тех систем собственные значения матриц которых по модулю строго больше 1. Данный факт сформулирован в следствии 6.

В качестве демонстрации основных результатов данной работы приведены примеры и иллюстрации построения множеств управляемости и достижимости для различных линейных систем с дискретным временем.

Список литературы

Ибрагимов Д.Н., Сиротин А.Н. О задаче оптимального быстродействия для линейной дискретной системы с ограниченным скалярным управлением на основе множеств 0-управляемости // АиТ. 2015. № 9. С. 3–30.
Пропой А.И. Элементы теории оптимальных дискретных процессов. М.: Наука, 1973. 256 с.
Сиротин А.Н., Формальский А.М. Области достижимости и управляемости линейных дискретных систем // Изв. АН. ТиСУ. 2002. № 4. С. 5–16.
Formalsky A.M., Sirotin A.N. On the Geometric Properties of Reachable and Controllable Sets for Linear Discrete Systems // J. Optimization Theory and Applications. 2004. V. 122. № 2. P. 17–44.
Сиротин А.Н. Точное аналитическое описание множеств достижимости асимптотически устойчивых линейных дискретных систем с ограниченным по l₁-норме скалярным управлением // Вестн. МАИ. 2008. Т. 15. № 2. С. 142–146.
Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука, 1973. 447 с.
Табак Д., Куо Б. Оптимальное управление и математическое программирование. М.: Наука, 1975. 280 с.
Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах и упражнениях. М.: Наука, 1991. 448 с.
Половинкин У.С., Балашов М.В. Элементы выпуклого и сильно выпуклого анализа. М.: Физматлит, 2007. 440 с.
Козорез Д.А., Красильщиков М.Н., Кружков Д.М., Сыпало К.И. Решение навигационной задачи при автономном выведении полезной нагрузки на геостационарную орбиту с помощью двигателя малой тяги // Изв. АН. ТиСУ. 2015. № 5. С. 106–118.
Козорез Д.А., Красильщиков М.Н., Кружков Д.М., Сыпало К.И. Интегрированная навигационная система космического аппарата на геостационарной и высокоэллиптической орбитах, функционирующая в условиях активных помех // Изв. АН. ТиСУ. 2013. № 3. С. 143–154.
Рокафеллар Р. Выпуклый анализ. М.: Мир, 1973. 471 с.
Ульянов П.Л., Бахвалов А.Н., Дьяченко М.И., Казарян К.С., Сифуэнтес П. Действительный анализ в задачах. М.: Физматлит, 2005. 416 с.
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1981. 544 с.
Хорн Р., Джонсон И. Матричный анализ. М.: Мир, 1989. 667 с.
Лейхтвейс К. Выпуклые множества. М.: Наука, 1983. 336 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал