Известия РАН. Теория и системы управления, 2022, № 4, стр. 22-30

УПРАВЛЕНИЕ АМПЛИТУДОЙ КОЛЕБАНИЙ МЕХАНИЧЕСКИХ СИСТЕМ

Ю. Ф. Голубев^*

Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

Поступила в редакцию 26.01.2022
После доработки 31.01.2022
Принята к публикации 28.03.2022

EDN: KSPRLT
DOI: 10.31857/S0002338822040084

Аннотация

Предложен оригинальный метод поиска оптимального управления амплитудой колебаний в окрестности положения равновесия склерономной многомерной механической системы. Одна степень свободы системы не поддается непосредственному управлению. На ее движение влияют другие, непосредственно управляемые степени свободы. В число непосредственно управляемых могут входить как позиционные, так и циклические координаты. Метод не содержит сопряженных переменных в смысле принципа максимума Л.С. Понтрягина и не увеличивает размерность анализируемой исходной системы дифференциальных уравнений. На примере конкретной маятниковой системы продемонстрирована эффективность применения предложенного метода.

Введение. Задачи управления амплитудой нелинейных колебаний представляют издавна значительный интерес для исследований как с теоретической, так и с практической точек зрения. К настоящему времени существует развитая теория резонансного возбуждения колебаний, которая широко используется в практических приложениях [1, 2]. Проблема построения оптимального управления как для линейных, так и для нелинейных колебательных систем имеет существенные отличия от резонансных постановок. Она часто ставится и исследуется в рамках принципа максимума Л.С. Понтрягина [3, 4]. Среди колебательных систем особый интерес вызывают колебательные системы с дефицитом управления, когда система содержит степени свободы, для которых невозможно непосредственное управление, а их требуемое изменение достигается опосредованно за счет подходящего управления по другим степеням свободы [5, 6]. Примеры решения некоторых задач с дефицитом управления системами, находящимися в окрестности положения равновесия и содержащими одну неуправляемую степень свободы, можно найти в [7–10]. Как следует из указанных работ, системы могут быть весьма непростыми. На первоначальном этапе исследования таких систем представляется разумным выбрать координаты управляемых степеней свободы в качестве функций управления, считая, что возможна их идеальная реализация. Основная трудность применения принципа максимума Понтрягина в таком случае состоит в том, что координаты управляемых степеней свободы, как правило, входят в уравнения движения вместе со своими производными. Из-за этого размерность фазового пространства может быть уменьшена лишь на число управляемых координат системы, что может быть недостаточно для эффективного решения задачи по методу Понтрягина.

В предлагаемой статье для решения задач оптимального управления колебаниями позиционных систем с дефицитом управления по одной степени свободы развивается оригинальный метод оптимизации, формализм которого основан на подходе Д.Е. Охоцимского, Т.М. Энеева [11] к решению проблем оптимального управления. Метод позволяет получить решение в виде синтеза управления колебаниями в классе кусочно-непрерывных управляющих координат в зависимости от неуправляемой координаты. Управление колебаниями понимается в смысле увеличения или уменьшения амплитуды колебаний, которая служит критерием оптимальности.

1. Постановка проблемы. Рассмотрим склерономную голономную механическую систему с кинетической энергией

$T = \frac{1}{2}\sum\limits_{i,j = 1}^n {{{a}_{{ij}}}({{q}_{1}}, \ldots ,{{q}_{n}}){{{\dot {q}}}_{i}}{{{\dot {q}}}_{j}}} ,\quad n \geqslant 2,$

где n – число степеней свободы системы, ${{q}_{i}}$ – обобщенные координаты, ${{\dot {q}}_{i}}$ – обобщенные скорости, а симметричная матрица $({{a}_{{ij}}})$ зависит от координат и положительно определена. Уравнения движения системы представим в форме уравнений Лагранжа 2-го рода

(1.1)

$\frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial {{{\dot {q}}}_{i}}}}} \right) - \frac{{\partial T}}{{\partial {{q}_{i}}}} = {{Q}_{i}},\quad i = \overline {1,n} ,$

в которых t – время, ${{Q}_{i}}$ – обобщенные силы. Пользуясь произволом в нумерации обобщенных координат, будем считать, что первая обобщенная координата не поддается непосредственному активному управлению, а остальные обобщенные силы могут быть сформированы нужным образом за счет доступного управляющего воздействия. Выделим первую обобщенную координату, обозначив ее буквой $x$:

${{q}_{1}} = x.$

Обобщенную силу ${{Q}_{1}}$ будем считать позиционной в том смысле, что она может зависеть только от x и других обобщенных координат, а от обобщенных скоростей не зависит. Пусть первыми в наборе $({{q}_{2}},...,{{q}_{n}})$ идут $s - 1$ координат, от которых обобщенная сила ${{Q}_{1}}$ зависит явно. Остальные $(n - s)$ координат не входят явно в выражение для ${{Q}_{1}}$. Все координаты переобозначим: ${{u}_{j}} = {{q}_{{j + 1}}}$, $j = \overline {1,s - 1} $ и ${{w}_{k}} = {{q}_{{s + k}}}$, $k = \overline {1,n - s} $, причем ${\mathbf{u}} = ({{u}_{1}},...,{{u}_{{s - 1}}}) \in {{R}^{{s - 1}}}$ – вектор координат, непосредственно влияющих на значение ${{Q}_{1}}$, ${\mathbf{w}} = ({{w}_{1}},...,{{w}_{{n - s}}}) \in {{R}^{{n - s}}}$ – вектор координат, от которых ${{Q}_{1}}$ явно не зависит, так что $\partial {{Q}_{1}}{\text{/}}\partial {{w}_{k}} = 0,$ $k = \overline {1,n - s} $. В число w-координат могут входить, например, циклические координаты. Кинетическая энергия примет вид

$Т = \frac{1}{2}\left[ {{{a}_{{11}}}{{{\dot {x}}}^{2}} + 2\dot {x}\left( {\sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} } } \right)} \right] + T{\kern 1pt} *,$

где $s - 1$ – число u-координат и

$T{\kern 1pt} *(x,{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}}) = \frac{1}{2}\left( {\sum\limits_{j,r = 1}^{s - 1} {{{a}_{{j + 1,r + 1}}}{{{\dot {u}}}_{j}}{{{\dot {u}}}_{r}}} + 2\sum\limits_{j = 1}^{s - 1} {\sum\limits_{k = 1}^{n - s} {{{a}_{{j + 1,k + s}}}{{{\dot {u}}}_{j}}{{{\dot {w}}}_{k}}} + \sum\limits_{k,r = 1}^{n - s} {{{a}_{{k + s,r + s}}}{{{\dot {w}}}_{k}}{{{\dot {w}}}_{r}}} } } \right).$

В системе (1.1) выделим уравнение для координаты x:

(1.2)

$\frac{d}{{dt}}\left( {{{a}_{{11}}}\dot {x} + \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} } \right) - \frac{{\partial T}}{{\partial x}} = F(x,{\mathbf{u}}),$

где $F(x,{\mathbf{u}}) = {{Q}_{1}}(x,{{u}_{1}}, \cdots ,{{u}_{{s - 1}}})$. Примем координату x в качестве независимой переменной на участке ее монотонного изменения: $\dot {x} \ne 0$ и обозначим буквой ${\mathbf{y}} = ({\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}},{\mathbf{w}}{\kern 1pt} ')$, где ${\mathbf{u}}{\kern 1pt} ' = d{\mathbf{u}}{\text{/}}dx$, ${\mathbf{w}}{\kern 1pt} ' = d{\mathbf{w}}{\text{/}}dx$, вектор управляющих координат и их производных по координате $x$. Тогда уравнение (1.2) преобразуется к виду

(1.3)

$\dot {x}\frac{d}{{dx}}\left[ {f(x,{\mathbf{y}})\dot {x}} \right] - p(x,{\mathbf{y}}){{\dot {x}}^{2}} = F(x,{\mathbf{u}}),$

где

$f(x,{\mathbf{y}}) = {{a}_{{11}}} + \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}u_{j}^{'}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}w_{k}^{'}} ,$

$p(x,{\mathbf{y}}) = \frac{1}{2}\left( {\frac{{\partial {{a}_{{11}}}}}{{\partial x}} + 2\sum\limits_{j = 1}^{s - 1} {\frac{{\partial {{a}_{{1,j + 1}}}}}{{\partial x}}u_{j}^{'} + } 2\sum\limits_{k = 1}^{n - s} {\frac{{\partial {{a}_{{1,s + k}}}}}{{\partial x}}w_{k}^{'}} } \right) + \frac{{\partial T{\kern 1pt} *(x,{\mathbf{y}})}}{{\partial x}}.$

Будем считать, что векторы ${\mathbf{u}} = {\mathbf{u}}(x)$, ${\mathbf{w}} = {\mathbf{w}}(x)$ каким-либо образом назначены и ограничены:

(1.4)

$\begin{array}{*{20}{c}} {\left| {u_{j}^{m} \leqslant {{u}_{j}}(x) \leqslant u_{j}^{M}} \right|,} \\ {\left| {\dot {u}_{j}^{m} \leqslant {{{\dot {u}}}_{j}}(x) \leqslant \dot {u}_{j}^{M}} \right|,} \end{array},\quad \begin{array}{*{20}{c}} {\left| {w_{k}^{m} \leqslant {{w}_{k}}(x) \leqslant w_{k}^{M}} \right|,} \\ {\left| {\dot {w}_{k}^{m} \leqslant {{{\dot {w}}}_{k}}(x) \leqslant \dot {w}_{k}^{M}} \right|,} \end{array}\quad j = \overline {1,s - 1} ,\quad k = \overline {1,n - s} .$

Эти вектор-функции будем рассматривать как функции управления системой. Тогда обобщенные силы ${{Q}_{2}},...,{{Q}_{n}}$ вычисляются в соответствии с уравнениями (1.1) таким образом, чтобы указанные вектор-функции ${\mathbf{u}}(x)$, ${\mathbf{w}}(x)$ реализовались. Предположим, что это сделано, так что ограничения (1.4) удовлетворяются, и можно написать уравнение

(1.5)

$\int\limits_{{{x}_{0}}}^x {\lambda \left\{ {F(x,{\mathbf{u}}) + p(x,{\mathbf{y}}){{{\dot {x}}}^{2}} - \dot {x}\frac{d}{{dx}}\left[ {f(x,{\mathbf{y}})\dot {x}} \right]} \right\}} dx = 0,$

где x₀ – начальное значение независимой переменной x, $\lambda (x,{\mathbf{y}})$ – любая функция. Уравнение (1.5) эквивалентно уравнению (1.3). Заметим, что если $f(x,{\mathbf{y}}) \ne 0$, то уравнение (1.3) допускает интегрирующий множитель. Выберем его в качестве $\lambda $:

(1.6)

$\lambda = f(x,{\mathbf{y}})\exp \left( { - \int\limits_{{{x}_{0}}}^x {\frac{{2p(x,{\mathbf{y}})}}{{f(x,{\mathbf{y}})}}dx} } \right),\quad f(x,{\mathbf{y}}) \ne 0.$

Тогда равенство (1.5) можно преобразовать к виду

$\int\limits_{{{x}_{0}}}^x {\lambda F(x,{\mathbf{u}})dx} - \frac{1}{2}\left. {[{{{\dot {x}}}^{2}}f(x,{\mathbf{y}})\lambda (x,{\mathbf{y}})]} \right|_{{{{x}_{0}}}}^{x} = 0$

или

(1.7)

$\int\limits_{{{x}_{0}}}^x {\lambda F(x,{\mathbf{u}})dx} = \frac{1}{2}\left. {\left[ {f{\kern 1pt} *(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}})\lambda {\kern 1pt} *(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}})} \right]} \right|_{{{{x}_{0}}}}^{x},$

где

(1.8)

$\begin{array}{*{20}{c}} {f{\kern 1pt} *(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}}) = {{a}_{{11}}}\dot {x} + \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} ,} \\ {\lambda {\kern 1pt} *(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}}) = f{\kern 1pt} *(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}})\exp \left( { - \int\limits_{{{x}_{0}}}^x {\frac{{2p(x,{\mathbf{y}})}}{{f(x,{\mathbf{y}})}}dx} } \right).} \end{array}$

В том случае, когда $\dot {x} = \dot {x}(x)$ обращается в нуль, интеграл в левой части равенства (1.7) становится несобственным из-за того, что при $\dot {x} = 0$ значения ${\mathbf{u}}{\kern 1pt} ' = {\mathbf{\dot {u}}}{\text{/}}\dot {x}$ и ${\mathbf{w}}{\kern 1pt} ' = {\mathbf{\dot {w}}}{\text{/}}\dot {x}$ могут стать бесконечно большими. Однако та же формула (1.7) показывает, что этот интеграл существует и принимает конечное значение. Заметим, что переменные $f{\kern 1pt} *$ и $\lambda {\kern 1pt} *$ не содержат отмеченной особенности.

Предположим, что силовая функция

(1.9)

$U(x,{\mathbf{u}}( \cdot )) = \int\limits_{{{x}_{0}}}^x {F(\tau ,{\mathbf{u}}(\tau ))} d\tau $

имеет изолированный максимум по координате $x$ при ${\mathbf{u}}(\tau ) \equiv 0$ и этот максимум остается изолированным, когда ${\mathbf{u}}(\tau )$ меняется. Будем рассматривать движение в окрестности этого максимума. Пусть начальные условия выбраны так, что равенство ${{\dot {x}}_{0}} = \dot {x}({{x}_{0}}) = 0$ выполнено, когда $x = {{x}_{0}}$. Назовем амплитудой колебаний величину $J = {{x}_{1}} - {{x}_{0}}$, где ${{x}_{1}} > {{x}_{0}}$ – следующее значение координаты x, когда ${{\dot {x}}_{1}} = \dot {x}({{x}_{1}})$ обращается в ноль. В этом случае аргумент изолированного максимума силовой функции $U(x,{\mathbf{u}}( \cdot ))$ будет принадлежать отрезку $[{{x}_{0}},{{x}_{1}}]$. В общем случае этот аргумент может меняться в зависимости от выбранных вектор-функций ${\mathbf{u}}(x)$, ${\mathbf{w}}(x)$. На концах отрезка должно быть выполнено

(1.10)

${{\dot {x}}_{0}} = {{\dot {x}}_{1}} = 0,$

а также

(1.11)

$\begin{array}{*{20}{c}} {f{\kern 1pt} *({{x}_{0}},{{{\dot {x}}}_{0}},{\mathbf{u}}({{x}_{0}}),{\mathbf{\dot {u}}}({{x}_{0}}),{\mathbf{w}}({{x}_{0}}),{\mathbf{\dot {w}}}({{x}_{0}})) = \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}({{x}_{0}})} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}({{x}_{0}}),} } \\ {f{\kern 1pt} *({{x}_{1}},{{{\dot {x}}}_{1}},{\mathbf{u}}({{x}_{1}}),{\mathbf{\dot {u}}}({{x}_{1}}),{\mathbf{w}}({{x}_{1}}),{\mathbf{\dot {w}}}({{x}_{1}})) = \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} ({{x}_{1}}) + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}({{x}_{1}}).} } \end{array}$

Требуется найти кусочно-непрерывные управления ${\mathbf{u}}(x)$, ${\mathbf{w}}(x)$, при которых достигается максимум (минимум) функционала J.

Теперь рассмотрим обратное движение маятника. Для того, чтобы сохранить смысл введенного функционала, обозначим $\xi = - x$. Пусть ${{{\mathbf{y}}}_{\xi }} = ({\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}},{\mathbf{w}}_{\xi }^{'})$, где ${\mathbf{u}}_{\xi }^{'} = d{\mathbf{u}}{\text{/}}d\xi $, ${\mathbf{w}}_{\xi }^{'} = d{\mathbf{w}}{\text{/}}d\xi $, вектор управляющих координат и их производных по координате $\xi $ в этом случае. Уравнение (1.2) принимает вид

(1.12)

$\frac{d}{{dt}}\left( {{{a}_{{11}}}\dot {\xi } - \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} - \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} } \right) - \frac{{\partial T}}{{\partial \xi }} = - F( - \xi ,{\mathbf{u}}).$

Уравнение (1.3) можно представить как

(1.13)

$\dot {\xi }\frac{d}{{d\xi }}\left[ {{{f}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }})\dot {\xi }} \right] - {{p}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }}){{\dot {\xi }}^{2}} = - F( - \xi ,{\mathbf{u}}),$

где

${{f}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }}) = {{a}_{{11}}} - \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}u_{{j\xi }}^{'}} - \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}w_{{k\xi }}^{'}} ,$

${{p}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }}) = \frac{1}{2}\left( {\frac{{\partial {{a}_{{11}}}}}{{\partial \xi }} + 2\sum\limits_{j = 1}^{s - 1} {\frac{{\partial {{a}_{{1,j + 1}}}}}{{\partial \xi }}u_{{j\xi }}^{'} + \;} 2\sum\limits_{k = 1}^{n - s} {\frac{{\partial {{a}_{{1,s + k}}}}}{{\partial \xi }}w_{{k\xi }}^{'}} } \right) + \frac{{\partial T{\kern 1pt} {\text{*}}(x,{{{\mathbf{y}}}_{\xi }})}}{{\partial \xi }}.$

Следовательно, получаем

(1.14)

${{\lambda }_{\xi }} = {{f}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }})\exp \left( { - \int\limits_{{{\xi }_{0}}}^\xi {\frac{{2{{p}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }})}}{{{{f}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }})}}d\xi } } \right),$

и формулу (1.7) можно переписать следующим образом:

(1.15)

$\int\limits_{{{\xi }_{0}}}^\xi {{{\lambda }_{\xi }}F( - \xi ,{\mathbf{u}})d\xi } = - \frac{1}{2}\left. {[f_{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}})\lambda _{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}})]{\kern 1pt} {\kern 1pt} } \right|_{{{{\xi }_{0}}}}^{\xi },$

где

$f_{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}}) = {{a}_{{11}}}\dot {\xi } - \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} - \sum\limits_{k = 1}^{n - s + 1} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} ,$

$\lambda _{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}}) = f_{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{w}},{\mathbf{\dot {w}}})\exp \left( { - \int\limits_{{{\xi }_{0}}}^\xi {\frac{{2{{p}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }})}}{{{{f}_{\xi }}( - \xi ,{{{\mathbf{y}}}_{\xi }})}}d\xi } } \right).$

Амплитуда колебаний имеет вид $J = {{\xi }_{1}} - {{\xi }_{0}}$, где ${{\xi }_{1}} > {{\xi }_{0}}$, ${{\dot {\xi }}_{0}} = \dot {\xi }({{\xi }_{0}}) = 0$, ${{\dot {\xi }}_{1}} = \dot {\xi }({{\xi }_{1}}) = 0$ и $\dot {\xi }(\xi ) \ne 0$, если $\xi \in ({{\xi }_{0}},{{\xi }_{1}})$. Требуется найти кусочно-непрерывные управления ${\mathbf{u}}(\xi )$, ${\mathbf{w}}(\xi )$, при которых значение функционала J максимально (минимально).

2. Оптимальное раскачивание (успокоение) колебаний. Пусть λ определенa формулой (1.6). Тогда справедливы следующие теоремы.

Теорема 1 (принцип наилучшего раскачивания). Предположим, что движение системы описывается уравнением (1.2) и существуют две точки ${{x}_{0}}$ и ${{x}_{1}}$, причем ${{x}_{0}} < {{x}_{1}}$ и ${{\dot {x}}_{0}} = {{\dot {x}}_{1}} = 0$. Тогда справедливы следующие утверждения.

I. Необходимыми условиями оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{M}}(x)$, ${{{\mathbf{w}}}_{M}}({{x}_{1}})$, которые, будучи стесненными ограничениями (1.4), при фиксированном значении ${{x}_{0}}$ обеспечивают максимум величины ${{x}_{1}}$, служат уравнения

(2.1)

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{M}}(x) = \arg \mathop {\max }\limits_{\mathbf{u}} \text{[}\chi (x,{{{\mathbf{u}}}_{М}},{\mathbf{u}}_{М}^{'},{{{\mathbf{w}}}_{M}},{\mathbf{w}}_{М}^{'})F(x,{\mathbf{u}})],} \\ {{{{{\mathbf{\dot {w}}}}}_{M}}({{x}_{1}}) = \arg \mathop {\min }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{1}},{{{\mathbf{u}}}_{M}},{{{\mathbf{w}}}_{M}}){{{\dot {w}}}_{k}}} } \right],} \end{array}$

где $\chi = {\text{sign}}[f(x,{\mathbf{y}}(x))f({{x}_{1}} - 0,{\mathbf{y}}({{x}_{1}} - 0))]$.

II. Необходимыми условиями оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{m}}(x)$, ${{{\mathbf{\dot {w}}}}_{m}}({{x}_{0}})$, которые, будучи стесненными ограничениями (1.4), при фиксированном значении x₁ обеспечивают минимум величины x₀, служат уравнения

(2.2)

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{m}}(x) = \arg \mathop {\min }\limits_{\mathbf{u}} \text{[}\chi (x,{{{\mathbf{u}}}_{m}},{\mathbf{u}}_{m}^{'},{{{\mathbf{w}}}_{m}},{\mathbf{w}}_{m}^{'})F(x,{\mathbf{u}})],} \\ {{{{{\mathbf{\dot {w}}}}}_{m}}({{x}_{0}}) = \arg \mathop {\max }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{0}},{{{\mathbf{u}}}_{m}},{{{\mathbf{w}}}_{m}}){{{\dot {w}}}_{k}}} } \right],} \end{array}$

где $\chi = {\text{sign}}[f(x,{\mathbf{y}}(x))f({{x}_{0}} + 0,{\mathbf{y}}({{x}_{0}} + 0))]$.

Теорема 2 (принцип оптимального успокоения колебаний). Предположим, что движение системы описывается уравнениями (1.2) и имеются две точки x₀ и x₁, такие, что ${{x}_{0}} < {{x}_{1}}$ ${{\dot {x}}_{0}} = {{\dot {x}}_{1}} = 0$. Тогда справедливы следующие утверждения.

I. Необходимые условия оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{m}}(\tau )$, ${{{\mathbf{\dot {w}}}}_{m}}({{x}_{1}})$, которые, будучи стесненными ограничениями (1.4), при фиксированном значении x₀ обеспечивают минимум величины x₁, выражаются равенствами

(2.3)

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{m}}(x) = \arg \mathop {\min }\limits_{\mathbf{u}} \text{[}\chi (x,{{{\mathbf{u}}}_{m}},{\mathbf{u}}_{m}^{'},{{{\mathbf{w}}}_{m}},{\mathbf{w}}_{m}^{'})F(x,{\mathbf{u}})],} \\ {{{{{\mathbf{\dot {w}}}}}_{m}}({{x}_{1}}) = \arg \mathop {\max }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{1}},{{{\mathbf{u}}}_{m}},{{{\mathbf{w}}}_{m}}){{{\dot {w}}}_{k}}} } \right],} \end{array}$

где $\chi = {\text{sign}}[f(x,{\mathbf{y}}(x))f({{x}_{1}} - 0,{\mathbf{y}}({{x}_{1}} - 0))]$.

II. Необходимые условия оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{M}}(x)$, ${{{\mathbf{\dot {w}}}}_{M}}({{x}_{0}})$, которые, будучи стесненными ограничениями (1.4), при фиксированном значении x₁ обеспечивают максимум величины x₀, выражаются уравнениями

(2.4)

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{M}}(x) = \arg \mathop {\max }\limits_{\mathbf{u}} \text{[}\chi (x,{{{\mathbf{u}}}_{M}},{\mathbf{u}}_{М}^{'},{{{\mathbf{w}}}_{M}},{\mathbf{w}}_{М}^{'})F(x,{\mathbf{u}})],} \\ {{{{{\mathbf{\dot {w}}}}}_{M}}({{x}_{0}}) = \arg \mathop {\min }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{0}},{{{\mathbf{u}}}_{M}},{{{\mathbf{w}}}_{M}}){{{\dot {w}}}_{k}}} } \right]{\text{,}}} \end{array}$

где $\chi = {\text{sign}}[f(x,{\mathbf{y}}(x))f({{x}_{0}} + 0,{\mathbf{y}}({{x}_{0}} + 0))]$.

Доказательство приведенных теорем достигается применением формул (1.7) и (1.15), а также с учетом того, что в уравнении (1.2) коэффициент ${{a}_{{11}}} > 0$. Обозначим

$\Upsilon = F(x,{\mathbf{u}}) + p(x,{\mathbf{y}}){{\dot {x}}^{2}} - \dot {x}\frac{d}{{dx}}\left[ {f(x,{\mathbf{y}})\dot {x}} \right].$

При варьировании управляющих функций будем считать тождественно выполненным уравнение движения: $\Upsilon \equiv 0$. Интегрирующий множитель будет меняться вместе с изменением управления. Вместе с тем вариация тождества (1.5) примет вид

$\int\limits_{{{x}_{0}}}^x {(\Upsilon \delta \lambda + \lambda \delta \Upsilon )dx} = \int\limits_{{{x}_{0}}}^x {\lambda \delta \Upsilon dx} = 0.$

Поэтому при анализе влияния управления в формулах (1.7) и (1.15) множители λ и ${{\lambda }_{\xi }}$ играют вспомогательную роль и не участвуют в процессе оптимизации. Они служат лишь для тождественного преобразования уравнения движения. Заметим также, что из формул (1.6) и (1.14) следует, что знаки множителей λ и ${{\lambda }_{\xi }}$ совпадают со знаками функций $f(x,{\mathbf{y}})$ и $f( - \xi ,{{{\mathbf{y}}}_{\xi }})$ соответственно.

Рассмотрим сначала утверждение I теоремы 1. Пусть значение координаты $x = {{x}_{1}}$ соответствует максимально достижимому отклонению системы от положения равновесия, но первое равенство формулы (2.1) в какой-нибудь внутренней точке отрезка [${{x}_{0}}$, ${{x}_{1}}$] нарушено. Тогда, как следует из формулы (1.7), в этой точке можно за счет управления ${\mathbf{u}}$, оставив значения других управлений неизменными, увеличить подынтегральную функцию в (1.7), а за счет этого увеличить значение скорости ${{\dot {x}}_{1}} > 0$. Тогда вырастет и новое значение координаты $x = {{x}_{1}}$, при котором скорость $\dot {x}$ сделается равной нулю. Полученное противоречие доказывает необходимость выполнения первого соотношения равенства (2.1). Второе соотношение равенства (2.1) аналогичным образом следует из того, что функции f* в (1.8), (1.11) линейно зависят от скоростей системы.

Для доказательства утверждения II теоремы 1 следует воспользоваться формулой (1.15) с последующей интерпретацией полученного результата в терминах независимой переменной $x$. Действительно, тогда должно быть

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{m}} = \arg \mathop {\max }\limits_{\mathbf{u}} \text{[} - \chi (\xi ,{{{\mathbf{u}}}_{М}},{\mathbf{u}}_{М}^{'},{{{\mathbf{w}}}_{M}},{\mathbf{w}}_{М}^{'})F( - \xi ,{\mathbf{u}})] = \arg \mathop {\min }\limits_{\mathbf{u}} [\chi (x,{{{\mathbf{u}}}_{m}},{\mathbf{u}}_{m}^{'},{{{\mathbf{w}}}_{m}},{\mathbf{w}}_{m}^{'})F(x,{\mathbf{u}})],} \\ {{{{{\mathbf{\dot {w}}}}}_{m}} = \arg \mathop {\min }\limits_{{\mathbf{\dot {w}}}} \left[ { - \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{\xi }_{1}},{{{\mathbf{u}}}_{M}},{{{\mathbf{w}}}_{M}}){{{\dot {w}}}_{k}}} } \right] = \arg \mathop {\max }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{0}},{{{\mathbf{u}}}_{m}},{{{\mathbf{w}}}_{m}}){{{\dot {w}}}_{k}}} } \right].} \end{array}$

Теорема 2 является взаимной по отношению к теореме 1, и поэтому доказательство теоремы 2 вполне аналогично доказательству теоремы 1.

Подробное доказательство приведенных выше теорем с помощью метода первой вариации читатель может найти в [12].

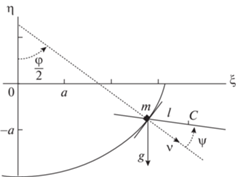
3. Пример. Маятник с точкой подвеса на перевернутой циклоиде. Материальная точка массы m движется без трения в вертикальной плоскости по перевернутой циклоиде (брахистохроне). К этой точке подвешен стержень, имеющий массу M и центральный момент инерции I. Стержень способен совершать колебания в той же плоскости. Требуется, управляя движением стержня, заставить точку m двигаться по циклоиде с возрастающей амплитудой колебаний около ее нижней точки. Обозначим буквой l расстояние от центра масс $С$ стержня до точки подвеса. Пусть ${\mathbf{\nu }}$ − внешняя нормаль к циклоиде в точке подвеса стержня, а $\psi $ − угол между стержнем и вектором ${\mathbf{\nu }}$. Угол $\psi $ примем в качестве управления с целью раскачивания системы, ограничив его допустимые значения: ${{\psi }_{m}} \leqslant \psi \leqslant {{\psi }_{M}}$ (рисунок).

Рисунок.

Маятник с точкой подвеса на циклоиде

Для описания движения введем абсолютную правоориентированную декартову систему координат $O\xi \eta \zeta $. Ось $O\eta $ направим вертикально вверх. Ось $O\xi $ расположим в плоскости движения. Тогда ось $O\zeta $ будет перпендикулярна указанной плоскости. Уравнение перевернутой циклоиды представим в виде

$\xi = a(\varphi + \sin \varphi ),\quad \eta = - a(1 + \cos \varphi ),\quad \zeta = 0,$

где $a > 0$ − постоянная, а $\varphi $ − обобщенная координата, задающая положение точки m на циклоиде. Циклоида выпукла вниз. Ее внешняя нормаль ${\mathbf{\nu }} = ({{\nu }_{\xi }},{{\nu }_{\eta }},0)$ имеет координаты

${{\nu }_{\xi }} = \sin \frac{\varphi }{2},\quad {{\nu }_{\eta }} = - \cos \frac{\varphi }{2}.$

Таким образом, вектор ${\mathbf{\nu }}$ образует с отрицательным направлением оси $O\eta $ угол $\varphi {\text{/}}2$.

Центр масс стержня имеет координаты

${{\xi }_{с}} = a(\varphi + \sin \varphi ) + l\sin \left( {\frac{\varphi }{2} + \psi } \right),\quad {{\eta }_{с}} = - a(1 + \cos \varphi ) - l\cos \left( {\frac{\varphi }{2} + \psi } \right).$

${{\dot {\xi }}_{с}} = 2a\dot {\varphi }{{\cos }^{2}}\frac{\varphi }{2} + l\left( {\frac{{\dot {\varphi }}}{2} + \dot {\psi }} \right)\cos \left( {\frac{\varphi }{2} + \psi } \right),\quad {{\dot {\eta }}_{с}} = a\dot {\varphi }\sin \varphi + l\left( {\frac{{\dot {\varphi }}}{2} + \dot {\psi }} \right)\sin \left( {\frac{\varphi }{2} + \psi } \right).$

Кинетическая энергия системы принимает вид

$T = 2(m + M){{a}^{2}}{{\dot {\varphi }}^{2}}{{\cos }^{2}}\left( {\frac{\varphi }{2}} \right) + 2Mla\dot {\varphi }\left( {\frac{{\dot {\varphi }}}{2} + \dot {\psi }} \right){{\cos }^{2}}\left( {\frac{\varphi }{2}} \right)\cos \psi + \frac{{M{{l}^{2}} + I}}{2}{{\left( {\frac{{\dot {\varphi }}}{2} + \dot {\psi }} \right)}^{2}}.$

Найдем силовую функцию:

$U = mga(1 + \cos \varphi ) + Mg\left[ {a(1 + \cos \varphi ) + l\cos \left( {\frac{\varphi }{2} + \psi } \right)} \right].$

Система уравнений Лагранжа записывается следующим образом:

(3.1)

$\begin{array}{*{20}{c}} {\frac{d}{{dt}}({{A}_{\psi }}\dot {\varphi } + {{B}_{\psi }}\dot {\psi }) + {{C}_{\psi }} = - Mlg\sin \left( {\frac{\varphi }{2} + \psi } \right) + {{Q}_{\psi }},} \\ {\frac{d}{{dt}}({{A}_{\varphi }}\dot {\varphi } + {{B}_{\varphi }}\dot {\psi }) + {{C}_{\varphi }} = - (m + M)ga\sin \varphi - \frac{{Mgl}}{2}\sin \left( {\frac{\varphi }{2} + \psi } \right),} \end{array}$

где

$\begin{array}{*{20}{c}} {{{A}_{\psi }} = \left( {2Mla{{{\cos }}^{2}}\left( {\frac{\varphi }{2}} \right)\cos \psi + \frac{{M{{l}^{2}} + I}}{2}} \right),{\text{ }}} \\ {{{B}_{\psi }} = (M{{l}^{2}} + I),{\text{ }}{{C}_{\psi }} = 2Mla\dot {\varphi }\left( {\frac{{\dot {\varphi }}}{2} + \dot {\psi }} \right){{{\cos }}^{2}}\left( {\frac{\varphi }{2}} \right)\sin \psi .} \end{array}$

(3.2)

$\left\{ {\begin{array}{*{20}{c}} {{{A}_{\varphi }} = 4(m + M){{a}^{2}}{{{\cos }}^{2}}\left( {\frac{\varphi }{2}} \right) + 2Mla{{{\cos }}^{2}}\left( {\frac{\varphi }{2}} \right)\cos \psi + \frac{{M{{l}^{2}} + I}}{4},{\text{ }}} \\ {{{B}_{\varphi }} = 2Mla{{{\cos }}^{2}}\left( {\frac{\varphi }{2}} \right)\cos \psi + \frac{{M{{l}^{2}} + I}}{2},{\text{ }}} \\ {{{C}_{\varphi }} = \left[ {2(m + M){{a}^{2}}{{{\dot {\varphi }}}^{2}} + 2Mla\dot {\varphi }\left( {\frac{{\dot {\varphi }}}{2} + \dot {\psi }} \right)\cos \psi } \right]\sin \varphi ,{\text{ }}} \end{array}} \right.$

${{Q}_{\psi }}$ − обобщенная сила, обеспечивающая требуемое изменение угла $\psi $.

В уравнениях (3.1) в качестве управляющей координаты выбирается угол $\psi $. В соответствии с уравнением (1.3) получим

(3.3)

$f = {{A}_{\varphi }} + {{B}_{\varphi }}\psi {\kern 1pt} ',\quad p = - \left[ {2(m + M){{a}^{2}} + 2Mla\left( {\frac{1}{2} + \psi {\kern 1pt} '} \right)\cos \psi } \right]\sin \varphi ,$

где $\psi {\kern 1pt} '$ − производная по $\varphi $. Знак множителя $\lambda $, вычисляемого по формуле (1.6), совпадает со знаком функции f. Правая часть второго уравнения (3.1) зависит от угла $\psi $. Оптимизируемая по величине $\psi $ функция в формулировке теорем 1 и 2 принимает вид

(3.4)

$\Phi = \chi (x,{{{\mathbf{u}}}_{m}},{\mathbf{u}}_{m}^{'},{\mathbf{w}}_{m}^{'})F(x,{\mathbf{u}}) = - \chi \left[ {(m + M)ga\sin \varphi + \frac{{Mgl}}{2}\sin \left( {\frac{\varphi }{2} + \psi } \right)} \right].$

Естественно принять ${\text{|}}\psi {\text{|}} \leqslant \pi {\text{/}}2$, так как при превышении этих пределов конструкция системы может быть нарушена. Экстремальные значения функции $\Phi $ достигаются при

$\psi = \pm \frac{\pi }{2} - \frac{\varphi }{2} \to \psi {\kern 1pt} ' = - \frac{1}{2}.$

Следовательно, для указанных экстремалей будем иметь

$f = {{A}_{\varphi }} - \frac{{{{B}_{\varphi }}}}{2} = 4(m + M){{a}^{2}}{{\cos }^{2}}\left( {\frac{\varphi }{2}} \right) + Mla{{\cos }^{2}}\left( {\frac{\varphi }{2}} \right)\cos \psi > 0.$

Поэтому коэффициент $\chi > 0$. Сузим допустимые границы изменения угла $\psi $:

$ - \frac{\pi }{2} < {{\psi }_{m}} < 0,\quad 0 < {{\psi }_{M}} < \frac{\pi }{2}.$

Тогда оптимальными могут быть также режимы постоянства функции $\psi (\varphi )$, для которых $\psi {\kern 1pt} ' = 0$, и будет выполнено

$f = {{A}_{\varphi }} = 4(m + M){{a}^{2}}{{\cos }^{2}}\left( {\frac{\varphi }{2}} \right) + 2Mla{{\cos }^{2}}\left( {\frac{\varphi }{2}} \right)\cos \psi + \frac{{M{{l}^{2}} + I}}{4} > 0.$

Следовательно, и в этом случае оказывается $\chi > 0$.

Применим утверждение I теоремы 1. Пусть ${{\varphi }_{0}} < 0$ есть левая граница отклонения по углу $\varphi $, а ${{\varphi }_{1}} > 0$ − соответственно правая граница, и в начальный момент $\varphi = {{\varphi }_{0}}$. Из формулы (2.1) видим, что наилучший способ достичь максимума положительного полуколебания состоит в применении правила

(3.5)

$\psi = \left\{ {\begin{array}{*{20}{l}} {{{\psi }_{M}},\quad {\text{если}}\quad \frac{\varphi }{2} + {{\psi }_{M}} < - \frac{\pi }{2},} \\ { - \frac{\pi }{2} - \frac{\varphi }{2},\quad {\text{если}}\quad \frac{\varphi }{2} + {{\psi }_{m}} \leqslant - \frac{\pi }{2} \leqslant \frac{\varphi }{2} + {{\psi }_{M}},} \\ {{{\psi }_{m}},\quad {\text{если}}\quad \frac{\varphi }{2} + {{\psi }_{m}} > - \frac{\pi }{2}.} \end{array}} \right.$

Применим утверждение II теоремы 1. Пусть теперь в начальный момент $\varphi = {{\varphi }_{1}} > 0$. Тогда, напротив, требуется минимизировать значение ${{\varphi }_{0}}$ отрицательного полуразмаха. Из (2.2) заключаем, что наилучший режим для достижения минимума отклонения отрицательного полуразмаха состоит в применении формулы

(3.6)

$\psi = \left\{ {\begin{array}{*{20}{l}} {{{\psi }_{m}},\quad {\text{если}}\quad \frac{\varphi }{2} + {{\psi }_{m}} > \frac{\pi }{2},} \\ {\frac{\pi }{2} - \frac{\varphi }{2},\quad {\text{если}}\quad \frac{\varphi }{2} + {{\psi }_{m}} \leqslant \frac{\pi }{2} \leqslant \frac{\varphi }{2} + {{\psi }_{M}},} \\ {{{\psi }_{M}},\quad {\text{если}}\quad \frac{\varphi }{2} + {{\psi }_{M}} < \frac{\pi }{2}.} \end{array}} \right.$

В итоге получается синтез управления для оптимального раскачивания маятника: после достижения максимального положительного отклонения маятника следует применять формулы (3.3); после достижения минимального отрицательного отклонения − формулы (3.2) и т.д.

Из теоремы 2 выводится синтез управления для оптимального успокоения колебаний маятника: после достижения максимального положительного отклонения маятника следует применять формулы (3.2), после достижения минимального отрицательного отклонения − формулы (3.3) и т.д.

Когда зависимость $\psi (\varphi )$ установлена, второе уравнение системы (3.1) становится замкнутым и его можно решать различными известными методами [2]. В частности, для решения можно применить формулу (1.7). После определения функции $\varphi (t)$ становится возможным из первого уравнения (3.1) найти обобщенную силу ${{Q}_{\psi }}$, обеспечивающую требуемое изменение угла $\psi $.

Из системы уравнений (3.1) видим, что при l = 0 угол $\psi $ становится циклической координатой. Тогда, чтобы обеспечить раскачивание, достаточно воспользоваться правилами разд. 2 для управления скоростями в конце полуразмаха.

Заключение. Применение предложенных алгоритмов управления, получаемых из необходимых условий оптимальности (2.1)–(2.4), предполагает учет информации о моментах времени достижения экстремальных значений оптимизируемой координаты и информации о направлении соответствующего полуколебания. Условия оптимальности (2.1)–(2.4) не содержат сопряженных переменных в смысле принципа максимума Л.С. Понтрягина [4]. Это облегчает применение указанных условий для рассмотренного класса задач. Дополнительным преимуществом предложенного метода служит то, что закон оптимального управления получается непосредственно в виде зависимости от оптимизируемой координаты. Используя предложенные условия оптимальности, можно получить аналитические решения для некоторых новых нетривиальных модельных задач. Эти условия упрощают решение соответствующих задач в многомерном пространстве управляющих функций по сравнению с известными методами. Они эффективны как для задач раскачивания, так и для задач успокоения колебаний.

Список литературы

Магнус К. Колебания: Введение в исследование колебательных систем. М.: Мир, 1982. 304 с.
Арнольд В.И. Обыкновенные дифференциальные уравнения. Изд. 2, испр. М.: МЦНМО, 2018. 344 с. ISBN 978-5-94057-907-6.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1976. 393 с.
Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980. 384 с.
Фантони И., Лозано Р. Нелинейное управление механическими системами с дефицитом управляющих воздействий / Пер. с франц. Ижевск: К-Динамика, 2012. 312 с. ISBN 978-5-906268-01-3.
Формальский А.М. Управление движением неустойчивых объектов. М.: Физматлит, 2012. 232 с. ISBN 978-5-9221-1460-8.
Голубев Ю.Ф., Хайруллин Р.З. К построению оптимальных режимов раскачивания двузвенного физического маятника // ПММ. 2000. Т. 64. Вып. 2. С. 217–226. ISSN 0032-8235.
Голубев Ю.Ф., Корянов В.В., Мелкумова Е.В. Приведение инсектоморфного робота в рабочее состояние из аварийного положения “вверх ногами” // Изв. РАН. ТиСУ. 2019. № 6. С. 163–176. ISSN: 0002-3388.https://doi.org/10.1134/S0002338819060052
Мартыненко Ю.Г., Формальский А.М. Управление продольным движением одноколесного аппарата по неровной поверхности // Изв. РАН. ТиСУ. 2005. № 4. С. 165–173.
Лавровский Э.К., Формальский А.М. О качении колеса посредством управления его дисбалансом // ПММ. Т. 70. Вып. 3. 2006. С. 371–383.
Охоцимский Д.Е., Энеев Т.М. Некоторые вариационные задачи, связанные с запуском искусственного спутника Земли // УФН. 1957. Т. 63. Вып. 1а. С. 5–32.
Golubev Yu.F. Optimal Control for Nonlinear Oscillations of Natural Mechanical Systems // Lobachevskii J. Math. 2021. V. 42. № 11. P. 2596–2607. ISSN: 1995-0802. https://doi.org/10.1134/S199508022111010X

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Теория и системы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал