Известия РАН. Теория и системы управления, 2022, № 5, стр. 131-151
ИССЛЕДОВАНИЯ И ОПТИМИЗАЦИЯ ЭТАПА КРЕЙСЕРСКОГО ПОЛЕТА САМОЛЕТОВ ГРАЖДАНСКОЙ АВИАЦИИ В ЗАДАЧЕ ВЕРТИКАЛЬНОЙ НАВИГАЦИИ
А. А. Голубева a, *, Н. В. Куланов a, **
a ФНЦ ФГУП “ГосНИИАС”
Москва, Россия
* E-mail: aagolubeva@2200.gosniias.ru
** E-mail: nvkulanov@2200.gosniias.ru
Поступила в редакцию 15.12.2021
После доработки 02.03.2022
Принята к публикации 28.03.2022
- EDN: AQDEZY
- DOI: 10.31857/S0002338822040096
Аннотация
Решение задачи формирования высотно-скоростного профиля полета самолетов гражданской и военно-транспортной авиации на этапе крейсерского полета и оптимизации по экономическому критерию проводится с использованием динамической модели движения центра масс в вертикальной плоскости. В модели учитывается изменение массы самолета и систематическая составляющая скорости ветра. Аэродинамические характеристики самолета и его вес, а также высотно-скоростные характеристики и дроссельные характеристики двигателей приближены к современному типовому среднемагистральному самолету. Для заданных сценариев полета найдены оптимальные законы управления и проведена оценка влияния на них возмущающих факторов в виде скорости ветра и отклонения температуры воздуха от стандартного значения. Сформулированы условия, при выполнении которых целесообразно переходить на большие значения числа Маха и эшелон полета.
Введение. В настоящее время разработка современных систем самолетовождения (ССВ) является одним из важнейших направлений в создании бортового оборудования самолетов гражданской авиации. К числу основных задач ССВ относятся:
1) формирование горизонтального маршрута полета, проходящего через заданные точки на поверхности Земли от аэродрома вылета до аэродрома прилета;
2) формирование высотно-скоростного профиля полета воздушного судна (ВС) в соответствии с заданными авиакомпанией (АК) требованиями по эффективности использования его в данном конкретном полете;
3) формирование в бортовую систему управления (БСУ) управляющих сигналов и команд, обеспечивающих реализацию рассчитанных по п.п. 1, 2 горизонтального и высотно-скоростного профилей полета;
4) прогноз требуемых значений отдельных параметров полета в заданных точках маршрута (например, так называемая задача 4D навигации) с расчетом времени прибытия в конечный пункт маршрута и затрат топлива на весь полет;
5) формирование необходимых “подсказок” и сигналов экипажу, помогающих выполнить предписанные ему действия.
Наибольшие сложности в научном плане связаны с решением второй и четвертой задач. Именно они определяют основное научное содержание задачи вертикальной навигации и позволяют отнести ее к классу задач управления и прогноза, а не к навигации в обычном понимании этого термина. Решение этих задач должно проводиться на борту ВС непрерывно в процессе полета по сформированному в п. 1 маршруту при заданных аэродинамических характеристиках конкретного ВС и характеристиках его двигателей, а также с учетом заданного АК критерия эффективности и доступной информации о состоянии атмосферы. При этом в соответствии с требованиями международных стандартов ошибка в прогнозе времени прибытия должна быть меньше 30 с, а в отдельных случаях – 5 с.
Критерием эффективности для самолетов гражданской авиации принимается определяемый АК экономический критерий в виде стоимости конкретного полета. Он является линейной комбинацией стоимости затраченного топлива и времени полета, связанных так называемым индексом стоимости.
Вопросам оптимизации режимов полета ВС и предсказания траекторий уделялось значительное внимание в работах сотрудников различных организаций, например, [1–6]. Их общей чертой является то, что в них не в полной мере учитываются наиболее важные для задачи вертикальной навигации особенности полета ВС. В частности:
используются некоторые абстрактные характеристики ВС и двигателей;
не всегда корректно учитываются изменение массы ВС, скорости ветра на высотах полета, отличие параметров атмосферы от стандартных значений;
роль АК и системы управления воздушным движением (СУВД) при формировании критериев эффективности;
ограничения, накладываемые на режимы полета ВС руководствами по летной эксплуатации (РЛЭ).
Данная статья является продолжением работ [7, 8], где представлены результаты исследования режимов взлет и набор высоты. Здесь применительно к крейсерскому полету предлагается методика и приводятся результаты решения задачи оптимизации полета ВС с учетом существенных, но обычно не учитываемых факторов.
1. Режимы движения ВС (сценарии) на этапе крейсерского полета. Режимы движения ВС на этапе крейсерского полета задаются в РЛЭ каждого конкретного ВС. Кроме того, они определяются АК и СУВД. Чтобы в наибольшей степени охватить возможное множество возникающих при этом режимов в качестве типовых, на этапе крейсерского полета будем рассматривать следующие:
1) полет с оптимальным (либо с заданным Мзад) значением числа Маха Мopt = const на заданной высоте Hзад;
2) полет на оптимальной (либо заданной Hзад) высоте Hopt = const с заданным числом Мзад;
3) полет с оптимальным значением числа Мopt = const на оптимальной высоте Hopt = const.
4) полет с переходом с текущей высоты H на оптимальную высоту Hopt (либо переход с текущего значения числа М на Мopt);
5) полет с переходом на очередной оптимальный эшелон;
6) оптимальный по выбранному критерию полет с обеспечением заданного времени прибытия Tзад в очередную точку маршрута.
Здесь заданные значения высоты и числа Маха формируются экипажем ВС в соответствии с руководящими документами и указаниями АК и СУВД.
Оптимальные значения этих параметров должны рассчитываться на борту ВС (в процессе предполетной подготовки и в полете) по заданным АК критериям оптимальности в зависимости от:
текущих параметров полета;
доступной информации о состоянии атмосферы;
имеющихся в бортовой базе данных по актуальным аэродинамическим характеристикам ВС и его двигателей.
2. Критерии оптимизации. В настоящее время в качестве основного критерия при формировании вертикального профиля полета ВС принимаются прямые эксплуатационные расходы (C), которые складываются из стоимости затраченного топлива и времени полета. АК заинтересована в минимизации C и поэтому требует, чтобы ССВ обеспечила в каждом конкретном полете реализацию траектории с минимизацией прямых эксплуатационных расходов. При этом в стоимости времени учитывается множество факторов, к которым относятся: стоимость погрузоразгрузочных работ, стоимость аэронавигационного сопровождения полета ВС, аренда и амортизация ВС, различные регламентные работы, зарплата и страховка экипажа и др. Очевидно, что критерий C для этапа крейсерского полета можно записать в виде
где qт – расход топлива в единицу времени, Cт, Ct – стоимость единицы топлива и времени соответственно, tk – длительность участка крейсерского полета.Учитывая, что стоимость топлива Cт для конкретного маршрута полета является величиной постоянной, критерий стоимости полета можно заменить критерием относительной стоимости IC , т.е. отношением стоимости полета C к величине стоимости единицы топлива Cт:
где $CI = {{C}_{t}}{\text{/}}{{C}_{{\text{т}}}}$ и называется индексом стоимости (CostIndex).Заметим, что критерий IC имеет размерность расхода топлива (кг, т, …), поэтому его можно рассматривать как приведенный расход топлива.
Наряду с критерием относительной стоимости или приведенного топлива (2.1) будем считать значение фактического расхода топлива Iт и полное время полета It = tk, как имеющее в ряде случаев важное самостоятельное значение.
3. Модель движения ВС. При решении любой задачи, связанной с исследованием и оптимизацией движения какого-либо объекта, построение модели его движения – одна из важнейших составляющих методики решения поставленной задачи. Здесь должна быть найдена та золотая середина, которая бы охватывала все существенные особенности рассматриваемого явления и, в то же время, позволяла бы довести решение до конца с использованием предполагаемых методов.
К числу основных особенностей, характерных для этапа крейсерского полета, относятся:
доходящая до нескольких часов длительность и большая протяженность этапа;
наличие на высотах полета значительной горизонтальной составляющей скорости ветра, достигающей сотен километров в час;
существенное изменение в процессе полета массы ВС;
движение ВС в поле тяготения Земли.
Анализ имеющихся в научно-технической литературе моделей движения ВС показывает, что они в полной мере не учитывают эти особенности. Это связано с тем, что основное внимание уделяется либо вопросам динамики полета, либо оценкам потенциальных возможностей и разработке методов оптимизации, в которых неизбежно (в угоду предполагаемым методам исследования) проводятся существенные упрощения модели. Длительность и протяженность полета предполагают использование полных моделей движения ВС с учетом формы Земли и ее вращения, имеющихся, например, в публикациях [9–11].
Значительная продолжительность этапа полета и сравнительно небольшие длительности переходных процессов при отработке углов ориентации ВС позволяют в описании модели движения ВС ограничиться только движением центра масс. Так поступают, например, в задачах управления траекториями аэрокосмических аппаратов [10, 11].
В полной модели движения твердого тела переменной массы, каковым является ВС, относительно Земли помимо активных сил и сил гравитации должны участвовать переносное и кориолисово ускорения, ускорение от изменения массы и систематических составляющих скорости ветра. Как показывают расчеты, дополнительные ускорения от этих факторов могут достигать значений (2–4) × 10–3 g. Понятно, что при формировании законов управления такими величинами, по сравнению с ускорениями от активных сил, можно пренебречь. Однако в задачах прогноза на длительных интервалах времени, что имеет место в задачах вертикальной навигации, не учет их приводит к ошибкам в несколько десятков километров за час полета или несколько минут в оценке времени прибытия в заданную точку маршрута.
По этим причинам модели для решения задач управления (п. 2) и прогноза (п. 4) должны быть различны. В качестве основы для разработки “прогнозных” моделей могут использоваться соотношения (1.16) публикации [10] после коррекции их в направлении более строгого учета изменения массы ВС и скорости ветра.
3.1. Уравнения движения центра масс ВС. При разработке модели движения ВС для решения задач формирования вертикального профиля полета ввиду достаточной малости значений переносного и кориолисового ускорения можно отказаться от их учета. В этом случае движение ВС рассматривается как движение его центра масс в равномерном гравитационном поле относительно плоской поверхности Земли. Соответствующая этой модели система дифференциальных уравнений, описывающая движение центра масс, получится из теоремы об изменении количества движений материальной точки.
Как показано в [7, 8], при принятых допущениях уравнения движения центра масс ВС при формировании профиля полета имеют вид
(3.1)
$\begin{gathered} mV\frac{{d\theta }}{{dt}} = T\sin {{\alpha }_{{\text{т}}}} + Y - mg\cos \theta - {{q}_{{\text{c}}}}{{U}_{{\text{в}}}}\sin \theta , \\ \frac{{dH}}{{dt}} = V\sin \theta , \\ \frac{{dL}}{{dt}} = V\cos \theta + {{U}_{{\text{в}}}}, \\ \end{gathered} $Входящие в систему уравнений (3.1) силы R, Y определяются соотношениями:
где ${{C}_{X}}$, ${{C}_{Y}}$ – коэффициенты соответствующих аэродинамических сил; $S$ – характерная площадь крыла ВС; $\rho $ – плотности воздуха на высоте H.Аэродинамические коэффициенты СX, СY в общем случае являются функциями большого числа переменных, однако в траекторных задачах принято использовать их балансировочные значения в виде функций
где Fl – параметр, определяющий конфигурацию крыла.Входящие в уравнения (3.1) сила тяги Т и секундный расход топлива qc обычно задаются таблицами или графиками вида
(3.4)
$\begin{gathered} T = T(\delta ,{{H}_{{\text{б}}}},M,\Delta {{T}^{0}}), \\ {{q}_{{\text{c}}}} = {{q}_{{\text{c}}}}(\delta ,{{H}_{{\text{б}}}},M,\Delta {{T}^{0}}), \\ \end{gathered} $Из анализа соотношений (3.1)–(3.4) видно, что при известных (таблицы, графики, аналитические выражения и т.д.) зависимостях ${{C}_{X}} = {{C}_{X}}(\alpha ,M,Fl)$, ${{C}_{Y}} = {{C}_{Y}}(\alpha ,M,Fl)$, $T = T(\delta ,{{H}_{{\text{б}}}},M,\Delta {{T}^{0}})$, ${{q}_{{\text{c}}}} = {{q}_{{\text{c}}}}(\delta ,{{H}_{{\text{б}}}},M,\Delta {{T}^{0}})$ система уравнений (3.1) однозначно определяет динамику изменения фазовых переменных H, L, V, θ, m при заданных $\alpha (\xi )$, $\delta (\xi )$, где $\xi $ – какой-либо монотонный скалярный параметр, например время t или дальность L.
Функции
являются в данном случае для системы (3.1) функциями управления или управляющими функциями, на которые наложены ограничения:(3.6)
$\begin{gathered} {{\alpha }_{{\min }}} \leqslant \alpha \leqslant {{\alpha }_{{\max }}}, \\ {{\delta }_{{\min }}} \leqslant \delta \leqslant {{\delta }_{{\max }}}. \\ \end{gathered} $Соответствующие ограничения могут быть наложены и на фазовые координаты модели.
Как видно из соотношений (3.1)–(3.6), данная модель отличается от большинства известных тем, что в ней корректно учитываются изменение в процессе полета массы ВС и влияние горизонтальной составляющей скорости ветра.
3.2. Модель активных сил. Значения аэродинамических коэффициентов, а также высотно-скоростные и дроссельные характеристики двигателей ВС обычно задаются в виде таблиц на сетке их аргументов. Такой способ задания не позволяет получать с достаточной точностью производные от этих величин, что обычно требуется при использовании методов оптимизации и построении вычислительных алгоритмов.
Как показали исследования, эффективным методом преобразования заданных табличных значений в соотношения с требуемыми свойствами непрерывности является метод последовательной полиномиальной аппроксимации, суть которого на примере СX, СY понятна из рассмотрения соотношения
(3.7)
${{C}_{{X/Y}}} = {{A}_{0}}(M) + {{A}_{1}}(M)\alpha + {{A}_{2}}(M){{\alpha }^{2}} + {{A}_{3}}(M){{\alpha }^{3}},$Как можно видеть, в этом методе в зависимости от предполагаемого в дальнейшем применения, выбирается последовательность аргументов, по которым проводятся последовательная полиномиальная аппроксимация исходных таблиц и далее – коэффициентов предыдущей аппроксимации.
Аналогичные выражения получаются при аппроксимации значений тяги двигателей Т и секундного расхода топлива qc по четырем переменным δ, M, Hб, ΔT0.
Такая аппроксимация обеспечивает для системы (3.1) непрерывность правых частей и их производных не ниже второго порядка, что достаточно для применения современных методов оптимизации и вычислительной математики.
3.3. Модель атмосферы. Особое место в модели движения ВС имеет модель атмосферы. Это связано с тем, что полет ВС практически всегда проходит в условиях отличных от стандартных (принятых в ГОСТ 4401-81), а задачи вертикальной навигации должны решаться для текущих условий полета. По этой причине необходимо иметь модель атмосферы, учитывающую отличия реальной атмосферы от стандартной, в частности по давлению на уровне моря и температуре воздуха.
Полагая, что атмосфера Земли в целом находится в равновесии, для построения модели воспользуемся основным уравнением статики атмосферы (3.8), которое справедливо для любого газа. Оно выражает условие равновесия между двумя силами, действующими на единицу массы воздуха по вертикали: силой вертикального барического градиента и силой тяжести:
где $\rho ,\;p$ – массовая плотность и давление воздуха; g – ускорение силы тяжести; h – геометрическая высота относительно среднего уровня моря.Дополнив (3.8) соотношением Менделеева–Клайперона, определяющим связь между температурой Т, давлением p и плотностью $\rho $ воздуха
где ${{R}_{{{\kern 1pt} {\text{c}}}}}$ = 287.05287 – удельная газовая постоянная сухого воздуха, из (3.8), (3.9) получим дифференциальное уравнение для определения давления p как функции высоты h:Отсюда следует, что зависимость давления сухого воздуха P от высоты h в предположении о постоянстве g определяется только видом зависимости температуры воздуха от высоты, т.е. $p(h) = F(T(h))$.
Задаваясь различными законами изменения температуры Т по высоте h, из (3.9), (3.10) можно получить различные модели атмосферы. Для задач вертикальной навигации наибольший интерес представляют следующие две модели атмосферы:
стандартная атмосфера по ГОСТ 4401-81;
так называемая квазистандартная атмосфера, учитывающая возможные отклонения ΔT температуры и давления ΔP от стандартных значений.
В первом случае функция F имеет вид
(3.11)
$T(h) = \left\{ {\begin{array}{*{20}{l}} {{{T}_{0}} - ah,\quad {\text{если}}\quad h \leqslant 11{\text{ км,}}} \\ {{{T}_{{11}}},\quad {\text{если}}\quad h > 11{\text{ км,}}} \end{array}} \right.$Во втором случае функция F сохраняет вид (3.11), но могут меняться значения параметров ${{T}_{0}}$ и a , а также значение давления на уровне моря ${{P}_{0}}$.
При таком способе построения функции F решение уравнения (3.10) имеет единый вид для обеих моделей атмосферы:
(3.12)
$T(h) = \left\{ {\begin{array}{*{20}{l}} {P_{0}^{*}{{{\left( {1 - \frac{a}{{T_{0}^{*}}}h} \right)}}^{{\frac{{{{k}_{P}}}}{a}}}},\quad {\text{если}}\quad h \leqslant 11{\text{ км,}}} \\ {{{P}_{{{\kern 1pt} 11}}}{\kern 1pt} {{e}^{{\frac{{{{K}_{P}}}}{{{{T}_{{11}}}}}(h - 11)}}},\quad {\text{если}}\quad h > 11{\text{ км,}}} \end{array}} \right.$Выражения (3.12) однозначно определяют значения давления воздуха на высоте h как в случае стандартной, так и квазистандартной моделях атмосферы. Далее, используя уравнение Менделеева–Клайперона, получаем соотношение для нахождения плотности воздуха на высоте h:
Выражения (3.12), (3.13) полностью определяют обе требуемые модели атмосферы и показывают влияние температуры воздуха на ее параметры.
4. Постановка задачи. Принципиальное влияние на постановку задачи оказывает принятый в гражданской и транспортной авиации подход к формированию высотно-скоростного профиля полета ВС. Суть его заключается в том, что для АК и СУВД важно знать (и задавать) текущие значения параметров режима полета ВС, какими могут служить высота, скорость, угол наклона траектории, вертикальная скорость и др. Поэтому целью данной работы прежде всего является исследование влияния этих параметров на значения критериев качества и нахождение их оптимальных значений, а не поиск оптимальных законов управления при перелете ВС из точки А в точку В. Целесообразность такого подхода связана с тем, что в современных ВС гражданской и транспортной авиации собственно управлением (созданием целенаправленных воздействий на органы управления ВС) занимается бортовая система управления, а ССВ задает ей необходимые значения параметров режима полета (уставки), обеспечивающие выполнение целей управления.
Множество указанных выше конкретных сценариев этапа крейсерского полета приводит к множеству постановок задач для каждого из возможных сценариев, которые рассматриваются далее.
5. Вектор параметров модели. Анализируя уравнения модели (3.1)–(3.6) и определение критерия оптимизации (2.1), можно видеть, что в данном случае значение критерия зависит от следующего набора параметров:
параметры режима полета: Мзад, Нзад;
параметр, задаваемый авиакомпанией: CostIndex (CI);
вес ВС в начале этапа полета (m);
дальность полета L;
составляющая ветра на направление полета (Uв);
отклонение температуры воздуха на барометрической высоте от стандартного значения (ΔT0).
Заметим, что здесь, так же как и в (3.1), под Uв понимается не проекция ветра на направление полета, а составляющая ветра, получаемая из рассмотрения навигационного треугольника.
6. Оптимизация сценариев 1–3. В этих сценариях требуется найти оптимальные по критерию (2.1) значения какого-то одного (сценарии 1, 2) или обоих (сценарий 3) параметров режима полета ВС при заданных значениях других параметрах. Так как по условиям реализации сценариев предполагается, что как оптимизируемые, так и заданные параметры постоянны на каждом отдельном этапе полета, то задача сводится к процедуре поиска минимальных значений некоторой функции
где F – значение оптимизируемого критерия (Iт, IС); pупр, pзад – вектор управляющих и заданных параметров соответственно.Дополнив (6.1) условиями
приходим к классической задаче поиска минимального значения функции (6.1) при ограничениях на область определения переменных в виде (6.2). Особенность данной задачи состоит в том, что ее решение должно проводиться в два этапа.На первом из них для заданного вектора ${{p}_{{{\text{зад}}}}}$ необходимо найти законы формирования управляющих функций (3.5), обеспечивающие требуемые свойства вектору ${{p}_{{{\text{упр}}}}}$, и провести интегрирование системы уравнений (3.1) с учетом соотношений (3.2)–(3.6).
В сценариях 1, 2 вектор ${{p}_{{{\text{упр}}}}}$ состоит из одной компоненты: Мзад в сценарии 1 и Нзад в сценарии 2. В сценарии 3 вектор pупр имеет две компоненты Мзад и Нзад. Остальные параметры модели образуют вектор pзад. Эту задачу будем называть задачей управления. Решение ее позволяет получить значение функции F, соответствующее выбранной паре векторов ${{p}_{{{\text{упр}}}}}$ и ${{p}_{{{\text{зад}}}}}$.
На втором этапе проводится собственно оптимизация функции F по вектору ${{p}_{{{\text{упр}}}}}$, его будем называть этапом оптимизации.
Каждый из этапов имеет различные постановки задач и методы решения, поэтому рассмотрим их отдельно.
6.1. Этап управления. Как можно понять из описания сценариев 1–3, для них задача управлений формулируется одинаково. Для системы (3.1) при заданном векторе ${{p}_{{{\text{зад}}}}}$ требуется найти такие законы формирования управляющих функций $\alpha = \alpha (\xi )$, $\delta = \delta (\xi )$, при которых после окончания переходного процесса выполняются условия
(6.3)
$H = {{H}_{{{\text{зад}}}}} = {\text{const,}}\quad M = {{M}_{{{\text{зад}}}}} = {\text{const}}.$Интегрирование системы (3.1) здесь ведется из начального вектора фазовых координат до заданного значения конечной дальности L. Заметим, что задача интегрирования системы (3.1) формально поставлена корректно в том смысле, что имеются две управляющие функции (3.5), обеспечивающие требуемое поведение двух параметров режима полета (6.3).
6.1.1. Возможные подходы к получению уравнений управляемой системы. При формировании законов управления (3.5) системы (3.1) можно использовать различные подходы, к числу которых относятся методы построения пропорционально-интегрально-дифференцирующих (ПИД) регуляторов, методы концепции обратных задач динамики и методы теории оптимального управления.
В частности, в первой группе этих методов можно положить
(6.4)
$\begin{gathered} ({{\tau }_{\alpha }}p + 1)\alpha = {{K}_{1}}(H - {{H}_{{{\text{зад}}}}}) + \frac{{{{K}_{2}}}}{p}\int\limits_0^t {(H - {{H}_{{{\text{зад}}}}})dt} + {{K}_{3}}p\frac{d}{{dt}}(H - {{H}_{{{\text{зад}}}}}), \hfill \\ ({{\tau }_{\delta }}p + 1)\delta = {{K}_{4}}(M - {{M}_{{{\text{зад}}}}}) + \frac{{{{K}_{5}}}}{p}\int\limits_0^t {(M - {{M}_{{{\text{зад}}}}})dt} + {{K}_{6}}p\frac{d}{{dt}}(M - {{M}_{{{\text{зад}}}}}), \hfill \\ \end{gathered} $При использовании ПИД-регуляторов система уравнений модели (3.1) дополняется двумя уравнениями (6.4), динамика которых определяется значениями постоянных времени ${{\tau }_{\alpha }},{{\tau }_{\delta }}$, оказывающих существенное влияние на допустимый шаг интегрирования расширенной системы уравнений.
Как показали результаты моделирования, для каждого режима полета можно подобрать параметры законов управления (6.4), обеспечивающие в рассматриваемых диапазонах изменения высоты и скорости полета ВС приемлемое качество переходных процессов. Основным недостатком метода ПИД-регуляторов оказалось значительное ограничение допустимого шага интегрирования (единицы секунд) расширенной системы по сравнению с исходной, что приводит к существенному увеличению времени расчета траектории полета.
В методе концепции обратных задач динамики необходимо задаться в системе (3.1) желаемым законом изменения фазовых переменных $V$ и $\theta $, например
(6.5)
$({{\tau }_{V}}p + 1)V = {{V}_{{{\text{зад}}}}},\quad ({{\tau }_{\theta }}p + 1){\kern 1pt} {\kern 1pt} \theta = {{\theta }_{{{\text{зад}}}}},$С учетом этого система (3.1) принимает вид
Необходимые для интегрирования этой системы значения отклонения рукоятки управления двигателем $\delta = \delta (\xi )$ (а, следовательно, значения расхода топлива qc) находим из решения системы уравнений:
(6.7)
$\begin{gathered} T\cos {{\alpha }_{{\text{т}}}} - R - mg\sin \theta + {{q}_{{\text{c}}}}(V + {{U}_{{\text{в}}}}\cos \theta ) - m({{V}_{{{\text{зад}}}}} - V){\text{/}}{{\tau }_{V}} = 0, \\ T\sin {{\alpha }_{{\text{т}}}} + Y - mg\cos \theta - {{q}_{{\text{c}}}}{{U}_{{\text{в}}}}\sin \theta - mV({{\theta }_{{{\text{зад}}}}} - \theta ){\text{/}}{{\tau }_{V}} = 0. \\ \end{gathered} $Сравнивая (3.1) и (6.6), можно видеть, что использование концепции обратных задач динамики обеспечивает существенное упрощение интегрируемых уравнений. Кроме того, так как $({{\tau }_{V}},{{\tau }_{\theta }}) > ({{\tau }_{\alpha }},{{\tau }_{\delta }})$, полученные уравнения, по сравнению с ПИД-регулятором, допускают применение большего шага интегрирования. Однако за эти положительные свойства приходится платить необходимостью решения уравнений (6.7) на каждом шаге интегрирования системы (6.6).
При решении поставленных задач методом теории оптимального управления Понтрягина Л.С. [12] управляемая система описывается уравнениями (3.1) без какого-либо расширения, а условия (6.3) выступают как ограничения на фазовый вектор. Известные сложности решения таких задач даже для одного варианта условий (6.3) делают бесперспективным применение этого метода на втором этапе решения задачи при поиске оптимальных значений Mзад и Hзад.
Анализ рассмотренных подходов к построению модели управляемой системы показывает, что способ, основанный на использовании метода обратных задач динамики, более предпочтителен по сравнению с двумя другими. Это связано с тем, что здесь в рассматриваемой системе (6.6) можно исключить первые два уравнения и решать задачу для установившихся значений V и $\theta $. Возможность такого подхода базируется на результатах работы [13], где показано, что учет переходных процессов в рассматриваемых задачах практически не влияет на критерии качества управления.
С помощью данного предположения все составляющие фазового вектора, кроме m, становятся известными, а в системе (6.6) остаются только два последние уравнения, которые должны интегрироваться с учетом выполнения двух соотношений:
(6.8)
$\begin{gathered} {{F}_{1}}(\delta ,\alpha ) = T\cos {{\alpha }_{{\text{т}}}} - R + {{q}_{{\text{c}}}}(V + {{U}_{{\text{в}}}}) = 0, \\ {{F}_{2}}(\delta ,\alpha ) = T\sin {{\alpha }_{{\text{т}}}} + Y - mg = 0, \\ \end{gathered} $Таким образом, задача управления как определение управляющих функций системы (3.1), обеспечивающих выполнение условий (6.3), свелась к решению уравнений (6.8) относительно $\delta = \delta ( \cdot )$ и $\alpha = \alpha ( \cdot )$.
6.1.2. Способы решения системы уравнений (6.8). Как известно, общих методов решения систем подобного типа не существует и успех решения зависит от наличия в них тех или иных особенностей. В данном случае такой особенностью является линейность системы (6.8) относительно переменных T, qc. Это позволяет получить следующие решения $T{\kern 1pt} {\text{*}},q{\kern 1pt} *$:
(6.9)
$T{\kern 1pt} * = \frac{{{{b}_{2}}}}{{{{a}_{{21}}}}},\quad q{\kern 1pt} * = \frac{{{{b}_{1}}{{a}_{{21}}} - {{b}_{2}}{{a}_{{11}}}}}{{{{a}_{{12}}}{{a}_{{21}}}}},$В соответствии с принятой ранее формой аппроксимации активных сил запишем
Отсюда следует, что левые части соотношений (6.9) являются полиномами третьей степени относительно δ, а правые части – функциями α. Поэтому (6.9) представим как
(6.10)
$\begin{gathered} f(x) = {{a}_{0}}{{x}^{3}} + {{a}_{1}}{{x}^{2}} + {{a}_{2}}x + {{a}_{3}} = 0, \\ g(x) = {{b}_{0}}{{x}^{3}} + {{b}_{1}}{{x}^{2}} + {{b}_{2}}x + {{b}_{3}} = 0, \\ \end{gathered} $Решение системы алгебраических уравнений (6.10) проведем с использованием теории полиномов [14, 15]. Первым шагом этого метода является построение так называемого результанта полиномов $R(f,g)$:
(6.11)
$R(f,g) = \left| {\begin{array}{*{20}{c}} {{{a}_{0}}}&{{{a}_{1}}}&{{{a}_{2}}}&{{{a}_{3}}}&0&0 \\ 0&{{{a}_{0}}}&{{{a}_{1}}}&{{{a}_{2}}}&{{{a}_{3}}}&0 \\ 0&0&{{{a}_{0}}}&{{{a}_{1}}}&{{{a}_{2}}}&{{{a}_{3}}} \\ 0&0&{{{b}_{0}}}&{{{b}_{1}}}&{{{b}_{2}}}&{{{b}_{3}}} \\ 0&{{{b}_{0}}}&{{{b}_{1}}}&{{{b}_{2}}}&{{{b}_{3}}}&0 \\ {{{b}_{0}}}&{{{b}_{1}}}&{{{b}_{2}}}&{{{b}_{3}}}&0&0 \end{array}} \right|.$Вычеркиванием из (6.11) первых и последних строк и столбцов получаем первый субрезультант ${{R}_{1}}(f,g)$ полиномов $f(x),\;g(x)$:
Вычеркиванием из (6.11) первой и последней строки, а также первого и предпоследнего столбцов находим $\det {{M}_{1}}$:
Далее пользуемся теоремой о существовании решения системы алгебраических уравнений, в соответствии с которой для того, чтобы полиномы $f(x),\;g(x)$ имели только один общий корень x* необходимо и достаточно, чтобы $R(f,g) = 0,$ а ${{R}_{{{\kern 1pt} 1}}}(f,g) \ne 0$. При этом
Наличие данной теоремы обуславливает целесообразность использования для решения системы (6.10) рассмотренного способа, хотя возможны и другие решения.
Конкретное применение предлагаемого метода сводится к получению выражений для $R(f,g)$, ${{R}_{1}}(f,g)$ и $\det {{M}_{1}}$ как функций коэффициентов ${{a}_{i}},{{b}_{i}},i = 0,3$. Проведя необходимые преобразования, находим
(6.13)
$\begin{gathered} {{R}_{1}}(f,g) = {{K}_{{01}}}({{K}_{{03}}} + {{K}_{{12}}}) - K_{{02}}^{2}, \\ \det {{M}_{1}} = {{K}_{{13}}}{{K}_{{01}}} - {{K}_{{03}}}{{K}_{{02}}}, \\ R(f,g) = {{K}_{{01}}}({{S}_{{02}}} - K_{{13}}^{2} + {{K}_{{23}}}({{K}_{{12}}} + {{K}_{{03}}})) + {{K}_{{02}}}({{S}_{{01}}} - {{K}_{{02}}}{{K}_{{23}}}) - K_{{03}}^{3} + 2{{a}_{3}}{{b}_{3}}{{S}_{{12}}}, \\ \end{gathered} $Первые два выражения (6.13) позволяют вычислить $x{\kern 1pt} *$ по соотношению (6.12) и, таким образом, найти значение отклонения рукоятки управления двигателем $\delta {\kern 1pt} *$, обеспечивающее (совместно c углом атаки $\alpha {\kern 1pt} *$) выдерживание заданных значений высоты и скорости. Значение угла атаки $\alpha {\kern 1pt} *$ находим из условия $R(f,g) = 0$. Если имеется несколько решений этого уравнения, то из них выбирается то, которое удовлетворяет заданным ограничениям (3.6).
Как показали результаты моделирований, предлагаемый метод дает возможность существенно увеличить допустимый шаг интегрирования модели движения. Так, если в основу модели принять соотношения (6.6), (6.7), то допустимый шаг интегрирования не превышает 2 с, а предлагаемый метод позволяет увеличить шаг интегрирования до 500 с и более. Одной из особенностей его является необходимость решения уравнения $R(f,g) = 0$ на каждом шаге интегрирования, что предполагает использование методов численного решения подобного рода уравнений. Так как эти методы основаны на выполнении тех или иных итерационных процедур, то данный метод будем называть итерационным.
Помимо рассмотренного, существует и другой метод решения уравнений (6.8), в котором практически отсутствует необходимость численного решения уравнений типа $R(f,g) = 0$.
Суть его заключается в переходе от конечных уравнений (6.8) к их дифференциальным аналогам, поэтому он называется дифференциальным. Для этого заметим, что в (6.8) участвует параметр m (масса ВС), следовательно решения $\alpha {\kern 1pt} *$ и $\delta {\kern 1pt} *$ являются функциями m. Так как уравнения (6.8) должны выполняться при любых значениях m, то производная от левых частей этих уравнений по m равна нулю, т.е.
(6.14)
$\begin{gathered} \frac{{d{{F}_{1}}}}{{dm}} = {{F}_{{1\delta }}}\frac{{d\delta }}{{dm}} + {{F}_{{1\alpha }}}\frac{{d\alpha }}{{dm}} + {{F}_{{1m}}} = 0, \\ \frac{{d{{F}_{2}}}}{{dm}} = {{F}_{{2\delta }}}\frac{{d\delta }}{{dm}} + {{F}_{{2\alpha }}}\frac{{d\alpha }}{{dm}} + {{F}_{{2m}}} = 0, \\ \end{gathered} $Проведя необходимые преобразования, получим
(6.15)
$\begin{gathered} \frac{{d\delta }}{{dm}} = g\frac{{mg - Y + {{R}_{\alpha }}}}{\Delta }, \\ \frac{{d\alpha }}{{dm}} = g\frac{{T\cos {{\alpha }_{{\text{т}}}} + {{q}_{\delta }}(V + {{U}_{{\text{в}}}})}}{\Delta }, \\ \Delta = (V\cos {{\alpha }_{{\text{т}}}} + {{q}_{\delta }}(V + {{U}_{{\text{в}}}}))(T\cos {{\alpha }_{{\text{т}}}} + {{Y}_{\alpha }}) + (T\sin {{\alpha }_{{\text{т}}}} + {{R}_{\alpha }}){{T}_{\delta }}\sin {{\alpha }_{{\text{т}}}}, \\ \end{gathered} $Уравнения (6.15) являются дифференциальными аналогами уравнений (6.8), они определяют искомые управляющие функции $\delta = \delta ( \cdot )$ и $\alpha = \alpha ( \cdot )$ как решения системы уравнений:
(6.16)
$\begin{gathered} \frac{{d\alpha }}{{dt}} = - \frac{{d\alpha }}{{dm}}{{q}_{{\text{c}}}}, \\ \frac{{d\delta }}{{dt}} = - \frac{{d\delta }}{{dm}}{{q}_{{\text{c}}}}, \\ \end{gathered} $Эти уравнения описывают движение центра масс ВС при полете его на заданной высоте $H = {{H}_{{{\text{зад}}}}}$ = const со скоростью $M = {{M}_{{{\text{зад}}}}} = {\text{const}}$. В таком режиме полета при заданной дальности неизвестными являются время и расход топлива, которые и определяются в процессе решения системы уравнений (6.16).
Как показывают результаты моделирования, оба предлагаемых способа достаточно близки по затратам времени моделирования на движения центра масс ВС, причем первый из них дает завышенное (на несколько килограмм) значение расхода топлива, а второй – такого же порядка заниженное значение.
6.2. Этап оптимизации. Использование итерационного или дифференциального методов решения соотношений (6.8) обеспечивает построение модели объекта управления и позволяет провести моделирование режима полета ВС при любых заданных значениях высоты и скорости, а следовательно, и рассчитать значения критериев стоимости ${{I}_{C}}$, расхода топлива Iт и времени полета ${{I}_{t}}$ на дальность L. При заданном значении CI эти критерии, как следует из (2.1), связаны соотношением ${{I}_{C}} = {{I}_{{\text{т}}}} + {{I}_{t}}CI$. Поэтому фактически для расчета всех критериев достаточно найти только значение Iт, что можно выполнить, например, путем интегрирования системы уравнений (6.16) до заданной дальности Lзад. Заметим, что начальные условия $\alpha (0)$ и $\delta (0)$ для системы (6.16) всегда получаются с помощью итерационного метода решения соотношений (6.8).
Как можно видеть, в сценариях 1, 2 задача оптимизации сводится к поиску оптимального значения управляющего параметра M или H при заданных значениях всех остальных параметров сценария. В сценарии 3 оптимизацию критериев необходимо провести по двум параметрам. Таким образом, задача оптимизации параметров в сценариях 1–3 свелась к классической задаче нелинейного программирования, для которой имеется множество эффективных методов решения. Выбор конкретного из них определяется целью проводимого исследования и практическим использованием результатов. В данном случае работа направлена на создание методической основы для разработки алгоритмического обеспечения бортового вычислителя ССВ. Это предъявляет ряд требований к вычислительному методу, к числу которых относятся: предсказуемость времени выполнения расчетов, глобальность полученного решения и простота контроля процесса вычислений. С другой стороны, требования к методу диктуются свойствами оптимизируемых функций, такими, как непрерывность, дифференцируемость и количество локальных оптимумов.
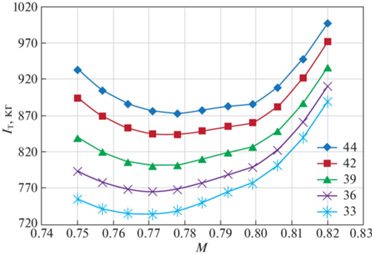
Проведенное исследование показало, что в рассматриваемом диапазоне высот и скоростей полета среднемагистральных ВС типа SSJ-100 типичный вид зависимости ${{I}_{{\text{т}}}} = {{I}_{{\text{т}}}}(M{\text{/}}m)$ для значений массы m = 33–44 т имеет вид, представленный на рис. 1.
Показанный на рис. 1 характер зависимости ${{I}_{{\text{т}}}} = {{I}_{{\text{т}}}}(M{\text{/}}m)$ сохраняется для других значений параметров сценария, что позволяет сделать вывод о непрерывности, выпуклости и унимодальности критерия расхода топлива ${{I}_{{\text{т}}}}$, а следовательно, и критерия стоимости ${{I}_{C}}$, во всей области определения параметров. Кроме того, на рис. 1 просматривается одна специфическая особенность зависимости ${{I}_{{\text{т}}}} = {{I}_{{\text{т}}}}(M{\text{/}}m)$ от числа М. Она проявляется в том, что в диапазонах чисел М = = 0.778–0.799 ее значения изменяются практически по линейному закону. Это обстоятельство оказывает существенное влияние на выбор метода поиска оптимальных значений Мopt и Hopt и характер их зависимостей от параметров модели.
Учитывая сформулированные выше требования к методу оптимизации и показанный на рис. 1 характер зависимости критериев ${{I}_{{\text{т}}}}$ и ${{I}_{C}}$ от числа М в статье в качестве рабочего используется сочетание прямого метода поиска минимума методом перебора с первой итерацией метода квадратичной параболы. Главными достоинствами такого способа является возможность получения глобального минимума и постоянное количество расчетов оптимизируемой функции (что существенно при организации вычислительного процесса в бортовых вычислителях). Единственным параметром такого способа поиска минимума выступает количество интервалов N, на которое разбивается область оптимизируемых переменных (6.4).
Будем считать, что ошибка в определении Мopt не должна превосходить нескольких тысячных долей единицы, а ошибка в определении Hopt допускается в пределах сотни метров. Учитывая, что ошибка в методе перебора задается соотношением $\varepsilon \leqslant (b - a){\text{/}}N$, где a, b – границы области определения, а ошибка первой итерации метода квадратичной параболы пропорциональна ${{\varepsilon }^{3}}$, в данном случае с достаточной степенью надежности можно принять N = 10.
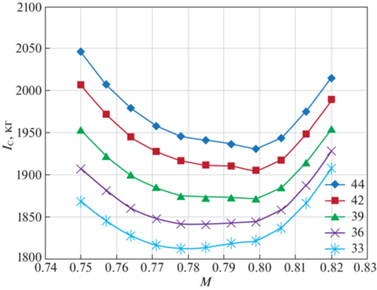
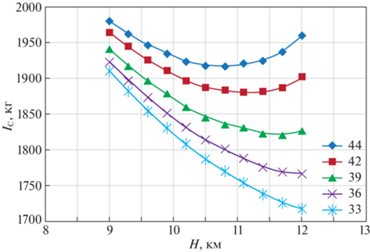
Таким образом, все необходимые модели и методы оптимизации подготовлены для практического решения поставленных задач. Остался последний вопрос: нужно ли этим вообще заниматься и что с этого можно получить? Для ответа на этот вопрос рассмотрим показанные на рис. 2, 3 результаты расчетов значений критериев стоимости ${{I}_{С}}$ как функции числа Маха и высоты для различных значений массы m.
Результаты обработки представленных на рис. 1–3 графиков показаны в табл. 1, 2, где первая относится к рис. 2, а вторая – к рис. 3.
Таблица 1
| Вес | Критерий | Min | Max | Ср. ар. | Дельта | % |
|---|---|---|---|---|---|---|
| 44 | IC | 1930.91 | 2046.58 | 1970.81 | 115.67 | 5.87 |
| IT | 873.06 | 997.38 | 906.46 | 124.32 | 13.71 | |
| It | 2036.21 | 2226.26 | 2128.69 | 190.05 | 8.93 | |
| 42 | IC | 1905.00 | 2006.64 | 1940.55 | 101.64 | 5.24 |
| IT | 842.82 | 970.82 | 876.20 | 128.00 | 14.61 | |
| It | 2036.21 | 2226.26 | 2128.69 | 190.05 | 8.93 | |
| 40 | IC | 1871.44 | 1955.18 | 1900.72 | 83.74 | 4.41 |
| IT | 801.65 | 937.07 | 836.37 | 135.43 | 16.19 | |
| It | 2036.21 | 2226.26 | 2128.69 | 190.05 | 8.93 | |
| 38 | IC | 1840.94 | 1928.28 | 1867.16 | 87.34 | 4.68 |
| IT | 764.99 | 910.18 | 802.82 | 145.19 | 18.08 | |
| It | 2036.21 | 2226.26 | 2128.69 | 190.05 | 8.93 | |
| 36 | IC | 1811.93 | 1907.84 | 1839.52 | 95.92 | 5.21 |
| IT | 733.77 | 889.74 | 775.17 | 155.96 | 20.12 | |
| It | 2036.21 | 2226.26 | 2128.69 | 190.05 | 8.93 |
Таблица 2
| Вес | Критерий | Min | Max | Ср. ар. | Дельта | % |
|---|---|---|---|---|---|---|
| 44 | IC | 1917.80 | 1981.45 | 1939.21 | 63.65 | 3.28 |
| IT | 861.67 | 952.77 | 890.89 | 91.10 | 10.23 | |
| It | 2057.37 | 2118.20 | 2096.64 | 60.83 | 2.90 | |
| 42 | IC | 1880.47 | 1963.79 | 1905.35 | 83.33 | 4.37 |
| IT | 821.37 | 935.11 | 857.02 | 113.74 | 13.27 | |
| It | 2057.37 | 2118.20 | 2096.64 | 60.83 | 2.90 | |
| 40 | IC | 1821.77 | 1941.31 | 1862.01 | 119.54 | 6.42 |
| IT | 762.67 | 912.63 | 813.69 | 149.96 | 18.43 | |
| It | 2057.37 | 2118.20 | 2096.64 | 60.83 | 2.90 | |
| 38 | IC | 1766.59 | 1923.48 | 1826.59 | 156.89 | 8.59 |
| IT | 707.49 | 894.79 | 778.26 | 187.30 | 24.07 | |
| It | 2057.37 | 2118.20 | 2096.64 | 60.83 | 2.90 | |
| 36 | IC | 1717.96 | 1910.15 | 1798.21 | 192.19 | 10.69 |
| IT | 658.86 | 881.46 | 749.88 | 222.60 | 29.68 | |
| It | 2057.37 | 2118.20 | 2096.64 | 60.83 | 2.90 |
В этих таблицах для каждого значения массы ВС приведены минимальные (Min), максимальные (Max) и среднеарифметические (Cр.ар.) значения критериев (IC, ${{I}_{{\text{т}}}}$, It), а также величины разброса значений в абсолютном (Дельта) и процентном (%) измерениях. Как можно видеть из табл. 1, экономия топлива за счет оптимального выбора числа М может достигать 15–20%, сокращение времени – порядка 9% и выигрыш по стоимости составляет 4.5–5% (последние цифры соответствуют значению CI = 0.5). За счет оптимального выбора высоты экономия топлива, как видно из табл. 2, может составлять 10–30%, времени – порядка 3% и стоимости – порядка 3–10%. Эти результаты говорят о практической значимости рассматриваемых далее задач оптимизации сценариев полета ВС.
6.2.1. Исследование и оптимизация сценария 1. В этом сценарии требуется найти оптимальное значение числа Маха при заданных значениях всех других перечисленных в разд. 5 параметрах. Для этого интервал возможных значений числа М разбивается на 10 равных частей и для каждой точки ${{M}_{i}}$ проводится интегрирование системы уравнений (6.16). При этом все остальные значения параметров модели остаются постоянными. По полученным в процессе интегрирования на заданную дальность L значениям времени и расходу топлива формируются массивы значений ${{I}_{t}}(i) = {{I}_{t}}({{M}_{i}}{\text{/}}p)$ и ${{I}_{т}}(i) = {{I}_{т}}({{M}_{i}}{\text{/}}p)$, $i = \overline {1,11} $, где p – множество других (кроме ${{М}_{i}}$) параметров модели. Далее по заданному значению $CI$ рассчитывается массив ${{I}_{C}}(i) = {{I}_{C}}({{M}_{i}}{\text{/}}p)$. В соответствии с предлагаемым выше способом оптимизации на множестве 11 значений ${{I}_{C}}(i)$ находится минимальное, и затем методом квадратичной параболы с учетом ограничений рассчитывается Мopt. Очевидно, что при этом получаем
Первые четыре параметра будем называть параметрами сценария 1, а два других – возмущающими параметрами.
Как можно понять, среди всего множества параметров особое место занимает дальность полета L, так как она определяет длительность интегрирования системы уравнений (6.16) и получающиеся значения критериев IC, ${{I}_{{\text{т}}}}$. Расчеты показали, что при $L < 1000{\kern 1pt} - {\kern 1pt} 1200$ км значения Мopt c точностью порядка 0.001 практически не зависят от L. Поэтому в множестве параметров сценария 1 остались три параметра H, m, CI, влияние которых на значения Мopt необходимо исследовать. Разработанный алгоритм поиска Мopt позволил решить задачу исследования влияния на значение Мopt всей совокупности его параметров.
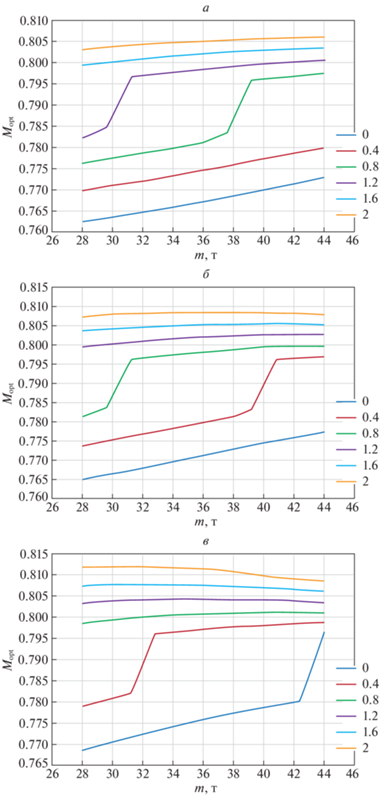
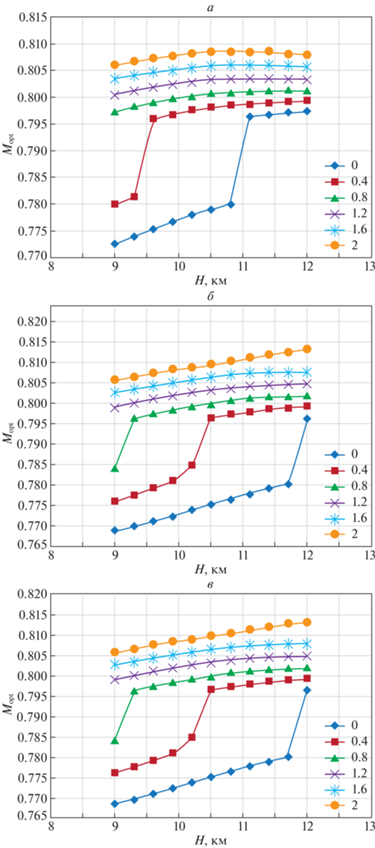
Результаты расчетов зависимости ${{M}_{{opt}}} = {{M}_{{opt}}}(m,CI{\text{/}}H)$ для H = 9; 10; 11 км показаны на рис. 4, а зависимость ${{M}_{{opt}}} = {{M}_{{opt}}}(H,CI{\text{/}}m)$ для m = 44; 38; 32 т – на рис. 5.
Представленные на рис. 4, 5 графики зависимостей Мopt от параметров сценария m, H,CI характеризуются наличием в них “изломов”. Согласно исследованиям, эти изломы являются следствием дискретного отображения соответствующих зависимостей, в которых имеются разрывы первого рода. Эти разрывы связаны с существованием показанных на рис. 1 (в диапазоне изменения числа М = 0.778–0.799) площадок с практически “постоянным” углом наклона. Заметим, что разрывы в зависимостях Мopt от параметров сценария приводят к соответствующим разрывам в значениях времени полета ${{I}_{t}}$ и затрат топлива ${{I}_{{\text{т}}}}$, в то время как критерий стоимости ${{I}_{С}}$ сохраняет непрерывность.
Анализ приведенных результатов позволяет сделать следующие выводы:
рабочий диапазон значений CI, в котором обеспечивается выполнение заданного ограничения на число М < 0.82, ограничен значением CI < 2 кг/с;
зависимости Мopt от m и Н в диапазоне значений 0 < CI < 2 имеют разрывы первого рода, в которых происходит скачкообразное возрастание значения Мopt при увеличении m, Н или CI;
значения Мopt существенно зависят от заданного значения CI;
при CI < 1 значения Мopt возрастают с увеличением массы m и высоты Н полета ВС;
при CI > тенденция возрастания Мopt снижается и даже переходит в противоположную.
При этом экономия топлива за счет оптимального выбора числа М может достигать 15–20%, а сокращение времени – порядка 9%.
Исследование влияния на значения Мopt возмущающих факторов в виде ветра и отклонения температуры воздуха от стандартного значения показало следующее:
наличие ветра не меняет характер поведения зависимостей, а влияет только на значения Мopt;
встречный ветер по сравнению с попутным оказывает большее влияние на Мopt;
степень влияния ветра на Мopt зависит от значений CI;
при встречном ветре Мopt увеличивается, а при попутном ветре уменьшается с увеличением модуля скорости ветра;
при встречном ветре порядка 100 км/ч увеличение Мopt (в зависимости от m, H, CI) может достигать значения 0.02, а при попутном уменьшение Мopt может достигать значения –0.015;
изменение температуры воздуха в пределах ±20° практически не влияет на значение Мopt.
6.2.2. Результаты исследования и оптимизации сценариев 2–5. В сценарии 2 задача заключается в определении оптимального значения высоты Нopt при заданных всех остальных значениях параметров полета. Параметрами сценария здесь являются M, m, CI, L, а внешними (возмущающими) служат Uв, ΔT, поэтому в общем случае можем записать
Проверка параметров сценария по степени влияния их на значения критериев оптимальности показала, что на дальностях полета 1000–1200 км с точностью $ \pm $50 м влиянием дальности можно пренебречь. Другие параметры сценария существенно влияют на критерии оптимальности. При этом типичный вид зависимости ${{H}_{{opt}}} = H(M,m{\text{/}}CI)$ для различных значений возмущающих параметров имеет вид, представленный на рис. 6.
Рассмотренные на рис. 6 зависимости получены при значении CI = 2 и стандартных значениях состояния атмосферы. Влияние CI на вид зависимости ${{H}_{{opt}}} = H(M,m{\text{/}}CI)$ прежде всего проявляется в величине скачка в точках разрыва, который примерно пропорционален значению CI и отсутствует при CI = 0. Ветер оказывает существенное влияние на вид зависимостей Hopt = = $H(M,m{\text{/}}CI)$, которое отражается в величине скачка и смещении области его расположения. При этом имеет место такая тенденция, что с увеличением (алгебраическим) скорости ветра величина скачка уменьшается и он смещается в область больших значений веса ВС.
Завершая рассмотрение сценария 2, заметим, что за счет оптимального выбора высоты экономия топлива может составлять 10–30%, а времени – порядка 3%.
В сценарии 3 задача заключается в определении оптимальных значений высоты Нopt и числа Mopt при заданных всех остальных значениях параметров полета. Параметрами этого сценария являются $m,CI,L$, а возмущающими служат Uв и ΔT. Отличие этой задачи от двух предыдущих состоит в том, что здесь рассматривается оптимизация критериев IC, Iт по двум переменным H и M.
Полученные по результатам расчетов (при отсутствии ветра и в стандартной атмосфере) зависимости Mopt = M(m, CI) и Hopt = H(m, CI) без ветра и при стандартной атмосфере показаны на рис. 7.
Рис. 7.
Зависимость Mopt и Нopt от веса ВС для различных значений CI без ветра и при стандартной атмосфере
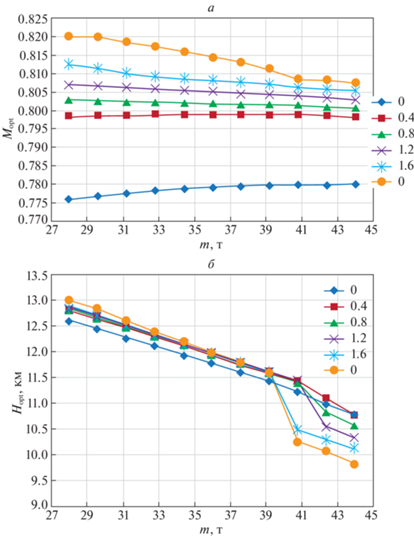
Представленные на рис. 7 результаты позволяют сделать следующие выводы:
при выполнении условия 0 < CI < 1.2 значение Mopt практически не зависит от массы ВС, а значение Нopt линейно уменьшается с увеличением массы и практически не зависит от значения CI;
при CI > 1.2 значения Mopt и Нopt проявляют зависимость от обоих аргументов (m, CI), которая усиливается с увеличением значения CI;
при CI = 0, что соответствует оптимизации по критерию расхода топлива, оптимальное значение числа Маха изменяется в узком диапазоне 0.775 < Mopt < 0.78, а оптимальное значение высоты с увеличением веса ВС плавно и без скачков уменьшается с 12 500 до 10 700 м.
Исследование влияния на значения Mopt и Нopt (полученных в отсутствие возмущений) скорости ветра и температуры воздуха показало, что:
в целом характер зависимостей Mopt = M(m, CI) и Hopt = H(m, CI) не меняется;
наиболее существенное влияние на Mopt и Нopt оказывает встречный ветер, и оно эквивалентно увеличению значения CI, т.е. изменение скорости ветра от нуля до –100 м/с приводит к таким же изменениям, как и увеличение CI от 0 до 2.0 (кроме того, следует отметить, что влияние ветра на значение Нopt сказывается только в области больших весов ВС);
температура воздуха практически не влияет на оптимальное значение числа Маха, влияние ΔT на оптимальное значение Нopt ограничено значением $ \approx {\kern 1pt} 500{\kern 1pt} - {\kern 1pt} 700\;{\text{м}}$ и имеет место в области средних и больших весов ВС.
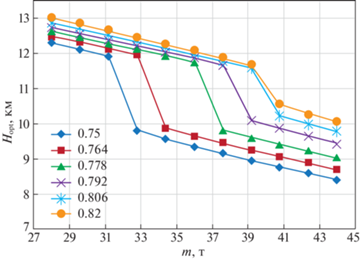
Оптимизация сценариев 4–6, связанных с переходом на оптимальную высоту либо на оптимальное значение числа М в зависимости от текущего изменения веса ВС, проводится в соответствии с результатами, приведенными на рис. 2–4. В частности, при заданном значении шага изменения числа М по зависимостям рис. 4, 5 можно найти те значения массы, при которых целесообразно увеличивать число М, а по рис. 6 можно определить значения m, при которых следует переходить на следующий эшелон полета.
6.2.3. Оптимизация полета с выполнением заданного времени прибытия в очередную точку маршрута. Формально эту задачу можно свести к классической изопериметрической задаче, где в качестве управлений выступают высота Hзад и скорость Mзад, на которые наложены ограничения:
(6.18)
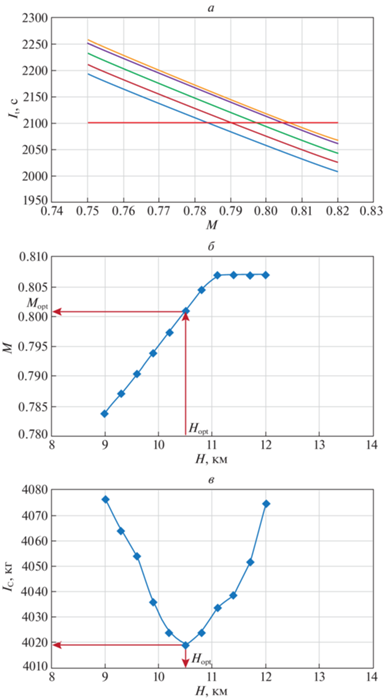
${{H}_{{\min }}} \leqslant {{H}_{{{\text{зад}}}}} \leqslant {{H}_{{\max }}},\quad {{M}_{{\min }}} \leqslant {{M}_{{{\text{зад}}}}} \leqslant {{M}_{{\max }}}.$Однако в данном случае более удобно она решается графо-аналитическим методом, суть которого при заданных значениях дальности полета L и времени прибытия Tзад заключается в следующем:
1. Разобьем диапазоны (6.18) возможного изменения переменных Hзад и Mзад на некоторое количество отрезков точками Hi, $i = \overline {1,{{i}_{h}}} $, Mj, $j = \overline {1,{{j}_{m}}} $.
2. Для каждого значения высоты Нi и всех значений Mj, $j = \overline {1,{{j}_{m}}} $, получим путем интегрирования системы уравнений (6.16) сечения функции ${{I}_{t}} = F({{M}_{{{\text{зад}}}}}{\text{/}}{{H}_{{{\text{зад}}}}})$ плоскостями Hзад = Hi. Эти сечения показаны на рис. 6, а.
3. Если Tзад принадлежит диапазону значений ${{I}_{t}}$, образованному сечениями ${{I}_{t}} = F({{M}_{{{\text{зад}}}}}{\text{/}}{{H}_{{{\text{зад}}}}})$, то проводим линию ${{I}_{t}} = {{T}_{{{\text{зад}}}}}$ (на рис. 8, а Tзад = 2100 с) и находим точки пересечения ее с полученными сечениями.
4. Для этих точек находим соответствующие им значения числа Маха Mj, $j = \overline {1,{{j}_{m}}} $, которые вместе со значениями Hi, $i = \overline {1,{{i}_{h}}} $ образуют линию f (Hзад, Mзад) = 0, показанную на рис 8, б. Каждая точка этой линии (по построению) определяет пару значений Hзад, Мзад, при полете с которыми обеспечивается требуемое время прибытия в заданный пункт маршрута.
5. Для каждой точки этой линии путем интегрирования системы уравнений (6.16) находим значения критерия (стоимости) IC = IC (H) и значение H = Hopt, в котором стоимость минимальна. Эта точка показана на рисунке 8, в.
6. С этим значением Hopt поднимаемся на рис. 8, б, где по функции f (Hзад, Mзад) = 0 находим значение Mopt.
Таким образом, проведена оптимизация всех рассмотренных сценариев полета ВС и исследовано влияние параметров полета на значения критериев оптимизации.
Заключение. Как показали результаты моделирования, предлагаемый подход к оптимизации этапа крейсерского полета по критериям стоимости и затратам топлива позволяет получить решение задач для множества типовых сценариев полета ВС. Характер зависимостей оптимального числа М от веса ВС хорошо коррелируется с данными, полученными в работе [12]. Результаты расчетов, проведенные для ВС типа SSJ-100, показывают, что за счет оптимизации высоты полета и числа М можно сократить затраты топлива более чем на 10–15% и время полета – на 3–9%. При этом для обеспечения выполнения ограничений на число М диапазон значений CI следует рассматривать в пределах 0–2 кг/с. Учитывая, что в гражданской авиации экономия 1% топлива считается хорошим результатам, полученные оценки показывают практическую значимость предлагаемой методики решения задачи оптимизации и целесообразность реализации ее при разработке бортовых алгоритмов ССВ.
Список литературы
Федоров Л.П. Некоторые вопросы оптимизации траектории полета дальних самолетов // Тр. ЦАГИ. 1973. Вып. 1488.
Косминков К.Ю. Оптимизация режима полета дозвукового пассажирского самолета при заданных дальности и времени полета // Тр. ЦАГИ. 1984. Вып. 2231.
Скрипниченко С.Ю. Оптимизация режимов полета самолета по экономическим критериям. М.: Машиностроение, 1988.
Губарева Е.А., Мозжорина Т.Ю. Оптимизация программы полета дозвукового пассажирского самолета на участке крейсерского полета // Инженерный журнал: Наука и инновации. 2014. Вып. 12.
Киселев В.Ю., Монаков А.А. Предсказание траектории воздушного судна в автоматизированных системах управления воздушным движением // Информационно-управляющие системы. 2015. № 4.
Велищанский М.А. Движение летательного аппарата в вертикальной плоскости при наличии ограничений на состояния // Вестн. МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 3.
Голубева А.А., Куланов Н.В. Методика и оптимизация этапа набора высоты в задаче вертикальной навигации самолетов гражданской и военно-транспортной авиации // Изв. РАН. ТиСУ. 2021. № 4.
Голубева А.А., Куланов Н.В. Методика выбора значений параметров этапа взлет самолетов гражданской, военно-транспортной авиации и беспилотных летательных аппаратов // Изв. РАН. ТиСУ. 2019. № 6.
Горбатенко С.А., Макашов Э.М., Полушкин Ю.Ф., Шефтель Л.В. Механика полета. Общие сведения. Уравнения движения: Инж. справочник. М.: Машиностроение, 1969.
Лазарев Ю.Н. Управление траекториями аэрокосмических аппаратов. Самара: Самар. науч. центр РАН, 2007.
Шкадов Л.М., Буханов Р.С., Илларионов В.Ф., Плохих В.П. Механика оптимального пространственного движения летательных аппаратов в атмосфере. М.: Машиностроение, 1972.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969.
Александров В.А., Зыбин Е.Ю., Косьянчук В.В., Сельвесюк Н.И., Тремба А.А., Хлебников М.В. Оптимизация высотно-скоростного профиля крейсерского полета воздушного судна при фиксированном времени прибытия // АиТ. 2021. № 7. С. 69–85.
Кострикин А.И. Введение в алгебру. Ч. I. Основы алгебры: учебник для вузов. 3-е изд. М.: Физматлит, 2004. 272 с.
Калинина Е.А., Утешев А.Ю. Теория исключений. Учебное пособие. СПб.: Из-во НИИ Химии СПбГУ, 2002.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления