Известия РАН. Теория и системы управления, 2022, № 5, стр. 118-130
ТРАЕКТОРИИ ГРАЖДАНСКОГО СВЕРХЗВУКОВОГО САМОЛЕТА, ОПТИМАЛЬНЫЕ ПО РАСХОДУ ТОПЛИВА
С. А. Кумакшев a, *, А. М. Шматков a, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: kumak@ipmnet.ru
** E-mail: shmatkov@ipmnet.ru
Поступила в редакцию 17.03.2022
После доработки 21.03.2022
Принята к публикации 28.03.2022
- EDN: MDJTLG
- DOI: 10.31857/S0002338822040126
Аннотация
Построены оптимальные по расходу топлива траектории движения сверхзвукового пассажирского самолета. Применена математическая модель авиалайнера, детально описывающая свойства аппарата, которые связаны с конструктивными особенностями самолета. Для оптимизации не было использовано предварительное разбиение траектории на отдельные участки с последующей компоновкой из них оптимального решения. Весь перелет был рассмотрен как единый процесс. Для вычислений применили классический метод динамического программирования.
Введение. Проблему выбора наилучшей траектории для самолета исследуют давно. Исходно цель состояла в достижении заданной высоты при минимизации времени движения или расхода топлива, однако с ростом скорости самолетов потребовалось одновременно с этим получать необходимую скорость полета [1]. При этом оптимизацию крейсерского участка траектории проводили отдельно [2]. Для воздушных судов, движущихся с дозвуковой скоростью, можно было произвести дополнительную декомпозицию задачи и тем самым упростить решение [3]. Резкий рост цен на нефть, вызвавший удорожание авиационного топлива, повысил актуальность его экономии. В связи с этим потребовалось значительно более точно учитывать как аэродинамические ограничения, так и ограничения на тягу двигателей [4]. В дальнейшем математические модели продолжали усложняться [5], для чего потребовалось применение моделей, во все большей степени основывающихся на использовании численных методов [6]. С помощью более мощных бортовых компьютеров стала возможной оптимизация траекторий по расходу топлива в режиме реального времени с учетом текущих воздушных потоков [7, 8]. В последние годы все больше внимания уделяют снижению различных воздействий со стороны самолета на окружающую среду [9, 10], что тесно связано с проблемой экономии топлива [11]. Также возникают задачи экономии электрической энергии, поскольку появились воздушные суда, использующие соответствующие источники [12].
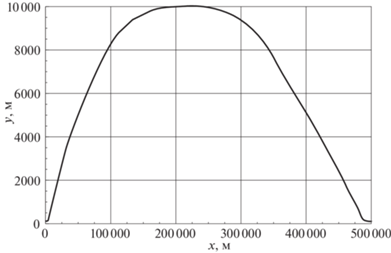
Выбор наилучшей траектории зависит от большого числа разнообразных факторов [13]. Стандартный коммерческий полет имеет траекторию [14], которая значительно отличается от типичной дозвуковой траектории, оптимальной по расходу топлива, пример которой [15] показан на рис. 1. Наиболее заметное отличие – отсутствие крейсерского этапа полета. Причина в том, что с точки зрения теории для экономии топлива оказывается целесообразным сначала набрать большую высоту полета, преобразовав внутреннюю энергию топлива в потенциальную энергию дозвукового самолета, а затем постепенно использовать этот резерв в процессе снижения до конечной точки полета. На практике приходится учитывать многочисленные ограничения, не связанные напрямую с техническими характеристиками самолета. Наиболее очевидным является то, что по современным воздушным трассам одновременно движется большое количество воздушных судов [16]. Следовательно, использование траекторий с постоянно изменяющейся высотой значительно усложнит управление воздушным движением и создаст риск столкновения в воздухе. Поэтому перелет между крупными центрами авиационных перевозок происходит, как правило, на постоянной высоте. Экипаж может сам (или по указанию авиадиспетчера) выбрать один из разрешенных эшелонов полета. Изменения эшелона во время полета случаются нечасто. Таким образом, возможности экономии топлива за счет глобальной оптимизации траектории дозвукового гражданского лайнера существенно ограничены, и на практике необходимо применять только локальную оптимизацию [17, 18]. Локальные решения, принимаемые в процессе полета, зависят во многом от бортовых автоматических систем [19]. Используемые в них алгоритмы формируют на основе общего подхода к глобальной оптимизации [20]. Он, как правило, начинается с разбиения траектории на три этапа: взлет, крейсерский режим и посадка. Далее рассматривают три отдельные задачи [14, 21] и строят полное решение [22, 23]. Для этого применяют разнообразные численные методы [24, 25], но они, как правило, дают только субоптимальные траектории. Точные зависимости должны соответствовать принципу максимума Понтрягина [26], однако использование этого принципа затруднено большим количеством фазовых ограничений. Другим способом получения точных решений является метод динамического программирования Беллмана [27].
В статье применена математическая модель сверхзвукового пассажирского самолета, максимально приближенная к аналогичным моделям дозвуковых воздушных судов22. Она учитывает самые разнообразные и весьма сложные конструктивные ограничения, которые наложены как на управляющие параметры, так и на фазовые переменные. Это обстоятельство делает применение принципа максимума крайне затруднительным, но существенно облегчает использование метода динамического программирования в классической форме, поскольку уменьшает количество вариантов возможных перемещений центра масс самолета, которые нужно перебрать. Этот метод позволяет провести оптимизацию всей траектории целиком без предварительного разделения на участки и последующей стыковки полученных фрагментов. В отличие от ограничений, накладываемых особенностями конструкции, многочисленные ограничения, наложенные действующими правилами на допустимые траектории движения гражданских самолетов, не были учтены совершенно. Однако в результате вычислений выяснилось, что оптимальные решения весьма удобны для применения в рамках указанных ограничений. Данная работа представляет собой расширенное изложение кратко описанных ранее результатов [28].
Заметим, что в статье все размерные величины представлены в системе единиц СИ.
1. Уравнения движения. Для минимизации расхода топлива важно найти оптимальное управление в вертикальной плоскости. Поэтому будем полагать, что вся траектория полета находится в этой плоскости. Пусть масса самолета в текущий момент времени равна $m$. Обозначим абсциссу и ординату центра масс самолета в земной системе координат через $x$ и $y$ соответственно, через $\theta $ – величину угла, который составляет с осью абсцисс вектор скорости этого центра, причем модуль вектора равен V. Предположим, что значение угла наклона траектории $\theta $ удовлетворяет ограничению $ - 45^\circ \leqslant \theta \leqslant 45^\circ $. Заметим, что для приведенных далее примеров оптимальных траекторий $ - 11^\circ < \theta < 6^\circ $.
Уравнения движения самолета имеют следующий вид [29]:
Здесь через $g = 9.81$ м/с2 обозначено ускорение свободного падения, а функция ${{Q}_{t}}$ задает секундный расход топлива, зависящий от числа Маха $M$, высоты полета $y$ и тяги $P$. Будем полагать, что вектор силы тяги с модулем $P$ всегда направлен вдоль вектора скорости. Величины ${{n}_{x}}$ и ${{n}_{y}}$ – проекции отношения суммы векторов тяги и полной аэродинамической силы к величине силы тяжести на вектор скорости центра масс самолета и ось, ортогональную вектору скорости и направленную к верхней части самолета соответственно.
Поскольку сила лобового сопротивления направлена против вектора скорости, то тангенциальная перегрузка
(1.2)
${{n}_{x}} = \frac{P}{{mg}} - \frac{{qS{{C}_{x}}}}{{mg}}{\kern 1pt} ,\quad q = \frac{{\rho (y){{V}^{2}}}}{2}{\kern 1pt} ,$(1.3)
$\begin{gathered} {{D}_{M}} = {{c}_{{00}}} + {{c}_{{01}}}{{k}_{M}}(M - {{M}_{0}}) + {{c}_{{02}}}k_{M}^{2}{{(M - {{M}_{0}})}^{2}}, \\ {{D}_{C}} = {{k}_{y}}({{C}_{y}} - {{C}_{{y0}}})({{c}_{{10}}} + {{c}_{{11}}}{{k}_{M}}(M - {{M}_{0}}) + {{c}_{{12}}}k_{M}^{2}{{(M - {{M}_{0}})}^{2}}), \\ \end{gathered} $В формуле (1.3) введены заданные постоянные величины ${{C}_{{y0}}} = 0.305$, ${{k}_{y}} = 1.63934$, ${{M}_{0}} = 1.35$, ${{k}_{M}} = 0.526316$. Параметры cij и ${{b}_{{kj}}}$ обозначают заданные константы согласно табл. 1 и 2.
Таблица 1.
Значения cij для $i = 0,1$ и $j = \overline {0,2} $
| ${{c}_{{i0}}}$ | ${{c}_{{i1}}}$ | ${{c}_{{i2}}}$ |
|---|---|---|
| 1 | 8.56798 | 20.889 |
| –1.95247 | –15.671 | –32.4513 |
Таблица 2.
Значения ${{b}_{{kj}}}$ для $k = \overline {0,4} $ и $j = \overline {0,6} $
| ${{b}_{{i0}}}$ | ${{b}_{{i1}}}$ | ${{b}_{{i2}}}$ | ${{b}_{{i3}}}$ | ${{b}_{{i4}}}$ | ${{b}_{{i5}}}$ | ${{b}_{{i6}}}$ |
|---|---|---|---|---|---|---|
| 0.053994 | 0.525011 | 1.65896 | 1.37706 | –0.106878 | 0.624163 | 2.72471 |
| –0.0146431 | 0.020673 | 1.49412 | 7.03404 | 11.3274 | –3.7583 | –16.1524 |
| –0.0519696 | –0.566926 | –1.05058 | 5.84359 | 20.0796 | –11.0012 | –54.2533 |
| –0.149042 | –1.34689 | –5.61298 | –18.4137 | –33.5839 | 5.75549 | 50.3087 |
| 0.118336 | 1.71543 | 2.39537 | –34.9937 | –98.1452 | 59.7578 | 250.8 |
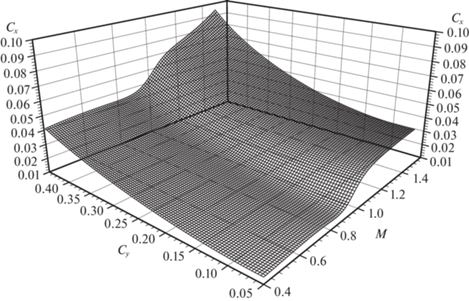
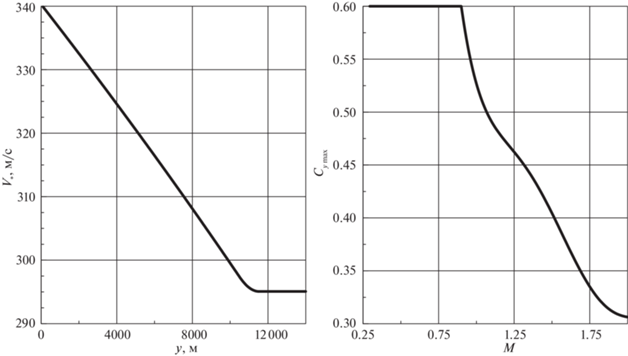
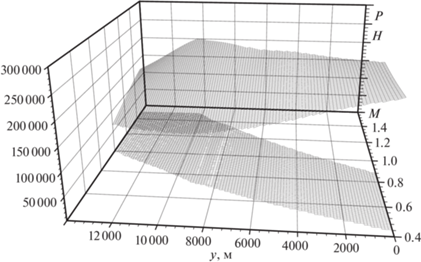
Зависимость (1.3) представлена на рис. 2. Заметим, что число Маха M определено как M = = $V{\text{/}}{{V}_{*}}$, причем скорость звука ${{V}_{*}} = {{V}_{*}}(y)$ показана на рис. 3 слева.
Нормальная скоростная перегрузка определяется формулой
Пусть выполняется условие $0 \leqslant {{n}_{y}} \leqslant n_{y}^{{\max }}$, где $n_{y}^{{\max }} = 4$. Заметим, что для приведенных далее примеров оптимальных траекторий справедливо неравенство $0.8 < {{n}_{y}} < 1.3$.
Величина коэффициента подъемной силы должна удовлетворять условию $0 \leqslant {{C}_{y}} \leqslant {{C}_{{y\max }}}(M)$ и
(1.5)
${{C}_{{y\max }}}(M) = \left\{ {\begin{array}{*{20}{l}} {{{C}_{{y1}}},\quad M < {{M}_{c}},} \\ {{{C}_{{y1}}} + (M - {{M}_{c}})\sum\limits_{i = 0}^4 {{M}_{{ci}}}{{M}^{i}},\quad M \geqslant {{M}_{c}}.} \end{array}} \right.$Здесь ${{C}_{{y1}}} = 0.6$ и ${{M}_{c}} = 0.9$. Значения ${{M}_{{ci}}}$ даны в табл. 3. Функция ${{C}_{{y\max }}} = {{C}_{{y\max }}}(M)$ приведена на рис. 3 справа.
Таблица 3.
Значения ${{M}_{{ci}}}$ для $i = \overline {0,4} $
| ${{M}_{{c0}}}$ | ${{M}_{{c1}}}$ | ${{M}_{{c2}}}$ | ${{M}_{{c3}}}$ | ${{M}_{{c4}}}$ |
|---|---|---|---|---|
| –13.7464 | 30.9773 | –26.6324 | 10.0843 | –1.41375 |
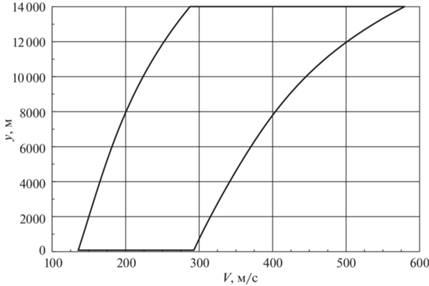
Высота полета y должна быть не меньше 100 м и не больше 14000 м. Модуль $V$ вектора скорости ограничен снизу величиной Vmin, а сверху – величиной ${{V}_{{\max }}}$:
(1.6)
${{V}_{{\min }}} = \sum\limits_{j = 0}^3 {{h}_{j}}{{(y - {{y}_{0}})}^{j}},\quad {{V}_{{\max }}} = \sum\limits_{i = 0}^4 {{H}_{i}}{{(y - {{y}_{0}})}^{i}},$Таблица 4.
Значения ${{H}_{i}}$ для $i = \overline {0,4} $
| ${{H}_{0}}$ | ${{H}_{1}}$ | ${{H}_{2}}$ | ${{H}_{3}}$ | ${{H}_{4}}$ |
|---|---|---|---|---|
| 387.176 | 1.66418 × 10–2 | 7.60218 × 10–7 | 8.21839 × 10–11 | 5.30230 × 10–15 |
Таблица 5.
Значения ${{h}_{j}}$ for $j = \overline {0,3} $
| ${{h}_{0}}$ | ${{h}_{1}}$ | ${{h}_{2}}$ | ${{h}_{3}}$ |
|---|---|---|---|
| 191.006 | 9.57611 × 10–3 | 4.26035 × 10–7 | 2.78953 × 10–11 |
Суммарная тяга двигателей $P$ ограничена сверху и снизу величинами ${{P}_{{\max }}}$ и ${{P}_{{\min }}}$ соответственно. Они определены следующими соотношениями:
(1.7)
$\begin{gathered} {{D}_{{\min }}} = \sum\limits_{i = 0}^3 (\xi _{{0i}}^{*} + \xi _{{1i}}^{*}{{\lambda }_{M}}(M - {{M}_{p}}))\lambda _{y}^{i}{{(y - {{y}_{p}})}^{i}}, \\ {{P}_{{\max }}} = D_{{\max }}^{{ - 1}}\sum\limits_{i = 0}^7 \left( {\sum\limits_{j = 0}^5 {{\eta }_{{ij}}}\lambda _{M}^{j}{{{(M - {{M}_{p}})}}^{j}}} \right)\lambda _{y}^{i}{{(y - {{y}_{p}})}^{i}}, \\ \end{gathered} $Таблица 6.
Значения $\xi _{{0i}}^{*}$ для $i = \overline {0,3} $
| $\xi _{{00}}^{*}$ | $\xi _{{01}}^{*}$ | $\xi _{{02}}^{*}$ | $\xi _{{03}}^{*}$ |
|---|---|---|---|
| 0.833333 | –14.8184 | 80.5036 | 61.0632 |
Таблица 7.
Значения $\xi _{{1i}}^{*}$ для $i = \overline {0,3} $
| $\xi _{{10}}^{*}$ | $\xi _{{11}}^{*}$ | $\xi _{{12}}^{*}$ | $\xi _{{13}}^{*}$ |
|---|---|---|---|
| –4.82486 | 97.4383 | –601.624 | 1092.67 |
Таблица 8.
Значения ${{\xi }_{{ij}}}$ для $i = \overline {0,4} $ и $j = \overline {0,2} $
| ${{\xi }_{{i0}}}$ | ${{\xi }_{{i1}}}$ | ${{\xi }_{{i2}}}$ |
|---|---|---|
| 758.995 | –4567.95 | 4232.93 |
| –13823 | 89014.1 | –100407 |
| 67057.7 | –498041 | 731444 |
| 67717.2 | 348166 | –1.72372 × 106 |
| –212169 | 501622 | 1.06713 × 106 |
Таблица 9.
Значения $\eta _{{ji}}^{*}$ для $j = \overline {0,2} $ и $i = \overline {0,3} $
| $\eta _{{j0}}^{*}$ | $\eta _{{j1}}^{*}$ | $\eta _{{j2}}^{*}$ | $\eta _{{j3}}^{*}$ |
|---|---|---|---|
| 0.833333 | 0.367113 | 12.6041 | 29.0280 |
| 5.12608 | –37.2538 | –180.062 | 228.569 |
| 14.0470 | –152.093 | 598.407 | 1235.07 |
Таблица 10.
Значения ${{\eta }_{{ij}}}$ для $i = \overline {0,7} $ и $j = \overline {0,5} $
| ${{\eta }_{{i0}}}$ | ${{\eta }_{{i1}}}$ | ${{\eta }_{{i2}}}$ | ${{\eta }_{{i3}}}$ | ${{\eta }_{{i4}}}$ | ${{\eta }_{{i5}}}$ |
|---|---|---|---|---|---|
| 19280.6 | 139444 | 457777 | 422679 | 151535 | 37198.4 |
| –6584.98 | –957338 | –5.02766 × 106 | –4.00434 × 106 | 3.8336 × 106 | 7.10484 × 106 |
| 260832 | –3.2056 × 106 | 9.74563 × 106 | 3.34046 × 106 | –4.7405 × 107 | –8.97828 × 107 |
| 296231 | 1.31656 × 107 | 4.10711 × 107 | 1.70711 × 108 | 2.67929 × 108 | 8.09869 × 107 |
| –1.1145 × 106 | –2.31839 × 106 | –7.00327 × 107 | –3.15096 × 108 | –2.79845 × 108 | 4.29642 × 107 |
| –2.85568 × 107 | –1.1652 × 108 | –5.93709 × 108 | –1.1059 × 109 | –4.89287 × 108 | |
| 1.9564 × 106 | 2.30552 × 107 | 4.03068 × 108 | 2.189 × 109 | 3.61881 × 109 | 2.80674 × 109 |
| –1.89517 × 106 | 5.19449 × 106 | –2.82164 × 108 | –1.61854 × 109 | –4.08609 × 109 | –2.23579 × 109 |
Скорость расхода топлива определена с помощью полинома
(1.8)
${{Q}_{t}} = \sum\limits_{k = 0}^3 \left( {\sum\limits_{i = 0}^2 \left( {\sum\limits_{j = 0}^5 {{\chi }_{{kij}}}\zeta _{P}^{j}{{{(P - {{P}_{q}})}}^{j}}} \right)\zeta _{M}^{i}{{{(M - {{M}_{q}})}}^{i}}} \right)\zeta _{y}^{k}{{(y - {{y}_{q}})}^{k}},$Таблица 11.
Значения ${{\chi }_{{kij}}}$. Каждый из четырех блоков соответствует значению индекса $k = \overline {0,3} $ в порядке возрастания и содержит данные для $i = \overline {0,2} $ и $j = \overline {0,5} $
| ${{\chi }_{{0i0}}}$ | ${{\chi }_{{0i1}}}$ | ${{\chi }_{{0i2}}}$ | ${{\chi }_{{0i3}}}$ | ${{\chi }_{{0i4}}}$ | ${{\chi }_{{0i5}}}$ |
|---|---|---|---|---|---|
| 6.91868 | 20.23 | –7.02744 | –22.2448 | 140.477 | 199.532 |
| 0.259048 | –9.80678 | –11.9578 | 10.2475 | –463.874 | –972.726 |
| 10.7416 | 28.2658 | –54.6752 | 147.246 | 998.464 | 821.872 |
| ${{\chi }_{{1i0}}}$ | ${{\chi }_{{1i1}}}$ | ${{\chi }_{{1i2}}}$ | ${{\chi }_{{1i3}}}$ | ${{\chi }_{{1i4}}}$ | ${{\chi }_{{1i5}}}$ |
| 0.49976 | –17.8734 | –0.298142 | 315.634 | 324.562 | –355.916 |
| –22.9026 | –41.8508 | 123.088 | –652.49 | –2859 | –1939.09 |
| 13.3055 | –46.6298 | –242.898 | 1025.71 | 5231.22 | 5583.6 |
| ${{\chi }_{{2i0}}}$ | ${{\chi }_{{2i1}}}$ | ${{\chi }_{{2i2}}}$ | ${{\chi }_{{2i3}}}$ | ${{\chi }_{{2i4}}}$ | ${{\chi }_{{2i5}}}$ |
| 2.05478 | 14.5837 | 154.249 | 377.15 | 189.587 | 4.09526 |
| 4.28556 | 139.001 | –21.8526 | –2502.32 | –4610.68 | –1246.87 |
| –54.6038 | –359.476 | 296.872 | 3879.98 | 5277.72 | 2047.04 |
| ${{\chi }_{{3i0}}}$ | ${{\chi }_{{3i1}}}$ | ${{\chi }_{{3i2}}}$ | ${{\chi }_{{3i3}}}$ | ${{\chi }_{{3i4}}}$ | ${{\chi }_{{3i5}}}$ |
| 7.85532 | 65.3292 | 153.677 | 28.5226 | 63.6594 | 504.47 |
| 78.3572 | 382.776 | –133.377 | –2087.3 | –3441.84 | –4271.34 |
| –31.595 | –14.1883 | 1212.21 | 2937.3 | –2762.48 | –8853.4 |
Задача состоит в выборе таких функций ${{C}_{y}}(t)$ и $P(t)$, чтобы функционал
определяющий суммарный расход топлива, имел наименьшее возможное значение. Через T обозначено требуемое время движения из заданной начальной точки траектории в конечную при заданных начальной и конечной скоростях.Так как, согласно наложенным условиям, значение выражения $V\cos \theta $ никогда не обращается в нуль, можно заменить независимую переменную в (1.1) и использовать дальность x вместо времени. Получим
(1.10)
$\begin{gathered} \frac{{d\theta }}{{dx}} = \frac{g}{{{{V}^{2}}}}\left( {\frac{{{{n}_{y}}}}{{\cos \theta }} - 1} \right), \\ \frac{{dy}}{{dx}} = \tan \theta , \\ \frac{{dm}}{{dx}} = - \frac{{{{Q}_{t}}(M,y,P)}}{{V\cos \theta }}{\kern 1pt} , \\ \end{gathered} $Граничные условия примут вид
(1.11)
$\begin{gathered} V({{x}_{0}}) = {{V}_{0}},\quad \theta ({{x}_{0}}) = {{\theta }_{0}},\quad m({{x}_{0}}) = {{m}_{0}},\quad t({{x}_{0}}) = 0, \\ V({{x}_{T}}) = {{V}_{T}},\quad \theta ({{x}_{T}}) = {{\theta }_{T}},\quad t({{x}_{T}}) = T, \\ \end{gathered} $Решение задачи поиска траектории, минимизирующей функционал (1.12) для системы дифференциальных уравнений (1.10) с начальными условиями (1.11) и удовлетворяющей всем указанным выше условиям, было проведено численно классическим методом динамического программирования. Подробное описание алгоритма можно найти в статье [30].
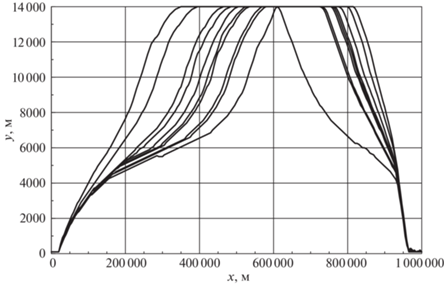
2. Оптимальные решения. Площадь крыла самолета была взята равной $S = 110.16$ м2. Были выбраны следующие граничные условия (1.11) , одинаковые для всех описанных далее случаев: ${{V}_{0}} = 140$ м/с, ${{\theta }_{0}} = 0$, ${{m}_{0}} = 6 \times {{10}^{4}}$ кг, ${{x}_{T}} = {{10}^{6}}$ м, ${{V}_{T}} = 140$ м/с, ${{\theta }_{T}} = 0$. Все последующие рисунки соответствуют 10 разным случаям, отличающимся друг от друга длительностью полета. Последняя заключена в диапазоне от 48 до 58 мин. На каждом рисунке представлено по 10 графиков – по одному для каждой из длительностей. Соответствие между длительностью и кривой для каждого из рисунков указано отдельно. Опишем наиболее интересные свойства полученных решений.
На рис. 6 приведены оптимальные траектории, на которых видны участки набора высоты, крейсерского режима и снижения перед посадкой. Чем меньше общее время движения, тем за меньшее время происходит набор высоты, дольше движение в крейсерском режиме и быстрее происходит снижение. Для самого длительного из представленных перелетов крейсерский режим практически отсутствует. Можно заметить, что по отношению к общему времени движения чувствительность скорости набора высоты больше, чем скорости снижения.
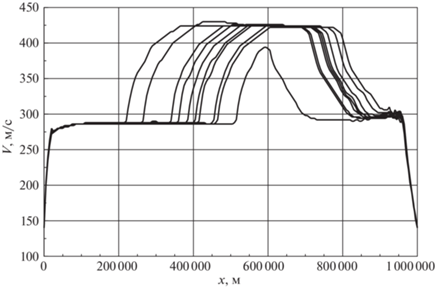
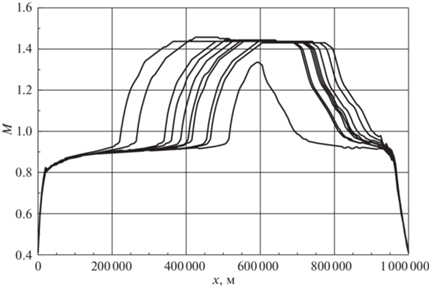
На рис. 7 показаны зависимости скорости движения самолета от дальности. Видно, что типичный график состоит из семи участков. На начальном участке траектории скорость одинаково быстро растет во всех случаях. Потом в течение некоторого времени происходит движение с постоянной скоростью, практически не зависящей от общей длительности полета. Затем на некотором удалении от начальной точки траектории начинается резкий набор скорости до значения, характерного для крейсерского режима. Чем меньше общее время движения, тем меньше соответствующая дальность. Полет на крейсерском режиме характеризуется практически постоянной скоростью, одинаковой для всех рассмотренных случаев. Далее виден участок, на котором скорость резко падает почти до того же самого значения, которое было до ее роста при переходе к крейсерскому режиму. Указанное уменьшение скорости начинается тем ближе к начальной точке траектории, чем больше общее время движения. Потом виден участок, на котором скорость почти постоянна и слабо отличается от одной траектории к другой. Завершающее движение происходит при резком снижении скорости, практически одинаковом для всех случаев. Как и на рис. 6, самый длительный перелет не имеет участка, характерного для крейсерского режима. Из рис. 8 видно, что участки, предшествующие выходу на крейсерский режим и следующие после него, соответствуют дозвуковым режимам полета. На том участке до крейсерского режима, где скорость движения почти одинакова для всех вариантов, число Маха медленно увеличивается. Переход к сверхзвуковому полету происходит при очень быстром росте скорости. В рамках крейсерского режима число Маха практически постоянно и равно приблизительно 1.44, а на участке примерного постоянства скорости после окончания этого режима число Маха медленно уменьшается. При этом сам выход из крейсерского режима происходит хотя и с быстрым уменьшением данного числа, однако менее резким, чем при переходе к сверхзвуковому полету.
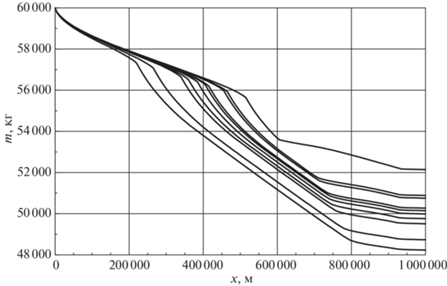
На рис. 9 показано, как меняется полная масса лайнера с изменением расстояния от пункта вылета. Чем больше время движения и меньше расход топлива, тем больше масса самолета и, следовательно, тем выше находится соответствующий график. Видно, что максимальная скорость расхода топлива почти постоянна и практически не зависит от времени перелета. Она имеет место на участке, где начинается быстрый рост скорости перед выходом на сверхзвуковой режим, и участке, соответствующем крейсерскому полету. На этапе снижения скорости к постоянной дозвуковой и последующего движения с этой скоростью секундный расход топлива резко падает до примерно равного для всех случаев значения, меньшего по сравнению с использованным для набора высоты и выхода на постоянную дозвуковую скорость на начальном участке. При завершении полета скорость расхода топлива минимальна и почти не зависит от общего времени движения.
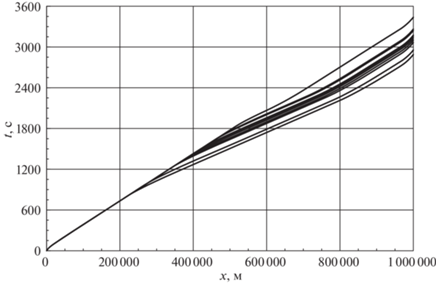
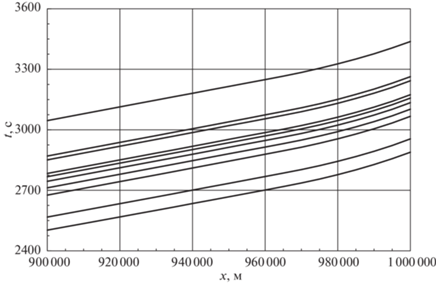
Графики на рис. 10 показывают, сколько времени необходимо самолету, чтобы удалиться от начальной точки на соответствующее расстояние. Чем выше находится кривая, тем больше экономия топлива на описываемой ею траектории. На рис. 11 показаны участки графиков, изображенных на рис. 10, вблизи конечной точки. Это позволяет лучше увидеть, как отличается полное время полета для разных траекторий. Как видно из рис. 9 и 11, экономия приблизительно 7.5% топлива увеличивает время полета на величину около 16%.
Заключение. Полученные решения кажутся удобными для реализации. Оптимальные траектории близки к тем, которые удовлетворяют действующим в гражданской авиации обычным правилам, хотя для дозвуковых аппаратов такое явление нехарактерно.
Крейсерский полет, обеспечивающий минимум расхода топлива, происходит на большой высоте, значительно превышающей обычную для дозвуковых пассажирских самолетов. Это позволяет исключить происшествия, вызванные отличиями в скоростях разных летательных аппаратов.
В близких к авиационным узлам зонах, характеризующихся высокой интенсивностью движения, участки оптимальных траекторий незначительно отличаются для различных длительностей полета. Это дает возможность соответствующей унификации без заметного роста расхода топлива.
Начальные участки траекторий незначительно отличаются друг от друга, а разница между конечными участками – еще меньше. Это дает возможность унифицировать элементы движения самолета на небольшом удалении от аэродромов взлета и посадки. Данное обстоятельство очень важно для оптимизации интенсивного воздушного движения в районах крупных транспортных узлов.
Полет со скоростью, превышающей скорость звука, сопровождается распространением ударных волн, которые оказывают значительное акустическое воздействие на живые организмы, а иногда – и на элементы зданий и сооружений. Расчеты, результаты которых приведены в данной работе, показывают, что оптимальное движение на сверхзвуковой скорости начинается и заканчивается на высоте около 6 км, а крейсерская часть полета проходит на высоте 14 км. Акустическое воздействие в этих условиях можно считать допустимым.
Еще одним полезным свойством полученных траекторий является удобство реализации оптимального управления, так как, например, основные отличия скоростей движения для разных случаев сводятся к изменению времен перехода с одной скорости на другую, что видно из представленных графиков.
Список литературы
Rutowski E.S. Energy Approach to the General Aircraft Performance Problem // J. Aeronaut. Sci. 1954. V. 21. № 3. P. 187–195.
Zagalsky N.R., Irons R.P., Schultz R.L. Energy State Approximation and Minimum-fuel fixed-range Trajectories // J. Aircr. 1971. V. 8. № 6. P. 488–490.
Calise A.J. Extended Energy Management for Flight Performance Optimization // AIAA J. 1977. V. 15. № 3. P. 314–321.
Erzberger H., Lee H. Constrained Optimum Trajectories with Specified Range // J. Guid. Control. 1980. V. 3. № 1. P. 78–85.
Grimm W., Well K.H., Oberle H.J. Periodic Control for Minimum-fuel Aircraft Trajectories // J. Guid. Control Dyn. 1986. V. 9. № 2. P. 169–174.
Raivio T., Ehtamo H., Hämäläinen R.P. Aircraft Trajectory Optimization Using Nonlinear Programming // System Modelling and Optimization. Boston: Springer, 1996. P. 435–441.
Langelaan J.W. Long Distance/Duration Trajectory Optimization for Small UAVs // AIAA Guidance, Navigation and Control Conf. South Carolina: Hilton Head, 2007. P. 3654–3667.
Rosenow J., Lindner M., Scheiderer J. Advanced Flight Planning and the Benefit of In-flight Aircraft Trajectory Optimization // Sustainability. 2021. V. 13. № 3. P. 1383–1401.
Wan J., Zhang H., Liu F., Lv W., Zhao Y. Optimization of Aircraft Climb Trajectory Considering Environmental Impact Under RTA Constraints // J. Adv. Transp. 2020. V. 2020. P. 1–17.
Lim Y., Gardi A.G.M., Sabatini R. Optimal Aircraft Trajectories to Minimize the Radiative Impact of Contrails and CO2 // Energy Procedia. 2017. V. 110. P. 446–452.
Dias M.V., Comendador V.F.G., Carretero J.G.-H., Valdis R.M. Environmental Benefits in Terms of Fuel Efficiency and Noise when Introducing Continuous Climb Operations as Part of Terminal Airspace Operation // Int. J. Sustain. Transp. 2020. V. 14. № 12. P. 903–913.
Li Y., Zhang Z., Zhang J. Research on Trim Simulation and Flight Test of a General Electric Aircraft // J. Phys. Conf. Ser. 2021. V. 1802. P. 1–10.
Rosenow J., Förster S., Lindner M., Fricke H. Multi-objective Trajectory Optimization // Int. Transportation. 2016. V. 68. № 1. P. 40–43.
Murrieta-Mendoza A., Botez R.M. Methodology for Vertical-navigation Flight-trajectory Cost Calculation Using a Performance Database // J. Aerosp. Inf. Syst. 2015. V. 12. № 8. P. 519–532.
Kumakshev S.A., Shmatkov A.M. Flight Trajectory Optimization Without Decomposition Into Separate Stages // IOP Conf. Ser. Mater. Sci. Eng. 2018. V. 468. 012033.
Vishnyakova L.V., Popov A.S. Selection of Airspace Structure and Aerodrome Infrastructure During Their Modernization by Methods of Mathematical Modeling // J. Comput. Syst. Sci. Int. 2021. V. 60. № 6. P. 918–955.
Golubeva A.A., Kulanov N.V. Method for Selecting the Parameter Values of the Takeoff Phase of Civil and Military Transport AC, as well as Unmanned Aerial Vehicles // J. Comput. Syst. Sci. Int. 2020. V. 59. № 1. P. 105–121.
Golubeva A.A., Kananadze S.S., Kulanov N.V. Methodology and Results of Optimizing the Ascent Stage in the Problem of Vertical Navigation of Civil and Military Transport Aircraft // J. Comput. Syst. Sci. Int. 2021. V. 60. № 4. P. 654–672.
Blakelock J.H. Automatic Control of Aircraft and Missiles, 2nd edition. N.Y.: Wiley, 1991.
Rosenow J., Strunck D., Fricke H. Trajectory Optimization in Daily Operations // CEAS Aeronaut. J. 2020. V. 11. P. 333–343.
Alligier R. Predictive Distribution of Mass and Speed Profile to Improve Aircraft Climb Prediction // J. Air Transp. 2020. V. 28. № 3. P. 114–123.
Franco A., Rivas D. Optimization of Multiphase Aircraft Trajectories Using Hybrid Optimal Control // J. Guid. Control Dyn. 2015. V. 38. № 3. P. 452–467.
Murrieta-Mendoza A., Romain C., Botez R.M. 3D Cruise Trajectory Optimization Inspired by a Shortest Path Algorithm // Aerospace. 2020. № 7. P. 99–119.
Soler M., Olivares A., Staffetti E. Multiphase Optimal Control Framework for Commercial Aircraft Four-dimensional Flight-planning Problems // J. Aircr. 2015. V. 52. № 1. P. 274–286.
Garcia-Heras J., Soler M., Saez F.J. Collocation Methods to Minimum-fuel Trajectory Problems with Required Time of Arrival in ATM // J. Aerosp. Inf. Syst. 2016. V. 13. № 7. P. 243–265.
Pontryagin L.S., Boltyanskii V.G., Gamkrelidze R.V., Mishchenko E.F. The Mathematical Theory of Optimal Processes. N. Y.: Wiley Interscience, 1963.
Bellman R. Dynamic Programming. Princeton: Princeton University Press, 1957.
Кумакшев С.А., Шматков A.M. Оптимальные по расходу топлива траектории сверхзвукового пассажирского самолета // Доклады Российской академии наук. Физика, технические науки. 2022. Т. 504. C. 59–64.
Бочкарев А.Ф., Андреевский В.В., Белоконов В.М. и др. Аэромеханика самолета: динамика полета. М.: Машиностроение, 1985.
Grevtsov N.M., Kumakshev S.A., Shmatkov A.M. Optimization of the Flight Trajectory of a Non-manoeuvrable Aircraft to Minimize Fuel Consumption by the Dynamic Programming Method // J. Appl. Math. Mech. 2017. V. 81. № 5. P. 368–374.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления