Известия РАН. Теория и системы управления, 2022, № 6, стр. 150-160
ФРЕЙМОВАЯ РЕГУЛЯРИЗАЦИЯ СВЕРТОЧНОЙ НЕЙРОННОЙ СЕТИ В ЗАДАЧАХ КЛАССИФИКАЦИИ ИЗОБРАЖЕНИЙ
А. Н. Гнеушев a, b, *, А. Д. Григорьев a, **, И. А. Матвеев b, ***
a МФТИ
Долгопрудный, МО, Россия
b ФИЦ ИУ РАН
Москва, Россия
* E-mail: gneushev@ccas.ru
** E-mail: grigorev.ad@phystech.edu
*** E-mail: matveev@ccas.ru
Поступила в редакцию 06.07.2022
После доработки 09.07.2022
Принята к публикации 01.08.2022
- EDN: QDGILN
- DOI: 10.31857/S0002338822060087
Аннотация
Рассматривается задача регуляризации параметров нейронной сети для увеличения эффективности использования их избыточности и повышения устойчивости к реализациям входных данных, не содержащихся в обучающей выборке. Предлагается представление системы весовых векторов нейросетевого слоя в виде фрейма в пространстве весов, вводится регуляризация в виде штрафа за несоблюдение достаточного условия фрейма. Предложенный метод накладывает меньшие ограничения на веса модели, чем существующие способы увеличения эффективности, основанные на ортогонализации. Метод обобщается на сверточные слои в блочно-теплицевом представлении и применим к сверточным нейронным сетям. Вычислительный эксперимент на выборках CIFAR-10, CIFAR-100 и SVHN показал превосходство предложенного метода регуляризации по точности классификации, обобщающей способности и устойчивости к состязательным атакам по сравнению с базовыми подходами.
0. Введение. Информационные интеллектуальные системы, использующие искусственные нейронные сети для анализа данных, являются неотъемлемой частью современных решений широкого круга задач. В частности, важным направлением является автоматизация анализа изображений и построение интеллектуальных видеосистем для промышленных и бытовых нужд. Глубокие нейронные сети с большим количеством параметров способны с высокой точностью описывать сложные нелинейные зависимости. Высокая размерность пространства параметров делает задачу их подбора и оптимизации весьма сложной. В частности, избыточное число параметров приводит к корреляции нейронов сети, что снижает обобщающую способность и приводит к неэффективному использованию вычислительных ресурсов. Проблему избыточности параметров модели можно переформулировать в задачу увеличения эффективности параметризации. Решается она изменением структуры нейронной сети или повышением (оптимизацией) разнообразия нейронов в каждом из слоев. В структурных подходах можно уменьшать число параметров во время обучения [1, 2] или прореживать их после обучения [3, 4]. Оптимизационные подходы работают непосредственно при обучении.
Особый интерес представляет регуляризация параметров. Она нацелена прежде всего на предотвращение переобучения, т.е. повышение обобщающей способности модели [5–7]. Классический метод регуляризации на основе введения штрафа на норму весов ограничивает их абсолютные значения и тем самым предотвращает возможный рост нормы градиентов параметров, что существенно облегчает обучение нейросетевых моделей стандартными градиентными методами [5].
Предложено множество способов регуляризации параметров, ориентированных на повышение их разнообразия. Один из успешных подходов основан на обеспечении углового разнообразия векторов нейронов [8]. Угловое разнообразие векторов можно характеризовать как сумму попарных угловых расстояний (энергию). Такая регуляризация подразумевает минимизацию энергии при достижения более равномерно распределенной в пространстве и, следовательно, разнообразной конфигурации векторов. Альтернативный подход к повышению разнообразия векторов связан с их ортогонализацией [9–11]. В [12] предлагается метод ортогональной инициализации, ускоряющий сходимость на ранних этапах обучения, однако далее в процессе обучения ортогональность не сохраняется. Для поддержания ортогональности вводится регуляризация (система штрафов). Ортогональность весов в слое позволяет сохранить энергию входного сигнала, что минимизирует потерю информации о сигнале [9, 12]. В работах [9, 10] предлагаются разные подходы к ортогонализации параметров нейросетевого слоя. В [9] регуляризатор является фробениусовой нормой разности матрицы Грама векторов весов и единичной матрицы:
(0.1)
$R({\mathbf{W}}) = \left( {\begin{array}{*{20}{l}} {{\text{||}}{{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} - \mathbb{I}{\text{||}},\quad m \geqslant n,} \\ {{\text{||}}{\mathbf{W}}{{{\mathbf{W}}}^{{\text{T}}}} - \mathbb{I}{\text{||}},\quad m < n,} \end{array}} \right.$В [10] ортогональная регуляризация основана на свойстве спектральной ограниченной изометрии и заключается в минимизации спектральной нормы матрицы, определенной как разность матрицы Грама системы весов и единичной матрицы:
Здесь $\sigma ({\mathbf{A}})$ – спектральная норма матрицы, для симметричных положительно определенных вещественнозначных матриц численно равная квадратному корню наибольшего собственного числа: $\sigma ({\mathbf{A}}) = \sqrt {{{\lambda }_{{\max }}}({\mathbf{A}})} $. Ортогональность достигается за счет наложения штрафа в случае отличия сингулярных чисел матрицы весов от единицы.Несмотря на то, что описанные подходы показывают многообещающие результаты в задаче классификации на эталонных выборках, условие ортогональности вводит довольно жесткие ограничения на параметры нейронного слоя. В случае избыточности параметров, когда число нейронов больше размерности входного сигнала, снижается фактическая емкость нейросетевой модели [13].
В работе обобщается подход ортогональной регуляризации для увеличения эффективности избыточного множества параметров нейронной сети и повышения устойчивости нейросетевой модели в задачах классификации. Параметры слоя нейронной сети предлагается рассматривать как семейство векторов в евклидовом пространстве, такое, что проекция входных данных на эту систему является устойчивой и полной. В этом случае гарантируется сохранение энергии входного сигнала и его информации в условиях переопределенной системы параметров, характерной для нейронной сети. В отличие от методов ортогонализации параметров предлагается более общий подход, а именно построение фрейма в евклидовом векторном пространстве параметров каждого слоя. Полнота и устойчивость фреймового представления аналогичны базису. Исходя из этого, в данной работе предлагается новая функция потерь, которая накладывает слабые ограничения на параметры модели, но обеспечивает базисные свойства для нейросетевого слоя, достаточные для восстановления входного сигнала на входе слоя по его выходу. Фреймовое представление позволяет рассматривать каждый слой нейронной сети как суперпозицию набора линейных преобразований, осуществляющих выделение признаков без потерь информации, и нелинейных функций активации, выбирающих значимые для решения задачи признаки. Многослойная нейросеть, соответственно, является суперпозицией таких чередующихся преобразований.
1. Постановка задачи. Дана выборка $\mathfrak{D} = \{ {{\vec {x}}_{i}},{{y}_{i}}\} _{{i = 1}}^{N}$, где ${{\vec {x}}_{i}} \in {{\mathbb{R}}^{n}}$ – объект, ${{y}_{i}} \in \{ 1, \ldots ,C\} $ – метка класса данного объекта, C – число классов в выборке, N – размер выборки.
Задана параметрическая модель $\varphi (\vec {x}\,{\text{|}}\,\Theta )$ из семейства ${{\Phi }_{L}}$ глубоких нейронных сетей следующего вида:
(1.1)
$\varphi (\vec {x}\,{\text{|}}\,\Theta ) = ({{\mathcal{H}}_{L}} \circ {{\mathcal{F}}_{L}} \circ \ldots \circ {{\mathcal{H}}_{j}} \circ {{\mathcal{F}}_{j}} \circ \ldots \circ {{\mathcal{H}}_{1}} \circ {{\mathcal{F}}_{1}})(\vec {x}\,{\text{|}}\,\Theta ),$(1.2)
$\left( {{{\mathcal{H}}_{j}} \circ {{\mathcal{F}}_{j}}} \right)(\vec {z}) = {{\mathcal{H}}_{j}}\left( {{{\mathcal{F}}_{j}}(\vec {z})} \right) = {{\mathcal{H}}_{j}}\left( {{{{\mathbf{W}}}_{j}}\vec {z}} \right),\quad \forall \vec {z} \in {{\mathbb{R}}^{{{{n}_{j}}}}},\quad j = \overline {1,L} ,$Ставится задача мультиклассовой классификации, решение которой ищется методом минимизации эмпирического риска по заданной выборке $\mathfrak{D}$:
(1.3)
$\hat {\Theta } = \arg \mathop {\min }\limits_\Theta \frac{1}{N}\sum\limits_{i = 1}^N \ell (\varphi ({{\vec {x}}_{i}}\,{\text{|}}\,\Theta ),{{y}_{i}}) + \gamma \widetilde R(\Theta ),$Регуляризация матрицы ${{{\mathbf{W}}}_{j}}^{{\text{T}}} = (\vec {w}_{1}^{j} \ldots \vec {w}_{{{{m}_{j}}}}^{j})$ каждого из слоев $j = \overline {1,L} $ направлена на минимизацию потерь информации на линейной части нейросетевого слоя ${{\mathcal{F}}_{j}}(\vec {z}) = {{{\mathbf{W}}}_{j}}\vec {z}$ путем построения системы векторов $\{ \vec {w}_{k}^{j}\} _{{k = 1}}^{{{{m}_{j}}}}$, линейно восстанавливающих вход $\vec {z}$ по выходу ${{\mathcal{F}}_{j}}(\vec {z})$:
(1.5)
$\forall \vec {z} \in {{\mathbb{R}}^{{{{n}_{j}}}}}\quad \exists \vec {c} = \vec {c}\left( {{{\mathcal{F}}_{j}}(\vec {z})\,{\text{|}}\,{{{\mathbf{W}}}_{j}}} \right):\;\vec {z} = \sum\limits_{k = 1}^m {{c}_{k}}\vec {w}_{k}^{j}.$Существует неединственная матрица Wj, удовлетворяющая условию (1.5) обратимости оператора ${{\mathcal{F}}_{j}}$ при избыточном множестве векторов $\{ \vec {w}_{1}^{j}, \ldots ,\vec {w}_{{{{m}_{j}}}}^{j}\} $.
2. Модель фрейма для сверточного слоя. Рассмотрим задачу регуляризации векторов весов нейронов некоторого слоя с точки зрения увеличения их разнообразия, тем самым минимизируя потери информации на этом слое даже тех данных, которые слабо представлены в обучающей выборке.
В случае представления слоя в виде линейного оператора (1.2) с квадратной матрицей весов условие ортогональности данной матрицы ведет к существованию обратного оператора для данного слоя. В частности, веса слоя образуют базис и любой вход $\vec {z} \in {{\mathbb{R}}^{n}}$ раскладывается по базисной системе векторов с уникальными коэффициентами. Тогда линейный оператор $\mathcal{F}$ будет обладать максимальной обобщающей способностью, поскольку может преобразовывать и представлять в ${{\mathbb{R}}^{n}}$ без потерь любой пример $\vec {z}$ вне обучающей выборки.
Предложим модель $\mathcal{F}:{{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{m}}$ нейросетевого слоя с сохранением свойства обратимости, но при этом содержащую избыточное число параметров (m > n), что характерно для сверточных слоев нейронной сети. Условие обратимости гарантирует, что в избыточном множестве весов модели найдется базис и, таким образом, сохраняется обобщающая способность представлять любой вход $\vec {z} \in {{\mathbb{R}}^{n}}$ без потерь в ${{\mathbb{R}}^{m}}$. Избыточность весов снижает степень ограничений при обучении модели и может способствовать устойчивость модели.
Линейный оператор $\mathcal{F}$ с матрицей ${\mathbf{W}}$ непрерывен и, следовательно, ограничен:
(2.1)
$\exists \;0 < B < \infty :\;{\text{||}}{\mathbf{W}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant B{\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}}\quad {\text{для}}\quad \forall \vec {z} \in {{\mathbb{R}}^{n}}$Требование устойчивого восстановления $\vec {z}$ по образу ${\mathbf{W}}\vec {z}$ означает, что если ${\text{||}}{\mathbf{W}}\vec {z}{\text{|}}{{{\text{|}}}^{2}}$ мало, то и ${\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}}$ также должна быть малой, т.е $\exists \;\alpha < \infty :\;{\text{||}}{\mathbf{W}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant 1 \Rightarrow {\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant \alpha $. Следуя рассуждениям [14], пусть $\vec {\tilde {z}} = \vec {z}{\text{/||}}{\mathbf{W}}\vec {z}{\text{||}}$ для $\forall \vec {z} \in {{\mathbb{R}}^{n}}$, тогда из условия ${\text{||}}{\mathbf{W}}\vec {\tilde {z}}{\text{|}}{{{\text{|}}}^{2}} \leqslant 1$ вытекает ${\text{||}}\vec {\tilde {z}}{\text{|}}{{{\text{|}}}^{2}} \leqslant \alpha $, откуда получаем выражение ${\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}}/{\text{||}}{\mathbf{W}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant \alpha $ или при $A = {{\alpha }^{{ - 1}}} > 0$:
(2.2)
$A{\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant {\text{||}}{\mathbf{W}}\vec {z}{\text{|}}{{{\text{|}}}^{2}}\quad {\text{для}}\quad \forall \vec {z} \in {{\mathbb{R}}^{n}}.$Если выражение (2.2) выполняется, то для $\forall {{\vec {z}}_{1}},{{\vec {z}}_{2}} \in {{\mathbb{R}}^{n}}$ расстояние ${\text{||}}{{\vec {z}}_{1}} - {{\vec {z}}_{2}}{\text{||}}$ не может быть сколько угодно большим, если величина ${\text{||}}{\mathbf{W}}{{\vec {z}}_{1}} - {\mathbf{W}}{{\vec {z}}_{2}}{\text{|}}{{{\text{|}}}^{2}}$ мала. Таким образом, выражение (2.2) является условием устойчивости.
2.1. Фреймовое представление нейросетевого слоя. Условия (2.1) и (2.2) определяют фрейм в пространстве ${{\mathbb{R}}^{m}}$. Фреймы были введены в работах, связанных с разложениями функций из ${{\mathbb{L}}^{2}}([0,1])$ по комплексным экспонентам, и рассматриваются как базовая структура для построения избыточных систем вейвлетов в Гильбертовом пространстве [14]. Отсчеты ядер сверточных слоев нейронной сети можно рассматривать как реализации семейства функций с компактным носителем. Визуализация сверточных ядер нейронной сети [15], обученной на большой выборке изображений, подтверждает аналогию с вейвлетами. Соответствующие профили напоминают типичные решетчатые фильтры, характерные для функций Габора и гауссовских вейвлетов. Такая аналогия приводит к представлению, что обученная нейронная сеть должна содержать как веса полносвязного слоя, так и сверточные ядра, которые определяют подпространства, обладающие определенной структурой для представления промежуточных разложений входных данных. Таким образом, устойчивость этих разложений и полнота подпространств определяется свойствами системы весов линейных слоев нейросети. Используя идеи из [14], будем рассматривать линейные слои обученной нейронной сети как фреймовую структуру.
Определение [16]. Набор векторов $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m} \subset {{\mathbb{R}}^{n}}$ называется фреймом в ${{\mathbb{R}}^{n}}$, если $\exists {\kern 1pt} A,B$ : $0 < A \leqslant B < \infty :{\kern 1pt} \;\forall \vec {z} \in {{\mathbb{R}}^{n}}$ выполнено неравенство фрейма:
(2.3)
$A{\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant \sum\limits_{i = 1}^m {\text{|}}\langle \vec {z},{{\vec {w}}_{i}}\rangle {{{\text{|}}}^{2}} \leqslant B{\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}},$Фрейм обладает рядом свойств, которые делают естественным его использование для описания нейросетевого слоя. Полнота фрейма $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m} \subset {{\mathbb{R}}^{n}}$ в ${{\mathbb{R}}^{n}}$ и его избыточность при $m > n$ во многом характерны для слоя нейросети и позволяют точнее его описывать. Фреймовая система гарантированно содержит подсистему, образующую базис в ${{\mathbb{R}}^{n}}$. В частности, если векторы фрейма линейно независимы, то сам фрейм является базисом.
Полная ортогональная система – частный случай фрейма. В связи с этим ортогональная регуляризация (0.1) параметров нейросетевого слоя вида (1.2) соответствует частному случаю построения жесткого фрейма с границами $A = B = 1$ (фрейм Парсеваля–Стеклова). В действительности равенство ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} = \mathbb{I}$ необходимо и достаточно для того, чтобы строки матрицы W образовывали фрейм Парсеваля–Стеклова [16]. Более того, фрейм является естественным обобщением полных ортогональных систем с точки зрения сингулярных чисел матрицы ${\mathbf{W}}$, спектра матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$. Для ортогональной системы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} = \mathbb{I}$, все собственные значения равны 1. Если строки $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m}$ матрицы W образуют фрейм, то собственные числа ${{\lambda }_{1}}, \ldots ,{{\lambda }_{n}}$ матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$ ограничены границами фрейма:
Для жесткого фрейма $A = B$ все сингулярные числа матрицы W одинаковы. В данном случае множество векторов пространства наиболее равномерно представляется векторами фреймовой системы, т.е. элементы фрейма максимально разнообразны.
Ограниченность спектра для фреймового представления линейного оператора с матрицей W позволяет оценить константу Липшица $\mathcal{L}$ данного оператора, равную спектральной норме матрицы W:
(2.5)
$\mathcal{L} = {\text{||}}{\mathbf{W}}{\text{|}}{{{\text{|}}}_{2}} = \sigma ({\mathbf{W}}) \leqslant \sqrt B .$Одним из важнейших свойств фрейма $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m} \subset {{\mathbb{R}}^{n}}$ является возможность разложения произвольного элемента пространства по дуальному фрейму $\{ {{\widetilde {\vec {w}}}_{i}}\} _{{i = 1}}^{m}$, элементы которого определяются как ${{\widetilde {\vec {w}}}_{i}} = {{({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}})}^{{ - 1}}}{{\vec {w}}_{i}}$, ${{{\mathbf{W}}}^{{\text{T}}}} = \left[ {{{{\vec {w}}}_{1}} \ldots {{{\vec {w}}}_{m}}} \right]$, $i = \overline {1,m} $:
(2.6)
$\vec {z} = \sum\limits_{i = 1}^m \langle \vec {z},{{\vec {w}}_{i}}\rangle {{\widetilde {\vec {w}}}_{i}},\quad \forall \vec {z} \in {{\mathbb{R}}^{n}}.$Разложение по дуальному фрейму задает решение переопределенной системы линейных алгебраических уравнений (СЛАУ) $\vec {u} = {\mathbf{W}}\vec {z}$, где ${{{\mathbf{W}}}^{{\text{T}}}} = \left[ {{{{\vec {w}}}_{1}} \ldots {{{\vec {w}}}_{m}}} \right]$, строки $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m}$ матрицы W образуют фрейм. Причем фрейм дает устойчивое решение задачи восстановления входа: $\vec {z} = ({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}{{)}^{{ - 1}}}{{{\mathbf{W}}}^{{\text{T}}}}\vec {u}$. Обусловленность задачи ограничена отношением границ фрейма:
(2.7)
$\kappa ({\mathbf{W}}) = {\text{||}}{{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}{\text{||}}\;{\text{||}}{{({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}})}^{{ - 1}}}{\text{||}} = \frac{{{\text{|}}{{\lambda }_{{\max }}}({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}){\text{|}}}}{{{\text{|}}{{\lambda }_{{\min }}}({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}){\text{|}}}} \leqslant \frac{B}{A}.$В случае жесткого фрейма обусловленность задачи оптимальна: $\kappa ({\mathbf{W}}) = 1$.
Приведенные свойства делают до некоторой степени естественным использование фрейма в качестве модели слоя нейросети. Пусть нейросетевой слой, подобно (1.2), задан линейным оператором $\mathcal{F}:{{\mathbb{R}}^{n}} \to {{\mathbb{R}}^{m}}$ с матрицей ${\mathbf{W}} \in {{\mathbb{R}}^{{m \times n}}}:{\kern 1pt} \;m \geqslant n,{\kern 1pt} $ $\mathcal{F}(\vec {z}) = {\mathbf{W}}\vec {z},$ $\forall \vec {z} \in {{\mathbb{R}}^{n}}$; ${{{\mathbf{W}}}^{{\text{T}}}} = \left[ {{{{\vec {w}}}_{1}} \ldots {{{\vec {w}}}_{m}}} \right]$. Предлагается рассматривать строки $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m}$ матрицы W в качестве фреймовой системы векторов. Наличие разложения по дуальному фрейму (2.6) позволяет сформулировать следующее утверждение.
Утверждение. Для обратимости линейной части нейросетевого слоя $\mathcal{F}(\vec {z}) = {\mathbf{W}}\vec {z}$ необходимо и достаточно, чтобы строки $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m}$ матрицы W образовывали фрейм в ${{\mathbb{R}}^{n}}$.
Доказательство. Необходимость. Пусть линейная часть слоя $\mathcal{F}(\vec {z}) = {\mathbf{W}}\vec {z}$ обратима. Покажем, что строки $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m}$ матрицы W образуют фрейм в ${{\mathbb{R}}^{n}}$.
Обратимость соответствует линейной восстановимости (1.5) произвольного входа $\vec {z} \in {{\mathbb{R}}^{n}}$ по системе $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m}$, т.е. система полна в ${{\mathbb{R}}^{n}}$. Полная система в ${{\mathbb{R}}^{n}}$ является фреймом в данном пространстве [16].
Достаточность. Пусть строки $\{ {{\vec {w}}_{k}}\} _{{k = 1}}^{m}$ матрицы W – фрейм в ${{\mathbb{R}}^{n}}$. Покажем, что линейный оператор $\mathcal{F}(\vec {z}) = {\mathbf{W}}\vec {z}$ обратим.
Воспользуемся свойством (2.6) разложения входа по дуальному фрейму:
(2.8)
$\vec {z} = \sum\limits_{i = 1}^m \langle \vec {z},{{\vec {w}}_{i}}\rangle {{\widetilde {\vec {w}}}_{i}} = \sum\limits_{i = 1}^m {{({\mathbf{W}}\vec {z})}_{i}}{\kern 1pt} {{\widetilde {\vec {w}}}_{i}} = \sum\limits_{i = 1}^m {{(\mathcal{F}(\vec {z}))}_{i}}{\kern 1pt} {{\widetilde {\vec {w}}}_{i}},\quad \forall \vec {z} \in {{\mathbb{R}}^{n}},$(2.9)
$\vec {z} = \sum\limits_{i = 1}^m \underbrace {{{{\left( {\mathcal{F}(\vec {z})} \right)}}_{i}}{{{({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}})}}^{{ - 1}}}}_{{{{\tilde {c}}}_{i}}(\mathcal{F}(\vec {z}),{\mathbf{W}})}{{\vec {w}}_{i}} = \sum\limits_{i = 1}^m {{\tilde {c}}_{i}}{{\vec {w}}_{i}},\quad \forall \vec {z} \in {{\mathbb{R}}^{n}},$2.2. Фреймовая регуляризация. Ввиду того что явная параметризация нейросетевого слоя в качестве фрейма не представляется возможной, предлагается построение регуляризатора, накладывающего штраф за несоблюдение достаточного условия фрейма.
Фреймовое неравенство (2.3) для нейросетевого слоя вида (1.2) записывается как
(2.10)
$A{\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant {\text{||}}{\mathbf{W}}\vec {z}{\text{|}}{{{\text{|}}}^{2}} \leqslant B{\text{||}}\vec {z}{\text{|}}{{{\text{|}}}^{2}},\quad \forall \vec {z} \in {{\mathbb{R}}^{n}},$(2.11)
$\left( {\begin{array}{*{20}{c}} {{{{\vec {z}}}^{{\text{T}}}}({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} - A{\kern 1pt} \mathbb{I})\vec {z} \geqslant 0,\quad \forall \vec {z} \in {{\mathbb{R}}^{n}},} \\ {{{{\vec {z}}}^{{\text{T}}}}( - {{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} + B{\kern 1pt} \mathbb{I})\vec {z} \geqslant 0,\quad \forall \vec {z} \in {{\mathbb{R}}^{n}}.} \end{array}} \right.$Неравенства данной системы соответствуют положительной полуопределенности матрицы $({{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} - A{\kern 1pt} \mathbb{I})$ и $( - {{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} + B{\kern 1pt} \mathbb{I})$ соответственно. Регуляризатор для произвольной матрицы W весов слоя определяется путем введения штрафа за нарушение этих неравенств, пользуясь следующим достаточным условием положительной полуопределенности матрицы, являющимся следствием теоремы Гершгорина [17].
Матрица ${\mathbf{V}} \in {{\mathbb{R}}^{{m \times m}}}$ положительно полуопределена, если она обладает свойством диагонального преобладания:
Пусть ${\mathbf{V}} = {{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$, $M(v) = \min \{ v,0\} $. Введем фреймовый регуляризатор для отдельного нейросетевого слоя с матрицей весов W:
(2.12)
$R({\mathbf{W}}) = \frac{1}{n}\sum\limits_{i = 1}^n \underbrace {M{{{\left( {{{v}_{{ii}}} - A - \sum\limits_{j = 1,j \ne i}^n {\text{|}}\,{{v}_{{ij}}}{\text{|}}} \right)}}^{2}}}_{{\text{штраф }}i{\text{ - й строки (}}{{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} - A{\kern 1pt} \mathbb{I})} + \underbrace {M{{{\left( { - {{v}_{{ii}}} + B - \sum\limits_{j = 1,j \ne i}^n {\text{|}}{{v}_{{ij}}}{\text{|}}} \right)}}^{2}}}_{{\text{штраф }}i{\text{ - й строки }}( - {{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}} + B{\kern 1pt} \mathbb{I})},$Отметим, что обычно применяемый штраф на ${{L}_{2}}$ норму весов (weight decay [5]) конкурирует с предложенной фреймовой регуляризацией, поскольку независимо уменьшает диагональное доминирование матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$ путем минимизации диагональных элементов – квадратов весов слоя. Более того, условие с верхней границей $B$ при фреймовой регуляризации обобщает подход ограничения нормы весов [5] и не нуждается в использовании данного штрафа.
2.3. Фреймовая регуляризация сверточных слоев. Особый интерес представляет класс нейросетевых моделей, состоящий из сверточных нейронных сетей, в силу успешности их применения во многих задачах обработки изображений и компьютерного зрения. Сверточный слой удовлетворяет линейному представлению (1.2) в случае, если размерность входа не снижается. В качестве матрицы W весов линейного представления сверточного слоя выступает блочно-теплицева матрица, составленная из параметров свертки.
На практике размерность матрицы W оказывается слишком высокой для эффективного вычисления матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$, что накладывает ограничения на применимость предложенного метода в исходном виде. Ввиду разреженности блочно-теплицевой матрицы W предлагается использовать алгоритм вычисления ненулевых элементов каждой из строк матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$ на основе свертки ядер с самими собой, предложенный в работе [11]. Эффективность алгоритма обусловлена конечным набором возможных пространственных пересечений двух сверточных ядер (рис. 2).
Отличительной особенностью предложенного регуляризатора (2.12) является инвариантность его значений к позициям внедиагональных элементов каждой из строк матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$. Данное свойство фреймового регуляризатора позволяет успешно вычислять его значения на основе приведенного выше алгоритма вычисления ненулевых элементов матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$.
3. Численные эксперименты. В данной работе вычислительные эксперименты разделяются на три набора по направлению исследований. В рамках первой группы экспериментов проводится сравнение предложенного метода регуляризации с существующими в рамках задачи мультиклассовой классификации. Вторая группа экспериментов посвящена исследованию обобщающей способности моделей, обученных с разными видами регуляризаций, при смене домена. Третье направление экспериментов связано с изучением устойчивости моделей к состязательным атакам.
3.1. Классификация изображений. В табл. 1 приведены характеристики трех баз данных, CIFAR-10, CIFAR-100 [18] и SVHN [19], использованных в вычислительных экспериментах по мультиклассовой классификации. В качестве моделей взяты сверточные нейронные сети архитектур ResNet-34 и ResNet-50 [20]. Функция потерь задана в виде (1.3), (1.4) с фреймовым регуляризатором (2.12). Границы фрейма брались из множеств $A \in \{ 0.05,0.1,0.25,0.5,1.0\} $ и $B \in \{ 0.05,0.1,0.25,0.5,1.0,2.0,4.0\} $ с условием A ≤ B. Найденная по серии обучений модели наилучшая пара границ $A$, $B$ использовалась для сравнения с другими методами регуляризации. Модели обучались на 200 эпохах с размером батча 128, оптимизатором выступал Adam с начальным шагом 0.01 и мультипликативным уменьшением шага с коэффициентом 0.1 на 100, 150 и 180 эпохах [21].
Таблица 1.
Описание выборок
| Выборка | Число изображений | Число классов |
|---|---|---|
| CIFAR-10 | 60 000 | 10 |
| CIFAR-100 | 60 000 | 100 |
| SVHN | ~100 000 | 10 |
Проведено сравнение предложенного метода фреймовой регуляризации с существующими подходами: минимизацией гиперсферической потенциальной энергии (minimum hyperspherical energy) [8], спектральной ограниченной изометрии (spectral restricted isometry property) [10] и подходами к ортогонализации (weights orthogonalization, orthogonal convolutions) [9, 11]. Ортогонализация применялась к сверточным слоям в представлении im2col, для последних двух из указанных методов использовалось блочно-теплицево представление [22]. Показателем качества решения взята стандартная в задачах классификации мера – точность (accuracy). В силу сбалансированности классов во всех используемых выборках применение этой меры оправдано.
В табл. 2 представлена зависимость точности классификации модели ResNet-34, обученной на выборке CIFAR-100 с фреймовой регуляризацией, от различных значений границ фрейма. Наилучшая точность достигалась для значений границ $A = 0.25$, $B = 0.5$. Эти значения взяты для фреймовой регуляризации (2.12) во всех дальнейших экспериментах. Следует отметить, что (2.12) является обобщением регуляризации по ${{L}_{2}}$ норме. Эксперименты показали, что при фреймовой регуляризации штраф на ${{L}_{2}}$ норму весов [5] ухудшает результаты, так как конкурирует за влияние на диагональные элементы матрицы ${{{\mathbf{W}}}^{{\text{T}}}}{\mathbf{W}}$. Поэтому данный штраф не включен в целевую функцию предлагаемого метода. Этим метод отличается от ранее известных, где наряду с иными различными регуляризаторами присутствует и регуляризатор по ${{L}_{2}}$ норме. Сравнение методов регуляризации представлено в табл. 3 и 4.
Таблица 2.
Точность (в %) модели ResNet-34 c фреймовой регуляризацией для выборки CIFAR-100 при различных значениях границ фрейма
| A | B | ||||||
|---|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 4.0 | |
| 0.05 | 76.81 | 76.88 | 77.02 | 77.06 | 76.95 | 76.91 | 76.90 |
| 0.1 | – | 77.19 | 77.36 | 77.41 | 77.33 | 77.21 | 77.01 |
| 0.25 | – | – | 77.53 | 77.61 | 77.57 | 77.39 | 77.21 |
| 0.5 | – | – | – | 77.26 | 77.20 | 77.13 | 77.10 |
| 1.0 | – | – | – | – | 76.79 | 76.74 | 76.75 |
Таблица 3.
Точность (в %) методов регуляризации (ResNet-34)
| Метод регуляризации | CIFAR-10 | CIFAR-100 | SVHN |
|---|---|---|---|
| Без регуляризации | 94.53 ± 0.03 | 75.58 ± 0.08 | 96.50 ± 0.03 |
| Minimum hyperspherical energy | 94.58 ± 0.04 | 75.78 ± 0.08 | 96.59 ± 0.03 |
| Weights orthogonalization | 94.59 ± 0.04 | 75.98 ± 0.08 | 96.51 ± 0.02 |
| Spectral restricted isometry property | 94.72 ± 0.03 | 76.24 ± 0.09 | 96.57 ± 0.03 |
| Orthogonal convolutions | 95.03 ± 0.04 | 76.57 ± 0.06 | 96.66 ± 0.02 |
| Фреймовая регуляризация | 95.17 ± 0.05 | 77.61 ± 0.07 | 96.85 ± 0.02 |
Таблица 4.
Точность (в %) методов регуляризации (ResNet-50)
| Метод регуляризации | CIFAR-10 | CIFAR-100 | SVHN |
|---|---|---|---|
| Без регуляризации | 94.83 ± 0.04 | 77.20 ± 0.07 | 96.92 ± 0.03 |
| Minimum hyperspherical energy | 94.88 ± 0.03 | 77.34 ± 0.06 | 96.94 ± 0.02 |
| Weights orthogonalization | 94.92 ± 0.04 | 77.38 ± 0.06 | 96.91 ± 0.03 |
| Spectral restricted isometry property | 95.01 ± 0.03 | 77.40 ± 0.07 | 96.95 ± 0.03 |
| Orthogonal convolutions | 95.29 ± 0.03 | 77.77 ± 0.07 | 97.01 ± 0.02 |
| Фреймовая регуляризация | 95.25 ± 0.04 | 78.35 ± 0.06 | 97.10 ± 0.02 |
Полученные результаты показывают, что предложенный метод значимо превосходит базовые подходы с точки зрения качества классификации на выборках CIFAR-100 и SVHN для обеих нейросетевых моделей. На выборке CIFAR-10 метод сравним по качеству с лучшим из имеющихся базовых.
3.2. Устойчивость к смене домена. Произведено сравнение предложенного метода регуляризации на основе фрейма с базовыми методами с точки зрения устойчивости к смене домена. Модели архитектуры ResNet-34, обучались на выборке CIFAR-10 с разными видами регуляризации. Далее расчитывалась их точность на исходном домене CIFAR-10 и на новых доменах, которые задавались выборками CIFAR-10-C и CINIC-10 [23, 24]. CIFAR-10-C [24] является аугментированной версией выборки CIFAR-10 с 19 разными типами возмущений, среди которых присутствуют нормальный шум, размытие, изменение контрастности и пр. CINIC-10 [23] – подвыборка ImageNet [25], включающая классы из CIFAR-10. Результаты работы методов при смене домена приведены в табл. 5.
Таблица 5.
Точность (в %) методов регуляризации на разных доменах
| Метод регуляризации | CIFAR-10 | CIFAR-10-C | CINIC-100 |
|---|---|---|---|
| Без регуляризации | 94.53 ± 0.03 | 74.77 ± 0.25 | 67.91 ± 0.35 |
| Orthogonal Convolutions | 94.52 ± 0.01 | 76.27 ± 0.19 | 69.87 ± 0.29 |
| Фреймовая регуляризация | 94.53 ± 0.01 | 76.65 ± 0.15 | 71.20 ± 0.32 |
Модель, обученная с предложенным методом регуляризации на основе фреймового представления слоя, обладает существенно более высокой обобщающей способностью по сравнению с моделью, обученной без регуляризации, направленной на повышение разнообразия параметров. Фреймовая регуляризация обладает несколько более высокой устойчивостью к смене домена по сравнению с ортогональной регуляризацией.
3.3. Устойчивость к состязательным атакам. Исследована устойчивость моделей, обученных с разными видами регуляризации, к состязательным атакам. В качестве метода состязательной атаки использовался подход SimBA, представляющий из себя итеративную атаку типа “черный ящик” [26]. Итерация атаки производится путем добавления к входу модели случайного вектора из ортонормированного базиса во входном пространстве с малым весом, знак которого определяется исходя из значений выхода модели для данного видоизмененного входа. Векторы ортонормированного базиса в конечномерном пространстве входов однозначно отвечают элементам входного тензора: содержат единственную единицу на заданной позиции, остальные компоненты – нули. Таким образом, итерация атаки является возмущением строго одного элемента входного тензора.
Эффективность атаки оценивается по доле успешных атак (attack success rate – ASR) при заданном числе итераций. Успешность атаки в задаче классификации соответствует изменению предсказания модели для видоизмененного атакой входа, атака производится только для верно классифицированных объектов.
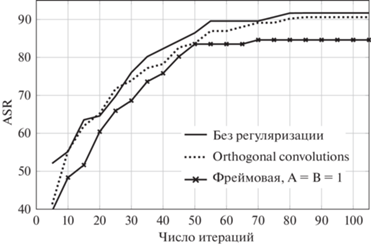
Результаты успешности атак на модели, обученные с разными регуляризациями, отображены в табл. 6. На рис. 3 представлена зависимость доли успешных атак от числа итераций метода SimBA.
Таблица 6.
Зависимость доли успешных атак (в %) от числа итераций
| Метод регуляризации | Число итераций | ||||
|---|---|---|---|---|---|
| 1 | 10 | 50 | 100 | 1000 | |
| Без регуляризации | 52.08 | 59.37 | 84.38 | 92.71 | 93.75 |
| Orthogonal convolutions | 41.30 | 57.61 | 83.69 | 91.30 | 92.06 |
| Фреймовая регуляризация | 39.56 | 49.45 | 80.20 | 84.61 | 86.81 |
Исходя из полученных результатов, заключается, что модель, обученная с предложенным методом регуляризации, существенно более устойчива к исследованной состязательной атаке по сравнению с моделью, обученной без регуляризации. Фреймовое представление нейросетевых слоев позволяет ограничить сверху константу Липшица (2.5), что делает модель более устойчивой по отношению к малому возмущению входа. Для модели, обученной с фреймовой регуляризацией, требуется до ~1.4 раза большего числа итераций для достижения доли успешных атак ASR = 70% в сравнении с ортогональной регуляризацией, что может объясняться тем, что фреймовая регуляризация позволяет достигать более ограниченного спектра весов слоя.
Заключение. Поставлена задача регуляризации нейронной сети, направленная на увеличение эффективности избыточного множества параметров и повышения устойчивости модели. Изучены существующие подходы и выявлены их недостатки. В частности, ортогонализация параметров нейросетевого слоя является избыточно жестким ограничением и, фактически, ортогональность весов не достигается. Для увеличения разнообразия параметров нейронной сети обобщен метод ортогонализации и предложена модель нейросетевого слоя, представляющая параметры в виде фрейма. Такое представление делает разложение входного сигнала по весам слоя полным и устойчивым, исключает потерю информации на данном слое. На основе предложенной модели разработан фреймовый регуляризатор, накладывающий штраф на параметры за несоблюдение достаточного условия фрейма. Проведен вычислительный эксперимент по оценке качества разработанного метода в сравнении с альтернативными подходами в задачах классификации изображений, увеличения обобщающей способности и устойчивости к состязательным атакам. Показано превосходство моделей, обученных с помощью фреймовой регуляризации, с точки зрения точности классификации и устойчивости модели по сравнению с базовыми методами регуляризации параметров.
Для дальнейшего развития работы планируется исследовать зависимость точности модели от количества ее параметров при использовании фреймовой регуляризации, сравнение предложенного подхода с другими методами увеличения эффективности и обобщающей способности на больших обучающих и тестовых данных.
Список литературы
Liu C., Zoph B., Neumann M. et al. Progressive Neural Architecture Search // Proc. European Conf. Computer Vision (ECCV). Munich, Germany, 2018. P. 19–34.
Tan M., Le Q. Efficientnet: Rethinking Model Scaling for Convolutional Neural Networks // Proc. 36th Intern. Conf. Machine Learning. Long Beach, CA, USA, 2019. P. 6105–6114.
Molchanov P., Tyree S., Karras T. et al. Pruning Convolutional Neural Networks for Resource Efficient Inference // Proc. Intern. Conf. Learning Representations. Toulon, France, 2017. P. 1–17.
Molchanov P., Mallya A., Tyree S. et al. Importance Estimation for Neural Network Pruning // Proc. IEEE/CVF Conf. Computer Vision and Pattern Recognition. Long Beach, CA, USA, 2019. P. 11264–11272.
Krogh A., Hertz J. A Simple Weight Decay Can Improve Generalization // Advances in Neural Information Processing Systems. 1992. № 4. P. 950–957.
Srivastava N., Hinton G., Krizhevsky A. et al. Dropout: A Simple Way to Prevent Neural Networks from Overfitting // The Journal of Machine Learning Research. 2014. V. 15. № 1. P. 1929–1958.
Ioffe S., Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift // Proc. Intern. Conf. Machine Learning. Lille, France, 2015. P. 448–456.
Liu W., Lin R., Liu Z. et al. Learning towards Minimum Hyperspherical Energy // Proc. 32nd Conf. Neural Information Processing Systems. Montreal, Canada, 2018. V. 31.
Xie D., Xiong J., Pu S. All You Need Is Beyond a Good Init: Exploring Better Solution for Training Extremely Deep Convolutional Neural Networks with Orthonormality and Modulation // Proc. IEEE Conf. Computer Vision and Pattern Recognition. Honolulu, HI, USA, 2017. P. 6176–6185.
Bansal N., Chen X., Wang Z. Can We Gain More from Orthogonality Regularizations in Training Deep Networks? // Proc. 32nd Conf. Neural Information Processing Systems. Montreal, Canada, 2018. V. 31.
Wang J., Chen Y., Chakraborty R., Yu S. X. Orthogonal Convolutional Neural Networks // Proc. IEEE/CVF Conf. Computer Vision and Pattern Recognition. Seattle, WA, USA, 2020. P. 11505–11515.
Saxe A., McClelland J., Ganguli S. Exact Solutions to the Nonlinear Dynamics of Learning in Deep Linear Neural Networks // Proc. 2nd Intern. Conf. Learning Representations. Banff, AB, Canada, 2014. P. 1–22.
Григорьев А.Д., Гнеушев А.Н. Регуляризация параметров нейронной сети на основе неравенства Рисса // Математические методы распознавания образов: Тез. докл. 20-й Всероссийской конф. с международным участием. М.: Российская академия наук, 2021. С. 121–122.
Добеши И. Десять лекций по вейвлетам. Москва, Ижевск: РХД. 2001. 463 с.
Krizhevsky A., Sutskever I., Hinton G.E. ImageNet Classification with Deep Convolutional Neural Networks // Comm. ACM. 2012. V. 60. P. 84–90.
Casazza P.G., Kutyniok G. Finite Frames: Theory and Applications. Springer Science & Business Media, 2012.
Bell H.E. Gershgorin’s Theorem and the Zeros of Polynomials // The American Mathematical Monthly. 1965. V.72. № 3. P. 292–295.
Krizhevsky A. Learning Multiple Layers of Features from Tiny Images [Электронный ресурс] // cs.toronto.edu. 2009. Дата обновления: 08.04.2009. URL: https://www.cs.toronto.edu/ kriz/learning-features-2009-TR.pdf (дата обращения: 01.06.2022).
Netzer Y., Wang T., Coates A. et al. Reading Digits in Natural Images with Unsupervised Feature Learning // Neural Information Processing Systems Workshop on Deep Learning and Unsupervised Feature Learning. Granada, Spain, 2011.
He K., Zhang X., Ren S., Sun J. Deep Residual Learning for Image Recognition // Proc. IEEE Conf. Computer Vision and Pattern Recognition. Las Vegas, NV, USA, 2016. P. 770–778.
Kingma D.P., Ba J. Adam: A Method for Stochastic Optimization // Proc. Intern. Conf. Learning Representations. San Diego, CA, USA, 2015. P. 1–13.
Chellapilla K., Puri S., Simard P. High Performance Convolutional Neural Networks for Document Processing // Proc. Tenth Intern. Workshop Frontiers in Handwriting Recognition. La Baule, France. 2006. P. 1–7.
Darlow L., Crowley E., Antoniou A., Storkey A. Cinic-10 is not Imagenet or Cifar-10 [Электронный ресурс] // arXiv.org. 2018. Дата обновления: 02.https://doi.org/10.2018. URL: https://arxiv.org/abs/1810.03505 (дата обращения: 01.06.2022).
Hendrycks D., Dietterich T. Benchmarking Neural Network Robustness to Common Corruptions and Perturbations // Proc. 7th Intern. Conf. Learning Representations. New Orleans, LA, USA, 2019. P. 1–16.
Deng J., Dong W., Socher R. et al. ImageNet: A Large-scale Hierarchical Image Database // Proc. IEEE Conf. Computer Vision and Pattern Recognition. Miami, FL, USA, 2009. P. 248–255.
Guo C., Gardner J., You Y. et al. Simple Black-box Adversarial Attacks // Proc. Intern. Conf. Machine Learning. Long Beach, CA, USA, 2019. P. 2484–2493.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления