Известия РАН. Теория и системы управления, 2023, № 1, стр. 106-122

Введение. Рассматривается задача проведения декомпозиции множества альтернатив с последующим упорядочиванием подмножества наиболее предпочтительных вариантов. При решении задач с большим числом альтернатив возникает необходимость использовать полиномиальные алгоритмы, так как современные вычислительные средства не в состоянии решать алгоритмы класса NP (non-deterministic polynomial) за приемлемое время [1]. Но многие переборные алгоритмы обладают преимуществом перед полиномиальными, обеспечивая наибольшую степень согласованности агрегированного отношения с профилем исходных предпочтений (экспертов или по критериям качества). Задачи с большим числом альтернатив возникают, в частности, при выборе наиболее успешных проектов или предприятий с целью инвестирования каким-либо венчурным фондом. В этом случае целесообразно предварительно отбросить заведомо худшие варианты и работать далее с подмножеством наиболее предпочтительных альтернатив.

Практически все алгоритмы группового выбора требуют от экспертов ранжирования альтернатив, что невозможно осуществить при большом количестве вариантов. Алгоритмы, предложенные в статье, основываются на профиле исходных предпочтений, содержащем произвольные бинарные отношения. Ранжирования альтернатив не требуется, достаточно попарно сравнить хорошо известные экспертам варианты. При необходимости ЛПР (лицо, принимающее решения) может дополнить информацию, но уже только на множестве наилучших альтернатив.

Статья является продолжением работы [2], в которой предложен алгоритм разбиения орграфа на уровни предпочтения. Уровни предпочтения позволяют провести декомпозицию первоначальной задачи и исключить из рассмотрения заведомо худшие альтернативы, тем самым уменьшить время работы алгоритма и сделать возможным использование даже алгоритмов класса NP.

Одним из наиболее математически обоснованных алгоритмов класса NP является построение медианы Кемени [3] – ранжирования альтернатив, минимально удаленные от экспертных предпочтений. Согласованность предпочтений измеряется расстоянием Хэмминга между матрицами смежности соответствующих им орграфов. Ж.-А. Кондорсе еще в XVIII в. предложил выбирать в качестве группового решения ранжирование альтернатив, соответствующее максимальному числу отданных за него голосов экспертов [4]. Такому ранжированию удовлетворял Гамильтонов путь максимальной длины в нагруженном голосами экспертов орграфе. Эту же идею использует и М. Шульце [5], предложивший метод выбора победителя в голосовании, который в настоящее время часто применяется. Алгоритмы нахождения Гамильтоновых путей [6] и построения медианы Кемени являются переборными и, следовательно, могут быть применены только для очень небольшого числа альтернатив.

Предлагаемая в статье процедура нахождения подмножества наиболее предпочтительных альтернатив имеет полиномиальную сложность. Она базируется на предварительном построении мажоритарного графа. В [7] показано, что отношение, имеющее минимальное суммарное расстояние до исходных предпочтений, находится по правилу большинства, т.е. соответствует мажоритарному графу. Алгоритм построения мажоритарного графа имеет вычислительную сложность $O(m{{n}^{2}})$ от числа экспертов m и альтернатив $n$. И хотя мажоритарный граф может быть нетранзитивным, содержать противоречивые контуры [8, 9], именно его целесообразно выбирать в качестве основы для декомпозиции исходной задачи. Разбиение мажоритарного графа на уровни предпочтения дает возможность в дальнейшем работать только с наилучшими альтернативами, но при необходимости можно ранжировать альтернативы каждого уровня предпочтения.

В статье для ранжирования наиболее предпочтительных альтернатив разработан алгоритм построения агрегированного полного квазипорядка (нестрогого ранжирования), который включает в себя участие ЛПР для получения дополнительной информации о предпочтениях альтернатив.

Строгий линейный порядок (строгое ранжирование) предлагается получить с помощью Гамильтоновых путей максимальной длины [10, 11]. Длина пути соответствует суммарному числу голосов экспертов по всем дугам пути. В статье разработан алгоритм нахождения Гамильтоновых путей в компоненте сильной связности орграфа методом возведения в степень матрицы смежности. Алгоритм базируется на изложенной в [11] процедуре нахождения Гамильтоновых циклов в неориентированном графе. Также предлагается алгоритм нахождения Гамильтоновых путей в исходном орграфе на основе путей, построенных на уровнях предпочтения мажоритарного графа. В этом случае сложность алгоритма нахождения Гамильтонова пути совпадает со сложностью нахождения Гамильтонова пути в компоненте сильной связности орграфа, имеющей наибольшее число вершин.

1. Постановка задачи. Задано множество альтернатив $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$, причем число альтернатив достаточно велико. Профиль исходных предпочтений (экспертов или по критериям качества) – бинарные отношения ${{\rho }_{1}},~{{\rho }_{2}}, \ldots ,{{\rho }_{m}}$ на множестве A: упорядоченная пара альтернатив из $A$ ${{a}_{i}},~{{a}_{j}} \in {{\rho }_{t}}$, где $t = 1, \ldots ,m$, если элемент ${{a}_{i}}$ не более предпочтителен, чем элемент¹¹ a_j. Требуется найти строгое или нестрогое ранжирование $\tilde {\rho }$ наилучших альтернатив $\tilde {A} \subseteq A$ по предпочтительности.

Под строгим ранжированием будем понимать отношение строгого порядка (антирефлексивное и транзитивное), при котором все альтернативы попарно сравнимы. Под нестрогим ранжированием – отношение полного квазипорядка (рефлексивное и транзитивное).

Из постановки задачи следует, что ее решение разбивается на две части:

1) выделение подмножества наилучших альтернатив $\tilde {A} \subseteq A$;

2) ранжирование альтернатив из подмножества $\tilde {A}$.

Решение первой части задачи сводится к приведенному авторами алгоритму разбиения мажоритарного графа на уровни предпочтения [2]. Наилучшие альтернативы будут находиться на нулевом уровне предпочтения. Для получения нестрогого и строгого ранжирования альтернатив разработаны два метода:

1) достроение отношения до полного квазипорядка;

2) нахождение Гамильтоновых путей максимальной длины.

Алгоритм в [2] позволяет выделить подмножество наилучших альтернатив $\tilde {A} \subseteq A$. Опишем его.

Произвольному бинарному отношению $\rho $, заданному на множестве $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$, поставим в соответствие орграф $G = \langle A,~\rho \rangle $ с множеством вершин A и множеством дуг $\rho $. Множество дуг – это множество упорядоченных пар $\langle {{a}_{i}},~{{a}_{j}}\rangle $ $\left( {{{a}_{i}},~{{a}_{j}} \in A} \right)$, входящих в отношение $\rho $.

Матрица смежности орграфа $R = {\text{||}}{{r}_{{ij}}}{\text{||}}$ определяется как квадратная матрица порядка n с элементами:

Таким образом, профиль исходных предпочтений ${{\rho }_{1}},~{{\rho }_{2}}, \ldots ,{{\rho }_{m}}$ будем задавать матрицами смежности ${{R}^{1}},{{R}^{2}}, \ldots ,{{R}^{m}}$ соответствующих орграфов.

Проведем декомпозиции исходной задачи на уровни предпочтения мажоритарного графа. На первом этапе построим мажоритарный граф ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $, классический [7] или дополнительно нагруженный весами (голосами экспертов) на дугах [8, 9]. Процедура нахождения мажоритарного графа (правило большинства) сводится к суммированию матриц смежности ${{R}^{1}},{{R}^{2}}, \ldots ,{{R}^{m}}$ исходных предпочтений. Таким образом вычислительная сложность алгоритма будет $O(m{{n}^{2}}),~$ где $m$ – число экспертов, n – число альтернатив. На втором этапе декомпозиции разобьем мажоритарный граф на уровни предпочтения, воспользовавшись алгоритмом, приведенным в [2].

Опишем суть алгоритма разбиения на уровни предпочтения произвольного орграфа $G = \langle A,\rho \rangle $ с множеством вершин $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$ $\left( {A \ne \emptyset } \right)$ и множеством дуг $\rho $, хотя в рассматриваемых в статье задачах будем использовать мажоритарный граф ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $.

Для орграфа $G = \langle A,~\rho \rangle $ построим граф конденсации $\bar {G} = \langle \bar {A},~\bar {\rho }\rangle $ с множеством вершин-компонент сильной связности графа $G$: $\bar {A} = \left\{ {{{S}_{1}},~{{S}_{2}}, \ldots ,{{S}_{k}}} \right\}$, дуга $\langle {{S}_{i}},~{{S}_{j}}\rangle \in \bar {\rho }~$ тогда и только тогда, когда существует хотя бы одна дуга в графе G, исходящая из вершины компоненты сильной связности ${{S}_{i}}$ и заходящая в вершину компоненты сильной связности ${{S}_{j}}$.

Граф конденсации по построению не имеет контуров, следовательно, его можно разбить на уровни, используя алгоритм Демукрона [10] (в разных работах может различаться последовательность уровней, но суть определения и алгоритма не меняется). Обозначим уровни графа конденсации ${{\bar {N}}_{0}},{{\bar {N}}_{1}}, \ldots ,{{\bar {N}}_{s}}$.

Определение 1. Уровнями предпочтения графа $G = \langle A,~\rho \rangle $ назовем множества вершин ${{P}_{0}},~{{P}_{1}}, \ldots ,~{{P}_{s}}$, такие, что уровню P_i  принадлежат вершины компонент сильной связности уровня ${{\bar {N}}_{i}}$ графа $\bar {G} = \langle \bar {A},~\bar {\rho }\rangle $ ($i = 1, \ldots ,s$).

Из определения 1 следуют основные этапы разбиения произвольного графа $G = \langle A,~\rho \rangle $ на уровни предпочтения.

Алгоритм 1. Разбиение орграфа $G = \langle A,~\rho \rangle $ на уровни предпочтения.

1. Найдем компоненты сильной связности ${{S}_{1}},~{{S}_{2}}, \ldots ,{{S}_{k}}$ орграфа $G = \langle A,~\rho \rangle $.

2. Построим для орграфа $G = \langle A,~\rho \rangle $ граф конденсации $\bar {G} = \langle \bar {A},~\bar {\rho }\rangle $.

3. Воспользовавшись алгоритмом Демукрона, разобьем граф $\bar {G} = \langle \bar {A},~\bar {\rho }\rangle $ на уровни ${{\bar {N}}_{0}},~{{\bar {N}}_{1}}, \ldots ,~{{\bar {N}}_{s}}$.

4. Вершины уровней предпочтения ${{P}_{0}},~{{P}_{1}}, \ldots ,~{{P}_{s}}$ являются вершинами соответствующих компонент сильной связности уровней ${{\bar {N}}_{0}},~{{\bar {N}}_{1}}, \ldots ,~{{\bar {N}}_{s}}$ графа $\bar {G} = \langle \bar {A},~\bar {\rho }\rangle $.

5. Восстановим дуги орграфа $G = \langle A,~\rho \rangle $.

В [2] предложен и обоснован более простой алгоритм разбиения орграфа на уровни предпочтения.

Отношение $\rho $ на $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$ разобьем на симметричную Symρ и асимметричную Asρ части. К Symρ относятся все такие пары, для которых выполняется следующее условие: $\langle {{a}_{i}},~{{a}_{j}}\rangle \in \rho $ и $\langle {{a}_{j}},~{{a}_{i}}\rangle \in \rho $ одновременно $({{a}_{i}},~{{a}_{j}}$ ∈ A). Асимметричная часть: $As~\rho = \rho {{\backslash }}Sym~\rho $ (если $\langle {{a}_{i}},~{{a}_{j}}\rangle \in As~\rho $, то $\langle {{a}_{j}},~{{a}_{i}}\rangle \notin As~\rho $). Обозначим через Trρ транзитивное замыкание отношения $\rho $ – наименьшее транзитивное отношение, содержащее $\rho $.

Алгоритм 2. Разбиение орграфа $G = \langle A,~\rho \rangle $ на уровни предпочтения.

1. Строим орграф ${{G}_{{As}}} = \langle A,~As\left( {Tr\rho } \right)\rangle $ отношения $As\left( {Tr\rho } \right)$.

2. Разбиваем орграф ${{G}_{{As}}} = \langle A,~As(Tr\rho )\rangle $ на уровни, используя алгоритм Демукрона.

3. Восстанавливаем дуги исходного орграфа $G = \langle A,~\rho \rangle $.

Полученные в п. 2 уровни будем сразу обозначать ${{P}_{0}},~{{P}_{1}}, \ldots ,~{{P}_{s}}$, поскольку они содержат вершины уровней предпочтения исходного орграфа $G = \langle A,~\rho \rangle $.

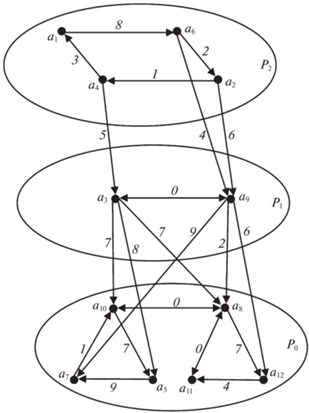
Пример 1. Выбор наилучших моделей дронов для наблюдения за возникновением пожаров. Разбиение мажоритарного графа на уровни предпочтения. В МЧС было принято решение закупить дроны для наблюдения за возникновением лесных пожаров. По стоимости и дальности полета было отобрано 12 моделей $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{{12}}}} \right\}$. Затем пять экспертов провели попарное сравнение моделей, в результате чего были получены отношения ${{\rho }_{1}},~{{\rho }_{2}},~{{\rho }_{3}},~{{\rho }_{4}},~{{\rho }_{5}}$ и соответствующие им матрицы ${{R}^{1}},{{R}^{2}},~{{R}^{3}},~{{R}^{4}},{{R}^{5}}$.

По данному профилю экспертных предпочтений на множестве A был построен нагруженный мажоритарный граф [9]. Используя алгоритм 2, разобьем мажоритарный граф на уровни предпочтения.

Матрица смежности мажоритарного графа ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $ имеет следующий вид:

Определим матрицу смежности $Tr{{R}_{\Sigma }}$, воспользовавшись формулой

или модифицированным алгоритмом Уоршалла [6]:

Вычислим матрицу $As\left( {Tr{{R}_{\Sigma }}} \right)$ по определению асимметричной части отношения: заменим на нули в матрице $Tr{{R}_{\Sigma }}$ симметричные относительно главной диагонали единицы (вместе с диагональю). Затем, используя алгоритм Демукрона, разобьем орграф асимметричной части с матрицей смежности $As\left( {Tr{{R}_{\Sigma }}} \right)$ на уровни:

Согласно алгоритму Демукрона, суммируем элементы строк и записываем сумму в первый столбец матрицы итераций L. Соответствующие нулям первого столбца L альтернативы принадлежат нулевому уровню: ${{a}_{5}},{{a}_{7}},{{a}_{8}},{{a}_{{10}}},{{a}_{{11}}},{{a}_{{12}}} \in {{P}_{0}}$. Обнуляем столбцы с соответствующими номерами альтернатив (обводим 1 – $\boxed1$). И опять суммируем элементы строк, считая $\boxed1$ нулями. Записываем сумму во второй столбец матрицы итераций L, а элементы уровня ${{P}_{0}}$ помечаем звездочкой. Соответствующие нулям второго столбца L альтернативы принадлежат первому уровню предпочтения: ${{a}_{3}},{{a}_{9}} \in {{P}_{1}}$. Обнулив третий и девятый столбцы (обводим 1 – $\boxed{\boxed1}$), получим $As\left( {Tr{{R}_{\Sigma }}} \right) = \left( 0 \right)$. Следовательно, все оставшиеся альтернативы принадлежат второму уровню предпочтения (см. третий столбец L): ${{a}_{1}},{{a}_{2}},{{a}_{4}},{{a}_{6}} \in {{P}_{2}}$.

Расположим вершины-альтернативы по уровням предпочтения и восстановим все дуги орграфа ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $ (рис. 1).

Проведение декомпозиции задачи с помощью разбиения множества альтернатив на уровни предпочтения позволяет удалить из рассмотрения наименее предпочтительные альтернативы, расположенные на уровнях ${{P}_{1}}$ и ${{P}_{2}}$, оставив наилучшие альтернативы уровня ${{P}_{0}}$: подмножество $\tilde {A}~ = \left\{ {{{a}_{5}},~{{a}_{7}},~{{a}_{8}},~{{a}_{{10}}},~{{a}_{{11}}},{{a}_{{12}}}} \right\}$.

На дугах нагруженного мажоритарного графа проставлены веса – разность числа экспертов, предпочитающих одну альтернативу другой. Они понадобятся в следующем разделе для упорядочения наилучших альтернатив подмножества $\tilde {A}$.

2. Достроение произвольного отношения до полного квазипорядка. Для упорядочения наилучших альтернатив $\tilde {A}$ уровня ${{P}_{0}}$ будем использовать процедуру непротиворечивого агрегирования отношений [9]. В качестве агрегированного будем строить отношение квазипорядка (рефлексивное и транзитивное отношение). Алгоритм нахождения отношения квазипорядка основывается на предварительном построении нагруженного мажоритарного графа, который может содержать дуги из симметричной и асимметричной частей отношения. Дуги из симметричной части указывают на равноценность соответствующих альтернатив.

Для нахождения агрегированного квазипорядка $\hat {\rho }$ предварительно разрушим противоречивые контуры мажоритарного графа ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $, если они есть. Контур отношения ${{\rho }_{\Sigma }}$ будем считать противоречивым, если в нем хотя бы одна пара $\langle {{a}_{i}},~{{a}_{j}}\rangle $ принадлежит асимметричной части отношения: $\langle {{a}_{i}},~{{a}_{j}}\rangle \in As{{\rho }_{\Sigma }}$ $\left( {{{a}_{i}},~{{a}_{j}} \in A} \right)$. Отношение $\rho $ называется противоречивым, если оно содержит противоречивый контур. Таким образом, агрегированное отношение не должно содержать контуров, в которых не все элементы равноценны. Отсутствие таких контуров – необходимое условие для осуществления однозначного непустого выбора наилучших альтернатив. Этому условию удовлетворяет отношение квазипорядка.

Алгоритм 3. Построение отношения $\rho $, не содержащего противоречивых контуров по ${{\rho }_{\Sigma }}$.

1. Проверяем граф ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $ на наличие противоречивых контуров. Если таких контуров нет, то граф ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $ без весов на дугах и есть искомый граф $G = \langle A,~\rho \rangle $ и ${{\rho }_{{{\Sigma }}}} = \rho $. Если противоречивые контуры есть, переходим к п. 2.

2. Из графа ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $ удаляем все дуги $\langle {{a}_{i}},~{{a}_{j}}\rangle \in As{{\rho }_{{{\Sigma }}}}$ $({{a}_{i}},~{{a}_{j}} \in A)$, которые принадлежат какому-либо противоречивому контуру и имеют наименьший вес. Переходим к п. 1.

Искомое агрегированное отношение предпочтения $\hat {\rho }$ должно быть квазипорядком. Найдем $\hat {\rho }$ по формуле: $\hat {\rho } = e \cup {\text{Tr}}\rho $, где e – тождественное отношение. Матрица смежности $\hat {R}$ отношения $\hat {\rho }$ согласно формуле, имеет вид

Работа данного алгоритма основывается на нахождении отношения ${{\rho }_{K}}$, содержащего контуры отношения ${{\rho }_{{{\Sigma }}}}$. Матрицу смежности ${{R}_{K}}$ графа отношения ${{\rho }_{K}}$, содержащего все контуры отношения ${{\rho }_{{{\Sigma }}}}$, вычислим по формуле:

где ${{\hat {R}}_{{{\Sigma }}}}$ – матрица смежности отношения ${\text{Tr}}{{\rho }_{{{\Sigma }}}}$, T – транспонирование матрицы.

При реализации алгоритма для построения отношения $\rho $, не содержащего противоречивых контуров, можно выделить только дуги противоречивых контуров из $As{{\rho }_{\Sigma }}$. Матрица $As{{R}_{K}} = As{{R}_{\Sigma }}~\& ~Sym\left( {Tr{{R}_{\Sigma }}} \right)$. Заметим, что для произвольного отношения q с матрицей смежности Q матрицы смежности отношений $As~q$ и $Sym~q$ находятся соответственно следующим образом:

Таким образом, для построения агрегированного квазипорядка на множестве наилучших альтернатив необходимо:

1) разрушить противоречивые контуры уровня ${{P}_{0}}$;

2) построить агрегированный квазипорядок по формуле $\hat {R} = {\text{E}} \vee TrR$.

Отношение квазипорядка допускает наличие несравнимых альтернатив, что не позволит найти ранжирование всех альтернатив. При необходимости квазипорядок можно достроить до полного.

Отношение квазипорядка $q$ на $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$, при котором все элементы из $A$ сравнимы между собой, называется полным квазипорядком. По определению полный квазипорядок является нестрогим ранжированием элементов множества $A$.

Приведем определение и утверждения, которые необходимы для построения полного квазипорядка. Отношение квазипорядка q порождает разбиение множества $A$, на котором он задан, на классы эквивалентности.

Определение 2. Классом эквивалентности ${{[{{a}_{i}}]}_{q}}$, порожденным элементом ${{a}_{i}} \in ~A$ относительно квазипорядка q, называется подмножество $A$, состоящее из всех тех элементов ${{a}_{j}} \in A$, для которых одновременно выполняется $\langle {{a}_{i}},{{a}_{j}}\rangle \in q$ и $\langle {{a}_{j}},{{a}_{i}}\rangle \in q$.

Таким образом, классы эквивалентности отношения квазипорядка состоят из равноценных альтернатив. Следующее утверждение позволит легко найти классы эквивалентности произвольного квазипорядка q, заданного на множестве $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$. Рассмотрим симметричную часть квазипорядка $q:~{\text{\;}}(Sym~q = q \cap {{q}^{{ - 1}}})$ и матрицу смежности $Sym~Q = Q~\& ~{{Q}^{Т}}$ соответствующего этому отношению орграфа.

Утверждение 1. Для любого класса эквивалентности $C = \left\{ {{{a}_{{{{i}_{1}}}}},~ \ldots ,{{a}_{{{{i}_{k}}}}}} \right\}$, порожденного квазипорядком q на $A$, номера элементов этого класса полностью совпадают с единицами хотя бы одной из строк матрицы смежности $Sym~Q = {\text{||}}s{{q}_{{ji}}}{\text{||}}$, т.е. в $Sym~Q$ существует  j-я строка, такая, что $s{{q}_{{ji}}} = 1$ для всех $i = {{i}_{1}}, \ldots ,{{i}_{k}}$.

Для доказательства утверждения 1 нам потребуется лемма.

Лемма. Всякое отношение квазипорядка q на A порождает разбиение множества A = = $\{ {{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}\} $ на классы эквивалентности относительно этого отношения.

Доказательства утверждения 1 и леммы приведены в Приложении.

Алгоритм 4. Достроение квазипорядка до полного.

1. Находим классы эквивалентности в отношении квазипорядка (утверждение 1).

2. Упорядочиваем несравнимые классы эквивалентности произвольным образом. При этом достаточно сравнить любые два элемента из разных классов, а затем взять транзитивное замыкание полученного отношения.

При практической реализации алгоритма упорядочение классов эквивалентности осуществляется в диалоговом режиме с ЛПР. Непротиворечивость введенной ЛПР информации обеспечивается взятием транзитивного замыкания текущего отношения после каждого проведенного ЛПР сравнения альтернатив.

На последнем этапе ранжирования альтернатив уровня ${{P}_{0}}$ опять разбиваем построенный полный квазипорядок на уровни предпочтения. Получаем нестрогое ранжирование альтернатив. В случае необходимости ЛПР может попарно сравнить альтернативы и на других уровнях предпочтения орграфа агрегированного отношения, например для исключения из рассмотрения худших альтернатив.

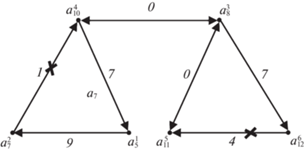
Пример 2. Нестрогое ранжирование моделей дронов. Построение полного квазипорядка для подмножества наилучших альтернатив. Найдем агрегированный квазипорядок $\tilde {\rho }$ на множестве наилучших альтернатив $\tilde {A} \subseteq A$ уровня P₀ из примера 1. Для удобства составления матриц добавим альтернативам верхний индекс – номер по порядку: ${{a}_{5}} \to a_{5}^{1},\,\,~{{a}_{7}} \to a_{7}^{2},~\,\,{{a}_{8}} \to a_{8}^{3}$, ${{a}_{{10}}} \to a_{{10}}^{4}$, ${{a}_{{11}}} \to a_{{11}}^{5},~\,\,{{a}_{{12}}} \to a_{{12}}^{6}.$ Подграф уровня P₀ изображен на рис. 2.

Легко видеть, что все дуги принадлежат противоречивым контурам. Разрушим эти контуры, удалив дуги наименьшего веса из $As{{\rho }_{\Sigma }}$. Очевидно, что придется удалить две дуги: весом 1 – $\langle a_{7}^{2},a_{{10}}^{4}\rangle $ и весом 4 – $\langle a_{{12}}^{6},a_{{11}}^{5}\rangle $ (на рис. 2 зачеркнуты крестиком). Матрица смежности полученного подграфа без противоречивых контуров имеет вид

Матрицу смежности агрегированного квазипорядка найдем по формуле $\hat {R} = {\text{E}} \vee TrR$. В данном примере матрица $TrR$ легко записывается по рис. 2. По определению транзитивного замыкания отношения, если существует путь из вершины ${{a}_{i}}$ в ${{a}_{j}}$, то элемент матрицs $TrR$ с индексами (ij) равен единице. Добавив единицы на диагонали, окончательно получим:

Вычислим матрицу $Sym\hat {R}$, по которой легко определим классы эквивалентности:

Найдем классы эквивалентности, используя утверждение 1. Каждая строка матрицы $Sym\hat {R}$ определяет класс эквивалентности: ${{C}_{1}} = \{ a_{5}^{1}\} ,{{C}_{2}} = \{ a_{7}^{2}\} ,{{C}_{3}} = \{ a_{8}^{3},~a_{{10}}^{4},~a_{{11}}^{5}\} $, ${{C}_{4}} = \{ a_{{12}}^{6}\} $. Упорядочим эти классы. Необходимо сравнить элементы $a_{5}^{1}$ и $a_{{12}}^{6}$, $a_{7}^{2}$ и $a_{{12}}^{6}$ из классов с несравнимыми элементами. Для пар альтернатив ЛПР задается вопрос, является ли одна из альтернатив предпочтительнее другой, или они равноценны (достаточно из каждого класса эквивалентности взять по одному любому элементу)? Введенная ЛПР информация не может быть противоречивой, так как на каждом шаге опроса берется транзитивное замыкание текущего отношения. Пусть в данном примере ЛПР ответило, что альтернатива $a_{{12}}^{6}$ менее предпочтительна, чем $a_{5}^{1}$. Так как $a_{5}^{1}$ менее предпочтительна, чем $a_{7}^{2}$, по транзитивности получим, что $a_{{12}}^{6}$ менее предпочтительна, чем $a_{7}^{2}$, и все классы, а значит, и все альтернативы сравнимы между собой. Матрица смежности полного квазипорядка имеет вид

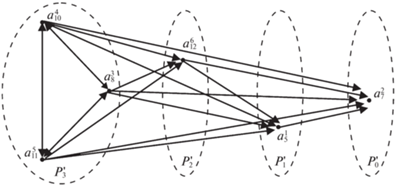
По упорядочению элементов из различных классов делаем вывод, что классы эквивалентности, начиная с наилучшего, упорядочены следующим образом: ${{C}_{2}} - {{C}_{1}} - {{C}_{4}} - {{C}_{3}}$. В общем случае порядок классов эквивалентности можно установить разбиением орграфа на уровни предпочтения, классы эквивалентности в отношении квазипорядка соответствуют компонентам сильной связанности. На рис. 3 изображен орграф полного квазипорядка с вершинами, расположенными по уровням предпочтения.

Полученное разбиение задает нестрогое ранжирование альтернатив (полный квазипорядок $\tilde {\rho }$) на множестве наилучших альтернатив $\tilde {A} \subseteq A$ уровня P₀:

Наилучшей является модель дрона ${{a}_{7}}$ ($a_{7}^{2}$).

3. Строгое ранжирование альтернатив с помощью Гамильтоновых путей максимальной длины в орграфе. Рассмотрим алгоритмы нахождения агрегированного строгого ранжирования альтернатив, соответствующего Гамильтонову пути в нагруженном мажоритарном графе. Напомним, что Гамильтоновым называется путь, проходящий через все вершины графа, причем ровно по одному разу. В качестве искомого ранжирования выбирают последовательность альтернатив, соответствующую Гамильтонову пути с заданными характеристиками: максимальная длина или наибольшая сила [4, 5]. Максимальная длина пути отождествляется с максимальным числом голосов экспертов, отданным за соответствующее вершинам пути ранжирование альтернатив, наибольшая сила – наибольшая по сравнению со всеми Гамильтоновыми путями в данном орграфе минимальная длина дуги пути.

Алгоритмы нахождения Гамильтоновых путей принадлежат классу сложности NP и обычно применяются только для графов с небольшим числом вершин. Уменьшим вычислительную сложность данной задачи, предварительно проведя декомпозицию мажоритарного графа на уровни предпочтения. В этом случае сложность алгоритма будет равна сложности выбранной процедуры поиска Гамильтоновых путей для компоненты сильной связанности с наибольшим числом вершин.

Как и в разд. 1, опишем алгоритм в общем случае для произвольного орграфа $G = \langle A,~\rho \rangle $, хотя для упорядочения альтернатив будем использовать мажоритарный граф ${{G}_{\Sigma }} = \langle A,~{{\rho }_{\Sigma }}\rangle $.

Пусть для орграфа $G = \langle A,~\rho \rangle $ с множеством вершин $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$ построен граф конденсации $\bar {G} = \langle \bar {A},~\bar {\rho }\rangle $. Используя алгоритм Демукрона, разобьем его на уровни ${{\bar {N}}_{0}},~{{\bar {N}}_{1}}, \ldots ,~{{\bar {N}}_{s}}$. Справедливо следующее утверждение.

Утверждение 2. Если в графе конденсации $\bar {G} = \langle \bar {A},~\bar {\rho }\rangle $ одному уровню принадлежат несколько вершин, то орграф $G = \langle A,~\rho \rangle $ не содержит Гамильтоновых путей.

Доказательство утверждения 2 приведено в Приложении.

Следствие 1. Если орграф содержит Гамильтонов путь, то все уровни разбиения его графа конденсации содержат ровно по одной вершине. (Соответственно каждый из уровней предпочтения орграфа ${{P}_{0}},~{{P}_{1}}, \ldots ,~{{P}_{s}}$ содержит вершины одной компоненты сильной связанности.)

Доказательство непосредственно следует из утверждения 2.

Будем считать, что компонента сильной связности с одной вершиной содержит Гамильтонов путь длиной 0. Для простоты описания алгоритма переобозначим номера компонент сильной связности: полагаем, что вершины компоненты S_i совпадают с вершинами уровня предпочтения P_i, $i = 0, \ldots ,~s$. Тогда справедливо утверждение.

Утверждение 3. В Гамильтоновом пути орграфа вершины любой компоненты сильной связности стоят последовательно. Другими словами, в Гамильтоновом пути орграфа не существует двух вершин из одной компоненты сильной связности, между которыми стоят вершины из других компонент сильной связности.

Следствие 2. Если хотя бы одна компонента сильной связности орграфа не содержит Гамильтоновых путей, то и сам орграф не содержит Гамильтоновых путей.

Доказательства утверждения 3 и следствия 2 приведены в приложении.

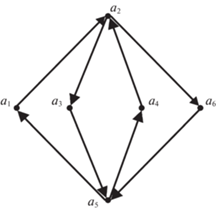
Следующий пример показывает, что в сильно связанном орграфе может не быть Гамильтоновых путей.

Пример 3. Сильно связный орграф, не содержащий Гамильтоновых путей. Легко убедиться, что орграф, изображенный на рис. 4, сильно связный и не содержит Гамильтоновых путей. В орграфе есть пути длиной 5, но они не являются Гамильтоновыми.

Пусть для орграфа $G = \langle A,~\rho \rangle $ построены уровни предпочтения ${{P}_{0}},~{{P}_{1}}, \ldots ,~{{P}_{s}}$, и пусть каждому уровню принадлежит ровно одна компонента сильной связности орграфа, причем компонента ${{S}_{i}}$ принадлежит уровню ${{P}_{i}},~i = 0, \ldots ,s$. Каждая компонента сильной связности ${{S}_{i}}$ содержит Гамильтоновы пути.

Алгоритм 5. Построение Гамильтоновых путей орграфа $G = \langle A,~\rho \rangle $ по Гамильтоновым путям компонент сильной связности ${{S}_{0}},~{{S}_{1}}, \ldots ,{{S}_{s}}$.

1. Разобьем орграф $G = \langle A,~\rho \rangle $ на уровни предпочтения ${{P}_{0}},~{{P}_{1}}, \ldots ,~{{P}_{s}}$. Если на каждом уровне все вершины принадлежат только одной компоненте сильной связности, переходим к п. 2, иначе в орграфе $G = \langle A,~\rho \rangle $ Гамильтоновых путей нет.

2. Для каждой компоненты сильной связности ${{S}_{i}},~i = 0, \ldots ,s,$ найдем Гамильтоновы пути. Если в какой-то компоненте Гамильтоновых путей нет, то и орграф $G = \langle A,~\rho \rangle $ Гамильтоновых путей не содержит. Иначе переходим к п. 3.

3. Последовательно соединяем Гамильтоновы пути уровней предпочтения ${{P}_{0}},~{{P}_{1}}, \ldots ,~{{P}_{s}}$. Из последней вершины Гамильтонова пути уровня ${{P}_{k}}$ должна исходить дуга и заходить в первую вершину Гамильтонова пути уровня ${{P}_{{k - 1}}}~$ для $k = s, \ldots ,1$. Перечислив все возможные варианты, получим Гамильтоновы пути мажоритарного графа.

Для нахождения Гамильтоновых путей в компонентах сильной связности модифицируем алгоритм для нахождения Гамильтоновых циклов [11] в неориентированном графе. Следующее утверждение необходимо для обоснования алгоритма поиска Гамильтоновых путей.

Рассмотрим орграф $G = \langle A,~\rho \rangle $ отношения q с множеством вершин $A = \left\{ {{{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}} \right\}$ и матрицей смежности Q.

Утверждение 4. Число путей длиной $k$ из вершины ${{a}_{i}}$ в ${{a}_{j}}$ орграфа $G = \langle A,~\rho \rangle $ с матрицей смежности $Q = \left| {\left| {{{q}_{{ij}}}} \right|} \right|$ определяет элемент $q_{{ij}}^{k}$ матрицы ${{Q}^{k}} = \left| {\left| {q_{{ij}}^{k}} \right|} \right|$.

В этом утверждении при возведении в степень используется обычная алгебраическая операция умножения матриц. Пусть Q – матрица смежности орграфа $G = \langle A,~\rho \rangle $.

Алгоритм 6. Нахождение Гамильтоновых путей по матрице смежности $Q$ орграфа $G = \langle A,~\rho \rangle $.

0. Обозначим последовательно вершины ${{a}_{1}},~{{a}_{2}}, \ldots ,{{a}_{n}}$ графа буквами $a,~b,~c, \ldots $ (чтобы не возникали дополнительные трудности с индексами).

Выпишем вспомогательную матрицу $H$ следующим образом: на место единиц в матрице смежности Q напишем буквы, обозначающие вершины, причем в первом столбце – $a$, во втором – $b$ и т. д.

1. Положим ${{Q}_{1}} = Q.$

2. Вычислим $Q_{2}^{'} = H{{Q}_{1}}$ и ${{Q}_{2}} = F(Q_{2}^{'})$. В матрицах $Q_{i}^{'}$ указаны промежуточные вершины путей длины $i = 2,..,n - 1$. Первая вершина добавляется в начало пути в соответствии со строкой матрицы, а последняя – в соответствии со столбцом; $F(Q_{i}^{'})$ – преобразование обнуления элементов матрицы $Q_{i}^{'}$, если они соответствуют путям с повторяющимися вершинами, в частности, контурам. Поскольку все диагональные элементы соответствуют контурам, можно ставить нули еще в матрицах $Q_{i}^{'}$.

3. Вычислим $Q_{3}^{'} = H{{Q}_{2}}$, где ${{Q}_{3}} = F(Q_{3}^{'})$.

……………………………..

(n – 1), $Q_{{n - 1}}^{'} = H{{Q}_{{n - 2}}}$, где ${{Q}_{{n - 1}}} = F(Q_{{n - 1}}^{'})$.

Если элементы матриц состоят из нескольких слагаемых, следовательно, существует несколько путей.

Обоснование алгоритма 6 приведено в Приложении.

Пример 4. Нахождение Гамильтоновых путей орграфа по Гамильтоновым путям компонент сильной связности. Найдем Гамильтоновы пути максимальной длины в мажоритарном графе из примера 1 как на множестве наилучших альтернатив $\tilde {A} \subseteq A$ уровня ${{P}_{0}}$, так и на множестве всех вершин A орграфа. Гамильтонов путь максимальной длины уровня ${{P}_{0}}$ будет определять строгое ранжирование $\tilde {\rho }$ на множестве наилучших альтернатив $\tilde {A} \subseteq A$.

Орграф уже разбит на уровни предпочтения ${{P}_{0}},~{{P}_{1}},{{P}_{2}}$, каждый из которых сдержит вершины одной компоненты сильной связанности: ${{P}_{0}} \to {{S}_{0}},~{{P}_{1}} \to {{S}_{1}},{{P}_{2}} \to {{S}_{2}}$ (рис. 1). Гамильтоновы пути в компонентах сильной связности ${{S}_{1}}$ и ${{S}_{2}}$ легко найти из рис. 1. Компонента ${{S}_{1}}$ содержит два Гамильтоновых пути: ${{a}_{3}},~{{a}_{9}}~и~{{a}_{9}},~{{a}_{3}}$, компонента ${{S}_{2}}$ – четыре Гамильтоновых пути: ${{a}_{1}},~{{a}_{6}},{{a}_{2}},{{a}_{4}};~\,\,{{a}_{2}},{{a}_{4}},{{a}_{1}},{{a}_{6}};\,\,~{{a}_{4}},{{a}_{1}},{{a}_{6}},{{a}_{2}};~{\text{\;}}{{a}_{6}},{{a}_{2}},{{a}_{4}},{{a}_{1}}.$

Найдем Гамильтоновы пути в компоненте сильной связанности ${{S}_{0}}$, используя алгоритм 5. Будем придерживаться обозначений этого алгоритма. Выпишем матрицу смежности $Q$ орграфа компоненты ${{S}_{0}}$ (рис. 1 и 2). Чтобы не мешали индексы, вершины переобозначим следующим образом: ${{a}_{5}} \to a,{{a}_{7}} \to b,{{a}_{8}} \to c$, ${{a}_{{10}}} \to d,{{a}_{{11}}} \to e,{{a}_{{12}}} \to f$:

0. Согласно алгоритму, выпишем вспомогательную матрицу H, соответствующую матрице смежности с обозначением вершин буквами:

1. Положим ${{Q}_{1}} = Q = \left( {\begin{array}{*{20}{c}} 0&1&0&0&0&0 \\ 0&0&0&1&0&0 \\ 0&0&0&1&1&1 \\ 1&0&1&0&0&0 \\ 0&0&1&0&0&0 \\ 0&0&0&0&1&0 \end{array}} \right).$

2. Вычислим $Q_{2}^{'}$ и ${{Q}_{2}}$:

Обнулим контуры длиной 2 на диагонали.

Обнулим контуры длиной 3 на диагонали (можно было сразу поставить нули) и пути с повторяющимися вершинами:

Обнулим пути с повторяющимися вершинами:

Обнулим пути с повторяющимися вершинами:

Подграф уровня ${{P}_{0}}$ содержит два Гамильтоновых пути: $a,b,d,c,f,e$ и $f,e,c,d,a,b$. В обозначениях мажоритарного графа ${{a}_{5}},~{{a}_{7}},{{a}_{{10}}},{{a}_{8}},~{{a}_{{12}}},{{a}_{{11}}}$ и ${{a}_{{12}}},~{{a}_{{11}}},{{a}_{8}},{{a}_{{10}}},~{{a}_{5}},{{a}_{7}}$.

Найдем Гамильтоновы пути в мажоритарном графе (рис. 1), соединив пути трех уровней предпочтения. Согласно алгоритму 4, из последней вершины Гамильтонова пути уровня ${{P}_{2}}$ должна исходить дуга и заходить в первую вершину Гамильтонова пути уровня ${{P}_{1}}$, а из последней вершины Гамильтонова пути уровня ${{P}_{1}}$ должна исходить дуга и заходить в первую вершину Гамильтонова пути уровня ${{P}_{0}}$. Получим Гамильтоновы пути мажоритарного графа: ${{a}_{1}},~{{a}_{6}},{{a}_{2}},{{a}_{4}},~{{a}_{3}},~{{a}_{9}},~{{a}_{{12}}},~~{{a}_{{11}}},~{{a}_{8}},{{a}_{{10}}},~{{a}_{5}},{{a}_{7}}$ и ${{a}_{2}},{{a}_{4}},{{a}_{1}},{{a}_{6}},{{a}_{9}},~{{a}_{3}},{{a}_{5}},~{{a}_{7}},{{a}_{{10}}},{{a}_{8}},~{{a}_{{12}}},{{a}_{{11}}}$ и ${{a}_{4}},{{a}_{1}},{{a}_{6}},{{a}_{2}},{{a}_{9}},~{{a}_{3}},~{{a}_{5}},~~{{a}_{7}},~{{a}_{{10}}},{{a}_{8}},~{{a}_{{12}}},{{a}_{{11}}}$.

Используя веса на дугах мажоритарного графа (рис. 1), выберем путь максимальной длины. Этому пути будет соответствовать искомое упорядочение альтернатив по предпочтению:

путь ${{a}_{1}},~{{a}_{6}},{{a}_{2}},{{a}_{4}},~{{a}_{3}},~{{a}_{9}},{{a}_{{12}}},~{{a}_{{11}}},{{a}_{8}},{{a}_{{10}}},~{{a}_{5}},{{a}_{7}}$ – длина 42,

путь ${{a}_{2}},{{a}_{4}},{{a}_{1}},{{a}_{6}},{{a}_{9}},~{{a}_{3}},{{a}_{5}},~{{a}_{7}},{{a}_{{10}}},{{a}_{8}},~{{a}_{{12}}},{{a}_{{11}}}$ – длина 45,

путь ${{a}_{4}},{{a}_{1}},{{a}_{6}},{{a}_{2}},{{a}_{9}},~{{a}_{3}},{{a}_{5}},~{{a}_{7}},{{a}_{{10}}},{{a}_{8}},~{{a}_{{12}}},{{a}_{{11}}}$ – длина 48.

Искомое упорядочение альтернатив соответствует третьему пути длиной 48:

Наиболее предпочтительная альтернатива – a₁₁.

В этом примере ту же наилучшую альтернативу дадут и Гамильтоновы пути уровня ${{P}_{0}}{\text{:}}$ путь ${{a}_{{12}}},~{{a}_{{11}}},{{a}_{8}},{{a}_{{10}}},~{{a}_{5}},{{a}_{7}}$ имеет длину 20; а путь ${{a}_{5}},~{{a}_{7}},{{a}_{{10}}},{{a}_{8}},~{{a}_{{12}}},{{a}_{{11}}}$ большей длины – 21. Ему соответствует строгое ранжирование $\tilde {\rho }$ наилучших альтернатив $\tilde {A} \subseteq A$: ${{a}_{{11}}} - {{a}_{{12}}} - {{a}_{8}} - {{a}_{{10}}} - {{a}_{7}} - {{a}_{5}}$.

Итак, существенно сократив перебор при поиске Гамильтоновых путей, удалось уменьшить сложность алгоритма: вместо поиска путей в мажоритарном графе с 12 вершинами требуется найти пути максимально с 6 вершинами в компоненте сильной связанности ${{S}_{0}}$.

Заключение. В задачах принятия решений при получении агрегированного отношения с большим числом альтернатив целесообразно предварительно провести декомпозицию на уровни предпочтения орграфа. Это поможет значительно уменьшить вычислительную сложность алгоритма и при необходимости для ранжирования альтернатив использовать даже переборные («медленные») процедуры принятия решений. По желанию ЛПР можно упорядочить альтернативы на всех уровнях предпочтения мажоритарного графа. Предложены два метода ранжирования альтернатив: построение полного квазипорядка и нахождение Гамильтоновых путей максимальной длины.