Известия РАН. Теория и системы управления, 2023, № 4, стр. 153-167
СТАБИЛИЗАЦИЯ ПРОГРАММНЫХ ДВИЖЕНИЙ МЕХАНИЧЕСКИХ СИСТЕМ С УЧЕТОМ ОГРАНИЧЕНИЙ
А. Е. Голубев *
* E-mail: v-algolu@hotmail.com
Поступила в редакцию 14.03.2023
После доработки 29.03.2023
Принята к публикации 03.04.2023
- EDN: OCLSAO
- DOI: 10.31857/S0002338823040054
Аннотация
Рассматривается задача стабилизации программных траекторий механических систем с учетом ограничений на значения обобщенных координат, скоростей и ускорений. Управление строится при помощи метода бэкстеппинга в сочетании с использованием логарифмических барьерных функций Ляпунова. Полученные в работе стабилизирующие обратные связи в отличие от аналогичных известных результатов не приводят к неограниченному росту значений переменных управления при приближении переменных состояния системы к граничным значениям. В качестве примера рассмотрена задача построения и стабилизации траектории пространственного движения подводного аппарата.
Введение. Разработка методов решения задач построения и стабилизации траекторий движения динамических систем с учетом различных ограничений является одной из популярных и важных тем исследований последних десятилетий. Актуальность исследований обусловлена требованиями безопасности к переходным процессам при управлении техническими системами, подразумевающими, что при отслеживании программной траектории движения обьекта управления переменные состояния системы должны находиться в рамках допустимых значений. Отметим также, что в последнее время все большую популярность среди исследователей приобретают задачи группового управления (см., например, [1]), в процессе решения которых от отдельных объектов управления в группе требуется нахождение в отдельной области пространства, непересекающейся с зонами движения других обьектов [2].
Конструктивные аналитические методы синтеза нелинейных законов управления на основе использования нелинейных моделей движения обьектов управления были предложены и активно исследовались на рубеже 1990-х и 2000-х годов. Наиболее популярными подходами к синтезу нелинейных обратных связей являются метод обратных задач динамики [3], в общем случае базирующийся на применении дифференциально-геометрического аппарата [4, 5], а также метод бэкстеппинга [6] и методы, использующие свойства пассивности механических систем [7].
Результаты, связанные с возможностью учета различного рода ограничений при синтезе нелинейных законов управления с помощью указанных методов, появились позднее [8, 9]. Наиболее эффективным с точки зрения возможностей учета ограничений на состояние системы является метод бэкстеппинга [6]. В сочетании с использованием барьерных функций [10] метод бэкстеппинга позволяет строить стабилизирующие обратные связи, гарантирующие выполнение ограничений на состояние системы [8, 9, 11–16]. Отметим, что предлагаемые в большинстве работ обратные связи, полученные на основе применения барьерных функций Ляпунова в методе бэкстеппинга, приводят к значениям управляющих переменных, неограниченно возрастающих при приближении переменных состояния к граничным значениям [8, 9, 11, 12]. Однако неограниченный рост значений переменных управления будет нежелательным, так как может приводить к насыщению управляющих воздействий и излишнему расходу ресурса управления. Одним из способов решения указанной проблемы является, например, расширение динамики системы за счет использования производных управляющих переменных, предложенное в [14].
В работе решается задача синтеза обратных связей по состоянию, стабилизирующих программные траектории движения механических систем, которые описываются уравнениями Эйлера–Лагранжа, с учетом ограничений на абсолютные величины обобщенных координат, скоростей и ускорений. Управление строится на основе метода бэкстеппинга с помощью логарифмических барьерных функций Ляпунова. Полученные в работе стабилизирующие обратные связи в отличие от аналогичных известных результатов не приводят к неограниченному росту значений переменных управления при приближении переменных состояния к граничным значениям. В качестве примера рассмотрена задача построения и стабилизации траектории пространственного движения подводного аппарата.
1. Постановка задачи. Рассматривается задача стабилизации программных движений динамических систем, имеющих структуру уравнений Эйлера–Лагранжа и записанных следующим образом:
(1.1)
$M\left( q \right)\ddot {q} + C\left( {q,\dot {q}} \right)\dot {q} + D\dot {q} + G\left( q \right) = \tau .$Здесь $q = {{\left( {{{q}_{1}}, \ldots ,{{q}_{m}}} \right)}^{{\text{T}}}} \in {{\mathbb{R}}^{m}}$ – вектор обобщенных координат; $\tau = {{\left( {{{\tau }_{1}}, \ldots ,{{\tau }_{m}}} \right)}^{{\text{T}}}} \in {{\mathbb{R}}^{m}}$ – вектор управляющих сил и моментов; M(q) – матрица кинетической энергии, $M(q) = {{M}^{{\text{T}}}}(q) > 0$ при всех $q \in {{\mathbb{R}}^{m}}$; $C\left( {q,\dot {q}} \right)\dot {q}$ – центробежные и кориолисовы силы; $D\dot {q}$ – демпфирование; G(q) = ${{\left[ {\partial {{\Pi }}(q){\text{/}}\partial q} \right]}^{{\text{T}}}}$, где Π(q) – потенциальная энергия системы.
Будем полагать, что для системы (1.1), например с использованием результатов работы [17], построено программное движение $q = P\left( t \right)$, $\tau = {{\tau }_{P}}\left( t \right)$, $t \in \left[ {0,T} \right]$, удовлетворяющее фиксированным начальным и конечным условиям на переменные состояния q, $\dot {q}$ системы:
(1.2)
$q\left( 0 \right) = {{q}_{0}},\quad \dot {q}\left( 0 \right) = {{\dot {q}}_{0}},\quad q\left( T \right) = {{q}_{*}},\quad \dot {q}\left( T \right) = {{\dot {q}}_{*}},$(1.3)
$\left| {{{q}_{i}}\left( t \right)} \right| \leqslant {{B}_{i}},\quad {\text{|}}{{\dot {q}}_{i}}\left( t \right)\left| { \leqslant {{N}_{i}},\quad } \right|{{\ddot {q}}_{i}}\left( t \right){\text{|}} \leqslant {{Q}_{i}}\quad {\text{при}}\;{\text{всех}}\quad t \in \left[ {0,T} \right],$Обозначим i-ю компоненту вектор-функции P(t) через pi(t) и определим соответствующие ошибки отслеживания ${{\xi }_{{1i}}} = {{q}_{i}} - {{p}_{i}}\left( t \right)$, $i \in \overline {1,m} $, программной траектории $q = P\left( t \right)$. Отметим, что при стабилизации программной траектории $q = P\left( t \right)$, $t \in \left[ {0,T} \right]$, можно при необходимости рассмотреть значения pi(t) при $t \geqslant T$, доопределив соответствующие функции, например, значениями ${{p}_{i}}\left( t \right) = {{p}_{i}}\left( T \right)$ при $t \geqslant T$. Далее, без ограничения общности будем полагать, что функции pi(t) определены при всех $t \geqslant 0$, а также являются дважды непрерывно дифференцируемыми.
Задача. Требуется выбрать компоненты вектора управляющих воздействий $\tau $ в системе (1.1) в виде обратных связей по состоянию системы таким образом, чтобы при всех $i \in \overline {1,m} $ для произвольных значений ${{\xi }_{{1i}}}\left( 0 \right)$ и ${{\dot {\xi }}_{{1i}}}\left( 0 \right)$ было гарантировано выполнение условий $\left| {{{\xi }_{{1i}}}\left( t \right)} \right| \to 0$ при $t \to + \infty $ с учетом ограничений:
(1.4)
$\left| {{{\xi }_{{1i}}}\left( t \right)} \right| \leqslant {{\varepsilon }_{{1i}}},\quad \left| {{{{\dot {\xi }}}_{{1i}}}\left( t \right)} \right| \leqslant {{\varepsilon }_{{2i}}},\quad \left| {{{{\ddot {\xi }}}_{{1i}}}\left( t \right)} \right| \leqslant {{\varepsilon }_{{3i}}},\quad t \geqslant 0.$Здесь ${{\varepsilon }_{{1i}}}$, ${{\varepsilon }_{{2i}}}$ и ${{\varepsilon }_{{3i}}}$ – некоторые заданные положительные константы, удовлетворяющие соответственно условиям ${{\varepsilon }_{{1i}}} \geqslant \left| {{{\xi }_{{1i}}}\left( 0 \right)} \right|$, ${{\varepsilon }_{{2i}}} \geqslant \left| {{{{\dot {\xi }}}_{{1i}}}\left( 0 \right)} \right|$ и ${{\varepsilon }_{{3i}}} \geqslant \left| {{{{\ddot {\xi }}}_{{1i}}}\left( 0 \right)} \right|$.
2. Стабилизация программных траекторий с учетом ограничений. Заметим, что одним из хорошо известных и широко используемых методов синтеза нелинейных стабилирующих законов управления является метод линеаризации обратной связью (см., например, [5]). В результате применения метода линеаризации обратной связью для решения задачи стабилизации программной траектории $q = P\left( t \right)$ системы (1.1) получим следующее управление:
(2.1)
$\tau = C\left( {q,\dot {q}} \right)\dot {q} + D\dot {q} + G\left( q \right) + M\left( q \right)\left( {\ddot {P}\left( t \right) - {{{\tilde {K}}}_{1}}{{\xi }_{1}} - {{{\tilde {K}}}_{2}}{{{\dot {\xi }}}_{1}}} \right),$Замкнутую обратной связью (2.1) систему (1.1) можно записать в виде
(2.2)
${{\ddot {\xi }}_{1}} = - {{\tilde {K}}_{1}}{{\xi }_{1}} - {{\tilde {K}}_{2}}{{\dot {\xi }}_{1}}.$Положение равновесия ${{\xi }_{1}} = 0$, ${{\dot {\xi }}_{1}} = 0$ линейной системы (2.2) асимптотически устойчиво в целом. Однако известно [18], что за счет выбора элементов матриц ${{\tilde {K}}_{1}}$ и ${{\tilde {K}}_{2}}$ явным образом обеспечить выполнение для решений системы (2.2) ограничений (1.4) затруднительно. Поэтому закон управления (2.1) далее в работе будет модифицирован.
Для синтеза управления, стабилизирующего программную траекторию $q = P\left( t \right)$ системы (1.1) с учетом ограничений (1.4), воспользуемся идеями метода бэкстеппинга [6] в сочетании с логарифмическими барьерными функциями Ляпунова [8].
При построении управления рассмотрим сначала функцию
Для удобства используем переменные ${{\xi }_{{2i}}} = {{\dot {q}}_{i}} - {{\alpha }_{{1i}}}\left( {{{\xi }_{1}}} \right)$, где ${{\alpha }_{{1i}}}\left( \cdot \right)$ – непрерывно дифференцируемые функции, определяемые далее. Тогда выражение для ${{\dot {V}}_{1}}\left( {{{\xi }_{1}}} \right)$ можно представить следующим образом:
Выбрав ${{\alpha }_{{1i}}}\left( {{{\xi }_{1}}} \right) = - {{\kappa }_{{1i}}}{{\xi }_{{1i}}} + {{\dot {p}}_{i}}\left( t \right)$, где ${{\kappa }_{{1i}}} > 0$ – положительные коэффициенты усиления, получим
В качестве функции Ляпунова замкнутой управлением системы используем функцию
Производная по времени функции ${{V}_{2}}\left( {{{\xi }_{1}},{{\xi }_{2}}} \right)$ в силу системы (1.1) запишется следующим образом:
Для удобства дальнейших рассуждений представим последнее слагаемое в выражении для ${{\dot {V}}_{2}}\left( {{{\xi }_{1}},{{\xi }_{2}}} \right)$ в виде скалярного произведения векторов:
Далее, принимая во внимание соотношение (1.1), имеем
(2.3)
$\begin{gathered} {{{\dot {V}}}_{2}}\left( {{{\xi }_{1}},{{\xi }_{2}}} \right) = - \mathop \sum \limits_{i = 1}^m \frac{{{{k}_{{1i}}}{{\kappa }_{{1i}}}\xi _{{1i}}^{2}}}{{\varepsilon _{{1i}}^{2} - \xi _{{1i}}^{2}}} + \mathop \sum \limits_{i = 1}^m \frac{{{{k}_{{1i}}}{{\xi }_{{1i}}}{{\xi }_{{2i}}}}}{{\varepsilon _{{1i}}^{2} - \xi _{{1i}}^{2}}} + \\ \, + a\left( {{{M}^{{ - 1}}}\left( q \right)\left( { - C\left( {q,\dot {q}} \right)\dot {q} - D\dot {q} - G\left( q \right) + \tau } \right) - \ddot {P}\left( t \right) + {{K}_{1}}{{{\dot {\xi }}}_{1}}} \right). \\ \end{gathered} $Стабилизирующее программную траекторию q = P(t) системы (1.1) управление выберем следующим образом:
(2.4)
$\tau = C\left( {q,\dot {q}} \right)\dot {q} + D\dot {q} + G\left( q \right) + M\left( q \right)\left( {\ddot {P}\left( t \right) - {{K}_{1}}{{{\dot {\xi }}}_{1}} - {{K}_{2}}{{\xi }_{2}} - b} \right),$Подставив управление (2.4) в выражение (2.3), получим
В результате выделения полных квадратов по соответствующим переменным справедлива следующая оценка:
Таким образом, производная по времени функции ${{V}_{2}}\left( {{{\xi }_{1}},{{\xi }_{2}}} \right)$ в силу системы (1.1) с управлением (2.4) отрицательно определена в области
Заметим, что для любых положительных коэффициентов усиления ${{\kappa }_{{1i}}}$, ${{\kappa }_{{2i}}}$ в управлении (2.4) за счет выбора положительных постоянных ${{k}_{{1i}}}$, ${{k}_{{2i}}}$ в функции Ляпунова ${{V}_{2}}\left( {{{\xi }_{1}},{{\xi }_{2}}} \right)$ значения величин $\sqrt {\varepsilon _{{1i}}^{2} - {{k}_{{1i}}}{\text{/}}\left( {2{{k}_{{2i}}}{{\kappa }_{{1i}}}} \right)} $ можно сделать сколь угодно близкими к соответствующим значениям констант ${{\varepsilon }_{{1i}}}$.
Система (1.1), замкнутая управлением (2.4), с учетом соотношения ${{\xi }_{2}} = {{\dot {\xi }}_{1}} + {{K}_{1}}{{\xi }_{1}}$ может быть представлена в виде
(2.5)
${{\ddot {\xi }}_{1}} = - {{K}_{2}}{{K}_{1}}{{\xi }_{1}} - \left( {{{K}_{1}} + {{K}_{2}}} \right){{\dot {\xi }}_{1}} - b.$Тогда в силу справедливости при всех $t \geqslant 0$ неравенств
(2.6)
$\{ {{(\xi _{1}^{{\text{T}}},\dot {\xi }_{1}^{{\text{T}}})}^{{\text{T}}}} \in {{\mathbb{R}}^{{2m}}}:\,\left| {{{\xi }_{{1i}}}} \right| < {{\varepsilon }_{{1i}}},\,\,{\text{|}}{{\dot {\xi }}_{{1i}}}{\text{|}} < {{\varepsilon }_{{2i}}},\,\,i \in \overline {1,m} \} ,$Далее, в силу равенства $q = {{\xi }_{1}} + P\left( t \right)$ для компонент qi(t) любого решения q = q(t) систе-мы (1.1), замкнутой управлением (2.4), с начальной точкой в множестве (2.6) при всех $t \geqslant 0$ и $i \in \overline {1,m} $ верны следующие оценки:
Дополнительно, с учетом уравнения (2.5) для любого $t \geqslant 0$ и $i \in \overline {1,m} $ имеют место неравенства
Здесь постоянные Bi, Ni и Qi взяты из ограничений (1.3), выполняющихся для программной траектории q = P(t).
Заметим, что правые части систем (2.2) и (2.5) при соотношениях коэффициентов усиления ${{\tilde {\kappa }}_{{1i}}} = {{\kappa }_{{1i}}}{{\kappa }_{{2i}}}$ и ${{\tilde {\kappa }}_{{2i}}} = {{\kappa }_{{1i}}} + {{\kappa }_{{2i}}}$ различаются за счет присутствия в правой части системы (2.5) слагаемого b, i-я компонента bi которого в переменных ${{\xi }_{{1i}}}$, ${{\dot {\xi }}_{{1i}}}$ имеет вид
(2.7)
$ = ({{\dot {\xi }}_{{1i}}} + {{\kappa }_{{1i}}}{{\xi }_{{1i}}})({{({{\varepsilon }_{{2i}}} - {{\kappa }_{{1i}}}{{\varepsilon }_{{1i}}})}^{2}} - {{({{\dot {\xi }}_{{1i}}} + {{\kappa }_{{1i}}}{{\xi }_{{1i}}})}^{2}}).$Таким образом, наличие дополнительного слагаемого b в обратной связи (2.4) по сравнению с законом управления (2.1), найденным при помощи метода линеаризации обратной связью, обеспечивает выполнение ограничений (1.4). Отметим, что при стремлении $\left| {{{\xi }_{{1i}}}} \right| \to {{\varepsilon }_{{1i}}} - 0$ и/или $\left| {{{{\dot {\xi }}}_{{1i}}}} \right| \to {{\varepsilon }_{{2i}}} - 0$ для любого i соответствующая функция (2.7) не является неограниченно возрастающей и имеет конечный предел. В этом свойстве дополнительной стабилизирующей компоненты b в обратной связи (2.4) заключается существенное отличие предлагаемого в работе способа применения метода бэкстеппинга от других работ, например [9, 11, 12]. Полученные в [9, 11, 12] обратные связи на основе метода бэкстеппинга приводят к значениям управляющих переменных, неограниченно возрастающих при приближении переменных состояния к граничным значениям.
Так, по аналогии с результатами работ [9, 12] можно предложить следующую стабилизирующую обратную связь:
(2.8)
$\tau = C\left( {q,\dot {q}} \right)\dot {q} + D\dot {q} + G\left( q \right) + M\left( q \right)\left( {\ddot {P}\left( t \right) - {{K}_{1}}{{{\dot {\xi }}}_{1}} - {{K}_{2}}{{\xi }_{2}} - \bar {b}} \right),$Производная по времени функции ${{V}_{2}}\left( {{{\xi }_{1}},{{\xi }_{2}}} \right)$ в силу системы (1.1) c управлением (2.8) примет вид
Однако, несмотря на то, что управление (2.8) также будет решением задачи cтабилизации программной траектории q = P(t) системы (1.1) с учетом ограничений (1.4), при стремлении $\left| {{{\xi }_{{1i}}}} \right| \to {{\varepsilon }_{{1i}}} - 0$ для любого i соответствующая i-я компонента вектор-функции $\bar {b}$ может неограниченно возрастать. Следовательно, полученная в настоящей работе стабилизирующая обратная связь (2.4) предпочтительнее управления (2.8).
3. Решение задачи управления пространственным движением подводного аппарата. Для описания движения аппарата используются две системы координат: инерциальная земная система координат $Oxyz$ и неинерциальная система координат ${{O}_{b}}{{x}_{b}}{{y}_{b}}{{z}_{b}}$, жестко связанная с корпусом подводного аппарата. Начало ${{O}_{b}}$ неинерциальной системы координат обычно выбирается совпадающим с центром тяжести или центром плавучести корпуса аппарата, а направления осей ${{O}_{b}}{{x}_{b}}$, ${{O}_{b}}{{y}_{b}}$ и ${{O}_{b}}{{z}_{b}}$ фиксируются вдоль главных осей инерции корпуса. Продольная ось ${{O}_{b}}{{x}_{b}}$ направлена вдоль корпуса от хвостовой части к передней, поперечная ось ${{O}_{b}}{{y}_{b}}$ выбирается ортогонально правому борту корпуса аппарата в горизонтальной плоскости, а нормальная ось ${{O}_{b}}{{z}_{b}}$ ориентирована сверху вниз [20].
Поступательное движение аппарата описывается координатами ${{\eta }_{1}} = {{\left( {x,y,z} \right)}^{{\text{T}}}}$ точки Ob в инерциальной системе координат $Oxyz$ и координатами ${{\nu }_{1}} = {{\left( {u,{v},w} \right)}^{{\text{T}}}}$ вектора скорости точки Ob в неинерциальной системе координат ${{O}_{b}}{{x}_{b}}{{y}_{b}}{{z}_{b}}$. Вращательное движение корпуса аппарата задается при помощи угловых координат ${{\eta }_{2}} = {{\left( {\varphi ,\theta ,\psi } \right)}^{{\text{T}}}}$ поворота неинерциальной системы координат ${{O}_{b}}{{x}_{b}}{{y}_{b}}{{z}_{b}}$ относительно инерциальной системы координат $Oxyz$, где $\varphi $ – угол крена, $\theta $ – угол тангажа, $\psi $ – угол рысканья, а также вектора ${{\nu }_{2}} = {{\left( {p,q,r} \right)}^{{\text{T}}}}$ угловых скоростей вращения корпуса аппарата относительно соответствующих осей ${{O}_{b}}{{x}_{b}}$, ${{O}_{b}}{{y}_{b}}$ и ${{O}_{b}}{{z}_{b}}$ неинерциальной системы координат ${{O}_{b}}{{x}_{b}}{{y}_{b}}{{z}_{b}}$ [20].
Координаты вектора скорости точки Ob в инерциальной и неинерциальной системах координат, согласно монографии [20], связаны соответственно соотношениями
(3.1)
${{\dot {\eta }}_{1}} = {{J}_{1}}\left( {{{\eta }_{2}}} \right){{\nu }_{1}},\quad {{\nu }_{1}} = J_{1}^{{ - 1}}\left( {{{\eta }_{2}}} \right){{\dot {\eta }}_{1}},$Далее, угловые скорости вращения корпуса аппарата вокруг осей неинерциальной системы координат ${{O}_{b}}{{x}_{b}}{{y}_{b}}{{z}_{b}}$ пересчитываются в производные по времени угловых координат ${{\eta }_{2}}$ следующим образом [20]:
гдеВ итоге, кинематика движения подводного аппарата может быть записана в виде
где $\eta = {{(\eta _{1}^{{\text{T}}},\eta _{2}^{{\text{T}}})}^{{\text{T}}}}$, $\nu = {{(\nu _{1}^{{\text{T}}},\nu _{2}^{{\text{T}}})}^{{\text{T}}}}$,Здесь ${{O}_{{3 \times 3}}}$ – нулевая матрица размера 3 × 3.
Динамические уравнения поступательного и вращательного движения корпуса подводного аппарата в векторных обозначениях представлены ниже [20]:
где ${{\tau }_{{RB}}} = {{\left( {{{F}_{{{{x}_{b}}}}},{{F}_{{{{y}_{b}}}}},{{F}_{{{{z}_{b}}}}},{{\tau }_{{{{x}_{b}}}}},{{\tau }_{{{{y}_{b}}}}},{{\tau }_{{{{z}_{b}}}}}} \right)}^{{\text{T}}}}$,Здесь ${{M}_{{RB}}}$ – матрица инерции твердого тела, ${{C}_{{RB}}}\left( \nu \right)$ – матрица кориолисовых и центростремительных сил, m – масса аппарата, ${{r}_{G}} = {{\left( {{{x}_{G}},{{y}_{G}},{{z}_{G}}} \right)}^{{\text{T}}}}$ – координаты центра масс корпуса аппарата в подвижной системе координат ${{O}_{b}}{{x}_{b}}{{y}_{b}}{{z}_{b}}$; ${{I}_{x}}$, ${{I}_{y}}$, ${{I}_{z}}$ – моменты инерции корпуса относительно осей ${{O}_{b}}{{x}_{b}}$, ${{O}_{b}}{{y}_{b}}$ и ${{O}_{b}}{{z}_{b}}$ соответственно; ${{I}_{{xy}}}$, ${{I}_{{xz}}}$, ${{I}_{{yz}}}$ – центробежные моменты инерции; ${{F}_{{{{x}_{b}}}}}$, ${{F}_{{{{y}_{b}}}}}$, ${{F}_{{{{z}_{b}}}}}$ – проекции равнодействующей всех приложенных к корпусу аппарата сил на оси ${{O}_{b}}{{x}_{b}}$, ${{O}_{b}}{{y}_{b}}$ и ${{O}_{b}}{{z}_{b}}$; ${{\tau }_{{{{x}_{b}}}}}$, ${{\tau }_{{{{y}_{b}}}}}$, ${{\tau }_{{{{z}_{b}}}}}$ – суммарные моменты сил, действующих на корпус, вокруг осей ${{O}_{b}}{{x}_{b}}$, ${{O}_{b}}{{y}_{b}}$ и ${{O}_{b}}{{z}_{b}}$. В частности, если оси ${{O}_{b}}{{x}_{b}}$, ${{O}_{b}}{{y}_{b}}$ и ${{O}_{b}}{{z}_{b}}$ направлены вдоль главных осей инерции корпуса аппарата, то имеют место равенства ${{I}_{{xy}}} = {{I}_{{xz}}} = {{I}_{{yz}}} = 0$.
Внешние силы и моменты, действующие на корпус подводного аппарата, характеризуются компонентами вектора τRB в правой части динамической системы (3.3), который имеет следующую структуру:
где τH включает влияние присоединенной массы воды, гидродинамического демпфирования, гравитации и выталкивающей силы; τ представляет собой силы и моменты, создаваемые управляющими органами аппарата.Компонета τH в соотношении (3.4), согласно [20], имеет вид
(3.5)
${{\tau }_{H}} = - {{M}_{A}}\dot {\nu } - {{C}_{A}}\left( \nu \right)\nu - D\left( \nu \right)\nu - g\left( \eta \right),$Матрица CA(ν) гидродинамических кориолисовых и центростремительных сил является кососимметрической при всех $\nu \in {{\mathbb{R}}^{6}}$, матрица D(ν) гидродинамического демпфирования – положительно определенной при всех $\nu \in {{\mathbb{R}}^{6}}$, слагаемое g(η) характеризует действие силы тяжести и выталкивающей силы на корпус аппарата и определяется далее. Элементы матрицы MA добавочной инерции представляют собой коэффициенты линеаризации соответствующих компонент сил и моментов, связанных с влиянием присоединенной массы воды, в окрестности нулевых значений скоростей. В частности, в случае малых скоростей движения подводного аппарата, согласно [20], имеют место равенства: ${{X}_{{{\dot {v}}}}} = 0$, ${{X}_{{\dot {w}}}} = 0$, ${{X}_{{\dot {p}}}} = 0$, ${{X}_{{\dot {q}}}} = 0$, ${{X}_{{\dot {r}}}} = 0$, ${{Y}_{{\dot {u}}}} = 0$, ${{Y}_{{\dot {w}}}} = 0$, ${{Y}_{{\dot {p}}}} = 0$, ${{Y}_{{\dot {q}}}} = 0$, ${{Y}_{{\dot {r}}}} = 0$, ${{Z}_{{\dot {u}}}} = 0$, ${{Z}_{{{\dot {v}}}}} = 0$, ${{Z}_{{\dot {p}}}} = 0$, ${{Z}_{{\dot {q}}}} = 0$, ${{Z}_{{\dot {r}}}} = 0$, ${{K}_{{\dot {u}}}} = 0$, ${{K}_{{{\dot {v}}}}} = 0$, ${{K}_{{\dot {w}}}} = 0$, ${{K}_{{\dot {q}}}} = 0$, ${{K}_{{\dot {r}}}} = 0$, ${{M}_{{\dot {u}}}} = 0$, ${{M}_{{{\dot {v}}}}} = 0$, ${{M}_{{\dot {w}}}} = 0$, ${{M}_{{\dot {p}}}} = 0$, ${{M}_{{\dot {r}}}} = 0$, ${{N}_{{\dot {u}}}} = 0$, ${{N}_{{{\dot {v}}}}} = 0$, ${{N}_{{\dot {w}}}} = 0$, ${{N}_{{\dot {p}}}} = 0$, ${{N}_{{\dot {q}}}} = 0$ и D(ν) = –diag(Xu + + ${{X}_{{u\left| u \right|}}}\left| u \right|,{{Y}_{{v}}} + {{Y}_{{{v}\left| {v} \right|}}}\left| {v} \right|,{{Z}_{w}} + {{Z}_{{w\left| w \right|}}}\left| w \right|,{{K}_{p}} + {{K}_{{p\left| p \right|}}}\left| p \right|,{{M}_{q}} + {{M}_{{q\left| q \right|}}}\left| q \right|,{{N}_{r}} + {{N}_{{r\left| r \right|}}}\left| r \right|)$, где Xu, ${{Y}_{{v}}}$, ${{Z}_{w}}$, Kp, Mq, ${{N}_{r}}$ и ${{X}_{{u\left| u \right|}}}$, ${{Y}_{{v\left| v \right|}}}$, ${{Z}_{{w\left| w \right|}}}$, ${{K}_{{p\left| p \right|}}}$, ${{M}_{{q\left| q \right|}}}$, ${{N}_{{r\left| r \right|}}}$ – некоторые отрицательные коэффициенты.
Вектор-функция $g\left( \eta \right)$ в выражении (3.5), описывающая влияние величины силы тяжести $W = mg$ и величины выталкивающей силы $B = \rho gV$ на динамику корпуса аппарата, записывается следующим образом [20]:
(3.6)
$\begin{gathered} g\left( \eta \right) = - \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \; \end{array}{{f}_{G}}\left( {{{\eta }_{2}}} \right) + {{f}_{B}}\left( {{{\eta }_{2}}} \right)} \\ {{{r}_{G}} \times {{f}_{G}}\left( {{{\eta }_{2}}} \right) + {{r}_{B}} \times {{f}_{B}}\left( {{{\eta }_{2}}} \right)} \end{array}} \right)~, \\ {{f}_{G}}\left( {{{\eta }_{2}}} \right) = J_{1}^{{ - 1}}\left( {{{\eta }_{2}}} \right)\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \; \end{array}0} \\ 0 \\ W \end{array}} \right),\quad {{f}_{B}}\left( {{{\eta }_{2}}} \right) = - J_{1}^{{ - 1}}\left( {{{\eta }_{2}}} \right)\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \; \end{array}0} \\ 0 \\ B \end{array}} \right)~, \\ \end{gathered} $(3.7)
$g\left( \eta \right) = \left( {\begin{array}{*{20}{c}} {\left( {W - B} \right)\sin \theta } \\ { - \left( {W - B} \right)\cos \theta \sin \varphi } \\ { - \left( {W - B} \right)\cos \theta \cos \varphi } \\ { - \left( {{{y}_{G}}W - {{y}_{B}}B} \right)\cos \theta \cos \varphi + \left( {{{z}_{G}}W - {{z}_{B}}B} \right)\cos \theta \sin \varphi } \\ {\left( {{{z}_{G}}W - {{z}_{B}}B} \right)\sin \theta + \left( {{{x}_{G}}W - {{x}_{B}}B} \right)\cos \theta \cos \varphi } \\ { - \left( {{{x}_{G}}W - {{x}_{B}}B} \right)\cos \theta \sin \varphi - \left( {{{y}_{G}}W - {{y}_{B}}B} \right)\sin \theta } \end{array}} \right).$В итоге, принимая во внимание соотношения (3.2) – (3.7), получим следующую математическую модель движения подводного аппaрата, записанную относительно неинерциальной системы координат ${{O}_{b}}{{x}_{b}}{{y}_{b}}{{z}_{b}}$:
(3.8)
$M\dot {\nu } + C\left( \nu \right)\nu + D\left( \nu \right)\nu + g\left( \eta \right) = \tau ,\quad \dot {\eta } = J\left( \eta \right)\nu ,$Тогда с учетом равенства (3.2) уравнения движения корпуса аппарата в векторном виде относительно инерциальной земной системы координат $Oxyz$ примут вид
(3.9)
${{M}_{\eta }}\left( \eta \right)\ddot {\eta } + {{C}_{\eta }}\left( {\eta ,\nu } \right)\dot {\eta } + {{D}_{\eta }}\left( {\eta ,\nu } \right)\dot {\eta } + g\left( \eta \right) = \tau ,\quad \nu = {{J}^{{ - 1}}}\left( \eta \right)\dot {\eta },$Для построения программной траектории $\eta = P\left( t \right)$, $t \in \left[ {0,T} \right]$, движения корпуса подводного аппарата воспользуемся результатами, полученными в работе [17]. Используем далее обозначения ${{x}_{{11}}} = x$, ${{x}_{{12}}} = y$, ${{x}_{{13}}} = z$, ${{x}_{{14}}} = \varphi $, ${{x}_{{15}}} = \theta $, ${{x}_{{16}}} = \psi $ и перепишем условия (1.2):
В частности, рассмотрим, например, значения ${{\dot {x}}_{{0i}}} = {{\dot {x}}_{{*i}}} = 0$, $i = \overline {1,6} $, и дополнительно потребуем, чтобы искомая программная траектория удовлетворяла условиям ${{\ddot {x}}_{{1i}}}\left( 0 \right) = 0$ и ${{\ddot {x}}_{{1i}}}\left( T \right) = 0$, $i = \overline {1,6} $. Будем также полагать, что время движения T не задано в постановке задачи.
Фиксируем произвольные положительные значения T1, T3, T5 и ${{\varepsilon }_{1}} > 1$, ${{\varepsilon }_{2}} > 1$. Для синтеза программной траектории из начальной точки ${{\left( {{{x}_{{01}}},0, \ldots ,{{x}_{{06}}},0} \right)}^{{\text{T}}}}$ в конечную точку ${{\left( {{{x}_{{*1}}},0, \ldots ,{{x}_{{*6}}},0} \right)}^{{\text{T}}}}$ в фазовом пространстве ${{\left( {x,\dot {x},y,\dot {y},z,\dot {z},\varphi ,\dot {\varphi },\theta ,\dot {\theta },\psi ,\dot {\psi }} \right)}^{{\text{T}}}}$ системы (3.9) используем дополнительные промежуточные точки с координатами ${{\left( {{{x}_{{j1}}},{{{\dot {x}}}_{{j1}}}, \ldots ,{{x}_{{j6}}},{{{\dot {x}}}_{{j6}}}} \right)}^{{\text{T}}}}$, $j = \overline {1,4} $, где значения ${{x}_{{ji}}}$, ${{\dot {x}}_{{ji}}}$, $j = \overline {1,4} $, $i = \overline {1,6} $, удовлетворяют условиям ${{\dot {x}}_{{2i}}} = {{\dot {x}}_{{3i}}}$ и соответствующим соотношениям [17]:
Программная траектория η = P(t), $t \in \left[ {0,T} \right]$, запишется покомпонентно следующим образом:
(3.10)
${{x}_{{1i}}} = {{p}_{i}}\left( t \right) = \left\{ {{{p}_{{ji}}}\left( t \right),t \in \left[ {\mathop \sum \limits_{k = 0}^{j - 1} {{T}_{k}},\mathop \sum \limits_{k = 0}^j {{T}_{k}}} \right],j = \overline {1,5} } \right\},\quad i = \overline {1,6} ,$Здесь коэффициенты ${{c}_{{1{{i}_{j}}}}}$, ${{c}_{{2{{i}_{j}}}}}$ следующие [17]:
Далее, согласно работе [17], для выполнения ограничений $\left| {{{{\dot {x}}}_{{1i}}}\left( t \right)} \right| \leqslant {{N}_{i}}$ и $\left| {{{{\ddot {x}}}_{{1i}}}\left( t \right)} \right| \leqslant {{Q}_{i}}$ при всех $t \in \left[ {0,T} \right]$, $i = \overline {1,6} $, на значения первых и вторых производных по времени соответствующих функций (3.10) необходимо и достаточно, чтобы выбранные значения T1, T3, T5 и ${{\varepsilon }_{1}} > 1$, ${{\varepsilon }_{2}} > 1$ удовлетворяли следующим неравенствам:
Дополнительно, если для любого $i = \overline {1,6} $ выполнены условия
Наконец, управление, стабилизирующее программную траекторию $\eta = P\left( t \right)$, $t \in \left[ {0,T} \right]$, системы (3.9), покомпонентно заданную соотношениями (3.10), с учетом соответствующих ограничений (1.4), согласно формуле (2.4), запишется следующим образом:
(3.11)
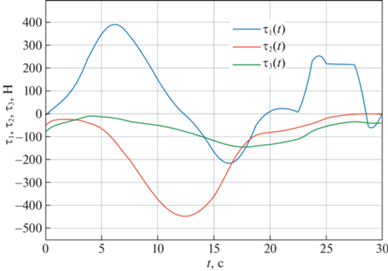
$\begin{gathered} \tau = {{C}_{\eta }}\left( {\eta ,\nu } \right)\dot {\eta } + {{D}_{\eta }}\left( {\eta ,\nu } \right)\dot {\eta } + g\left( \eta \right) + {{M}_{\eta }}\left( \eta \right)(\ddot {P}\left( t \right)~\, - \\ - \,{{K}_{2}}{{K}_{1}}{{\xi }_{1}} - \left( {{{K}_{1}} + {{K}_{2}}} \right){{{\dot {\xi }}}_{1}} - b), \\ \end{gathered} $Результаты численного моделирования системы (3.9) с управлением (3.11) представлены на рис. 1–8 для следующих значений физических и геометрических параметров модели, соответствующих подводному аппарату Kambara [21, 22]: m = 117 кг, g = 9.81 м ⋅ с–2, B = 1108 Н, ${{I}_{x}} = 10.7$ кг ⋅ м2, ${{I}_{y}}\, = \,11.8$ кг ⋅ м2, ${{I}_{z}} = 13.4$ кг ⋅ м2, ${{x}_{G}} = 0$ м, ${{y}_{G}} = 0$ м, ${{z}_{G}} = 0$ м, ${{x}_{B}} = - 0.017$ м, ${{y}_{B}}\, = \,\,0$ м, ${{z}_{B}} = - 0.115$ м, ${{X}_{{\dot {u}}}} = - 58.4$ кг, ${{Y}_{{\dot {v}}}} = - 23.8$ кг, ${{Z}_{{\dot {w}}}} = - 23.8$ кг, ${{K}_{{\dot {p}}}} = - 3.38$ кг ⋅ м2/рад, ${{M}_{{\dot {q}}}} = - 1.18$ кг ⋅ м2/рад, ${{N}_{{\dot {r}}}} = - 2.67$ кг ⋅ м2/рад, ${{X}_{u}} = - 120$ кг/с, ${{Y}_{v}} = - 90$ кг/с, ${{Z}_{w}} = - 150$ кг/с, ${{K}_{p}} = - 15$ Н ⋅ м ⋅ с/рад, ${{M}_{q}} = - 15$ Н ⋅ м ⋅ с/рад, ${{N}_{r}} = - 18$ Н ⋅ м ⋅ с/рад, ${{X}_{{u\left| u \right|}}} = - 90$ кг/м, ${{Y}_{{{v}\left| {v} \right|}}} = - 90$ кг/м, ${{Z}_{{w\left| w \right|}}} = - 120$ кг/м, ${{K}_{{p\left| p \right|}}} = - 10$ кг ⋅ м2/рад2, ${{M}_{{q\left| q \right|}}} = - 12$ кг ⋅ м2/рад2, ${{N}_{{r\left| r \right|}}} = - 15$ кг ⋅ м2/рад2.
Рис. 1.
Координаты ${{\eta }_{1}} = {{\left( {x,y,z} \right)}^{{\text{T}}}}$ центра масс корпуса аппарата как функции времени и их программные значения $x = {{p}_{1}}\left( t \right),~~y = {{p}_{2}}\left( t \right),~~z = {{p}_{3}}\left( t \right)$
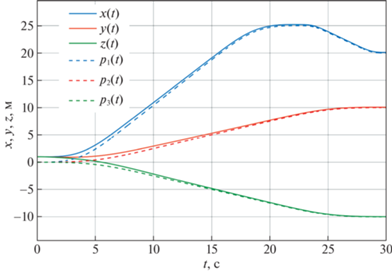
Рис. 2.
Координаты вектора скорости ${{\dot {\eta }}_{1}} = {{\left( {\dot {x},\dot {y},\dot {z}} \right)}^{{\text{T}}}}$ поступательного движения центра масс корпуса аппарата как функции времени и их программные значения $\dot {x} = {{\dot {p}}_{1}}\left( t \right),~~\dot {y} = {{\dot {p}}_{2}}\left( t \right),~~\dot {z} = {{\dot {p}}_{3}}\left( t \right)$
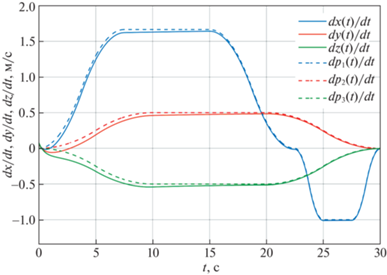
Рис. 3.
Угловые координаты ${{\eta }_{2}} = {{\left( {\varphi ,\theta ,\psi } \right)}^{{\text{T}}}}$ вращения корпуса аппарата вокруг центра масс как функции времени и их программные значения $\varphi = {{p}_{4}}\left( t \right),~~\theta = {{p}_{5}}\left( t \right),~~\psi = {{p}_{6}}\left( t \right)$
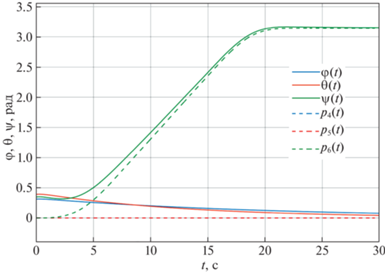
Рис. 4.
Угловые скорости ${{\dot {\eta }}_{2}} = {{\left( {\dot {\varphi },\dot {\theta },\dot {\psi }} \right)}^{{\text{T}}}}$ вращения корпуса аппарата вокруг центра масс как функции времени и их программные значения $\dot {\varphi } = {{\dot {p}}_{4}}\left( t \right),~\dot {\theta } = {{\dot {p}}_{5}}\left( t \right),\dot {\psi } = {{\dot {p}}_{6}}\left( t \right)$
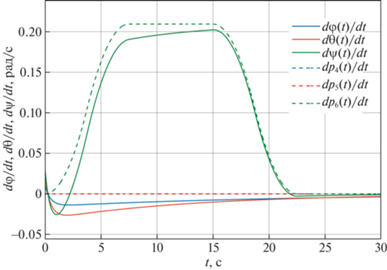
Рис. 5.
Координаты вектора ускорения ${{\ddot {\eta }}_{1}} = {{\left( {\ddot {x},\ddot {y},\ddot {z}} \right)}^{{\text{T}}}}$ поступательного движения центра масс корпуса аппарата как функции времени и их программные значения $\ddot {x} = {{\ddot {p}}_{1}}\left( t \right),~~\ddot {y} = {{\ddot {p}}_{2}}\left( t \right),~\ddot {z} = {{\ddot {p}}_{3}}\left( t \right)$
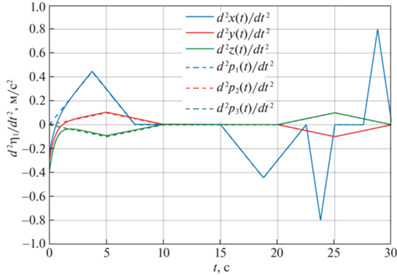
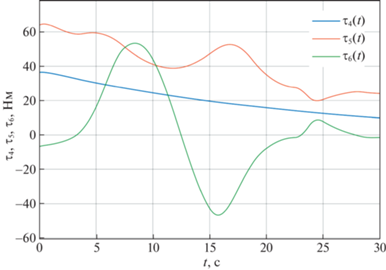
Рис. 6.
Угловые ускорения ${{\ddot {\eta }}_{2}} = {{\left( {\ddot {\varphi },\ddot {\theta },\ddot {\psi }} \right)}^{{\text{T}}}}$ вращения корпуса аппарата вокруг центра масс как функции времени и их программные значения $\ddot {\varphi } = {{\ddot {p}}_{4}}\left( t \right),\ddot {\theta } = {{\ddot {p}}_{5}}\left( t \right),\ddot {\psi } = {{\ddot {p}}_{6}}\left( t \right)$
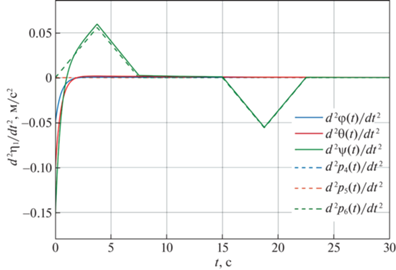
Построена программная траектория смещения центра масс корпуса аппарата из начала координат ${{\eta }_{1}} = {{\left( {0,0,0} \right)}^{{\text{T}}}}$ в точку с координатами ${{\eta }_{1}} = {{\left( {20,10, - 10} \right)}^{{\text{T}}}}$ и пространственного разворота корпуса на 180° по углу рысканья ψ. В качестве начальных и конечных значений переменных состояния системы (3.9) для программной траектории рассматривались соответственно $\eta \left( 0 \right) = {{\eta }_{0}} = {{\left( {0,0,0,0,0,0} \right)}^{{\text{T}}}}$, $\dot {\eta }\left( 0 \right) = {{\dot {\eta }}_{0}} = {{\left( {0,0,0,0,0,0} \right)}^{{\text{T}}}}$ и $\eta \left( T \right) = {{\eta }_{*}} = {{\left( {20,10, - 10,0,0,\pi } \right)}^{{\text{T}}}}$, $\dot {\eta }\left( T \right) = {{\dot {\eta }}_{*}}$ = = (0, 0, 0, 0, 0, 0)T. При планировании программной траектории были выбраны значения $T = 30$ с, ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 2$, ${{T}_{1}} = T{\text{/}}\left( {3{{\varepsilon }_{1}}} \right)$, ${{T}_{5}} = T{\text{/}}\left( {3{{\varepsilon }_{2}}} \right)$.
Для численного моделирования процесса стабилизации построенной программной траектории были использованы следующие начальные значения: ${{\xi }_{1}}\left( 0 \right) = {{\left( {1,1,1,\pi {\text{/}}10,\pi {\text{/}}8,\pi {\text{/}}9} \right)}^{{\text{T}}}}$ и ${{\dot {\xi }}_{1}}(0) = {{(0.05,0.06,0.08,0.01,0.02,0.03)}^{{\text{T}}}}$ соответствующих переменных отклонения и их производных, в также значения параметров управления (3.11): ${{\varepsilon }_{{1i}}} = 1.001\left| {{{\xi }_{{1i}}}\left( 0 \right)} \right|,\,\,{{\varepsilon }_{{2i}}} = 1.5\left| {{{{\dot {\xi }}}_{{1i}}}\left( 0 \right)} \right|,$ ${{\kappa }_{{1i}}} = 0.999{{\varepsilon }_{{2i}}}{\text{/}}{{\varepsilon }_{{1i}}},\,\,{{\kappa }_{{2i}}} = 2,\,\,i = \overline {1,6} .$.
Заключение. Рассмотрена задача стабилизации программных траекторий движения механических систем с учетом ограничений на значения обобщенных координат, скоростей и ускорений. Для построения стабилизирующих законов управления применен метод бэкстеппинга, использующий логарифмические барьерные функции Ляпунова. Полученные в работе стабилизирующие обратные связи в отличие от аналогичных известных результатов не приводят к неограниченному росту значений переменных управления при приближении переменных состояния системы к граничным значениям. В качестве примера решена задача построения и стабилизации траектории пространственного движения подводного аппарата. Отметим, что возможность учета ограничений на значения обобщенных координат при построении и стабилизации траекторий движения механических систем важна, например, при решении задач группового управления, когда от отдельных объектов управления в группе может требоваться нахождение в отдельной области пространства, непересекающейся с зонами движения других обьектов. Выполнение ограничений на значения обобщенных скоростей позволяют, например, учитывать требования малости соответствующих скоростей движения при использовании в математических моделях линеаризованных выражений для сил и моментов.
Список литературы
Olfati-Saber R. Flocking for Multi-agent Dynamic Systems: Algorithms and Theory // IEEE Trans. Automat. Contr. 2006. V. 51 (3). P. 401–420.
Liu H., Chen G., Tian X. Cooperative Formation Control for Multiple Surface Vessels Based on Barrier Lyapunov Function and Self-structuring Neural Networks // Ocean Engineering. 2020. V. 216. 108163.
Крутько П.Д. Обратные задачи динамики управляемых систем. Нелинейные модели. М.: Наука, 1988. 326 с.
Isidori A. Nonlinear Control Systems. 3rd ed. London: Springer-Verlag, 1995. 549 p.
Краснощеченко В.И., Крищенко А.П. Нелинейные системы: геометрические методы анализа и синтеза. М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. 520 с.
Krstić M., Kanellakopoulos I., Kokotović P.V. Nonlinear and Adaptive Control Design. New York: John Wiley and Sons, 1995. 563 p.
Ortega R., Loria A., Nicklasson P.J., Sira-Ramirez H. Passivity-based Control of Euler-Lagrange Systems: Mechanical, Electrical and Electromechanical Applications. London: Springer-Verlag, 1998. 543 p.
Ngo K.B., Mahony R., Jiang Z.P. Integrator Backstepping Using Barrier Functions for Systems with Multiple State Constraints // Proc. 44th IEEE Conf. on Decision and Control, and the European Control Conf. Seville, Spain, 2005. P. 8306–8312.
Tee K.P., Ge S.S., Tay E.H. Barrier Lyapunov Functions for the Control of Output-constrained Nonlinear Systems // Automatica. 2009. V. 45 (4). P. 918–927.
Boyd S., Vandenberghe L. Convex Optimization. Cambridge: University Press, 2009. 716 p.
Niu B., Zhao J. Barrier Lyapunov Functions for the Output Tracking Control of Constrained Nonlinear Switched Systems // Systems and Control Letters. 2013. V. 62 (10). P. 963–971.
Sachan K., Padhi R. Barrier Lyapunov Function Based Output-constrained Control of Nonlinear Euler-Lagrange Systems // Proc. 15th Intern. Conf. on Control, Automation, Robotics and Vision (ICARCV). Singapore, 2018. P. 686–691.
Golubev A.E., Botkin N.D., Krishchenko A.P. Backstepping Control of Aircraft Take-off in Windshear // IFAC-PapersOnLine. 2019. V. 52 (16). P. 712–717.
Garg T., Roy S.B. Barrier Lyapunov Function Based Controller Design for Euler-Lagrange Systems with Reduced Control Effort // IFAC-PapersOnLine. 2020. V. 53 (1). P. 459–464.
Wang X., Xu J., Lv M., Zhang L., Zhao Z. Barrier Lyapunov Function-based Fixed-time FTC for High-order Nonlinear Systems with Predefined Tracking Accuracy // Nonlinear Dynamics. 2022. V. 110. P. 381–394.
Golubev A., Kovtanyuk A., Lampe R. Modeling of Cerebral Blood Flow Autoregulation Using Mathematical Control Theory // Mathematics. 2022. V. 10 (12). 2060.
Голубев А.Е. Построение программных движений механических систем с учетом ограничений при помощи многочленов третьего порядка // Изв. РАН. ТиСУ. 2021. № 2. С. 126–137.
Sussmann H.J., Kokotovic P.V. The Peaking Phenomenon and the Global Stabilization of Nonlinear Systems // IEEE Transactions on Automatic Control. 1991. V. 36 (4). P. 424–440.
Khalil H.K. Nonlinear Systems. 3rd ed. Upper Saddle River: Prentice Hall, 2002.
Fossen T.I. Guidance and Control of Ocean Vehicles. Chichester: John Wiley and Sons, 1994.
Silpa-Anan C., Zelinsky A. Kambara: Past, Present, and Future // Proc. 2001 Australian Conf. on Robotics and Automation. Sydney, 2001. P. 61–66.
Silpa-Anan C. Autonomous Underwater Robot: Vision and Control. Master thesis. Canberra: Australian National University, 2001. https://doi.org/10.25911/5d626dd9b96ec.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления