Известия РАН. Теория и системы управления, 2023, № 5, стр. 3-15
ГЛОБАЛЬНАЯ УСТОЙЧИВОСТЬ ГИБРИДНОЙ АФФИННОЙ СИСТЕМЫ 4-ГО ПОРЯДКА
Ю. В. Морозов a, *, А. В. Пестерев a, **
a ИПУ РАН
Москва, Россия
* E-mail: tot1983@inbox.ru
** E-mail: alexanderpesterev.ap@gmail.com
Поступила в редакцию 03.11.2022
После доработки 23.03.2023
Принята к публикации 03.04.2023
- EDN: OCWYZV
- DOI: 10.31857/S0002338823040108
Аннотация
Исследуемая гибридная аффинная система возникает при применении импульсного управления специального вида к цепочке четырех интеграторов. Цель управления – стабилизировать систему в начале координат так, чтобы система приближалась к состоянию равновесия по заданной желаемой (целевой) траектории. Целевая траектория определена неявно как траектория интегратора второго порядка, стабилизируемого с помощью обратной связи в виде вложенных сатураторов. Задача исследования – найти диапазон изменения коэффициентов обратной связи, при которых система глобально устойчива. Показано, что задача сводится к более простой задаче установления устойчивости линейной системы второго порядка с переключениями с зависящим от состояния законом переключений. Доказано, что последняя устойчива при любом законе переключений.
Введение. Гибридными системами называют динамические системы, которые демонстрируют как непрерывное, так и дискретное поведение, т.е. системы, состояния которых могут меняться не только непрерывно, но и скачками [1]. Исследуемая в статье гибридная аффинная система возникает при применении импульсного управления специального вида для стабилизации цепочки четырех интеграторов. Задача стабилизации цепочек интеграторов широко обсуждалась в литературе в течение нескольких последних десятилетий (например, [2–6] и приведенные там ссылки). Интерес к данной проблематике обусловлен тем, что управления, разработанные для цепочек интеграторов, легко обобщаются на более широкие классы систем [5]. Более того, во многих приложениях исходные модели, например модели механических планарных систем, заданы в виде цепочек интеграторов.
Задачей настоящего исследования было нахождение управления, глобально стабилизирующего интегратор 4-го порядка, при дополнительном условии асимптотического следования вдоль желаемой траектории при приближении к состоянию равновесия. Целевая траектория определена неявно как траектория более простой эталонной системы 2-го порядка, расширенная до четырехмерного пространства. В качестве эталонной системы рассматривается цепочка двух интеграторов, замкнутая заданной обратной связью в виде вложенных сатураторов с коэффициентами обратной связи, выбранными так, чтобы обеспечить желаемые характеристики целевой траектории. Искомая обратная связь, обеспечивающая глобальную стабилизацию интегратора 4-го порядка, получена в виде суммы кусочно-непрерывного и импульсного управления. Показано, что система, замкнутая такой обратной связью, является гибридной аффинной системой.
Настоящая публикация не претендует на разработку общего метода или инструмента для исследования гибридных систем и/или систем с переключениями. Рассматривается конкретная, нетривиальная гибридная аффинная система. Цель работы – установить условия ее глобальной устойчивости. Так как система нелинейна, к ней неприменимы хорошо известные методы исследования линейных систем, основанные, например, на критериях Михайлова и Рауса–Гурвица. Известные же методы исследования устойчивости нелинейных систем напрямую неприменимы к гибридным системам и системам с переключениями, для которых разработан ряд специальных методов [1, 7–9]. Однако ни один из обсуждаемых в цитированной выше литературе методов оказался неприменим к рассмотренной в статье гибридной аффинной системе. Полученное доказательство глобальной устойчивости основано на сведении исходной задачи к исследованию устойчивости более простой системы 2-го порядка с переключениями. Цель статьи, таким образом, состоит в следующем: 1) разработать новый закон управления, стабилизизирующий интегратор 4-го порядка; 2) показать, что замкнутая система является гибридной системой; 3) исследовать глобальную устойчивость полученной гибридной системы.
В разд. 1 статьи формулируется задача стабилизации интегратора 4-го порядка при дополнительном условии асимптотического следования вдоль заданной траектории и предлагается обратная связь, обеспечивающая желаемые характеристики процесса перехода к состоянию равновесия. Показано, что система, замкнутая такой обратной связью, является гибридной аффинной системой с зависящим от состояния законом переключения. Главный результат работы представлен в разд. 1. Исследование устойчивости рассматриваемой гибридной системы сведено к исследованию устойчивости линейной системы 2-го порядка с переключениями. Доказательство устойчивости последней при любых законах переключения, что гарантирует глобальную устойчивость исходной системы, приведено в Приложении, где также доказан вспомогательный результат о глобальной устойчивости интегратора 2-го порядка, замкнутого обратной связью в виде вложенных сатураторов. В разд. 3 приведены результаты численных экспериментов, иллюстрирующих изложение.
1. Потановка задачи. Постановку задачи разобьем на два этапа.
1.1. Стабилизация интегратора 4-го порядка. Рассмотрим интегратор 4-го порядка:
(1.1)
${{\dot {x}}_{1}} = {{x}_{2}},\quad {{\dot {x}}_{2}} = {{x}_{3}},\quad {{\dot {x}}_{3}} = {{x}_{4}},\quad {{\dot {x}}_{4}} = U(x),$(1.2)
${{\dot {w}}_{1}} = {{w}_{2}},\quad {{\dot {w}}_{2}} = {{U}_{1}}({{w}_{1}},{{w}_{2}}),\quad {{w}_{1}}(0) = {{x}_{1}}(0),\quad {{w}_{2}}(0) = {{x}_{2}}(0)$(1.3)
${\text{|}}{{U}_{1}}({{w}_{1}},{{w}_{2}}){\text{|}} \leqslant {{U}_{{{\text{max}}}}},\quad {\text{|}}{{w}_{2}}(t){\text{|}} \leqslant {{V}_{{{\text{max}}}}}.$Для стабилизации системы (1.2) применим негладкую обратную связь U1 в виде вложенных сатураторов:
(1.4)
${{U}_{1}}({{w}_{1}},{{w}_{2}}) = - {{k}_{4}}{\text{sat}}({{k}_{3}}({{w}_{2}} + {{k}_{2}}{\text{sat}}({{k}_{1}}{{w}_{1}}))),$Вблизи нуля система (1.2), (1.4) линейна: ${{\dot {x}}_{1}} = {{x}_{2}}$, ${{\dot {x}}_{2}} = - {{k}_{1}}{{k}_{2}}{{k}_{3}}{{k}_{4}}{{x}_{1}} - {{k}_{3}}{{k}_{4}}{{x}_{2}}$ и имеет в нуле устойчивое положение равновесия при любых ${{k}_{i}} > 0$, $i = \overline {1,4} $. Если ${{k}_{3}}{{k}_{4}} < 4{{k}_{1}}{{k}_{2}}$, то x = 0 – фокус; иначе – узел. Последний случай представляется более практичным, так как не приводит к осцилляциям вокруг нуля, поэтому далее будем считать, что коэффициенты контроллера удовлетворяют неравенству ${{k}_{3}}{{k}_{4}} \geqslant 4{{k}_{1}}{{k}_{2}}$.
Обратные связи в виде вложенных сатураторов применялись в ряде работ по стабилизации цепочек интеграторов ([2, 3, 10–13] и приведенные там ссылки). Однако авторам не известны работы, результаты которых могли бы быть использованы для установления устойчивости системы (1.2), (1.4). Общий случай n-мерного интегратора обсуждается, например, в [2, 3]. Глобальная устойчивость системы, замкнутой обратной связи в виде n вложенных сатураторов, при этом была доказана только для случая, когда предельные значения вложенных функций насыщения удовлетворяют определенным неравенствам [2], Theorem 2.1, которые не выполняются для обратной связи (1.4). В [11, 12] для стабилизации интегратора 2-го порядка применяется обратная связь вида (1.4), отличающаяся от (1.4) тем, что аргументом внутреннего сатуратора является скорость ${{w}_{2}}$, а не отклонение ${{w}_{1}}$, как в (1.4) (в [12] аргумент внешнего сатуратора дополнительно зависит от квадрата скорости $w_{2}^{2}$). Доказательство глобальной устойчивости в обеих работах основано на существовании функции Ляпунова в виде суммы квадратичного и интегрального членов. Для системы (1.2), (1.4), однако, указанный прием не применим, так как функцию Ляпунова такого вида не удается найти.
Условия глобальной устойчивости системы (1.2), (1.4) сформулированы в следующей лемме, доказательство которой приведено в Приложении.
Лемма 1. Пусть ${{k}_{i}} > 0$, $i = \overline {1,4} $ и ${{k}_{3}}{{k}_{4}} \geqslant 4{{k}_{1}}{{k}_{2}}$. Тогда система (1.2), замкнутая обратной связью (1.4), глобально устойчива.
Чтобы уменьшить количество параметров, будем выбирать коэффициенты ${{k}_{1}}$ и ${{k}_{3}}$ в (1.4) при заданных значениях ресурса управления ${{k}_{4}}$ и максимальной скорости ${{k}_{2}}$ из однопараметрического семейства, параметризованного показателем $\lambda $:
(1.5)
${{k}_{1}} = \lambda {\text{/}}2{{k}_{2}},\quad {{k}_{3}} = 2\lambda {\text{/}}{{k}_{4}},\quad \lambda > 0.$При таком выборе коэффициентов характеристическое уравнение системы (1.2), (1.4) имеет два одинаковых корня: ${{\lambda }_{1}} = {{\lambda }_{2}} = - \lambda $, т.е. начало координат является устойчивым вырожденным узлом, а система (1.2), (1.4) в окрестности нуля принимает вид
(1.6)
${{\dot {w}}_{1}} = {{w}_{2}},\quad {{\dot {w}}_{2}} = - {{\lambda }^{2}}{{w}_{1}} - 2\lambda {{w}_{2}}.$Кроме того, без потери общности положим далее ${{U}_{{{\text{max}}}}} = 1$ и ${{V}_{{{\text{max}}}}} = 1$ (${{k}_{4}} = {{k}_{2}} = 1$).
Возвращаясь теперь к исследуемой системе (1.1), наложим на ее решение дополнительное условие
(1.7)
$\mathop {\lim }\limits_{t \to \infty } {{x}_{3}}(t) = {{U}_{1}}({{x}_{1}}(t),{{x}_{2}}(t)),\quad \mathop {\lim }\limits_{t \to \infty } {{x}_{4}}(t) = {{\dot {U}}_{1}}({{x}_{1}}(t),{{x}_{2}}(t))$(1.8)
$U(x) = {{\ddot {U}}_{1}}({{x}_{1}},{{x}_{2}}) + {{\beta }_{1}}({{U}_{1}}({{x}_{1}},{{x}_{2}}) - {{x}_{3}}) + {{\beta }_{2}}({{\dot {U}}_{1}}({{x}_{1}},{{x}_{2}}) - {{x}_{4}}),$Как и в случае коэффициентов ${{k}_{1}}$ и ${{k}_{3}}$, ограничимся для простоты выбором ${{\beta }_{1}}$ и ${{\beta }_{2}}$ из однопараметрического семейства и при этом масштабируем их с помощью показателя $\lambda $ [14]:
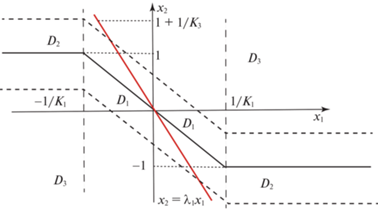
уменьшив таким образом количество параметров до двух: $\lambda $ и $\xi $. Далее докажем, что обратная связь (1.8) стабилизирует интегратор 4-го порядка, и определим диапазон изменения параметров $\lambda $ и $\xi $, для которых замкнутая система (1.1), (1.8) глобально устойчива и при этом выполняются условия (1.7). Покажем сначала, что система (1.1), (1.8) является гибридной аффинной системой.1.2. Эквивалентная гибридная аффинная система. Рассмотрим разбиение плоскости $({{x}_{1}},{{x}_{2}})$ на три множества (рис. 1). Ко множеству ${{D}_{1}}$ отнесем все точки, в которых оба сатуратора не насыщены:
Из формулы (1.4) с учетом (1.5) видно, что ${{U}_{1}}$ – кусочно-линейная функция:
Производные ${{U}_{1}}$ в силу системы (1.2) определены формулами
Подставляя выражения для ${{U}_{1}}$, ${{\dot {U}}_{1}}$ и ${{\ddot {U}}_{1}}$ в уравнение замкнутой системы (1.1), (1.8), получаем аффинную систему с переключениями:
(1.9)
$\dot {x} = {{A}_{{\sigma (x)}}}(\lambda ,\xi )x + {{b}_{{\sigma (x)}}}(\lambda ,\xi ),\quad \sigma (x) \in \{ 1,2,3\} ,$Переключения между системами зависят от состояния, согласно закону
(1.10)
$\sigma (x) = \left\{ \begin{gathered} 1,\quad x \in {{D}_{1}} \times {{R}^{2}}, \hfill \\ 2,\quad x \in {{D}_{2}} \times {{R}^{2}}, \hfill \\ 3,\quad x \in {{D}_{3}} \times {{R}^{2}}. \hfill \\ \end{gathered} \right.$Так как ${{\dot {U}}_{1}}$ меняется скачком при пересечении границы $\Gamma $, функция ${{\ddot {U}}_{1}}$ претерпевает разрыв второго рода в этот момент, а управление U(x) имеет как кусочно-непрерывную, так и импульсную составляющие. На множестве $\Gamma \times {{R}^{2}}$ (jump set [1]) вектор состояния меняется скачком, так что отображение (1.9) (flow map [1]) следует дополнить отображением
(1.11)
${{x}^{ + }} = {{x}^{ - }} + \Delta {{\dot {U}}_{1}}({{x}_{1}},{{x}_{2}})q,\;({{x}_{1}},{{x}_{2}}) \in \Gamma ,$Таким образом, представления (1.1), (1.8) и (1.9), (1.11) эквивалентны, т.е. замкнутая система (1.1), (1.8) является гибридной, и исследование ее устойчивости сводится к исследованию глобальной устойчивости системы (1.9), (1.11).
2. Доказательство глобальной устойчивости. Легко видеть, что области ${{D}_{2}}$ и ${{D}_{3}}$ не включают начала координат и вторая и третья системы в (1.9) не имеют стационарных положений равновесия. Следовательно, необходимым условием устойчивости начала координат является гурвицевость матрицы A1. Вычисляя характеристический полином A1 и применяя критерий Раусса–Гурвица или Льенара–Шипарда [15], нетрудно доказать что эта матрица гурвицева при любых $\lambda > 0$ и $\xi > 3$. Далее будет показано, что эти условия не только необходимы для глобальной устойчивости системы (1.9), но и достаточны. Для этого сначала будет показано, что задача исследования устойчивости рассматриваемой гибридной системы 4-го порядка сводится к исследованию устойчивости системы 2-го порядка с переключениями. Затем будет доказано, что последняя устойчива при любом законе переключения.
2.1. Сведение исследования устойчивости гибридной системы 4-го порядка к исследованию устойчивости системы 2-го порядка с переключениями. Для начала избавимся от разрывной переменной ${{x}_{4}}$, введя новые переменные состояния ${{\delta }_{1}}$ и ${{\delta }_{2}}$ вместо ${{x}_{3}}$ и ${{x}_{4}}$:
Так как скачки ${{\dot {U}}_{1}}$ и ${{x}_{4}}$ при пересечении границы $\Gamma \times {{R}^{2}}$ компенсируют друг друга, переменная ${{\delta }_{2}}$ непрерывна, так что ее можно дифференцировать в обычном смысле. Введем обозначения $d{{U}_{1}}{\text{/}}dt$ и $d{{\dot {U}}_{1}}{\text{/}}dt$ для производных функций ${{U}_{1}}$ и ${{\dot {U}}_{1}}$ в силу системы (1.1), сохранив обозначения с помощью точки над символом для производных этих функций в силу системы (1.2). Для производных ${{\delta }_{1}}$ и ${{\delta }_{2}}$ в силу (1.1) имеем:
Переписывая (1.9) в новых переменных, получаем
(2.1)
${{\dot {x}}_{1}} = {{x}_{2}},\quad {{\dot {x}}_{2}} = {{U}_{1}}({{x}_{1}},{{x}_{2}}) - {{\delta }_{1}},$(2.2)
$\left( {\begin{array}{*{20}{c}} {{{{\dot {\delta }}}_{1}}} \\ {{{{\dot {\delta }}}_{2}}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} { - \frac{{\partial {{U}_{1}}}}{{\partial {{x}_{2}}}}}&1 \\ { - \left( {\frac{{\partial {{{\dot {U}}}_{1}}}}{{\partial {{x}_{2}}}} + {{\lambda }^{2}}{{\xi }^{2}}} \right)}&{ - 2\lambda \xi } \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{{\delta }_{1}}} \\ {{{\delta }_{2}}} \end{array}} \right).$Из (2.1) видно, что компоненты решения ${{x}_{1}}$, ${{x}_{2}}$ стремятся к решению эталонной системы (1.2) тогда и только тогда, когда ${{\delta }_{1}}$ стремится к нулю. Это условие выполняется, когда нулевое решение $\delta $-подсистемы (2.2) глобально устойчиво. Принимая во внимание, что частные производные ${{U}_{1}}$ и ${{\dot {U}}_{1}}$ не зависят от $x$:
(2.4)
${{C}_{1}} = \left[ {\begin{array}{*{20}{c}} {2\lambda }&1 \\ { - {{\lambda }^{2}}({{\xi }^{2}} + 3)}&{ - 2\lambda \xi } \end{array}} \right],$(2.5)
${{C}_{2}} = \left[ {\begin{array}{*{20}{c}} {2\lambda }&1 \\ { - {{\lambda }^{2}}({{\xi }^{2}} + 4)}&{ - 2\lambda \xi } \end{array}} \right],$(2.6)
${{C}_{3}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ { - {{\lambda }^{2}}{{\xi }^{2}}}&{ - 2\lambda \xi } \end{array}} \right],$2.2. Устойчивость системы 2-го порядка с переключениями. Хотя матрицы ${{C}_{i}}$ в правой части (2.3) не зависят от переменных ${{x}_{1}}$ и ${{x}_{2}}$, решение $\delta $-подсистемы (2.3) зависит от динамики x-подсистемы, так как от состояния $x$-подсистемы зависят моменты переключения в (2.3). Тем не менее, оказывается, что динамика x-подсистемы не влияет на устойчивость системы (2.3). А именно справедлива следующая лемма, доказательство которой приведено в Приложении.
Лемма 2. Система с переключениями (2.3) устойчива при любых законах переключения тогда и только тогда, когда $\lambda > 0$ и $\xi > 3$.
Устойчивость системы (2.3) при произвольных переключениях означает, что она устойчива и при любом зависящем от состояния законе переключения. Следовательно, условия λ > 0 и $\xi > 3$ достаточны для глобальной устойчивости гибридной системы (1.9), (1.11). Принимая во внимание, что, как установлено в начале данного раздела, эти условия необходимы для глобальной устойчивости, получаем следующее утверждение.
Теорема. Нулевое решение гибридной системы (1.9), (1.11) глобально устойчиво тогда и только тогда, когда λ > 0 и $\xi > 3$.
3. Численные примеры. С целью иллюстрации рассмотрим стабилизацию интегратора 4-го порядка с помощью обратной связи (1.8) с параметрами $\lambda = 1.5$ и $\xi = 4.0$ (${{\beta }_{1}} = 36$ и ${{\beta }_{2}} = 12$). Предельные значения управления и скорости эталонной системы с обратной связью (1.4) были принятыми равными единице: ${{k}_{2}} = {{k}_{4}} = 1$, а значения ${{k}_{1}} = 0.75$ и ${{k}_{3}} = 3.0$ двух других коэффициентов выбраны так, чтобы обеспечить целевую экспоненциальную скорость убывания отклонения $\lambda = 1.5$.
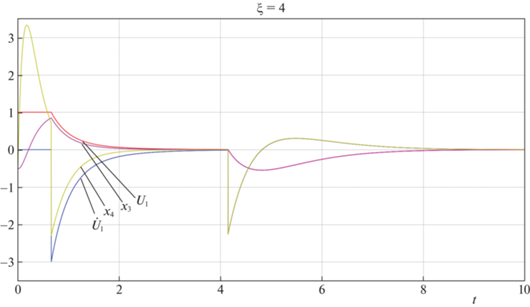
Рисунки 2 и 3 демонстрируют графики переменных состояния для начальных условий ${{x}_{1}}(0)$ = = –5.0, ${{x}_{2}}(0) = 0.5$, ${{x}_{3}}(0) = - 0.5$ и ${{x}_{4}} = - 1.0$. Начальные невязки, таким образом, равны ${{\delta }_{1}}(0) = {{U}_{1}}({{x}_{1}}(0),{{x}_{2}}(0)) - {{x}_{3}}(0) = 1.5$ и ${{\delta }_{2}}(0) = {{\dot {U}}_{1}}({{x}_{1}}(0),{{x}_{2}}(0)) - {{x}_{4}}(0) = 1.0$. На рис. 2 показаны отклонения и скорости (${{x}_{1}}$, ${{x}_{2}}$) и (${{w}_{1}}$, ${{w}_{2}}$) исследуемой и эталонной систем, а на рис. 3 для сравнения представлены переменные ${{x}_{3}}$ и ${{x}_{4}}$ и функции ${{U}_{1}}({{x}_{1}},{{x}_{2}})$ и ${{\dot {U}}_{1}}({{x}_{1}},{{x}_{2}})$. Видно, что невязки ${{\delta }_{1}}$ и ${{\delta }_{2}}$ быстро убывают и становятся практически равными нулю при $t > {{t}_{d}} \approx 3$. Первые две компоненты вектора состояния интегратора 4-го порядка ведут себя аналогично переменным состояния интегратора 2-го порядка в том смысле, что графики одного из них могут быть получены из графиков другого сдвигом вдоль оси времени: ${{x}_{i}}(t) \approx {{w}_{i}}(t - {{t}_{d}})$, $i = 1,2$, for $t > {{t}_{d}}$ (рис. 2). Время задержки ${{t}_{d}}$ зависит как от параметров $\lambda $ и $\xi $, так и от начальных условий.
Рис. 2.
Графики отклонений и скоростей (${{x}_{1}}$, ${{x}_{2}}$) и (${{w}_{1}}$, ${{w}_{2}}$) исследуемой и эталонной систем ($\xi = 4.0$).
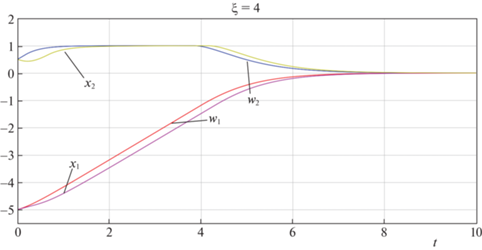
Рис. 3.
Графики переменных ${{x}_{3}}$ и ${{x}_{4}}$ и функций ${{U}_{1}}({{x}_{1}},{{x}_{2}})$ и ${{\dot {U}}_{1}}({{x}_{1}},{{x}_{2}})$ ($\xi = 4.0$).
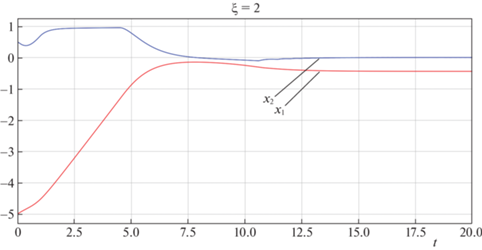
Наконец, для демонстрации отсутствия устойчивости нулевого решения при $\xi \leqslant 3$ на рис. 4 показаны графики ${{x}_{1}}$ и ${{x}_{2}}$ для $\xi = 2.0$. Из рисунка видно, что система останавливается на некотором расстоянии от начала координат.
Заключение. Рассмотрена задача стабилизации цепочки четырех интеграторов при дополнительном условии следования вдоль целевой траектории вблизи состояния равновесия. Целевая траектория определена неявно как траектория эталонной системы. В качестве эталонной системы взят интегратор 2-го порядка, стабилизируемый с помощью обратной связи в виде вложенных сатураторов. Предложен новый закон управления в виде комбинации кусочно-непрерывной и импульсной составляющих. Показано, что система, замкнутая таким законом управления, является гибридной аффинной системой и что задача исследования ее устойчивости сводится к исследованию устойчивости более простой системы 2-го порядка с переключениями. Определена область значений параметров обратной связи, обеспечивающих глобальную устойчивость исследуемой системы.
Список литературы
Goebel R., Sanfelice R.G., Teel A.R. Hybrid Dynamical Systems: Modeling, Stability, and Robustness. New Jersey: Princeton University Press, 2012.
Teel A.R. Global Stabilization and Restricted Tracking for Multiple Integrators with Bounded Controls // Systems & Control Letters. 1992. V. 18. P. 165–171.
Teel A.R. A Nonlinear Small Gain Theorem for the Analysis of Control Systems with Saturation // Trans. Autom. Contr. IEEE. 1996. V. 41. P. 1256–1270.
Pao L., Franklin G. Proximate Time-optimal Control of Third-order Servomechanisms // IEEE Transactions on Automatic Control. 1993. V. 38. P. 560–580.
Polyakov A., Efimov D., Perruquetti W. Robust Stabilization of Mimo Systems in Finite/fixed Time // Int. J. Robust. Nonlinear Control. 2016. V. 26. P. 69–90.
Kurzhanski A.B., Varaiya P. Solution Examples on Ellipsoidal Methods: Computation in High Dimensions. Cham: Springer, 2014. Ch. 4. P. 147–196.
Lin H., Antsaklis P.J. Stability and Stabilizability of Switched Linear Systems: A Survey of Recent Results // IEEE Transactions on Automatic Control 2009. V. 54. P. 308–322.
Pyatnitskiy E., Rapoport L. Criteria of Asymptotic Stability of Differential Inclusions and Periodic Motions of Time-varying Nonlinear Control Systems // IEEE Transactions on Circuits and Systems. Fundamental Theory and Applications. 1996. V. 43. P. 219–229.
Serieye M., Albea-Sánchez C., Seuret A., Jungers M. Stabilization of Switched Affine Systems via Multiple Shifted Lyapunov Functions // IFAC-PapersOnLine. 2020. V. 53. P. 6133–6138.
Pesterev A.V., Morozov Y.V. Optimizing Coefficients of a Controller in the Point Stabilization Problem for a Robot-wheel // Optimization and Applications. Montenegro. 2021. V. 13078. P. 191–202.
Olfati-Saber R. Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles. Ph.D. Thesis. Cambridge: Massachusetts Institute of Technology. Dept. of Electrical Engineering and Computer Science, 2001.
Hua M.-D., Samson C. Time Sub-optimal Nonlinear Pi and Pid Controllers Applied to Longitudinal Headway Car Control// International Journal of Control. 2011. V. 84. P. 1717–1728.
Marconi L., Isidori A. Robust Global Stabilization of a Class of Uncertain Feedforward Nonlinear Systems // Systems & Control Letters. 2000. V. 41. P. 281–290.
Pesterev A.V., Morozov Y.V. Stabilization of a Cart with Inverted Pendulum // Automation and Remote Control. 2022. V. 83. P. 78–91.
Gantmacher F. Matrix theory. 5th ed. M.: Fizmatlit, 2010.
Andronov A.A., Leontovich E., Gordon I.I., Maier A. Qualitative Theory of Second-order Dynamic Systems. New Jersey: Wiley, 1973.
Boyd S., Ghaoui L.E., Feron E., Balakrishnan V. Linear Matrix Inequalities in System and Control Theory. Philadelphia: SIAM, 1994.
Pesterev A.V. Construction of the Best Ellipsoidal Approximation of the Attraction Domain in Stabilization Problem for a Wheeled Robot // Automation and Remote Control. 2011. V. 72. P. 512–528.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Теория и системы управления