Известия РАН. Теория и системы управления, 2023, № 6, стр. 33-49

Введение. Возрастание требований к качеству управления современными технологическими объектами делает актуальным применение соответствующих автоматических систем на базе безынерционных и интегрирующих регуляторов состояния (РС) полного порядка [1, 2]. Когда получение оперативной информации о значениях всех основных координат состояния объекта является затруднительным, необходимое качество управления может обеспечиваться путем использования динамических регуляторов с дробно-рациональным представлением их передаточных функций (ПФ) полиномами повышенного порядка, получивших название полиномиальных регуляторов (ПР) [3–5].

Однако, являясь во многих случаях равноценной альтернативой РС, ПР и системы автоматического управления (САУ) на их основе оказываются такими же, а иногда и более чувствительными к вариациям внутренних параметров объекта управления (ОУ). В итоге практическая реализация таких систем существенно осложняется проблемой робастности (параметрической грубости) из-за недостаточной параметрической определенности и стабильности большинства реальных ОУ.

Несмотря на значительные успехи в области решения проблемы [6–8] универсальных и высокоэффективных методов синтеза робастных САУ, даже в линейной постановке пока не выработано, что делает актуальным продолжение исследований в этом направлении. Выполненные ранее работы [5, 9, 10] позволили установить, что значительные возможности повышения робастных свойств линейных и линеаризованных САУ имеют классические методы модального управления (МУ), реализуемого как на базе РС, так и на основе ПР.

Исследованиями, проведенными в [11], было показано, что улучшение робастных свойств синтезируемых САУ может достигаться предварительным повышением степени управляемости состояния ОУ. На этой базе в [11] разработан эффективный итерационный метод структурно-параметрического синтеза робастных систем с РС с помощью грамианов управляемости ОУ, коррекции их сингулярных чисел предварительным регулятором (предрегулятором) и последующего синтеза основного РС для скорректированного объекта методом МУ.

Очевидно, подобный подход может быть использован и при синтезе робастных САУ на базе ПР. Однако при этом следует учитывать, что для эффективного управления состоянием динамических ОУ на основе ПР потребуется предварительное повышение не только степени управляемости объекта, но и степени наблюдаемости, приводящих в итоге к снижению его вырожденности.

В качестве наиболее эффективных для оценки степени управляемости и наблюдаемости следует указать алгебраические критерии [9, 10] в виде норм матриц преобразования расчетной модели объекта к каноническим формам управляемости и наблюдаемости (КФУ и КФН), а также диагональные формы грамианов управляемости и наблюдаемости [12, 13]. При этом первые позволяют получить более точные количественные оценки системных свойств объекта, но не указывают пути их улучшения. Вторые дают менее точные оценки, но могут использоваться для формирования моделей ОУ с желаемыми свойствами управляемости и наблюдаемости.

В работе предлагается итерационный метод синтеза робастных САУ с ПР “входа-выхода”, на каждом шаге которого целенаправленно изменяются сингулярные числа грамианов управляемости или наблюдаемости, формируется предрегулятор, преобразующий структуру расчетной модели объекта в направлении повышения управляемости и наблюдаемости с учетом имеющихся возможностей и ограничений, рассчитываются параметры основного регулятора и выполняется оценка робастных свойств синтезированной системы в заданных интервалах изменения внутренних параметров.

Исследование сопровождается конкретными числовыми примерами синтеза параметрически грубых систем управления, обеспечивающими наглядную иллюстрацию полученных результатов. Расчетная часть работы выполняется средствами программного комплекса MatLab.

1. Постановка задачи. Будем рассматривать одноканальные системы управления с ПР, имеющие общую структуру (в изображениях сигналов), представленную на рис. 1. Здесь приняты следующие обозначения: s – переменная Лапласа; g, y – входной (задающий) и выходной скалярные сигналы; u – скалярное управляющее воздействие на объект, x – вектор координат состояния с размерностью n; ${\mathbf{A}},~{\mathbf{B}}$ и С – постоянные матрицы состояния, входа и выхода объекта с размерностями $n \times n$, $n \times 1$ и $1 \times n$ соответственно. Здесь n – порядок объекта; ${\mathbf{A}}',~\,\,{\mathbf{B}}'~$ и ${\mathbf{C}}'$ – матрицы предрегулятора, согласованные по размерностям с соответствующими матрицами объекта; B(s) – гурвицев полином числителя ПФ объекта; R(s), C(s) – полиномы ПФ технически реализуемого регулятора минимального порядка, для которого $\deg R\left( s \right) = \deg C\left( s \right) = n - 1$. ПР реализует обратную связь по выходу ОУ, согласно операторному уравнению

При этом контурная часть ПР обеспечивает желаемое распределение полюсов системы, а его внеконтурная часть (префильтр) компенсирует влияние нулей объекта и контурной части регулятора.

Соответствующее дифференциальное описание ОУ имеет вид

где в общем случае матрицы A и ${\mathbf{B}}$ носят интервальный характер.

Компоненты матриц A, B и С, которые можно изменять введением дополнительных каналов управления и связей координат для повышения управляемости и наблюдаемости, отмечаются единичными значениями соответствующих элементов двоичных матриц-масок ${{{\mathbf{E}}}_{1}},{{{\mathbf{E}}}_{2}}$ и E₃, согласованных с ними по размерностям, на фоне нулевых значений остальных элементов. Так, например, при

имеем где $ \circ $ – символ покомпонентного матричного произведения Адамара. В итоге матрица-маска E₁ скрывает элементы $a_{{12}}^{{\text{'}}}$ и $a_{{21}}^{{\text{'}}}$ матрицы ${\mathbf{A}}{\kern 1pt} '$, сохраняя элементы $a_{{11}}^{{\text{'}}}$ и $a_{{22}}^{{\text{'}}}$, которые можно использовать для формирования новой матрицы (${\mathbf{A}} + {\mathbf{A}}{\kern 1pt} '\, \circ {{{\mathbf{E}}}_{1}}$) улучшенной расчетной модели ОУ, предназначенной для синтеза ПР.

Будем проводить синтез робастной системы управления с ПР методом полиномиального модального управления [3–5] при номинальных значениях параметров ОУ путем решения полиномиального уравнения синтеза:

где A(s) – гурвицев полином знаменателя ПФ объекта $H\left( s \right) = {\mathbf{C}}~{{\left( {{\mathbf{I}} - s~{\mathbf{A}}} \right)}^{{ - 1}}}~{\mathbf{B}}$, $D\left( s \right)$ – желаемый характеристический полином (ХП) ПФ замкнутой системы.

Требуется синтезировать робастную САУ, сохраняющую устойчивость и заданные показатели качества при вариациях параметров ОУ и ПР в определенных пределах. Предполагается, что заданный ОУ обладает свойствами управляемости и наблюдаемости, а интервальная матрица A является гурвицевой, что обеспечивает возможность вычисления грамианов.

Будем решать задачу путем повышения степени управляемости и степени наблюдаемости объекта за счет преобразования подобия матриц A, B и C к виду, приближающему структуру объекта соответственно к КФУ и КФН. При этом для определения матриц преобразования координатного базиса объекта используем математический аппарат грамианов управляемости, наблюдаемости и их сингулярных разложений.

2. Улучшение системных свойств объектов управления с помощью грамианов. Рассмотрим возможности преобразования структуры ОУ в направлениях повышения его управляемости и наблюдаемости. Для этого предлагается использовать математический аппарат грамианов управляемости G_c и наблюдаемости G_o [13–16], определяемых выражениями:

где t – время. Для одномерного объекта грамианы представляют собой матрицы размерностью $n \times n$.

С целью количественной оценки системных свойств ОУ применяя процедуры сингулярного разложения, приводящие грамианы к виду

где ${{{\mathbf{\Sigma }}}_{{\text{c}}}} = {\text{diag}}\left\{ {{{\sigma }_{{c1}}},{{\sigma }_{{c2}}}, \ldots ,{{\sigma }_{{cn}}}} \right\}$, ${{{\mathbf{\Sigma }}}_{o}} = {\text{diag}}\left\{ {{{\sigma }_{{o1}}},{{\sigma }_{{o2}}}, \ldots ,{{\sigma }_{{on}}}} \right\}$ – диагональные матрицы, состоящие из выстроенных в порядке убывания сингулярных чисел грамианов управляемости и наблюдаемости; U_c и V_o – матрицы преобразования грамианов к диагональной форме. Относительно малые значения сингулярных чисел являются признаками плохой управляемости или плохой наблюдаемости координат состояния объекта.

В качестве более точной оценки системных свойств ОУ удобно использовать [9, 10] нормы матриц преобразования координат состояния из КФУ и КФН, согласованных с объектом по входу и выходу, в исходный координатный базис:

где u_ij и ${{{v}}_{{ij}}}$ – элементы матриц преобразования координат ${{{\mathbf{P}}}_{U}} = {\mathbf{\bar {U}}}~{{{\mathbf{U}}}^{{ - 1}}}$ и ${{{\mathbf{P}}}_{V}} = {\mathbf{\tilde {V}}}~{{{\mathbf{V}}}^{{ - 1}}}$, находящиеся на пересечении строки i и столбца  j; ${\mathbf{\bar {U}}}$ и ${\mathbf{\tilde {V}}}$ – матрицы управляемости и наблюдаемости соответственно в КФУ и КФН; U и V – матрицы управляемости и наблюдаемости в собственных координатах объекта. По мере приближения объекта к КФУ и КФН соответствующие значения ${\text{||}}{{{\mathbf{P}}}_{U}}{\text{|}}{{{\text{|}}}_{1}}$ и ${\text{||}}{{{\mathbf{P}}}_{V}}{\text{|}}{{{\text{|}}}_{1}}$ стремятся к единице.

Количественной оценкой степени вырожденности ОУ может служить норма матрицы преобразования координат из КФУ в КФН ${\text{||}}{{{\mathbf{P}}}_{{\bar {U}\tilde {U}}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{\mathbf{\bar {U}}}~{{{\mathbf{\tilde {V}}}}^{{ - 1}}}{\text{|}}{{{\text{|}}}_{1}}$ или норма матрицы обратного преобразования ${\text{||}}{{{\mathbf{P}}}_{{\tilde {V}\bar {V}}}}{\text{|}}{{{\text{|}}}_{1}} = {\text{||}}{\mathbf{\tilde {V}}}~{{{\mathbf{\bar {V}}}}^{{ - 1}}}{\text{|}}{{{\text{|}}}_{1}}$, величины которых неограниченно возрастают при сближении нулей и полюсов ПФ объекта.

Помимо проведения системного анализа математический аппарат грамианов позволяет решать и обратные задачи, т.е. формировать математические модели объектов с заданными значениями степеней управляемости и наблюдаемости. Примерами таких задач является получение сбалансированной формы модели ОУ с одинаковыми управляемостью и наблюдаемостью [12, 14, 15], для которой соответствующие грамианы совпадают: ${\mathbf{G}}_{c}^{{''}} = {\mathbf{G}}_{o}^{{''}} = {\text{diag}}\left\{ {{{{{\sigma }}}_{1}},{{{{\sigma }}}_{2}}, \ldots ,{{{{\sigma }}}_{n}}} \right\}$, а также формирование оптимальной структуры наблюдателей состояния [17] с определенным соотношением свойств управляемости и наблюдаемости для повышения их параметрической грубости. Подобный подход, основанный на целенаправленном итерационном изменении сингулярных чисел грамиана управляемости с последующим вычислением соответствующих матриц ${\mathbf{\hat {A}}}$, ${\mathbf{\hat {B}}}$ и ${\mathbf{\hat {C}}}$ улучшенной расчетной модели, был успешно использован в [11] для решения задач синтеза робастных САУ с РС.

Руководствуясь [11], можно дополнить предложенный алгоритм коррекции степени управляемости модели ОУ аналогичным алгоритмом коррекции степени ее наблюдаемости и сформировать на этой основе комплексную итерационную процедуру улучшения системных свойств модели объекта, предназначенной для синтеза ПР.

Сущность процедуры заключается в том, что для исходной матричной модели объекта принудительно увеличивают малые значения сингулярных чисел грамиана управляемости и грамиана наблюдаемости:

Затем определяют матрицы ${\mathbf{\hat {A}}}$, ${\mathbf{\hat {B}}}$, ${\mathbf{\hat {C}}}$, а также ${{{\mathbf{\hat {U}}}}_{c}}$ и ${{{\mathbf{\hat {V}}}}_{o}}$ модели объекта, переведенной в новую систему координат путем преобразования подобия с использованием соотношений:

Руководствуясь аналогиями с [14], а также результатами [11], получаем следующие выражения для определения матриц преобразования T через исходные и новые значения матриц диагонального разложения грамианов управляемости и наблюдаемости:

или

Справедливость этих выражений для матриц T может быть показана их подстановкой в матричные уравнения, соответствующие сингулярным представлениям грамианов управляемости и наблюдаемости в исходной и преобразованной системах координат:

Для определения значений матриц преобразования T, согласно (2.3), (2.4), требуются новые значения матриц ${{{\mathbf{\hat {U}}}}_{c}}$ и ${{{\mathbf{\hat {V}}}}_{o}}$, точные значения которых могут быть получены только после сингулярных разложений грамианов в новой системе координат. В качестве выхода из этой ситуации предлагается организация пошаговой итерационной процедуры, согласно которой изменениями структуры объекта в пределах одного (малого) шага коррекции сингулярных чисел грамианов пренебрегают, полагая ${{{\mathbf{\hat {U}}}}_{c}} = {{{\mathbf{U}}}_{c}}$ и ${{{\mathbf{\hat {V}}}}_{o}} = {{{\mathbf{V}}}_{o}}$, но изменяя значения обеих матриц после завершения преобразования подобия (2.2) и сингулярного разложения (2.1) на следующем шаге расчета.

Предлагаемая процедура коррекции системных свойств объекта реализуется путем изменения его параметров или введения в его структуру дополнительных прямых и обратных связей, формируемых предрегулятором, который описывается соответствующими матрицами:

Новая версия ПР рассчитывается по скорректированной предрегулятором ПФ объекта, определяемой следующим образом

где ${\mathbf{\hat {A}}}{\kern 1pt} ' = {\mathbf{A}} + {\mathbf{A}}{\kern 1pt} '{{{\mathbf{E}}}_{1}}$, ${\mathbf{\hat {B}}}{\kern 1pt} ' = {\mathbf{B}} + {\mathbf{B}}{\kern 1pt} '{{{\mathbf{E}}}_{2}}$, ${\mathbf{\hat {C}}}{\kern 1pt} ' = {\mathbf{C}} + {\mathbf{C}}{\kern 1pt} '{{{\mathbf{E}}}_{3}}$; $\hat {B}\left( s \right)$, $\hat {A}\left( s \right)$ – новые полиномы ПФ скорректированной модели ОУ.

Поскольку в расчете не накладывается ограничение на изменение передаточной функции H(s) и матриц U_c, V_o исходного объекта, то для получения желаемых сингулярных чисел ${{{\mathbf{\hat {\Sigma }}}}_{c}}$ и ${{{\mathbf{\hat {\Sigma }}}}_{o}}$ можно варьировать только часть элементов матриц ${\mathbf{A}}{\kern 1pt} ',$ ${\mathbf{B}}{\kern 1pt} '$ и ${\mathbf{C}}'$, задаваемых соответствующими двоичными матрицами-масками ${{{\mathbf{E}}}_{1}},{{{\mathbf{E}}}_{2}}$ и E₃ путем поэлементного умножения.

С учетом особенностей ОУ следует проанализировать возможность воздействия не на все, а только на одну или две из указанных матриц для минимизации структуры синтезируемого предрегулятора. Разработанная процедура формирует основу для синтеза основного ПР, позволяющего обеспечить существенное улучшение робастных свойств создаваемых САУ.

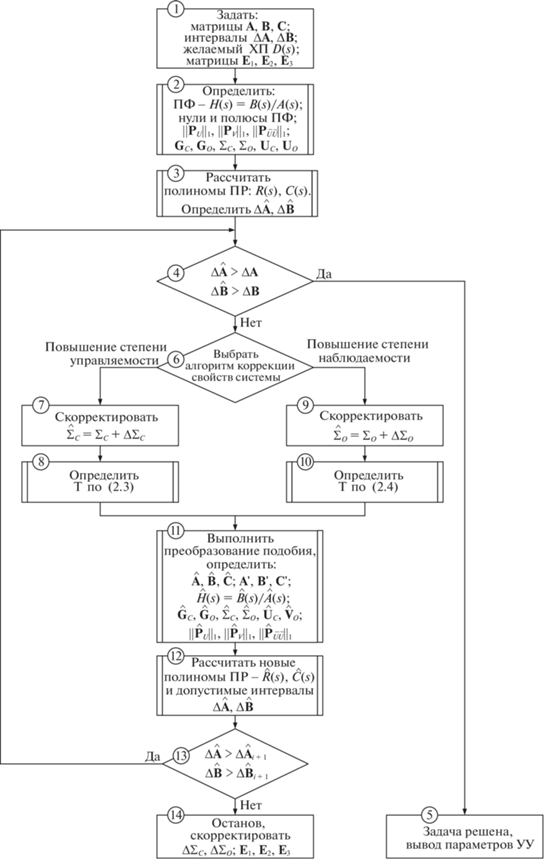
3. Структурно-параметрический синтез робастных систем с ПР. На базе предложенной комплексной процедуры улучшения системных свойств управляемого объекта был разработан и реализован алгоритм автоматизированного синтеза робастных систем управления с динамическими регуляторами, содержащий этапы анализа, преобразования матричной модели объекта и синтеза основного ПР методом полиномиального модального управления, поясняемый блок-схемой на рис. 2.

На начальном этапе (блок 1) задаются матрицы объекта и интервалы их варьирования, формируется желаемый ХП синтезируемой САУ и двоичные матрицы-маски, определяющие допустимые вариации элементов матриц расчетной модели ОУ. Затем (блок 2) определяются передаточная функция “входа-выхода” объекта, ее нули и полюсы; оцениваются степени управляемости, наблюдаемости и вырожденности ОУ, вычисляются грамианы управляемости и наблюдаемости, а также выполняются сингулярные разложения грамианов. Далее (блок 3) осуществляется первая попытка синтеза ПР по исходной модели ОУ, т.е. рассчитываются параметры полиномов регулятора, и методом вычислительных экспериментов определяются матричные интервалы сохранения робастной устойчивости и желаемых показателей качества синтезированной САУ.

На первом этапе основного итерационного цикла (блок 4) проверяется условие достижения требуемых робастных свойств системы. При его выполнении процедура синтеза САУ завершается (блок 5), и задача считается решенной. В противоположном случае инициируется алгоритм коррекции системных свойств объекта.

На этом этапе автоматизированного синтеза САУ (блок 6) разработчик, основываясь на результатах анализа свойств ОУ и предыдущих расчетов, должен задать направление коррекции системных свойств объекта (повышение управляемости или наблюдаемости). При этом в первом случае корректировке подвергаются сингулярные числа грамиана управляемости (блок 7), более подробно описанной в [11], после чего по формуле (2.3) определяется соответствующее численное выражение матрицы преобразования координат (блок 8). Во втором случае аналогичным образом корректируются сингулярные числа грамиана наблюдаемости (блок 9), а нахождение матрицы преобразования подобия (блок 10) осуществляется по формуле (2.4).

На основе полученной любым из методов матрицы координатного преобразования в блоке 11 определяют новые (преобразованные) выражения матриц объекта, его передаточной функции, корректирующих матриц предрегулятора, грамианов управляемости и наблюдаемости, а также элементов их сингулярных разложений. Затем (блок 12) по полученным выражениям полиномов преобразованной ПФ рассчитывают новые выражения полиномов ПР и методом вычислительного эксперимента определяют допустимые матричные интервалы сохранения заданных свойств синтезированной САУ.

В завершение каждого шага основного итерационного цикла (блок 13) осуществляется оценка его успешности и целесообразности последующих итераций или необходимости останова для корректировки условий задачи, прежде всего назначением новых значений ступеней изменений сингулярных чисел или выражений двоичных матричных масок. При этом решение о прекращении расчетов принимается в том случае, если значения матричных интервалов, обусловленных вариациями параметров ОУ, оказываются меньшими их значений, полученных на предыдущем итерационном шаге, и задача робастного синтеза оказывается нерешенной.

Для продолжения расчета осуществляется возврат к началу основного итерационного цикла (блок 4) с последующим повтором расчетных процедур в случае малых значений робастных интервалов или переходу к заключительному этапу (блок 15) при достижении требуемых робастных свойств синтезированной САУ с выводом параметров синтезированного управляющего устройства (УУ).

Следует отметить, что при синтезе систем с ПР, в отличие от САУ с РС, имеются два пути улучшения робастных свойств – через повышение управляемости и наблюдаемости, что расширяет функциональные возможности разработчика. Однако у таких систем, как правило, не все координаты состояния ОУ являются доступными для измерения, что затрудняет коррекцию его системных свойств и требует решения проблемы формирования корректирующих предрегуляторов.

Для иллюстрации разработанного метода синтеза робастных САУ с ПР и определения путей преодоления указанных трудностей рассмотрим конкретные примеры его применения для объектов различной степени сложности, использованных ранее в [11, 18, 19].

Пример. Рассмотрим процедуру синтеза робастной САУ с ПР для двухканального объекта третьего порядка [11], матрицы которого с учетом возможных вариаций параметров имеют следующий вид:

Примем в качестве желаемого ХП полином Ньютона $D\left( s \right) = {{\left( {s + 15.5} \right)}^{3}}$, определяющий требования к быстродействию и качеству переходных процессов синтезируемой САУ при номинальных значениях параметров ОУ. Требуется обеспечить сохранение апериодического характера переходных процессов с изменениями быстродействия не более 10% в заданных интервалах вариаций параметров объекта и 20%-ных вариациях собственных параметров регулятора.

Предположим, что для управления данным ОУ доступны первая и третья координаты состояния и возможно дополнительное воздействие по второму каналу. В этом случае двоичные матричные маски ${{{\mathbf{E}}}_{1}},{{{\mathbf{E}}}_{2}}$ и E₃, определяющие доступные для коррекции элементы матрицы А (матрицы B и C не меняются), задаются как

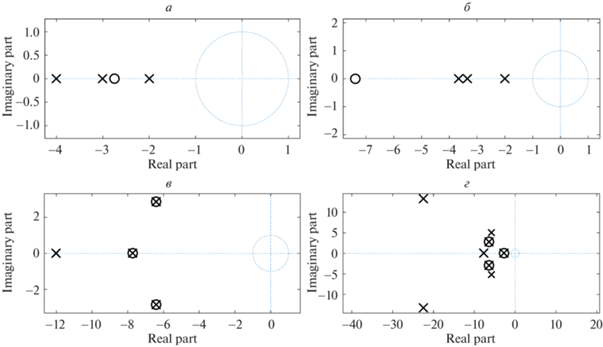
Расчет передаточной функции заданного ОУ приводит к следующим выражениям ее полиномов с соответствующими значениями нуля и полюсов, представленными на рис. 3, а:

Количественные показатели управляемости, наблюдаемости и вырожденности ОУ приобретают следующие числовые значения: ${{\left\| {{{{\mathbf{P}}}_{U}}} \right\|}_{1}} = 31.5,{{\left\| {{{{\mathbf{P}}}_{V}}} \right\|}_{1}} = 33.5,$ ${{\left\| {{{{\mathbf{P}}}_{{\bar {U}\tilde {U}}}}} \right\|}_{1}} = 220.17$, свидетельствуя о низком уровне системных свойств заданного объекта и проблемах достижения робастного управления.

Расчет и последующее сингулярное разложение грамианов дают результаты:

Полученные распределения сингулярных чисел грамианов с многократным отличием их меньших значений также подтверждают тенденцию объекта к вырождению с потерей управляемости и наблюдаемости.

Как следствие, полученные при синтезе выражения полиномов регулятора

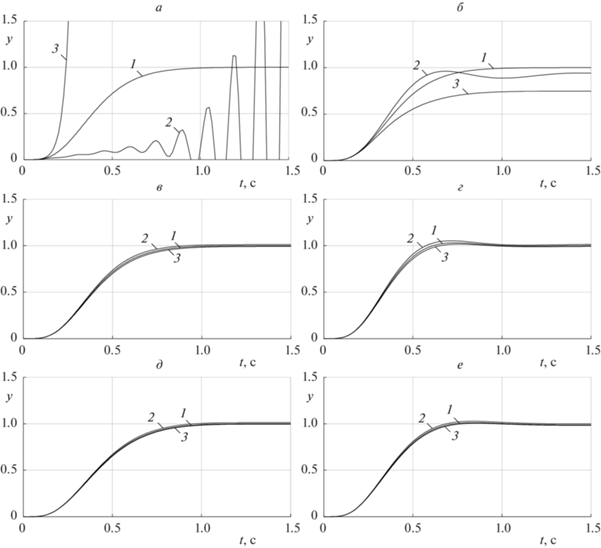
приобретают коэффициенты разного знака, что придает ему неминимально-фазовый (неустойчивый) характер и, как свидетельствуют переходные характеристики на рис. 4, а, не позволяет обеспечить желаемые робастные свойства системы при заданных вариациях параметров.

Итерационная коррекция минимального сингулярного числа грамиана наблюдаемости по изложенной методике с шагом ${{\Delta }}{{{\mathbf{\Sigma }}}_{o}} = 1.34 \times {{10}^{{ - 5}}}$ позволяет в определенной мере улучшить системные свойства ОУ и робастные свойства полученной САУ за счет формирования нового распределения сингулярных чисел обоих грамианов соответствующим предрегулятором, изменения ПФ объекта и синтеза новой версии ПР:

Однако, как показывают переходные характеристики на рис. 4, б, поставленную задачу синтеза робастной САУ с ПР нельзя признать решенной.

Дополнительная коррекция минимального сингулярного числа грамиана управляемости с шагом ${{\Delta }}{{{\mathbf{\Sigma }}}_{c}} = 1.25 \times {{10}^{{ - 4}}}$ позволяет существенно улучшить системные свойства ОУ и окончательно сформировать управляющее устройство, позволяющее обеспечить требуемое качество САУ:

Новые распределения нуля и полюсов скорректированного объекта и синтезированной САУ представлены соответственно на рис. 3, б, в. Приведенные на рис. 4, в переходные характеристики синтезированной системы при номинальных и варьированных значениях параметров ОУ иллюстрируют полное решение поставленной задачи. Сохранение достигнутого результата при вариациях собственных параметров регулятора в пределах ±20%, превышающих возможные погрешности как при его цифровой, так и при аналоговой реализации, подтверждают соответствующие переходные характеристики на рис. 4, в.

Таким образом, возможность коррекции как управляемости, так и наблюдаемости ОУ позволяет в данном примере достичь желаемого уровня робастности САУ, даже при отсутствии возможности контроля одной из трех координат состояния.

Аналогичный пример успешного синтеза более сложной робастной системы полиномиального управления натяжением упругого длинномерного материала в составе технологического агрегата приведен в Приложении. Однако во всех случаях остается открытым вопрос о том, как обеспечить необходимое улучшение системных свойств ОУ в наиболее типичном для САУ с ПР “входа-выхода” в случае контроля только одной – выходной (регулируемой) координаты объекта.

4. Синтез робастных САУ с ПР по улучшенной расчетной модели объекта. Попытки улучшения робастных свойств САУ с динамическими регуляторами, использующими ограниченный состав переменных состояния ОУ или только одну – выходную координату без применения полноразмерных наблюдателей состояния, которые направили бы разработчика в другой класс систем с новой проблематикой, привели к довольно неожиданному результату. Была выявлена возможность исключения из состава робастной САУ, синтезированной разработанным методом, отдельных связей, формируемых предрегулятором, или полного отключения последнего с незначительным изменением достигнутого результата, т.е. сохранением требуемых показателей качества в заданных интервалах робастности.

В качестве иллюстрации, в дополнение к примеру 1, на рис. 3, г приведено новое распределение полюсов синтезированной САУ, формируемое после отключения предрегулятора, а на рис. 4, д, е – соответствующие переходные характеристики системы в заданных интервалах изменения параметров ОУ и ПР. Важно отметить, что нуль системы возвращается при этом в исходное состояние, определяемое нулем объекта.

Сравнительный анализ полученных результатов показывает, что система, синтезированная по улучшенной в отношении управляемости, наблюдаемости и вырожденности расчетной модели объекта, в значительной мере сохраняет достигнутые показатели качества даже без использования в ее реальной структуре того предрегулятора, который обеспечил улучшение системных свойств модели объекта при синтезе САУ.

Для оценки степени общности выявленного эффекта были проведены аналогичные вычислительные экспериментами с объектом и системами из Приложения. Результаты, полученные при формировании управлений объектом более высокого порядка с более сложным распределением нулей и полюсов, представленные на рис. 5, также подтверждают наличие указанной закономерности.

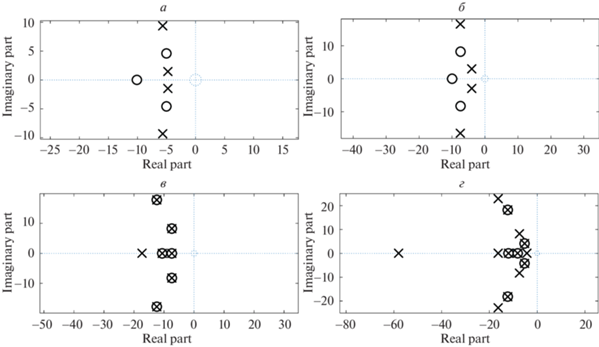
Кроме этого, были проведены аналогичные исследования в отношении синтезированных ранее [11, 17, 18] робастных систем с безынерционными регуляторами состояния, которые также показали возможность в значительной степени сохранять достигнутые результаты при исключении корректирующих модели ОУ предрегуляторов из реальных систем управления.

Однако кажущийся парадоксальным результат имеет тем не менее вполне логичные объяснения. Действительно, при синтезе регуляторов робастных систем расчет обычно ведется по исходной модели ОУ с номинальными значениями параметров. Но при успешном решении задачи система оказывается способной обеспечить требуемые показатели качества при значительных параметрических вариациях реального ОУ, и это не считается парадоксальным. В разработанном методе синтез основного регулятора осуществляется по модели ОУ с предрегулятором, т.е. по улучшенной расчетной модели объекта. В таком случае достижение робастных свойств полученной САУ также допускает значительные изменения расчетной модели, в том числе частичное или полное исключение из нее корректирующего предрегулятора при переходе к управлению реальным объектом.

Выявленной закономерности можно дать и соответствующее “энергетическое” объяснение. При синтезе робастных САУ улучшение системных свойств ОУ достигается коррекцией меньших сингулярных чисел грамианов управляемости и наблюдаемости, т.е. относительно малыми энергетическими воздействиями на объект, формируемыми предрегуляторами. Однако этого оказывается вполне достаточно для сохранения робастных свойств системы при малых энергетических изменениях в объекте относительно расчетной модели, вызываемых отключением корректирующего предрегулятора.

Следует также отметить, что выявленные закономерности вполне согласуются с результатами более ранних исследований в области робастного модального управления. Так при формировании оптимального управления мехатронными системами по обобщенному критерию точности, быстродействия, робастности и энергетических затрат на управление [19] было показано, что близкие переходные характеристики САУ могут наблюдаться при существенно различных параметрах регулятора и показателей робастности. В [20] значительное улучшение робастных свойств мехатронных систем как с безынерционными РС, так и с ПР достигалось принудительными изменениями отдельных параметров регуляторов, синтезированных по номинальным параметрам объекта, и сопровождалось малыми вариациями переходных характеристик САУ. А в исследованиях [21], посвященных выявлению взаимосвязи степени вырожденности ОУ с робастными свойствами САУ, было установлено, что при повышении различий близких нулей и полюсов (размеров диполей) всего лишь до 10–15% вырожденность объектов резко снижается, что существенно облегчает достижение заданных робастных свойств синтезируемых систем малыми структурно-параметрическими воздействиями на исходный ОУ.

Синтез САУ по улучшенной модели объекта можно рассматривать как одну из версий более общего метода М.М. Лаврентьева, разработанного в [22] для решения некорректных задач путем замены исходного уравнения близким ему корректным уравнением и использованного позднее, например в [23, 24].

Таким образом, полученные результаты работы согласуются с логикой и свойствами робастного управления и являются вполне закономерными. Более того, они предоставляют разработчику САУ новые творческие возможности улучшения их робастных свойств за счет использования виртуальных каналов управления и связей, т.е. таких корректировок матриц A, B и C, которые могут присутствовать только в расчетной модели объекта для улучшения ее системных свойств, но не применяться в реальной системе.

Так, в расчетном примере может быть сделано допущение об использовании в предрегуляторе всех координат состояния объекта. Применение разработанного метода позволяет получить следующие результаты расчета:

Соответствующие переходные характеристики синтезированной САУ, полученные как при наличии, так и при отсутствии в ее структуре корректирующего предрегулятора, оказываются аналогичными приведенным на рис. 4, в, г , что также свидетельствует об успешном решении поставленной задачи робастного управления.

В результате анализа разработанного метода синтеза управления по улучшенной модели объекта, условно названного методом СУМО, неизбежно возникает вопрос о целесообразности его наполнения итерационной грамианной коррекцией модели ОУ с помощью достаточно сложных матричных вычислений.

Казалось бы, для успешного синтеза эффективного ПР можно использовать метод модального управления, задав желаемое распределение полюсов, которое формируется в системе после отключения предрегулятора (рис. 3, г и 5, г). Однако при этом остается неясным, как отыскать это распределение и с какими значениями нулей его применять при синтезе регулятора, ведь информация о них оказывается утраченной после отключения предрегулятора.

Безусловно, можно организовать процедуру оптимального поиска такого распределения нулей и полюсов, но это потребует разрешения соответствующей проблематики: формирование обобщенного критерия оптимальности с определенной схемой компромиссов между частными критериями, поиск эффективного метода оптимизации с хорошей сходимостью и возможностью надежного отыскания глобального экстремума и др. Попытки обойти эти трудности применением регулярного сканирования с полным перебором возможных значений как нулей, так и полюсов в довольно широкой области действительных и комплексных чисел с малым значением шага потребуют больших вычислительных затрат при повышении порядка ОУ. Кроме того, в этом случае будут утрачены потенциальные возможности улучшения качества управления редуцированным предрегулятором с использованием доступных координат реального объекта.

Попытки заменить поиск желаемых нулей и полюсов непосредственным поиском соответствующих параметров ПР порождают аналогичные проблемы и могут приводить к определенным потерям качества управления.

В то же время с помощью разработанного грамианного подхода, дополненного возможностями метода СУМО, можно осуществлять целенаправленное улучшение системных свойств объекта с контролем степени управляемости, наблюдаемости и вырожденности на каждом этапе расчета и обеспечивать более оперативное решение задач робастного управления с заданными показателями качества. Применение разработанного программного обеспечения, реализующего автоматизацию расчетных процедур с использованием стандартных матричных библиотек, а также наглядное представление результатов позволяют выполнять структурно-параметрический синтез робастных САУ за несколько секунд машинного времени на обычном персональном компьютере средней вычислительной мощности.

Безусловно, для успешного решения задачи синтеза робастной САУ разработанным методом в расчетной модели ОУ должны содержаться потенциальные возможности необходимого повышения степени управляемости и наблюдаемости, которые выявляются и эффективно используются в ходе выполняемых матрично-грамианных и полиномиальных расчетов.

Заключение. Успешное решение задачи структурно-параметрического синтеза робастных систем управления с полиномиальными регуляторами, способных обеспечивать и сохранять желаемые показатели качества в заданных пределах изменения параметров объекта и регулятора, может быть достигнуто разработанным методом путем предварительной итерационной коррекции сингулярных чисел грамианов управляемости и наблюдаемости, формирования соответствующего предрегулятора, преобразующего структуру и параметры расчетной модели объекта в направлении улучшения системных свойств, синтеза основного регулятора по улучшенной модели ОУ и редуцирования корректирующего предрегулятора исходя из имеющихся возможностей управления реальным объектом.