1. На главную
  2. Электронные версии
  3. Теплоэнергетика
  4. № 9, 2022

Теплоэнергетика, 2022, № 9, стр. 78-88

Современные методы численного моделирования радиационного теплопереноса в селективных газах (обзор)

В. А. Кузнецов *

Белгородский государственный технологический университет им. В.Г. Шухова
308012 Белгород, ул. Костюкова, д. 46, Россия

* E-mail: kousnezow@mail.ru

Поступила в редакцию 21.11.2021
После доработки 20.12.2021
Принята к публикации 26.01.2022

Полный текст (PDF)

Аннотация

Радиационный теплоперенос в газообразной среде печей и топок представляет собой важнейший теплообменный процесс, от которого зависит эффективность работы промышленных установок. Это объясняет большой интерес инженеров-теплотехников к современным методам численного моделирования радиационного переноса. Теплоперенос в высокотемпературных газах математически описывается дифференциальным уравнением радиационного переноса совместно с транспортными уравнениями тепловой конвекции. Основная проблема состоит в том, что трехатомные газы, такие как водяной пар и углекислый газ, излучают и поглощают радиационную энергию селективно, вследствие чего их коэффициенты поглощения становятся переменными в пространственных координатах. Благодаря достижениям последних десятилетий в инфракрасной спектроскопии были созданы благоприятные условия для разработки хорошо обоснованных моделей, позволяющих находить коэффициенты поглощения важнейших трехатомных газов. Полинейный расчет радиационного переноса в миллионе спектральных линий уступил место модели узкой полосы спектра с коррелированным коэффициентом поглощения и затем глобальным полноспектровым моделям. Наряду с моделями коэффициента поглощения совершенствуются методы численного решения дифференциального уравнения радиационного переноса. Как результат, в настоящее время более десятка различных моделей и методов могут применяться для расчета теплообмена излучением в промышленных установках. Предлагаемый обзор частично устраняет недостаток публикаций, в которых сравниваются разные подходы к численному исследованию радиационных проблем. В нем прослеживается, вплоть до нашего времени, более чем двадцатилетнее последовательное развитие математических моделей радиационного теплопереноса в селективных газах. Основные методы итерационного решения дифференциального уравнения радиационного переноса также включены в обзор. В то же время, чтобы не усложнять анализ моделей, в обзоре не отражена избыточная информация, относящаяся к граничным условиям и к рассеиванию лучей. Для обеспечения однозначности используемых понятий обзор предваряется короткой теоретической справкой.

Ключевые слова: тепловое излучение, селективные газы, селективное поглощение излучения, радиационный теплоперенос, численное моделирование

Радиационный теплообмен часто используется в промышленных установках, поэтому инженерам нужны простые и достаточно точные математические модели для численного исследования высокотемпературных энергетических и технологических процессов.

Первоначально методы расчета радиационного теплопереноса были основаны на традиционных теоретических и экспериментальных знаниях [1, 2]. Быстрое развитие вычислительной техники позволило применять численное моделирование для виртуального воспроизведения тепловых процессов. Новые модели и методы рассмотрены в нескольких обзорных статьях, например [3, 4].

Основные проблемы моделирования радиационного переноса возникают из-за селективного излучения и поглощения энергии трехатомными газами, вследствие чего спектральный состав лучей изменяется по их длине. Некоторые проблемы возникают также из-за необходимости исследовать одновременно огромное количество лучей, проходящих во всех направлениях в объеме селективной среды.

Для преодоления этих трудностей были предложены хорошо обоснованные усложненные модели. Хотя более простые численные подходы имеют обычно меньшую точность, тем не менее они также находят применение в вычислительном исследовании высокотемпературных процессов. Кроме того, такие численные подходы могут легче вписываться в универсальные алгоритмы моделирования теплопереноса одновременно излучением и конвекцией, что упрощает математические модели и уменьшает объем компьютерных вычислений.

Главная цель данной статьи состоит в том, чтобы помочь инженерам ориентироваться в разнообразии численных методов, применяемых для моделирования теплопередачи излучением. Поэтому в статье только кратко рассматриваются наиболее представительные модели и методы без их углубленного анализа. Способы постановки граничных условий, необходимых для однозначности вычислительных результатов, практически исключены из обзора. Рассмотрены только излучающие и поглощающие газы, не содержащие частиц, способных рассеивать лучи. Изложены также некоторые теоретические понятия с целью исключить расхождения в их интерпретации. (Опытные специалисты могут пропустить этот раздел, рассматривая его как справочный.)

ИСПОЛЬЗУЕМЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Для сохранения адекватности обзора в нем применены те же обозначения, что и в большинстве рассмотренных источников. Коэффициент поглощения среды обозначается, как правило, символом k, напрямую входящим в англоязычные названия многих статей и математических моделей.

Как известно, абсолютно черное тело испускает тепловое излучение, зависящее в его полном спектре только от температуры:

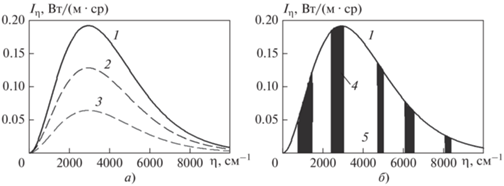
${{I}_{b}} = \left( {{\sigma \mathord{\left/ {\vphantom {\sigma \pi }} \right. \kern-0em} \pi }} \right){{T}^{4}},$
где Ib – интенсивность излучения в полном спектре абсолютно черного тела, Вт/(м2 ∙ ср); σ – постоянная Стефана‒Больцмана, Вт/(м2 ∙ К4); T – термодинамическая температура, К.

Как и другие радиационные свойства, интенсивность излучения имеет спектральную зависимость от волнового числа η, которое представляет собой обратную функцию длины электромагнитной волны. Спектральная интенсивность Ibη излучения абсолютно черного тела, изменяющаяся в соответствии с функцией Планка, представлена кривой 1 на рисунке. Такой же спектр характерен для равновесного излучения в замкнутой системе нечерных тел, находящихся при одинаковой температуре. Кривые 2 и 3 на рисунке a показывают зависимости спектральной интенсивности серого излучения Iη от волнового числа η: они изменяются пропорционально функции Планка (кривая 1), образуя два идеализированных серых спектра с разными уровнями собственного излучения среды.

Трехатомные газы, такие как углекислый газ CO2 или водяной пар H2O, испускают и поглощают радиационную энергию селективно в миллионах спектральных линий, находящихся, в основном, в широких вибрационно-вращательных полосах. Широкие полосы разделены в спектре “окнами”, где излучение почти не поглощается. При увеличении оптической толщины газового объема спектральная интенсивность Iη в широких полосах спектра возрастает, приближаясь к значениям Ibη, в то время как излучением в “окнах” спектра можно пренебречь. Такой идеализированный антисерый спектр показан на рисунке б. Он состоит из абсолютно черных полос поглощения, разделенных полностью прозрачными “окнами”.

В нерассеивающей газообразной среде изменение спектральной интенсивности Iη вдоль ординаты s, совпадающей с направлением луча, определяется спектральным дифференциальным уравнением [3]:

$\frac{{\partial {{I}_{{\eta s}}}}}{{\partial s}} = {{k}_{\eta }}\left( {{{I}_{{b\eta }}} - {{I}_{{\eta s}}}} \right),$
где Iηs – спектральная интенсивность излучения среды вдоль ординаты s, Вт/(м ∙ ср); kη – спектральный коэффициент поглощения, м‒1.

Интегрирование этого спектрального уравнения по всему спектру приводит к дифференциальному уравнению радиационного переноса, которое лежит в основе различных математических моделей. Для селективно излучающего и поглощающего газа оно может быть записано следующим образом:

(1)
$\frac{{\partial {{I}_{s}}}}{{\partial s}} = {{k}_{b}}{{I}_{b}} - {{k}_{s}}{{I}_{s}},$
где Is – интенсивность излучения, распространяющегося вдоль луча, Вт/(м2 ср); ${{k}_{b}} = \frac{1}{{{{I}_{b}}}}\int_0^\infty {{{k}_{\eta }}} {{I}_{{b\eta }}}{\text{d}}\eta $ ‒ планковский коэффициент поглощения, средний по спектру, м‒1, зависящий только от радиационных свойств газа и его температуры; ${{k}_{s}} = \frac{1}{{{{I}_{s}}}}\int_0^\infty {{{k}_{\eta }}} {{I}_{{\eta s}}}{\text{d}}\eta $ – локальный коэффициент поглощения, м‒1, изменяющийся вдоль луча.

Особенность локального коэффициента поглощения ks состоит в том, что он зависит от спектрального распределения интенсивности падающего излучения Iηs, что сильно затрудняет его определение.

Уравнение (1) может быть проинтегрировано по сферическому телесному углу ω = 4π. Результат представляет собой уравнение сохранения радиационной энергии, которое при известной дивергенции вектора потока излучения можно было бы рассматривать как вторую форму уравнения радиационного переноса:

(2)
${\text{div}}\,{{{\mathbf{q}}}_{{rad}}} = 4\pi {{k}_{b}}{{I}_{b}} - {{k}_{\omega }}{{G}_{\omega }},$
где ${{{\mathbf{q}}}_{{rad}}}$ ‒ вектор потока излучения, Вт/м2; ${{G}_{\omega }} = \int_{4\pi } {{{I}_{s}}{\text{d}}} \omega $ ‒ сферическое падающее излучение, Вт/м2; ${{k}_{\omega }} = \frac{1}{{{{G}_{\omega }}}}\int_{4\pi } {{{k}_{s}}} {{I}_{s}}{\text{d}}\omega $ ‒ локальный коэффициент поглощения, м‒1, средний по сферическому телесному углу.

Дивергенция вектора потока излучения, взятая с отрицательным знаком, рассматривается как объемный радиационный источник тепла:

(3)
${{S}_{{rad}}} \equiv - {\text{div}}{{{\mathbf{q}}}_{{rad}}} = {{k}_{\omega }}{{G}_{\omega }} - 4\pi {{k}_{b}}{{I}_{b}}.$

Радиационный источник тепла Srad, Вт/м3, необходим для вычисления распределения температуры газа в расчетной области с помощью дифференциального уравнения конвективного теплопереноса, пример которого записан далее:

$\frac{{\partial \rho h}}{{\partial \tau }} + \sum\limits_{i = 1}^3 {\frac{{\partial \rho {{u}_{i}}h}}{{\partial {{x}_{i}}}}} - \sum\limits_{i = 1}^3 {\frac{\partial }{{\partial {{x}_{i}}}}\left( {{{\lambda }_{{eff}}}\frac{{\partial T}}{{\partial {{x}_{i}}}}} \right)} = {{Q}_{V}} + {{S}_{{rad}}},$
где τ – время, с; xi – пространственные координаты, м; h – энтальпия газа, Дж/кг; ui – компоненты скорости, м/с; ρ – плотность газа, кг/м3; λeff – эффективная теплопроводность газа, Вт/(м ∙ К); QV – объемное тепловыделение при горении, Вт/м3.

Это уравнение дает представление о вкладе радиационного источника тепла Srad в алгоритм расчета температурного поля. Начальные и граничные условия к нему формулируются при численном решении конкретной задачи.

МЕТОДЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ПОГЛОЩЕНИЯ СЕЛЕКТИВНЫХ ГАЗОВ

Экспериментальное определение коэффициентов поглощения трехатомных газов, выполненное в 30-х годах прошлого столетия, было обобщено в [1]. Исследовалась способность изотермического газа поглощать энергию из узкого пучка лучей, испускаемого абсолютно черным телом той же температуры. Первый член в правой части уравнения (1), примененного к этому пучку лучей, равняется нулю, а само уравнение при таком упрощении может быть сведено к формуле поглощательной способности Ā изотермического газа:

(4)
$\bar {A}\left( l \right) \equiv \frac{{{{I}_{{abs}}}}}{{{{I}_{b}}}} = 1 - {\text{exp}}\left( { - kl} \right),$
где Iabs – поглощенная часть интенсивности излучения на длине пути l пучка лучей; k – изотермический коэффициент поглощения, средний на этой длине.

Уравнение (4) может использоваться также для определения излучательной способности газа. Когда изотермический газ испускает столько же энергии (Iemi), сколько поглощает (Iabs), его излучательная способность Ē(l) равняется его поглощательной способности Ā(l), т.е.

(5)
$\bar {E}\left( l \right) \equiv \frac{{{{I}_{{emi}}}}}{{{{I}_{b}}}} = 1 - {\text{exp}}\left( { - kl} \right).$

Формулы (4) и (5) предназначались для практически замкнутых объемов изотермического однородного газа, в которых эффективная длина луча leff была определена как радиус эквивалентной полусферы [1]. Тем не менее, средний изотермический коэффициент k мало подходит для применения в уравнениях (1) или (2), в которых локальные коэффициенты поглощения ks и kω зависят от радиационных свойств неизотермических газов и спектрального состава падающего излучения.

В настоящее время, когда спектральные коэффициенты поглощения трехатомных газов могут быть получены из спектроскопических данных высокого разрешения [5], решение уравнения радиационного переноса полинейным методом LBL (line-by-line) дает наиболее точные результаты. Но этот численный метод, примененный приблизительно к миллиону спектральных линий, является столь трудоемким, что его результаты используются только в качестве эталона в простейших радиационных задачах. На практике инженеры обращаются к приближенным значениям коэффициентов поглощения.

Коэффициенты поглощения в узких полосах спектра

Когда стало доступно довольно большое количество результатов спектроскопических исследований, были предложены и реализованы модели узкой полосы спектра. В статистической узкополосной модели SNB (statistical narrowband) [6] полагается, что функция Планка Ibη может рассматриваться как постоянная величина Ibi в малых спектральных интервалах Δηi. Тогда для каждой i-й узкой полосы спектра может быть определен “сглаженный” планковский коэффициент поглощения kbi, а также вычислен средний коэффициент поглощения ki. Необходимые для этого спектральные параметры трехатомных газов получены на основе спектроскопических данных высокого разрешения [7].

Усреднение узкополосных коэффициентов поглощения kbi и ki по спектру изотермического газа приводит к локальному планковскому коэффициенту поглощения kb для уравнения (1) и к среднему изотермическому коэффициенту поглощения k для уравнений (4) и (5):

(6)
${{k}_{b}}\left( T \right) = \frac{1}{{{{I}_{b}}}}\sum\limits_{i = 1}^n {{{k}_{{bi}}}} {{I}_{{bi}}};\,\,\,\,k\left( {T,l} \right) = \frac{1}{{{{I}_{b}}}}\sum\limits_{i = 1}^n {{{k}_{i}}{{I}_{{bi}}}} ,$
где Ibi – значение функции Планка в i-й узкой полосе; n – общее число узких полос; T – температура газа; l – длина луча.

Таким образом, в модели SNB используются изотермические коэффициенты поглощения ki, средние по длине лучей, что ограничивает способы решения уравнения радиационного переноса. Для преодоления этого недостатка была развита более совершенная узкополосная модель c коррелированными коэффициентами поглощения SNBCK (statistical narrowband correlated-k), в полосах которой применен алгоритм расчета локальных коэффициентов поглощения ksi [8].

Сравнительные тестовые расчеты для высокотемпературных смесей CO2 и H2O показали, что результаты, полученные с помощью модели SNBCK, находятся в хорошем соответствии с эталонными результатами модели LBL [9]. Несмотря на это, были разработаны менее точные широкополосные модели в связи с тем, что узкополосный подход, требующий нескольких сот решений спектрального уравнения радиационного переноса, является вычислительно затратным. Затем было обосновано несколько глобальных моделей повышенной точности.

Коэффициенты поглощения в полном спектре

Одной из первых была предложена модель SLW с основанной на спектральных линиях взвешенной суммой серых газов (spectral-line-based weighted sum of gray gases), коэффициенты поглощения и веса которой были найдены по спектроскопическим базам данных высокого разрешения [10]. Чтобы метод SLW мог быть лучше согласован с пространственными изменениями температуры, несколько групп “горячих” и “холодных” спектральных линий с различными минимальными энергетическими уровнями были выделены в модели с функцией распределения поглощения ADF (absorption distribution function) [11].

Во всех глобальных моделях выполняется операция k-распределения (k-distribution) для предотвращения повторного вычисления одинаковых значений спектрального коэффициента поглощения в линиях спектра. С этой целью используются кумулятивные функции распределения [12]. В результате перестроенный спектральный коэффициент поглощения kη монотонно увеличивается в функциональном пространстве. Когда кумулятивные частоты и соответствующие им веса функции Планка становятся известными, спектральные коэффициенты поглощения могут быть проинтегрированы численно и усреднены в полном спектре.

Модель k-распределения в полном спектре FSK (full spectrum k-distribution) [13] и ее разновидности содержат в себе лучшие достижения узкополосных и глобальных подходов. Они стали самым успешным инструментом для численного моделирования радиационного теплопереноса. Модель FSK дает точные результаты для изотермического однородного газа, когда справочный коэффициент поглощения, оцененный единожды в эталонных условиях, может быть применен ко всей излучающей среде. Для умеренных изменений температуры и концентрационного состава среды были предложены модели с коррелированными FSCK (correlated-k) и масштабированными FSSK (scaled-k) коэффициентами поглощения [4]. Новые коэффициенты поглощения определяются путем корректировки справочного коэффициента в соответствии с локальным состоянием неоднородного неизотермического газа.

Полноспектровая FSCK-модель и несколько широкополосных моделей сравнивались между собой при вычислении радиационного переноса в виртуальной трехмерной печи [14]. Эталоном служила узкополосная модель SNBCK. Модель k‑распределения в полном спектре с коррелированным коэффициентом поглощения FSCK продемонстрировала замечательную точность, предсказав значения радиационного источника тепла и результирующего потока излучения на стенах со средней относительной погрешностью менее 2%. Погрешность тестируемых широкополосных моделей составляла чаще всего от 10 до 30%.

Хотя и достигнута высокая точность результатов [15], глобальные модели продолжают развиваться, в основном путем объединения разных известных методов. Например, модель полного спектра FSCK была объединена с методом поверхностного отклика RSM (response surface method), основанным на применении радиальных базисных функций. Вычислительное время комбинированной модели FSCK-RSM оказалось не больше половины времени, затрачиваемого при использовании собственно модели FSCK [16].

Основной недостаток глобальных моделей заключается в чрезмерной сложности нахождения локального коэффициента поглощения. Как правило, эти модели требуют специальных знаний в области газовых спектров и нуждаются в справочных таблицах или вспомогательных базах данных [17]. Неудивительно, что сегодня более простые математические модели все еще находят применение в инженерной практике.

Коэффициенты поглощения в неполном инфракрасном спектре

Следует принимать во внимание, что радиационная энергия лучей не поглощается полностью в ограниченных газовых объемах. Способы определения коэффициентов поглощения в неизотермических не однородных газовых смесях становятся проще, если непоглощенное газами излучение абсолютно черного тела частично или полностью исключается из расчета. В этом случае идеализированные серые или антисерые спектры (см. рисунок) могут найти применение.

Модель взвешенной суммы серых газов WSGG (weighted sum of gray gases). Прямая замена переменных коэффициентов поглощения их средним значением приводит к недопустимым неточностям. Намного более точные результаты могут быть достигнуты с помощью модели взвешенной суммы серых газов. Ее методы предусматривают деление всего спектра на несколько участков, которые условно ассоциируются с фиктивными серыми газами. Один из этих участков должен быть полностью прозрачным для теплового излучения [1]. Коэффициент поглощения κj каждого j-го фиктивного серого газа постоянен как по волновым числам, так и по длине лучей. Его значения получены по спектральным данным высокого разрешения трехатомных газов.

В этом методе излучательная способность газового слоя (5) определяется как сумма ее парциальных значений, найденных для каждого фиктивного газа, т.е. условного серого газа, излучающего в выделенной ему части спектра. Часто излучательная способность состоит из пяти слагаемых [18]:

$\bar {E}\left( l \right) = \sum\limits_{j = 0}^4 {{{a}_{j}}\left[ {1 - {\text{exp}}\left( { - {{\kappa }_{j}}l} \right)} \right]} ,$
где ${{a}_{j}} = \sum\nolimits_{n = 0}^N {{{b}_{{j,n}}}{{T}^{4}}} $ – весовой фактор, который предложено находить с помощью его полиномиальной зависимости от температуры T; bj,n – полиномиальные коэффициенты.

Весовой коэффициент для прозрачной части спектра при κ0 = 0 определяют так, чтобы обеспечить выполнение закона сохранения энергии:

${{a}_{0}} = 1 - \sum\limits_{j = 1}^4 {{{a}_{j}}} .$

Уравнение радиационного переноса (1) должно быть записано и решено отдельно для каждого фиктивного газа:

$\frac{{\partial {{I}_{j}}}}{{\partial s}} = {{\kappa }_{j}}\left( {{{a}_{j}}{{I}_{b}} - {{I}_{j}}} \right).$

Радиационный источник тепла (3) получает в модели WSGG следующую форму:

${{S}_{{rad}}} = \int\limits_{4\pi } {\sum\limits_{j = 0}^4 {{{\kappa }_{j}}\left( {{{I}_{j}} - {{a}_{j}}{{I}_{b}}} \right)} } \,{\text{d}}\omega {\kern 1pt} {\kern 1pt} .$

Согласование WSGG c базами спектроскопических данных обычно применялось к фиксированным соотношениям молярных концентраций углекислого газа и водяного пара в газовых смесях. В последнее время такое ограничение было преодолено разработкой процедуры суперпозиции переменных концентраций излучающих газов [19].

Сравнение модели WSGG и эталонного метода LBL показало относительно хорошее совпадение значений рассчитанного радиационного теплопереноса в неизотермической неоднородной газовой смеси в виртуальной цилиндрической печи [20]. Средняя относительная погрешность вычисления радиационного источника тепла в модели WSGG с постоянным соотношением концентраций углекислого газа и водяного пара составила менее 2%. Максимальная погрешность повысилась до 8.5% вблизи центра печи. Модель WSGG с переменным отношением концентраций, работавшая в 6 раз медленнее, имела максимальную погрешность 6.6%.

Модель эквивалентного антисерого спектра. Бóльшая часть излучения проходит через объем селективных газов без поглощения. Непоглощенная радиационная энергия не подчиняется уравнению переноса (1) и поэтому может быть исключена из него. Оставшаяся энергия лучей, распределившаяся по отдельным частям спектра, составляет полностью поглощаемую часть эквивалентного антисерого спектра [21].

Интегрирование по волновым числам позволяет объединить эти спектральные части в единую полосу поглощения, поглощательная способность которой Āabs соответствует уравнению (4):

(7)
${{\bar {A}}_{{abs}}}\left( l \right) \equiv \frac{{{{I}_{{abs}}}}}{{{{I}_{b}}}} = \frac{1}{{{{I}_{b}}}}\int\limits_0^\infty {{{{\bar {A}}}_{\eta }}} {{I}_{{b\eta }}}{\text{d}}\eta = 1 - {\text{exp}}\left( { - kl} \right),$
где Iabs – поглощенная часть интенсивности излучения абсолютно черного тела; Āη – спектральная поглощательная способность на длине пучка лучей l.

Таким образом, каждому спектру изотермического селективного газа можно поставить в соответствие эквивалентный антисерый аналог. Равенство поглощательных способностей газа Ā(l) из уравнения (4) и Āabs(l) из уравнения (7) рассматривается как условие спектральной эквивалентности селективного газа и некоторой гипотетической антисерой среды. Следует принимать во внимание, что ширина полосы поглощения Δηabs в антисером спектре газа равняется его поглощательной способности Āabs. В соответствии с уравнением (5), излучательная способность Ēabs изотермического газа в полосе поглощения эквивалентного антисерого спектра равняется поглощательной способности Āabs этой полосы поглощения.

Суть метода эквивалентного антисерого спектра сводится к следующим утверждениям. Уравнение (1) радиационного переноса для эквивалентного антисерого спектра неизотермического неоднородного газа может быть записано следующим образом:

(8)
$\frac{{\partial \Delta {{I}_{s}}}}{{\partial s}} = {{k}_{b}}{{I}_{b}} - {{\kappa }_{s}}\Delta {{I}_{s}},$
где ΔIs – интенсивность излучения в антисерой полосе поглощения; κs – локальный коэффициент поглощения в этой полосе.

Интегрирование уравнения (8) по сферическому телесному углу ω = 4π приводит к соответствующему дифференциальному уравнению сохранения радиационной энергии

(9)
${\text{div}}\,{{{\mathbf{q}}}_{{rad}}} = 4\pi {{k}_{b}}{{I}_{b}} - {{\kappa }_{\omega }}\Delta {{G}_{\omega }},$
где $\Delta {{G}_{\omega }} = \int_{4\pi } {\Delta {{I}_{s}}{\text{d}}} \omega $ ‒ сферическое падающее излучение в полосе поглощения эквивалентного антисерого спектра; κω – локальный коэффициент поглощения, средний по сферическому телесному углу.

При равновесном излучении левая часть уравнения (8) равняется нулю и коэффициент κs превращается в локально-равновесный коэффициент поглощения κb в антисером спектре. Тогда с помощью уравнения (5), примененного к излучательной способности антисерого спектра, этот коэффициент поглощения определится следующим образом:

(10)
${{\kappa }_{b}} = \frac{{{{k}_{b}}}}{{{{{\bar {E}}}_{{emi}}}}} = \frac{{{{k}_{b}}}}{{1 - {\text{exp}}\left( { - kl} \right)}}.$

Значение локально-равновесного коэффициента поглощения κb может быть вычислено условно также и для неизотермического неоднородного газа по его локальным радиационным свойствам и температуре. При этом ширина Δηabs полосы поглощения эквивалентного антисерого спектра становится пространственной переменной.

В полосе поглощения максимальной ширины Δηmax может проходить все излучение антисерого спектра, в то время как более узкая часть полосы способна пропускать лишь его долю. Эту долю можно оценить как соотношение поглощательных способностей более узкой части полосы поглощения Āabs и полосы поглощения максимальной ширины Āmax. С помощью этого соотношения и гипотезы о том, что ширина антисерых полос поглощения практически не зависит от спектральной структуры падающего излучения, уравнение (10) преобразовано в следующую формулу, определяющую локальный коэффициент поглощения κω в уравнении (9) сохранения радиационной энергии:

${{\kappa }_{\omega }} \approx \frac{1}{{\Delta G}}\int\limits_{4\pi } {{{\kappa }_{b}}} \Delta {{I}_{s}}\frac{{{{{\bar {A}}}_{{abs}}}}}{{{{{\bar {A}}}_{{{\text{max}}}}}}}{\text{d}}\omega \,{\text{ = }}\frac{{{{k}_{b}}}}{{1 - {\text{exp}}\left( { - {{k}_{{{\text{max}}}}}{{l}_{\operatorname{m} }}} \right)}},$
где lm – средняя длина луча, аналогичная эффективной длине луча leff, определенной в [1]; kb – средний планковский коэффициент поглощения; kmax – максимальное значение (в вычислительной области) среднего изотермического коэффициента поглощения.

Как показано в [22], средние изотермические коэффициенты поглощения, найденные по формулам (6), могут быть удовлетворительно обобщены с помощью интерполяционных функций, что заметно упрощает модель.

МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЯ РАДИАЦИОННОГО ТЕПЛОПЕРЕНОСА

Как правило, радиационный теплоперенос от высокотемпературных газов к стенам печей и топок осуществляется совместно с конвективной теплоотдачей. Эти процессы невозможно разделить. Например, вблизи стен тепло радиационного источника поглощается, температура среды повышается и конвективная теплоотдача к стенам заметно возрастает.

Следует иметь в виду, что численное решение задач радиационного переноса, результаты которого сравниваются с эталоном, чаще всего бывает выполнено без учета тепловой конвекции. В таком случае распределение температуры в расчетной области не является результатом полноценного расчета; оно выбрано, по большей части, произвольно [9, 14, 20]. Намного больше полезной информации может быть получено при совместном решении дифференциальных уравнений радиационного и конвективного теплопереноса, в том числе о распределении температуры газов и турбулентно-радиационном взаимодействии (TRI) [23–25].

Метод дискретных ординат

При использовании метода дискретных ординат (DOM) должна быть выполнена одновременно пространственная и угловая дискретизация уравнения радиационного переноса (1). Эта же пространственная дискретизация используется и для решения задачи конвективного переноса.

Угловая дискретизация выполняется посредством дискретного набора ординат, разделяющих сферический телесный угол 4π радиан на части с соответствующими угловыми весами. Например, при моделировании крупномасштабной печи [23] каждый октант телесного угла разделялся на 3 × 3 части, что привело к 72 дискретным ординатам, локально закрепленным в каждом из узлов пространственной сетки.

Уравнение радиационного переноса для каждой дискретной ординаты m (число дискретных ординат равно M) в методе дискретных ординат принимает следующую форму:

(11)
${{\mu }_{m}}\frac{{\partial {{I}^{m}}}}{{\partial x}} + {{\eta }_{m}}\frac{{\partial {{I}^{m}}}}{{\partial y}} + {{\xi }_{m}}\frac{{\partial {{I}^{m}}}}{{\partial z}} = {{k}_{b}}{{I}_{b}} - {{k}_{s}}{{I}^{m}},$
где Im – интенсивность излучения вдоль дискретной ординаты с номером m; µm, ηm и ξm – направляющие косинусы дискретной ординаты m относительно декартовых осей x, y и z.

Все M уравнений (11) должны быть снабжены граничными условиями на поверхности стен. После этого система дискретных уравнений может быть решена численно относительно интенсивностей излучения I m посредством итераций на пространственной сетке. Когда все значения интенсивности излучения будут найдены, вычисляется радиационный источник тепла в каждом из узлов пространственной сетки посредством модифицированного уравнения (3):

${{S}_{{rad}}} = \sum\limits_1^M {k_{s}^{m}I_{s}^{m}{{w}^{m}} - 4\pi {{k}_{b}}{{I}_{b}}} ,$
где wm – угловой вес дискретной ординаты m.

Современные подходы к численному моделированию расширяют возможности метода дискретных ординат. В частности, он хорошо сочетается со статистическими процедурами, способствующими его улучшению [26].

Метод сферических гармоник

Чтобы создать метод сферических гармоник, интенсивность излучения Is разлагают в ряд по полиномам Лежандра Pn. Затем усеченные ряды подставляют в уравнение (1), откуда получают систему приближенных дифференциальных уравнений с требуемыми пространственными функциями [2]. Нечетные приближения P1 и P3 лучше согласуются с граничными условиями. Их индексы соответствуют максимальному номеру члена Pn полинома Лежандра, оставленного в усеченных рядах.

Чрезмерно трудоемкий, но довольно точный метод P3 не нашел широкого применения в инженерной практике, в то время как приближение P1 стало популярным благодаря возможности очень быстро решать с его помощью уравнения радиационного переноса [27, 28]. В способе P1 уравнение сохранения (2) дополнено приближенным соотношением, представленным здесь в следующей градиентной форме:

(12)
${{{\mathbf{q}}}_{{rad}}} \approx - \frac{1}{{3{{k}_{\omega }}}}{\text{grad}}{{G}_{\omega }}.$

Уравнения (2) и (12) могут быть приведены к дифференциальному уравнению второго порядка в частных производных, имеющему в декартовых координатах следующий вид:

(13)
$\begin{gathered} \frac{\partial }{{\partial x}}\left( {\frac{{\partial {{G}_{\omega }}}}{{{{k}_{\omega }}\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{\partial {{G}_{\omega }}}}{{{{k}_{\omega }}\partial y}}} \right) + \\ + \,\,\frac{\partial }{{\partial z}}\left( {\frac{{\partial {{G}_{\omega }}}}{{{{k}_{\omega }}\partial z}}} \right) + 3\left( {4{{k}_{b}}\sigma {{T}^{4}} - {{k}_{\omega }}{{G}_{\omega }}} \right) = 0. \\ \end{gathered} $

Решение уравнения (13) при соответствующих граничных условиях дает сферическое падающее излучение Gω. После этого радиационный источник тепла Srad может быть определен по уравнению (3) в каждом узле сетки. Однако точность этой процедуры сомнительна. В [29] показано, что метод дискретных ординат имеет более высокую точность по сравнению с радиационным методом P1 при оценке температуры стен и потока газов в камере сгорания. В первую очередь, это касается случаев, когда градиентное соотношение (12), которое не является надежным при определении температуры вблизи стен, используется для постановки граничных условий, как, например, в условиях Маршака [3].

Метод радиационной диффузии

Метод радиационной диффузии, ослабляющий недостатки приближения P1, был разработан в рамках модели эквивалентного антисерого спектра. Для удобства его формулировки в величину ΔGω была введена условная лучистая температура Tray:

$\Delta {{G}_{\omega }} = \int\limits_{4\pi } {\Delta {{I}_{s}}{\text{d}}} \omega = 4\sigma T_{{ray}}^{4}.$

Две отличительные особенности присущи этому методу [21]. Во-первых, в уравнении (12) вместо величины Gω использована более точная диффузионная функция F. Таким образом,

(14)
${{{\mathbf{q}}}_{{rad}}} = - \frac{{4\sigma }}{{3{{\kappa }_{\omega }}}}{\text{grad}}F,$
где

$F = T_{{ray}}^{4} + \frac{1}{3}\left( {T_{{ray}}^{4} - \frac{{{{k}_{b}}}}{{{{\kappa }_{\omega }}}}{{T}^{4}}} \right).$

В этом случае уравнение (13) приобретает следующую форму с неизвестной функцией F:

(15)
$\begin{gathered} \frac{\partial }{{\partial x}}\left( {\frac{{\partial F}}{{{{\kappa }_{\omega }}\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{\partial F}}{{{{\kappa }_{\omega }}\partial y}}} \right) + \\ + \,\,\frac{\partial }{{\partial z}}\left( {\frac{{\partial F}}{{{{\kappa }_{\omega }}\partial z}}} \right) + \frac{9}{4}\left( {{{k}_{b}}{{T}^{4}} - {{\kappa }_{\omega }}F} \right) = 0. \\ \end{gathered} $

Во-вторых, введено понятие гипотетической неограниченной среды, обладающей радиационными свойствами и температурой реального газа, ограниченного стенами. В то время как при определении температуры вблизи стен уравнение (14) становится неверным, оно остается достаточно точным во всей расчетной области неограниченной среды, где стены отсутствуют.

Метод предусматривает решение уравнения (15) дважды при разных граничных условиях для гипотетической среды и для объема газов, ограниченного стенами. Физические величины, найденные для неограниченной среды, помогают корректно формулировать граничные условия на поверхности стен.

Радиационный источник тепла может быть рассчитан по формуле

${{S}_{{rad}}} = 3\sigma \left( {{{\kappa }_{\omega }}F - {{k}_{b}}{{T}^{4}}} \right).$

В такой же форме это выражение вводится в уравнение конвективного теплопереноса для того, чтобы найти распределение термодинамической температуры T в расчетной области.

Статистические методы в моделировании радиационного переноса

Статистические приближения Монте-Карло в их классическом виде хорошо приспособлены для решения задач радиационного теплопереноса в устройствах сложной формы, но требуют значительных вычислительных ресурсов для получения достоверных результатов [3]. В настоящее время применяются усовершенствованные статистические модели [30, 31].

Статистические методы часто реализуются как эффективный вспомогательный инструмент в различных моделях радиационного переноса. Например, статистические способы вычислений были применены в методе DRESOR (distribution of ratios of energy scattered or reflected) для решения задач радиационного переноса в разных средах [32].

Как правило, эффективность статистических процедур возрастает при многократных повторениях одних и тех же операций. Сравнение двух методов было выполнено в условиях применения модели узкой полосы SNBCK к радиационному переносу в трехмерной виртуальной печи [33]. В этой работе сообщается, что при числе угловых направлений равном 800 время, потребовавшееся на решение одной и той же задачи традиционным методом дискретных ординат, было приблизительно в 7 раз больше времени, затраченного методом DRESOR.

Другие способы решения уравнения радиационного переноса

Существует еще несколько способов решения уравнения радиационного переноса, которые используются реже. Среди них зональный численный метод, который считается эффективным для расчета радиационного теплообмена в трехмерных печах, заполненных газами [2, 34]. Вычислительная область в них разделяется на поверхностные и объемные зоны, каждая из которых обменивается радиационной энергией со всеми другими зонами.

Основные недостатки зонального метода связаны с плохой совместимостью в нем радиационных и конвективных алгоритмов. Как правило, число радиационных зон намного меньше количества ячеек сетки, необходимого для расчета конвективного теплопереноса. Поэтому метод применяется, главным образом, в тех случаях, когда конвективным тепловым потоком можно пренебречь.

В методе дискретного переноса DTM (discrete transfer method) лучи прослеживаются в заданных направлениях от дискретных точек, расположенных на границе вычислительной области, до другой границы [35]. В ячейках сетки, пересекаемых лучами, вычисляются локальные интенсивности излучения Is и радиационные источники тепла Srad.

Метод трассирования лучей RTM (ray-tracing method) был применен в модели статистической узкой полосы спектра SNB [6]. Его особенность состоит в вычислении эволюции излучательной способности Ē вдоль выбранных лучей с применением средних изотермических коэффициентов поглощения.

ВЫВОДЫ

1. С помощью математических моделей радиационного теплопереноса в селективной среде, рассмотренных в настоящем обзоре, решаются две основные проблемы: нахождение достаточно точных локальных коэффициентов поглощения радиационной энергии и повышение эффективности численного метода, применяемого для интегрирования дифференциального уравнения радиационного переноса.

2. Достаточно точные локальные коэффициенты поглощения удалось получить с помощью узкополосной модели с коррелированным коэффициентом поглощения (SNBCK). Однако необходимость многократно решать уравнение радиационного переноса в сотнях узких полос спектра ограничивает применение этой модели в инженерной практике.

В глобальных моделях, использующих кумулятивные функции для усреднения коэффициентов поглощения в полном спектре, итерационное решение уравнения радиационного переноса выполняется однократно. Среди них модель c коррелированным коэффициентом поглощения (FSCK) обычно считается наилучшей. К недостаткам глобальных моделей можно отнести повышенную сложность их алгоритмов, что стимулирует применение в инженерной практике менее точных упрощенных моделей.

3. Метод дискретных ординат (DOM) считается одним из лучших для численного решения дифференциального уравнения радиационного переноса. Его точность, как и время, затраченное на компьютерные вычисления, зависит от числа дискретных ординат. Отмечается, что применение статистического способа вычислений повышает эффективность DOM.

Уравнение радиационного переноса, приведенное к сферическому телесному углу, решают, как правило, быстрым, но недостаточно точным приближением P1 метода сферических гармоник. Основные недостатки этого приближения устранены в методе радиационной диффузии.

4. Представленный здесь обзор можно рассматривать как своеобразный путеводитель для инженеров по многочисленным методам моделирования радиационного теплопереноса в селективных газах. Такие же или подобные методы применяются для газов, содержащих твердые или жидкие частицы, рассеивающие лучи. Несомненно, что в последнем случае вычислительные алгоритмы становятся более сложными.

Идеализированные серый (а) и антисерый (б) спектры. 1 – функция Планка Ibη при 1500 К; 2, 3 – интенсивности излучения двух серых спектров; 4 – полосы поглощения антисерого спектра; 5 – спектральные “окна”

Список литературы

  1. Hottel H.C., Sarofim A.F. Radiative transfer. N.Y.: McGraw-Hill Book Company, 1967.

  2. Оцисик М.Н. Сложный теплообмен. М.: Мир, 1976.

  3. Viskanta R., Mengüç M.P. Radiation heat transfer in combustion systems // Prog. Energy Combust. Sci. 1987. V. 13. Is. 2. P. 97–160. https://doi.org/10.1016/0360-1285(87)90008-6

  4. Modest M.F. The treatment of nongray properties in radiative heat transfer: from past to present // J. Heat Transfer. 2013. V. 135. Is. 6. P. 061801. https://doi.org/10.1115/1.4023596

  5. HITEMP, the high-temperature molecular spectroscopic database / L.S. Rothman, I.E. Gordon, R.J. Barber, H. Dothe, R.R. Gamache, A. Goldman, V.I. Perevalov, S.A. Tashkun, J. Tennyson // J. Quant. Spectrosc. Radiat. Transfer. 2010. V. 111. Is. 15. P. 2139–2150. https://doi.org/10.1016/j.jqsrt.2010.05.001

  6. Liu F. Numerical solutions of three-dimensional non-grey gas radiative transfer using the statistical narrow-band model // J. Heat Transfer. 1999. V. 121. Is. 1. P. 200–203. https://doi.org/10.1115/1.2825944

  7. Riviére P., Soufiani A. Updated band model parameters for H2O, CO2, CH4 and CO radiation at high temperature // Int. J. Heat Mass Transfer. 2012. V. 55. Is. 13‒14. P. 3349–3358. https://doi.org/10.1016/j.ijheatmasstransfer.2012.03.019

  8. Liu F., Smallwood G.J. An efficient approach for the implementation of the SNB based correlated-k method and its evaluation // J. Quant. Spectrosc. Radiat. Transfer. 2004. V. 84. Is. 4. P. 465–475. https://doi.org/10.1016/S0022-4073(03)00263-2

  9. Chu H., Liu F., Zhou H. Calculations of gas radiation heat transfer in a two-dimensional rectangular enclosure using the line-by-line approach and the statistical narrow-band correlated-k model // Int. J. Therm. Sci. 2012. V. 59. P. 66–74. https://doi.org/10.1016/j.ijthermalsci.2012.04.003

  10. Denison M.K., Webb B.W. A spectral line-based weighted-sum-of-gray-gases model for arbitrary RTE solvers // Int. J. Heat Mass Transfer. 1993. V. 115. Is. 4. P. 1004–1012. https://doi.org/10.1115/1.2911354

  11. A fictitious-gas-based absorption distribution function global model for radiative transferring hot gases / L. Pierrot, P. Rivière, A. Soufiani, J. Taine // J. Quant. Spectrosc. Radiat. Transfer. 1999. V. 62. Is. 5. P. 609–624. https://doi.org/10.1016/S0022-4073(98)00124-1

  12. Solovjov V.P., Webb B.W. The cumulative wavenumber method for modeling radiative transfer in gas mixtures with soot // J. Quant. Spectrosc. Radiat. Transfer. 2005. V. 93. Is. 1‒3. P. 273–287. https://doi.org/10.1016/j.jqsrt.2004.08.037

  13. Wang C., Modest M.F., He B. Improvement of full-spectrum k-distribution method using quadrature transformation // Int. J. Therm. Sci. 2016. V. 108. P. 100–107. https://doi.org/10.1016/j.ijthermalsci.2016.05.005

  14. Assessment of several gas radiation models for radiative heat transfer calculations in a three-dimensional oxy-fuel furnace under coal-fired conditions / V. Kez, J.L. Consalvi, F. Liu, J. Strӧhle, B. Epple // Int. J. Therm. Sci. 2017. V. 120. P. 289–302. https://doi.org/10.1016/j.ijthermalsci.2017.06.017

  15. The impact of radiative heat transfer in combustion processes and its modeling – with a focus on turbulent flames / F. Liu, J.-L. Consalvi, P.J. Coelho, F. André, M. Gu, V.P. Solovjov, B.W. Webb // Fuel. 2020 V. 281. P. 118555. https://doi.org/10.1016/j.fuel.2020.118555

  16. An improved full-spectrum correlated-k-distribution model for non-gray radiative heat transfer in combustion gas mixtures / S. Zheng, R. Sui, Y. Yang, Y. Sun, H. Zhou, Q. Lu // Int. Commun. Heat Mass Transfer. 2020. V. 114. P. 104566. https://doi.org/10.1016/j.icheatmasstransfer.2020.104566

  17. A full-spectrum k-distribution look-up table for radiative transfer in nonhomogeneous gaseous media / C. Wang, W. Ge, M. Modest, B. He // J. Quant. Spectrosc. Radiat. Transfer. 2016. V. 168. Is. 1. P. 46–56. https://doi.org/10.1016/j.jqsrt.2015.08.017

  18. WSGG correlations based on HITEMP2010 for computation of thermal radiation in non-isothermal, non-homogeneous H2O/CO2 mixtures / L.J. Dorigon, G. Duciak, R. Brittes, F. Cassol, M. Galarҫa, F.H.R. Franҫa // Int. J. Heat Mass Transfer. 2013. V. 64. P. 863–873. https://doi.org/10.1016/j.ijheatmasstransfer.2013.05.010

  19. Application of the weighted-sum-of-gray-gases model for media composed of arbitrary concentrations of H2O, CO2 and soot / F. Cassol, R. Brittes, F.H.R. França, O.A. Ezekoye // Int. J. Heat Mass Transfer. 2014. V. 79. P. 796–806. https://doi.org/10.1016/j.ijheatmasstransfer.2014.08.032

  20. Evaluation of gas radiation heat transfer in a 2D axisymmetric geometry using the line-by-line integration and WSGG models / F.R. Centeno, R. Brittes, F.H.R. França, O.A. Ezekoye // J. Quant. Spectrosc. Radiat. Transfer. 2015. V. 156. P. 1–11. https://doi.org/10.1016/j.jqsrt.2015.01.015

  21. Кузнецов В.А. Математическая модель радиационного теплообмена в селективных газах диффузионного факела // ИФЖ. 2017. Т. 90. № 2. Март‒апрель. С. 381–390.

  22. Трулёв А.В., Кузнецов В.А. Способ расчета поглощательных свойств трехатомных газов // Теплоэнергетика. 2013. № 6. С. 55–58. https://doi.org/10.1134/S0040363613060118

  23. Prediction of the radiative heat transfer in small and large scale oxy-coal furnaces / X. Yang, A. Clements, J. Szuhánszki, X. Huang, O.F. Moguel, J. Li, J. Gibbins, Zh. Liu, Ch. Zheng, D. Ingham, L. Ma, B. Nimmo, M. Pourkashanian // Appl. Energy. 2018. V. 211. P. 523–537. https://doi.org/10.1016/j.apenergy.2017.11.070

  24. Sikic I., Dembele S., Wen J. Non-gray radiative heat transfer modelling in LES-CFD simulated methanol pool fires // J. Quant. Spectrosc. Radiat. Transfer. 2019. V. 234. September. P. 78–89. https://doi.org/10.1016/j.jqsrt.2019.06.004

  25. A detailed modeling study of radiative heat transfer in a heavy-duty diesel engine / Ch. Paul, S.F. Fernandez, D.C. Haworth, S. Roy, M.F. Modest // Combust. Flame. 2019. V. 200. P. 325–341. https://doi.org/10.1016/j.combustflame.2018.11.032

  26. Konzen P.H.A., Guidi L.F., Richter Th. Quasi-random discrete ordinates method for neutron transport problems // Ann. Nucl. Energy. 2019. V. 133. P. 275–282. https://doi.org/10.1016/j.anucene.2019.05.017

  27. Numerical simulation of conjugate heat transfer and surface radiative heat transfer using the P1 thermal radiation model: Parametric study in benchmark cases / C. Cintolesi, H. Nilsson, A. Petronio, V. Armenio // Int. J. Heat Mass Transfer. 2017. V. 107. P. 956–971. https://doi.org/10.1016/j.ijheatmasstransfer.2016.11.006

  28. Diffusion approximation of the radiative-conductive heat transfer model with Fresnel matching conditions / A.Yu. Chebotarev, G.V. Grenkin, A.E. Kovtanyuk, N.D. Botkin, K.-H. Hoffmann // Commun. Nonlinear Sci. Numer. Simul. 2018. V. 57. P. 290–298. https://doi.org/10.1016/j.cnsns.2017.10.004

  29. Assessment of numerical radiation models on the heat transfer of an aero-engine combustion chamber / A.A.A. Gamil, T. Nikolaidis, I. Lelaj, P. Laskaridis // Case Stud. Therm. Eng. 2020. V. 22. P. 100772. https://doi.org/10.1016/j.csite.2020.100772

  30. Assessment of randomized Quasi-Monte Carlo method efficiency in radiative heat transfer simulations / L. Palluotto, N. Dumont, P. Rodrigues, O. Gicquel, R. Vicquelin // J. Quant. Spectrosc. Radiat. Transfer. 2019. V. 236. P. 106570. https://doi.org/10.1016/j.jqsrt.2019.07.013

  31. Bidirectional Monte-Carlo method for thermal radiation transfer in participating medium / X. Zhang, Q. Ai, K. Song, H. Tan // AIMS Energy. 2021. V. 9. Is. 3. P. 603–622. https://doi.org/10.3934/energy.2021029

  32. Non-gray radiation study of gas and soot mixtures in one-dimensional planar layer by DRESOR / Zh. Shu, Q. Chaobo, H. Zhifeng, Zh. Huaichun // J. Quant. Spectrosc. Radiat. Transfer. 2018. V. 217. P. 425–431. https://doi.org/10.1016/j.jqsrt.2018.06.020

  33. Yang Y., Zheng S., Lu Q. Numerical solutions of non-gray gases and particles radiative transfer in three-dimensional combustion system using DRESOR and SNBCK // Int. J. Therm. Sci. 2021. V 161. March. P. 106783. https://doi.org/10.1016/j.ijthermalsci.2020.106783

  34. Zonal modeling of radiative heat transfer in industrial furnaces using simplified model for exchange area calculation / H. Ebrahimi, A. Zamaniyan, J.S.S. Mohammadzadeh, A.A. Khalili // Appl. Math. Modell. 2013. V. 37. Is. 16‒17. P. 8004–8015. https://doi.org/10.1016/j.apm.2013.02.053

  35. Feldheim V., Lybaert P. Solution of radiative heat transfer problems with the discrete transfer method applied to triangular meshes // J. Comput. Appl. Math. 2004. V. 168. Is. 1‒2. P. 179–190. https://doi.org/10.1016/j.cam.2003.05.016

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплоэнергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал