Теплофизика высоких температур, 2019, T. 57, № 1, стр. 66-71
Влияние компонентов тензора теплопроводности теплозащитного материала на величину тепловых потоков от газодинамического пограничного слоя
В. Ф. Формалев 1, *, С. А. Колесник 1, **, Е. Л. Кузнецова 1, ***
1 Московский авиационный институт (национальный исследовательский университет),
Москва, Россия
* E-mail: formalev38@yandex.ru
** E-mail: sergey@oviont.com
*** E-mail: lareyna@mail.ru
Поступила в редакцию 10.05.2018
После доработки 10.10.2018
Принята к публикации 18.06.2018
Аннотация
На основе впервые полученного аналитического решения задачи теплопереноса в анизотропном композиционном материале в условиях конвективно-кондуктивного теплообмена при обтекании высокотемпературным газодинамическим пограничным слоем исследовано влияние компонентов тензора теплопроводности теплозащитного материала на тепловые потоки от газа к телу. Такой анализ позволил установить заметное снижение тепловых потоков к боковой поверхности затупленного анизотропного тела при использовании теплозащитного материала с высокой степенью продольной анизотропии (например, пиролитических графитов, у которых отношение продольного коэффициента теплопроводности к поперечному может достигать ста и более). Основной вклад в уменьшение тепловых потоков вносит уменьшение величины градиента температур на границе газа и тела со стороны газа за счет повышения температуры тела вниз по потоку. Кроме этого, при росте температуры газа на стенке увеличивается динамическая вязкость и снижается плотность, что уменьшает локальные числа Рейнольдса и содействует уменьшению тепловых потоков. Анализируются численные результаты.
ВВЕДЕНИЕ
В условиях высокоинтенсивного аэрогазодинамического нагрева элементов конструкций гиперзвуковых летательных аппаратов в качестве теплозащитных материалов используются анизотропные материалы (графиты, графитосодержащие, композиционные материалы и др.). Теплозащитные материалы с высокой степенью продольной анизотропии (отношения продольного компонента тензора теплопроводности к поперечному) можно использовать для регулирования тепловых потоков от газодинамического пограничного слоя. Действительно, если спроектировать анизотропную теплозащиту так, чтобы продольная анизотропия составляла десятки, а то и сотни единиц, то появляется возможность канализировать тепловые потоки в теле от непосредственно затупления в хвостовую часть затупленного тела, что приводит к повышению температуры хвостовой части, уменьшению модуля градиента температуры на границе “газ–тело” со стороны газа и, как следствие, к уменьшению тепловых потоков от газа к боковой поверхности затупленного тела.
Целью данной работы является анализ влияния чисел Фурье, определяемых по продольному коэффициенту теплопроводности анизотропного теплозащитного материала, на тепловой поток к боковой поверхности затупленного тела от газодинамического пограничного слоя. На основе полученного аналитического решения третьей начально-краевой задачи теплопроводности в анизотропной тепловой защите исследован конвективно-кондуктивный теплообмен на границе “газ–твердое тело”.
Аналогичные аналитические решения задач теплопроводности рассматривались в работах Зарубина В.С., Кувыркина Г.Н., Савельевой И. [1], Карташова Э.М. [2], Аттеткова А.В., Волкова И.К. [3] и в [4–6]. В работах Кудинова И.В., Кудинова В.А., Котовой Е.В. [7], Кирсанова Ю.А. [8], а также авторов [9, 10] исследуется сопряженный теплообмен на границах анизотропных тел от газодинамических течений. Однако аналитическое решение двумерной задачи анизотропной теплопроводности в условиях конвективно-кондуктивного теплообмена получено и исследовано впервые.
ПОСТАНОВКА ЗАДАЧИ
Рассматривается теплоперенос в анизотропной полосе неограниченной длины толщиной $\delta $ (рис. 1), на границе $y = 0$ которого приложен переменный в направлении оси $0x$ конвективный тепловой поток экспоненциального характера, причем точка с координатами $x = 0,$ $y = 0$ является критической точкой, в окрестности которой наблюдается максимальный уровень теплового потока при обтекании высокотемпературным газодинамическим пограничным слоем. Математическая формулировка задачи содержит следующие уравнения для определения функции $T\left( {x,y,t} \right){\text{:}}$
(1)
$\begin{gathered} c\rho \frac{{\partial T}}{{\partial t}} = {{\lambda }_{{11}}}\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + {{\lambda }_{{12}}}\frac{{{{\partial }^{2}}T}}{{\partial x\partial y}} + {{\lambda }_{{21}}}\frac{{{{\partial }^{2}}T}}{{\partial y\partial x}} + {{\lambda }_{{22}}}\frac{{{{\partial }^{2}}T}}{{\partial {{y}^{2}}}}, \\ x \in \left( { - \infty ,\infty } \right),\,\,\,\,y \in \left( {0,\delta } \right),\,\,\,\,t > 0; \\ \end{gathered} $(2)
$\begin{gathered} {{\left( {{{\lambda }_{{21}}}\frac{{\partial T}}{{\partial x}} + {{\lambda }_{{22}}}\frac{{\partial T}}{{\partial y}}} \right)}_{{y = 0}}} = \\ = {{\alpha }_{1}}\left( x \right)\left( {{{T}_{e}} - T\left( {x,0,t} \right)} \right)\eta \left( {{{l}_{1}} - \left| x \right|} \right), \\ x \in \left( { - \infty ,\infty } \right),\,\,\,\,t > 0; \\ \end{gathered} $(3)
${{\left( {{{\lambda }_{{21}}}\frac{{\partial T}}{{\partial x}} + {{\lambda }_{{22}}}\frac{{\partial T}}{{\partial y}}} \right)}_{{y = \delta }}} = 0,\,\,\,\,x \in \left( { - \infty ,\infty } \right),\,\,\,\,t > 0;$(4)
$T\left( {x,y,0} \right) = 0,\,\,\,\,x \in \left( { - \infty ,\infty } \right),\,\,\,\,y \in \left[ {0,\delta } \right].$Рис. 1.
Расчетная схема и системы координат $\left( {{{q}_{1}}\left( x \right) = {{\alpha }_{1}}\left( x \right)\left( {{{T}_{e}} - T\left( {x,0,t} \right)} \right)\eta \left( {{{l}_{1}} - \left| x \right|} \right)} \right).$
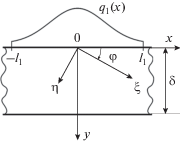
В соотношениях (1)–(4) введены следующие обозначения: c – теплоемкость в Дж/(кг K), ρ – плотность в кг/м3, $T\left( {x,y,t} \right)$ – температура в K, $x,y$ – декартовы координаты в м, t – время в с, ${{\alpha }_{1}}(x)$ – коэффициент теплоотдачи в Вт/(м2 К), ${{T}_{e}}$ – эффективная температура пограничного слоя в K, $q\left( x \right)$ – плотность теплового потока в Вт/м2, ${{T}_{0}}$ – начальная температура в K, ${{\lambda }_{{ij}}},$ $i,j = \overline {1,2} $ – компоненты тензора теплопроводности в Вт/(м K), $\eta \left( z \right)$ – функция Хэвисайда.
Компоненты ${{\lambda }_{{ij}}},$ $i,j = \overline {1,2} $ вычисляются следующим образом:
(5)
$\begin{gathered} {{\lambda }_{{11}}} = {{\lambda }_{\xi }}{{\cos }^{2}}\varphi + {{\lambda }_{\eta }}{{\sin }^{2}}\varphi , \\ {{\lambda }_{{12}}} = {{\lambda }_{{21}}} = \left( {{{\lambda }_{\xi }} - {{\lambda }_{\eta }}} \right)\sin \varphi \cos \varphi , \\ {{\lambda }_{{22}}} = {{\lambda }_{\xi }}{{\sin }^{2}}\varphi + {{\lambda }_{\eta }}{{\cos }^{2}}\varphi , \\ \end{gathered} $Для решения задачи (1)–(5) делается следующее предположение: коэффициент теплоотдачи ${{\alpha }_{1}}\left( x \right)$ имеет экспоненциальный вид
(6)
${{\alpha }_{1}}\left( x \right) = {{\alpha }_{0}}\exp ( - k{{x}^{2}})\eta \left( {{{l}_{1}} - \left| x \right|} \right),\,\,\,\,x \in \left( { - \infty ,\infty } \right).$Если начальная температура (4) равна некоторому постоянному значению ${{T}_{0}},$
(7)
$T\left( {x,y,0} \right) = {{T}_{0}},\,\,\,x \in \left( { - \infty ,\infty } \right),\,\,\,y \in \left[ {0,\delta } \right],\,\,\,t = 0,$В этом случае к итоговому решению необходимо добавить величину ${{T}_{0}}.$
МЕТОД РЕШЕНИЯ
Для решения задачи (1)–(8) используем метод построения граничной функции влияния (функции Грина), для чего граница области $y = 0$ и $y = \delta $ разбивается на $2J$ отрезков $\Delta {{\xi }_{j}},$ в центре ${{\xi }_{j}}$ каждого из которых вместо граничного условия (2) используется граничное условие вида
(9)
$\begin{gathered} - {{\left( {{{\lambda }_{{21}}}\frac{{\partial T}}{{\partial x}} + {{\lambda }_{{22}}}\frac{{\partial T}}{{\partial y}}} \right)}_{{y = 0}}} - {{\alpha }_{1}}\left( x \right)T\left( {x,0,t} \right) = \\ = - {{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\delta \left( {x - {{\xi }_{j}}} \right); \\ {{\xi }_{j}} \in \left( {\Delta {{\xi }_{j}}} \right),\,\,\,\,j \in \left( { - {{J}_{1}},{{J}_{1}}} \right),\,\,\,\,t > 0, \\ \end{gathered} $На боковых границах тепловые потоки в соответствии с (2), (3) и (6) равны нулю. Если в результате решения задачи (1), (3)–(9) получено $T\left( {x,{{\xi }_{j}},y,t} \right),$ то это решение является распределением температуры в расчетной области $x \in \left( { - \infty ,\infty } \right),$ $y \in \left( {0,\delta } \right),$ $t > 0$ под действием точечного источника теплоты ${{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\delta \left( {x - {{\xi }_{j}}} \right),$ приложенного в точке ${{\xi }_{j}} \in \Delta {{\xi }_{j}},$ $j \in \left( { - {{J}_{1}},{{J}_{1}}} \right).$ Оно называется граничной функцией источника и обозначается
Если функция источника $G\left( {x,{{\xi }_{j}},y,t} \right)$ найдена, то приближенное решение задачи (1), (9), (3)–(8) определяется суммой
Пределом этих интегральных сумм при $\Delta {{\xi }_{j}} \to 0$ будет решение задачи (1), (9), (3)–(8)
(11)
$\begin{gathered} T\left( {x,y,t} \right) = \mathop {\lim }\limits_{\Delta \xi \to 0} \bar {T}\left( {x,y,t} \right) = \\ = \oint\limits_C {G\left( {x,\xi ,y,t} \right){{T}_{e}}{{\alpha }_{1}}\left( \xi \right)d\xi ,} \\ \end{gathered} $Для нахождения функции источника (10) применим к задаче (1), (9), (3)–(8) преобразования Фурье по переменной x и Лапласа – по переменной t:
Приходим к следующей краевой задаче для обыкновенного дифференциального уравнения с мнимыми коэффициентами относительно функции источника ${{G}_{{\omega ,p}}}\left( y \right) = {{T}_{{\omega ,p}}}\left( y \right)\,:$
(12)
$\begin{gathered} \frac{{{{\partial }^{2}}{{G}_{{\omega ,p}}}}}{{\partial {{y}^{2}}}} + 2i\omega \frac{{{{\lambda }_{{12}}}}}{{{{\lambda }_{{22}}}}}\frac{{\partial {{G}_{{\omega ,p}}}}}{{\partial y}} - \frac{{{{\lambda }_{{11}}}{{\omega }^{2}} + c\rho p}}{{{{\lambda }_{{22}}}}}{{G}_{{\omega ,p}}} = 0, \\ 0 < y < \delta ; \\ \end{gathered} $(13)
$\begin{gathered} \frac{{\partial {{G}_{{\omega ,p}}}}}{{\partial y}} + \frac{{i\omega {{\lambda }_{{12}}} + {{{\bar {\alpha }}}_{1}}}}{{{{\lambda }_{{22}}}}}{{G}_{{\omega ,p}}} = \frac{{{{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)}}{{{{\lambda }_{{22}}}p}}\exp \left( { - i\omega {{\xi }_{j}}} \right), \\ y = 0; \\ \end{gathered} $(14)
${{\lambda }_{{22}}}\frac{{\partial {{G}_{{\omega ,p}}}}}{{\partial y}} + i\omega {{\lambda }_{{12}}}{{G}_{{\omega ,p}}} = 0,\,\,\,\,y = \delta ,$(15)
${{\bar {\alpha }}_{1}} = \frac{{{{\alpha }_{0}}}}{{{{l}_{1}}}}\int\limits_0^{{{l}_{1}}} {\exp ( - k{{x}^{2}})dx = \frac{{{{\alpha }_{0}}}}{{2{{l}_{1}}}}\sqrt {\frac{\pi }{k}} {\kern 1pt} {\text{erf(}}\sqrt k {{l}_{1}}{\text{)}}.} $Решением задачи (12)–(14) является функция
(16)
$\begin{gathered} {{G}_{{\omega ,p}}}\left( {{{\xi }_{j}},t} \right) = \exp \left( { - i\omega \alpha y} \right){{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\exp \left( { - i\omega {{\xi }_{j}}} \right) \times \\ \times \,\,\frac{{\exp \left( { - {{K}_{{\omega ,p}}}\left( {\delta - y} \right) + \exp ({{K}_{{\omega ,p}}}\left( {\delta - y} \right)} \right)}}{{p\left[ {{{\lambda }_{{22}}}{{K}_{{\omega ,p}}}\left( {\exp \left( { - {{K}_{{\omega ,p}}}\delta } \right) - \exp \left( {{{K}_{{\omega ,p}}}\delta } \right)} \right) + {{{\bar {\alpha }}}_{1}}\left( {\exp \left( {{{K}_{{\omega ,p}}}\delta } \right) + \exp \left( { - {{K}_{{\omega ,p}}}\delta } \right)} \right)} \right]}}. \\ \end{gathered} $Обратное преобразование Лапласа выражения (16) осуществим по формуле Меллина [11, 12]
(17)
$\begin{gathered} {{G}_{w}}\left( {{{\xi }_{j}},y,t} \right) = \frac{{\exp \left( { - i\omega \alpha y} \right)}}{{{{\lambda }_{{22}}}}}{{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\exp \left( { - i\omega {{\xi }_{j}}} \right) \times \\ \times \,\,\frac{1}{{2\pi i}}\int\limits_{\sigma - i\infty }^{\sigma + i\infty } {\frac{{\left[ {\exp } \right.\left. {\left( { - {{K}_{{\omega ,p}}}\left( {\delta - y} \right) + \exp ({{K}_{{\omega ,p}}}\left( {\delta - y} \right)} \right)} \right]\exp \left( {pt} \right)dp}}{{p\left[ {{{K}_{{\omega ,p}}}\left( {\exp \left( { - {{K}_{{\omega ,p}}}\delta } \right) - \exp \left( {{{K}_{{\omega ,p}}}\delta } \right)} \right) + \frac{{{{{\bar {\alpha }}}_{1}}}}{{{{\lambda }_{{22}}}}}\left( {\exp \left( {{{K}_{{\omega ,p}}}\delta } \right) + \exp \left( { - {{K}_{{\omega ,p}}}\delta } \right)} \right)} \right]}}} . \\ \end{gathered} $Вычислить интеграл в (17) без предварительного преобразования не удается. Поэтому рассмотрим два предельных случая: 1) большая толщина $\delta $ (т.е. тело сплошное или полубесконечное), 2) малая толщина $\left( {{{K}_{{\omega ,p}}}\delta \sim 1} \right).$
В первом случае после деления числителя и знаменателя подынтегральной функции в (17) на $\exp \left( {{{K}_{{\omega ,p}}}\delta } \right)$ получим
(18)
$\begin{gathered} {{G}_{\omega }}\left( {{{\xi }_{j}},y,t} \right) = \frac{{\exp \left( { - i\omega \alpha y} \right)}}{{{{\lambda }_{{22}}}}}{{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\exp \left( { - i\omega {{\xi }_{j}}} \right) \times \\ \times \,\,\frac{1}{{2\pi i}}\int\limits_{\sigma - i\infty }^{\sigma + i\infty } {\frac{{\exp \left( { - \sqrt {\beta {{\omega }^{2}} + \gamma p} y} \right)}}{{p\left[ { - \sqrt {\beta {{\omega }^{2}} + \gamma p} } \right] + \frac{{{{{\bar {\alpha }}}_{1}}}}{{{{\lambda }_{{22}}}}}}}\exp \left( {pt} \right)dp.} \\ \end{gathered} $Во втором случае все экспоненты в [17 ] , зависящие от $\delta ,$ разложим в ряды Тейлора с удержанием линейных членов.
(19)
$\begin{gathered} {{G}_{\omega }}\left( {{{\xi }_{j}},y,t} \right) = \exp \left( { - i\omega \alpha y} \right){{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\exp \left( { - i\omega {{\xi }_{j}}} \right) \times \\ \times \,\,\frac{1}{{c\rho \delta }}\frac{1}{{2\pi i}}\int\limits_{\sigma - i\infty }^{\sigma + i\infty } {\frac{{\exp \left( {pt} \right)dp}}{{p\left[ {p - \left( {\frac{{\beta {{\omega }^{2}}}}{\gamma } + \frac{{{{{\bar {\alpha }}}_{1}}}}{{c\rho \delta }}} \right)} \right]}}.} \\ \end{gathered} $На основе теоремы о произведении двух изображений ${1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0em} p}$ и [p – (${{\beta {{\omega }^{2}}} \mathord{\left/ {\vphantom {{\beta {{\omega }^{2}}} \gamma }} \right. \kern-0em} \gamma } + {{{{{\bar {\alpha }}}_{1}}} \mathord{\left/ {\vphantom {{{{{\bar {\alpha }}}_{1}}} {c\rho \delta }}} \right. \kern-0em} {c\rho \delta }}$)]–1 из выражения (19) находим
(20)
$\begin{gathered} {{G}_{\omega }}\left( {{{\xi }_{j}},y,t} \right) = \frac{{\exp \left( { - i\omega \alpha y} \right){{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\exp \left( { - i\omega {{\xi }_{j}}} \right)}}{{c\rho \delta }} \times \\ \times \,\,\int\limits_0^t {\eta \left( \tau \right)} \exp \left[ {\left( {\frac{{\beta {{\omega }^{2}}}}{\gamma } + \frac{{{{{\bar {\alpha }}}_{1}}}}{{c\rho \delta }}} \right)\left( {t - \tau } \right)} \right]d\tau , \\ \end{gathered} $При вычислении интеграла в (18) используем теорему о произведении изображений F1(p) = ${1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0em} p} \Leftrightarrow \eta \left( t \right)$ и
(21)
${{F}_{2}}\left( p \right) = \frac{{\exp \left( { - \sqrt {\beta {{\omega }^{2}} + \gamma p} y} \right)}}{{ - \sqrt {\beta {{\omega }^{2}} + \gamma p} + {{{{{\bar {\alpha }}}_{1}}} \mathord{\left/ {\vphantom {{{{{\bar {\alpha }}}_{1}}} {{{\lambda }_{{22}}}}}} \right. \kern-0em} {{{\lambda }_{{22}}}}}}}.$Для изображения (21) оригиналом является функция [11, 12]
(22)
$\begin{gathered} {{f}_{2}}\left( t \right) = \frac{1}{{2\pi i}}\int\limits_{\sigma - i\infty }^{\sigma + i\infty } {\frac{{\exp \left( { - \sqrt {\beta {{\omega }^{2}} + \gamma p} y} \right)}}{{ - \sqrt {\beta {{\omega }^{2}} + \gamma p} + {{{{{\bar {\alpha }}}_{1}}} \mathord{\left/ {\vphantom {{{{{\bar {\alpha }}}_{1}}} {{{\lambda }_{{22}}}}}} \right. \kern-0em} {{{\lambda }_{{22}}}}}}}\exp \left( {pt} \right)dp = } \\ = \frac{1}{{\sqrt \gamma }}\exp \left( { - \frac{{\beta {{\omega }^{2}}}}{\gamma }t} \right)\exp \left( {\frac{{ - {{{\bar {\alpha }}}_{1}}y}}{{{{\lambda }_{{22}}}}} + \frac{{\bar {\alpha }_{1}^{2}t}}{{\lambda _{{22}}^{2}\gamma }}} \right) \times \\ \times \,\,\left\{ {\frac{1}{{\sqrt {\pi t} }}\exp \left[ { - \frac{{{{{\left( { - y\sqrt \gamma + \frac{{2{{{\bar {\alpha }}}_{1}}}}{{{{\lambda }_{{22}}}\sqrt \gamma }}t} \right)}}^{2}}}}{{4t}}} \right] - } \right. \\ - \,\,\frac{{{{{\bar {\alpha }}}_{1}}}}{{{{\lambda }_{{22}}}\sqrt \gamma }}{\text{erfc}}\left. {\left( {\frac{{ - y\sqrt \gamma }}{{2\sqrt t }} + \frac{{{{{\bar {\alpha }}}_{1}}\sqrt t }}{{{{\lambda }_{{22}}}\sqrt \gamma }}} \right)} \right\}. \\ \end{gathered} $Тогда в соответствии с (18) и (20)
(23)
$\begin{gathered} {{G}_{\omega }}\left( {{{\xi }_{j}},y,t} \right) = \frac{{{{T}_{e}}}}{{\sqrt \gamma {{\lambda }_{{22}}}}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)\exp \left( { - i\omega \left( {\alpha y + {{\xi }_{j}}} \right)} \right) \times \\ \times \,\,\exp \left( {\frac{{ - {{{\bar {\alpha }}}_{1}}y}}{{{{\lambda }_{{22}}}}}} \right)\int\limits_0^t {\eta \left( \tau \right)} \exp \left( { - \frac{{\beta {{\omega }^{2}}}}{\gamma } + \frac{{\bar {\alpha }_{1}^{2}}}{{\lambda _{{22}}^{2}\gamma }}} \right)\left( {t - \tau } \right) \times \\ \times \,\,\left\{ {\frac{1}{{\sqrt {\pi \left( {t - \tau } \right)} }}\exp \left[ { - \frac{{ - y\sqrt \gamma + \frac{{2{{{\bar {\alpha }}}_{1}}\left( {t - \tau } \right)}}{{{{\lambda }_{{22}}}\sqrt \gamma }}}}{{4\left( {t - \tau } \right)}}} \right] - \frac{{{{{\bar {\alpha }}}_{1}}}}{{{{\lambda }_{{22}}}\sqrt \gamma }} \times } \right. \\ \left. { \times \,\,{\text{erfc}}\left( {\frac{{ - y\sqrt \gamma }}{{2\sqrt {t - \tau } }} + \frac{{{{{\bar {\alpha }}}_{1}}\sqrt {t - \tau } }}{{{{\lambda }_{{22}}}\sqrt \gamma }}} \right)} \right\}d\tau . \\ \end{gathered} $Обратное преобразование Фурье от выражения (23) имеет вид
Несобственный интеграл по параметру преобразования Фурье в (24) вычисляется следующим образом:
(25)
$\begin{gathered} \int\limits_{ - \infty }^\infty {\exp \left[ { - i\omega \left( {\alpha y - x + {{\xi }_{j}}} \right)} \right]\exp \left( { - \frac{{\beta \left( {t - \tau } \right)}}{\gamma }{{\omega }^{2}}} \right)d\omega } = \\ = \,\,\frac{{\sqrt {\pi \gamma } }}{{\sqrt {\beta \left( {t - \tau } \right)} }}\exp \left( { - \frac{{{{{\left( {\alpha y - x + {{\xi }_{y}}} \right)}}^{2}}}}{{4\beta {{\left( {t - \tau } \right)} \mathord{\left/ {\vphantom {{\left( {t - \tau } \right)} \gamma }} \right. \kern-0em} \gamma }}}} \right). \\ \end{gathered} $Подставляя (25) в (24), получаем функцию источника $G\left( {x,{{\xi }_{j}},y,t} \right)$
(26)
$\begin{gathered} G\left( {x,{{\xi }_{j}},y,t} \right) = \frac{{{{T}_{e}}{{\alpha }_{1}}\left( {{{\xi }_{j}}} \right)}}{{{{\lambda }_{{22}}}2\pi }}\exp \left( {\frac{{ - {{{\bar {\alpha }}}_{1}}y}}{{{{\lambda }_{{22}}}}}} \right) \times \\ \times \,\,\int\limits_0^t {\eta \left( \tau \right)\frac{1}{{\sqrt {\beta \left( {t - \tau } \right)} }}\exp \left( { - \frac{{{{{\left( {\alpha y - x + {{\xi }_{j}}} \right)}}^{2}}}}{{4\beta {{\left( {t - \tau } \right)} \mathord{\left/ {\vphantom {{\left( {t - \tau } \right)} \gamma }} \right. \kern-0em} \gamma }}}} \right)} \times \\ \times \,\,\exp \left( {\frac{{\bar {\alpha }_{1}^{2}\left( {t - \tau } \right)}}{{\lambda _{{22}}^{2}\gamma }}} \right) \times \\ \times \,\,\left\{ {\frac{1}{{\sqrt {t - \tau } }}\exp \left[ { - {{{\left( {\frac{{ - y\sqrt \gamma }}{{2\sqrt {t - \tau } }} + \frac{{{{{\bar {\alpha }}}_{1}}\sqrt {t - \tau } }}{{{{\lambda }_{{22}}}\sqrt \gamma }}} \right)}}^{2}}} \right] - } \right. \\ - \,\,\left. {\frac{{{{{\bar {\alpha }}}_{1}}}}{{{{\lambda }_{{22}}}\sqrt \gamma }}{\text{erfc}}\left( {\frac{{ - y\sqrt \gamma }}{{2\sqrt {t - \tau } }} + \frac{{{{{\bar {\alpha }}}_{1}}\sqrt {t - \tau } }}{{{{\lambda }_{{22}}}\sqrt \gamma }}} \right)} \right\}d\tau . \\ \end{gathered} $Осталось подставить функцию (26) в (11), где замкнутый контур $C$ включает прямую $y = \delta ,$ а также достаточно удаленные от начала координат боковые границы, где коэффициент теплоотдачи принимается равным нулю.
Окончательно в случае $\delta \to \infty $ в соответствии с (11) и (26) находим решение третьей начально-краевой задачи в анизотропной области
(27)
$\begin{gathered} T\left( {x,y,t} \right) = \frac{{{{T}_{e}}\exp \left( {\frac{{ - {{{\bar {\alpha }}}_{1}}y}}{{{{\lambda }_{{22}}}}}} \right)}}{{2\pi {{\lambda }_{{22}}}}} \times \\ \times \,\,\int\limits_0^t {\int\limits_{ - {{l}_{1}}}^{{{l}_{1}}} {\left[ {\frac{{{{\alpha }_{1}}\left( \xi \right)}}{{\sqrt {\beta \left( {t - \tau } \right)} }}\exp \left( { - \frac{{{{{\left( {\alpha y - x + \xi } \right)}}^{2}}}}{{4\beta {{\left( {t - \tau } \right)} \mathord{\left/ {\vphantom {{\left( {t - \tau } \right)} \gamma }} \right. \kern-0em} \gamma }}}} \right)d\xi } \right]} \times } \\ \times \,\,\exp \left( {{{A}^{2}}\left( {t - \tau } \right)} \right)\left\{ {\frac{1}{{\sqrt {t - \tau } }}} \right.\exp \left[ { - {{{\left( {A\sqrt {t - \tau } - \frac{B}{{\sqrt {t - \tau } }}} \right)}}^{2}}} \right] - \\ - \,\,A{\text{erfc}}\left. {\left( {A\sqrt {t - \tau } - \frac{B}{{\sqrt {t - \tau } }}} \right)} \right\}d\tau , \\ \end{gathered} $Для малых толщин $\delta $ аналогичное выражение будет получено из (20), для которого вначале необходимо выполнить обратное преобразование Фурье, а затем полученное выражение подставить в (11). В результате находим
АНАЛИЗ РЕЗУЛЬТАТОВ
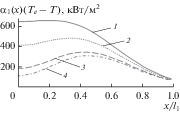
На рис. 2 и 3 представлены результаты расчетов температуры $T\left( {x,0,t} \right)$ границы $y = 0$ по (27) и тепловых потоков к этой границе в зависимости от чисел Фурье, рассчитанных по продольной теплопроводности ${{\lambda }_{\xi }}$ в ортотропном случае $(\varphi = {{0}^{0}},{{\lambda }_{{12}}} = 0)$ и ${\text{Fo}} = {{{{\lambda }_{\xi }}t} \mathord{\left/ {\vphantom {{{{\lambda }_{\xi }}t} {(c\rho l_{1}^{2})}}} \right. \kern-0em} {(c\rho l_{1}^{2})}}.$
Рис. 2.
Изменение температуры вдоль границы $y = 0{\text{:}}$ 1 = ${\text{Fo}} = 0.1,$ 2 – ${\text{Fo}} = 0.2,$ 3 $ - \,{\text{Fo}} = 0.4,$ 4 $ - \,{\text{Fo}} = 0.5.$
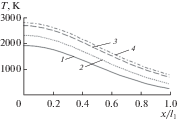
Рис. 3.
Изменение тепловых потоков к границе $y = 0{\text{:}}$ 1 $ - \,{\text{Fo}} = 0.1,$ 2 $ - \,{\text{Fo}} = 0.2,$ 3 $ - \,{\text{Fo}} = 0.4,$ 4 $ - \,{\text{Fo}} = 0.5.$
Входные данные принимали следующие значения: ${{\lambda }_{\xi }} = 100$ Вт/(м К), ${{\lambda }_{\eta }} = 5$ Вт/(м К), $c\rho = {{10}^{6}}$ Дж/(м3 К), ${{l}_{1}} = 0.1$ м, $\varphi = 0,$ ${{T}_{e}} = 3000$ К, ${{\alpha }_{1}}\left( x \right) = 600\exp ( - 3{{\bar {x}}^{2}})$ Вт/(м2 К), $\bar {x} = {x \mathord{\left/ {\vphantom {x {{{l}_{1}}}}} \right. \kern-0em} {{{l}_{1}}}},$ ${{\alpha }_{2}} = 0.$ Нумерация кривых соответствует различным значениям чисел ${\text{Fo:}}$ 1 – $0.1\left( {t = 10\,\,{\text{c}}} \right),$ 2 – ${\text{Fo}} = 0.2\left( {t = 20\,\,{\text{c}}} \right),$ 3 – ${\text{Fo}} = 0.4\left( {t = 40\,\,{\text{c}}} \right),$ 4 – ${\text{Fo}} = 0.5\left( {t = 50\,\,{\text{c}}} \right).$
На рис. 2 представлены распределения температур вдоль границы $y = 0$ правой половины пластины, поскольку в ортотропном случае ее прогрев симметричен относительно оси $0y$ (в анизотропном случае, когда $\varphi \ne 0$ и ${{\lambda }_{{12}}} \ne 0,$ температурное поле не обладает симметрией относительно оси $0y$). Ясно, что с ростом чисел ${\text{Fo}}$ температуры границы $y = 0$ растут. При этом, если точку $x = 0,$ $y = 0$ считать критической точкой затупленного тела, то хвостовая часть этого тела нагревается не только за счет конвективного теплового потока от пограничного слоя, но и вследствие перетока теплоты вдоль тела к периферийной его части из-за большой степени продольной анизотропии ${{{{\lambda }_{\xi }}} \mathord{\left/ {\vphantom {{{{\lambda }_{\xi }}} {{{\lambda }_{\eta }}}}} \right. \kern-0em} {{{\lambda }_{\eta }}}} = 20.$
Такой рост температуры наружной границы приводит к резкому уменьшению конвективных тепловых потоков ${{\alpha }_{1}}\left( x \right)\left( {{{T}_{e}} - T\left( {x,0,t} \right)} \right)$ за счет уменьшения градиента температуры на границе $y = 0$ со стороны газа (рис. 3). При этом тепловые потоки на периферии уменьшаются вследствие не только экспоненциального уменьшения коэффициента теплоотдачи, но и увеличения температуры границы $y = 0$ при перетоке теплоты на периферию внутри тела в результате высокой продольной теплопроводности по сравнению с поперечной (степень анизотропии ${{{{\lambda }_{\xi }}} \mathord{\left/ {\vphantom {{{{\lambda }_{\xi }}} {{{\lambda }_{\eta }}}}} \right. \kern-0em} {{{\lambda }_{\eta }}}} = 20$).
ЗАКЛЮЧЕНИЕ
На основе построения граничной функции источника (граничной функции Грина) и применения интегральных преобразований Фурье и Лапласа впервые получено аналитическое решение двумерной нестационарной задачи теплопроводности в анизотропной полосе в условиях конвективно-кондуктивного теплообмена на границах. Аналитические решения найдены в двух случаях: для сплошного анизотропного тела и тонкой анизотропной пластины. Полученные результаты показывают, что увеличение чисел ${\text{Fo,}}$ вычисленных по продольной теплопроводности ортотропного тела, существенно снижает тепловые потоки не только за счет уменьшения коэффициента теплоотдачи, но и за счет значительного продольного перетока теплоты из-за высокой степени продольной анизотропии.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, проект № 9.7100.2017/6.7, руководитель – Кузнецова Е.Л.
Список литературы
Zarubin V.S., Kuvyrkin G.N., Savelyeva I.Y. Two-Sided Thermal Resistance Estimates for Heat Transfer Through an Anisotropic Solid of Complex Shape // Int. J. Heat Mass Transfer. 2018. V. 116. P. 833.
Карташов Э.М. Математическое моделирование теплопроводности с двухфазным запаздыванием // ИФЖ. 2016. Т. 89. № 2. С. 338.
Аттетков А.В., Волков И.К. Температурное поле анизотропного полупространства, подвижная граница которого содержит пленочное покрытие // Изв. РАН. Энергетика. 2015. № 3. С. 39.
Формалев В.Ф., Колесник С.А. Аналитическое иcследование теплопереноса в анизотропной полосе при задании тепловых потоков на границах // ИФЖ. 2016. Т. 89. № 4. С. 973.
Формалев В.Ф., Колесник С.А., Кузнецова Е.Л. Нестационарный теплоперенос в анизотропном полупространстве в условиях теплообмена с окружающей средой, имеющей заданную температуру // ТВТ. 2016. Т. 54. № 6. С. 878.
Формалев В.Ф., Колесник С.А., Чипашвили А.А. Аналитическое исследование теплопереноса при пленочном охлаждении тел // ТВТ. 2006. Т. 44. № 1. С. 107.
Кудинов И.В., Кудинов В.А., Котова Е.В. Дополнительные граничные условия в нестационарных задачах теплопроводности // ТВТ. 2017. Т. 55. № 4. С. 556.
Кирсанов Ю.А. Влияние тепловой релаксации и термического демпфирования на переходные процессы при циклических граничных условиях // ТВТ. 2017. Т. 55. № 4. С. 549.
Формалев В.Ф., Колесник С.А. Об обратных граничных задачах теплопроводности по восстановлению тепловых потоков к анизотропным телам с нелинейными характеристиками теплопереноса // ТВТ. 2017. Т. 55. № 4. С. 564.
Формалев В.Ф., Колесник С.А. Сопряженный теплоперенос между пристенными газодинамическими течениями и анизотропными телами // ТВТ. 2007. Т. 45. № 1. С. 85.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Дёч Г. Руководство к практическому применению преобразования Лапласа. М.: Наука, 1965. 288 с.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур



