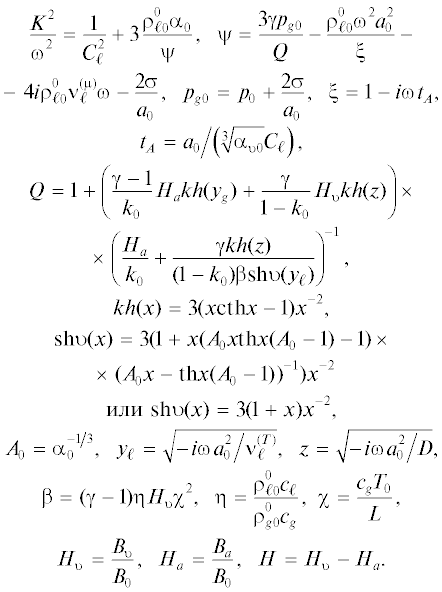Теплофизика высоких температур, 2019, T. 57, № 2, стр. 284-290
Особенности отражения и прохождения акустических волн на границе “чистой” и пузырьковой жидкостей при прямом их падении
В. Ш. Шагапов 1, М. Н. Галимзянов 1, 2, 3, *, И. И. Вдовенко 2
1 Институт механики им. Р.Р. Мавлютова УНЦ РАН,
Башкортостан, г. Уфа, Россия
2 ФГБОУ ВО Башкирский государственный университет,
Башкортостан, г. Уфа, Россия
3 ФГБОУ ВО Уфимский государственный авиационный технический университет
Башкортостан, г. Уфа, Россия
* E-mail: monk@anrb.ru
Поступила в редакцию 19.12.2017
После доработки 05.06.2018
Принята к публикации 16.03.2018
Аннотация
Изучены особенности отражения и преломления гармонических волн на границе раздела “чистой” жидкости и жидкости с пузырьками с парогазовой смесью при прямом их падении. Проведен численный анализ влияния изменения равновесной температуры T0 системы в диапазоне 300 ≤ T0 ≤ 373 K для двух начальных размеров пузырьков a0 = 10–6 и 10–3 м. Изучено влияние частот возмущений на коэффициенты отражения и преломления звука при прямом падении. Показано, что при падении волны со стороны пузырьковой жидкости на границу может реализоваться условие полного внутреннего отражения.
ВВЕДЕНИЕ
В морской воде из-за снижения ее плотности или скорости звука по различным причинам на некоторых глубинах может возникнуть слой, в котором возможно сверхдальнее распространение звука. Этот слой называется подводным звуковым каналом. Обычно на глубине нескольких сотен метров находится слой, где величина скорости звука минимальна. Причем скорость звука выше глубины этого слоя увеличивается за счет роста температуры воды, а ниже – вследствие повышения давления. Это явление было открыто независимо американскими учеными М. Ирвингом и Дж. Ворцелем [1] и советскими учеными Л.М. Бреховских и Л.Д. Розенбергом [2, 3]. Подводные звуковые каналы могут возникнуть за счет изменения солености воды, наличия нанопузырьков, из-за жизнедеятельности микроорганизмов, миграции пузырьков со дна и т.д.
В работе [4] был рассмотрен случай распространения волнового импульса в жидкости, содержащей пузырьки. Были выявлены критерии гашения пузырьковым экраном волнового импульса в зависимости от начальных параметров системы. Установлено, что пузырьковой слой с достаточно небольшим начальным объемным содержанием пузырьков способен полностью погасить волновой сигнал.
В работах [5, 6] численно решалась задача о прямом падении волны сжатия на твердую стенку, полностью или частично покрытую пузырьковой областью конечных размеров. В результате исследований установлено, что, когда по твердой стенке, имеющей пристенную пузырьковую завесу конечных размеров, “бьет” волновой импульс, завеса, в зависимости от параметров (размеров пузырьковой зоны, объемного содержания газа в завесе, радиуса пузырьков) может существенно уменьшить или увеличить воздействие импульсного сигнала. Пристенная пузырьковая зона влияет и на участки, которые находятся на некотором расстоянии от завесы. В случае, когда твердая стенка полностью покрыта пузырьковой областью, можно в зависимости от начальных параметров волнового импульса подобрать такие параметры пузырьковой области, которые обеспечивали бы полное гашение сигнала.
В работах [7–11] изучена динамика слабых и акустических волн в многофракционных смесях жидкости с парогазовыми и газовыми пузырьками различных размеров и разного состава с фазовыми превращениями. Показано, что дисперсия и диссипация акустических волн во многом зависит от присутствия в составе дисперсной фазы пузырьков различных фракций. Проведено сравнение с экспериментальными данными.
В случае “теплых” и кипящих жидкостей из-за фазовых переходов и действия капиллярных сил волновые свойства пузырьковых жидкостей гораздо разнообразнее. В данной работе анализируется влияние равновесной температуры, степени диспергированности объемного содержания пузырьковой фазы на динамику отражения и прохождения акустической волны при прямом падении на границу раздела пузырьковой и “чистой” жидкостей.
ОСНОВНЫЕ УРАВНЕНИЯ
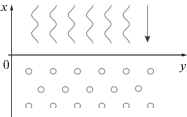
Рассмотрим двумерные акустические волны. Вертикальную ось $Ox$ направим перпендикулярно к плоскости раздела между однофазной и двухфазной средами в сторону “чистой” жидкости, а начало координат ($x = 0$) положим на границе раздела. Горизонтальная ось $Oy$ направлена вдоль границы раздела (рис. 1).
Пусть жидкость в зоне $x > 0$ находится при температуре ${{T}_{0}}$ и под давлением ${{p}_{0}},$ а в жидкости в зоне $x < 0$, находящейся при той же температуре и давлении, имеются сферические пузырьки радиусом ${{a}_{0}},$ которые содержат пар и нерастворимый в жидкой фазе газ. Тогда в случае механического и теплового равновесия рассматриваемой системы (жидкость–парогазовые пузырьки) при состояниях, достаточно далеких от критического, выполняются следующие условия:
(1)
${{p}_{{\upsilon 0}}} + {{p}_{{a0}}} = {{p}_{0}} + \frac{{2\sigma }}{{{{a}_{0}}}},\,\,\,\,{{p}_{{\upsilon 0}}} = {{p}_{s}}({{T}_{0}}),$Рассмотрим распространение малых возмущений в описанной системе в одномерном случае (плоский слой), используя односкоростное приближение. Полагая, что жидкость является акустически сжимаемой, можем записать линеаризованное уравнение
(2)
$\frac{1}{{C_{\ell }^{2}}}\frac{{\partial {{p}_{\ell }}}}{{\partial t}} + \rho _{{\ell 0}}^{0}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial \upsilon }}{{\partial y}}} \right) - 3\rho _{{\ell 0}}^{0}\frac{{{{\alpha }_{0}}}}{{{{a}_{0}}}}\frac{{\partial a}}{{\partial t}} = 0,$Уравнения импульсов имеют вид
(3)
$\rho _{{\ell 0}}^{0}\frac{{\partial u}}{{\partial t}} + \frac{{\partial {{p}_{\ell }}}}{{\partial x}} = 0,\,\,\,\,\rho _{{\ell 0}}^{0}\frac{{\partial \upsilon }}{{\partial t}} + \frac{{\partial {{p}_{\ell }}}}{{\partial y}} = 0.$Отметим, что уравнения (2) и (3) записаны с учетом малости слагаемых вида ${{\left( {\rho _{{\upsilon 0}}^{0} + \rho _{{a0}}^{0}} \right)} \mathord{\left/ {\vphantom {{\left( {\rho _{{\upsilon 0}}^{0} + \rho _{{a0}}^{0}} \right)} {\rho _{{l0}}^{0}}}} \right. \kern-0em} {\rho _{{l0}}^{0}}}$ и ${{\alpha }_{0}}$ по сравнению с единицей.
Примем, что возмущения давления в жидкости pl и пузырьках ${{p}_{g}} = {{p}_{\upsilon }} + {{p}_{a}}$ связаны уравнением Рэлея–Ламба, которое после линеаризации с учетом капиллярных сил имеет вид
Здесь $\nu _{\ell }^{{(\mu )}}$ – кинематическая вязкость жидкости.
В дальнейшем давление парогазовой смеси в пузырьках ${{p}_{g}}$ будем считать однородным (${{\partial {{p}_{g}}} \mathord{\left/ {\vphantom {{\partial {{p}_{g}}} {\partial r}}} \right. \kern-0em} {\partial r}} = 0$ – условие гомобаричности [8]), парциальные плотности пара, газа и температуры – неоднородными (${{\partial \rho _{\upsilon }^{'}} \mathord{\left/ {\vphantom {{\partial \rho _{\upsilon }^{'}} {\partial r}}} \right. \kern-0em} {\partial r}} \ne 0,$ ${{\partial \rho _{a}^{'}} \mathord{\left/ {\vphantom {{\partial \rho _{a}^{'}} {\partial r}}} \right. \kern-0em} {\partial r}} \ne 0,$ ${{\partial T_{g}^{'}} \mathord{\left/ {\vphantom {{\partial T_{g}^{'}} {\partial r}}} \right. \kern-0em} {\partial r}} \ne 0$). Знак “штрих” наверху означает, что эти параметры зависят, помимо $x,t,$ еще от радиальной координаты, отсчитываемой от центра пузырька.
Будем считать, что для парогазовой смеси в пузырьках выполняется закон Дальтона. Тогда уравнение Клапейрона–Менделеева можно записать в виде
(4)
$\begin{gathered} {{p}_{g}} = \rho _{g}^{'}B_{g}^{'}T_{g}^{'},\,\,\,\,B_{g}^{'} = {{B}_{a}} + ({{B}_{\upsilon }} - {{B}_{a}})k{\text{'}}, \\ k{\text{'}} = k_{\upsilon }^{'} = \frac{{\rho _{\upsilon }^{0}{\text{'}}}}{{\rho _{g}^{0}{\text{'}}}},\,\,\,\,\rho _{g}^{0}{\text{'}} = \rho _{\upsilon }^{0}{\text{'}} + \rho _{a}^{0}{\text{',}} \\ \end{gathered} $Запишем уравнение сохранения массы пузырьков
(5)
$\frac{{\partial {{m}_{g}}}}{{\partial t}} + u\frac{{\partial {{m}_{g}}}}{{\partial x}} + \upsilon \frac{{\partial {{m}_{g}}}}{{\partial y}} = 4\pi {{a}^{2}}j,\,\,\,\,{{m}_{g}} = \int\limits_0^a 4 \pi {{r}^{2}}\rho _{g}^{0}{\text{'}}dr,$Используя уравнение состояния (4) и последнее условие из (5), после линеаризации можем получить
(6)
$\begin{gathered} \frac{1}{{{{\rho }_{{g0}}}}}\frac{{\partial {{p}_{g}}}}{{\partial t}} + \frac{3}{{{{a}_{0}}}}\frac{{\partial a}}{{\partial t}} - \frac{3}{{a_{0}^{3}}} \times \\ \times \,\,\int\limits_0^a {{{r}^{2}}\left( {\frac{{{{B}_{\upsilon }} - {{B}_{a}}}}{{{{B}_{{g0}}}}}\frac{{\partial k{\text{'}}}}{{\partial t}} + \frac{1}{{{{T}_{0}}}}\frac{{\partial T{\kern 1pt} {\text{'}}}}{{\partial t}}} \right)} dr = \frac{{3j}}{{{{\rho }_{{g0}}}{{a}_{0}}}} \\ ({{B}_{{g0}}} = {{B}_{a}} + ({{B}_{\upsilon }} - {{B}_{a}}){{k}_{0}}). \\ \end{gathered} $Для учета межфазного тепломассообмена запишем уравнение теплопроводности и диффузии внутри пузырька и уравнение теплопроводности в жидкости вокруг пузырька
(7)
$\begin{gathered} \rho _{{g0}}^{0}{{c}_{g}}\frac{{\partial T_{g}^{'}}}{{\partial t}} = \frac{{{{\lambda }_{g}}}}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{\lambda }_{g}}{{r}^{2}}\frac{{\partial {{T}_{g}}}}{{\partial r}}} \right) + \frac{{\partial {{P}_{g}}}}{{\partial t}}, \\ \frac{{\partial k{\text{'}}}}{{\partial t}} = \frac{D}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}{{r}^{2}}\frac{{\partial k{\text{'}}}}{{\partial r}}\,\,\,(0 < r < {{a}_{0}}), \\ \rho _{{\ell 0}}^{0}{{c}_{\ell }}\frac{{\partial T_{\ell }^{'}}}{{\partial t}} = \frac{{{{\lambda }_{\ell }}}}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial T_{\ell }^{'}}}{{\partial r}}} \right)({{a}_{0}} < r < {{a}_{0}}\alpha _{{g0}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}). \\ \end{gathered} $На поверхности раздела фаз ($r = {{a}_{0}}$) зададим граничные условия, следующие из условий баланса тепла и массы:
(8)
$\begin{gathered} {{p}_{g}} = \rho _{{g(a)}}^{0}({{B}_{a}} + ({{B}_{\upsilon }} - {{B}_{a}}){{k}_{{(a)}}}){{T}_{{(a)}}}, \\ {{p}_{{\upsilon (a)}}} = {{p}_{s}}({{T}_{{(a)}}}) = \rho _{{g(a)}}^{0}{{B}_{a}}{{k}_{{(a)}}}{{T}_{{(a)}}}. \\ \end{gathered} $Здесь ${{p}_{\upsilon }}_{{(a)}}$ – парциальное давление на поверхности пузырька.
Из (8) следует
(9)
$\frac{{{{p}_{s}}({{T}_{{(a)}}})}}{{{{p}_{g}}}} = \frac{{{{B}_{\upsilon }}{{k}_{{(a)}}}}}{{{{B}_{a}} + ({{B}_{\upsilon }} - {{B}_{a}}){{k}_{{(a)}}}}}.$Кроме того, на поверхности раздела фаз для системы пар–вода должно выполняться уравнение Клапейрона–Клаузиуса
(10)
$\frac{{d{{p}_{{\upsilon (a)}}}}}{{d{{T}_{{(a)}}}}} = \frac{{\rho _{g}^{0}{{k}_{{(a)}}}L}}{{{{T}_{{(a)}}}}}.$Проведем линеаризацию уравнения (9). Для этого параметры ${{T}_{{(a)}}}$ и ${{k}_{{(a)}}}$ представим в следующем виде:
причемТогда из уравнения (9) с учетом (10), исключая верхние штрихи, можем получить
(11)
$\begin{gathered} \frac{{\rho _{{g0}}^{0}}}{{{{T}_{{g0}}}}}\frac{{{{T}_{{(a)}}}}}{{{{T}_{0}}}} - \frac{{{{B}_{\upsilon }}}}{{{{B}_{{g0}}}}}\frac{{{{p}_{g}}}}{{{{p}_{{g0}}}}} = \\ = \frac{{{{B}_{\upsilon }}{{B}_{a}}}}{{B_{{g0}}^{2}}}\frac{{{{k}_{{(a)}}}}}{{{{k}_{0}}}}\,\,({{B}_{{g0}}} = {{B}_{a}} + ({{B}_{\upsilon }} - {{B}_{a}}){{k}_{0}}). \\ \end{gathered} $Кроме того, для поля температур и концентрации пара должны выполняться следующие граничные условия:
(12)
$\begin{gathered} \frac{{\partial k{\text{'}}}}{{\partial r}} = 0,\,\,\,\,\frac{{\partial T_{g}^{'}}}{{\partial r}} = 0\,\,(r = 0); \\ T_{\ell }^{'} = 0\,\,(r = \infty )\,\,{\text{и л и }}\,\,\frac{{\partial T_{\ell }^{'}}}{{\partial r}} = 0\,\,(r = {{a}_{*}} = {{a}_{0}}\alpha _{0}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}). \\ \end{gathered} $Здесь ${{a}_{*}}$ – радиус ячейки в рамках ячеистой схемы [13]. Последнее условие в (12) – условие адиабатичности ячейки. В тех случаях, когда температурная неравновесность в жидкости вблизи пузырьков реализуется на расстояниях значительно меньших, чем межпузырьковые расстояния, вместо этого условия примем условие изотермичности вдали от пузырька ($T_{i}^{'} = 0,$ $r = \infty $).
Из уравнения (6) с учетом (7), (11) и граничных условий (12) можем получить
Запишем также выражение, аналогичное (6), для исходного равновесного состояния
Приведенные выше уравнения являются замкнутыми при заданных значениях параметров для искомого состояния смеси ${{P}_{{g0}}},$ ${{T}_{0}},$ ${{a}_{0}}$ и ${{\alpha }_{0}},$ а также коэффициентов, зависящих от теплофизических свойств системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть на плоскую границу раздела между “чистой” и газонасыщенной жидкостями падает плоская гармоническая волна. Будем полагать, как и в случае обычных однофазных сред, что отраженная от границы и преломленная волны являются плоскими гармоническими волнами [14]. Тогда в зоне воды малые возмущения представляют собой сумму двух гармонических волн, а в зоне пузырьковой жидкости – одну гармоническую волну. Возмущения, соответствующие падающей, отраженной и преломленной волнам, обозначим верхними индексами (0), (r) и (s). В рамках принятой модели пузырьковой жидкости вязкостные и теплообменные процессы учитываются лишь при межфазных взаимодействиях, смесь односкоростная, тензор напряжений – шаровой, жидкость – изотермическая. Поэтому на границе $x = 0,$ как и в случае однофазных сред, можно ограничиться лишь двумя граничными условиями: непрерывности давления и нормальной компоненты скорости:
(13)
$\begin{gathered} {{p}^{{(0)}}} + {{p}^{{(r)}}} = {{p}^{{(s)}}}, \\ {{\upsilon }^{{(0)}}}\cos {{\theta }^{{(0)}}} - {{\upsilon }^{{(r)}}}\cos {{\theta }^{{(r)}}} = {{\upsilon }^{{(s)}}}\cos {{\theta }^{{(s)}}}. \\ \end{gathered} $Здесь ${{\theta }^{{(0)}}},$ ${{\theta }^{{(r)}}}$ и ${{\theta }^{{(s)}}}$ – углы падения; ${{\upsilon }^{{(0)}}},$ ${{\upsilon }^{{(r)}}}$ и ${{\upsilon }^{{(s)}}}$ – возмущения скорости, соответствующие плоским падающим, отраженным и преломленным волнам. Тогда для падающей, отраженной и преломленной волн можем записать
Для волновых чисел K(0) и K(r) имеет место ${{K}^{{(0)}}} = {{K}^{{(r)}}} = {\omega \mathord{\left/ {\vphantom {\omega {{{C}_{\ell }}}}} \right. \kern-0em} {{{C}_{\ell }}}}.$
Волновое число K(s) определяется из дисперсионного уравнения
Данное дисперсионное уравнение следует из условия существования нетривиального решения приведенной выше системы в виде плоской затухающей бегущей волны
(15)
$\begin{gathered} \left( {p,\upsilon ,a,n} \right) = {{A}_{{(p)}}},{{A}_{{(\upsilon )}}},{{A}_{{(a)}}},{{A}_{{(n)}}}\exp [i\left( {Kx - \omega t} \right)], \\ T = {{A}_{{(T)}}}(r)\exp [i\left( {Kx - \omega t} \right)], \\ k = {{A}_{{(k)}}}(r)\exp [i\left( {Kx - \omega t} \right)]\,\,\,\, \\ \left( {K = k + i\delta ,{{C}_{p}} = {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k}} \right), \\ \end{gathered} $Амплитуды возмущений скоростей связаны с амплитудами давления выражениями вида
(16)
$A_{{(\upsilon )}}^{{(0)}} = \frac{{A_{{(p)}}^{{(0)}}}}{{{{\rho }_{{\ell 0}}}{{C}_{\ell }}}},\,\,\,A_{{(\upsilon )}}^{{(r)}} = - \frac{{A_{{(p)}}^{{(r)}}}}{{{{\rho }_{{\ell 0}}}{{C}_{\ell }}}},\,\,\,\,A_{{(\upsilon )}}^{{(s)}} = \frac{{{{K}^{{(s)}}}}}{\omega }\frac{{A_{{(p)}}^{{(s)}}}}{{\rho _{{\ell 0}}^{0}}}.$При этом для распределения концентраций и температуры внутри пузырьков будем иметь
Распределение температуры в жидкости при условиях адиабатичности или изотермичности ячеек описывается выражением
На основе условий (13) для решений вида (15) с учетом (16) при x = 0 получим
(17)
$\begin{gathered} A_{{(p)}}^{{(0)}}\exp \left( {i{{K}^{{(0)}}}n_{y}^{{(0)}}y} \right) + A_{{(p)}}^{{(r)}}\exp \left( {i{{K}^{{(r)}}}n_{y}^{{(r)}}y} \right) = \\ = A_{{(p)}}^{{(s)}}\exp \left( {i{{K}^{{(s)}}}n_{y}^{{(s)}}y} \right), \\ A_{{(p)}}^{{(0)}}\cos {{\theta }^{{(0)}}}\exp \left( {i{{K}^{{(0)}}}n_{y}^{{(0)}}y} \right) - \\ - \,\,A_{{(p)}}^{{(r)}}\cos {{\theta }^{{(r)}}}\exp \left( {i{{K}^{{(r)}}}n_{y}^{{(r)}}y} \right) = \\ = A_{{(p)}}^{{(s)}}\cos {{\theta }^{{(s)}}}\frac{{{{K}^{{(s)}}}}}{\omega }{{C}_{a}}\exp \left( {i{{K}^{{(s)}}}n_{y}^{{(s)}}y} \right). \\ \end{gathered} $Чтобы эти уравнения удовлетворялись для любых значений y, должны выполняться равенства
Отсюда имеем
(19)
$\sin {{\theta }^{{(0)}}} = \sin {{\theta }^{{(r)}}},\,\,\,\,\sin {{\theta }^{{(0)}}} = \left( {{{{{K}^{{(s)}}}} \mathord{\left/ {\vphantom {{{{K}^{{(s)}}}} \omega }} \right. \kern-0em} \omega }} \right){{C}_{\ell }}\sin {{\theta }^{{(s)}}}.$Поскольку определяемое из (14) волновое число K(s) – комплексное, то, как это следует из второго равенства (18), угол преломления также имеет мнимую часть.
Для коэффициентов отражения и преломления, определенных как R = ${{A_{{(p)}}^{{(r)}}} \mathord{\left/ {\vphantom {{A_{{(p)}}^{{(r)}}} {A_{{(p)}}^{{(0)}}}}} \right. \kern-0em} {A_{{(p)}}^{{(0)}}}}$ и S = ${{A_{{(p)}}^{{(s)}}} \mathord{\left/ {\vphantom {{A_{{(p)}}^{{(s)}}} {A_{{(p)}}^{{(0)}}}}} \right. \kern-0em} {A_{{(p)}}^{{(0)}}}},$ на основе (17) с учетом (18) получим
В том случае, когда волна падает со стороны пузырьковой жидкости на границу раздела, вместо второго равенства (19) имеем
Волновое число ${{K}^{{(0)}}}$ определяется из дисперсионного уравнения (14).
Для коэффициентов преломления и отражения в этом случае будем иметь
РЕЗУЛЬТАТЫ РАСЧЕТОВ
На рис. 2 и 3 представлены зависимости фазовой скорости (а) и коэффициента затухания (б) от частоты возмущений при ${{P}_{0}} = 0.1$ МПа и ${{\alpha }_{0}} = {{10}^{{ - 2}}}.$ Линии 1–3 соответствуют (здесь и в дальнейшем) значениям фазовой температуры ${{T}_{0}} = 300,$ 353, 373 К.
Рис. 2.
Дисперсионные зависимости при различных температурах (${{\alpha }_{0}} = {{10}^{{ - 2}}},$ ${{a}_{0}} = {{10}^{{ - 3}}}$ м).
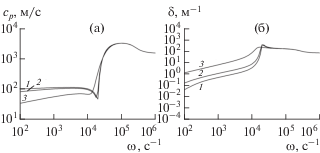
Рис. 3.
Дисперсионные зависимости при различных температурах (${{\alpha }_{0}} = {{10}^{{ - 2}}},$ ${{a}_{0}} = {{10}^{{ - 6}}}$ м).
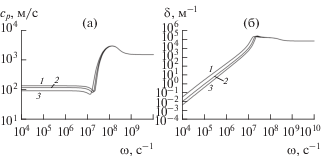
Дисперсионные зависимости, приведенные на рисунках, получены, соответственно, для крупнодисперсной (${{a}_{0}} = {{10}^{{ - 3}}}$ м, рис. 2) и мелкодисперсной (${{a}_{0}} = {{10}^{{ - 6}}}$ м, рис. 3) систем. Массовое паросодержание в пузырьках при указанных выше трех значениях температуры составляет для крупнодисперсной смеси ${{k}_{0}} = 0.023,$ 0.361, 0.996 и для мелкодисперсной смеси ${{k}_{0}} = 0.001,$ 0.147, 0.347.
Из сравнения кривых, представленных на рис. 2 и 3, видно, что в случае крупнодисперсной пузырьковой системы для низкочастотного диапазона ($\omega \leqslant {{\omega }_{R}},$ ${{\omega }_{R}} = a_{0}^{{ - 1}}\sqrt {{{3\gamma {{p}_{0}}} \mathord{\left/ {\vphantom {{3\gamma {{p}_{0}}} {\rho _{{\ell 0}}^{0}}}} \right. \kern-0em} {\rho _{{\ell 0}}^{0}}}} $ – миннаэртовская частота собственных колебаний пузырьков) наблюдается значительное влияние температуры на величину фазовой скорости (оно может различаться в сотни раз). Кроме того, когда система находится в точке кипения (${{T}_{0}} = 373$ К), отмечается сильная зависимость фазовой скорости от частоты возмущений. Это связано с тем, что при низких частотах повышается роль фазовых переходов и за счет них парогазовые пузырьки с небольшим массовым содержанием инертного газа (${{k}_{0}} = 0.996$) становятся менее упругими. Совершенно иную картину можно видеть вблизи низких частот для мелкодисперсной смеси (рис. 3). Здесь наблюдаются, во-первых, для всех трех значений температуры постоянство фазовой скорости, а во-вторых, достаточно слабая зависимость от величины равновесной температуры. Такая особенность в этом случае связана с повышением массовой концентрации инертного газа в пузырьках k0. Когда система находится в точке кипения, k0 составляет 0.347. Поэтому упругость пузырьков в основном определяется массовым содержанием газа. Отмеченные особенности фазовой скорости в зависимости от дисперсности и температуры системы предсказывают наличие определенных эффектов при прямом и косом падении гармонических волн на границу раздела между жидкостью и ее смесью с газовыми пузырьками.
Зависимости модулей и аргументов $\varphi $ и $\psi $ коэффициентов отражения и преломления от круговой частоты гармонических волн, падающих со стороны “чистой” жидкости на пузырьковую смесь с ${{a}_{0}} = {{10}^{{ - 3}}}$ м, для трех значений температуры представлены на рис. 4. На рис. 4–7 штриховые линии соответствуют изменениям угла.
Рис. 4.
Влияние равновесной температуры ${{T}_{0}}$ на коэффициенты отражения и преломления при прямом падении волны со стороны “чистой” жидкости при ${{\alpha }_{0}} = {{10}^{{ - 2}}},$ ${{a}_{0}} = {{10}^{{ - 3}}}$ м.
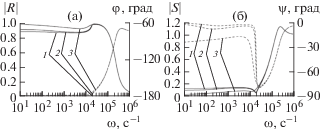
Рис. 5.
Влияние равновесной температуры ${{T}_{0}}$ на коэффициенты отражения и преломления при прямом падении волны со стороны “чистой” жидкости при ${{\alpha }_{0}} = {{10}^{{ - 2}}},$ ${{a}_{0}} = {{10}^{{ - 6}}}$ м.
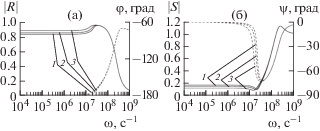
Рис. 6.
Зависимость коэффициентов отражения и преломления при прямом падении волны со стороны пузырьковой жидкости на границу раздела при ${{\alpha }_{0}} = {{10}^{{ - 2}}},$ ${{a}_{0}} = {{10}^{{ - 3}}}$ м.

Рис. 7.
Зависимость коэффициентов отражения и преломления при прямом падении волны со стороны пузырьковой жидкости на границу раздела при ${{\alpha }_{0}} = {{10}^{{ - 2}}},$ ${{a}_{0}} = {{10}^{{ - 6}}}$ м.

Из представленных графиков следует, что для низкочастотного диапазона ($\omega < {{\omega }_{R}}$) $\varphi \approx $ –180°, следовательно $R = - \left| R \right|.$ Соответственно, отраженная волна имеет отрицательную амплитуду. Причем наибольшая амплитуда отраженной волны ($R \approx 1$) реализуется для случая, когда система находится при точке кипения (${{T}_{0}} = 373$ К). Что касается проходящей волны, ее амплитуда для всех трех температур составляет меньше 10% ($\left| S \right| \leqslant 0.1$) от амплитуды падающей волны. Наименьшая амплитуда для падающей волны реализуется также при точке кипения. Отметим, что высокочастотные ветви кривых ($\omega > {{10}^{4}}$ с–1) для всех этих значений температуры сливаются. Это связано с тем, что при высоких частотах из-за инерции радиальное движение пузырьков “замораживается”. Поэтому акустический импеданс пузырьковой жидкости определяется скоростью звука “чистой” жидкости.
Для случая, когда пузырьковая жидкость мелкодисперсная (${{a}_{0}} = {{10}^{{ - 6}}}$ м), зависимости коэффициентов отражения и преломления представлены на рис. 5. Согласно расчетам, кривые для трех значений отличаются и для низкочастотного диапазона ($\omega < {{\omega }_{R}}$). Отмеченные отличия коэффициентов отражения и преломления в этом случае значительно меньше.
На рис. 6 и 7 приведены зависимости коэффициентов отражения и преломления (их модули и аргументы) при прямом падении волны со стороны пузырьковой жидкости в “чистую” жидкость для крупнодисперсной (${{a}_{0}} = {{10}^{{ - 3}}}$ м, рис. 6) и мелкодисперсной (${{a}_{0}} = {{10}^{{ - 6}}}$ м, рис. 7) систем. Видно, что аналогично случаю падения волны со стороны “чистой” жидкости в пузырьковую жидкость, в низкочастотной области ($\omega < {{\omega }_{R}}$) для $\varphi = 0^\circ ,$ следовательно $R = \left| R \right|.$ Что касается проходящей волны, ее амплитуда для всех трех температур увеличивается почти в два раза ($\left| S \right| \sim 1.9$). Это связано с тем, что по отношению к “чистой” жидкости пузырьковая жидкость является акустически более мягкой средой. Наибольшая амплитуда отраженной волны реализуется также в точке кипения.
Из результатов расчета видно, что в диапазоне частот ${{\omega }_{R}} < \omega < {{\omega }_{C}}$ (${{\omega }_{C}} = {{\omega }_{R}}\sqrt {1 + {{\rho _{{\ell 0}}^{0}{{\alpha }_{{g0}}}C_{\ell }^{2}} \mathord{\left/ {\vphantom {{\rho _{{\ell 0}}^{0}{{\alpha }_{{g0}}}C_{\ell }^{2}} {\gamma {{p}_{0}}}}} \right. \kern-0em} {\gamma {{p}_{0}}}}} $) величины коэффициента затухания и фазовой скорости принимают аномально высокие значения, поэтому данная зона частот соответствует полосе непропускания. Вне этого диапазона ($\omega > {{\omega }_{C}}$) скорость звука и коэффициент затухания стремятся к значениям
Хочется отметить, что проведение экспериментальных работ по рассматриваемой тематике представляется весьма сложным. Поэтому для апробации полученных результатов было проведено сравнение с результатами [8]. В предельном случае для параметров среды и волны, использованных в [8], а именно при отсутствии механизма диффузии, результаты, полученные по описанной выше модели, хорошо согласуются с приведенными в [8]. Использование фундаментальных законов механики и хорошее совпадение с данными других авторов позволяет говорить о достоверности результатов, изложенных в настоящей статье.
ЗАКЛЮЧЕНИЕ
Исследование гармонических волн в жидкости с паровоздушными пузырьками размером ${{a}_{0}} = {{10}^{{ - 3}}}$ м показало, что при изменении равновесной температуры от ${{T}_{0}} = 300$ К до точки кипения ${{T}_{0}} = 373$ К вблизи низких частот ($\omega \leqslant {{\omega }_{R}},$ ${{\omega }_{R}} = a_{0}^{{ - 1}}\sqrt {{{3\gamma {{p}_{0}}} \mathord{\left/ {\vphantom {{3\gamma {{p}_{0}}} {\rho _{{\ell 0}}^{0}}}} \right. \kern-0em} {\rho _{{\ell 0}}^{0}}}} $ – собственная частота пузырьков) коэффициент затухания меняется в десятки и сотни раз в зависимости от частоты возмущений. В случае же мелкодисперсных смесей (${{a}_{0}} = {{10}^{{ - 6}}}$ м) изменение фазовой скорости и коэффициента затухания гораздо слабее (не более двух раз). Это связано со снижением роли фазовых переходов для мелкодисперсных систем из-за роста массовой концентрации газа в пузырьках, связанного с действием капиллярных сил на межфазной поверхности.
Из результатов расчета видно, что в диапазоне частот ${{\omega }_{R}} < \omega < {{\omega }_{C}}$ (${{\omega }_{C}} = {{\omega }_{R}}\sqrt {1 + {{\rho _{{\ell 0}}^{0}{{\alpha }_{{g0}}}C_{\ell }^{2}} \mathord{\left/ {\vphantom {{\rho _{{\ell 0}}^{0}{{\alpha }_{{g0}}}C_{\ell }^{2}} {\gamma {{p}_{0}}}}} \right. \kern-0em} {\gamma {{p}_{0}}}}} $) коэффициент затухания и фазовая скорость принимают аномально высокие значения, поэтому данный диапазон соответствует полосе непропускания.
Показано, что при падении волны со стороны “чистой” жидкости на границу раздела она проходит в пузырьковую жидкость.
Данная статья расширяет результаты, которые были получены ранее и опубликованы в [15].
Работа авторов В.Ш. Шагапова и М.Н. Галимзянова поддержана средствами государственного бюджета по госзаданию на 2017–2019 гг. (№ 0246-2019-0052). Работа И.И. Вдовенко частично поддержана грантом РФФИ (№ 17-41-020582-р_а).
Список литературы
Ирвинг М., Ворцель Д. Распространение звуков взрыва в мелкой воде // Распространении звука в океане. Сб. ст. М.: Изд-во иностр. лит., 1951. 157 с.
Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1975. 343 с.
Бреховских Л.М., Лысанов Ю.П. Теоретические основы акустики океана. Л.: Гидрометеоиздат, 1982. 264 с.
Нигматулин Р.И., Шагапов В.Ш., Гималтдинов И.К., Галимзянов М.Н. Двумерные волны давления в жидкости, содержащей пузырьковые зоны // Докл. РАН. 2001. Т. 378. № 6. С. 763.
Галимзянов М.Н. Распространение волн сжатия в пузырьковых зонах конечных размеров // Вестн. Удм. ун-та. Математика. Механика. Компьютерные науки. 2010. № 2. С. 57.
Галимзянов М.Н. Распространение волн давления в пузырьковых зонах конечных размеров // Изв. Саратовск. ун-та. Новая серия. Математика. Механика. Информатика. 2010. Т. 10. № 4. С. 27.
Гафиятов Р.Н., Губайдуллин Д.А., Никифоров А.А. Распространение акустических волн в двухфракционных пузырьковых жидкостях с учетом фазовых превращений в каждой из фракций // МЖГ. 2013. № 3. С. 92.
Шагапов В.Ш., Зайнуллина О.А. Распространение малых возмущений во вскипающей жидкости, содержащей газовые зародыши // ТВТ. 2015. Т. 53. № 1. С. 91.
Губайдуллин Д.А., Федоров Ю.В. Звуковые волны в жидкостях с полидисперсными парогазовыми и газовыми пузырьками // Изв. РАН. МЖГ. 2015. № 1. С. 67.
Губайдуллин Д.А., Никифоров А.А., Гафиятов Р.Н. Акустические волны в многофракционных пузырьковых жидкостях // ТВТ. 2015. Т. 53. № 2. С. 250.
Губайдуллин Д.А., Терегулова Е.А., Губайдуллина Д.Д. Распространение акустических волн в многофракционных газовзвесях // ТВТ. 2015. Т. 53. № 5. С. 752.
Нигматулин Р.И. Динамика многофазных сред. Т. 1, 2. М.: Наука, 1987. 464 с.
Шагапов В.Ш., Вахитова Н.К. О распространении малых возмущений в парожидкостных пузырьковых средах // ПМТФ. 1984. № 5. С. 34.
Исакович М.А. Общая акустика. М.: Наука, 1973.
Шагапов В.Ш., Галимзянов М.Н., Вдовенко И.И., Хабеев Н.С. Особенности распространения звука в теплой воде с воздушными пузырьками // ИФЖ. 2018. Т. 91. № 4. С. 912.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур