Теплофизика высоких температур, 2019, T. 57, № 2, стр. 262-268
Трехмерное численное моделирование развития неустойчивости контактной границы сталкивающихся металлических пластин в газодинамическом приближении
С. В. Фортова 1, *, П. С. Уткин 1, Т. С. Казакова 2
1 Институт автоматизации проектирования РАН,
Москва, Россия
2 Московский физико-технический институт,
г. Долгопрудный, Россия
* E-mail: sfortova@mail.ru
Поступила в редакцию 23.08.2018
После доработки 10.10.2018
Принята к публикации 23.08.2018
Аннотация
Представлены результаты численного моделирования развития начальной стадии неустойчивости контактной границы соударяющихся металлических пластин. Математическая модель основывается на системе уравнений Эйлера для среды, подчиняющейся двучленному уравнению состояния. Параметры уравнения состояния откалиброваны по расчетно-экспериментальным данным на основе реальных широкодиапазонных уравнений состояния металлов. Вычислительный алгоритм основан на схеме Harten–Lax–van Leer. Начальное синусоидальное возмущение контактной границы между пластинами после прохождения волн разрежения от свободных границ пластин приобретает кратерообразную форму, что качественно соответствует натурным опытам.
ВВЕДЕНИЕ
Проблема взрывного упрочнения и сварки взрывом является актуальной задачей при получении высокопрочных биметаллических соединений [1]. Сварка взрывом представляет собой соединение металлов при высокоскоростном ударе под действием энергии, выделяющейся продуктами конденсированного взрывчатого вещества. Данный процесс сопровождается сложными динамическими эффектами, которые являются предметом многих экспериментальных и численных исследований.
На примере высокоскоростного соударения свинцовой пластины с пластинами из других металлов в работе [2] экспериментально изучены особенности процессов, происходящих в приграничных слоях соударяемых пластин. При соударении имеет место деформация пластин с образованием в ряде случаев прочного соединения. В результате выделения большой энергии происходит частичное плавление соприкасающихся поверхностей и переход металлов в упругопластическое состояние. Таким образом, в течение некоторого времени (порядка 10 мкс) после удара металлы находятся в упругопластическом состоянии и способны деформироваться псевдожидким образом прежде, чем начнется процесс перехода к упругому состоянию. Косвенным доказательством этого факта является обнаружение на поверхности стальной пластины кратерообразных выплесков в сторону свинцовой пластины, объяснение которым было дано в предположении развития неустойчивости Релея–Тэйлора (РТ). Данный вид неустойчивости может реализовываться в волне разрежения (ВР), приходящей на границу раздела пластин со стороны свободной поверхности свинца, если распад разрыва протекал с образованием двух ударных волн (УВ). Ускорение в ВР направлено в сторону металла меньшей плотности, что является необходимым условием возникновения неустойчивости РТ (градиенты скорости и плотности имеют разные знаки).
В [3] детально описываются результаты численного моделирования взаимодействия металлических пластин. Рассмотрены три случая: пластин одной толщины и одинаковой плотности, пластин одинаковой плотности и разной толщины, а также случай, когда толщина и плотность пластин различны. В каждом из них процесс начинается с расхождения УВ от контактной границы металлов, затем УВ доходят до свободных границ и отраженные волны разрежения распространяются внутрь пластин. Во всех трех случаях значительную роль играют разница во времени между моментами отражения волн от границ пластин и разные локации взаимодействия распространяющихся волн. В результате соударения двух одинаковых пластин между ними происходит взаимный обмен импульсами и энергиями. Приграничные области пластин испытывают динамическое растяжение за счет остановки основной части метаемой пластины, ускорения другой пластины до начальной скорости метания и наличия линейного распределения скорости лишь в приграничных областях пластин. В процессе такого динамического растяжения происходит нарушение контакта между пластинами. В случае, когда пластины имеют разную толщину, УВ достигают свободных границ в разные моменты времени, вследствие чего отразившаяся ВР движется вдогонку УВ, еще не достигшей свободной границы более толстой пластины. В дальнейшем волны разрежения и сжатия взаимодействуют во внутренней области пластин, причем в отсутствие диссипации в системе это может продолжаться сколь угодно долго. Кроме того, сделано замечание, что размазанность ВР обусловлена механизмом ее распространения в среде малых возмущений. Головному участку волны соответствуют малые возмущения, распространяющиеся в сжатой среде, а хвостовому – в среде, полностью разгруженной до начальных значений плотности и давления. Протяженность фронта волны разрежения в более сжатой среде возникает из-за бóльшей скорости распространения малых возмущений, а не только по причине наличия псевдовязкости, как это происходит в УВ.
В [4] указано, что возникающее в момент столкновения пластин давление значительно превышает динамические пределы прочности соударяющихся металлов, поэтому предлагается использовать в первом приближении гидродинамическую модель, в которой давление p, внутренняя энергия ε и плотность ρ связаны соотношением вида
(1)
$p = \left( {\gamma - 1} \right)\rho \varepsilon + \left( {\rho - {{\rho }_{0}}} \right)c_{0}^{2},$В [5] моделируется столкновение пластин с искривленной формой контактной границы. Форма возмущения является синусоидальной, ее линейный размер порядка 1 мм. Расходящиеся УВ в таком случае имеют искривленную форму, а возникающие области высокого давления в области оси симметрии одной пластины и на границе области возмущения между УВ в области другой пластины приводят к деформации границы раздела сред и торможению на оси симметрии. Процесс роста давления в них продолжается до момента, пока они сами не станут источниками волн сжатия. Взаимодействие волн сжатия и искривленных фронтов первичных УВ приводит к выравниванию фронтов, однако деформация границы при сложившейся картине течения будет продолжаться до прихода ВР со свободных границ пластин. Волны разрежения, проходя через контактную границу, создают внешнее переменное ускорение, приводящее к развитию неустойчивости РТ на контактной границе.
Еще один вариант постановки задачи моделирования высокоскоростного столкновения металлических пластин рассмотрен в [6], где решаются трехмерные уравнения Эйлера и уравнение состояния (УРС) идеального газа. Кроме того, в рассматриваемой области присутствует внешнее ускорение, направленное в сторону стальной пластины и имеющее величину 107 м/с2, а в качестве начального возмущения используется точечное возмущение скорости в центре контактной границы между пластинами.
Данная работа является продолжением и развитием исследования [6]. Ее цель – численное исследование развития неустойчивости контактной границы металлических пластин при их высокоскоростном соударении в рамках газодинамического приближения с использованием двучленного уравнения состояния среды.
ПОСТАНОВКА ЗАДАЧИ
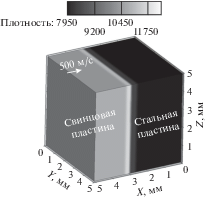
Рассмотрим взаимодействие свинцовой и стальной пластин в виде параллелепипедов с размерами 5 × 5 × 2 и 5 × 5 × 3 мм соответственно (рис. 1). Свинцовая пластина плотностью 11 300 кг/м3 налетает на покоящуюся стальную плотностью 7900 кг/м3 со скоростью 500 м/с. Всюду в начальный момент времени задается давление 105 Па. Предполагается, что в течение порядка 10 мкс металлы ведут себя как псевдожидкости [2], поэтому справедливы уравнения газовой динамики.
На поверхностях, параллельных разделу сред, заданы граничные условия втекания (табл. 1). До прихода на границу УВ задаются параметры втекания с начальными характеристиками свинцовой и стальной пластин. В момент прихода УВ на границу параметры втекания меняются таким образом, чтобы обеспечить формирование ВР, распространяющихся внутрь расчетной области. Данные параметры подбирались на основании анализа (p–v)-диаграмм [7], описывающих решение задачи о распаде разрыва на “свободных” границах пластин. На остальных границах устанавливаются периодические граничные условия.
Таблица 1.
Параметры граничных условий
| Плоскость X = 0 мм | Плоскость X = 5 мм | ||
|---|---|---|---|
| $t \leqslant 0.88{\text{ м к с }}$ | $t > 0.88{\text{ м к с }}$ | $t \leqslant 0.92{\text{ м к с }}$ | $t > 0.92{\text{ м к с }}$ |
| $\begin{gathered} \rho _{{{\text{in}}}}^{1} = 7900{\text{ }}{{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{3}}}}}} \hfill \\ u_{{{\text{in}}}}^{1} = \text{v}_{{{\text{in}}}}^{1} = w_{{{\text{in}}}}^{1} = 0{\text{ }}{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}} \hfill \\ p_{{{\text{in}}}}^{1} = {{10}^{5}}{\text{ П а }} \hfill \\ \end{gathered} $ | $\begin{gathered} \rho _{{{\text{in}}}}^{2} = 7900{\text{ }}{{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{3}}}}}} \hfill \\ u_{{{\text{in}}}}^{2} = - 544.8{\text{ }}{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}} \hfill \\ \text{v}_{{{\text{in}}}}^{2} = w_{{{\text{in}}}}^{2} = 0{\text{ }}{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}} \hfill \\ p_{{{\text{in}}}}^{2} = {{10}^{5}}{\text{ П а }} \hfill \\ \end{gathered} $ | $\begin{gathered} \rho _{{{\text{in}}}}^{1} = 11{\kern 1pt} 300{\text{ }}{{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{3}}}}}} \hfill \\ u_{{{\text{in}}}}^{1} = - 500{\text{ }}{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}} \hfill \\ \text{v}_{{{\text{in}}}}^{1} = w_{{{\text{in}}}}^{1} = 0{\text{ }}{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}} \hfill \\ p_{{{\text{in}}}}^{1} = {{10}^{5}}{\text{ П а }} \hfill \\ \end{gathered} $ | $\begin{gathered} \rho _{{{\text{in}}}}^{2} = 11{\kern 1pt} 300{\text{ }}{{{\text{к г }}} \mathord{\left/ {\vphantom {{{\text{к г }}} {{{{\text{м }}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м }}}^{{\text{3}}}}}} \hfill \\ u_{{{\text{in}}}}^{2} = - 45{\text{ }}{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}} \hfill \\ \text{v}_{{{\text{in}}}}^{2} = w_{{{\text{in}}}}^{2} = 0{\text{ }}{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {\text{с }}}} \right. \kern-0em} {\text{с }}} \hfill \\ p_{{{\text{in}}}}^{2} = {{10}^{5}}{\text{ П а }} \hfill \\ \end{gathered} $ |
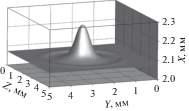
В некоторый момент времени после формирования УВ задается имеющее осесимметричную синусоидальную форму искривление контактной границы между пластинами в сторону более тяжелой (рис. 2). В качестве ориентира для выбора размеров возмущения взят линейный размер возмущения формы в [5]: 1 мм при толщине покоящейся пластины 4.68 и толщине метаемой 3.9 мм. Возмущение формы границы между пластинами в начальный момент времени представляет определенную сложность, поскольку в таком случае необходима более сложная обработка граничных условий, обеспечивающих возникновение ВР. При этом фронт УВ не будет параллелен свободной границе, т.е. УВ будет доходить до разных точек на границе в разные моменты времени. Но даже в случае плоской границы моменты переключения параметров втекания были подобраны для каждой границы экспериментально. Реализация более сложного варианта не представляется возможной без автоматизации процесса подбора или расчета параметров втекания. Поэтому был выбран момент времени после того, как УВ разойдутся от контактной границы на некоторое расстояние, чтобы не наложить возмущение на область, где они в этот момент распространяются, но до того момента, когда ВР достигнут контактной границы пластин. Форма возмущения плоской контактной границы s (x, y) = 0 определяется формулой (рис. 2)
(2)
$\begin{gathered} d\left( {y,z} \right) = A\sin \left( {y{\text{'}}} \right)\sin \left( {z{\text{'}}} \right), \\ y{\text{'}} = \frac{\pi }{B}\left| {y - {{y}_{0}}} \right| + \frac{\pi }{2},\,\,\,\,z{\text{'}} = \frac{\pi }{B}\left| {z - {{z}_{0}}} \right| + \frac{\pi }{2}, \\ y - {{y}_{0}} \in [ - \pi {\text{/}}2;\pi {\text{/}}2],\,\,\,z - {{z}_{0}} \in [ - \pi {\text{/}}2;\pi {\text{/}}2], \\ \end{gathered} $МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Математическая модель основывается на трехмерной системе уравнений Эйлера для среды с двучленным УРС, записанной в декартовой системе координат (x, y, z)
(3)
$\begin{gathered} {{{\mathbf{U}}}_{t}} + {{{\mathbf{F}}}_{x}}\left( {\mathbf{U}} \right) + {{{\mathbf{G}}}_{y}}\left( {\mathbf{U}} \right) + {{{\mathbf{H}}}_{z}}\left( {\mathbf{U}} \right) = {\mathbf{0}}, \\ {\mathbf{U}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u} \\ {\rho \text{v}} \\ {\rho w} \\ E \end{array}} \right],\,\,\,\,{\mathbf{F}} = \left[ {\begin{array}{*{20}{c}} {\rho u} \\ {\rho {{u}^{2}} + p} \\ {\rho u\text{v}} \\ {\rho uw} \\ {\left( {E + p} \right)u} \end{array}} \right], \\ {\mathbf{G}} = \left[ {\begin{array}{*{20}{c}} {\rho \text{v}} \\ {\rho \text{v}u} \\ {\rho {{\text{v}}^{2}} + p} \\ {\rho \text{v}w} \\ {\left( {E + p} \right)\text{v}} \end{array}} \right],\,\,\,\,{\mathbf{H}} = \left[ {\begin{array}{*{20}{c}} {\rho w} \\ {\rho wu} \\ {\rho w\text{v}} \\ {\rho {{w}^{2}} + p} \\ {\left( {E + p} \right)w} \end{array}} \right], \\ E = \frac{\rho }{2}\left( {{{u}^{2}} + {{\text{v}}^{2}} + {{w}^{2}}} \right) + \rho \varepsilon \left( {p,\rho } \right),\,\,\,\,\varepsilon \left( {p,\rho } \right) = \frac{{p + \gamma {{p}_{0}}}}{{\rho \left( {\gamma - 1} \right)}}. \\ \end{gathered} $Здесь ρ, u, $\text{v},$ w, E, p, ε, γ – плотность, три компоненты скорости, полная энергия на единицу объема среды, давление, удельная внутренняя энергия и показатель адиабаты газа, U – вектор консервативных переменных, F(U), G(U) и H(U) – векторы потоков вдоль осей x, y и z соответственно. УРС (3), известное в англоязычной литературе как “stiffened gas equation of state”, является несколько более простым вариантом двучленного УРС (1).
Параметры двучленного УРС были откалиброваны по расчетно-экспериментальным данным, чтобы обеспечить количественно разумные параметры УВ, которые образуются при соударении. Процесс подбора констант УРС изложен ниже.
ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ
Был использован метод расщепления по пространственным переменным. На каждом шаге по времени для каждого из трех пространственных направлений выполняется следующий алгоритм: поочередно из расчетной области выбираются одномерные слои, в каждом слое применяется одномерный метод Harten–Lax–van Leer (HLL), переменные обновляются, после чего полученные значения переменных становятся входными для расчета в другом направлении:
Здесь i, j и k – пространственные индексы ячеек структурированной расчетной сетки вдоль координатных направлений x, y и z соответственно; n – временнóй индекс; Lx, Ly и Lz – одномерные операторы разностной схемы в процедуре расщепления. Обозначим шаги расчетной сетки вдоль координатных направлений через hx, hy и hz. Опишем в качестве примера действие оператора Lx. Используется следующая конечно-объемная аппроксимация и явная схема Эйлера интегрирования по времени:
(4)
$\frac{{{\mathbf{\tilde {U}}}_{{i,j,k}}^{{n + 1}} - {\mathbf{U}}_{{i,j,k}}^{n}}}{{\Delta {{t}^{n}}}} + \frac{{{\mathbf{F}}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{{{\text{HLL}}}} - {\mathbf{F}}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{{{\text{HLL}}}}}}{{{{h}_{x}}}} = 0,$(5)
$\begin{gathered} {\mathbf{F}}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{{{\text{HLL}}}} = \frac{{S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ + }{\mathbf{F}}\left( {{\mathbf{U}}_{{i,j,k}}^{n}} \right) - S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ - }{\mathbf{F}}\left( {{\mathbf{U}}_{{i + 1,j,k}}^{n}} \right) + S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ + }S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ - }\left( {{\mathbf{U}}_{{i + 1,j,k}}^{n} - {\mathbf{U}}_{{i,j,k}}^{n}} \right)}}{{S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ + } - S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ - }}}, \\ S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ + } = \max \left( {u_{{i,j,k}}^{n} + c_{{i,j,k}}^{n},{\text{ }}u_{{i + 1,j,k}}^{n} + c_{{i + 1,j,k}}^{n},{\text{ }}0} \right),\,\,\,\,S_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}^{ - } = \min \left( {u_{{i,j,k}}^{n} - c_{{i,j,k}}^{n},{\text{ }}u_{{i + 1,j,k}}^{n} - c_{{i + 1,j,k}}^{n},{\text{ }}0} \right). \\ \end{gathered} $Шаг интегрирования по времени Δt n выбирается динамически для выполнения условия устойчивости [4]. Для двучленного УРС (2) скорость звука c задается выражением
Стоит обратить внимание, что численный поток HLL зависит только от скорости звука и не зависит от конкретного вида УРС среды, что делает данный метод привлекательным для моделирования течений сред со сложными УРС, в том числе заданными в табличном виде. Тильда над вектором переменных в (4) означает, что это не переменные на следующем временнóм шаге, а вектор входных данных для следующего этапа процедуры расщепления по пространственным направлениям.
Второй порядок аппроксимации достигнут с помощью кусочно-линейного восполнения сеточных функций консервативных переменных с использованием ограничителя minmod [8, 9]:
Для вектора функция minmod применяется покомпонентно. Численный поток HLL (5) тогда модифицируется следующим образом:
КАЛИБРОВКА ПАРАМЕТРОВ УРС И ВЕРИФИКАЦИЯ
Для воспроизведения количественно корректных характеристик процесса взаимодействия металлических пластин требуется откалибровать константы γ и p0 в двучленном УРС (3). Данные константы калибровались по характеристикам образовавшихся при соударении УВ с использованием расчетно-экспериментальных данных [10–12]. В табл. 2 приведено сравнение рассчитанных характеристик УВ для найденных значений γ = 3.0, p0 = 25 ГПа с данными [10–12], полученными с использованием реальных широкодиапазонных УРС стали и свинца. Через $D$ обозначена скорость УВ в лабораторной системе координат. В скобках приведены относительные погрешности рассчитанных характеристик в сравнении с [10–12]. Для найденных значений γ и p0 получено удовлетворительное согласие (по всем величинам отклонение не более 30%), позволяющее использовать данный набор параметров УРС для дальнейшей работы.
Таблица 2.
Рассчитанные характеристики УВ в стали и свинце
| Параметры за УВ в стали | |||
|---|---|---|---|
| p, ГПа | ρ, кг/м3 | u, м/с | D, км/с |
| 7.24 (–9%) | 8595 (+4%) | 272 (+29%) | 3.40 (–28%) |
| Параметры за УВ в свинце | |||
| 7.24 (–9%) | 12 294 (–5%) | 272 (+29%) | 2.38 (+21%) |
Верификация реализованного метода проводилась на тестах, приведенных в статье [13]. Расчетная область – отрезок [0,1]. Расчетная сетка – равномерная с числом ячеек 100. В начальный момент времени во всей расчетной области задаются одинаковые параметры, например
Рассмотрение производится в безразмерных переменных. На левой границе выставляется условие непротекания, на правой – условие втекания с параметрами, равными начальным условиям. Во всех тестах начальная скорость среды направлена в сторону стенки. Таким образом, происходит отражение от стенки с формированием отошедшей УВ. Среда описывается уравнением состояния вида (1) с константами
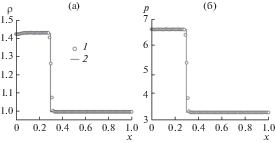
Рис. 3 иллюстрирует сравнение рассчитанных профилей давления и плотности среды с аналитическим решением задачи [4] на момент времени 0.13.
Рис. 3.
Результаты расчета теста из [13] для плотности среды (а) и давления (б): 1 – расчет авторов, 2 – точное решение.
РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
Форма возмущения в (2) описывалась значениями параметров A = 0.633 и B = 1.24 мм. Напомним, что возмущение формы происходило уже после того, как УВ разошлись на достаточное расстояние. Расчеты проводились на сетке 300 × 121 ×121. Вдоль каждого из координатных направлений сетка была равномерной.
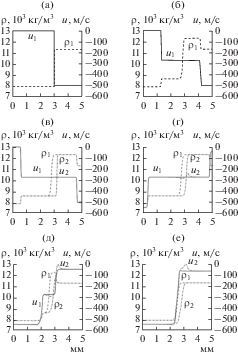
Рассмотрим сначала динамику процесса на одномерных распределениях вдоль выделенных направлений, параллельных оси x (рис. 4). Первое направление (индекс 1) проходит вдалеке от начального возмущения и фактически описывает решение соответствующей одномерной задачи. Второе – через геометрический центр возмущения (индекс 2). Рис. 4а соответствует моменту, когда стальная пластина еще покоится, а свинцовая пластина налетает на нее со скоростью 500 м/с. После столкновения от контактной границы расходятся две УВ (рис. 4б). В момент времени $t = 0.62{\text{ м к с }}$ накладывается синусоидальное возмущение формы, описанное выше. Поскольку на контактном разрыве давление и скорость непрерывны, изменяется лишь распределение плотности в расчетной области (рис. 4в). Когда УВ достигают свободных границ (это происходит в разное время), от последних внутрь пластин распространяются ВР (рис. 4г, 4д). Проходя через контактную границу (рис. 4е), ВР создают ускорение, которое и способствует возникновению неустойчивости РТ. Обратим внимание, что после прохождения ВР от свободных границ скорость среды в окрестности контактной границы изменяет знак, наблюдается ее локальной максимум (рис. 4д), что можно трактовать как начало формирования выплеска в сторону свинцовой пластины.
Рис. 4.
Начальное возмущение – выпуклость в сторону свинца; распределение плотности ρ и х-компоненты скорости u в двух срезах: вдоль границы вдали от возмущения ρ1, u1 и в центре симметрии пластин ρ2, u2: (а) t = 0, (б) 0.5, (в) 0.7, (г) 1.0, (д) 1.6, (е) 1.8 мкс.
Для визуализации структур в окрестности контактной границы проанализированы изоповерхности плотности, давления и продольной компоненты скорости. Рис. 5 иллюстрирует изоповерхность плотности 7200 кг/м3 в окрестности контактной границы между металлами. Начальное возмущение контактной границы, представленное на рис. 2, приобретает кратерообразную форму, качественно соответствующую наблюдаемым структурам в опытах [2].
ЗАКЛЮЧЕНИЕ
В работе представлен численный метод для исследования начальной стадии развития неустойчивости контактной границы металлических пластин при их высокоскоростном соударении. Решаются трехмерные уравнения Эйлера для среды с двучленным уравнением состояния в области со специально сконструированными граничными условиями, моделирующими свободные границы пластин. Вычислительный алгоритм второго порядка аппроксимации по пространственным переменным на гладких решениях основан на схеме Harten–Lax–van Leer. Проведена калибровка параметров уравнения состояния для задачи о соударении металлических пластин с использованием расчетно-экспериментальных данных сотрудников ОИВТ РАН и ИПХФ РАН.
Проведено численное исследование задачи высокоскоростного соударения свинцовой и металлической пластин в постановке, соответствующей натурным опытам [2]. Качественно и количественно верно воспроизведены стадии формирования ударных волн, их взаимодействие со свободными границами пластин с образованием волн разрежения, взаимодействие волн разрежения с контактной границей металлов. Исследовано развитие возмущения формы контактной границы после однократного прохождения через нее волн разрежения. Продемонстрировано, что начальное синусоидальное возмущение контактной границы между пластинами после прохождения волн разрежения от свободных границ пластин приобретает кратерообразную форму, что качественно соответствует натурным опытам [2].
Вместе с тем количественные характеристики полученной кратерообразной структуры отличаются от наблюдаемых в опытах [2]. К возможным причинам следует отнести несовершенство математической модели, а также связанную с этим постановку задачи. По-видимому, для получения более явного эффекта требуется моделирование на бóльших временах, учитывая многократное прохождение волн разрежения через контактную границу пластин. Для этого требуется переходить к многожидкостным моделям, когда металлы описываются сжимаемыми несмешивающимися континуумами, каждый из которых характеризуется своим уравнением состояния. Работа в данном направлении ведется [14]. Для лучшего количественного согласия с экспериментом также требуется применять более сложную модель среды, т.е. уравнение состояния (см. обзор [12]), которое позволит более точно учесть сложную динамику волн сжатия и разрежения на длительных временах.
Работа выполнена в ИАП РАН при поддержке Российского научного фонда (соглашение № 17-11-01293).
Список литературы
Дерибас А.А. Физика упрочнения и сварки взрывом. Новосибирск: Наука, 1972. 188 с.
Яковлев И.В. Неустойчивость границы раздела соударяющихся поверхностей металлов // ФГВ. 1973. Т. 9. № 3. С. 447.
Бабкин А.В. Численные методы в задачах физики быстропротекающих процессов. М.: Изд-во МГТУ им. Баумана, 2006. 520 с.
Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. М.: Наука, 1976. С. 309.
Демченко В.В., Сергеев М.А. Гидродинамическая неустойчивость при высокоскоростном ударе // Мат. мод. 2002. Т. 14. № 10. С. 87.
Белоцерковский О.М., Фортова С.В., Трошкин О.В., Пронина А.П., Ериклинцев И.В., Козлов С.А. Численное моделирование высокоскоростного столкновения металлических пластин // Мат. мод. 2016. Т. 28. № 2. С. 19.
Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, 1992. 424 с.
Колган В.П. Применение принципа минимальных значений производной к построению конечноразностных схем для расчета разрывных решений газовой динамики // Уч. запис. ЦАГИ. 1972. Т. 3. № 6. С. 68.
Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001. 608 с.
Fortov V.E., Khishchenko K.V., Levashov P.R., Lomonosov I.V. Wide-Range Multi-Phase Equations of State for Metals // Nuc. Instr. Meth. Phys. Res. Sect. A. 1998. V. 415. P. 604.
Shock Wave Database. Электронный ресурс, режим доступа: http://www.ihed.ras.ru/rusbank/.
Ломоносов И.В., Фортова С.В. Широкодиапазонные полуэмпирические уравнения состояния вещества для численного моделирования высокоэнергетических процессов // ТВТ. 2017. Т. 55. № 4. С. 596.
Glaister P. An Approximate Linearised Riemann Solver for the Euler Equations for Real Gases // J. Comp. Phys. 1988. V. 74. P. 382.
Utkin P.S., Fortova S.V. Mathematical Modeling of Impact of Two Metal Plates using Two-Fluid Approach // J. Phys.: Conf. Ser. 2018. V. 946. 012047.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур