Теплофизика высоких температур, 2019, T. 57, № 2, стр. 246-252

ВВЕДЕНИЕ

Движение фрагментов жидкости (пленки, ручейков, капель) по твердому телу исследуется в течение длительного времени как теоретически, так и экспериментально в приложении к проблемам энергетики, химической промышленности, безопасности полетов [1–6]. При этом широкие диапазоны управляющих параметров (скоростей и температур, определяющих режим обтекания, размеров капель, значений коэффициента поверхностного натяжения, теплофизических свойств жидкости), естественно, приводят к использованию математических моделей различного уровня сложности.

Достаточно подробно исследован случай капель, находящихся на вертикальной или наклонной плоскостях в неподвижном газе, а также обтекаемых газом в стоксовом режиме. Однако в случае скоростей, характерных для авиации (порядка десятков и сотен метров в секунду) [6, 7], исследование осложнено наличием пограничного слоя толщиной порядка размера самой капли, причем изменяющейся вдоль траектории последней. Кроме того, этот слой изобилует трехмерными и, вообще говоря, нестационарными структурами. В частности, предсказание места возникновения так называемого барьерного льда (наиболее коварного вида обледенения) требует исследования гидротермодинамики капли с учетом ее охлаждения до температуры замерзания и ниже. Эти факты также вызывают необходимость прибегать к упрощенным моделям динамики капли, движущейся в пограничном слое с изменяющимся отношением их масштабов.

В настоящей работе предложена физико-математическая модель гидродинамики капли, учитывающая вязкую и аэродинамическую силы, увлекающие каплю вдоль поверхности, поверхностное натяжение и диссипацию энергии в объеме, препятствующие движению капли. Дано описание экспериментов на аэродинамическом стенде, результаты которых послужили для валидации теоретической модели.

ФИЗИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ КАПЛИ НА ПЛОСКОЙ ПОВЕРХНОСТИ В ГАЗОВОМ ПОТОКЕ

В мировой литературе описаны многочисленные попытки построения математической модели капли на плоской поверхности. Отметим лишь некоторые результаты. Исследовалась зависимость нормальной и касательной компонент силы, действующей на частицу, движущуюся вблизи стенки или соприкасающуюся со стенкой. Ставшее классическим выражение “подъемной” силы Сэфмана описывает ее зависимость от градиента продольной скорости газа в пограничном слое и силы Стокса в безграничном потоке. Известно, что близость стенки и турбулизация потока приводят к противоположным результатам. Так, с одной стороны, в [8] получено, что подъемная сила шара у твердой поверхности может на один–два порядка “превышать величину, рассчитанную по известным выражениям”. С другой стороны, в [9] показано, что турбулизация потока, обтекающего свободный шар, которая проводит к росту коэффициента кинематической вязкости в 2000 раз в сравнении с молекулярной вязкостью, сопровождается значительным уменьшением коэффициентов сопротивления (в 4–7 раз) и теплообмена (в 3–6 раз).

В обзоре [10] сделано характерное замечание об одной из таких попыток учесть влияние стенки на аэродинамическую силу введением поправочного коэффициента, “который зависит от геометрии, температуры, свойств подложки, что ограничивает полезность модели”. Несмотря на эти данные, в [11] для коэффициента сопротивления C_D в функции от числа Рейнольдса частицы успешно использована стандартная зависимость, имеющая в качестве асимптотических выражения 24/Re_d (стоксов режим) и 0.44 (ньютонов предел). Здесь Re_d = d |u₁–u|/ν_a – число Рейнольдса частицы; d – диаметр капли, u – скорость капли, u₁ – скорость газа в пограничном слое на некотором характерном расстоянии от поверхности масштаба самой капли, ν_a – кинематическая вязкость воздуха.

В настоящей работе принята традиционная модель капли на обдуваемой газом поверхности, аналогичная использованной в работе [3], имеющая вид шарового сегмента при нулевой относительной скорости (рис. 1). Более того, в [3] при движении по поверхности капля сохраняет форму усеченного шара (рис. 1б), что соответствует нулевому значению Г = cos θ_R – cos θ_A = 0. Предложенная авторами система уравнений в качестве одного из наиболее важных содержит уравнение динамики

где ${{F}_{a}} = \frac{1}{2}{{C}_{D}}{{{\rho }}_{g}}{{S}_{ \bot }}\left| {{{u}_{1}} - u} \right|\left( {{{u}_{1}} - u} \right){{\xi }_{D}}$ – аэродинамическая сила, ${{F}_{{\sigma }}} = - 2b{\sigma (cos}{{{\theta }}_{R}} - \cos {{{\theta }}_{A}})$ – сила адгезии, ${{F}_{{\mu }}} = - {{{\mu }}_{l}}\frac{{\pi {{b}^{2}}}}{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}}}u$ – диссипативная сила, ${{F}_{{\alpha }}} = mg\sin {\alpha }$ – тангенциальная компонента силы тяжести;

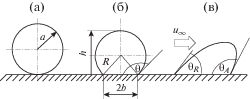
Здесь m – масса капли; μ_g, ρ_g – вязкость и плотность увлекающего газа; μ_l, ρ_l, σ – вязкость, плотность и коэффициент поверхностного натяжения воды; θ – статический угол смачивания; ξ_D – поправочный множитель, учитывающий близость капли к поверхности тела. Геометрические характеристики (рис. 1): a – радиус объемно-эквивалентной сферической капли, R – радиус сферической части поверхности капли, b – радиус пятна контакта, h – “высота” капли над плоскостью, g – ускорение земного тяготения, α – угол наклона плоскости, S_⊥ – площадь сечения капли, перпендикулярного поверхности модели.

В ряде работ также подтверждено, что, хотя центр масс капли смещается в направлении движения (относительно центра пятна контакта), его высота над поверхностью плоского тела почти не меняется. Поэтому можно считать, что высота усеченной капли h не зависит от гистерезиса угла смачивания Δθ = θ_A – θ_R. В ранних работах, в частности в [12], принималось, что значения наветренного (индекс R) и подветренного (индекс A) углов (рис. 1в) симметричны относительно стационарного значения θ. В настоящей работе такое предположение не используется. В [13] для капель радиусом около 1–3 мм получено, что гистерезис не зависит от размера капли. В настоящей работе также исследовались капли миллиметрового диапазона.

В правой части уравнения динамики капли первое слагаемое имитирует стоксову и аэродинамическую силы. Коэффициент ξ_D должен учитывать влияние подложки. Второе слагаемое моделирует влияние внутреннего трения, связанного с коэффициентом вязкости самой жидкости μ_l, причем отношение u/(h/2) имитирует градиент скорости внутреннего течения. В работе [14] в точно таком же виде представлены вязкие потери внутри капли, движущейся по поверхности. Отметим, что в ряде работ этим слагаемым пренебрегают на том основании, что поверхностное натяжение препятствует возникновению движения жидкости в объеме малой капли. По оценкам авторов, это слагаемое не превосходит 10% от аэродинамической силы. Третье слагаемое связано с тормозящим влиянием твердой подложки. Наконец, последнее слагаемое – компонента силы тяжести на наклонной плоскости.

В случае θ → π (идеально гидрофобная поверхность) имеем b = 0, h = d, R = d/2 (капля становится сферической) и при значениях ξ_g = 6π и ξ_D = 1 из уравнения (1) получаем уравнение динамики шара в безграничном потоке.

Теплообмен капли с увлекающим потоком газа и твердой подложкой оказывает влияние на ее динамику в основном через температурные зависимости вязкостей газа µ_g и жидкости µ_l. В рассмотренном диапазоне управляющих параметров это влияние оказалось несущественным, а влияние испарения капли вообще пренебрежимо малым. Поэтому соответствующие уравнения здесь не приводятся.

Для расчета скорости невязкого течения вдоль поверхности обтекаемого профиля использовался известный метод конформных отображений. Уравнение Лапласа для потенциала течения φ в любых прямоугольных криволинейных координатах ξ, η, являющихся конформным отображением декартовой сетки, имеет одинаковый вид [15]

Решение этого уравнения для безциркуляционного обтекания профиля может быть записано в виде

где А, γ – некоторые постоянные.

Для нахождения криволинейной системы координат, связанной с обтекаемым профилем, нужно конформно отобразить внешность профиля на внешность единичного круга, что, как правило, можно сделать лишь приближенно, используя, например, метод тригонометрической интерполяции [16]. Согласно этому методу, связь между декартовыми x, y и специальными криволинейными координатами определяется формулами

Единичная окружность разбивается на m равных частей и неизвестные коэффициенты a_n, b_n ищутся по формулам

где η_k – угловые координаты узловых точек окружности; x_k, y_k – заранее неизвестные декартовы координаты точек профиля, являющиеся конформными образами узловых точек окружности. Для отыскания x_k, y_k используется итерационная процедура, подробно изложенная в [16].

Для симметричного относительно оси х профиля, как в данном случае, имеем b_n = 0.

Компоненты скорости потока u_ξ, u_η, как известно, равны

где h_ξ = h_η – коэффициенты Ламе.

Константы A в выражении для φ определяются из условия, что скорость потока на бесконечности и_∞ задана. Если и_∞ направлена вдоль оси x, то γ = 0. В результате определяется скорость u_g, которая принимается равной скорости газа “над” пограничным слоем, тонким по сравнению с масштабами обтекаемого тела, зависящим от формы последнего.

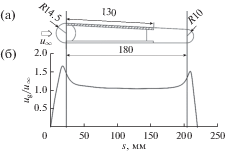
На рис. 2б приведен пример расчета скорости несжимаемого потока на поверхности профиля, используемого в экспериментах. Абсцисса s отсчитывается вдоль поверхности от передней линии растекания. Видно, что u_g/u_∞ нигде не достигает значения 2, характерного для цилиндра. Эти данные использованы для оценки значения скорости газа на внешней границе пограничного слоя.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА И РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ КИНЕМАТИКИ КАПЕЛЬ ВОДЫ НА ПОВЕРХНОСТИ ПРОФИЛЯ

Экспериментальные данные были получены на стенде в вентиляторной трубе незамкнутого типа с открытой рабочей частью и выходным сечением сопла 0.2 × 0.2 м² [7]. Подача воды в поток производилась с помощью водораспыливающей форсунки, установленной в тракте трубы.

Модель для исследований (см. рис. 2а) представляла собой профиль с полуцилиндрической передней кромкой и плоскими поверхностями сверху и снизу. На верхней поверхности устанавливались пластины из различного материала (в частности, гидрофобного), на которых исследовалось движение капли (заштрихованная пластина). Исследуемая пластина была с гладким кремнийорганическим покрытием на дюралюминиевой подложке.

В процессе эксперимента регистрировались скорость, температура и водность водовоздушного потока, температура и давление атмосферного воздуха, давление воды в водяной магистрали; проводилась видеосъемка исследуемого участка поверхности.

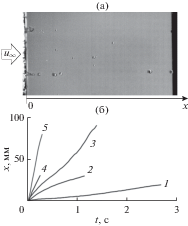
Модель для исследований устанавливалась в рабочей части аэродинамической трубы. Во время эксперимента производилась видеосъемка движения капель по исследуемой поверхности с частотой 85 кадр/с. По кадрам определялась координата капли x(t) и оценивался ее размер. Эти данные и являются основными экспериментальными результатами.

Как показали эксперименты, капли образуются до или сразу после того, как пленка воды, текущая по цилиндрической поверхности профиля, попадает на его верхний плоский участок (рис. 2). Таким образом, скачок кривизны профиля на линии соприкосновения цилиндрического и плоского участков поверхности служит своеобразным генератором капель. Напомним, что лабораторные эксперименты [5] подтвердили, что именно движение и отвердевание капель определяет основной механизм обледенения.

На снимках сверху капля видна на поверхности в виде овала, вытянутого по потоку, характерный размер капли d оценивался как ширина этого овала. Аналогично определялся размер капель и в работе [4].

На рис. 3 приведены координаты капель различных размеров в зависимости от времени. Выбраны участки траекторий, на которых скорость воздушного потока почти постоянна (рис. 2б). Видно, что более быстрые капли имеют больший размер. Существуют капли, движущиеся с одинаковой скоростью, хотя их размеры различны и их равномерное движение устанавливается в разных точках поверхности. Эти отличия можно отнести к непредсказуемому разбросу данных порядка 25%. Отличие скорости увлекающего газа на поверхности от скорости воздуха “на бесконечности” составляет значительно меньшую величину (рис. 2б), поэтому можно положить ${{u}_{1}} \approx {{u}_{\infty }}.$

ВАЛИДАЦИЯ ТЕОРЕТИЧЕСКОЙ МОДЕЛИ

Эксперименты проводились при следующем наборе входных данных: скорость u_∞ = 20 и 40 м/с, давление p = 10⁵ Па, температура набегающего потока T_∞ = 288 K, температура поверхности T_w = = 288 K, статический угол смачивания ее водой θ = 85°. Для физических свойств воды (индекс l) и воздуха (g) приняты следующие значения: µ_l = = 10^–3 кг/(м с), σ = 0.073 Н/м, ρ_g = 1.36 кг/м³, ν_g = = 1.5 × 10^–5 м²/с.

С учетом этих значений при радиусе цилиндрической части модели R_w и длине пластины l = = 0.1 м числа Рейнольдса не превосходят 3 × 10⁵, что соответствует ламинарному обтеканию [17]. Оценки толщины пограничного слоя на линии растекания (s = 0) дают δ₀ ~ 50 мкм, а в конце пластины δ(l) ~ 0.3 мм, что заметно меньше высоты h использованных в эксперименте капель.

На рис. 4 собраны результаты нескольких экспериментов [4, 18, 19], в которых поверхности предварительно обрабатывались различными способами (неоднократно отмечалось, например, [20], что без такой предварительной обработки углы смачивания зависят от многих случайных факторов). В результате как для гидрофобной, так и для гидрофильной поверхностей в этих работах удалось добиться небольших значений гистерезиса угла смачивания. Соответственно, форма капли, движущейся по поверхности, должна оставаться почти такой же, как и в покое, что оправдывает упомянутое выше предположение, принятое в более ранних работах [3, 12].

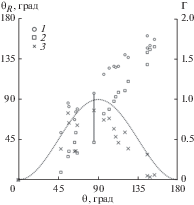
Можно отметить следующие общие черты зависимости Г от стационарного угла смачивания θ: Г равен нулю при θ = 0 и π и наибольшего значения достигает при θ ≈ π/2. На этом же рисунке отмечены результаты измерений углов θ_А = 43° и θ_R = 95° на наклонной плоскости, полученные в настоящей работе (θ = 85°) и соответствующие началу движения капли. На основе этих данных при численной обработке было принято значение гистерезиса Г ≈ 0.8. Для качественных оценок использована простая зависимость (пунктир)

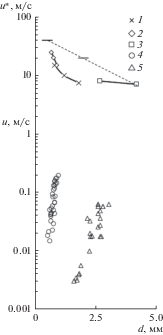
На рис. 5 в верхней части приведены экспериментальные значения скорости газа $u_{\infty }^{*},$ при которых капля начинает движение по гидрофобной поверхности [4, 18]. Авторы [4, 18] предлагают зависимость вида $u_{\infty }^{*}$ ~ d^–m, m = 0.5–1. Здесь же горизонтальными штрихами (демонстрирующими экспериментальный разброс диаметра капли ±0.3 мм) приведены результаты расчета скорости по уравнению (1) при θ = 85°, C_D = 0.5 и ξ_D = 1. Видно, что они хорошо коррелируют с результатами [18], полученными при близких значениях θ. Значения числа Рейнольдса для капель Re_d > 10³, что позволило принять для C_D предел Ньютона. Заметим, что значения $u_{\infty }^{*}$ меньше соответствующих значений скорости потока воздуха u_∞ = 20 и 40 м/с. Это вполне коррелирует с утверждением, что такие капли уже должны двигаться по поверхности. Кроме того, скорость воздуха u_g на экспериментальном участке плоскости над пограничным слоем несколько больше, чем u_∞, а скорость u₁ газа в пограничном слое меньше чем u_g. Эти два фактора имеют тенденцию компенсировать друг друга, что и позволило принять оценку u₁≈ u_∞.

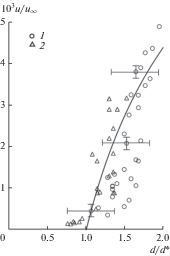
В нижней части рис. 5 представлены результаты измерений скорости движения капель, выполненных в настоящей работе. Эти же данные приведены на рис. 6 в координатах, нормированных на скорость невозмущенного потока u_∞ и критическое значение диаметра d * капли, начинающей движение. Здесь же дана аппроксимирующая кривая

Приведем также некоторые соображения, использованные при оценке характеристик пограничного слоя, которые особенно важны для более мелких частиц. Динамика частицы существенно определяется значением характерной скорости газа u₁, увлекающего каплю. Очевидно, что по мере продвижения вдоль поверхности капля все больше погружается в утолщающийся пограничный слой и, вообще говоря, может остановиться под действием адгезии. Значение u₁, в свою очередь, зависит от структуры пограничного слоя. В настоящей работе внимание акцентировалось на отношении характерного размера (высоты капли h) к толщине пограничного слоя δ. Использовались некоторые модельные представления [17, 21] зависимости средней продольной компоненты скорости газа от нормальной координаты: для турбулентного пограничного слоя, образовавшегося при обтекании пластины ламинарным потоком, ${u \mathord{\left/ {\vphantom {u {{{u}_{\infty }}}}} \right. \kern-0em} {{{u}_{\infty }}}} = {{{\text{[}}{y \mathord{\left/ {\vphantom {y {\delta }}} \right. \kern-0em} {\delta }}\left( x \right){\text{]}}}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}},$ $\delta {\kern 1pt} \left( x \right)\sim {{x}^{{{4 \mathord{\left/ {\vphantom {4 5}} \right. \kern-0em} 5}}}};$ для кусочно-линейной зависимости ${u \mathord{\left/ {\vphantom {u {{{u}_{\infty }}}}} \right. \kern-0em} {{{u}_{\infty }}}} = {y \mathord{\left/ {\vphantom {y \delta }} \right. \kern-0em} \delta }\left( x \right)$ при $y < \delta $ и ${u \mathord{\left/ {\vphantom {u {{{u}_{\infty }}}}} \right. \kern-0em} {{{u}_{\infty }}}} = 1$ при $y > \delta ;$ далее в виде

приведенном в классической монографии [21], а также зависимости, полученной экспериментально [22] в условиях, сходных с реализованными в настоящей работе, ${u \mathord{\left/ {\vphantom {u {{{u}_{\infty }}}}} \right. \kern-0em} {{{u}_{\infty }}}} = 1 - {\text{exp}}\left[ { - 0.89{{{({y \mathord{\left/ {\vphantom {y {{{\delta }_{*}}}}} \right. \kern-0em} {{{\delta }_{*}}}})}}^{{1.37}}}} \right],$ ${{\delta }_{*}} \cong \left( {1.72 \pm 0.54} \right)u_{\infty }^{{ - \left( {0.52 \pm 0.17} \right)}}$ при степени турбулентности потока 0.2–0.5%. В настоящей работе принималась зависимость (4), причем скорость газа u₁ вычислялась в точке y = h/2. Толщина δ оценивалась выражением в котором начальное значение рассчитывалось как в случае обтекания цилиндрической части профиля: при 0 < s < R_wπ/2 толщина пограничного слоя интерполировалась выражением которое при s = R_wπ/2 (x = 0) определяет величину δ₀ (см. выше численные оценки δ₀ и δ(l)), Re = = 2R_wu_∞/ν_a.

ЗАКЛЮЧЕНИЕ

Рассмотрены результаты предшествующих исследований динамики капель воды на горизонтальной поверхности, обдуваемой воздухом. В уравнении динамики учтены силы, увлекающие каплю, а также силы адгезии и диссипативная сила внутреннего трения, тормозящие ее. Приведены результаты экспериментальных исследований кинематики капли воды при наборе управляющих параметров, характерном для авиационной практики.

Уравнение динамики капли на поверхности тела, с одной стороны, может рассматриваться как определение гистерезиса угла смачивания, зависящего от относительной скорости обдуваемой воздухом частицы, ее размера и стационарного угла смачивания. C другой стороны, практически важно выполнить как раз противоположное требование – предсказать значение скорости движения капли, для чего необходимо знать заранее величину этого гистерезиса. Между тем последний является результатом различных воздействий на поверхность обтекаемого тела (например, механической, термической или химической обработки). Определенным выходом здесь является измерение гистерезиса на наклонной плоскости, при котором начинается движение капли. Если учесть, что скорость капли на два–три порядка меньше скорости газа, и пренебречь тем, что точки приложения равнодействующих силы тяготения и аэродинамической силы различны, то можно считать, что измеренный таким образом гистерезис приблизительно равен тому, что реализуется при движении капли. В настоящей работе принята эта точка зрения. В результате экспериментальные данные, полученные для различных скоростей потока, достаточно “кучно” ложатся на одну зависимость вида

где d * определяется уравнением (1) при u = 0, а геометрические параметры движущейся капли зависят только от стационарного угла смачивания, согласно выражениям (2) и (3). Для определения отношения скоростей u₁/u_∞ в случае капель с размером, соизмеримым с локальной толщиной пограничного слоя, можно использовать его модели, например (4). Для крупных капель, рассмотренных в настоящей работе, это отношение близко к единице.

Исследования выполнены за счет гранта Российского научного фонда (проект № 16-19-10 472).