1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 57, № 2, 2019

Теплофизика высоких температур, 2019, T. 57, № 2, стр. 234-245

Уточненное решение вариационной задачи идентификации математических моделей теплообмена с сосредоточенными параметрами

А. Г. Викулов 1, *, А. В. Ненарокомов 1, **

1 Московский авиационный институт (национальный исследовательский университет),
Москва, Россия

* E-mail: viarticle@yandex.ru
** E-mail: aleksey.nenarokomov@mai.ru

Поступила в редакцию 26.04.2017
После доработки 28.06.2017
Принята к публикации 26.04.2017

Полный текст (PDF)

Аннотация

В рамках проблемы математической корректности задач параметрической идентификации математических моделей теплообмена с сосредоточенными параметрами найдено уточненное решение вариационной задачи определения шага спуска метода итерационной регуляризации. Полученные результаты применены для идентификации тепловой математической модели составной части космического аппарата и подтверждены вычислительными экспериментами.

ВВЕДЕНИЕ

За последние 30 лет в журнале “Теплофизика высоких температур” обратным задачам теплообмена посвящено более двадцати статей. Опубликованные работы можно классифицировать по нескольким направлениям.

1. По направлению диагностики тепломассообмена на границе твердого тела при его обтекании потоком жидкости или газа представлены методика и результаты расчетно-экспериментального исследования теплообмена в окрестности критической точки калориметрической модели, обтекаемой высокоэнтальпийным двухфазным потоком при различной концентрации твердых частиц; неизвестные параметры уравнения теплового баланса определены из решения обратной задачи теплообмена методом итерационной регуляризации [1, 2]. Показан метод диагностики внешнего теплового воздействия на элементы конструкции, теплоперенос в которых описывается трехмерным уравнением теплопроводности в различных системах координат на примере исследования внешнего теплового воздействия на элементы конструкции автоматической межпланетной станции “Марс-96” на этапе ее выведения после сброса головного обтекателя [3]. Рассмотрены нестационарные задачи теплопроводности, возникающие в связи с восстановлением плотности теплового потока и температуры на поверхности модели в высокоэнтальпийных аэродинамических установках кратковременного действия по измерениям температуры внутримодельными тепловыми датчиками [4], а также метод решения обратной граничной задачи теплопроводности по восстановлению тепловых потоков к элементам конструкций летательных аппаратов, изготовленных из анизотропных материалов [5]. Предложены улучшенные алгоритмы решения обратной задачи по определению характеристик теплообмена на разрушаемой поверхности твердого тела [6, 7]. Рассмотрены процесс теплообмена и основные характеристики гетерогенного потока газ–твердые частицы, вызывающие усиление конвективного теплообмена в окрестности критической точки моделей при лобовом натекании в условиях эрозионного разрушения [8].

2. Задачи идентификации коэффициентов уравнения теплопроводности (теплового баланса) в частных производных (модель с распределенными параметрами) представлены наиболее широко. Проведена одновременная идентификация теплопроводности и удельной объемной теплоемкости искусственных алмазов решением многопараметрических обратных задач теплопроводности с использованием алгоритма итерационного фильтра [9]. Разработаны эффективные приемы улучшения качества предложенного алгоритма с применением процедур итерационной и шаговой регуляризации решения задачи идентификации локальных (числом более двух) параметров теплообмена для модельных задач различной сложности [10]. Предложен новый итерационный алгоритм определения комплекса теплофизических характеристик, зависящих от температуры, из решения коэффициентной обратной задачи теплопроводности при условии обеспечения единственности решения [11]. Описана статистическая математическая модель волокнистого высокопористого композиционного материала, существенно расширяющая возможности экспериментальных методов и позволяющая сопоставлением результатов расчета и эксперимента получать радиационные и теплофизические свойства материала, ранее практически недоступные определению [12]. Предложен метод решения обратной задачи по определению коэффициентов и углов ориентации главных осей тензора теплопроводности анизотропного материала, основанный на разложении в ряд Тейлора функционала невязки с получением векторов приращения искомых коэффициентов и дальнейшим использованием этих векторов в итерационных алгоритмах градиентного спуска [13]. Разработана методология решения обратных коэффициентных задач теплопроводности по определению компонентов тензора теплопроводности, зависящих от температуры, на основе введения квадратичного функционала невязки, его линеаризации, итерационного алгоритма минимизации и метода параметрической идентификации с учетом погрешностей определения экспериментальных значений температур. Разработанная методология позволяет определять как линейные, так и нелинейные характеристики анизотропных теплозащитных материалов, используемых в авиационной и ракетно-космической технике [14]. Предложен замкнутый метод восстановления тепловых потоков к анизотропным телам в условиях аэрогазодинамического нагрева по экспериментальным данным температур в пространственно-временны́х узлах, построенный на основе аппроксимации пространственной зависимости теплового потока линейной комбинацией базисных функций с искомыми коэффициентами (параметрами), определяемыми с помощью минимизации квадратичного функционала невязки между экспериментальными и теоретическими значениями температур по неявному методу градиентного спуска, а также на основе построения и численного решения задач по определению коэффициентов чувствительности [15]. По измеренным в диапазоне длин волн от 0.5 до 18 мкм спектрам полного отражения двух слоев разной толщины решением обратной задачи переноса излучения определены оптические параметры кварцевой керамики – показатели поглощения и рассеяния. Рассчитаны спектры полусферических коэффициентов излучения, а также интегральные коэффициенты теплового излучения в диапазоне температур от 20 до 1400°C. В диапазоне значений от 7 до 11% изучено влияние пористости на оптические параметры и коэффициенты излучения [16].

3. Задачи оптимизации характеристик конструкции, связанные с исследованием тепловых режимов объектов, рассмотрены как обратные задачи математической физики. Представлен алгоритм выбора толщин многослойной теплоизоляции минимальной массы, примененный для выбора толщины теплозащитного покрытия космического аппарата [17]. Предложен новый абсолютно устойчивый метод численного решения задач теплопереноса, позволивший решить задачу оптимального выбора количества слоев и их характеристик в пакетах многослойных пластин экранно-вакуумной теплоизоляции (ЭВТИ) космических аппаратов при продолжительном воздействии солнечного теплового потока. Получены многочисленные результаты, показавшие малую инерционность прогрева такой изоляции, что потребовало введения инерционной теплоизоляции на внутренней поверхности ЭВТИ [18].

4. Ретроспективная задача определения профиля температуры в начальном сечении по измерениям статической температуры в некотором сечении вниз по течению решена в оптимизационной постановке с использованием уравнений двумерного сверхзвукового течения вязкого теплопроводного сжимаемого газа. Приведена формулировка сопряженной задачи, позволяющая рассчитывать градиент невязки с минимальными затратами компьютерного времени. Представлены результаты численных экспериментов по расчету градиента невязки и решению обратной задачи конвекции [19]. Получено решение ретроспективной обратной задачи теплопроводности, поставленной как условно корректная задача оптимального управления объектом с распределенными параметрами при помощи учета ограничений на вторую производную искомого управления, соответствующего сужению множества управляющих воздействий до класса непрерывных и непрерывно-дифференцируемых функций. Предварительная параметризация управляющих воздействий позволяет сформулировать задачу математического программирования, решение которой основывается на аналитическом методе минимаксной оптимизации, использующем альтернансные свойства искомых оптимальных температурных отклонений [20].

5. Исследован термодинамический подход к формулированию вариационных принципов в обратных задачах теплообмена, позволяющий определить физически обоснованные условия для обеспечения единственности решения. Показано, что принцип минимума возникновения энтропии в стационарном состоянии корректен для одномерной геометрии при произвольных зависимостях теплопроводности и теплоемкости от температуры в некоторой области значений этих коэффициентов. В связи с отсутствием в данном случае вариационного описания предложен вариационный принцип, который определен как принцип минимума алгебраической суммы квадратов диссипативных потоков [21].

6. Особый интерес представляет возможность использования метода нейронных сетей для решения обратных задач, показанная на примере коэффициентной обратной задачи теплопереноса. Предложен способ настройки нейронной сети. Рассчитаны погрешности восстановления искомых параметров в зависимости от свойств среды и числа нейронов внутреннего слоя. Проведено сравнение результатов восстановления параметров с результатами, получаемыми методом подбора [22].

Выделяя методы термодинамических вариационных принципов и нейронных сетей, констатируем, что рассмотренные обратные задачи теплообмена решены методом итерационной регуляризации (МИР) [23], некоторые – с улучшенными алгоритмами и методиками определения отдельных параметров. Практически все из них основаны на дифференциальных уравнениях в частных производных, позволяющих подробно анализировать теплофизические и радиационные свойства материалов и отдельных элементов конструкций преимущественно ракетно-космической техники.

Представление технических систем в виде множеств взаимодействующих элементов приводит к росту сложности постановок теплофизических задач при использовании математических моделей с распределенными параметрами и трудоемкости их решения. В этой связи интересны математические модели с сосредоточенными параметрами, основанные на обыкновенных дифференциальных уравнениях [24]. Такие модели являются в определенном смысле переходным звеном к описанию теплофизических систем методом нейронных сетей.

Метод итерационной регуляризации адаптирован для математических моделей теплообмена с сосредоточенными параметрами: получены аналитические выражения для расчета неопределенных множителей Лагранжа при определении градиента функционала невязки температуры и расчета шага спуска, работоспособность которых подтверждена численными экспериментами; полученные результаты обобщены для технических, в частности, космических систем [25].

Тепловые процессы (в первую очередь, излучение) в технических системах нелинейны. Применимость метода итерационной регуляризации строго не доказана для нелинейных задач. В то же время вариационный метод Тихонова [26] теоретически обоснован в частных нелинейных случаях, но не имеет единого подхода к определению параметра регуляризации при неизвестной точности задания исходных данных. Анализ вариационного метода Тихонова и метода итерационной регуляризации задач идентификации тепловых математических моделей с сосредоточенными параметрами позволил разработать модифицированный метод итерационной регуляризации на основе вариационного метода, а также комбинированную методику аналитического определения параметра регуляризации (шага спуска) на основе минимизации функционала температурной невязки и сглаживающего функционала, работоспособность которой подтверждена вычислительными экспериментами [27]. Полученные результаты применены для идентификации математических моделей составных частей космических аппаратов, в частности теплового сопротивления и излучательной способности ЭВТИ [28].

В настоящей работе приведено уточненное решение вариационной задачи определения неопределенных множителей Лагранжа и параметра регуляризации (шага спуска), позволившее уменьшить количество итераций для решения ранее рассмотренных задач идентификации математических моделей с сосредоточенными параметрами [25, 27, 28].

ВАРИАЦИОННАЯ ЗАДАЧА ОПРЕДЕЛЕНИЯ НЕОПРЕДЕЛЕННЫХ МНОЖИТЕЛЕЙ ЛАГРАНЖА И ШАГА СПУСКА

Процессы теплообмена формализуются в виде математических моделей, средства выражения которых зависят от метода математического описания. Поскольку в дальнейшем речь пойдет о моделях с сосредоточенными параметрами, рассмотрим устойчивость решения системы [29]

(1)
${{{\mathbf{z}}}_{\tau }} = {\mathbf{f}}\left( {\tau ,{\mathbf{z}}} \right).$

Если f не зависит явно от τ, система (1) в координатной форме принимает следующий вид [29]:

(2)
$\frac{{d{{Т }_{i}}}}{{d\tau }} = {{f}_{i}}\left( {{{T}_{1}},...,{{T}_{N}}} \right)\,\,\,\,\left( {i = 1,...,N} \right).$

В краевой постановке неизвестной является N-мерная вектор-функция z с компонентами T1, …, TN. Для ее определения достаточно начального условия

${\mathbf{z}}\left( 0 \right) = {{{\mathbf{z}}}_{0}}.$

Устойчивость решения краевых задач на основе системы (2) полностью определяется характером функций fi в правой части уравнений.

Задача идентификации функций fi в правой части уравнений системы (2) некорректна по двум причинам. Во-первых, полный набор коэффициентов функций fi линейно зависим, а количество коэффициентов в общем виде больше числа N уравнений – решение неединственно. Такая ситуация имеет место при разложении функций fi в ряд Тейлора в окрестности гипотетической точки (0,…,0) по членам первого приближения. Пренебрегая членами ряда с производными второго порядка и учитывая, что вблизи абсолютного нуля решение системы (2) стремится к тривиальному, т.е. fi(0,…,0) = 0, получаем так называемую систему первого приближения [29]

(3)
$\frac{{d{{T}_{i}}}}{{d\tau }} = \sum\limits_{k = 1}^N {{{a}_{{ik}}}{{T}_{k}}} ,$
или в матричном виде [29]
$\frac{d}{{d\tau }}\left( {\begin{array}{*{20}{c}} {{{T}_{1}}} \\ {...} \\ {{{T}_{N}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{...}&{{{a}_{{1N}}}} \\ {...}&{}&{} \\ {{{a}_{{N1}}}}&{...}&{{{a}_{{NN}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{T}_{1}}} \\ {...} \\ {{{T}_{N}}} \end{array}} \right),$
где aik = ∂fi/∂Tk – элементы матрицы членов первого приближения (i = 1 ,…, N; k = 1 ,…, N).

Во-вторых, наличие производных по времени в уравнениях системы (3) допускает плохую обусловленность решения (свойство математической модели сохранять корректность решения при малых изменениях левой и правой части) относительно искомых коэффициентов: малым изменениям температур могут отвечать большие (выходящие за допустимые пределы) изменения решения [23] – решение неустойчиво.

Для решения задачи идентификации необходимо дополнительное условие, в качестве которого используются температуры точек, измеренные в определенные моменты времени τj:

(4)
$T_{i}^{{\left( 0 \right)}}\left( {{{{\tau }}_{j}}} \right) = T_{{ij}}^{{\left( 0 \right)}}\,\,\,\,\left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right).$

В методе итерационной регуляризации функционал температурной невязки записывается в виде [23]

(5)
$\begin{gathered} J\left[ {\mathbf{z}} \right] = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\left( {{{T}_{i}}\left( {{{{\tau }}_{j}}} \right) - T_{i}^{{\left( 0 \right)}}\left( {{{{\tau }}_{j}}} \right)} \right)}}^{2}}} } = \\ = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\left( {{{T}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right)}}^{2}}} } . \\ \end{gathered} $

Минимизация функционала осуществляется методами сопряженных градиентов и скорейшего спуска. Номер последней итерации выбирается по принципу итерационной регуляризации из условия [23]

(6)
$J\left[ {\mathbf{z}} \right] \leqslant {\delta }_{Т }^{2},$
где ${\delta }_{Т }^{2}$ – среднеквадратичная ошибка температурных измерений [23]:
(7)
${\delta }_{T}^{2} = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{\sigma }_{{ij}}^{2}} } ,$
${\sigma }_{{ij}}^{2}$ – дисперсия данного измерения температуры.

Для каждого промежутка времени [τj – 1, τj] на основе системы (3) записывается следующая математическая модель [25]:

(8)
$\begin{gathered} \frac{{d{{T}_{{ij}}}}}{{d{\tau }}} = \sum\limits_{k = 1}^N {{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right){{T}_{{kj}}}} ,\,\,\,\,{\tau } \in \left[ {{{{\tau }}_{{j - 1}}},{{{\tau }}_{j}}} \right] \\ \left( {i = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right), \\ \end{gathered} $
с общим начальным условием
(9)
${{T}_{i}}\left( {{{{\tau }}_{0}}} \right) = {{T}_{{i0}}}\,\,\,\,\left( {i = 1,2,...,N} \right)$
и условием непрерывности

(10)
$\begin{gathered} \left\{ \begin{gathered} {{T}_{i}}\left( {{{{\tau }}_{j}} - 0} \right) = {{T}_{i}}\left( {{{{\tau }}_{j}} + 0} \right) \hfill \\ {{{\tau }}_{0}} = {{{\tau }}_{{\min }}},\;{{{\tau }}_{{{{M}_{i}} + 1}}} = {{{\tau }}_{{\max }}} \hfill \\ \end{gathered} \right\} \\ \left( {i = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right). \\ \end{gathered} $

Функционал Лагранжа для задачи условной минимизации (4)–(10) принимает вид [25]

$\begin{gathered} L = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\left( {{{T}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right)}}^{2}}} } + \\ + \,\,\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {\int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)\left( { - \frac{{d{{T}_{{ij}}}}}{{d{\tau }}} + \sum\limits_{k = 1}^N {{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right){{T}_{{kj}}}} } \right)} } } d{\tau } + \\ + \,\,\sum\limits_{i = 1}^N {{{{\eta }}_{i}}\left( {{{T}_{i}}\left( {{{{\tau }}_{0}}} \right) - {{T}_{{i0}}}} \right)} + \\ + \,\,\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\mu }}_{{ij}}}\left( {{{T}_{i}}\left( {{{{\tau }}_{j}} - 0} \right) - {{T}_{i}}\left( {{{{\tau }}_{j}} + 0} \right)} \right)} } , \\ \end{gathered} $
где ψij, ηi, μij – неопределенные множители Лагранжа, соответствующие условиям (8)–(10).

Пусть искомые коэффициенты aik получили вариации δaik (i = 1, …, N; k = 1, …, N). Тогда температура изменится на некоторую величину υij(τ) (i = 1, …, N; j = 1, …, Mi), а вариация температуры υij(τ) удовлетворяет следующей краевой задаче:

(11)
$\begin{gathered} \frac{{d{{{\upsilon }}_{{ij}}}}}{{d{\tau }}} = \sum\limits_{k = 1}^N {{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right)\frac{{\partial {{T}_{{kj}}}}}{{\partial {{T}_{{ij}}}}}{{{\upsilon }}_{{ij}}}} + \\ + \,\,\sum\limits_{k = 1}^N {\frac{{\partial {{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right)}}{{\partial {{T}_{{ij}}}}}{{T}_{{kj}}}{{{\upsilon }}_{{ij}}}} + \sum\limits_{k = 1}^N {{\delta }{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right){{T}_{{kj}}}} , \\ {\tau } \in \left[ {{{{\tau }}_{{j - 1}}},{{{\tau }}_{j}}} \right]\,\,\,\,\left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right) \\ \end{gathered} $
с начальным условием
(12)
${{{\upsilon }}_{i}}\left( {{{{\tau }}_{0}}} \right) = 0\,\,\,\,\left( {i = 1,2,...,N} \right)$
и условием непрерывности

(13)
$\begin{gathered} \left\{ \begin{gathered} {{{\upsilon }}_{i}}\left( {{{{\tau }}_{j}} - 0} \right) = {{{\upsilon }}_{i}}\left( {{{{\tau }}_{j}} + 0} \right), \hfill \\ {{{\tau }}_{0}} = {{{\tau }}_{{\min }}},\;{{{\tau }}_{{{{M}_{i}} + 1}}} = {{{\tau }}_{{\max }}} \hfill \\ \end{gathered} \right\} \\ \left( {i = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right). \\ \end{gathered} $

Выражение линейной части приращения минимизируемого функционала имеет вид [25]

${\delta }J = 2\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {\left( {{{T}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right){{{\upsilon }}_{{ij}}}} } .$

Вариация функционала Лагранжа в виде линейной части приращения этого функционала представляется следующим образом [25]:

${\delta }L = {\delta }J + {\delta }{{L}_{1}} + {\delta }{{L}_{2}} + {\delta }{{L}_{3}},$
где

$\begin{gathered} {\delta }{{L}_{1}} = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)} } \left[ { - \frac{{d{{{\upsilon }}_{{ij}}}}}{{d{\tau }}} + \sum\limits_{k = 1}^N {\frac{{\partial {{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right)}}{{\partial {{T}_{{ij}}}}}{{T}_{{kj}}}{{{\upsilon }}_{{ij}}}} } \right. + \\ \left. { + \,\,\sum\limits_{k = 1}^N {{\delta }{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right){{T}_{{kj}}}} } \right]d{\tau ,} \\ {\delta }{{L}_{2}} = \sum\limits_{i = 1}^N {{{{\eta }}_{i}}{{{\upsilon }}_{i}}\left( {{{{\tau }}_{0}}} \right)} , \\ {\delta }{{L}_{3}} = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\mu }}_{{ij}}}\left( {{{{\upsilon }}_{i}}\left( {{{{\tau }}_{{j - 0}}}} \right) - {{{\upsilon }}_{i}}\left( {{{{\tau }}_{{j + 0}}}} \right)} \right)} } \\ \left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right). \\ \end{gathered} $

Из условия стационарности функционала Лагранжа δL = 0 следует

${\delta }J = - {\delta }{{L}_{1}} - {\delta }{{L}_{2}} - {\delta }{{L}_{3}}.$

Предполагая, что поведение решения системы (11)–(13) определяется членами первого приближения, имеем

(14)
$\begin{gathered} {\delta }J = - {\delta }{{L}_{1}} = \\ = - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)\left[ { - \frac{{d{{{\upsilon }}_{{ij}}}}}{{d{\tau }}} + \sum\limits_{k = 1}^N {{\delta }{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right){{T}_{{kj}}}} } \right]d{\tau }} } = \\ = - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {\sum\limits_{k = 1}^N {{{{\psi }}_{{ij}}}\left( {\tau } \right){\delta }{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right){{T}_{{kj}}}d{\tau }} } } + \\ + \,\,\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)d{{{\upsilon }}_{{ij}}}} } . \\ \end{gathered} $

В частном случае, когда искомые параметры aik являются только функциями времени, выражение (14) может рассматриваться как дифференциал функционала невязки. Так как по определению дифференциала Фреше

(15)
$\begin{gathered} {\delta }J = \left( {{\mathbf{J}}_{{\mathbf{a}}}^{'},{\delta }{\mathbf{a}}} \right) + O\left( {{\delta }{{{\mathbf{a}}}^{2}}} \right) = \\ = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {\sum\limits_{k = 1}^N {J_{{{{a}_{{ikj}}}}}^{'}{\delta }{{a}_{{ikj}}}} } } + O\left( {{\delta }{{{\mathbf{a}}}^{2}}} \right), \\ \end{gathered} $
то, сравнивая подынтегральные выражения (14), (15) и принимая во внимание (11), получаем выражение производной функционала
(16)
$dJ_{{{{a}_{{ikj}}}}}^{'} = - {{{\psi }}_{{ij}}}\left( {\tau } \right){{T}_{{kj}}}d{\tau } \Rightarrow J_{{{{a}_{{ikj}}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right){{T}_{{kj}}}d{\tau }} ,$
где коэффициенты ψij могут быть найдены из сопряженной краевой задачи, которая решается в “обратном” времени [23]:
$\begin{gathered} - \frac{{d{{{\psi }}_{{ij}}}}}{{d{\tau '}}} = \sum\limits_{k = 1}^N {{{a}_{{ik}}}\left( {{{{\tau }}_{{\max }}} - {\tau '}} \right){{{\psi }}_{{kj}}}} \\ \left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right) \\ \end{gathered} $
с начальным условием
(17)
${{{\psi }}_{i}}\left( {{{{\tau }}_{{\max }}}} \right) = {{{\psi }}_{{i,{{M}_{i}} + 1}}} = 0\,\,\,\,\left( {i = 1,2,...,N} \right)$
и условием непрерывности

(18)
$\begin{gathered} \left\{ \begin{gathered} {{{\psi }}_{i}}({\tau }_{j}^{'} - 0) = {{{\psi }}_{i}}({\tau }_{j}^{'} + 0), \\ {\tau }_{0}^{'} = {{{\tau }}_{{\min }}},{\tau }_{{{{M}_{i}} + 1}}^{'} = {{{\tau }}_{{\max }}} \\ \end{gathered} \right\} \\ \left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right). \\ \end{gathered} $

Предложим другой способ определения множителей ψij. Для этого продифференцируем уравнение (14) по времени [25]:

(19)
$\begin{gathered} 2\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {\left( {\frac{{d{{T}_{{ij}}}}}{{d\tau }}{{{\upsilon }}_{{ij}}} + \left( {{{T}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right)\frac{{d{{{\upsilon }}_{{ij}}}}}{{d{\tau }}}} \right) = } } \\ = - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)\left[ { - \frac{{d{{{\upsilon }}_{{ij}}}}}{{d{\tau }}} + \sum\limits_{k = 1}^N {{\delta }{{a}_{{ik}}}\left( {{{T}_{{ij}}},{{T}_{{kj}}},{\tau }} \right){{T}_{{kj}}}} } \right]} } . \\ \end{gathered} $

Приравнивая множители при одинаковых степенях слагаемых в левой и правой частях уравнения (19), получим выражение для множителей [25]

(20)
${{{\psi }}_{{ij}}} = 2\left( {{{T}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right),$
где температуры Tij являются решением краевой задачи (8)–(10).

Если искомые функции aik зависят как от времени, так и от температуры, они параметризуются при помощи некоторой системы базисных функций {$\gamma _{{ikn}}^{a}$ = γa (Tin, Tkn)} (i = 1, …, N; k = 1, …, N; n = 1, …, $N_{{ik}}^{a}$) [25]

${{a}_{{ik}}}\left( {{{T}_{i}},{{T}_{k}},{\tau }} \right) = \sum\limits_{n = 1}^{N_{{ik}}^{a}} {{{A}_{{ikn}}}\left( {\tau } \right)} { \gamma }_{{ikn}}^{a}.$

Подставляя в (14) вариации

${\delta }{{a}_{{ik}}}\left( {{{T}_{i}},{{T}_{k}},{\tau }} \right) = \sum\limits_{n = 1}^{N_{{ik}}^{a}} {{\delta }{{A}_{{ikn}}}\left( {\tau } \right)} { \gamma }_{{ikn}}^{a},$
получим следующее выражение для вариации функционала:

${\delta }J = - {{L}_{1}} = - \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)\sum\limits_{k = 1}^N {{{T}_{{kj}}}\sum\limits_{n = 1}^{N_{{ik}}^{a}} {{\delta }{{A}_{{ikn}}}\left( {\tau } \right)} { \gamma }_{{ikn}}^{a}} d{\tau }} } .$

Тогда градиент функционала будет равен [25]

(21)
$dJ_{{{{A}_{{ikn}}}}}^{'} = - {{{\psi }}_{{ij}}}{{T}_{{kj}}}{\gamma }_{{ikn}}^{a}d{\tau } \Rightarrow J_{{{{A}_{{ikn}}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}{{T}_{{kj}}}{\gamma }_{{ikn}}^{a}d{\tau }} .$

Чтобы определить шаг спуска итерационного алгоритма решения задачи идентификации из условия минимизации температурного функционала [23]

(22)
${{{\beta }}^{{\left( l \right)}}}:\;J\left( {{{{\mathbf{a}}}^{{\left( l \right)}}}} \right) = \mathop {\inf }\limits_{\beta } J\left( {{{{\mathbf{a}}}^{{\left( {l - 1} \right)}}} - {{{\beta }}^{{\left( l \right)}}}{{{\mathbf{\xi }}}^{{\left( l \right)}}}} \right),$
будем считать приращение вектора характеристик на текущей итерации вариацией δaik, которая вызывает вариацию температуры υij(τ) (i = = 1, …, N; j = 1, …, Mi). Согласно (11) вариация υij(τ) в первом приближении удовлетворяет краевой задаче
(23)
$\begin{gathered} \frac{{d{{{\upsilon }}_{{ij}}}}}{{d{\tau }}} = - \sum\limits_{k = 1}^N {{{{\beta }}_{{ij}}}{{{\xi }}_{{ikj}}}{{T}_{{kj}}}} , \\ {\tau } \in \left[ {{{{\tau }}_{{j - 1}}},{{{\tau }}_{j}}} \right]\,\,\,\,\left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right) \\ \end{gathered} $
с начальным условием
(24)
${{{\upsilon }}_{i}}\left( {{{{\tau }}_{0}}} \right) = 0\,\,\,\,\left( {i = 1,2,...,N} \right)$
и условием непрерывности

(25)
$\begin{gathered} \left\{ \begin{gathered} {{{\upsilon }}_{i}}\left( {{{{\tau }}_{j}} - 0} \right) = {{{\upsilon }}_{i}}\left( {{{{\tau }}_{j}} + 0} \right), \hfill \\ {{{\tau }}_{0}} = {{{\tau }}_{{\min }}},\;{{{\tau }}_{{{{M}_{i}} + 1}}} = {{{\tau }}_{{\max }}} \hfill \\ \end{gathered} \right\} \\ \left( {i = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right). \\ \end{gathered} $

Тогда функционал температурной невязки на итерации l запишется как

(26)
$J\left( {{\mathbf{a}} + {\delta }{\mathbf{a}}} \right) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {{{{\left( {{{T}_{{ij}}} + {{{\upsilon }}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right)}}^{2}}} } .$

Из условия (22) шаг спуска β минимизирует функционал (26), поэтому в процессе минимизации должен являться аргументом температуры Tij(τ, βij) и вариации температуры υij(τ, βij):

(27)
$\begin{gathered} 2\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^{{{M}_{i}}} {\left( {{{T}_{{ij}}} + {{{\upsilon }}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right)\frac{\partial }{{\partial {{{\beta }}_{{ij}}}}}\left( {{{T}_{{ij}}} + {{{\upsilon }}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right) = 0} } , \Rightarrow \\ \Rightarrow \left[ \begin{gathered} {{T}_{{ij}}} + {{{\upsilon }}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}} = 0, \\ \frac{\partial }{{\partial {{{\beta }}_{{ij}}}}}\left( {{{T}_{{ij}}} + {{{\upsilon }}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right) = 0 \\ \end{gathered} \right] \Rightarrow \\ \Rightarrow \left\{ \begin{gathered} {{{\upsilon }}_{{ij}}} = T_{{ij}}^{{\left( 0 \right)}} - {{T}_{{ij}}}, \\ \frac{\partial }{{\partial {{{\beta }}_{{ij}}}}}\left( {{{T}_{{ij}}} + {{{\upsilon }}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right) = 0 \\ \end{gathered} \right\}. \\ \end{gathered} $

Подставляя вариации температуры из (27) в (23), имеем

(28)
$\begin{gathered} - \frac{{d{{T}_{{ij}}}}}{{d{\tau }}} = - \sum\limits_{k = 1}^N {{{{\beta }}_{{ij}}}{{{\xi }}_{{ikj}}}{{T}_{{kj}}}} \Rightarrow \\ \Rightarrow \,\,{{{\beta }}_{{ij}}} = \frac{{\frac{{d{{T}_{{ij}}}}}{{d{\tau }}}}}{{\sum\limits_{k = 1}^N {{{{\xi }}_{{ikj}}}{{T}_{{kj}}}} }} = \frac{{\sum\limits_{k = 1}^N {{{a}_{{ikj}}}{{T}_{{kj}}}} }}{{\sum\limits_{k = 1}^N {{{{\xi }}_{{ikj}}}{{T}_{{kj}}}} }}, \\ {\tau } \in \left[ {{{{\tau }}_{{j - 1}}},{{{\tau }}_{j}}} \right]\,\,\,\,\left( {i = 1,2,...,N;\,\,j = 1,2,...,{{M}_{i}}} \right), \\ \end{gathered} $
где температуры Tij являются решением краевой задачи (8)–(10) на текущей итерации. Из (28) следует, что шаг спуска β = βij вычисляется NMi раз и является индивидуальным для каждой строки искомой матрицы коэффициентов aik на каждом временнóм участке.

По теореме о неявной функции для идентификации одной координаты вектора требуется измерение одной температуры. Задача определения всех строк (столбцов) матрицы αik (i = 1, …, N, k = 1, 2, …, N) имеет неединственное решение и при наличии дополнительных условий решается приближенно с использованием вариационного принципа и методической возможности метода итерационной регуляризации вычислять единый шаг спуска для каждого искомого вектора [25].

Приведенные рассуждения справедливы не только для рассмотренной гипотетической системы, но и обобщаются для процессов, описываемых теплофизическим уравнением теплопроводности, применительно к техническим, в частности, космическим системам.

ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ТЕПЛООБМЕНА В КОСМИЧЕСКИХ АППАРАТАХ

Математическая модель с сосредоточенными параметрами, описывающая теплообмен в космической системе, представляет собой систему обыкновенных дифференциальных уравнений относительно температур материальных точек, являющихся эквивалентами элементов системы по массе, теплофизическим и радиационно-оптическим характеристикам. В случае теплофизических задач системами целесообразно называть составные части космического аппарата (КА), бортовые системы или аппарат в целом. Материальные точки условно считаются изотермическими, что подразумевает равенство зависящих от времени среднемассовых температур модельной точки и технического элемента.

Состояние термодинамически открытой технической системы из N элементов характеризуется вектором z = {Ti} (i = 1, …, N), который должен удовлетворять следующей системе уравнений [25]:

(29)
$\begin{gathered} {{C}_{i}}\left( {{{T}_{i}},{\tau }} \right)\frac{{d{{T}_{i}}}}{{d{\tau }}} = \sum\limits_{k = 1}^N {{{{\alpha }}_{{ik}}}\left( {\tau } \right)} \left( {{{T}_{k}} - {{T}_{i}}} \right) + \\ + \,\,\sum\limits_{k = 1}^N {{{{\varphi }}_{{ik}}}\left( {\tau } \right){{F}_{i}}{\sigma }} \left( {{{T}_{k}}^{4} - {{T}_{i}}^{4}} \right) + \\ + \,\,{{E}_{i}}\left( {{{T}_{i}},{\tau }} \right) + {{Q}_{i}}\left( {\tau } \right),\,\,\,\,{\tau } \in \left[ {{{{\tau }}_{{\min }}},{{{\tau }}_{{\max }}}} \right], \\ {{T}_{i}}\left( {{{{\tau }}_{{\min }}}} \right) = {{T}_{{i0}}}\,\,\,\,\left( {i = 1,2,...,N} \right), \\ \end{gathered} $
где Сi – абсолютная теплоемкость i-го элемента; αik – матрица проводимостей конвективного или кондуктивного теплообмена между элементами; φik – матрица угловых коэффициентов; σ – постоянная Стефана–Больцмана; Ei – тепловая мощность, подводимая к i-му элементу из окружающего пространства; Qi – тепловая мощность, выделяемая в i-м элементе; Ti0 – начальное значение температуры. Поскольку σ, Fi – известные величины, далее вместо матрицы угловых коэффициентов будем использовать матрицу коэффициентов излучения χik(τ) = φik(τ)Fiσ, Вт/К4.

Для решения задачи идентификации характеристик Ci(Ti, τ), Ei(Ti, τ), Qi(τ), αik(Ti, Tk, τ), χik(τ) методом итерационной регуляризации используется дополнительное условие (4), функционал-невязка (5) и условие регуляризации (6).

Для каждого промежутка времени [τj – 1, τj] на основе системы (29) записывается следующая математическая модель:

(30)
$\begin{gathered} {{C}_{i}}\left( {{{T}_{i}},{\tau }} \right)\frac{{d{{T}_{{ij}}}}}{{d{\tau }}} = \sum\limits_{k = 1}^N {{{{\alpha }}_{{ik}}}\left( {\tau } \right)} \left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right) + \\ + \,\,\sum\limits_{k = 1}^N {{{{\chi }}_{{ik}}}\left( {\tau } \right)} \left( {T_{{kj}}^{4} - T_{{ij}}^{4}} \right) + \\ + \,\,{{E}_{i}}\left( {{{T}_{i}},{\tau }} \right) + {{Q}_{i}}\left( {\tau } \right),\,\,\,\,{\tau } \in \left[ {{{{\tau }}_{{j - 1}}},{{{\tau }}_{j}}} \right] \\ \left( {i = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right) \\ \end{gathered} $
с общим начальным условием
(31)
${{T}_{i}}\left( {{{{\tau }}_{0}}} \right) = {{T}_{{i0}}},\,\,\,\,\left( {i = 1,\;2,...,N} \right)$
и условием непрерывности

(32)
$\begin{gathered} \left\{ \begin{gathered} {{T}_{i}}\left( {{{{\tau }}_{j}} - 0} \right) = {{T}_{i}}\left( {{{{\tau }}_{j}} + 0} \right), \hfill \\ {{{\tau }}_{0}} = {{{\tau }}_{{\min }}},\;{{{\tau }}_{{{{M}_{i}} + 1}}} = {{{\tau }}_{{\max }}} \hfill \\ \end{gathered} \right\} \\ \left( {i = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right). \\ \end{gathered} $

В частном случае, когда искомые функции зависят только от времени Ci(τ), Ei(τ), Qi(τ), αik(τ), χik(τ), задача решается в функциональном пространстве. Градиент функционала (5) определяется по аналогии с выражением (16) [25]:

$\begin{gathered} J_{{{{C}_{i}}}}^{'} = \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)\frac{{\partial {{T}_{{ij}}}}}{{\partial {\tau }}}} d{\tau } = \int\limits_{{{T}_{{i,j - 1}}}}^{{{T}_{{ij}}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)} d{{T}_{{ij}}}, \\ J_{{{{E}_{i}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)d{\tau }} ,\,\,\,\,J_{{{{Q}_{i}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)d{\tau }} , \\ J_{{{{{\alpha }}_{{ik}}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)\left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right)d{\tau }} , \\ J_{{{{{\chi }}_{{ik}}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {\tau } \right)\left( {T_{{kj}}^{4} - T_{{ij}}^{4}} \right)d{\tau }} \\ \left( {i = 1,\;2,\;...,\;N;\;k = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right), \\ \end{gathered} $
где ψij – решение задачи, сопряженной с линеаризованной формой исходной задачи [23]:
$\begin{gathered} - {{C}_{i}}\left( {{{T}_{i}},{\tau '}} \right)\frac{{d{{{\psi }}_{{ij}}}}}{{d{\tau '}}} = \sum\limits_{k = 1}^N {{{{\alpha }}_{{ik}}}\left( {{\tau '}} \right)} \left( { - {{{\psi }}_{{ij}}}} \right) + \\ + \,\,4\sum\limits_{k = 1}^N {{{{\chi }}_{{ik}}}\left( {{\tau '}} \right)} \left( { - {{T}_{{ij}}}^{3}{{{\psi }}_{{ij}}}} \right),\,\,\,\,{\tau '} \in \left[ {{{{\tau }}_{{j - 1}}},\;{{{\tau }}_{j}}} \right], \\ {\tau }_{0}^{'} = {{{\tau }}_{{\min }}},\,\,\,\,{\tau }_{{{{M}_{i}} + 1}}^{'} = {{{\tau }}_{{\max }}} \\ \left( {i = 1,\;2,\;...,\;N;j = 1,\;2,\;...,\;{{M}_{i}}} \right). \\ \end{gathered} $
с начальным условием (17) и условием непрерывности (18). Возможен и способ определения ψij по выражению (20). В этом случае, приравнивая коэффициенты при производной вариации температуры по времени в левой и правой частях уравнения, которое строится аналогично (19), необходимо принять во внимание наличие теплоемкости при производной вариации температуры в правой части [25]:

(33)
${{{\psi }}_{{ij}}} = \frac{2}{{{{C}_{i}}\left( {{{T}_{i}},{\tau }} \right)}}\left( {{{T}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right).$

Если искомые характеристики Ci(Ti, τ), Ei(Ti, τ), αik(Ti, Tk, τ) зависят как от времени, так и от температуры, задача идентификации решается в параметрическом пространстве. Характеристики параметризуются некоторыми системами функций {$\eta _{{in}}^{C}$ = ηC(Tin)} (n = 1, 2 …, $N_{i}^{C}$), {$\eta _{{in}}^{E}$ = ηE(Tin)} (n = 1, 2 …, $N_{i}^{E}$), {$\eta _{{ikn}}^{\alpha }$ = ηα (Tin, Tkn)} (n = 1, …, $N_{{ik}}^{\alpha }$) [25]:

$\begin{gathered} {{C}_{i}}\left( {{{T}_{i}},{\tau }} \right) = \sum\limits_{n = 1}^{N_{i}^{C}} {{{c}_{{in}}}\left( {\tau } \right)} {\eta }_{{in}}^{C},\,\,\,\,{{E}_{i}}\left( {{{T}_{i}},{\tau }} \right) = \sum\limits_{n = 1}^{N_{i}^{E}} {{{e}_{{in}}}\left( {\tau } \right)} {\eta }_{{in}}^{E}, \\ {{{\alpha }}_{{ik}}}\left( {{{T}_{i}},{{T}_{k}},{\tau }} \right) = \sum\limits_{n = 1}^{N_{{ik}}^{a}} {{{A}_{{ikn}}}\left( {\tau } \right)} {\eta }_{{ikn}}^{a}. \\ \end{gathered} $

Градиент функционала (5) определяется по аналогии с выражением (21) [25]:

$\begin{gathered} J_{{{{c}_{{in}}}}}^{'} = \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\frac{{\partial {{T}_{{ij}}}}}{{\partial {\tau }}}{\eta }_{{in}}^{C}d{\tau }} = \int\limits_{{{T}_{{i,j - 1}}}}^{{{T}_{{ij}}}} {{{{\psi }}_{{ij}}}{\eta }_{{in}}^{C}d{{T}_{{ij}}}} , \\ J_{{{{e}_{{in}}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}{\eta }_{{in}}^{E}d{\tau }} , \\ J_{{{{A}_{{ikn}}}}}^{'} = - \int\limits_{{{{\tau }}_{{j - 1}}}}^{{{{\tau }}_{j}}} {{{{\psi }}_{{ij}}}\left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right){\eta }_{{ikn}}^{\alpha }d{\tau }} , \\ \end{gathered} $
где ψji – решение задачи, сопряженной с линеаризованной формой исходной задачи:
$\begin{gathered} - {{C}_{i}}\left( {{{T}_{i}},{\tau '}} \right)\frac{{d{{{\psi }}_{{ij}}}}}{{d{\tau '}}} = \sum\limits_{k = 1}^N {{{{\alpha }}_{{ik}}}\left( {{\tau '}} \right)} \left( { - {{{\psi }}_{{ij}}}} \right) + \\ + \,\,4\sum\limits_{k = 1}^N {{{{\chi }}_{{ik}}}\left( {{\tau '}} \right)} \left( { - T_{{ij}}^{3}{{{\psi }}_{{ij}}}} \right) + {{{\psi }}_{{ij}}}\frac{{\partial {{E}_{i}}\left( {{{T}_{i}},{\tau '}} \right)}}{{\partial {{T}_{{ij}}}}}, \\ {\tau } \in \left[ {{{{\tau }}_{{j - 1}}},{{{\tau }}_{j}}} \right],\,\,\,\,{{{\tau }}_{0}} = {{{\tau }}_{{\min }}},\,\,\,\,{{{\tau }}_{{{{M}_{i}} + 1}}} = {{{\tau }}_{{\max }}} \\ \left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right) \\ \end{gathered} $
с начальным условием (17) и условием непрерывности (18). При решении задачи в пространстве параметров множители Лагранжа ψij также могут быть определены по выражению (33).

Для определения шага спуска по условию (22) будем считать приращение вектора каждой искомой характеристики на текущей итерации вариацией δ, которая вызывает отдельную вариацию температуры υij(τ, δ) (i = 1, …, N; j = 1, …, Mi). Тогда по аналогии с (28) получаем следующие выражения:

$\begin{gathered} {\beta }_{{ij}}^{C} = - \frac{{{{C}_{i}}\left( {{{T}_{i}},{\tau }} \right)}}{{{\xi }_{i}^{C}}} \times \\ \times \,\,\left[ {1 + \frac{{\left( { - \sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} - \sum\limits_{k = 1}^N {4T_{{ij}}^{3}{{{\chi }}_{{ikj}}}} } \right)\left( {T_{{ij}}^{{\left( 0 \right)}} - {{T}_{{ij}}}} \right)}}{{\sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} \left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right) + \sum\limits_{k = 1}^N {{{{\chi }}_{{ikj}}}} {\kern 1pt} \left( {T_{{kj}}^{4} - T_{{ij}}^{4}} \right) + {{E}_{{ij}}} + {{Q}_{{ij}}}}}} \right], \\ \end{gathered} $
$\begin{gathered} {\beta }_{{ij}}^{E} = \frac{1}{{{\xi }_{{ij}}^{E}}}\left[ {\left( { - \sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} - \sum\limits_{k = 1}^N {4T_{{ij}}^{3}{{{\chi }}_{{ikj}}}} } \right)\left( {T_{{ij}}^{{\left( 0 \right)}} - {{T}_{{ij}}}} \right)} \right. + \\ + \,\,\left. {\sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} \left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right) + \sum\limits_{k = 1}^N {{{{\chi }}_{{ikj}}}} \left( {T_{{kj}}^{4} - T_{{ij}}^{4}} \right) + {{E}_{{ij}}} + {{Q}_{{ij}}}} \right], \\ \end{gathered} $
$\begin{gathered} {\beta }_{{ij}}^{Q} = \frac{1}{{{\xi }_{{ij}}^{Q}}}\left[ {\left( { - \sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} - \sum\limits_{k = 1}^N {4T_{{ij}}^{3}{{{\chi }}_{{ikj}}}} } \right)\left( {T_{{ij}}^{{\left( 0 \right)}} - {{T}_{{ij}}}} \right)} \right. + \\ + \left. {\sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} \left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right) + \sum\limits_{k = 1}^N {{{{\chi }}_{{ikj}}}} \left( {T_{{kj}}^{4} - T_{{ij}}^{4}} \right) + {{E}_{{ij}}} + {{Q}_{{ij}}}} \right], \\ \end{gathered} $
$\begin{gathered} {\beta }_{{ij}}^{\alpha } = \frac{1}{{\sum\limits_{k = 1}^N {{\xi }_{{ikj}}^{{\alpha }}\left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right)} }} \times \\ \times \,\,\left[ {\left( { - \sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} - \sum\limits_{k = 1}^N {4T_{{ij}}^{3}{{{\chi }}_{{ikj}}}} } \right)\left( {T_{{ij}}^{{\left( 0 \right)}} - {{T}_{{ij}}}} \right)} \right. + \\ + \,\,\left. {\sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} \left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right) + \sum\limits_{k = 1}^N {{{{\chi }}_{{ikj}}}} \left( {T_{{kj}}^{4} - T_{{ij}}^{4}} \right) + {{E}_{{ij}}} + {{Q}_{{ij}}}} \right], \\ \end{gathered} $
$\begin{gathered} {\beta }_{{ikj}}^{\chi } = \frac{1}{{\sum\limits_{k = 1}^N {{\xi }_{{ikj}}^{\chi }\left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right)} }} \times \\ \times \,\,\left[ {\left( { - \sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} - \sum\limits_{k = 1}^N {4T_{{ij}}^{3}{{{\chi }}_{{ikj}}}} } \right)\left( {T_{{ij}}^{{\left( 0 \right)}} - {{T}_{{ij}}}} \right)} \right. + \\ + \,\,\left. {\sum\limits_{k = 1}^N {{{{\alpha }}_{{ikj}}}} \left( {{{T}_{{kj}}} - {{T}_{{ij}}}} \right) + \sum\limits_{k = 1}^N {{{{\chi }}_{{ikj}}}} \left( {T_{{kj}}^{4} - T_{{ij}}^{4}} \right) + {{E}_{{ij}}} + {{Q}_{{ij}}}} \right], \\ \end{gathered} $
${\tau } \in \left[ {{{{\tau }}_{{j - 1}}},{{{\tau }}_{j}}} \right]\,\,\,\,\left( {i = 1,2,...,N;j = 1,2,...,{{M}_{i}}} \right).$

Для каждого вектора характеристик Ci, Ei, Qi или каждой строки искомых матриц коэффициентов αik, χik (i = 1, …, N; k = 1, …, N) шаг спуска β = βij (i = 1, …, N) вычисляется NM раз и является индивидуальным. Так как система уравнений (30)–(32) решается на каждом временнóм шаге при наличии всех уравнений, временнáя сетка одинакова для всех узлов: Mi = M.

ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

С целью проверки работоспособности полученных выражений для расчета шага спуска в методе итерационной регуляризации [25] или обратного ему по значению параметра регуляризации модифицированного вариационного метода [27] проведен вычислительный эксперимент на примере идентификации тепловых проводимостей математической модели составной части КА (рис. 1).

Рис. 1.

Укрупненная модель с сосредоточенными параметрами составной части КА: 1 – несущая конструкция с аппаратурой, 2 – внутренняя часть оптической защиты, 3 – наружная часть оптической защиты, 4 – рама.

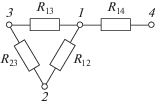
Идентификация выполнена по экспериментальным данным, полученным в тепловых вакуумных испытаниях составной части КА в режиме предельного нагрева от инфракрасных имитаторов с плотностью теплового потока до 900 Вт/м2 [25].

Задача решена для случая начального приближения, заданного достаточно произвольно:

${{{\mathbf{a}}}_{1}} = \left\{ {0,\;{{\alpha }_{{12}}},\;{{\alpha }_{{13}}},\;{{\alpha }_{{14}}}} \right\} = \left\{ {0,\;0.1,\;0.1,\;0} \right\}\,\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}{\text{,}}$
${{{\mathbf{a}}}_{2}} = \left\{ {{{\alpha }_{{21}}},\;0,\;{{\alpha }_{{23}}},\;0} \right\} = \left\{ {0.1,\;0,\;0.1,\;0} \right\}\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}{\text{,}}$
${{{\mathbf{a}}}_{3}} = \left\{ {{{\alpha }_{{31}}},\;{{\alpha }_{{32}}},\;0,\;0} \right\} = \left\{ {0.1,\;0.1,\;0,\;0} \right\}\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}{\text{,}}$
${{{\mathbf{a}}}_{4}} = \left\{ {{{\alpha }_{{41}}},\;0,\;0,\;0} \right\} = \left\{ {0,\;0,\;0,\;0} \right\}\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}.$

Определение допустимых диапазонов в итерационных процессах осуществляется по значениям искомых проводимостей, рассчитанных аналитически [30] и обеспечивающих значение 131.9 К2 суммарного критериального функционала (табл. 1):

${{{\mathbf{a}}}_{1}} = \left\{ {0,\;{{{\alpha }}_{{12}}},\;{{{\alpha }}_{{13}}},\;{{{\alpha }}_{{14}}}} \right\} = \left\{ {0,\;0.566,\;7.41,\;0} \right\}\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}{\text{,}}$
${{{\mathbf{a}}}_{2}} = \left\{ {{{{\alpha }}_{{21}}},\;0,\;{{{\alpha }}_{{23}}},\;0} \right\} = \left\{ {0.566,\;0,\;0.01,0} \right\}\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}{\text{,}}$
${{{\mathbf{a}}}_{3}} = \left\{ {{{{\alpha }}_{{31}}},\;{{{\alpha }}_{{32}}},\;0,\;0} \right\} = \left\{ {7.41,\;0.01,\;0,\;0} \right\}\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}{\text{,}}$
${{{\mathbf{a}}}_{4}} = \left\{ {{{{\alpha }}_{{41}}},\;0,\;0,\;0} \right\} = \left\{ {0,\;0,\;0,\;0} \right\}\,\,\,{{{\text{В т }}} \mathord{\left/ {\vphantom {{{\text{В т }}} {\text{К }}}} \right. \kern-0em} {\text{К }}}.$
Таблица 1.  

Спецификация итерационных процессов регуляризации в задаче идентификации тепловых проводимостей с неустойчивым решением

Метод Начальные приближения $\delta _{T}^{2},$ К2 m $J_{1}^{{\left( m \right)}},$ К2 $J_{2}^{{\left( m \right)}},$ К2 $J_{3}^{{\left( m \right)}},$ К2 J(m), К2
Аналитический Нет – – 23.0 64.8   44.2 131.9
МИР Произвольные 1.4 36 95.1 0.0 129.9 225.0
Метод Тихонова – 1.4 12 93.7 2.413 127.9 224.0

Поскольку пример является методическим, в нем выделено два предельных случая параметризации математической модели:

– α14 = α41 = 0, что исключает четвертое уравнение из системы и позволяет проверить, будет ли при таком условии идентифицированная функция α14(τ) стремиться к нулю;

– экспериментальная температура внутренней части оптической защиты 2 задана постоянной и равной $T_{2}^{{\left( 0 \right)}}$ = 273–10 К, что вызвано отсутствием измеренных температур для этого узла и позволяет проверить, будет ли расчетная температура T2 стремиться к постоянному значению.

Среднеквадратичная ошибка температурных измерений для всей системы

$\delta _{T}^{2} = \sum\limits_{i = 1}^N {D\left( {T_{i}^{{\left( 0 \right)}}} \right) = N} D\left( {T_{i}^{{\left( 0 \right)}}} \right) = 1.44\,\,{\text{K}}{\text{.}}$

Условие регуляризации (6) является пределом точности итерационного процесса, поэтому более рационально останавливать вычисления по условию $J_{i}^{{\left( l \right)}}$ ≥ $J_{i}^{{\left( {l - 1} \right)}}$ или замедлению сходимости при достижении приемлемых значений функционалов и достаточно гладких зависимостей для искомых функций.

Расчеты выполняются методом итерационной регуляризации [25] и вариационным методом Тихонова с определением параметра регуляризации по комбинированной методике [27] для задач идентификации с неустойчивым решением (рис. 2, 3, табл. 1, 2). Единственность решения обеспечивается упрощением исходной системы до вида, в котором все искомые функции относятся к одному узлу и выражаются через α23(τ), которая и регуляризуется.

Рис. 2.

Распределения значений функционалов J в зависимости от номера итерации в задаче идентификации с неустойчивым решением: (а) – метод итерационной регуляризации, (б) – вариационный метод Тихонова.

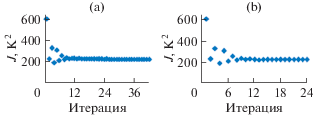
Рис. 3.

Корреляция временны́х зависимостей расчетных t и экспериментальных e температур узлов 1–4 в задаче идентификации с неустойчивым решением: (а) – на итерации 1; (б) – МИР, на итерации 36; (в) – вариационный метод Тихонова, на итерации 12.

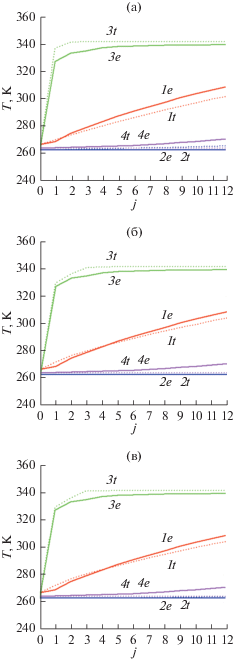
Таблица 2.  

Соответствие точек временнóй сетки времени испытаний

j 0 1 2 3 4 5 6 7 8 9 10 11 12
τ, с 0 1.20 × 103 2.40 × 103 3.60 × 103 4.80 × 103 6.00 × 103 7.20 × 103 8.40 × 103 9.60 × 103 1.08 × 104 1.20 × 104 1.32 × 104 1.44 × 104

По результатам идентификации проверена применимость методов в предельных методических случаях: α14 = α41 → 0, T2 → $T_{2}^{{\left( 0 \right)}}$ = 273–10 К.

Устойчивость решений проверяется сопоставлением функций, определенных по возмущенному температурному полю, с идентифицированными функциями, которые считаются “истинными”, а рассчитанное по ним температурное поле – “экспериментальным”. На “экспериментальное” поле накладывается нормальное возмущение, полученное как четыре (по числу узлов) массива из 13 значений с математическим ожиданием, равным нулю, и средним квадратичным отклонением 0.4, умноженных на С = 8 К.

В качестве “истинных” выбраны функции, идентифицированные соответствующим методом, рассчитанные по ним температуры представляются “экспериментальными”.

Результаты применения метода итерационной регуляризации в случае нормального возмущения показаны на рис 4, 5. В отличие от случая исходных экспериментальных температур идентифицированные функции определяются не на итерации 36, а на итерации 40, но являются близкими по значениям и характеру к идентифицированным при отсутствии возмущения.

Рис. 4.

Корреляция временны́х зависимостей расчетных t и возмущенных d температур узлов 1–4 на итерации 40 при нормальном возмущении (МИР).

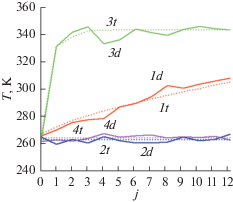
Рис 5.

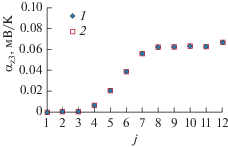
Временны́е зависимости искомых функций при нормальном возмущении “экспериментальной” температуры (МИР): 1 – идентифицированная (36 итераций), 2 – нормальное возмущение (40 итераций).

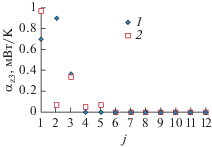
Результаты применения вариационного метода Тихонова показаны на рис. 6, 7. Как и в случае исходных экспериментальных температур идентифицированные функции определяются на итерации 12 по условию замедления сходимости температурного функционала и являются близкими по значениям и характеру к “истинным” функциям.

Рис. 6.

Корреляция временны́х зависимостей расчетных t и возмущенных d температур узлов 1–4 на итерации 12 при нормальном возмущении (вариационный метод Тихонова).

Рис. 7.

Временны́е зависимости искомых функций при нормальном возмущении “экспериментальной” температуры (вариационный метод Тихонова): 1 – идентифицированная (12 итераций), 2 – нормальное возмущение (12 итераций).

ЗАКЛЮЧЕНИЕ

1. Показано, что задача идентификации неизвестных функций матрицы тепловых связей математической тепловой модели с сосредоточенными параметрами, состоящей из обыкновенных дифференциальных уравнений, в общем виде имеет неединственное решение и может быть неустойчивой из-за плохой обусловленности. В случае неустойчивого решения применение методов итерационной регуляризации позволяет получить условно устойчивое решение при использовании экспериментальной температуры одного узла для идентификации одной координаты искомого вектора. Решение задачи в общем виде имеет неединственное решение и может находиться приближенно с использованием методической возможности расчета единого шага спуска (параметра регуляризации) для каждого искомого вектора. В этом случае требуется усиление вариационного принципа дополнительными условиями. Задача идентификации полного набора связей решается итерационно последовательным перебором узлов системы на каждой итерации при наличии первого приближения.

2. Получены аналитические выражения для вычисления неопределенных множителей Лагранжа, входящих в выражения градиента функционала температурной невязки в методе итерационной регуляризации, и уточненные аналитические выражения шага спуска (параметра регуляризации). При замене в выражении шага спуска метода итерационной регуляризации функции градиента функционала разностью значений искомого вектора на двух соседних итерациях получается выражение безразмерного шага спуска, обратного параметру регуляризации итерационного метода на основе вариационного метода Тихонова. Полученные выражения обобщены для технических, в частности, космических систем и проверены вычислительными экспериментами.

Работа выполнена в рамках государственного задания № 9.9074.2017/БЧ Минобрнауки России.

Список литературы

  1. Артюхин Е.А., Киллих В.Е., Ненарокомов А.В., Репин И.В. Исследование теплового взаимодействия материала с двухфазными потоками методом обратных задач // ТВТ. 1990. Т. 28. № 1. С. 111.

  2. Алифанов О.М., Артюхин Е.А., Ненарокомов А.В., Репин И.В. Определение характеристик теплового взаимодействия материалов с двухфазными потоками методом обратных задач // ТВТ. 1993. Т. 31. № 3. С. 450.

  3. Алифанов О.М., Ненарокомов А.В. Трехмерная граничная обратная задача теплопроводности // ТВТ. 1999. Т. 37. № 2. С. 231.

  4. Столяров Е.П. Моделирование процессов в тепловых датчиках на основе решения обратных задач теплопроводности // ТВТ. 2005. Т. 43. № 1. С. 71.

  5. Колесник С.А., Формалев В.Ф., Кузнецова Е.Л. О граничной обратной задаче теплопроводности по восстановлению тепловых потоков к границам анизотропных тел // ТВТ. 2015. Т. 53. № 1. С. 72.

  6. Артюхин Е.А., Ненарокомов А.В. Идентификация характеристик теплового взаимодействия материалов с газовыми потоками // ТВТ. 1990. Т. 28. № 2. С. 323.

  7. Будник С.А., Ненарокомов А.В. Оптимальное планирование измерений при определении характеристик теплового нагружения тел с подвижными границами // ТВТ. 1997. Т. 35. № 3. С. 453.

  8. Алифанов О.М., Репин И.В. Исследование теплообмена в гетерогенных потоках методом обратных задач теплопроводности // ТВТ. 1993. Т. 31. № 1. С. 78.

  9. Мацевитый Ю.М., Мултановский А.В. Одновременная идентификация теплофизических характеристик сверхтвердых материалов // ТВТ. 1990. Т. 28. № 5. С. 924.

  10. Мацевитый Ю.М., Мултановский А.В., Тимченко В.М. Моделирование тепловых процессов и идентификация локальных параметров теплообмена с помощью адаптивного итерационного фильтра // ТВТ. 1992. Т. 30. № 1. С. 82.

  11. Артюхин Е.А., Иванов Г.А., Ненарокомов А.В. Определение комплекса теплофизических характеристик материалов по данным нестационарных измерений температуры // ТВТ. 1993. Т. 31. № 2. С. 235.

  12. Алифанов О.М., Черепанов В.В. Математическое моделирование высокопористых волокнистых материалов и определение их физических свойств // ТВТ. 2009. Т. 47. № 3. С. 463.

  13. Кузнецова Е.Л. Решение обратных задач теплопроводности для получения характеристик анизотропных материалов // ТВТ. 2011. Т. 49. № 6. С. 912.

  14. Формалев В.Ф., Колесник С.А. Методология решения обратных коэффициентных задач по определению нелинейных теплофизических характеристик анизотропных тел // ТВТ. 2013. Т. 51. № 6. С. 875.

  15. Формалев В.Ф., Колесник С.А. Об обратных граничных задачах теплопроводности по восстановлению тепловых потоков к анизотропным телам с нелинейными характеристиками теплопереноса // ТВТ. 2017. Т. 55. № 4. С. 564.

  16. Миронов Р.А., Забежайлов М.О., Русин М.Ю., Черепанов В.В., Бородай С.П. Расчетно-экспериментальное определение температурной зависимости спектральных и интегральных коэффициентов излучения кварцевой керамики различной пористости // ТВТ. 2016. Т. 54. № 5. С. 724.

  17. Ненарокомов А.В. Проектирование системы многослойной теплоизоляции минимальной массы // ТВТ. 1997. Т. 35. № 6. С. 909.

  18. Формалев В.Ф., Колесник С.А., Селин И.А., Кузнецова Е.Л. Оптимальный выбор параметров экранно-вакуумной теплоизоляции космических аппаратов // ТВТ. 2017. Т. 55. № 1. С. 108.

  19. Алексеев А.K. К решению одной обратной ретроспективной задачи конвекции // ТВТ. 1999. Т. 37. № 4. С. 582.

  20. Дилигенская А.Н. Решение ретроспективной обратной задачи теплопроводности на основе параметрической оптимизации // ТВТ. 2018. Т. 56. № 3. С. 399.

  21. Плешанов А.С. Об экстремальных принципах в теории теплопроводности твердого тела // ТВТ. 2002. Т. 40. № 2. С. 323.

  22. Бердник В.В., Мухамедяров Р.Д. Применение метода нейронных сетей для решения обратной задачи теплопереноса // ТВТ. 2003. Т. 41. № 6. С. 942.

  23. Алифанов О.М. Обратные задачи теплообмена. М.: Машиностроение, 1988. 280 с.

  24. Викулов А.Г., Ненарокомов А.В. Идентификация тепловых связей в математических моделях космических систем // Тепловые процессы в технике. 2014. Т. 6. № 6. С. 274.

  25. Викулов А.Г., Ненарокомов А.В. Экстремальный метод идентификации тепловых математических моделей с сосредоточенными параметрами // Тепловые процессы в технике. 2015. Т. 7. № 7. С. 307.

  26. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука; Гл. ред. физ.-мат. лит., 1979. 288 с.

  27. Викулов А.Г., Ненарокомов А.В. Вариационный метод идентификации тепловых математических моделей с сосредоточенными параметрами // Тепловые процессы в технике. 2016. Т. 8. № 5. С. 214.

  28. Викулов А.Г., Ненарокомов А.В. Идентификация редуцированной математической модели экранно-вакуумной тепловой изоляции // Тепловые процессы в технике. 2016. Т. 8. № 11. С. 488.

  29. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. М.: Наука; Гл. ред. физ.-мат. лит., 1980. 288 с.

  30. Викулов А.Г., Викулов Д.Г. Электронная проводимость контактов твердых тел. Saarbrücken, Germany: Lambert Acad. Publ., 2011. 170 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал