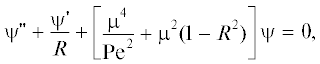1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 57, № 2, 2019

Теплофизика высоких температур, 2019, T. 57, № 2, стр. 308-311

Расчет теплообмена при ламинарном течении жидкости в цилиндрическом канале при наличии аксиальной теплопроводности

Ю. В. Видин 1, Р. В. Казаков 1, *

1 Сибирский федеральный университет
г. Красноярск, Россия

* E-mail: roman.kazakov@list.ru

Поступила в редакцию 05.07.2018
После доработки 10.10.2018
Принята к публикации 19.08.2018

Полный текст (PDF)

Аннотация

Предложен аналитический метод расчета собственных значений и собственных функций в задаче теплообмена для ламинарного потока жидкости в цилиндрическом канале с учетом аксиальной теплопроводности. Метод основан на использовании специальной гипергеометрической конфлюэнтной функции. С ее помощью удается найти точные реперные величины собственных чисел и собственных функций при определенных соотношениях между числами подобия Био и Пекле. Кроме этого, рекомендуемый способ позволяет выполнить необходимые математические вычислительные операции при произвольном сочетании названных чисел подобия с достаточной степенью точности, задавая соответствующий безразмерный комплекс α. Такой подход позволяет существенно ограничить (уменьшить) количество весомых членов бесконечного ряда применяемой гипергеометрической функции. Выведенные строгие и приближенные аналитические решения с использованием названных функций могут быть применены для теоретического анализа широкого класса теплофизических задач, в том числе и нелинейных.

ВВЕДЕНИЕ

Известно, что аналитический расчет процесса теплообмена при ламинарном течении жидкости в каналах с учетом ее аксиальной теплопроводности существенно усложняется [1–4]. С традиционными допущениями рассматриваемая задача может быть представлена при действующих на наружной поверхности граничных условиях третьего рода в следующем безразмерном виде [1]:

(1)
$\frac{{{{\partial }^{2}}\vartheta }}{{\partial {{R}^{2}}}} + \frac{1}{R}\frac{{\partial \vartheta }}{{\partial R}} + \frac{1}{{{\text{P}}{{{\text{e}}}^{2}}}}\frac{{{{\partial }^{2}}\vartheta }}{{\partial {{X}^{2}}}} = (1 - {{R}^{2}})\frac{{\partial \vartheta }}{{\partial X}},$
(2)
$\frac{{\partial \vartheta }}{{\partial R}} = 0\,\,{\text{п р и }}\,\,R = 0,$
(3)
$\frac{{\partial \vartheta }}{{\partial R}} = - {\text{Bi}}\vartheta \,\,{\text{п р и }}\,\,R = 1,$
(4)
$\vartheta = 1\,\,{\text{п р и }}\,\,X = 0.$

Общее решение этой задачи можно записать в форме бесконечного ряда

$\vartheta = \sum\limits_{n = 1}^\infty {{{A}_{n}}{{\psi }_{n}}(R)\exp ( - \mu _{n}^{2}X)} ,$
где собственные значения ${{\mu }_{n}}$ зависят от чисел подобия Bi и Pe.

РЕШЕНИЕ ЗАДАЧИ

В классической монографии [1] цитируется аналитическое решение задачи (1)–(4), полученное в работе [2] для случая, когда ${\text{Bi}} \Rightarrow \infty ,$ т.е. на поверхности трубы действует граничное условие первого рода. Согласно [2], собственные функции ${{\psi }_{n}}(R)$ представлены в виде бесконечного степенного ряда

${{\psi }_{n}}(R) = \sum\limits_{m = 0}^\infty {{{b}_{m}}{{R}^{m}}} ,$
где индекс m принимает четные значения (0, 2, 4…).

В монографиях [5–7] теоретически рассмотрены достаточно подробно и всесторонне процессы теплообмена при ламинарном движении жидкости в плоских и круглых каналах без учета осевой теплопроводности, т.е. когда ${\text{Pe}} \Rightarrow \infty $. При этом для решения задач были привлечены вырожденные гипергеометрические функции [8, 9]. По мнению авторов, применение таких функций является наиболее перспективным математическим направлением при исследовании тепловых процессов, подобных задаче (1)–(4).

Очевидно, что нахождение собственных значений ${{\mu }_{n}}$ и собственных функций ${{\psi }_{n}}(R)$ сводится к решению следующей задачи Штурма–Лиувилля:

(5)
(6)
$\psi {\text{'}} = 0\,\,{\text{п р и }}\,\,R = 0,$
(7)
$\psi {\text{'}} = - {\text{Bi}}\psi \,\,{\text{п р и }}\,\,R = 1.$

Представить интеграл дифференциального уравнения второго порядка (5) с принятыми граничными условиями (6) и (7) через элементарные функции в общем случае не удается. Поэтому здесь целесообразно использовать специальные функции. Как показано в [6], аналитическое решение задачи (5)–(7) можно записать в виде

(8)
$\psi = \exp \left( { - \mu \frac{{{{R}^{2}}}}{2}} \right){{F}_{a}}(\alpha ,\gamma ,\mu {{R}^{2}}),$
где ${{F}_{a}}(\alpha ,\gamma ,\mu {{R}^{2}})$ – конфлюэнтная гипергеометрическая функция [7, 8], определяемая как бесконечная сумма

(9)
$\begin{gathered} {{F}_{a}}(\alpha ,\gamma ,\mu {{R}^{2}}) = 1 + \frac{\alpha }{\gamma }\mu {{R}^{2}} + \frac{{\alpha (\alpha + 1)}}{{\gamma (\gamma + 1)}}\frac{{{{\mu }^{2}}{{R}^{4}}}}{{2!}} + \\ + \,\,\frac{{\alpha (\alpha + 1)(\alpha + 2)}}{{\gamma (\gamma + 1)(\gamma + 2)}}\frac{{{{\mu }^{3}}{{R}^{6}}}}{{3!}} + \\ + \,\,\frac{{\alpha (\alpha + 1)(\alpha + 2)(\alpha + 3)}}{{\gamma (\gamma + 1)(\gamma + 2)(\gamma + 3)}}\frac{{{{\mu }^{4}}{{R}^{8}}}}{{4!}} + ... + \\ + \,\,\frac{{\alpha (\alpha + 1)(\alpha + 2)...(\alpha + m - 1)}}{{\gamma (\gamma + 1)(\gamma + 2)...(\gamma + m - 1)}}\frac{{{{\mu }^{m}}{{R}^{{2m}}}}}{{m!}} + .... \\ \end{gathered} $

При этом для канала круглого сечения будут иметь место равенства

$\alpha = \frac{1}{4}\left( {2 - \mu - \frac{{{{\mu }^{3}}}}{{{\text{P}}{{{\text{e}}}^{2}}}}} \right)\,\,{\text{и }}\,\,\gamma = 1.$

При $\gamma = 1$ формула (9) примет вид

(10)
$\begin{gathered} {{F}_{a}}(\alpha ,1,\mu {{R}^{2}}) = 1 + \alpha \mu {{R}^{2}} + \frac{{\alpha (\alpha + 1){{\mu }^{2}}{{R}^{4}}}}{{{{{(2!)}}^{2}}}} + \\ + \,\,\alpha (\alpha + 1)(\alpha + 2)\frac{{{{\mu }^{3}}{{R}^{6}}}}{{{{{(3!)}}^{2}}}} + ... + \\ + \,\,\frac{{\alpha (\alpha + 1)(\alpha + 2)...(\alpha + m - 1){{\mu }^{m}}{{R}^{{2m}}}}}{{{{{(m!)}}^{2}}}}. \\ \end{gathered} $

После подстановки (8) в граничное условие (7), может быть получено характеристическое уравнение для определения собственных чисел ${{\mu }_{n}}$ рассматриваемой задачи в виде

(11)
$\mu - \frac{{2\alpha \mu + \alpha (\alpha + 1){{\mu }^{2}} + \frac{{\alpha (\alpha + 1)(\alpha + 2)}}{{3!}}{{\mu }^{3}} + ...}}{{1 + \alpha \mu + \frac{{\alpha (\alpha + 1)}}{{{{{(2!)}}^{2}}}}{{\mu }^{2}} + \frac{{\alpha (\alpha + 1)(\alpha + 2)}}{{{{{(3!)}}^{2}}}}{{\mu }^{3}} + ...}} = {\text{Bi}}{\text{.}}$

В частном случае, а именно при ${\text{Bi}} \Rightarrow \infty $ (граничное условие первого рода), формула (11) упрощается

(12)
$1 + \alpha \mu + \frac{{\alpha (\alpha + 1)}}{{{{{(2!)}}^{2}}}}{{\mu }^{2}} + \frac{{\alpha (\alpha + 1)(\alpha + 2)}}{{{{{(3!)}}^{2}}}}{{\mu }^{3}} + ... = 0.$

В монографиях [5–7] приведены подробные табличные значения трех первых корней ${{\mu }_{n}}$ уравнений (11) и (12) для широкого диапазона чисел Bi, рассчитанные при условии, что осевой растечки тепла в потоке жидкости нет, т.е. параметр ${\text{Pe}} \Rightarrow \infty $ и, следовательно, комплекс $\alpha $ равен $\alpha = \frac{1}{4}(2 - \mu ),$ что соответствует максимально возможным величинам этого коэффициента. В представленной таблице наряду с числовыми значениями корней ${{\mu }_{1}},\,\,{{\mu }_{2}},\,\,{{\mu }_{3}}$ указаны и соответствующие им ${{\alpha }_{{1\max }}},\,\,{{\alpha }_{{2\max }}},\,\,{{\alpha }_{{3\max }}}.$

Таблица 1.  

Значения первых трех характеристических чисел μn и αnmax для круглого канала при отсутствии аксиальной теплопроводности

Bi μ1 μ2 μ3 α1max α2max α3max
0 0 5.0675 9.1576 0.500 –0.767 –1.789
0.1 0.6183 5.1168 9.1750 0.345 –0.779 –1.794
0.2 0.8555 5.1641 9.2058 0.286 –0.791 –1.801
0.3 1.0258 5.2096 9.2359 0.244 –0.802 –1.809
0.4 1.1603 5.2532 9.2651 0.210 –0.813 –1.816
0.5 1.2716 5.2951 9.3063 0.182 –0.824 –1.827
0.6 1.3663 5.3349 9.3214 0.158 –0.834 –1.830
0.7 1.4482 5.3731 9.3484 0.138 –0.843 –1.837
0.8 1.5202 5.4097 9.3749 0.120 –0.852 –1.845
0.9 1.5841 5.4447 9.4002 0.104 –0.861 –1.850
1.0 1.6413 5.4782 9.4250 0.090 –0.870 –1.856
1.5 1.8569 5.6251 9.5390 0.036 –0.906 –1.885
2.0 2.0000 5.7439 9.6450 0.000 –0.936 –1.911
3.0 2.1787 5.9209 9.7976 –0.045 –0.980 –1.949
4.0 2.2857 6.0446 9.9193 –0.071 –1.011 –1.980
5.0 2.3568 6.1351 10.0137 –0.089 –1.034 –2.003
10.0 2.5168 6.3647 10.2755 –0.129 –1.091 –2.069
20.0 2.6069 6.5098 10.4500 –0.152 –1.127 –2.113
30.0 2.6386 6.5637 10.5259 –0.160 –1.141 –2.131
40.0 2.6547 6.5916 10.5624 –0.164 –1.148 –2.141
50.0 2.6645 6.6086 10.5849 –0.166 –1.152 –2.146
60.0 2.6710 6.6201 10.6001 –0.168 –1.155 –2.150
80.0 2.6793 6.6346 10.6194 –0.170 –1.159 –2.155
100.0 2.6845 6.6434 10.6312 –0.171 –1.161 –2.158
1000.0 2.7026 6.6790 10.6734 –0.176 –1.170 –2.168
∞ 2.7044 6.6790 10.6734 –0.176 –1.170 –2.168

При наличии осевого переноса тепла в потоке, т.е. когда число ${\text{Pe}} < \infty ,$ коэффициенты ${{\alpha }_{n}}$ будут обязательно меньше максимальных значений ${{\alpha }_{{n\max }}}.$

Нетрудно показать, что в тех случаях, когда параметр $\alpha $ оказывается нулевым или целым отрицательным числом, бесконечные ряды в зависимостях (10)–(12) обрываются и становятся конечными и, как правило, легко решаемыми.

Так, например, если при ${\text{Bi}} \Rightarrow \infty $ принять ${{\alpha }_{1}} = - 1,$ то согласно зависимости (12) первое собственное значение будет равно ${{\mu }_{1}} = 1$ и, следовательно, соответствующее этому рассматриваемому варианту число Pe = 0.4472. Тогда первая собственная функция записывается в простом виде ${{\psi }_{1}}(R) = {{(1 - R)}^{2}}\exp \left( { - \frac{{{{R}^{2}}}}{2}} \right).$

Другим интересным случаем является вариант, в котором ${\text{Bi}} = 1$ и ${\text{Pe}} = 1$. Тогда первое собственное число ${{\mu }_{1}}$ тоже равно единице ${{\mu }_{1}} = 1$ и, следовательно, параметр ${{\alpha }_{1}} = 0.$ Очевидно, что первая собственная функция ${{\psi }_{1}}(R)$ для такого сочетания Bi и Pe становится еще проще, а именно ${{\psi }_{1}}(R) = \exp \left( { - \frac{{{{R}^{2}}}}{2}} \right).$

Подобные примеры могут быть существенно расширены. Так, допустим, если снова принять $\alpha = - 1,$ тогда характеристическое уравнение (11) преобразуется в алгебраическое уравнение второй степени

${{\mu }^{2}} - (3 + {\text{Bi}})\mu + {\text{Bi}} = 0.$

Следовательно, при Bi = 1 первое и второе собственные числа ${{\mu }_{1}}$ и ${{\mu }_{2}}$ будут равны

${{\mu }_{1}} = \frac{{3 + {\text{Bi}}}}{2} - \sqrt {\frac{{{{{(3 + {\text{Bi}})}}^{2}}}}{4} - {\text{Bi}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{3 + 1}}{2} - \sqrt {4 - 1} = 0.268,$
${{\mu }_{2}} = \frac{{3 + {\text{Bi}}}}{2} + \sqrt {\frac{{{{{(3 + {\text{Bi}})}}^{2}}}}{4} - {\text{Bi}}} = 2 + \sqrt {4 - 1} = 3.732.$

Далее легко находятся соответствующие им значения Pe по выражениям

${\text{P}}{{{\text{e}}}_{1}} = \sqrt {\frac{{\mu _{1}^{3}}}{{2 - 4\alpha - {{\mu }_{1}}}}} = \sqrt {\frac{{{{{0.268}}^{3}}}}{{2 + 4 - 0.268}}} = 0.058,$
${\text{P}}{{{\text{e}}}_{2}} = \sqrt {\frac{{\mu _{2}^{3}}}{{2 - 4\alpha - {{\mu }_{2}}}}} = \sqrt {\frac{{{{{3.732}}^{3}}}}{{2 + 4 - 3.732}}} = 4.7872.$

Таким образом, в случае, когда ${\text{Bi}} = 1$ и ${\text{Pe}} = 0.058,$ первый корень характеристического уравнения (11) ${{\mu }_{1}} = 0.268$ и, следовательно, первая собственная функция ${{\psi }_{1}}(R)$ будет иметь вид ${{\psi }_{1}}(R) = (1 - 0.268{{R}^{2}})\exp ( - 0.134{{R}^{2}}).$

Если же ${\text{Bi}} = 1$ и ${\text{Pe}} = 4.7872,$ тогда второе собственное значение ${{\mu }_{2}} = 3.732$ и ${{\psi }_{2}}(R)$ = $ = (1 - 3.732{{R}^{2}})\exp ( - 1.866{{R}^{2}}).$

Естественно, что данные функции при указанных величинах чисел подобия Bi и Pe должны вполне удовлетворять задаче (7)–(9). Аналогичным способом выполняются расчеты и для других величин Bi.

Подобный анализ можно провести, например, и при величине параметра $\alpha = - 2.$ В этом случае характеристическое уравнение (11) преобразуется в алгебраическое соотношение третьей степени

(13)
$(5 + 2{\text{Bi}})\mu - \left( {4 + \frac{{{\text{Bi}}}}{2}} \right){{\mu }^{2}} + \frac{{{{\mu }^{3}}}}{2} - {\text{Bi}} = 0,$
которое при ${\text{Bi}} \Rightarrow \infty $ вырождается в квадратное ${{\mu }^{2}} - 4\mu + 2 = 0,$ и тогда ${{{\mu }}_{{\text{1}}}} = 0.5858$ и ${{{\mu }}_{{\text{2}}}} = 3.4142.$

Если же число Bi является конечным, то корни кубического уравнения (13) могут быть определены, например, с помощью известных формул Кардано. В частности, при Bi = 1 выражение принимает вид

${{\mu }^{3}} - 9{{\mu }^{2}} + 14\mu - 2 = 0.$

Отсюда следует, что

${{\mu }_{1}} = 0.1588,\,\,\,\,{{\mu }_{2}} = 1.7852,\,\,\,\,{{\mu }_{3}} = 7.0560.$

Далее рассчитываются соответствующие числа Pe

${\text{P}}{{{\text{e}}}_{1}} = \sqrt {\frac{{{{{0.159}}^{3}}}}{{10 - 0.159}}} = 0.0202,$
${\text{P}}{{{\text{e}}}_{2}} = \sqrt {\frac{{{{{1.785}}^{3}}}}{{10 - 1.785}}} = 0.8321,$
${\text{P}}{{{\text{e}}}_{3}} = \sqrt {\frac{{{{{7.056}}^{3}}}}{{10 - 7.056}}} = 10.924.$

Следовательно, при Bi = 1 и Pe = 0.0202 первая собственная функция ${{\psi }_{1}}(R)$ имеет вид

${{\psi }_{1}}(R) = (1 - 0.0318{{R}^{2}} + 0.0126{{R}^{4}})exp( - 0.0795{{R}^{2}}),$
при Bi = 1 и Pe = 0.08321
${{\psi }_{2}}(R) = (1 - 3.75{{R}^{2}} + 1.593{{R}^{4}})\exp ( - 0.8925{{R}^{2}})$
и при Bi = 1 и Pe = 10.924

${{\psi }_{3}}(R) = (1 - 14.112{{R}^{2}} + 24.894{{R}^{4}})\exp ( - 3.528{{R}^{2}}).$

ЗАКЛЮЧЕНИЕ

Итак, благодаря ряду свойств гипергеометрической функции (9), удается получить широкий спектр строгих аналитических решений задачи (5)–(7) для точечных комбинаций параметров Bi и Pe. Кроме того, во многих случаях, задавая приемлемый по величине комплекс α, можно свести уравнение (11) к сравнительно несложному алгебраическому выражению, обычно не выше четвертой степени. Это позволяет существенно расширить область определения приближенных аналитических решений уравнения (5) с граничными условиями (6), (7). Причем с инженерной точки зрения они, как правило, обладают вполне достаточной точностью.

Нетрудно также показать, что предлагаемый подход может быть применен и в случае, когда необходимо учесть влияние термического сопротивления стенки канала [5]. В работах [10, 11] приведены табличные данные функции (9) для ряда значений безразмерных параметров α и γ. Однако, по мнению авторов, целесообразно дополнить их для области малых и отрицательных величин коэффициентом α. Тогда, как это видно из приведенной в данной работе таблицы, оказывается возможным применение таких функций для эффективного исследования различных классов задач, подобных, в частности, рассматриваемой.

Список литературы

  1. Петухов Б.С. Теплообмен и сопротивление при ламинарном течении жидкости в трубах. М.: Энергия, 1967. 411 с.

  2. Лабунцов Д.А. Некоторые вопросы теории теплообмена при ламинарном течении жидкости в трубах // Теплоэнергетика. 1958. № 3.

  3. Видин Ю.В., Иванов В.В. Влияние аксиальной теплопроводности жидкости в трубах на процессе радиационно-конвективного охлаждения наружных поверхностей // Изв. вузов Северо-Кавказского региона. Техн. науки. 2014. № 5. С. 45.

  4. Генин Л.Г. Расчет температур жидкости и стенки при течении в трубах с учетом осевой теплопроводности // ТВТ. 1963. Т. 1. № 2. С. 247.

  5. Видин Ю.В., Иванов В.В., Медведев Г.Г. Расчет теплообмена при ламинарном течении жидкости в каналах. Красноярск: КПИ, 1971. 144 с.

  6. Видин Ю.В., Иванов В.В., Казаков Р.В. Инженерные методы расчета задач теплообмена. Красноярск: СФУ, 2014. 167 с.

  7. Видин Ю.В., Злобин В.С., Иванов В.В., Медведев Г.Г. Инженерные методы расчета задач нелинейного теплообмена при ламинарном течении жидкости в каналах. Красноярск: СФУ, 2015. 155 с.

  8. Маделунг Э. Математический аппарат физики. М.: Наука, 1968. 618 с.

  9. Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979. 830 с.

  10. Slater L.J. On the Evaluation of the Confluent Hypergeometric Function // Proc. Cambridge Philosoph. Society. 1953. V. 49. P. 612.

  11. Rushton S., Lang E.D. Tables of Confluent Hypergeometric Function // Sankhya. The Ind. J. Statist. 1954. V. 13. P. 377.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал