Теплофизика высоких температур, 2019, T. 57, № 3, стр. 453-458

Отражение акустических волн, падающих под прямым углом на границу раздела двух многофракционных газовзвесей

Д. А. Губайдуллин¹, Е. А. Терегулова^1, *, Д. Д. Губайдуллина¹

¹ Институт механики и машиностроения ФИЦ Казанский научный центр РАН
Казань, Россия

Поступила в редакцию 22.06.2018
После доработки 28.09.2018
Принята к публикации 10.10.2018

DOI: 10.1134/S0040364419030049

Аннотация

Изучены особенности отражения и преломления акустической волны, проходящей через границу двух многофракционных газовзвесей под прямым углом. Получены формулы для вычисления импеданса многофракционной газовзвеси, коэффициентов отражения и преломления. Построены зависимости модулей и аргументов коэффициента преломления и коэффициента отражения от безразмерной частоты.

ВВЕДЕНИЕ

Исследование акустических волн в дискретно-слоистых средах является актуальной задачей, что обусловлено широким распространением таких сред в природе и технологических процессах. С основными моделями и некоторыми результатами исследования акустических волн в многофазных средах можно ознакомиться в [1–12]. Проблемам изучения двухфазных течений с твердыми частицами, каплями и пузырями посвящены работы [13–15]. В [16–19] исследуется отражение и преломление акустических волн от границы раздела между чистым газом и смесью газа с различными включениями. Падение акустической волны под прямым углом на границу между чистым и запыленным воздухом изучалось в [16], под произвольным углом – в [17–19]. Установлено, что в случае падения волны на границу раздела со стороны парогазокапельной среды существует критический угол падения, при котором волна полностью отражается от границы. Также показано, что при определенном выборе объемного содержания включений и угла падения волны на границу раздела как со стороны газа, так и со стороны смеси в дисперсной системе наблюдается полное прохождение акустической волны через среду.

В данной работе изучаются особенности отражения и преломления акустической волны, падающей под прямым углом на границу раздела двух многофракционных газовзвесей.

ИМПЕДАНС МНОГОФРАКЦИОННОЙ ГАЗОВЗВЕСИ

При описании движения многофракционных газовзвесей методами механики сплошной среды принимаются справедливыми следующие допущения [1]:

– размеры включений в смеси многократно превышают молекулярно-кинетические размеры, т.е. включения содержат большое количество молекул;

– размеры включений во много раз меньше расстояний, на которых осредненные или макроскопические параметры смеси или фаз меняются существенно, т.е. много меньше характерных длин рассматриваемых волн (акустическая однородность);

– непосредственным взаимодействием и столкновением включений друг с другом и эффектами хаотического (в том числе броуновского) и внутреннего движения включений (вращения, деформации) можно пренебречь;

– отсутствуют процессы слипания (коагуляции), дробления и образования новых включений.

Предполагается также, что

– дисперсные включения являются твердыми (несжимаемыми и недеформируемыми) сферическими частицами;

– вязкость и теплопроводность проявляются лишь в процессе межфазного взаимодействия и не проявляются в макроскопических процессах переноса импульса и энергии;

– основными силами, действующими на частицу, являются силы Стокса и Бассэ;

– отсутствует массообмен между частицами и несущей средой;

– несущая среда – калорически совершенный газ;

– принята трехтемпературная схема теплообмена. Тепловые потоки извне ${{q}_{{1\Sigma }}}$ и изнутри ${{q}_{{2\Sigma }}}$ включения к его поверхности задаются соотношениями

${{q}_{{1\Sigma }}} = 2\pi r{{\lambda }_{1}}{\text{N}}{{{\text{u}}}_{1}}(T_{1}^{'} - T_{\Sigma }^{'}),\,\,\,\,{\text{N}}{{{\text{u}}}_{1}} = 2r{{\beta _{1}^{T}} \mathord{\left/ {\vphantom {{\beta _{1}^{T}} {{{\lambda }_{1}}}}} \right. \kern-0em} {{{\lambda }_{1}}}},$

${{q}_{{2\Sigma }}} = 2\pi r{{\lambda }_{2}}{\text{N}}{{{\text{u}}}_{2}}(T_{2}^{'} - T_{\Sigma }^{'}),\,\,\,\,{\text{N}}{{{\text{u}}}_{2}} = 2r{{\beta _{2}^{T}} \mathord{\left/ {\vphantom {{\beta _{2}^{T}} {{{\lambda }_{2}}}}} \right. \kern-0em} {{{\lambda }_{2}}}},$

где $r$ – радиус частицы, ${{T}_{1}}$ – температура несущей фазы, ${{T}_{\Sigma }}$ – температура в приповерхностном $\Sigma $-слое включения, ${{T}_{2}}$ – температура включений, ${\text{N}}{{{\text{u}}}_{1}}$ и $\beta _{1}^{T}$ – безразмерный (число Нуссельта) и размерный коэффициенты теплообмена несущей фазы с границей раздела частицы, ${\text{N}}{{{\text{u}}}_{{\text{2}}}}$ и $\beta _{2}^{T}$ – безразмерный (число Нуссельта) и размерный коэффициенты теплообмена частицы с границей раздела, $\lambda $ – коэффициент теплопроводности.

В рамках принятых предположений для изучения распространения акустических волн в многофракционных газовзвесях используется модель многоскоростного континуума [1]. Линеаризованная система уравнений возмущенного движения многофракционной газовзвеси с твердыми частицами разных материалов и размеров в декартовой системе координат, относительно которой невозмущенная среда покоится, записывается в виде [10]

$\frac{{\partial \rho _{1}^{'}}}{{\partial t}} + {{\rho }_{{10}}}\frac{{\partial \text{v}_{1}^{'}}}{{\partial z}} = 0,\,\,\,\,\frac{{\partial \rho _{j}^{'}}}{{\partial t}} + {{\rho }_{{j0}}}\frac{{\partial \text{v}_{j}^{'}}}{{\partial z}} = 0\,\,\left( {j = \overline {s1,sN} } \right),$

$\begin{gathered} \frac{{\partial \text{v}_{1}^{'}}}{{\partial t}} + \frac{1}{{{{\rho }_{{10}}}}}\frac{{\partial p_{1}^{'}}}{{\partial z}} + \sum\limits_{j \in \overline {s1,sN} } {\frac{{{{m}_{j}}}}{{{{\tau }_{{\text{v}j}}}}}} \left( {\text{v}_{1}^{'} - \text{v}_{j}^{'} + \sqrt {\frac{{{{\tau }_{{\mu 1j}}}}}{\pi }} _{{_{{_{{_{{}}}}}}}}^{{}}} \right. \times \\ \times \,\,\left. {\int\limits_{ - \infty }^t {\frac{\partial }{{\partial \tau }}\left( {\text{v}_{1}^{'} - \text{v}_{j}^{'}} \right)\frac{{d\tau }}{{\sqrt {t - \tau } }}} } \right) = 0, \\ \end{gathered} $

$\begin{gathered} \frac{{\partial \text{v}_{j}^{'}}}{{\partial t}} = \frac{1}{{{{\tau }_{{\text{v}j}}}}}\left( {\text{v}_{1}^{'} - \text{v}_{j}^{'} + \sqrt {\frac{{{{\tau }_{{\mu 1j}}}}}{\pi }} \int\limits_{ - \infty }^t {\frac{\partial }{{\partial \tau }}} \left( {\text{v}_{1}^{'} - \text{v}_{j}^{'}} \right)\frac{{d\tau }}{{\sqrt {t - \tau } }}} \right) \\ \left( {j = \overline {s1,sN} } \right),\,\,\,\,\frac{{\partial T_{1}^{'}}}{{\partial t}} = \frac{1}{{\rho _{{10}}^{ \circ }{{c}_{{p1}}}}}\frac{{\partial p_{1}^{'}}}{{\partial t}} - \sum\limits_{j \in \overline {s1,sN} } {{\text{N}}{{{\text{u}}}_{{1j}}}\frac{{T_{1}^{'} - T_{{\Sigma j}}^{'}}}{{{{\tau }_{{T1j}}}}}} , \\ \end{gathered} $

(1)

$\begin{gathered} \frac{{\partial T_{j}^{'}}}{{\partial t}} = - {\text{N}}{{{\text{u}}}_{{2j}}}\frac{{T_{j}^{'} - T_{{\Sigma j}}^{'}}}{{{{\tau }_{{T2j}}}}}, \\ \frac{{{{c}_{{p1}}}}}{{{{m}_{j}}}}{\text{N}}{{{\text{u}}}_{{1j}}}\frac{{T_{1}^{'} - T_{{\Sigma j}}^{'}}}{{{{\tau }_{{T1j}}}}} + {{c}_{j}}{\text{N}}{{{\text{u}}}_{{2j}}}\frac{{T_{j}^{'} - T_{{\Sigma j}}^{'}}}{{{{\tau }_{{T2j}}}}} = 0\,\left( {j = \overline {s1,sN} } \right), \\ p_{1}^{'} = \frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}\rho _{1}^{'} + \frac{{{{p}_{0}}}}{{{{T}_{0}}}}T_{1}^{'}, \\ \end{gathered} $

$\begin{gathered} {{\rho }_{{j0}}} = {{\alpha }_{{j0}}}\rho _{{j0}}^{ \circ },\,\,\,\,{{\alpha }_{{j0}}} = \frac{4}{3}\pi r_{j}^{3}{{n}_{{j0}}},\,\,\,\,\left( {j = \overline {s1,sN} } \right), \\ {{\alpha }_{{10}}} + \sum\limits_{j \in \overline {s1,sN} } {{{\alpha }_{{j0}}}} = 1,\,\,\,\,m = \sum\limits_{j \in \overline {s1,sN} } {{{m}_{j}}} , \\ \end{gathered} $

${{m}_{j}} = \frac{{{{\rho }_{{j0}}}}}{{{{\rho }_{{10}}}}},\,\,\,\,{{\tau }_{{\mu 1j}}} = \frac{{\rho _{{10}}^{ \circ }r_{j}^{2}}}{{{{\mu }_{1}}}},\,\,\,\,{{\tau }_{{\text{v}j}}} = \frac{2}{9}\frac{{\rho _{j}^{ \circ }r_{j}^{2}}}{{{{\mu }_{1}}}}\,\,\,\,\left( {j = \overline {s1,sN} } \right),$

$\begin{gathered} {{\tau }_{{T1j}}} = \frac{2}{3}\frac{{{{\alpha }_{{10}}}}}{{{{\alpha }_{{j0}}}}}{{\tau }_{{\lambda 1j}}},\,\,\,\,{{\tau }_{{T2j}}} = \frac{2}{3}{{\tau }_{{\lambda 2j}}},\,\,\,\,{{\tau }_{{\lambda 1j}}} = \frac{{\rho _{{10}}^{ \circ }r_{j}^{2}{{c}_{{p1}}}}}{{{{\lambda }_{1}}}}, \\ {{\tau }_{{\lambda 2j}}} = \frac{{\rho _{j}^{ \circ }r_{j}^{2}{{c}_{j}}}}{{{{\lambda }_{j}}}},\,\,\,\,m_{j}^{ \circ } = \frac{{\rho _{{10}}^{^\circ }}}{{\rho _{j}^{ \circ }}}\,\,\,\,\left( {j = \overline {s1,sN} } \right). \\ \end{gathered} $

Переменные с индексом 1 относятся к несущей фазе, с индексом j $\left( {j = \overline {s1,sN} } \right)$ – к частице j-го типа. Штрихи вверху используются для обозначения возмущения параметров, индекс 0 соответствует начальному невозмущенному состоянию, индекс Σ – к поверхности раздела. Здесь ${{n}_{{j0}}}$ – число частиц j-го типа в единице объема, $\rho $ – приведенная плотность, $\rho ^\circ $ – истинная плотность, $\text{v}$ – скорость, $\alpha $ – объемное содержание, $p$ – давление, ${{C}_{1}}$ – скорость звука в чистом газе, ${{c}_{p}}$ – теплоемкость газа при постоянном давлении, ${{c}_{j}}$ – теплоемкость частиц j-го типа, ${{m}_{j}}$ – массовое содержание частиц j-го типа, $m$ – суммарное массовое содержание всех частиц, ${{\tau }_{T}}$ – время релаксации температур, ${{\tau }_{\text{v}}}$ – время релаксации скорости, ${{\mu }_{1}}$ – коэффициент динамической вязкости несущей среды.

Дисперсионное соотношение, определяющее распространение акустических волн в многофракционных газовзвесях, получено в работе [10] и имеет вид

${{\left( {\frac{{{{C}_{1}}{{K}_{{\text{*}}}}}}{\omega }} \right)}^{2}} = V\left( \omega \right)D\left( \omega \right),$

где

$\begin{gathered} {{K}_{{\text{*}}}} = K + i{{K}_{{{\text{**}}}}},\,\,\,\,V\left( \omega \right) = 1 + \sum\limits_{j \in \overline {s1,sN} } {\frac{{{{m}_{j}}}}{{1 - i\omega \tau _{{\text{v}j}}^{ * }}}} , \\ D\left( \omega \right) = 1 + \left( {{{\gamma }_{1}} - 1} \right)\frac{{\sum\limits_{j \in \overline {s1,sN} } {\frac{{{{m}_{j}}{{{\bar {c}}}_{j}}}}{{1 - i\omega \bar {\tau }_{{Tj}}^{ * }}}} }}{{1 + \sum\limits_{j \in \overline {s1,sN} } {\frac{{{{m}_{j}}{{{\bar {c}}}_{j}}}}{{1 - i\omega \bar {\tau }_{{Tj}}^{ * }}}} }}, \\ \end{gathered} $

$\begin{gathered} {{{\bar {c}}}_{j}} = \frac{{{{c}_{j}}}}{{{{c}_{{p1}}}}},\,\,\,\,\tau _{{\text{v}j}}^{*} = {{\tau }_{{\text{v}j}}}{{\left[ {1 + \frac{{1 - i}}{{\sqrt 2 }}{{{\left( {\omega {{\tau }_{{\mu 1j}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]}^{{ - 1}}}, \\ \tau _{{T1j}}^{ * } = \frac{1}{{{\text{Nu}}_{{1j}}^{*}}}{{\tau }_{{T1j}}},\,\,\,\,\tau _{{T2j}}^{*} = \frac{1}{{{\text{Nu}}_{{2j}}^{*}}}{{\tau }_{{T2j}}}. \\ \end{gathered} $

Здесь ${{K}_{*}}$ – комплексное волновое число. Числа Нуссельта ${\text{Nu}}_{{1j}}^{*}\left( \omega \right)$ и ${\text{Nu}}_{{2j}}^{*}\left( \omega \right)$ определяются из решения сферически-симметричной задачи о теплообмене сферической частицы с газом в монохроматической волне и имеют вид [3]

${\text{Nu}}_{{1j}}^{*} = 2\left( {1 + {{z}_{{1j}}}} \right),\,\,\,\,{\text{Nu}}_{{T2j}}^{ * } = \frac{{2z_{{2j}}^{2}({\text{th}}{{z}_{{2j}}} - {{z}_{{2j}}})}}{{3{{z}_{{2j}}} - (3 - z_{{2j}}^{2}){\text{th}}{{z}_{{2j}}}}},$

где ${{z}_{{1j}}} = \frac{{1 - i}}{{\sqrt 2 }}{{(\omega {{\tau }_{{\lambda 1j}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, ${{z}_{{2j}}} = \frac{{1 - i}}{{\sqrt 2 }}{{(\omega {{\tau }_{{\lambda 2j}}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$

Для монохроматической волны, удовлетворяющей уравнению (1), справедливо соотношение

$\text{v}_{1}^{'}\left( {t,z} \right) = \frac{1}{{i\omega {{\rho }_{{10}}}V\left( \omega \right)}}\frac{{\partial p{\text{'}}}}{{\partial z}}.$

Импеданс (волновое сопротивление) определяется следующим образом:

$Z = \frac{{p{\text{'}}\left( {t,z} \right)}}{{\text{v}{\text{'}}\left( {t,z} \right)}}.$

Следовательно, при распространении звуковой волны в однородном пространстве импеданс имеет вид

$Z\left( \omega \right) = {{\rho }_{{10}}}V\left( \omega \right)\frac{\omega }{{{{K}_{{\text{*}}}}}}.$

Импеданс $Z\left( \omega \right)$ зависит от частоты $\omega $ и является комплексной величиной. Его можно переписать следующим образом:

$\begin{gathered} Z\left( \omega \right) = {{\rho }_{{10}}}{{C}_{p}}\left( \omega \right)\frac{{V\left( \omega \right)}}{{1 + i\frac{1}{{2\pi }}\sigma \left( \omega \right)}}, \\ {{C}_{p}} = \frac{\omega }{K},\,\,\,\,\sigma = 2\pi \frac{{{{K}_{{{\text{**}}}}}}}{K}, \\ \end{gathered} $

где ${{C}_{p}}$ – фазовая скорость звука, $\sigma $ – декремент затухания на длине волны.

Для чистого газа ${{C}_{p}}\left( \omega \right) = {{C}_{1}},$ $V\left( \omega \right) \equiv 1,$ $\sigma \left( \omega \right) \equiv 0,$ тогда $Z\left( \omega \right) = \rho _{{10}}^{ \circ }{{C}_{1}}.$

ГРАНИЧНЫЕ УСЛОВИЯ

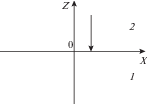
Пусть на границу раздела $z = 0$ двух многофракционных газовзвесей падает акустическая волна под прямым углом (рис. 1). Индекс $f$ относится к падающей волне, t – к прошедшей волне, r – к отраженной волне, 1 – к среде, из которой падает волна, 2 – к среде, в которую проходит волна.

Рис. 1.

Падение акустической волны на границу раздела двух сред.

Давление и скорость имеют вид

– в падающей волне

$\begin{gathered} {{p}_{f}}\left( {t,z} \right) = {{A}_{2}}\exp \left[ {i\left( { - {{K}_{{ * 2}}}z - \omega t} \right)} \right], \\ {{\text{v}}_{f}}\left( {t,z} \right) = - \frac{{{{K}_{{ * 2}}}}}{{\omega {{\rho }_{{20}}}{{V}_{2}}\left( \omega \right)}}{{p}_{f}}\left( {t,z} \right); \\ \end{gathered} $

– в отраженной волне

$\begin{gathered} {{p}_{r}}\left( {t,z} \right) = {{B}_{2}}\exp \left[ {i\left( {{{K}_{{ * 2}}}z - \omega t} \right)} \right], \\ {{\text{v}}_{r}}\left( {t,z} \right) = \frac{{{{K}_{{ * 2}}}}}{{\omega {{\rho }_{{20}}}{{V}_{2}}\left( \omega \right)}}{{p}_{r}}\left( {t,z} \right); \\ \end{gathered} $

– в прошедшей волне

$\begin{gathered} {{p}_{t}}\left( {t,z} \right) = {{A}_{1}}\exp \left[ {i\left( { - {{K}_{{ * 1}}}z - \omega t} \right)} \right], \\ {{\text{v}}_{t}}\left( {t,z} \right) = - \frac{{{{K}_{{ * 1}}}}}{{\omega {{\rho }_{{10}}}{{V}_{1}}\left( \omega \right)}}{{p}_{t}}\left( {t,z} \right). \\ \end{gathered} $

На границе раздела давление и нормальная составляющая скорости непрерывны [20]:

(2)

$\left\{ \begin{gathered} {{p}_{f}}\left( {t,0} \right) + {{p}_{r}}\left( {t,0} \right) = {{p}_{t}}\left( {t,0} \right), \hfill \\ {{\text{v}}_{f}}\left( {t,0} \right) + {{\text{v}}_{r}}\left( {t,0} \right) = {{\text{v}}_{t}}\left( {t,0} \right). \hfill \\ \end{gathered} \right.$

Далее граничные условия (2) переписываются в эквивалентной форме [21]

$\left\{ \begin{gathered} {{p}_{f}}\left( {t,0} \right) + {{p}_{r}}\left( {t,0} \right) = {{p}_{t}}\left( {t,0} \right), \hfill \\ {{{\tilde {Z}}}_{2}}\left( {t,0} \right) = {{Z}_{1}}, \hfill \\ \end{gathered} \right.$

где ${{\tilde {Z}}_{2}}\left( {t,z} \right) = - \frac{{{{p}_{f}}\left( {t,0} \right) + {{p}_{r}}\left( {t,0} \right)}}{{{{\text{v}}_{f}}\left( {t,0} \right) + {{\text{v}}_{r}}\left( {t,0} \right)}}$ – импеданс суммарного звукового поля в верхней полуплоскости. Второе условие означает непрерывность импеданса на границе раздела. Откуда получаем выражения для коэффициента отражения и коэффициента преломления

(3)

$R = \frac{{{{Z}_{1}} - {{Z}_{2}}}}{{{{Z}_{1}} + {{Z}_{2}}}},\,\,\,\,W = \frac{{2{{Z}_{1}}}}{{{{Z}_{1}} + {{Z}_{2}}}}.$

Поскольку $Z{}_{1}$ и ${{Z}_{2}}$ являются комплексными величинами, зависящими от $\omega ,$ то и коэффициенты отражения $(R)$ и преломления $(W)$ – комплексные величины, зависящие от $\omega .$

При ${{Z}_{1}} = {{Z}_{2}}$ коэффициент отражения $R = 0,$ а коэффициент преломления $W = 1,$ т.е. происходит полное прохождение акустической волны через границу сред. Условие ${{Z}_{1}} = {{Z}_{2}}$ означает, что

${{\rho }_{{10}}}{{C}_{{p1}}}\left( \omega \right)\frac{{{{V}_{1}}\left( \omega \right)}}{{1 + i\frac{1}{{2\pi }}{{\sigma }_{1}}\left( \omega \right)}} = {{\rho }_{{20}}}{{C}_{{p2}}}\left( \omega \right)\frac{{{{V}_{2}}\left( \omega \right)}}{{1 + i\frac{1}{{2\pi }}{{\sigma }_{2}}\left( \omega \right)}}.$

При $\omega \to 0$

$R = \frac{{{{\rho }_{{10}}}{{C}_{{e1}}} - {{\rho }_{{20}}}{{C}_{{e2}}}}}{{{{\rho }_{{10}}}{{C}_{{e1}}} + {{\rho }_{{20}}}{{C}_{{e2}}}}},\,\,\,\,W = \frac{{2{{\rho }_{{10}}}{{C}_{{e1}}}}}{{{{\rho }_{{10}}}{{C}_{{e1}}} + {{\rho }_{{20}}}{{C}_{{e2}}}}},$

где ${{C}_{{ei}}}$ $\left( {i = 1,{\text{ }}2} \right)$ – равновесная скорость звука, вычисляемая по формулам [10]

$\begin{gathered} {{C}_{{ei}}} = {{C}_{i}}{{\left( {\frac{{{{\gamma }_{{ei}}}}}{{{{M}_{i}}{{\gamma }_{i}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{M}_{i}} = 1 + \sum\limits_{j \in \overline {s1,s{{N}_{i}}} } {{{m}_{{ij}}}} , \\ {{\gamma }_{{ei}}} = \frac{{1 - \sum\limits_{j \in \overline {s1,s{{N}_{i}}} } {{{{\bar {c}}}_{{ij}}}{{m}_{{ij}}}} }}{{\frac{1}{{{{\gamma }_{i}}}} - \sum\limits_{j \in \overline {s1,s{{N}_{i}}} } {{{{\bar {c}}}_{{ij}}}{{m}_{{ij}}}} }},\,\,\,\,{{{\bar {с }}}_{{ij}}} = \frac{{{{c}_{{ij}}}}}{{{{c}_{{pi}}}}},\,\,\,\,\left( {i = 1,2} \right). \\ \end{gathered} $

При $\omega \to \infty $

$R = \frac{{{{\rho }_{{10}}}{{C}_{1}} - {{\rho }_{{20}}}{{C}_{2}}}}{{{{\rho }_{{10}}}{{C}_{1}} + {{\rho }_{{20}}}{{C}_{2}}}},\,\,\,\,W = \frac{{2{{\rho }_{{10}}}{{C}_{1}}}}{{{{\rho }_{{10}}}{{C}_{1}} + {{\rho }_{{20}}}{{C}_{2}}}}.$

где ${{C}_{i}}$ $\left( {i = 1,{\text{ }}2} \right)$ – скорость звука в чистом газе.

РЕЗУЛЬТАТЫ

В качестве примера рассмотрены особенности отражения и преломления акустических волн, падающих под прямым углом на границу раздела между следующими средами:

1) воздухом и двухфракционной смесью воздуха с частицами пороха и бериллия;

2) монодисперсной смесью воздуха с частицами пороха и двухфракционной смесью воздуха с частицами пороха и бериллия;

3) гелием и двухфракционной смесью воздуха с частицами пороха и бериллия;

4) монодисперсной смесью гелия с частицами пороха и двухфракционной смесью воздуха с частицами пороха и бериллия;

5) двухфракционной смесью гелия с частицами пороха и бериллия и двухфракционной смесью воздуха с частицами пороха и бериллия.

На рис. 2–6 построены зависимости модулей и аргументов коэффициентов отражения и преломления от безразмерной частоты $\omega {{\tau }_{{\text{v}s1}}}$ (кривые 1 – m = 0.3, 2 – 0.4, 3 – 0.5). Расчеты выполнены с помощью формул (3) при следующих теплофизических параметрах: для воздуха – $\rho _{{10}}^{ \circ } = 1.19$ кг/м³, ${{С }_{1}} = 343$ м/с, ${{c}_{{p1}}} = 1007$ м²/с² К, ${{\lambda }_{1}} = 0.0258$ кг м/с³ К, ${{\mu }_{1}} = 1.81 \times {{10}^{{ - 5}}}$ кг/м с, ${{\gamma }_{1}} = 1.4;$ для гелия – $\rho _{{10}}^{ \circ } = 0.164$ кг/м³, ${{С }_{1}} = 1005$ м/с, ${{c}_{{p1}}} = 5190$ м²/с² К, ${{\lambda }_{1}} = 0.149$ кг м/с³ К, ${{\mu }_{1}} = 1.94 \times {{10}^{{ - 5}}}$ кг/м с, ${{\gamma }_{1}} = 1.67;$ для частиц пороха – ${{r}_{{s1}}} = {{10}^{{ - 4}}}$ м, ${{\rho }_{{s1}}} = 1780$ кг/м³, ${{c}_{{s1}}} = 1460$ м²/с² К, ${{\lambda }_{{s1}}}$ = = 0.75 кг м/с³ К; частиц бериллия – ${{r}_{{s2}}} = {{10}^{{ - 5}}}$ м, ${{\rho }_{{s2}}} = 1840$ кг/м³, ${{c}_{{s2}}} = 1884$ м²/с² К, ${{\lambda }_{{s2}}}$ = = 201 кг м/с³ К; массовые содержания частиц пороха и бериллия в двухфракционной газовзвеси равны между собой.

Рис. 2.

Зависимости модулей и аргументов коэффициента отражения $\left( {\left| R \right|,\;{{\varphi }_{R}}} \right)$ и коэффициента преломления $\left( {\left| W \right|,\;{{\varphi }_{W}}} \right)$ от безразмерной частоты $\omega {{\tau }_{{\text{v}s1}}}$ при падении акустической волны под прямым углом со стороны воздуха на границу двухфракционной смеси воздуха с частицами пороха и бериллия при разном массовом содержании частиц.

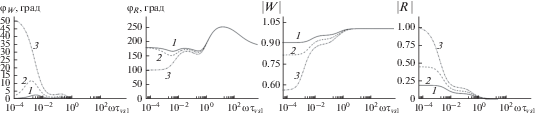
Рис. 3.

Зависимости модулей и аргументов коэффициента отражения $\left( {\left| R \right|,\;{{\varphi }_{R}}} \right)$ и коэффициента преломления $\left( {\left| W \right|,\;{{\varphi }_{W}}} \right)$ от безразмерной частоты $\omega {{\tau }_{{\text{v}s1}}}$ при падении акустической волны под прямым углом со стороны монодисперсной смеси воздуха с частицами пороха на границу двухфракционной смеси воздуха с частицами пороха и бериллия при разном массовом содержании частиц.

Рис. 4.

Зависимости модулей и аргументов коэффициента отражения $\left( {\left| R \right|,\;{{\varphi }_{R}}} \right)$ и коэффициента преломления $\left( {\left| W \right|,\;{{\varphi }_{W}}} \right)$ от безразмерной частоты $\omega {{\tau }_{{\text{v}s1}}}$ при падении акустической волны под прямым углом со стороны гелия на границу двухфракционной смеси воздуха с частицами пороха и бериллия при разном массовом содержании частиц.

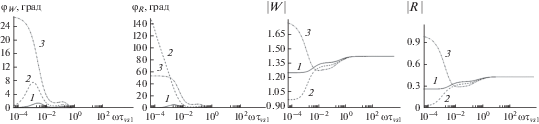
Рис. 5.

Зависимости модулей и аргументов коэффициента отражения $\left( {\left| R \right|,\;{{\varphi }_{R}}} \right)$ и коэффициента преломления $\left( {\left| W \right|,\;{{\varphi }_{W}}} \right)$ от безразмерной частоты $\omega {{\tau }_{{\text{v}s1}}}$ при падении акустической волны под прямым углом со стороны монодисперсной смеси гелия с частицами пороха на границу двухфракционной смеси воздуха с частицами пороха и бериллия при разном массовом содержании частиц.

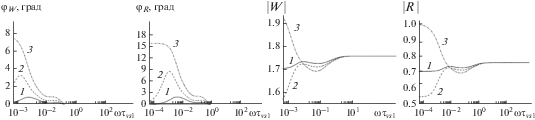
Рис. 6.

Зависимости модулей и аргументов коэффициента отражения $\left( {\left| R \right|,\;{{\varphi }_{R}}} \right)$ и коэффициента преломления $\left( {\left| W \right|,\;{{\varphi }_{W}}} \right)$ от безразмерной частоты $\omega {{\tau }_{{\text{v}s1}}}$ при падении акустической волны под прямым углом со стороны двухфракционной смеси гелия с частицами пороха и бериллия на границу двухфракционной смеси воздуха с частицами пороха и бериллия при разном массовом содержании частиц.

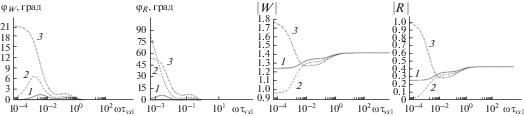
Из рис. 2, 3 видно, что коэффициенты отражения и преломления монотонно зависят от массового содержания. При стремлении $\omega \to \infty $ коэффициент отражения $R \approx 0,$ а коэффициент прохождения $W \approx 1,$ т.е. акустическая волна проходит практически полностью через границу раздела. Это происходит потому, что при $\omega \to \infty $ скорость звука в монодисперсной газовзвеси и многофракционной газовзвеси стремится к скорости звука в чистом газе (для рассмотренного примера – в воздухе).

Из рис. 4–6 видно, что коэффициенты отражения и преломления немонотонно зависят от массового содержания. При $\omega \to \infty $ коэффициент отражения $R \ne 0,$ а коэффициент прохождения $W \ne 1,$ т.е. существует отражение акустической волны от границы раздела двух сред.

ЗАКЛЮЧЕНИЕ

В работе изучены особенности отражения и преломления акустической волны, проходящей через границу двух многофракционных газовзвесей под прямым углом. Построены зависимости модулей коэффициентов отражения и преломления от безразмерной частоты при разных массовых содержаниях включений.

Установлена монотонная зависимость коэффициентов отражения и преломления от массового содержания частиц при падении акустической волны под прямым углом на границу раздела чистого газа и многофракционной газовзвеси, на границу раздела монодисперсной смеси газа с твердыми частицами и многофракционной газовзвеси при условии, что несущие среды – один и тот же газ.

Если же несущими средами являются газы с разными теплофизическими свойствами, то коэффициенты отражения и преломления немонотонно зависят от массового содержания частиц при падении акустической волны под прямым углом на границу раздела чистого газа и многофракционной газовзвеси, на границу раздела монодисперсной смеси газа с твердыми частицами и многофракционной газовзвеси, а также на границу раздела двух многофракционных газовзвесей.

Работа выполнена при финансовом содействии Российского научного фонда (проект № 15-11-10 016).

Список литературы

Нигматуллин Р.И. Основы механики гетерогенных сред. М.: Наука, 1978. 336 с.
Temkin S. Suspension Acoustics: An Introduction to the Physics of Suspension. Cambridge: Univ. Press, 2005. 398 p.
Губайдуллин Д.А. Динамика двухфазных парогазокапельных сред. Казань: Изд-во Казан. матем. об-ва, 1998. 153 с.
Нигматуллин Р.И., Ивандаев А.И., Губайдуллин Д.А. Эффект немонотонной зависимости диссипации звука от концентрации капель в акустике газовзвесей // ДАН. 1991. Т. 316. № 3. С. 601.
Губайдуллин Д.А., Ивандаев А.И. Влияние фазовых превращений на распространение звука в туманах. Сопоставление теории с экспериментом // ПМТФ. 1990. № 6. С. 27.
Губайдуллин Д.А., Ивандаев А.И. Распространение акустических возмущений в полидисперсных туманах // ТВТ. 1992. Т. 30. № 5. С. 935.
Гумеров Н.А. Длинные волны конечной амплитуды в полидисперсных газовзвесях // ПМТФ. 1990. № 4. С. 157.
Губайдуллин Д.А., Никифоров А.А., Уткина Е.А. Акустические волны в двухфракционных смесях газа с паром, каплями и твердыми частицами разных материалов и размеров при наличии фазовых превращений // Изв. РАН. МЖГ. 2011. № 1. С. 95.
Губайдуллин Д.А., Никифоров А.А., Уткина Е.А. Влияние фазовых превращений на распространение акустических волн в двухфракционных смесях газа с паром, каплями и твердыми частицами разных материалов и размеров // ТВТ. 2011. Т. 49. № 6. С. 942.
Губайдуллин Д.А., Терегулова Е.А., Губайдуллина Д.Д. Распространение акустических волн в многофракционных газовзвесях // ТВТ. 2015. Т. 53. № 5. С. 942.
Cole J.E., Dobbins R.A. Measurements of Attenuation and Dispersion of Sound by a Warm Air Fog // J. Atmospheric Sci. 1971. V. 28. № 2. P. 202.
Davidson G.A. Sound Propagation in Fogs // J. Atmospheric Sci. 1975. V. 32. № 11. P. 2201.
Вараксин А.Ю. Гидрогазодинамика и теплофизика двухфазных потоков: проблемы и достижения // ТВТ. 2013. Т. 51. № 3. С. 421.
Вараксин А.Ю. Кластеризация частиц в турбулентных и вихревых двухфазных потоках // ТВТ. 2014. Т. 52. № 5. С. 777.
Вараксин А.Ю. Влияние частиц на турбулентность несущего потока газа // ТВТ. 2015. Т. 53. № 3. С. 441.
Ishii R., Matsuhisa H. Steady Reflection, Absorption and Transmission of Small Disturbances by as Creen of Dusty Gas // J. Fluid Mech. 1983. V. 130. P. 259.
Шагапов В.Ш., Сарапулова В.В. Особенности преломления звука в атмосфере при тумане // Изв. РАН. Физика атмосферы и океана. 2014. Т. 50. № 6. С. 683.
Шагапов В.Ш., Сарапулова В.В. Особенности отражения и преломления акустических волн на границе раздела между газом и дисперсной системой // ПМТФ. 2015. Т. 56. № 5. С. 119.
Губайдуллин Д.А., Федоров Ю.В. Особенности отражения акустических волн от границы или слоя двухфазной среды // Акуст. журн. 2018. Т. 64. № 2. С. 162.
Ландау Л.Д. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1986. 736 с.
Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1973. 343 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал