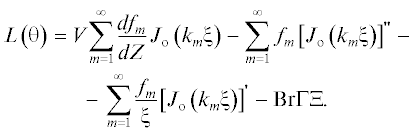Теплофизика высоких температур, 2019, T. 57, № 3, стр. 446-452

ВВЕДЕНИЕ

Даже в классическом варианте течения вязкой жидкости решение задачи Гретца–Нуссельта связано со значительными техническими трудностями. Обусловлено это тем, что решение соответствующей задачи Штурма–Лиувилля не выражается через элементарные функции. Между тем все большую актуальность приобретает эта задача применительно к теплообмену при течении неньютоновских жидкостей.

Из работ, посвященных течению бингамовской жидкости, можно отметить следующие. В [1] рассмотрен случай температурной стабилизации с постоянным тепловым потоком на стенке. Задача течения и теплообмена во входной области круглой трубы для жидкости Бингама решена численно в [2]. Предполагался ламинарный поток и постоянные свойства текучей среды. В [3] численно исследованы эффекты влияния реологических свойств степенной и пластической жидкости Бингама на характеристики потока и теплопередачу при ламинарной вынужденной конвекции через некруглые каналы. Рассмотрены два различных температурных граничных условия (постоянная температура стенки и постоянный тепловой поток на стенке).

В [4, 5] рассмотрен установившийся теплоперенос при сдвиговом течении Куэтта в плоском канале конечной длины. Задача решалась с учетом диссипации механической энергии при симметричных граничных условиях третьего рода на стенках канала.

Наиболее подробный анализ подходов различных авторов представлен в [6]. Основное внимание уделяется течению и теплообмену степенной жидкости и вязкопластической жидкости Бингама. Решение задачи получено в виде ряда. Задача Штурма–Лиувилля (поиск собственных функций и собственных чисел задачи) решалась численно.

Целью настоящей работы является получение приближенного решения задачи Гретца–Нуссельта с учетом диссипативного тепловыделения с указанием погрешности при вычислениях, получение расчетных формул для температуры и числа Нуссельта как для произвольного сечения канала, так и для участка термической стабилизации.

ПОСТАНОВКА ЗАДАЧИ

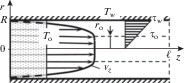
Схема течения и теплообмена представлена на рис. 1. Течение совершается вдоль оси z, в канале радиусом R, на участке длиной $\ell .$ Начальная температура жидкости (на входе) однородна по сечению Т₀. Реологические и теплофизические свойства жидкости постоянны. Температура стенок канала постоянна Т_w, причем выполняется соотношение Т_w ≠ Т₀. Для стенок канала используется граничное условие первого рода. Задача осесимметричная.

Поскольку справедливо соотношение ${{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{r}^{2}}}}} \right. \kern-0em} {\partial {{r}^{2}}}} \gg $ $ \gg {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}}}}} \right. \kern-0em} {\partial {{z}^{2}}}}$ (R $ \ll $ $\ell $), продольной теплопроводностью жидкости можно пренебречь, учитывается только теплопроводность в поперечном направлении. Задача стационарная.

Используются следующие безразмерные переменные и параметры:

Здесь T = T(z, r) – температура жидкости; a = = λ/ρC, λ, ρ, C – коэффициент температуропроводности, коэффициент теплопроводности, плотность и теплоемкость жидкости; ${{\text{v}}_{z}}$(r) – профиль осевой скорости (зависит от выбранной реологической модели течения); τ – касательное напряжение; γ = d${{\text{v}}_{z}}$/dr – скорость сдвига; ${{\text{v}}_{c}}$ – средняя скорость жидкости; V – безразмерная осевая скорость; Br – число Бринкмана; τ_w – касательное напряжение на стенке; γ_w – скорость сдвига у стенки; r_o – радиус пластического ядра; ${{\text{v}}_{{\text{o}}}}$ – скорость движения ядра; μ – пластическая вязкость; τ_о – предел текучести; θ – безразмерная температура; θ_m – среднеобъемная безразмерная температура; ξ – безразмерный радиус; ζ – безразмерный радиус пластического ядра. Безразмерная продольная координата Z может быть представлена в виде Z = z/(RPe), Pe = ${{\text{v}}_{c}}$R/a – число Пекле.

Температурное поле в жидкости описывается уравнением Фурье–Кирхгофа и краевыми условиями

Последнее слагаемое справа характеризует тепловыделение в потоке за счет внутреннего трения.

Линейное неоднородное уравнение относится к параболическому типу. Решение соответствующей задачи Штурма–Лиувилля при произвольном профиле осевой скорости не выражается через элементарные функции. Для получения приближенного решения использован метод Канторовича (метод приведения к обыкновенным дифференциальным уравнениям) [7]. Метод Канторовича обеспечивает среднеинтегральное приближение собственных функций задачи координатными функциями.

РЕШЕНИЕ ЗАДАЧИ

Поиск решения задачи (2) осуществляется в виде произведения двух функций

где J₀(k_sξ) – функция Бесселя нулевого порядка. Здесь k₁, k₂, k₃, … – положительные корни функции J_o(k_s). Координатные функции удовлетворяют граничным условиям и обладают свойством ортогональности в интервале ξ [0,1] с весом ξ.

Пусть выполняется условие ортогональности невязки уравнения Фурье–Кирхгофа (2) к каждой координатной функции на интервале от 0 до 1:

Невязка уравнения (2) имеет вид

После интегрирования по ξ, принимая во внимание взаимную ортогональность функций J₀(k_sξ) на интервале интегрирования (ненулевыми являются только диагональные элементы матрицы, у которых m = s), получаем систему уравнений для функций f_s(Z)

где ${{A}_{{1s}}} = \int_0^1 {V(\xi )J_{{\text{o}}}^{2}\left( {{{k}_{s}}\xi } \right)\xi d\xi } ,$ ${{A}_{{3s}}} = \int_0^1 {\Gamma \left( \xi \right)\Xi (\xi )} $× × ${{J}_{{\text{o}}}}\left( {{{k}_{s}}\xi } \right)\xi d\xi ,$ ${{A}_{{2s}}} = - \int\limits_0^1 {\left\{ {{{{\left[ {{{J}_{{\text{o}}}}\left( {{{k}_{s}}\xi } \right)} \right]}}^{{''}}} + \frac{1}{\xi }{{{\left[ {{{J}_{{\text{o}}}}\left( {{{k}_{s}}\xi } \right)} \right]}}^{'}}} \right\}} \,\,\,\,\,\, \times $

$ \times \,\,{{J}_{{\text{o}}}}\left( {{{k}_{s}}\xi } \right)\xi d\xi .$

Постоянные A_1s и A_3s определяются параметрами течения, в частности, используемой реологической моделью. Интеграл A_2s имеет аналитическое представление A_2s = 0.5[k_sJ₁(k_s)]².

Решение уравнения (4) имеет вид

Постоянную интегрирования С_s находим из граничного условия (Z = 0, θ = 1)

После умножения обеих частей этого равенства на координатную функцию и интегрирования с учетом взаимной ортогональности координатных функций получается

Таким образом, выражение для температуры (3) имеет вид

Следует отметить, что полученное решение (5) может использоваться как для анализа течения вязких жидкостей с любым реологическим уравнением состояния, так и для вязкопластических жидкостей Бингама, Гершеля–Балкли и др. Для последних эпюра осевой скорости складывается из зоны ядра и зоны вязкого течения (рис. 1).

Среднеобъемная температура жидкости в произвольном поперечном сечении определяется интегралом

Локальный коэффициент теплоотдачи α характеризует распределение теплового потока по длине канала. Он определяется из условия неразрывности теплового потока у стенки

где $\Delta T$ – локальный температурный напор

Рассматривается случай охлаждения жидкости (T_o > T_w, Br > 0). При отсутствии источников тепловыделения (Br = 0) результаты могут быть распространены на случай нагрева жидкости (T_o < T_w). Вариант T_o < T_w, Br ≠ 0 требует отдельного рассмотрения, поскольку в этом случае уравнение конвективного теплообмена Ньютона малопригодно для описания процесса. Это обусловлено наличием в знаменателе числа Нуссельта разности температур (8), которая в сечении инверсии направления теплового потока обращается в нуль (имеется в виду точка пересечения кривой среднеобъемной температуры с изотермой, отвечающей температуре стенки). Соответственно, число Нуссельта в указанном сечении претерпевает разрыв второго рода.

При переходе к безразмерным переменным (1) выражение (6) принимает вид

Учитывалось соотношение $2\int_0^1 {V\xi d\xi } = 1.$

Из совместного рассмотрения выражений (7), (8) для локального числа Нуссельта можем записать

где Nu = αR/λ – локальное число Нуссельта, ${{\theta }_{m}} = 2\int_0^1 {V\theta \xi d\xi } $ – безразмерная среднеобъемная температура.

В развернутой форме с учетом выражения (5) можем записать

Течение вязкопластической жидкости Бингама (τ = τ_о + μγ) достаточно подробно изучено и представлено в литературе. Основные закономерности течения в круглой трубе описываются следующими формулами: профилем скорости ${{\text{v}}_{z}}$ в зоне вязкого течения (r_o < r < R), скоростью пластического ядра ${{\text{v}}_{{\text{o}}}}$ (0 < r < r_o), расходом Q и средней скоростью ${{\text{v}}_{c}}{\text{:}}$

С учетом обозначений (1) получается следующее выражение для безразмерной скорости:

На рис. 2 представлены результаты анализа формулы (11). Пунктирными линиями показаны границы пластического ядра.

Распределение касательного напряжения по радиусу линейное (τ = τ_wξ), поэтому для всего сечения можем записать

С учетом выражений (11), (12) диссипативный множитель в уравнении энергии (2) имеет вид

Найдем коэффициенты A_1s и A_3s. Для коэффициента A_1s с учетом (11) можно записать

Аналогично, с учетом (13) для коэффициента A_3s имеем один интеграл, отвечающий зоне вязкого течения, в которой именно и сосредоточено тепловыделение за счет вязкого трения

Таким образом, температурное поле в жидкости описывается выражениями (5), (14), (15).

Согласно выражению (10), локальное число Нуссельта рассчитывается по формуле

Число Нуссельта зависит от продольной координаты и двух параметров: Nu(Z, Br, ζ).

ЧИСЛЕННЫЙ АНАЛИЗ РЕШЕНИЯ

При вычислении по формулам (5), (10) учитывались первые 50 членов рядов Фурье–Бесселя, что обеспечивало достаточную точность при малых Z. Корни уравнения ${{J}_{{\text{o}}}}\left( {{{k}_{s}}} \right) = 0$ взяты из справочника [8]: k₁ = 2.40482, k₂ = 5.520078, … k₅₀ = = 156.295.

На рис. 3а представлены распределения температур по длине зоны течения при отсутствии источников тепловыделения (Br = 0). Начальный всплеск объясняется проблемой сходимости ряда Фурье–Бесселя при малых значениях Z. Зависимости носят экспоненциальный характер. Теплообмен практически заканчивается при Z = 1. Видно, что быстрее происходит охлаждение жидкости, имеющей большое сечение пластического ядра (линия 1). Линия 3 отвечает жидкости, по свойствам близкой к вязким жидкостям (профиль скорости близок к параболическому). Видно, что такая жидкость охлаждается с наименьшей скоростью. Случай среднего размера ядра (2) занимает промежуточное положение.

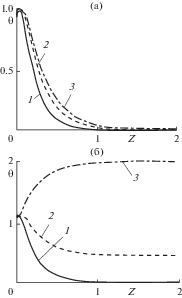
На рис. 3б представлена подобная зависимость, но при наличии тепловых источников (Br = 30). Видно, что характер зависимостей существенно меняется. В случае малого размера пластического ядра (линия 3) температура стабилизации превышает начальное значение. Зависимость носит асимптотический характер, и на расстоянии порядка Z = 1 наступает стабилизация температуры. В случае большого сечения пластического ядра (линия 1) диссипативный эффект повышения температуры проявляется незначительно. Это обусловлено существенным кондуктивным оттоком тепла к стенке и низким термическим сопротивлением тонкого слоя жидкости в зоне вязкого течения. Случай среднего размера ядра (линия 2) занимает промежуточное положение между указанными предельными случаями. При дальнейшем увеличении числа Бринкмана линии 2 и 3 смещаются вверх, температура жидкости повышается, превосходя начальную. Из сопоставления рис. 3а и 3б следует, что при наличии внутренних источников тепла появляется вторая (“верхняя” или “диссипативная”) асимптота в распределении температуры по длине канала.

На рис. 4а представлено распределение локального числа Нуссельта по длине трубы в условиях отсутствия объемных источников тепловыделения (Br = 0). График построен в двойных логарифмических координатах. Зависимости носят асимптотический характер, величина стабилизированного значения Нуссельта зависит от размера ядра. Термическая стабилизация наступает после Z = 1. Следует отметить, что линия 3 отвечает жидкости, по свойствам близкой к чисто вязкой жидкости. Она показывает наименьшее значение числа Нуссельта на участке стабилизации. На начальном участке канала (Z < 0.1) линии почти сливаются, следовательно, пластические свойства жидкости мало влияют на число Нуссельта, а сама зависимость в области Z < 0.03 описывается функцией Nu = 0.631Z ^–0.5. С уменьшением количества членов рядов (10) до s = 7 показатель степени снижается до –0.294.

На рис. 4б представлено распределение локального числа Нуссельта по длине зоны течения при интенсивности тепловыделений (Br = 30). Иллюстрируется влияние относительного размера пластического ядра. Характер влияния достаточно сложный. При сравнительно малых размерах ядра (линия 3) зависимость носит монотонный характер с горизонтальной асимптотой. Однако с увеличением размера ядра появляется локальный минимум в области значений Z от 0.1 до 1, далее значение числа Нуссельта возрастает и выходит на горизонтальную асимптоту. Причем при большом размере ядра (линия 1) стабилизация наступает в области Z > 4. При этом асимптотическое значение числа Нуссельта составляет Nu(Z = 10) = 96.363. В области малых протяженностей канала вязкая диссипация и размер ядра мало влияют на зависимость Nu(Z), которая описывается степенной функцией. Подобный расчет выполнен для малых интенсивностей тепловыделения (Br = 0.001). Обнаружилось запаздывание перехода Nu на диссипативную асимптоту: стабилизация наступала при Z > 5. Следовательно, для протяженных каналов при расчете теплообмена следует учитывать эффект саморазогрева, даже если расчетное значение числа Бринкмана незначительное.

В ньютоновском случае ζ = 0, Br = 0 расчетное асимптотическое значение числа Нуссельта при $Z \to \infty $ Nu_∞ = 2.09. Согласно [9], локальное число Нуссельта, приведенное к актуальному масштабу линейного размера R, составляло 2.18. Расхождение – 4.12%. Независимо от Br > 0 имеет место предельное соотношение Nu_∞ = 4.722. По данным [9], если использовать в качестве характерного размера радиус, Nu_∞ = 4.8. Расхождение – 1.6%. Следовательно, математическая модель теплообмена жидкости Бингама удовлетворительно согласуется с известными литературными данными. Приближенное решение задачи может использоваться для инженерного анализа и расчета теплообмена.

СТАБИЛИЗАЦИЯ ТЕПЛООБМЕНА НА БОЛЬШОМ УДАЛЕНИИ ОТ ВХОДА

На большом удалении от входа температурное поле стабилизируется $Z \to \infty ,$ ${{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial Z \to 0}}} \right. \kern-0em} {\partial Z \to 0}}.$ При этом температурное поле в жидкости описывается краевой задачей (2) без конвективного слагаемого в уравнении энергии

Интегрированием получим решение для зоны вязкого течения ζ < ξ < 1. Первое интегрирование

Учитывая, что на границе ядра производная от температуры равна нулю, можно записать

Разделив переменные и проинтегрировав в пределах от ξ до 1, получим

Температура на границе ядра

Непосредственно в ядре (0 < ξ < ζ) диссипативное тепловыделение отсутствует и краевая задача формулируется следующим образом:

В результате интегрирования, с учетом условия ограниченности функции на оси получим θ_∞ = θ_∞f = const. Кроме того, учитывая условие неразрывности теплового потока на границе ядра, имеем условие для обеих эпюр dθ_∞/dξ = = dθ_∞f/dξ = 0. Таким образом, поперечное распределение температуры на большом удалении от начала трубы описывается формулой

В случае ньютоновской жидкости (ζ = 0) для профиля температуры на бесконечности получаем известное выражение θ_∞ = Br(1 – ξ⁴)/16.

Согласно (17), температура пропорциональна числу Бринкмана. На рис. 5 показана зависимость температуры ядра от его относительного размера, вычисленная с помощью нижней формулы в (17). График построен в полулогарифмических координатах. Видно, что с увеличением размера ядра безразмерная температура саморазогрева уменьшается. Это обусловлено снижением термического сопротивления слоя жидкости в зоне вязкого течения.

Используя формулу (9) найдем число Нуссельта на большом удалении от входа. Согласно (17), для градиента температуры на стенке имеем

Для определения среднеобъемной температуры используем формулу, предусматривающую интегрирование в пределах ядра и зоны вязкого течения:

С учетом выражения для скорости (11) и температуры (17) можно записать

Таким образом, расчетное выражение для числа Нуссельта на бесконечном удалении от сечения входа имеет вид

Согласно полученному выражению, ${\text{N}}{{{\text{u}}}_{\infty }}$ не зависит от Br и полностью определяется ζ. Результаты численного анализа выражения (18) представлены на рис. 5 в полулогарифмических координатах (линия 1). Зависимость имеет две асимптоты: горизонтальную $\zeta \to 0,$ Nu_∞ = 4.8 и вертикальную $\zeta \to 1,$ ${\text{N}}{{{\text{u}}}_{\infty }} \to \infty .$ Первая отвечает течению число вязкой жидкости и соответствует известному значению [9]. Следовательно, в момент “трогания” (когда τ_w незначительно превышает τ_о) число Нуссельта равно бесконечности. Линия 2 отвечает приближенному решению (10), вычисленному для сечения Z = 10. Видно, что отклонение приближенного решения от точного появляется при ζ > 0.95. Следовательно, приближенное решение приводит к ошибке при относительно больших размерах пластического ядра. График на рис. 5 поясняет асимптотическое поведение числа Нуссельта, представленное на рис. 4.

ЗАКЛЮЧЕНИЕ

Получено приближенное решение задачи Гретца–Нуссельта для жидкости Бингама с учетом объемных источников тепла. Точность решения зависит от сходимости ряда Фурье–Бесселя и возрастает с увеличением числа членов. Полученные расчетные зависимости (5), (10) могут использоваться для исследования теплообмена других аномально вязких и вязкопластических неньютоновских жидкостей.

Предложено новое понятие “диссипативная асимптота числа Нуссельта”. Для протяженных каналов при расчете теплообмена следует учитывать эффект саморазогрева, даже если расчетное значение числа Бринкмана незначительное.

В области тепловой стабилизации температура пропорциональна числу Бринкмана, а число Нуссельта определяется относительным размером пластического ядра.