Теплофизика высоких температур, 2019, T. 57, № 3, стр. 437-445

ВВЕДЕНИЕ

Существует множество природных и технических процессов, для описания которых применяются модели парокапельных сред. На основе таких моделей решаются задачи метеорологии и климатологии, разрабатываются способы очистки промышленных выбросов, описывается городской микроклимат. В качестве рабочих сред парокапельные системы представлены в теплоэнергетике, аэрокосмической технике, двигателестроении. Описание гидро- и термодинамики таких сред требует применения моделей, учитывающих ряд взаимовлияющих физических процессов. В данной работе приводится модель и численный метод для описания динамики полидисперсных парокапельных систем со скоростным и температурным скольжением фаз, с учетом дробления, коагуляции, испарения капель и конденсации пара. В качестве примера выполнен расчет одного из режимов течения парокапельной смеси в коаксиальном канале разрабатываемого тепловоспринимающего элемента нагревателя-регазификатора сжиженного природного газа [1].

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ПОЛИДИСПЕРСНОЙ ПАРОКАПЕЛЬНОЙ СМЕСИ

Динамика полидисперсной парокапельной смеси описывается системами уравнений движения несущей среды и дисперсной фазы [2, 3], известными экспериментально-теоретическими моделями дробления и испарения капель различных фракций со скоростной неравновесностью относительно несущей среды [3–5], лагранжевой моделью Смолуховского [6], описывающей коагуляцию при парных столкновениях частиц, и равновесной моделью фазовых переходов в системе пар–мелкодисперсная фракция [5]. Основной шаг вычислительного алгоритма на каждом временнóм слое состоит в решении системы уравнений движения несущей среды и систем уравнений движения фракций дисперсной фазы в эйлеровой постановке [7]. На этом этапе находятся промежуточные значения плотности, скорости, температуры и давления несущей среды, скоростей и средних плотностей фракций дисперсной фазы. Затем анализируются условия возникновения фазовых переходов в системе пар–равновесная мелкодисперсная фракция и, если система находится в неравновесном состоянии, рассчитывается изменение массы, температуры фаз и давления смеси при переходе ее к термодинамически равновесному состоянию [5]. Следующий шаг состоит в анализе возможности реализации механизма дробления капель фракций со скоростной неравновесностью относительно несущей среды. Фиксируется момент времени, когда для данной фракции капель оказывается превышенным критическое число Вебера, и по истечении времени индукции рассчитывается уменьшение массы капель дробящихся фракций. На этом этапе считается, что капли-“осколки” пополняют равновесную мелкодисперсную фракцию. Если число Вебера для капли со скоростной неравновесностью относительно несущей среды меньше критического значения, а температура капли достигает температуры насыщения для давления в потоке, то реализуется механизм испарения капли, рассчитывается уменьшение ее массы и радиуса, корректируется изменение средней плотности и объемного содержания фракции, а также увеличение плотности пара. Если одновременно выполняются условия для дробления капли и ее испарения, то вначале капля дробится, а осколки от дробления пополняют равновесную фракцию. Ее испарение будет осуществлено на следующем временнóм шаге после анализа условий испарения–конденсации. Следующий шаг состоит в коррекции параметров системы за счет механизма коагуляции капель фракций с относительным скоростным скольжением [6, 7]. В ансамбле фракций в каждом узле дискретной сетки определяются фракции, для которых число Вебера меньше критического. Для этих фракций по модели Смолуховского рассчитывается увеличение массы капель-акцепторов, изменение их импульса и температуры, а также уменьшение концентрации капель-доноров. На основе новых значений массы капель, их радиусов и концентраций находятся новые значения объемного содержания и средней плотности всех капельных фракций. Таким образом, получаем параметры несущей и дисперсной фазы на текущем временнóм слое, после чего переходим к решению уравнений движения несущей среды и дисперсной фазы на следующем шаге по времени.

УРАВНЕНИЯ ДВИЖЕНИЯ НЕСУЩЕЙ СРЕДЫ И ДИСПЕРСНОЙ ФАЗЫ

Для описания движения полидисперсной смеси применяется система уравнений многоскоростной и многотемпературной газовзвеси, включающей в себя n фракций. В цилиндрической системе координат при осесимметричном течении системы уравнений для несущей среды и для дисперсной фазы имеют вид [3, 7]

Здесь ρ, Т, u, $\text{v},$ w, е, λ, μ, d_i, σ – плотность, температура, составляющие скорости по трем направлениям, удельная полная энергия, коэффициенты теплопроводности и вязкости несущей фазы, диаметр капли i-й фракции и коэффициент поверхностного натяжения жидкости. Величины с индексом i относятся к i-й фракции дисперсной фазы. Объемное содержание дисперсной фазы определяется суммированием объемных содержаний фракций: $\alpha = \sum\nolimits_{i{\text{ = 1,}}n} {{{\alpha }_{i}}} .$ Коэффициент аэродинамического сопротивления С_d рассчитывается с учетом поправки на сжимаемость среды ψ(М_i0) [3]. Система уравнений движения несущей среды содержит уравнение для азимутальной составляющей импульса, записанное в предположении об азимутальной симметрии потока при его вращении и без учета составляющих вязкого трения [8]. Составляющие сил аэродинамического сопротивления F_xi, F_yi, F_zi и тепловой поток Q_i на границе частица–газ определяются законом межфазного трения с учетом изменения формы капли в зависимости от чисел Вебера We_i и Лапласа Lp_i и законом теплообмена [3, 4]. Здесь I = = ρRT/(γ – 1) − внутренняя энергия газа; R, γ – газовая постоянная и постоянная адиабаты несущей среды. Температура несущей среды T = (γ − 1) × × (e/ρ − 0.5(u²+ ${{\text{v}}^{2}}$))/R. В уравнение сохранения полной энергии для несущей фазы входит тепловой поток, возникающий вследствие теплообмена между газом и частицами i-й фракции: Q_i = = 6α_iNu_iλ(T – T_i)/(2r_i)² , где Nu_i = 2r_iα^T/λ − число Нуссельта, r_i – радиус частиц i-й фракции. Число Нуссельта определяется при помощи известного приближения [4], использующего относительные числа Маха М_i0, Рейнольдса Re_i0 и Прандтля Pr.

Дисперсная фаза состоит из ряда фракций, каждая из которых образована частицами определенного размера. Динамика каждой фракции описывается уравнением сохранения средней плотности фракции, уравнениями сохранения компонент импульса и уравнением сохранения тепловой энергии [3, 7]:

Здесь α_i, ρ_i, e_i, Т_i , С_pi, ρ_i0 – объемное содержание, средняя плотность, тепловая энергия, температура, теплоемкость и плотность вещества i-й дисперсной фракции. Тепловая энергия i-й фракции определяется как e_i = ρ_iC_piT_i. Система уравнений движения каждой дисперсной фракции содержит уравнение для азимутальной составляющей импульса, записанное в предположении об азимутальной симметрии потока при его вращении [8].

РАВНОВЕСНАЯ МОДЕЛЬ ИСПАРЕНИЯ И КОНДЕНСАЦИИ КАПЕЛЬ МЕЛКОЙ ФРАКЦИИ

Парокапельная смесь, наряду с каплями сравнительно крупных фракций, содержит мелкую фракцию, температурным и скоростным скольжением которой относительно несущей среды можно пренебречь и считать, что испарение таких капель, или конденсация пара в случае отклонения температуры и давления от кривой фазового равновесия, описывается равновесной моделью фазовых переходов [5]. Испаряется при этом такая масса мелкодисперсной капельной фракции, или конденсируется такая масса пара, которая обеспечивает возвращение параметров несущей среды – давления и температуры на кривую фазового равновесия. Если масса мелкой капельной фракции недостаточна для того, чтобы система перешла в равновесное состояние, то мелкая фракция испаряется полностью, а затем начинается испарение капель крупных фракций – этот процесс продолжается до достижения равновесного давления и температуры, или до испарения всей жидкой фазы. При этом учитывается уменьшение температуры пара вследствие поглощения скрытой теплоты парообразования. Массовое содержание самой мелкой фракции может увеличиваться как вследствие дробления в потоке капель более крупных фракций, так и вследствие конденсации пара; уменьшение массового содержания мелких капель может происходить вследствие испарения и в результате коагуляции с более крупными каплями.

Давление пара определяется с учетом объемного содержания капель:

где ρ, R, Т – плотность, газовая постоянная и температура пара; ρ_l – суммарная средняя плотность капель по всем фракциям. Здесь учитывается, что часть объема ${{{{\rho }_{l}}} \mathord{\left/ {\vphantom {{{{\rho }_{l}}} {\rho _{l}^{0}}}} \right. \kern-0em} {\rho _{l}^{0}}}$ в смеси занимают капли ($\rho _{l}^{0}$ – истинная плотность жидкости в каплях).

В соответствие с моделью равновесных фазовых переходов конденсация пара происходит при увеличении парциального давления пара свыше давления насыщения ${{p}_{S}}(T).$ Капли испаряются при уменьшении парциального давления пара ниже ${{p}_{S}}(T)$. Схема равновесного фазового перехода приведена, например, в [5]. В результате конвективного и диффузионного переноса вещества, импульса и энергии изменяется парциальное давление пара р. При p(T) > p_s(T) избыточная масса пара $\delta {{m}_{\text{v}}}$ конденсируется, возрастает температура смеси от Т до Т ', а давление пара р(Т ') возвращается на кривую насыщения. Температура возрастает на δT ' = T  ' – T за счет выделения энергии при конденсации δQ = L$\delta {{m}_{\text{v}}},$ где L – скрытая теплота фазового перехода. Температура $T'$ определяется решением уравнения p(T ') = p_s(T  ').

Масса cконденсировавшегося в единице объема пара вычисляется из условия теплового баланса $\delta {{m}_{\text{v}}}$ = (ρ'С_pT  ' – ρС_pT)/L , где ρ, T, ρ', T  ' – плотность и температура пара до и после конденсации. Если p(T) < p_s(T) и в смеси содержится мелкодисперсная фракция, то испарение происходит по той же схеме, но с учетом того, что температура смеси и средняя плотность мелкодисперсной фракции снижаются.

Рассмотрим условие перехода подсистемы пар–мелкодисперсная капельная фракция в равновесное состояние. Для этого выразим текущее давление пара р через температуру и плотность нового равновесного состояния T  ' и приравняем его давлению насыщенного пара при температуре T ': ${{p}_{s}}(T{\kern 1pt} {\text{'}}) = {{\rho {\text{'}}RT{\kern 1pt} {\text{'}}} \mathord{\left/ {\vphantom {{\rho {\text{'}}RT{\kern 1pt} {\text{'}}} {(1 - {{\rho _{l}^{'}} \mathord{\left/ {\vphantom {{\rho _{l}^{'}} {\rho _{l}^{0}}}} \right. \kern-0em} {\rho _{l}^{0}}})}}} \right. \kern-0em} {(1 - {{\rho _{l}^{'}} \mathord{\left/ {\vphantom {{\rho _{l}^{'}} {\rho _{l}^{0}}}} \right. \kern-0em} {\rho _{l}^{0}}})}}.$

В это уравнение входят новые значения парциальных плотностей пара и капель ρ', $\rho _{l}^{'}.$ После фазового перехода ρ' = ρ – ρС_p(T ' – T)/L, $\rho _{l}^{'}$ = ρ_l + + ρС_p(T ' – T)/L, тогда как ρ, ρ_l, T соответствуют плотности пара, средней плотности капель и температуре смеси до наступления фазового перехода. Получаем уравнение для нового значения температуры пара после перехода системы в равновесное состояние

где для давления насыщенного пара метана применяется известная аппроксимация

Уравнение (1) с учетом (2) решается итерационным методом относительно нового значения температуры Т '. Итерационная процедура позволяет найти Т ' и в том случае, когда масса пара или масса мелких капель недостаточны для перехода системы в равновесие при конденсации или испарении. По Т ' определяются новые значения плотности пара ρ' = ρ – ρС_p(T ' – T)/L и средней плотности мелкодисперсной фракции $\rho _{l}^{'}$ = ρ_l + + ρС_p(T ' – T)/L. А по ним находится новое значение давления смеси.

МОДЕЛЬ ДРОБЛЕНИЯ КАПЕЛЬ

Если число Вебера ${\text{We}} = 2{{r}_{i}}{{\rho }_{{\text{ж }}}}{{{{{\left| {V - {{V}_{i}}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {V - {{V}_{i}}} \right|}}^{2}}} \sigma }} \right. \kern-0em} \sigma }$ для капли i-фракции больше критического, то ее движение сопровождается газодинамическим дроблением, приводящим к уменьшению массы таких частиц. В качестве механизма разрушения капли может быть выбран тарельчатый тип дробления, связанный со срывом пограничного слоя [2–4] и реализующийся при We_кр ≤ We < 1.7 × 10⁴/Lp^0.5. При этом диаметр отрывающихся частиц $d = 2.4\frac{{{{d}_{i}}}}{{\sqrt {{\text{R}}{{{\text{e}}}_{{i{\text{0}}}}}} }}{{\left( {\frac{{{{\mu }_{{\text{ж }}}}}}{\mu }} \right)}^{{0.5}}}{{\left( {\frac{\rho }{{{{\rho }_{{\text{ж }}}}}}} \right)}^{{0.25}}},$ где d_i – диаметр капель i-й фракции; μ_ж, μ, ρ_ж, ρ – коэффициенты динамической вязкости и плотность жидкости и пара [4]. Для описания процесса потери каплей массы при газодинамическом дроблении применимо полуэмпирическое уравнение [4]

Здесь m₁ – масса отрывающейся при дроблении капли, m_i – масса дробящейся капли i-й фракции, t – интервал времени с момента достижения критического значения числа Вебера для капли i-й фракции, t_i – время от начала деформации капли до начала ее дробления [4]:

Для решения обыкновенного дифференциального уравнения (3) применим метод рядов. Представим приближенно решение (3) рядом Тейлора, ограничившись членами до второго порядка:

Масса капли в текущий момент времени t известна. На следующем временнóм шаге она определяется рядом Тейлора (4). По массе дробящейся капли i-й фракции на новом временнóм шаге рассчитываются ее новый радиус и объем. Известное значение концентрации капель i-й фракции позволяет найти объемное содержание и новое значение средней плотности i-й фракции. Полагая, что отрывающиеся при дроблении капли-“осколки” переходят в самую мелкую фракцию смеси, находим увеличение средней плотности и концентрации капель этой фракции.

МОДЕЛЬ ПРОГРЕВА И ИСПАРЕНИЯ КАПЕЛЬ КРУПНЫХ ФРАКЦИЙ

Если для капли i-й фракции число Вебера превышает критическое значение, а ее температура достигла температуры насыщения, то на первом этапе процессом испарения с поверхности крупных капель пренебрегаем, так как унос массы неравновесной с несущей средой по скорости капли за счет дробления происходит более интенсивно [4], чем за счет испарения. Если же число Вебера меньше критического, а температура капли повысилась до температуры насыщения при текущем давлении, то требуется учесть уменьшение средней плотности дисперсной фазы за счет испарения крупных капель. Испарению капли предшествует ее нагрев до температуры насыщения, после чего начинается испарение с ее поверхности. Прогрев капли происходит за счет конвективного теплообмена в движущейся несущей среде. Коэффициент поверхностного теплообмена на поверхности капли α_p выражается через число Нуссельта, диаметр капли d и коэффициент теплопроводности несущей среды λ_г как α_p = Nuλ_г/d. Для определения числа Нуссельта используется известная из литературы [2–4] зависимость

Здесь М_отн = u_отн/с – относительное число Маха, где с – скорость звука, u_отн = |U – U_i| – скорость i-й фракции относительно несущей среды; Re = = ρ|U|d/µ – число Рейнольдса; Pr = µC_pг/λ_г – число Прандтля; µ, C_pг– динамическая вязкость и удельная изобарная теплоемкость несущей среды. В процессе нагрева до температуры насыщения k_исп = 1, после достижения каплей этой температуры k_исп = 0.6. С учетом температурной однородности температура движущейся в потоке капли описывается дифференциальным уравнением [4]

Для решения этого уравнения применим схему Эйлера:

Считаем, что до достижения каплей температуры насыщения испарением с ее поверхности можно пренебречь [4]. С момента времени достижения этой температуры при текущем давлении начинается интенсивное испарение с поверхности. Процесс испарения описывается уравнением

где L(T_p) – теплота парообразования жидкости при температуре Т_р, Т_s(p) – температура насыщения при давлении р, m – масса капли i-й фракции. Решение уравнения, описывающего изменение массы капли, будем искать по схеме Эйлера

При известной концентрации капель находим новое значение средней плотности и объемное содержание фракции, а также новое значение плотности пара.

МОДЕЛЬ КОАГУЛЯЦИИ КАПЕЛЬ

Если число Вебера для капли i-й фракции меньше критического значения (We_кр ≈ 10), то при столкновениях ее с частицами менее крупных фракций происходит их коагуляция, вследствие чего изменяются масса, концентрация, импульс и температура частицы i-й фракции. Этот процесс описывается лагранжевой моделью Смолуховского для коагуляции частиц при парных соударениях [6].

Масса m_i частицы i-й фракции (i = 2, …, n) возрастает за счет поглощения частиц j-х фракций меньшего размера с массой m_j ( j = 1, 2, …, i – 1):

где – константа коагуляции, d_i – диаметр частиц i-й фракции, d_j < d_i. Новое значение массы частиц i-й фракции в текущем узле конечно-разностной сетки позволяет определить новое значение радиуса частицы r_i. Уменьшение концентрации частиц j-х фракций вследствие поглощения их более крупными i-ми (i = j + 1, j + 2,…, n) описывается уравнением

Новое значение объемного содержания i-й фракции, изменившегося вследствие коагуляции, определяется как α_i = (4/3)π$r_{i}^{3}$n_i. Концентрация n_i рассчитывается через среднюю плотность и радиус i-й фракции на каждом шаге вычислений. Слияние мелких капель с более крупными приводит к изменению их скорости: ${{\partial {{w}_{i}}} \mathord{\left/ {\vphantom {{\partial {{w}_{i}}} {\partial t}}} \right. \kern-0em} {\partial t}} = \frac{1}{{{{m}_{i}}}}\sum\nolimits_{j = 1}^{i - 1} {{{k}_{{ij}}}\left( {{{w}_{j}} - {{w}_{i}}} \right){{m}_{j}}{{n}_{j}}} .$ Температура частицы i-й фракции после коагуляции с более мелкими находилась из соотношения T = = $\frac{1}{{Cm}}\left( {\sum\nolimits_{j = 1}^{i - 1} {{{k}_{{ij}}}{{n}_{j}}{{C}_{j}}} {{m}_{j}}{{T}_{j}} + {{C}_{i}}{{m}_{i}}{{T}_{i}}} \right),$ где T, C, m – температура, удельная массовая теплоемкость и масса частицы i-й фракции после коагуляции; T_i, C_i, m_i – те же параметры до коагуляции. Связанные с коагуляцией изменения скорости и температуры дисперсной фазы учитывались на каждом временнóм шаге основного алгоритма.

Далее переходим на следующий временнóй шаг и выполняем вычисления эйлерова этапа решения уравнений движения несущей среды и дисперсной фазы парокапельной смеси.

Система уравнений движения двухфазной полидисперсной парокапельной смеси записывалась в обобщенных криволинейных координатах [7, 9, 10] и решалась явным методом Мак-Кормака второго порядка с расщеплением пространственного оператора по направлениям и со схемой нелинейной коррекции [7, 9]. Для термодинамических характеристик жидкого метана и его пара были использованы известные из литературы аппроксимации [11]. Работоспособность модели определялась решением задач для отдельных механизмов (дробления и испарения капель, для равновесной модели фазовых переходов, для коагуляции полидисперсной смеси) и сопоставлением полученных результатов с известными из литературы, а также с решениями, полученными аналитически.

ОБЪЕКТ МОДЕЛИРОВАНИЯ И ПОСТАНОВКА ЗАДАЧИ

В качестве примера рассмотрим течение парокапельной смеси в тепловоспринимающем элементе трубного подогревателя-регазификатора сжиженного природного газа. Устройство выполнено в виде трубы Фильда, представляющей собой систему из двух концентрических труб, по которым движется парожидкостная смесь (рис. 1). Внешняя труба нагревается в огневой зоне. Поток сжиженного природного газа течет по внутренней трубе, на выходе из нее разворачивается и движется в противоположном направлении в зазоре между внутренней и внешней трубами, где происходит нагрев и испарение жидкости. Процесс установления стационарного режима и формирование фронта испарения в межтрубном зазоре зависит от расхода жидкости и внешнего теплового потока. Изменение расхода нарушает установившийся режим в тепловоспринимающем элементе и вызывает новый процесс установления термо- и гидродинамических параметров, сопровождающийся возникновением кризисных явлений при кипении жидкости на границе со стенкой и генерацией нестационарных колебаний.

Конструктивное исполнение нагревателя-регазификатора сжиженного природного газа, содержащего горелочное устройство, кожухотрубный теплообменник и тепловоспринимающие элементы (рис. 1), приведено в [1].

Для устранения длительных переходных процессов и кризисов кипения при смене расхода требуется модификация устройства, состоящая в том, что на входе во внутреннюю трубу жидкость диспергируется и далее движется в виде парокапельной смеси. При выходе из внутренней трубы поток разворачивается и движется в канале между коаксиально расположенными трубами, внешняя из которых нагрета. В этом случае происходит испарение диспергированной жидкости, что может позволить избежать нестационарных процессов, вызванных кризисом кипения жидкого метана на стенке внешней трубы. Для увеличения времени пребывания смеси в нагретой зоне и для транспортировки капель к нагретой стенке служит закрутка потока при его движении в межтрубном зазоре.

В процессе движения в зависимости от режима течения и интенсивности нагрева могут происходить процессы коагуляции, дробления, испарения капель и конденсации пара, влияющие на структуру и расход потока. Для выбора конструктивных параметров тепловоспринимающего элемента и режимов его работы – дисперсности на входе, перепада давления на входе-выходе, величины внешнего теплового потока – требуется моделирование процессов, сопровождающих течение парокапельной смеси.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

На рис. 2а показана геометрия расчетной области, построенная с учетом осевой симметрии канала, длина которого L = 1 м, радиусы внутренней и наружной труб R_вн = 0.05 м, R_н = 0.1 м. Парокапельная смесь втекает во внутреннюю трубу при х = 0 (область I на рис. 2а). Поток разворачивается в области II, протекает через внешний концентрический канал III и вытекает через сечение х = 0. Дисперсная фаза включает в себя пять капельных фракций. Радиус капель равновесной фракции составляет 1 мкм. Неравновесные по скорости с несущей средой фракции образованы каплями с начальными радиусами 10, 20, 50, 100 мкм. Начальные объемные содержания фракций одинаковы и составляют α_i = 0.0001 при плотности жидкого метана ρ_жидк = 416 кг/м³. Начальные температура и плотность пара Т₀ = 107 К, ρ₀ = 1.29 кг/м³. Начальная температура равновесной (R₀ = 1 мкм) фракции совпадает с начальной температурой пара и равна температуре насыщения для начального давления смеси р₀ = 71 499 Па.

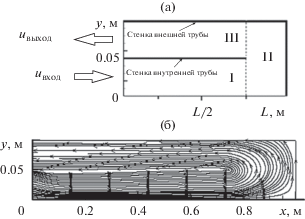
Температура капель крупных фракций составляет Т_i = 100 K. Оценка для скорости звука в несущей среде с = (γRT)^1/2 = 268 м/с, где γ = 1.3 – постоянная адиабаты, R = 518 Дж/(кг К) – газовая постоянная метана. Расчеты проводились на равномерной в осевом и радиальном направлении блочно-структурированной конечно-разностной сетке, включающей в себя три подобласти I−III и содержащей 200 × 100 узлов (рис. 2а). Граничные условия на линиях стыковки блоков задавались с учетом направления течения. Блоки I–III включают в себя узлы: I – 1 ≤ j ≤ 3nj/4, 1 ≤ k ≤ nk/2; II – 3nj/4 ≤ j ≤ nj, 1 ≤ k ≤ nk; III – 1 ≤ j ≤ 3nj/4, nk/2 ≤ k ≤ nk, где nj, nk – число узлов в осевом и радиальном направлении.

На входе в подобласть I при х = 0 задавались однородное граничное условие Неймана для давления и составляющие скорости несущей среды: u(t, x = 0) = 0.1M, $\text{v}$(t, x = 0) = 0. На выходе из области III (рис. 2а) при х = 0 задавалось давление несущей среды, а для остальных газодинамических функций ставилось однородное граничное условие Неймана. Для азимутальной составляющей скорости на оси симметрии при у = 0 и на боковых стенках (области I, III) принимались однородные граничные условия первого рода. Закрутка потока моделировалась заданием азимутальной составляющей скорости вблизи боковой границы области III при у = R_н − δ: w(x, R_н − δ) = ω(R_н − δ), где ω = −6πu(x, R_н − δ).

В начальный момент времени в области I задаются составляющие скорости потока. В приведенных ниже расчетах u(t = 0) = 0.1 M, v(t = 0) = 0, где М = |V|/c − число Маха. В областях II, III начальные скорости парокапельной смеси нулевые. На твердых стенках канала для скорости задается граничное условие прилипания, а для давления, плотности, температуры и энергии пара ставятся однородные граничные условия Неймана.

На рис. 2б показано поле скоростей пара, а на рис. 3 приведены пространственные распределения давления, плотности и температуры пара, сформировавшиеся в расчетной области к моменту времени t = 0.012 c. Параметры течения на входе в область I (при х = 0): р_вх = 110 кПа, ρ_вх = = 1.75 кг/м³, Т_вх = 112 К. В выходном сечении области III (при х = 0) р_вых= 71.5 кПа, ρ_вых = 1.29 кг/м³, Т_вых = 107 К.

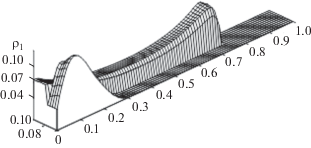
Движение парокапельной смеси сопровождается изменением ее дисперсности. На рис. 4 приводится зависимость параметров фракций смеси от времени в точке (х = 0.25 м, у = 0.075 м), принадлежащей области III. В начальный момент времени капли всех фракций неподвижны. Движение пара приводит к дроблению самой крупной фракции, радиус капель которой снижается от 100 до 93 мкм (рис. 4а). В результате ее средняя плотность уменьшается от 0.0416 до 0.033 кг/м³. “Осколки” от дробления переходят в самую мелкую равновесную фракцию, в результате чего ее средняя плотность возрастает с 0.0416 кг/м до 0.054 кг/м³ (рис. 4б). Расчеты показывают, что в поле течения существуют две зоны конденсации пара: на входе в область I вследствие влияния граничного условия и в области III (рис. 2а), где возникают условия для конденсации пара и роста средней плотности равновесной фракции (рис. 5). В результате в области III вследствие коагуляции наблюдается рост капель и средних плотностей всех крупных фракций (рис. 4а, 4б). Основным донором является равновесная мелкодисперсная фракция (R₀ = 1 мкм). Рост капель различных фракций происходит в потоке до тех пор, пока для них не будет достигнуто критическое значение числа Вебера (рис. 4а, 4в). При достижении числом Вебера критического значения (рис. 4в) коагуляция и рост капель сменяются их дроблением и уменьшением радиуса (рис. 4а). Можно отметить, что процесс коагуляции и последующего дробления капель с начальными радиусами 100, 50, 20 и 10 мкм в присутствии равновесной фракции с радиусом 1 мкм, играющей при коагуляции роль донора, приводит к тому, что к моменту времени t ≈ 0.045 c полидисперсная система крупных капель превращается в монодисперсную с радиусом капель R ≈ 45 мкм. К этому моменту времени процесс коагуляции для капель с начальным радиусом 10 мкм в системе R₀ = 1–10 мкм) сменяется дроблением. После образования монодисперсной системы процесс дробления протекает с меньшей скоростью (рис. 4а). К моменту времени t ≈ 0.075 c в системе присутствует две дисперсные капельные фракции: равновесная с радиусом капель R ≈ 1 мкм и фракция капель с радиусом R ≈ 32 мкм. Процесс сближения радиусов капель крупных фракций сопровождается установлением в системе двухскоростного режима: движение происходит со скоростью равновесной фракции и несущей среды и со скоростью монодисперсной крупной фракции с радиусом R ≈ 32 мкм (рис. 4г).

ЗАКЛЮЧЕНИЕ

Моделирование гидро- и термодинамики полидисперсной парокапельной смеси в коаксиальном цилиндрическом канале, учитывающее процессы испарения, коагуляции, дробления капель и конденсации пара, позволило сделать ряд выводов для рассмотренного режима течения:

− если в выходной части устройства (область III) температура пара ниже температуры насыщения для давления потока, то конденсация пара приводит к повышению концентрации и средней плотности мелкодисперсной фракции, являющейся донором в процессе коагуляции для всех остальных капельных фракций;

− большая концентрация фракции-донора, образовавшаяся при конденсации пара, приводит к интенсивной коагуляции и быстрому росту капель и средних плотностей всех неравновесных по скорости фракций;

− вследствие дальнейшего роста капель различных фракций в потоке возникают режимы течения с достижением и превышением критического числа Вебера, когда коагуляция капель сменяется дроблением;

− в результате конкурентного воздействия механизмов коагуляции и дробления в окрестности критического числа Вебера в потоке может произойти изменение структуры системы с переходом от полидисперсной многоскоростной смеси к двухскоростной с двумя преобладающими размерами капель.

Исследование выполнено при поддержке РФФИ и правительства Республики Татарстан (проект № 18-48-160017) и по госзаданию Минобрнауки России вузам (проект № 9.5542.2017/6.7).