Теплофизика высоких температур, 2019, T. 57, № 4, стр. 588-608

СОДЕРЖАНИЕ

Введение.

1. Основные характеристики процесса столкновений.

1.1. Частота и ядро столкновений.

1.2. Время и длина свободного пробега между столкновениями.

1.3. Столкновительное число Стокса.

2. Два подхода в теории столкновений частиц.

2.1. Цилиндрическая формулировка.

2.2. Сферическая формулировка.

2.3. Частные случаи.

3. Столкновения монодисперсных частиц в турбулентном потоке.

3.1. Частота столкновений монодисперсных частиц в изотропной турбулентности.

3.2. Частота столкновений частиц при совместном действии турбулентности и градиента осредненной скорости.

4. Столкновения бидисперсных частиц в однородном турбулентном потоке.

4.1. Частота столкновений бидисперсных частиц в изотропной турбулентности.

4.2. Частота столкновений частиц при совместном действии турбулентности и силы тяжести.

5. Развитые подходы для расчета процесса столкновения.

5.1. Методы определения места столкновения частиц (капель).

5.2. Методы определения характеристик частиц после столкновения.

5.3. Методы определения характеристик капель после столкновения.

6. Влияние столкновений на характеристики двухфазного потока.

6.1. Влияние столкновений на характеристики двухфазных турбулентных струйных течений.

6.2. Влияние столкновений на характеристики двухфазных турбулентных течений в каналах.

Заключение.

Список литературы.

ВВЕДЕНИЕ

Потоки сплошной среды, несущие дисперсную примесь в виде твердых частиц или жидких капель, имеют место в целом ряде природных явлений [1–8]: дожди, грады, воздушные и водяные смерчи, песчаные бури, извержения вулканов, лесные пожары и многие другие. Примерами технических устройств, в которых используются двухфазные течения, являются [9–14]: устройства термоподготовки угля в схемах энерготехнологического использования топлива, камеры сгорания тепловых двигателей, тракты твердотопливных реактивных двигателей, теплообменники с двухфазными рабочими телами, устройства песко- и дробеструйной обработки различных поверхностей, пневмотранспортеры сыпучих материалов, пылеуловители различных типов и т.п.

Турбулентные двухфазные течения – крайне сложный предмет для изучения. Добавление в поток дисперсной примеси в виде твердых частиц сильно осложняет картину течения. Во-первых, это связано с большим разнообразием свойств вводимых частиц (прежде всего, инерционности и концентрации), которые приводят к реализации многочисленных режимов (классов) течения газовзвеси [15, 16]. Во-вторых, теория однофазных турбулентных потоков далека от своего завершения.

Исследования турбулентных двухфазных течений имеют своей целью решение двух основных классов задач – изучение поведения взвешенных в потоке дисперсных частиц (капель) и их обратного влияния на характеристики несущего их течения. В двухфазных потоках могут иметь место различные столкновительные процессы [17]: столкновения частиц между собой (частица – частица); столкновения частиц с телом, обтекаемым двухфазным течением (частица – тело); столкновения частиц со стенками, ограничивающими двухфазный поток (частица – стенка). Все указанные столкновительные процессы могут оказывать определяющее влияние на формирование статистических характеристик движения частиц (капель), а следовательно, оказывать влияние на характеристики несущего их потока газа. Поэтому установление роли контактных взаимодействий в контексте решения двух основных задач изучения двухфазных потоков представляется чрезвычайно актуальным, а исследования турбулентных двухфазных течений приобретают исключительную сложность.

В настоящем обзоре описаны и проанализированы результаты расчетно-теоретических и экспериментальных работ, посвященных нахождению характеристик процесса столкновений частиц (капель) в турбулентных потоках, а также его влияния на параметры течения несущей газовой фазы.

1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПРОЦЕССА СТОЛКНОВЕНИЙ

1.1. Частота и ядро столкновений

Частота столкновений рассматриваемой частицы со всеми другими частицами ${{f}_{c}}$ при большом количестве частиц в двухфазной системе пропорциональна числовой концентрации (среднему числу частиц в единице объема) N

где $\beta $ – ядро столкновений. Данное название эта величина получила, поскольку присутствует в качестве подынтегральной функции (ядра) в уравнении для изменения (эволюции) размера частиц вследствие коагуляции.

Число столкновений частиц, принадлежащих к разным сортам, в единице объема в единицу времени определяется следующим соотношением:

где ${{f}_{{c12}}}{\kern 1pt} ,$ ${{f}_{{c21}}}$ – частоты столкновений соответственно частицы сорта 1 с частицами сорта 2 и частицы сорта 2 с частицами сорта 1; ${{N}_{1}},$ ${{N}_{2}}$ – средние числовые концентрации частиц сортов 1 и 2 соответственно.

1.2. Время и длина свободного пробега между столкновениями

Важной характеристикой движения частиц является среднее время между соударениями ${{\tau }_{c}},$ определяемое как

Времена между соударениями частиц, принадлежащих к разным сортам, имеют вид

где ${{\tau }_{{c12}}},$ ${{\tau }_{{c21}}}$ – времена между последовательными столкновениями соответственно частицы сорта 1 с частицами сорта 2 и частицы сорта 2 с частицами сорта 1.

Одним из ключевых понятий молекулярной физики является понятие средней длины свободного пробега молекулы, т.е. среднего расстояния, которое пролетает молекула от одного столкновения до следующего. По аналогии с этим понятием в теории двухфазных потоков широко используется термин длина “свободного пробега” частиц. Если известно значение средней скорости частиц, то легко определить средние длины свободного пробега частиц сортов 1 и 2 между последовательными столкновениями как

1.3. Столкновительное число Стокса

Процесс релаксации скоростей сталкивающихся частиц (капель) может быть охарактеризован столкновительным числом Стокса [17–19]

где ${{\tau }_{p}}$ – время динамической релаксации частиц, ${{\tau }_{c}}$ – характерное время между последовательными соударениями. Время динамической релаксации является комплексной характеристикой инерционности дисперсной фазы и представляется как где $C = \left\{ \begin{gathered} 1 + {{\operatorname{Re} _{p}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} \mathord{\left/ {\vphantom {{\operatorname{Re} _{p}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} 6}} \right. \kern-0em} 6}\,\,{\text{п р и }}\,\,{{\operatorname{Re} }_{p}} \leqslant {{10}^{3}}, \hfill \\ 0.11{{{{{\operatorname{Re} }}_{p}}} \mathord{\left/ {\vphantom {{{{{\operatorname{Re} }}_{p}}} 6}} \right. \kern-0em} 6}\,\,{\text{п р и }}\,\,{{\operatorname{Re} }_{p}} > {{10}^{3}}. \hfill \\ \end{gathered} \right.$

Здесь ${{\rho }_{p}}$ – плотность материала частицы, ${{d}_{p}}$ – ее диаметр, $\mu $ – динамическая вязкость несущего газа. В (9) ${{\tau }_{{p0}}}$ характеризует время динамической релаксации стоксовой частицы (капли) (${{\operatorname{Re} }_{p}} < 1$). Отметим, что инерционность стоксовой частицы зависит и от характеристик среды, в которой она движется. Выражение для ${{\tau }_{{p0}}}$ включает в себя коэффициент динамической вязкости среды. Поправочная функция $C$ учитывает влияние сил инерции на время релаксации нестоксовой частицы (капли). Таким образом, в случае движения нестоксовой частицы ее инерционность зависит также и от такого безразмерного комплекса, как число Рейнольдса частицы (капли), вычисляемое по относительной скорости между фазами и диаметру дисперсной примеси, т.е. ${{\operatorname{Re} }_{p}} = \left| {\mathbf{W}} \right|{{{{d}_{p}}} \mathord{\left/ {\vphantom {{{{d}_{p}}} \nu }} \right. \kern-0em} \nu } = \left| {{\mathbf{U}} - {\mathbf{V}}} \right|{{{{d}_{p}}} \mathord{\left/ {\vphantom {{{{d}_{p}}} \nu }} \right. \kern-0em} \nu }.$

Столкновительное число Стокса определяет степень влияния соударений на движение дисперсной фазы [17–19]. Если время динамической релаксации дисперсных включений малó по сравнению со временем между последовательными столкновениями (Stk_c → 0), то частицы (капли) быстро восстанавливают свою первоначальную скорость. В этом случае соударения практически не оказывают влияния на динамику дисперсной фазы. В другом предельном случае время между столкновениями намного меньше времени динамической релаксации частиц (капель) (Stk_c → ∞) и движение дисперсной фазы в значительной степени определяется процессами межчастичных (межкапельных) столкновений.

2. ДВА ПОДХОДА В ТЕОРИИ СТОЛКНОВЕНИЙ ЧАСТИЦ

Целью теоретического анализа процесса соударений частиц является нахождение ядра их столкновений. Данная характеристика напрямую связана с частотой соударений дисперсной фазы двухфазного потока – одной из ключевых характеристик межчастичных столкновений (см. 1.1).

В этом разделе рассмотрены два возможных подхода (формулировки) к определению ядра столкновений частиц.

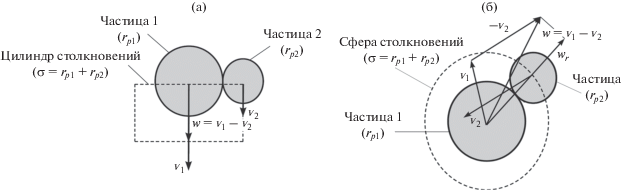
2.1. Цилиндрическая формулировка

Рассмотрим столкновения частиц сортов 1 и 2 с радиусами ${{r}_{{p1}}}$ и ${{r}_{{p2}}}.$ Согласно данному подходу вводится понятие о “цилиндре столкновений”. Центр рассматриваемой частицы радиусом ${{r}_{{p1}}}$ находится на оси цилиндра с радиусом, равным сумме радиусов соударяющихся частиц, т.е. $\sigma = {{r}_{{p1}}} + {{r}_{{p2}}}.$ В момент столкновения центр частицы сорта 2 находится на поверхности “цилиндра столкновений” (рис. 1а).

В рамках цилиндрической формулировки ядро столкновений $\beta $ связывается с полной относительной скоростью двух частиц ${\text{|}}{\mathbf{\bar {w}}}{\text{|}}$ и радиусом столкновений $\sigma $, равным для одинаковых частиц их диаметру ${{d}_{p}},$ следующим образом:

Из (10) видно, что ядро столкновений равно объему цилиндра с площадью поперечного сечения $\pi {\kern 1pt} {{\sigma }^{2}}$ и высотой, численно равной средней относительной скорости частиц различных сортов $\left| {{\mathbf{\bar {w}}}{\kern 1pt} } \right|.$

Отметим, что целый ряд развитых аналитических моделей столкновений частиц (например, [20–23]) основан на широко распространенной в статистической механике цилиндрической формулировке задачи.

2.2. Сферическая формулировка

Аналогично тому, как делалось выше, рассмотрим столкновения частиц сортов 1 и 2 с радиусами ${{r}_{{p1}}}$ и ${{r}_{{p2}}}.$ Согласно рассматриваемому подходу вводится понятие о “сфере столкновений”. Центр данной сферы находится в центре рассматриваемой частицы радиусом ${{r}_{{p1}}},$ а радиус сферы равен сумме радиусов соударяющихся частиц: $\sigma = {{r}_{{p1}}} + {{r}_{{p2}}}.$ В момент столкновения центр частицы сорта 2 находится на поверхности “сферы столкновений” (рис. 1б).

В рамках сферической формулировки задачи ядро столкновений $\beta $ выражается через осредненную радиальную компоненту относительной скорости $\left| {{{{\bar {w}}}_{r}}} \right|$ и радиус столкновений σ, равный для одинаковых частиц их диаметру ${{d}_{p}},$ при помощи соотношения

где w_r = wr – радиальная компонента относительной скорости между частицами; ${\mathbf{w}} = {{{\mathbf{v}}}_{1}} - {{{\mathbf{v}}}_{2}}$ – относительная скорость частиц; ${{{\mathbf{v}}}_{1}}$ и ${{{\mathbf{v}}}_{2}}$ – скорости частиц сортов 1 и 2; ${\mathbf{r}}$ – единичный вектор, направленный по линии удара от центра первой частицы к центру второй.

Из (11) видно, что ядро столкновений определяется как среднее значение объема жидкости (газа), входящего в “сферу столкновения” за единицу времени. Отметим очень важное обстоятельство. Так как внутри “сферы столкновений” нет источников (стоков), то объемы входящей и выходящей из нее жидкости должны быть равны между собой. Вследствие этого ядро столкновений, определяемое (11) как среднее значение входящего объема жидкости, находится как произведение половины поверхности “сферы столкновений” $2\pi {\kern 1pt} {{\sigma }^{2}}$ и осредненного значения радиальной компоненты относительной скорости ${\kern 1pt} \left| {{{{\bar {w}}}_{r}}} \right|.$

Разница этих формулировок для малых частиц связана с отличием продольной и поперечной структурных функций при малых расстояниях между двумя точками [24]. Проще говоря, эта разница определяется неравенством интенсивностей пульсаций относительных скоростей сталкивающихся частиц в разных направлениях.

В пионерской работе [25] делается вывод о том, что вид функции плотности вероятности (ФПВ) относительной скорости частиц, используемый при анализе, во многом определяет применимость той или иной формулировки. Однако, как показано в [26, 27], более корректной для ряда задач, например для определения частоты столкновений малоинерционных частиц в турбулентном потоке, является сферическая формулировка. Сделан вывод, что сферическое рассмотрение задачи является более общим, а цилиндрическая постановка приводит к сходным результатам только в некоторых частных случаях. Проанализируем их.

2.3. Частные случаи

Рассмотрим процессы столкновений частиц при их хаотическом движении и осаждении под действием силы тяжести с использованием обоих описанных выше подходов (формулировок).

Столкновения хаотически движущихся молекул (частиц). В этом случае отсутствует пространственная корреляция скоростей частиц, т.е.

Запишем ФПВ относительной скорости частиц w в виде

и найдем осредненную относительную скорость частиц как где $w = \left| {\mathbf{w}} \right|.$

Из (14) следуют выражения для осредненных значений радиальной компоненты относительной скорости и вектора относительной скорости

Подставляя (15) в (11) и (16) в (10), приходим к одному и тому же соотношению для ядра столкновений [25]

Таким образом, обе формулировки (сферическая и цилиндрическая) равнозначны при анализе столкновений хаотически движущихся частиц.

Столкновения частиц при гравитационном осаждении. В этом случае относительная скорость постоянна: ${\mathbf{w}} = ({\kern 1pt} \left| {{{{\mathbf{W}}}_{{ij}}}} \right|{\kern 1pt} ,0,0{\kern 1pt} ),$ где ${{{\mathbf{W}}}_{{ij}}}\, = {{{\mathbf{V}}}_{i}} - {{{\mathbf{V}}}_{j}}$ – относительная скорость витания частиц. Используя цилиндрическую постановку задачи, из (10) имеем

Для сферической формулировки можно получить [25]

Производя интегрирование (19), имеем [25]

Сравнивая (18) и (20), приходим к выводу о равнозначности обеих формулировок для случая гравитационного осаждения частиц.

Можно сделать заключение, что при пространственной корреляции скоростей частиц (отсутствует преимущественное направление движения), использование сферической формулировки является более корректным.

3. СТОЛКНОВЕНИЯ МОНОДИСПЕРСНЫХ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ

Турбулентность – один из основных механизмов, приводящих к столкновениям частиц друг с другом [24]. При вычислении частоты столкновений частиц и соответствующих “столкновительных членов” в уравнениях для характеристик дисперсной фазы обычно используются два основных допущения: 1) учитываются только парные столкновения, 2) процесс столкновений является марковским, т.е. не зависящим от предыдущих столкновений. Таким образом, с учетом описанных допущений для вычисления частоты столкновений необходимо определить ФПВ распределений скоростей двух частиц. Это может быть сделано двумя способами [24]. При первом способе допускается некорелированность (независимость) движения сталкивающихся частиц по аналогии с процессом столкновений молекул в кинетической теории газов [24, 28–30]. В этом случае двухчастичная ФПВ находится как произведение одночастичных ФПВ. Однако такой способ может использоваться для описания столкновений лишь относительно инерционных частиц, время релаксации которых ${{\tau }_{p}}$ много больше характерного времени взаимодействия с турбулентными вихрями ${{T}_{{Lp}}}$ (${{\tau }_{p}} \gg {{T}_{{Lp}}}$). Движение таких частиц не коррелировано и аналогично хаотическому движению молекул. Вторым способом является моделирование процесса столкновений двух частиц с учетом коррелированности их пульсационного движения из-за взаимодействия с турбулентными вихрями несущего потока. Коррелированность движения частиц должна учитываться, если ${{{{\tau }_{p}}} \mathord{\left/ {\vphantom {{{{\tau }_{p}}} {{{T}_{{Lp}}}}}} \right. \kern-0em} {{{T}_{{Lp}}}}} \leqslant 1.$

3.1. Частота столкновений монодисперсных частиц в изотропной турбулентности

Определение частоты столкновений твердых частиц (жидких капель) в турбулентных потоках представляет большой интерес для анализа целого ряда промышленных и метеорологических [31–33] процессов. Относительно простые решения указанной задачи могут быть получены в рамках приближения однородной изотропной турбулентности.

В этом разделе рассматриваются столкновения, обусловленные только взаимодействием частиц с турбулентными вихрями несущей среды. Другие многочисленные факторы (броуновское движение [34–37], гравитационная седиментация [38–41], электрические силы [42–48], гидродинамические силы [49–51] и др.) не учитываются.

Взаимодействие инерционных частиц с турбулентными вихрями приводит к двум основным факторам, дающим вклад в ядро столкновений [24]: 1) относительная скорость соседних частиц (турбулентный транспортный эффект), 2) неоднородное распределение частиц в пространстве (эффект кластеризации). Эффект кластеризации или аккумулирования проявляет себя как тенденция к росту концентрации частиц в областях малой завихренности вследствие действия центробежной силы [52, 53].

Известные аналитические решения задачи о столкновениях частиц в турбулентном потоке получены в предельных случаях безынерционных и высокоинерционных частиц [25, 54].

Теория [25] справедлива для частиц, время релаксации которых меньше колмогоровского временнóго микромасштаба (${{\tau }_{p}} < {{\tau }_{K}}$). Данные частицы полностью следуют турбулентным пульсациям скорости несущей среды и вовлекаются в движение самых мелких вихрей, ответственных за диссипацию энергии турбулентности. Решение [54] справедливо для другого предельного случая, когда время релаксации частиц много больше временнóго макромасштаба турбулентности (${{\tau }_{p}} \gg {{T}_{L}}$). Для таких частиц достаточно учитывать их взаимодействие с энергосодержащими вихрями, а вкладом взаимодействия с мелкомасштабной турбулентностью в ядро столкновений можно пренебречь. Максимальная сложность в определении ядра столкновений возникает в случае наличия в потоке частиц средней инерционности (${{\tau }_{K}} \leqslant {{\tau }_{p}} \leqslant {{T}_{L}}$), когда необходимо учитывать их взаимодействие со всем спектром турбулентных вихрей.

Рассмотрим кратко статистическую модель турбулентных столкновений, справедливую во всем диапазоне инерционности частиц [55–57].

Для определения $\left| {{\kern 1pt} {{{\bar {w}}}_{r}}} \right|$ плотность вероятности пульсационной составляющей радиальной относительной скорости задается распределением Гаусса

Здесь ${{W}_{r}}$ и $w_{r}^{'}$ – осредненная и пульсационная составляющие радиальной относительной скорости. Интенсивность пульсаций радиальной скорости двух частиц при соударении определяется как

В выражении (22) ${{\text{v}}^{{'2}}}$ – интенсивность пульсаций скоростей частиц, ${{\varsigma }_{{12}}}$ – коэффициент корреляции скоростей двух соударяющихся частиц из-за их взаимодействия с турбулентными вихрями несущей фазы, $\xi $ – коэффициент корреляции скоростей несущей фазы и частицы, $F(\sigma )$ – продольная компонента эйлеровой двухточечной корреляционной функции пульсаций скоростей при допущении о равенстве расстояния между частицами $r$ радиусу столкновений $\sigma $.

Для случая, когда отсутствует осредненное относительное движение частиц в радиальном направлении (${{W}_{r}} = 0$), распределение (21) позволяет выразить среднюю относительную радиальную скорость частиц через интенсивность пульсаций радиальной скорости

В [24] показано, что в однородной изотропной стационарной турбулентности при отсутствии осредненного скоростного скольжения кинетическая энергия пульсаций скорости частиц и ковариация скоростей жидкости и частицы совпадают и выражаются через кинетическую энергию пульсаций скорости жидкости как

где – коэффициент вовлечения частиц в турбулентное движение.

В случае экспоненциальной автокорреляционной функции ${{\Psi }_{{Lp}}}$ имеем

где ${{T}_{{Lp}}}$ – время взаимодействия частиц с энергоемкими турбулентными вихрями. С учетом (24) коэффициент корреляции скоростей жидкости и частицы принимает вид

Из (22) и (27) получаем соотношение для коэффициента корреляции скоростей двух частиц в момент столкновения

Из (28) следует вывод, что коэффициент корреляции скоростей частиц равен произведению коэффициента вовлечения частиц в турбулентное движение ${{f}_{u}}{\kern 1pt} $ и корреляционной функции ${\kern 1pt} F(\sigma ),$ учитывающей пространственную коррелированность скоростей жидкости на расстоянии радиуса столкновений $\sigma .$

В случае малоинерционных частиц (${\kern 1pt} {{d}_{p}} < \eta ,$ ${\kern 1pt} \eta = {{({{{{\nu }^{3}}} \mathord{\left/ {\vphantom {{{{\nu }^{3}}} \varepsilon }} \right. \kern-0em} \varepsilon })}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}$ – колмогоровский пространственный микромасштаб) [24] корреляционная функция определяется как

С учетом (22), (23), (28) и (29) средняя относительная радиальная скорость двух частиц представляется в виде

Подстановка (30) в (11) приводит к следующему соотношению для ядра столкновений:

Рассмотрим некоторые предельные случаи, вытекающие из (31).

Безынерционные частицы. Для безынерционных частиц (${{\tau }_{p}} = 0,$ ${{f}_{u}} = 1,$ $\text{v}{\text{'}} = u{\text{'}}$) выражение (31) преобразуется к виду [25]

Инерционный интервал. Большие числа Рейнольдса. В [24] анализируется инерционный интервал изменения времени релаксации частиц (${{\tau }_{K}} \ll {{\tau }_{p}} \ll {{T}_{L}}$) в пределе больших чисел Рейнольдса (${{\operatorname{Re} }_{\lambda }} \to \infty $). В соответствии с колмогоровской теорией локального подобия [58] в инерционном интервале структурная функция представляется известным образом, что приводит к следующим соотношениям для лагранжевой корреляционной функции ${\kern 1pt} {{\Psi }_{L}}(\tau )$ и коэффициента вовлечения частиц ${\kern 1pt} {{f}_{u}}{\text{:}}$

Подстановка (34) в соотношение (31) приводит к выражению для ядра столкновений в инерционном интервале

Высокоинерционные частицы. В другом предельном случае высокоинерционных частиц (${{\tau }_{p}} \to \infty ,$ ${{f}_{u}}{\kern 1pt} \to 0$) формула (31) переходит к виду [54]

3.2. Частота столкновений частиц при совместном действии турбулентности и градиента осредненной скорости

В [59] анализируется процесс столкновений частиц, обусловленный совместным влиянием турбулентных пульсаций несущего газа и осредненной составляющей скорости одной частицы относительно другой. Для определения средней радиальной компоненты относительной скорости $\left| {{{{\bar {w}}}_{r}}} \right|$ необходимо выполнить осреднение по случайному распределению ${{w}_{r}}$ и телесному углу, который характеризует пространственную ориентацию вектора скорости ${\mathbf{w}}$ относительно вектора ${\mathbf{r}},$ соединяющего центры сталкивающихся частиц:

где $\psi $ – азимутальный угол между вектором ${\mathbf{r}}$ и осью ${\mathbf{z}},$ направленной вертикально вверх; $\varphi $ – полярный угол в плоскости (x, y). Далее в [59] выполнено интегрирование (37) по ${{w}_{r}}$ с учетом распределения Гаусса (21):

Приведенное выражение учитывает как наличие пульсаций радиальной составляющей относительной скорости частиц вследствие турбулентных пульсаций скорости газа, так и наличие радиальной составляющей осредненной относительной скорости. При отсутствии осредненной относительной скорости (${{W}_{r}}$ = 0) выражение (38) переходит в соотношение (23), учитывающее только первый из двух упомянутых факторов.

Поле осредненной скорости газа зададим в виде однородного сдвига ${\mathbf{U}} = (sz,0,0).$ Примем допущение о том, что частицы полностью отслеживают осредненное движение несущей фазы, т.е. ${\mathbf{V}} = {\mathbf{U}}.$ В этом случае радиальная компонента относительной скорости ${{w}_{r}},$ обусловленная сдвигом скорости и действием силы тяжести, будет иметь следующий вид:

где $\sigma $ – радиус сферы столкновений ($\sigma = {{r}_{{p1}}} + {{r}_{{p2}}}$).

Из (11) и (38) с учетом (39) в [59] получено выражение для β, учитывающее влияние сдвига скорости, в виде ряда. Не будем приводить конечное соотношение для $\beta $ из-за его громоздкости. При ${{{{{(sR)}}^{2}}} \mathord{\left/ {\vphantom {{{{{(sR)}}^{2}}} {\overline {w_{r}^{{'2}}} }}} \right. \kern-0em} {\overline {w_{r}^{{'2}}} }} \to \infty $ найденный ряд сходится к классическому решению [34]

Также в [59] предложена следующая простая аппроксимация полученного громоздкого выражения:

где ${{\beta }_{t}}$ – турбулентная составляющая суммарного ядра столкновений, ${{\beta }_{s}}$ – составляющая ядра столкновений за счет сдвига скорости (определяется по (40)).

4. СТОЛКНОВЕНИЯ БИДИСПЕРСНЫХ ЧАСТИЦ В ОДНОРОДНОМ ТУРБУЛЕНТНОМ ПОТОКЕ

В разделе рассматриваются столкновения в системе частиц, состоящей из частиц двух сортов, в однородном турбулентном потоке, что имеет большое практическое значение, так как относительно легко обобщается на общий случай полидисперсной системы [24].

4.1. Частота столкновений бидисперсных частиц в изотропной турбулентности

Ниже приводятся основные положения обобщения аналитической модели для турбулентного ядра столкновений монодисперсных частиц, рассмотренной в разделе 3.1, на бидисперсную систему [60–62]. Эта модель справедлива во всем диапазоне инерционности частиц, так как учитывает взаимодействие частиц с турбулентными вихрями всех масштабов. Модель основана на допущении, что одноточечная ФПВ скоростей жидкости и частицы представляется в виде нормального распределения. Двухточечная ФПВ скорости жидкости предполагается гауссовой. ФПВ скоростей двух частиц определяется введением совместной двухточечной ФПВ скоростей жидкости и частиц в соответствии с подходом [55]. Интегрированием двухчастичной ФПВ по нормальным к вектору скорости, соединяющему центры частиц, компонентам скоростей в [24] получена ФПВ для распределения радиальных компонент скоростей частиц.

Двухчастичная ФПВ приводит к распределению (21) для радиальной компоненты относительной скорости пары частиц с интенсивностью пульсаций радиальной скорости двух частиц при контакте [24]

С учетом соотношения (24) для кинетической энергии пульсаций скоростей частиц и ковариации скоростей жидкости и частиц в однородной изотропной стационарной турбулентности коэффициент корреляции радиальных компонент скоростей сталкивающихся частиц примет вид [24]

Из (43) видно, что коэффициент корреляции скоростей частиц при контакте (столкновении) равен произведению среднегеометрического из коэффициентов вовлечения частиц в турбулентное движение и корреляционной функции, принимающей во внимание пространственную коррелированность скорости жидкости на расстоянии радиуса столкновений σ. Таким образом, радиальная относительная скорость сталкивающихся частиц согласно (23), (42) и (43) есть [24]

Для малоинерционных частиц (${\kern 1pt} {{d}_{p}} < \eta $) подстановка (29) и (44) в (11) дает следующее выражение для ядра столкновений:

В случае монодисперсных частиц (45) переходит в (31). Рассмотрим некоторые предельные случаи.

Безынерционные частицы. Для безынерционных частиц группы 2 (${{\tau }_{{p2}}} = 0,$ ${{f}_{{u2}}} = 1$) выражение (45) приобретает следующий вид:

Если частицы группы 1 также безынерционны (${{\tau }_{{p1}}} = 0,$ ${{f}_{{u1}}} = 1$), то выражение (45) переходит в полученную в [25] классическую формулу (32).

Инерционный интервал. Большие числа Рейнольдса. В инерционном интервале изменения времен динамической релаксации частиц (${{\tau }_{K}} \ll {{\tau }_{{p\alpha }}}{\kern 1pt} \ll {{T}_{L}}$) при больших числах Рейнольдса (${{\operatorname{Re} }_{\lambda }} \to \infty $) с учетом приведенного ранее соотношения (34) ядро столкновений (45) записывается как

Высокоинерционные частицы. В другом предельном случае высокоинерционных частиц (${{\tau }_{{p\alpha }}}{\kern 1pt} \to \infty $) их движение оказывается полностью некоррелированным (${{\varsigma }_{{12}}} \to 0$) и выражение (45) приводит к ядру столкновений [54]

являющемуся аналогом (36) для случая бидисперсных частиц.

4.2. Частота столкновений частиц при совместном действии турбулентности и силы тяжести

В [24] найдено ядро столкновений частиц в результате одновременного действия двух эффектов – турбулентности и средней относительной скорости частиц различных групп. В качестве причины возникновения осредненной скорости рассмотрено действие силы тяжести. Для нахождения $\left| {{{{\bar {w}}}_{r}}} \right|$ поступим аналогичным образом (см. 3.2). С этой целью необходимо выполнить осреднение по случайному распределению ${{w}_{r}}$ и телесному углу, который характеризует пространственную ориентацию вектора скорости w относительно вектора r, соединяющего центры сталкивающихся частиц согласно (37). В результате интегрирования с учетом гауссова распределения для пульсационной составляющей радиальной компоненты относительной скорости получим выражение (38).

Обусловленная силой тяжести радиальная компонента осредненной относительной скорости двух частиц определяется как

где ${{W}_{g}} = \left| {{{\tau }_{{p2}}} - {{\tau }_{{p1}}}} \right|{\kern 1pt} {\kern 1pt} g$ – разность скоростей седиментации (осаждения) двух частиц, $g$ – ускорение силы тяжести.

При интегрировании (38) с учетом (49) и последующей подстановки в (11) можно получить выражение для ядра столкновений, где принимается во внимание суммарное влияние турбулентности и силы тяжести:

Здесь $\Sigma = {{{{W}_{g}}} \mathord{\left/ {\vphantom {{{{W}_{g}}} {{{{(2\overline {w_{r}^{{'2}}} )}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{(2\overline {w_{r}^{{'2}}} )}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$ – параметр, учитывающий отношение эффектов гравитации и турбулентности на ядро столкновений.

При малых $\Sigma $ из (50) следует соотношение для ядра столкновений, совпадающее с решением [25] при слабом влиянии гравитации:

где ${{\beta }_{t}}$ – турбулентная составляющая ядра столкновений (45).

В другом предельном случае ($\Sigma \to \infty $) выражение (50) переходит в известное соотношение [17, 24] для ядра столкновений частиц под действием силы тяжести

В [24] отмечается, что соотношение (50) справедливо для учета влияния осредненной относительной скорости на ядро столкновений в изотропной турбулентности не только силы тяжести, но и любой другой внешней силы, вызывающей относительное движение частиц. Выражение (50) впервые получено в [54] и затем воспроизведено в [59, 62, 63].

5. РАЗВИТЫЕ ПОДХОДЫ ДЛЯ РАСЧЕТА ПРОЦЕССА СТОЛКНОВЕНИЯ

Обычно используемый для расчета столкновений алгоритм включает в себя две стадии. Первая предполагает определение места столкновения, вторая – характеристики частиц (капель) после соударения. Необходимо отметить, что в случае столкновения капель расчет характеристик осложняется, так как могут реализовываться различные режимы взаимодействия (отскок, коагуляция, слияние с последующим “растягивающим” или “возвратным” разделением).

5.1. Методы определения места столкновения частиц (капель)

Первым из основных двух этапов учета столкновений частиц (капель) в двухфазных потоках является определение координаты столкновений. На сегодняшний день развито три основных метода (подхода): 1) полностью детерминистский [64], 2) детерминистско-стохастический [65–67], 3) полностью стохастический [68, 69]. Первый подход предполагает полную геометрическую реконструкцию траекторий сталкивающихся частиц и является самым дорогостоящим с точки зрения затрат компьютерного времени. Второй требует определения вероятности столкновения для каждой пары частиц в пределах расчетной ячейки. Третий не требует никакой информации о соседних частицах, но предполагает генерацию фиктивной частицы.

Остановимся подробнее на описании третьего подхода. Учет межчастичного взаимодействия производится посредством генерации некой фиктивной частицы на каждом временнóм шаге расчета траектории движения “реальной” частицы. Характеристики генерируемой частицы, такие как диаметр и скорость, определяются исходя из ранее найденных функций распределений свойств частиц (размер, скорость) и корреляций пульсации скорости фиктивной частицы с ее размером. Например, пульсация скорости фиктивной частицы (индекс 2) определяется посредством следующего соотношения [55]:

где $R({\text{St}}{{{\text{k}}}_{L}}) = \exp ( - 0.55{\text{Stk}}_{L}^{{0.4}})$ – функция числа Стокса в крупномасштабном пульсационном движении (${\kern 1pt} {\text{St}}{{{\text{k}}}_{L}} = {{{{\tau }_{p}}} \mathord{\left/ {\vphantom {{{{\tau }_{p}}} {{{T}_{L}}}}} \right. \kern-0em} {{{T}_{L}}}},$ ${\kern 1pt} {{T}_{L}}$ – макромасштаб турбулентности), ${\kern 1pt} \text{v}_{{1,i}}^{'}$ – i-я составляющая пульсационной скорости “реальной” частицы (индекс 1), ${\kern 1pt} {{\sigma }_{i}}$ – i-я составляющая среднего значения (rms) скорости частицы в рассматриваемом контрольном объеме, ${\kern 1pt} {{\xi }_{n}}$ – случайное число, подчиняющееся гауссову распределению с математическим ожиданием, равным нулю, и среднеквадратичным отклонением, равным единице.

Затем производится вычисление частоты столкновений между рассматриваемой и фиктивной частицами как

где ${{{\mathbf{v}}}_{1}}$ и ${{{\mathbf{v}}}_{2}}$ – мгновенные скорости реальной и “фиктивной” частиц, $N$ – среднее число частиц в единице объема.

Вероятность столкновения является следующей простой функцией частоты столкновений и лагранжевого временнóго шага

Далее производится генерация равномерно распределенного случайного числа ${\kern 1pt} \Psi $, сравниваемого затем с вероятностью столкновения. Столкновение имеет место, если ${\kern 1pt} {{P}_{c}} > \Psi .$ В противном случае ${\kern 1pt} {{P}_{c}} < \Psi $ столкновение отсутствует, и составляющие скорости реальной частицы не претерпевают изменения.

5.2. Методы определения характеристик частиц после столкновения

Для расчета характеристик частиц после столкновения обычно используются следующие допущения: 1) частицы имеют сферическую форму, 2) рассматриваются только бинарные (парные) столкновения, 3) рассматриваются упругие столкновения (пластическая деформация частиц отсутствует), 4) столкновения происходят мгновенно.

Теоретическое описание процесса столкновений двух частиц в общей постановке на основе классической механики приводится в различных монографиях (например, [17, 70, 71]). Соотношения для определения трех проекций линейных и трех проекций угловых скоростей после соударения для первой и второй частиц выводятся с использованием законов сохранения импульса и момента импульса для сталкивающихся частиц.

Для примера приведем соотношения для нахождения линейных скоростей центров тяжести обеих частиц после соударения [17, 70, 71]

где ${\mathbf{v}}_{1}^{0}$ и ${\mathbf{v}}_{2}^{0}$ – соответствующие скорости до удара, ${{{\mathbf{w}}}^{0}}$ – относительная скорость центров тяжести частиц до соударения, ${\mathbf{n}}$ – единичный вектор, направленный по линии удара к центру второй частицы, ${\mathbf{\tau }}$ – единичный вектор, выходящий из точки касания и направленный перпендикулярно линии удара, ${{m}_{{p1}}}$ и ${{m}_{{p2}}}$ – массы частиц. Приведенные соотношения содержат две важные характеристики процесса столкновения – коэффициент восстановления ${{k}_{n}}$ и коэффициент трения ${{k}_{f}}.$

Коэффициент восстановления обычно представляют как

где ${\mathbf{w}}$ – относительная скорость центров тяжести частиц после соударения. Он изменяется в диапазоне от нуля до единицы. В случае абсолютно упругого удара ${{k}_{n}} = 1,$ а при абсолютно неупругом ударе ${{k}_{n}} = 0.$

Уравнения (56) и (57) соответствуют случаю, когда во время соударения обе частицы как бы скользят по поверхности друг друга. Если же скольжение частиц прекращается, то результаты будут другими [17, 70, 71]. Условие наличия скольжения имеет вид

где ${\mathbf{w}}_{{c\tau }}^{0}$ – тангенциальная составляющая относительной скорости соприкасающихся точек частиц до соударения.

Например, в работе [72], посвященной численному исследованию процессов пневмотранспорта частиц стекла (диаметр 130 мкм) в горизонтальном канале, было принято ${{k}_{n}} = 0.9$ и ${{k}_{f}} = 0.4.$

5.3. Методы определения характеристик капель после столкновения

Выше отмечалось, что в случае столкновения капель расчет характеристик осложняется вследствие реализации различных режимов взаимодействия (столкновение с отскоком, слияние (коагуляция), слияние с последующим разделением).

Процесс столкновения капель в общем виде определяется пятью безразмерными параметрами – числами Вебера We, Рейнольдса $\operatorname{Re} ,$ Онезорге Oh, ударным параметром $B$ и отношением размеров сталкивающихся капель $\Delta $, определяемыми следующим образом:

где ρ, σ, $\mu $ – плотность, поверхностное натяжение и динамическая вязкость материала капель соответственно; ${{V}_{r}}$ – относительная скорость; ${{d}_{{d0}}}$ – характерный диаметр капли для построения безразмерных параметров; $b$ – проекция расстояния между центрами капель на плоскость, перпендикулярную относительной скорости, в момент соударения (рис. 2); ${{r}_{{ds}}},$ ${{r}_{{dl}}},$ ${{d}_{{ds}}},$ ${{d}_{{dl}}}$ – радиусы и диаметры маленькой и большой капель соответственно.

Необходимо отметить, что ${\text{Oh}} = {{\sqrt {{\text{We}}} } \mathord{\left/ {\vphantom {{\sqrt {{\text{We}}} } {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }},$ т.е. из трех параметров ${\text{Oh,}}$ ${\text{We}}$ и $\operatorname{Re} $ только два являются независимыми. Таким образом, общее число независимых определяющих параметров будет равно четырем, а не пяти.

В случае столкновения капель разных размеров в качестве характерного размера принимается, как правило, диаметр мелкой капли, т.е. ${{d}_{{d0}}} = {{d}_{{ds}}}$ [73]. При столкновении капель одинакового размера ${{d}_{{ds}}} = {{d}_{{dl}}} = {{d}_{{d0}}}$ и $\Delta = 1.$ Ударный параметр изменяется в диапазоне $0 \leqslant B < 1.$ В случае центрального удара $B = 0.$

Схематичная карта возможных режимов столкновения капель в зависимости от величины двух определяющих критериев (${\text{We}}$ и $B$) приведена на рис. 3 [74]. На карте выделены пять основных областей, соответствующих различным режимам: отскоку, слиянию (коагуляции), слиянию с последующим “растягивающим” и “возвратным” разделениями. В работах [73–78] найдены конкретные числовые значения основных безразмерных параметров (We, B, $\Delta $), а также пограничные (между различными режимами) кривые и соответствующие им реперные точки для столкновений капель различной вязкости, имеющих большую разницу в размерах и т.п.

Например, в работе [75] найдено семейство кривых, определяющих нижнюю границу для отскока, в виде функций $B = f({\text{We}},\Delta ,\Psi ),$ где $\Psi $ – некоторый формпараметр, зависящий от степени деформации капель в течение соударения. Для капель этанола получено $\Psi = 3.351.$ В [76–78] найдены аналогичные семейства кривых, разделяющих режим слияния (коагуляции) и режимы растягивающего (stretching) и возвратного (reflexive) разделений.

Для расчета столкновения капель используются различные модели [79–83]. Большое распространение получили так называемые энергетические модели. В соответствии с ними критерием коагуляции является количество кинетической энергии, которое должно быть трансформировано в потенциальную и внутреннюю энергии перед тем, как капли коагулируют. В работе [84] эффективность коагуляции связывается с критическим значением относительной скорости капель при столкновении (в момент соударения). В [85] для фиксации перехода “соударение–коагуляция” используется критическое число Вебера ${\text{W}}{{{\text{e}}}_{{{\text{cr}}}}}.$ Оно достигается, когда капли переходят из режима соударения (отскока) в режим коагуляции (слияния). Такой подход восходит к работе [86], в которой различные режимы процесса столкновений характеризовались различными значениями числа Вебера. Критическое число ${\text{W}}{{{\text{e}}}_{{{\text{cr}}}}}$ найдено в экспериментах [87]. В [85], используя его, находят соответствующую разницу между кинетическими энергиями капель, где в качестве определяющей скорости выступает относительная скорость между двумя каплями в предположении, что обе капли имеют близкие по величине скорости. Затем найденная кинетическая энергия для ${\text{W}}{{{\text{e}}}_{{{\text{cr}}}}}$ интерпретируется как кинетическая энергия, необходимая для трансформации или диссипируемая вследствие вязкости до того момента, когда капли коагулируют (сольются).

Обозначим $\Delta {{E}_{{k{\text{cr}}}}}$ критическое значение кинетической энергии, которое должно трансформироваться или диссипировать, и определяемое как разность между начальным значением кинетической энергии ${{E}_{{k0}}}$ и в момент коагуляции ${{E}_{{kc}}}{\text{:}}$

где ${{m}_{{d\Sigma }}} = \sum\nolimits_{i = 1}^{N = 2} {{{m}_{i}}} $ – суммарная масса сталкивающихся капель, $N$ – их количество, $V_{{r{\text{cr}}}}^{{}}$ – критическое значение относительной скорости капель, которое связано с критическим числом Вебера ${\text{W}}{{{\text{e}}}_{{{\text{cr}}}}}$ как

Критерий коагуляции [85]:

если

коагуляция происходит;

если

коагуляция отсутствует.

Здесь текущее изменение кинетической энергии

где

– кинетическая энергия двух сталкивающихся капель, ${\mathbf{V}}$ – вектор относительной скорости, ${{{\mathbf{r}}}_{d}}$ – вектор расстояния между центрами масс двух сталкивающихся капель.

При проведении расчетов две капли мгновенно начинают рассматриваться как одна [85], если $\Delta {{E}_{{k{\text{cr}}}}}$ достигается.

Примеры столкновений двух капель при реализации режима отскока (${\text{We}} < {\text{W}}{{{\text{e}}}_{{{\text{cr}}}}}$) и режима слияния (${\text{We}} > {\text{W}}{{{\text{e}}}_{{{\text{cr}}}}}$) приведены на рис. 4 и 5 соответственно. Для рассматриваемого случая ${\text{W}}{{{\text{e}}}_{{{\text{cr}}}}} = 10.1.$

6. ВЛИЯНИЕ СТОЛКНОВЕНИЙ НА ХАРАКТЕРИСТИКИ ДВУХФАЗНОГО ПОТОКА

В этом разделе приводятся и анализируются лишь некоторые работы, демонстрирующие важность учета процесса межчастичных (межкапельных) столкновений при определении характеристик обеих фаз двухфазного потока.

6.1. Влияние столкновений на характеристики двухфазных турбулентных струйных течений

Имеется значительное количество исследований (например, [88–91]), в которых авторы пытались учесть влияние столкновений на характеристики турбулентных струйных течений.

В [88] развита математическая модель, позволяющая анализировать пульсационное движение частиц в двухфазном потоке с учетом их обратного влияния на характеристики несущей фазы и межчастичных столкновений. Модель основывается на уравнениях для отдельных компонент тензора напряжений Рейнольдса для дисперсной фазы, а также для смешанных моментов газа и частиц. Предложенные замыкающие соотношения позволили достичь приемлемого согласия между расчетными и экспериментальными данными.

В [89] выполнено численное моделирование нисходящей круглой струи воздуха, содержащей частицы стекла, при высоких массовых концентрациях дисперсной фазы (до $M{\kern 1pt} = 180\% $). Для $M{\kern 1pt} = 30{\kern 1pt} \% $ и 90% результаты хорошо описывают имеющиеся экспериментальные данные [90]. Для указанных значений массовых расходных концентраций не было выявлено различия в характеристиках двухфазной струи в случае учета межчастичных столкновений на основе стохастического подхода (см. раздел 5.1), развитого в [68]. Для $M{\kern 1pt} = 180\% $ данные экспериментов отсутствовали, но расчеты были выполнены. Учет межчастичных столкновений приводил к выполаживанию профиля осредненной скорости частиц и снижению (до 20%) анизотропии их пульсационных скоростей. Выявлен также эффект уширения (на 15%) поперечного сечения струи на расстоянии 40 диаметров от сопла. Это исследование показало, что в отсутствие стенок, ограничивающих течение, влияние столкновений между частицами начинается с более высоких значений концентрации последних.

В работе [91] проведено численное исследование влияния межчастичных столкновений на дисперсию частиц различной инерционности для трехмерной турбулентной двухфазной струи, истекающей из плоского горизонтального сопла. Для расчета движения воздуха использовался метод прямого численного моделирования (DNS), а для расчета поведения частиц – лагранжев траекторный метод и детерминистский подход (см. раздел 5.1) для учета их столкновений. Обратным влиянием частиц на течение несущего воздуха пренебрегалось. Число Стокса варьировалось в широком диапазоне 0.01–100 и определялось следующим образом:

где ${{\rho }_{p}}$ – плотность частиц, ${{d}_{p}}$ – диаметр частиц, $\mu $ – динамическая вязкость воздуха, ${{U}_{0}}$ – скорость воздуха на выходе из центра сопла, $D$ – высота плоского сопла.

Частицы для каждого расчетного случая вбрасывались порционно (по 462 штуки) через некоторые постоянные интервалы времени. Во время вбрасывания они располагались равномерно, при этом начальная скорость частиц равнялась локальной скорости воздуха.

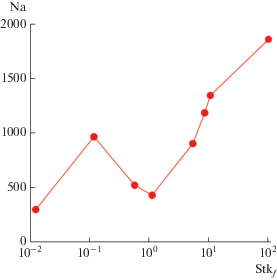
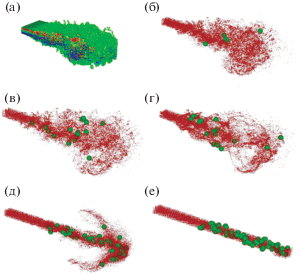
В результате расчетов визуализированы картины двухфазного течения: построены мгновенные расположения частиц различной инерционности с указанием мест их столкновений в разные моменты времени. Пример полученных пространственных расположений частиц в момент времени (безразмерное) $\bar {\tau } = 42$ показан на рис. 6. Обезразмеривание производилось с использованием значения скорости воздуха на выходе из центра сопла ${{U}_{0}}{\kern 1pt} $ и его высоты $D.$ Анализ дисперсии частиц различной инерционности позволил сделать следующие выводы. Малоинерционные частицы (${\text{St}}{{{\text{k}}}_{f}} = 0.01$ и 0.1) распределены в пространстве практически однородно вследствие их дисперсии турбулентными вихрями несущей фазы. Более инерционные частицы (${\text{St}}{{{\text{k}}}_{f}} = 1$) концентрируются преимущественно на внешних границах крупномасштабных турбулентных вихрей. Частицы, обладающие еще большей инерционностью (${\text{St}}{{{\text{k}}}_{f}} = 10$), практически не взаимодействуют с турбулентными вихрями. Наиболее инерционные частицы (${\text{St}}{{{\text{k}}}_{f}} = 100$) движутся почти прямолинейно и концентрируются в центральной области струи, где и сталкиваются между собой.

Также в [91] проанализировано влияние инерционности (числа Стокса) на среднее число столкновений, определяемое как

где $N$ – общее число столкновений в течение временнóго шага $\Delta {\tau }{\text{.}}$

Очевидно, что среднее число столкновений не является простой линейной функцией от числа ${\text{St}}{{{\text{k}}}_{f}}$ (рис. 7). Сначала оно растет с увеличением инерционности частиц и при ${\text{St}}{{{\text{k}}}_{f}} = 0.1$ достигает локального максимума, затем снижается и имеет локальный минимум при ${\text{St}}{{{\text{k}}}_{f}} = 1.$ В дальнейшем среднее число столкновений растет с увеличением числа Стокса.

Такое сложное поведение описанной зависимости определяется двумя основными факторами, каждый из которых вызывает эффект пересечения траекторий частиц и способствует межчастичным столкновениям: 1) частицы имеют тенденцию собираться (аккумулироваться) в областях низкой завихренности, что вызывает рост их локальной концентрации в струях [92–95]; 2) инерция частиц влияет на относительное движение соседних частиц, изменяя таким образом их относительную скорость.

Вследствие вышесказанного при малых числах Стокса увеличение числа столкновений (с ростом инерционности) объясняется влиянием эффекта аккумулирования частиц вследствие их взаимодействия с мелкомасштабными вихрями (при ${\text{St}}{{{\text{k}}}_{f}} = 0.1$ этот механизм играет главенствующую роль). При ${\text{St}}{{{\text{k}}}_{f}} = 1$ время динамической релаксации частиц сравнимо с характерным временем крупномасштабных вихрей. Для таких частиц эффект аккумулирования имеет место на начальной стадии развития струи, где доминируют крупномасштабные вихревые структуры. Однако по мере развития струи частицы, имеющие ${\text{St}}{{{\text{k}}}_{f}} = 1,$ не могут аккумулироваться и их распределение становится однородным, так как крупномасштабрые вихри сменяются мелкомасштабными. Из этого следует, что среднее число столкновений за все время “развития” струи становится минимальным. При дальнейшем росте инерционности (${\text{St}}{{{\text{k}}}_{f}} > 5$) воздействие несущего воздуха на частицы становится все меньше и меньше вследствие их большой инерционности. Такие частицы имеют прямолинейные траектории, движутся преимущественно в центральной области струи без дисперсии в вертикальном и поперечном направлениях, что способствует сокращению расстояний между ними. С ростом инерционности частицы имеют тенденцию сталкиваться все чаще и чаще.

Результаты [91] показали важность учета межчастичных столкновений даже в случае слабоконцентрированной двухфазной турбулентной струи.

6.2. Влияние столкновений на характеристики двухфазных турбулентных течений в каналах

Имеется целый ряд расчетно-теоретических исследований двухфазных турбулентных течений с частицами, в которых авторы пренебрегали столновениями частиц между собой (см., например, [96, 97]).

Первая попытка учета межчастичных столкновений была предпринята в [18], где исследовалось поведение частиц в вертикальной трубе без учета их обратного влияния на параметры течения несущей фазы. Было показано, что влиянием столкновений между частицами на их дисперсию в нормальном (по отношению к среднему течению) направлении нельзя пренебрегать даже в случае слабозапыленного потока, т.е. когда $\Phi = O({{10}^{{ - 4}}}).$ Отметим, что столкновения частиц рассчитывались на основе детерминистского подхода (см. раздел 5.1).

Дальнейшее изучение влияния столкновений между частицами на характеристики двухфазных потоков продолжено в целом ряде работ.

В [98] выполнено численное исследование условий формирования кластеров (областей повышенной концентрации частиц) в двухфазном воздушном потоке (скорость воздуха 5 м/с) в канале шириной 80 мм. Диаметр частиц равнялся 500 мкм, их плотность – 2620 кг/м³, массовая расходная концентрация дисперсной фазы на входе – 400%. Учет межчастичных столкновений проведен путем использования прямого моделирования по методу Монте-Карло (DSMC). Указанный метод, являющийся разновидностью детерминистско-стохастического подхода (см. раздел 5.1), впервые развит в работе [99]. Расчет столкновений частиц производился по алгоритму [100], учитывающему суммарную вероятность столкновений всех рассматриваемых в одной расчетной ячейке частиц в течение временнóго шага. В результате было показано, что нестабильность потока и формирование кластеров инициируются неупругостью (${{k}_{n}} = 0.94$) и трением (${{k}_{f}} = 0.28$) при межчастичных столкновениях.

Детальные экспериментальные исследования двухфазных потоков с частицами в горизонтальных каналах проведены в [101, 102]. В [102] использовались горизонтальные каналы прямоугольного сечения (высота 35 мм, ширина 350 мм) с гладкой (“нормальная” шероховатость) и шероховатой (“повышенная” шероховатость) стенками. Измерения показали, что средние глубины микронеровностей стенки (нержавеющая сталь) в продольном и поперечном направлениях равны $3.5{\kern 1pt} - {\kern 1pt} 4.3$ мкм и 7 мкм для гладкой и шероховатой стенок соответственно. В качестве дисперсной фазы в экспериментах применялись сферические частицы стекла с номинальными диаметрами 60, 100, 190 и 625 мкм. Массовая расходная концентрация частиц изменялась в диапазоне $M = 0{\kern 1pt} - {\kern 1pt} 10{0\% }.$ Эксперименты проводились для трех значений осредненной скорости несущего воздуха в центре канала: ${{U}_{{xc}}} = 14.25,$ ${{U}_{{xc}}} = 19.7$ и ${{U}_{{xc}}} = 25.6$ м/с.

Были выполнены подробные измерения осредненных и пульсационных (среднеквадратичных) скоростей несущего воздуха и частиц при различных концентрациях последних. Анализ полученных результатов позволил сделать следующие выводы о влиянии концентрации дисперсной фазы, размера частиц, шероховатости стенки на энергию пульсаций скорости частиц [102]:

1) повышенная шероховатость стенки приводит к существенному росту энергии пульсаций скорости частиц как в продольном, так и в нормальном направлениях;

2) рост концентрации частиц приводит к подавлению энергии пульсаций скорости частиц вследствие диссипации энергии из-за межчастичных столкновений;

3) увеличение размера частиц способствует росту энергии пульсаций дисперсной фазы, так как влияние повышенной шероховатости особенно значительно для крупных частиц;

4) степень снижения энергии пульсаций частиц с ростом концентрации особенно высока при повышенной шероховатости стенки и в случае движения малоинерционных частиц.

В большинстве описанных выше исследований не делался акцент на отличия параметров двухфазного течения с учетом и без учета межчастичных столкновений.

В работе [103] выполнено численное моделирование нисходящего развитого турбулентного двухфазного течения между двумя параллельными стенками на основе метода крупных вихрей (LES) для несущей фазы и лагранжевого траекторного метода для расчета движения частиц с использованием детерминистского подхода (см. раздел 5.1) к определению местоположения их соударений. Обнаружено, что учет межчастичных столкновений значительно улучшает совпадение получаемых результатов с имеющимися экспериментальными данными [104].

Показано, что столкновения интенсифицируют поперечное “перемешивание” дисперсной фазы, что приводит к выполаживанию профилей осредненной скорости и концентрации частиц. Проведена наглядная визуализация мгновенных картин двухфазного потока. Отчетливо показан эффект формирования “облаков” (скоплений) частиц небольшой инерционности вследствие их взаимодействия с турбулентными вихрями несущей фазы (так называемый эффект кластеризации) в случае, если межчастичные столкновения не учитывались. Появление “облаков” частиц изменяло результаты расчетов, проводимых с учетом обратного влияния частиц на несущую фазу и без учета последнего. Это является следствием модификации структуры турбулентности в случае эффекта кластеризации.

Учет межчастичных столкновений приводит к росту дисперсии частиц в поперечном направлении, что сказывается на их пространственном распределении. Влияние столкновений между частицами на эффект их аккумулирования (кластеризации) в плоскостях, параллельных стенкам канала, определяется соотношением между числами Стокса, построенными с использованием времени между соударениями и временны́м масштабом турбулентности.

В пристенной области межчастичные столкновения оказывают влияние на высокоинерционные частицы, в то время как в приосевой (центральной) области, напротив, – на движение малоинерционных частиц.

В [105] проведены расчеты двухфазных течений с частицами на основе эйлерова-лагранжева моделирования при высоких значениях концентрации последних. Используемые при проведении численного исследования расчетные сетки позволяли применить вихреразрешающие методы (LES) для расчета течения воздуха в условиях сложной геометрии и учитывать как обратное влияние частиц на несущую фазу, так и столкновения частиц между собой на основе детерминистского подхода (см. раздел 5.1). Развитая методология апробирована путем решения тестовых задач (плоское течение в канале, течение в камере сгорания). Результаты расчетов [105] и имеющиеся экспериментальные данные [106, 107] хорошо согласуются между собой.

Для турбулентного течения в плоском канале (${{M}_{0}} = 15\% ,$ ${{\Phi }_{0}} = 7.3 \times {{10}^{{ - 5}}}$ – средние по сечению канала концентрации) выявлено сильное влияние межчастичных столкновений на характеристики движения частиц вследствие реализации в пристенной области высокой локальной концентрации дисперсной фазы ($M \gg {{M}_{0}},$ $\Phi \gg {{\Phi }_{0}}$). Учет межчастичных столкновений приводил к выполаживанию профиля осредненной скорости частиц вследствие интенсивного обмена импульсом между ними. В пользу этого свидетельствует увеличение (до трех раз) поперечных пульсаций скорости частиц при учете столкновений. Что касается профиля продольных пульсаций скорости частиц, то он становился более пологим. Это легко объяснить следующим образом. Если частица движется из области, характеризующейся малой скоростью, в область с более высокой скоростью, то пульсация ее скорости будет меньшей в случае более пологого профиля осредненной скорости. Было также найдено, что присутствие частиц не оказывало влияния на профили осредненной скорости и продольных пульсаций скорости несущей фазы. Влияние дисперсной фазы на поперечные пульсации скорости воздуха было незначительным.

Для “холодного” течения в модели камеры сгорания при более высоких начальных концентрациях частиц (${{M}_{0}} = 22\% ,$ ${{\Phi }_{0}} = {{10}^{{ - 4}}}$ и ${{M}_{0}} = 110\% ,$ ${{\Phi }_{0}} = 5 \times {{10}^{{ - 4}}}$) не обнаружено различия в результатах в случае учета и неучета межчастичных столкновений вследствие уменьшения концентрации частиц в отрывной зоне ($M < {{M}_{0}}{\kern 1pt} ,$ $\Phi < {{\Phi }_{0}}$).

В [108] выполнено численное моделирование нисходящего полностью развитого турбулентного течения воздуха ($\operatorname{Re} = 13{\kern 1pt} 800$) в канале (ширина 4 см, длина 1 м), содержащего 50 мкм частицы стекла и 70 мкм частицы меди. Массовая концентрация частиц изменялась в диапазоне $M{\kern 1pt} = 2{\kern 1pt} - {\kern 1pt} 100\% .$ Расчеты выполнены на основе эйлерово-лагранжевого метода с учетом обратного влияния частиц на характеристики воздуха и межчастичных столкновений. Для условий постоянного расхода несущей фазы не выявлено влияния частиц на профиль осредненной скорости воздуха, что согласуется с данными экспериментов [104]. Учет столкновений между частицами приводил к выполаживанию профиля осредненной скорости дисперсной фазы. Межчастичные столкновения оказывали более сильное влияние на движение частиц меди. Эти частицы приводили также к более сильному изменению (подавлению) энергии турбулентности воздуха. Эффект подавления турбулентности возрастал с увеличением концентрации частиц, числа Стокса и расстояния от стенки. Интересным является тот факт, что неучет межчастичных столкновений изменял направление воздействия частиц на несущую среду с ламинаризирующего на турбулизирующий.

В [109] проведено численное исследование восходящего турбулентного течения в канале для очень высоких содержаний частиц – $M{\kern 1pt} = 1950\% $ ($\Phi = 1.3{\kern 1pt} \% $). Целью работы было установление как влияния частиц на характеристики несущей фазы, так и влияния межчастичных столкновений на параметры движения обеих фаз. Для достижения указанной цели выполнены три серии расчетов: 1) расчет турбулентного течения без частиц, 2) расчет турбулентного течения с частицами без учета их столкновений, 3) расчет турбулентного течения со сталкивающимися частицами.

Учет столкновений приводил к существенному изменению распределений (профилей) как осредненных, так и всех компонент (осевой, нормальной, азимутальной) пульсационных скоростей обеих фаз. Наличие межчастичных столкновений приводило к выполаживанию профиля осредненной скорости воздуха в центральной области течения, увеличивая при этом ее градиент вблизи стенки. Профиль осредненной скорости частиц также становился более пологим. При учете столкновений максимумы в распределениях осевых пульсаций скорости как воздуха, так и частиц сменялись на минимумы в центральной области течения. Здесь же выявлен рост (примерно в 1.5 раза) нормальных и азимутальных пульсаций скорости воздуха. Что касается аналогичных составляющих пульсаций скорости частиц, то их рост был еще более значительным (в 3–3.5 раза).

В заключение кратко остановимся на рассмотрении работ, посвященных проблеме эрозии. Эрозия – основная причина выхода из строя трубопроводов, транспортирующих газовзвеси (запыленные среды). В ранних работах исследовалось влияние скорости и концентрации песка на эрозию [110], изменение толщины стенки на разных расстояниях от входа в канал [111], а также для различных материалов трубы [112]. В более поздних экспериментальных работах применялись совершенные профилометры [113] и бесконтактные ультразвуковые приборы [114] для измерения глубины эрозии, а также PIV для измерения динамического скольжения между транспортирующим воздухом и частицами песка [115]. При проведении численных исследований использовались, как правило, лагранжевы траекторные методы [116–122] наряду со стохастическим подходом при учете межчастичных столкновений.

Остановимся на анализе одной из последних работ [122]. Чтобы предсказать явления эрозии в коленчатой алюминиевой трубе, в этом исследовании использованы нестационарные осредненные по Рейнольдсу уравнения Навье–Стокса при расчете несущей фазы вместе с лагранжевым траекторным подходом для частиц. Была предпринята попытка учета всех определяющих факторов (сила аэродинамического сопротивления, подъемная сила, вращение частиц, межчастичные столкновения, взаимодействие частиц со стенкой, межфазный обмен импульсом). Для выявления роли межчастичных столкновений расчеты выполнялись при шести разных значениях массовой концентрации ($M{\kern 1pt} = 3.85{\kern 1pt} - {\kern 1pt} 90\% $). Результаты вычислений выявили, что интенсивность эрозии в существенной степени связана с процессом взаимодействия частиц со стенками трубы. При этом определяющими параметрами процесса являются скорость частиц, угол их соударения со стенкой, а также частота столкновений. Показано, что при самой малой концентрации учет межчастичных столкновений не влиял на получаемые результаты. С ростом концентрации частиц межчастичное взаимодействие оказывало существенное влияние на все определяющие параметры процесса взаимодействия частиц со стенкой.

ЗАКЛЮЧЕНИЕ

Рассмотрены и проанализированы результаты расчетно-теоретических и экспериментальных исследований влияния столкновений частиц (капель) на параметры турбулентных двухфазных потоков. Описаны имеющиеся методы определения характеристик процесса столкновений монодисперсных (бидисперсных) частиц в однородной изотропной турбулентности, а также при совместном действии турбулентности, градиента осредненной скорости и силы тяжести. Приведены некоторые работы, демонстрирующие важность учета процесса межчастичных (межкапельных) столкновений при расчетах двухфазных потоков.

Отметим, что целый ряд принципиальных вопросов, касающихся столкновений частиц (капель), остался вне рассмотрения вследствие ограниченности объема обзора: случай существенного различия размеров сталкивающихся частиц [123]; влияние несферичности частиц [124–128]; генерация турбулентных следов за движущимися частицами [129]; наличие ударно-волновых процессов [130–133]; эффект кластеризации дисперсной фазы в турбулентных и вихревых потоках [52, 134–141]; особенности межчастичных соударений при обтекании тел двухфазными потоками [142–150] и др.

Работа выполнена при частичной поддержке Российского фонда фундаментальных исследований (проект № 18-08-01382).