Теплофизика высоких температур, 2019, T. 57, № 5, стр. 677-684

ВВЕДЕНИЕ

В статистической механике задача описания равновесных термодинамических свойств может быть решена в рамках одного из следующих подходов:

– компьютерное моделирование (численный эксперимент) методами молекулярной динамики или Монте-Карло;

– метод интегральных уравнений, связывающий потенциалы взаимодействия с функциями распределения;

– метод Гиббса, в котором поправки к термодинамическим функциям идеального состояния вычисляются с помощью конфигурационного интеграла (КИ).

Для реализации каждого из подходов необходимо задать конкретный вид потенциала межчастичного взаимодействия, определяющего свойства модели вещества.

Результаты расчетов свойств численными методами, представляемые обычно в виде таблиц или графиков, могут быть получены с высокой точностью и использованы, в частности, для проверки предположений, лежащих в основе интегральных уравнений, что может стимулировать развитие теории жидкого состояния.

Метод интегральных уравнений позволяет найти термодинамические соотношения в аналитической форме [1], если помимо потенциала взаимодействия известна и функция распределения.

Если задан только потенциал взаимодействия, то для получения аналитических соотношений, определяющих равновесные свойства, оказывается востребованным метод Гиббса, связанный с проблемой вычисления или оценки КИ. Следует отметить, что эта проблема, оставаясь одной из фундаментальных в статистической механике, имеет точное решение лишь для нескольких, весьма далеких от реальности модельных систем. К числу таких систем относятся модель Изинга и модель решеточного газа, модель Гейзенберга и одномерная модель Каца с бесконечным радиусом действия, приводящая к уравнению Ван-дер-Вальса [2].

Поскольку вид реального потенциала неизвестен, то для последовательного теоретического описания свойств методами статистической механики приходится использовать различные аппроксимации, отвечающие, по крайней мере, общим физическим представлениям о свойствах потенциальных функций.

Одной из таких функций, отражающих основные детали реальных взаимодействий, является линейная комбинация потенциалов Юкавы (или двойной потенциал Юкавы – DY-потенциал)

где a, A, b, B – положительные параметры.

Опубликовано немало работ [3–6], посвященных изучению термодинамических и структурных свойств жидкостей, в которых расчеты выполняются методами численного моделирования или интегральных уравнений на основе DY-потенциала, как правило, в сочетании с потенциалом твердых сфер. Приведенные ссылки, конечно, не исчерпывают всей библиографии по этой теме. Однако, несмотря на свою популярность, упрощенная модель (1) и ее модификация, учитывающая твердую сердцевину, не были исследованы в рамках подхода Гиббса (во всяком случае, таких исследований обнаружить не удалось).

В настоящей статье предпринимается попытка восполнить этот пробел и в качестве модели простой жидкости рассматривается система из $N$ одинаковых частиц массой ${{m}_{0}},$ расположенных в объеме $V$ и взаимодействующих посредством парного сферически симметричного потенциала ${v}(r).$

Программа описания свойств модельной системы состоит из следующих этапов:

1) нахождение свободной энергии и термодинамических функций системы с DY-потенциалом как функций параметров a, A, b, B;

2) редукция четырехпараметрической задачи к однопараметрической и определение с помощью нескольких экспериментальных величин значения управляющего параметра, обеспечивающего оптимальное согласование расчетов с экспериментом;

3) сопоставление теоретических зависимостей свойств, построенных с учетом значения управляющего параметра, с известными экспериментальными данными.

Для осуществления этой программы используются результаты работы [7], в которой КИ модельной системы преобразован к интегралу типа Лапласа и вычислен в квадратичном приближении метода перевала. В случае межатомного потенциала общего вида выражение для свободной энергии Гельмгольца определяется равенством [7]

где $\beta = {1 \mathord{\left/ {\vphantom {1 {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ – обратная температура, k_B – постоянная Больцмана, $n = {N \mathord{\left/ {\vphantom {N V}} \right. \kern-0em} V}$ – концентрация частиц, ${\tilde {v}}\left( k \right)$ – фурье-образ потенциала ${v}\left( r \right),$ ${{{\tilde {v}}}_{0}} = {\tilde {v}}(0)$ – его значение при $k = 0,$ ${{F}_{{{\text{id}}}}} = N{{k}_{{\text{B}}}}T\ln (n{{\lambda }^{3}}),$ ${{\lambda }^{2}} = \beta {{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} {2\pi {{m}_{0}}}}} \right. \kern-0em} {2\pi {{m}_{0}}}}$ – тепловая длина волны де Бройля, $h$ – постоянная Планка, $\Omega $ – область определения функции ${\tilde {v}}\left( k \right).$

Примеры применения выражения (2), полученного в [8] методом коллективных переменных и в [9] с помощью эргодической теоремы Вейля, можно найти в [10, 11], где для прогнозирования свойств привлекались различные потенциалы, допускающие разложение Фурье.

АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ

При использовании приближения (2) следует учесть условие устойчивости взаимодействия ${\tilde {v}}(k) \geqslant 0$ [12, 13], физическая трактовка которого состоит в том, что в системе невозможно скопление всех ее частиц в ограниченном объеме, другими словами, исключатся коллапс системы. Решение этого неравенства с фурье-образом

потенциала (1) определяет область изменения безразмерных параметров $\delta = {b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a}$ и $\varepsilon = {B \mathord{\left/ {\vphantom {B A}} \right. \kern-0em} A},$ состоящую из двух частей: сектора G₁ = $ = \left\{ {\left( {\delta ,\varepsilon } \right):0 < \delta < 1,\,\,0 < \varepsilon < {{\delta }^{2}}} \right\}$ и полосы G₂ = $ = \left\{ {\left( {\delta ,\varepsilon } \right):\delta \geqslant 1,\,\,0 \leqslant \varepsilon \leqslant 1} \right\},$ представленных на рис. 1. В секторе ${{G}_{1}}$ параметры $\delta $ и $\varepsilon $ принимают такие значения, при которых конкуренция первого слагаемого в (1), отвечающего за отталкивание на малых расстояниях, и второго, создающего притяжение на больших r, приводит к образованию потенциальной ямы. В полосе ${{G}_{2}}$ при $\delta \geqslant 1$ при любых $r$ в (1) доминирует первое слагаемое, поэтому потенциал преобразуется к отталкивательному потенциалу, подобному потенциалу Юкавы. Здесь ограничимся рассмотрением случая, когда параметры $\delta $ и $\varepsilon $ принимают значения из области ${{G}_{1}}.$

Интеграл $I\left( {n,\beta } \right),$ устанавливающий связь свободной энергии (2) с параметрами потенциала (1), равен

где $Q(x) = \sqrt {1 + {{\delta }^{2}} + xd + 2\delta q(x)} ,$ $q(x) = \sqrt {1 + xD} ,$ $x = n\beta w,$ $w = {A \mathord{\left/ {\vphantom {A {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}},$ $d = 1 - \varepsilon ,$ $D = 1 - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon {{{\delta }^{2}}}}} \right. \kern-0em} {{{\delta }^{2}}}}.$

Подстановка (3) в (2) дает выражение для свободной энергии системы с DY-потенциалом, используемое в дальнейших вычислениях. Покажем, что термодинамические величины, получаемые из свободной энергии, содержат только два безразмерных параметра $\delta $ и ε, отвечающих вкладу взаимодействия. Для этого запишем уравнение состояния (УС)

где $J(x) = 1 + {{\delta }^{3}} - \left( {{{Q}^{3}}(x) - 3\delta q(x)Q(x)} \right)$ – ‒ $3x\left[ {\delta \left( {q(x){{Q}_{1}}(x) + Q(x){{q}_{1}}(x)} \right) - {{Q}^{2}}(x){{Q}_{1}}(x)} \right],$ q₁(x) = $ = {D \mathord{\left/ {\vphantom {D {2q(x)}}} \right. \kern-0em} {2q(x)}},$ ${{Q}_{1}}(x) = {{\left( {d + 2\delta {{q}_{1}}(x)} \right)} \mathord{\left/ {\vphantom {{\left( {d + 2\delta {{q}_{1}}(x)} \right)} {2Q(x)}}} \right. \kern-0em} {2Q(x)}}.$

В критической точке (КТ) выполняются условия

где следующие ниже функции ${{J}_{1}}\left( x \right),$ ${{J}_{2}}\left( x \right)$ находятся дифференцированием $J\left( x \right)$ по $x$ и вычисляются в КТ:

Исключая отношение

из уравнений системы (5), приходим к уравнению относительно безразмерной неизвестной x_c = $ = {{n}_{c}}{{\beta }_{c}}w = x\left( {\delta ,\varepsilon } \right){\text{:}}$которое имеет универсальный характер, поскольку не содержит параметров конкретного вещества. С помощью (6) из УС (4) получим уравнение в приведенных координатах $\tau = {T \mathord{\left/ {\vphantom {T {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}},$ $\omega = {n \mathord{\left/ {\vphantom {n {{{n}_{c}}}}} \right. \kern-0em} {{{n}_{c}}}},$ $\Pi = {P \mathord{\left/ {\vphantom {P {{{P}_{c}}}}} \right. \kern-0em} {{{P}_{c}}}}{\text{:}}$ где функции $J\left( {\omega ,\tau } \right),$ ${{J}_{1}}\left( {\omega ,\tau } \right)$ построены из соответствующих функций $J\left( x \right),$ ${{J}_{1}}\left( x \right),$ определяемых после формул (4) и (5) с использованием замены $x = {{{{x}_{c}}\omega } \mathord{\left/ {\vphantom {{{{x}_{c}}\omega } \tau }} \right. \kern-0em} \tau }.$

С целью демонстрации предсказательных возможностей приближения (2) приведем несколько формул, получаемых из хорошо известных соотношений и используемых далее для расчета термодинамических свойств, о которых имеется соответствующая экспериментальная информация:

– молярная изобарная теплоемкость

${{C}_{V}}\left( \tau \right) = - {{T}^{2}}\left( {\frac{{{{\partial }^{2}}F}}{{\partial {{T}^{2}}}}} \right)$ = $C_{V}^{{{\text{id}}}} + R\frac{{q_{c}^{2}\omega }}{{{{J}_{1}}\left( {{{x}_{c}}} \right){{\tau }^{2}}}}{{J}_{1}}\left( {\omega ,\tau } \right),$ $C_{V}^{{{\text{id}}}} = \frac{3}{2}R,$ $R$ – универсальная газовая постоянная: – коэффициент Джоуля–Томсона – скорость звука где M – молярная масса вещества.

Функции (8)–(12) содержат только два параметра $\delta $ и ε, значения которых в секторе ${{G}_{1}}$ следует определить из условия наилучшего согласия с данными измерений.

Одним из индикаторов, дающих представление о качестве описания совокупности экспериментальных данных, служит функция

которая содержит экспериментальные $X_{i}^{{\exp }}$ и теоретические $X_{i}^{{{\text{theor}}}}\left( {\delta ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon } \right)$ значения $i$-го свойства, вычисляемые по заданным $P$ и $T.$ Конкуренция слагаемых, образующих сумму (13), может приводить к появлению минимума функции $\Phi \left( {\delta ,\,\varepsilon } \right).$ Поэтому для адекватного воспроизведения совокупности свойств необходимо найти такие значения $\delta $ и ε, при которых функция (13) достигает минимума.

Нахождение экстремума функции двух переменных сводится к решению системы нелинейных уравнений, вид которой зависит от свойств, входящих в (13). При этом неизвестно, какая из возможных систем имеет решение. Кроме того, для реализации какого-либо из численных методов требуется знание начального приближения. В общем случае ввиду перечисленных сложностей конкретных результатов на пути решения нелинейных систем достигнуто не было. Однако аналитическое решение задачи минимизации $\Phi \left( {\delta ,\,\varepsilon } \right)$ удается найти в асимптотическом случае при $\delta \to 1 - 0,$ если параметры $\delta $ и $\varepsilon $ связаны уравнением $\varepsilon = {{\delta }^{m}},$ $m > 2$ (далее предельный переход при $\delta \to 1 - 0$ вдоль кривых $\varepsilon = {{\delta }^{m}},$ $m > 2$ – единичный предел – Е-предел).

При анализе результатов численного решения уравнения (7) установлено, что его корни ${{x}_{c}}$ в Е-пределе неограниченно возрастают, однако произведения ${{x}_{c}}D$ и ${{x}_{c}}d,$ входящие во все вспомогательные функции $J\left( x \right),$ ${{J}_{1}}\left( x \right)$ и др. (см. экспликации к формулам (4), (5)), принимают конечные значения, зависящие только от m. Поэтому в Е-пределе вместо корня ${{x}_{c}}$ естественно использовать одну из двух величин ${{c}_{1}}\left( m \right) = {{x}_{c}}D$ или ${{c}_{2}}\left( m \right) = {{x}_{c}}d,$ связанных предельным соотношением $\mathop {\lim }\limits_{\delta \to 1 - 0} \frac{{{{c}_{2}}(m)}}{{{{c}_{1}}(m)}} = \mathop {\lim }\limits_{\delta \to 1 - 0} \frac{d}{D} = \frac{m}{{m - 2}} = {{L}_{m}},$ с помощью которого уравнение (7) преобразуется к уравнению относительно ${{c}_{1}}\left( m \right)$

Здесь функции $J_{1}^{{(E)}}\left( {{{c}_{1}}} \right),$ $J_{2}^{{(E)}}\left( {{{c}_{1}}} \right),$ ${{q}^{{(E)}}}\left( {{{c}_{1}}} \right)$ получены из соответствующих функций ${{J}_{1}}\left( x \right),$ ${{J}_{2}}\left( x \right),$ $q(x)$ заменой ${{x}_{c}}D$ на ${{c}_{1}}$ и ${{x}_{c}}d$ на ${{c}_{2}} = {{c}_{1}}{{L}_{m}},$ индекс $E$ обозначает, что функция получена в Е-пределе.

Трудности, возникающие при поиске точного аналитического решения уравнения (14), оказались непреодолимыми, однако по результатам численных расчетов возможно построение аппроксимант для ${{c}_{1}}\left( m \right)$ (или ${{c}_{2}}\left( m \right)$) различной точности. Так, при $2 < m < 15$ относительная погрешность формулы

(${{a}_{0}} = 1.3326,$ ${{a}_{1}} = 0.2392,$ ${{a}_{2}} = 2.5698,$ ${{a}_{3}} = - 6.0376$) не превышает 0.13%.

Для расчетов свойств в Е-пределе подобным изменениям с учетом равенства

получаемого из (6), должны быть подвергнуты и термодинамические функции. К примеру, критическая сжимаемость в переменных $m$ и ${{c}_{1}}\left( m \right)$ имеет вид Таким образом, термодинамические функции, и, следовательно, функция-индикатор (13) в Е-пределе $\Phi \left( m \right)$ утрачивают зависимость от $\delta $ и $\varepsilon $ и содержат только один параметр m. Кроме того, заметим, что переход к Е-пределу отражается и на исходном потенциале (1), преобразование которого к линейной комбинации потенциала Юкавы и экспоненциального потенциала показано в Приложении.

Выбор “управляющего” параметра $m$ связан с требованием наилучшего согласия свойств модельной системы с данными измерений, а температура Бойля T_B, как показали расчеты, весьма чувствительна к изменениям m. Поэтому при установлении оптимального значения $m$ в сумме (13) целесообразно учесть слагаемое, соответствующее температуре Бойля.

Извлекая из разложения УС (8) по степеням обратного объема множитель при 1/V ², получим второй вириальный коэффициент

и следующее из уравнения $B\left( T \right) = 0$ выражение для температуры Бойля которое в Е-пределе принимает вид

СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА С ЭКСПЕРИМЕНТОМ

Значение управляющего параметра $m = 4.2186,$ минимизирующее функцию-индикатор $\Phi \left( m \right),$ установлено с учетом следующих экспериментальных величин для аргона: ${{Z}_{c}} = 0.292,$ ${{{{T}_{B}}} \mathord{\left/ {\vphantom {{{{T}_{B}}} {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}} = 2.740$ [14], ${{\left( {{{\partial \Pi } \mathord{\left/ {\vphantom {{\partial \Pi } {\partial \tau }}} \right. \kern-0em} {\partial \tau }}} \right)}_{c}} = 6.0$ [15]. Расчет зависимостей термодинамических свойств от температуры $\tau = {T \mathord{\left/ {\vphantom {T {{{T}_{c}}}}} \right. \kern-0em} {{{T}_{c}}}}$ выполняется при постоянном давлении $\Pi = {P \mathord{\left/ {\vphantom {P {{{P}_{c}}}}} \right. \kern-0em} {{{P}_{c}}}}$ с привлечением значений плотности $\omega = {n \mathord{\left/ {\vphantom {n {{{n}_{c}}}}} \right. \kern-0em} {{{n}_{c}}}},$ вычисляемых с помощью УС (8).

Представленные на рис. 2 результаты расчета ${{C}_{P}}\left( T \right)$ при P = 10 МПа показывают, что теоретические кривые 1, 3, в отличие от экспериментальной кривой 4, имеют минимумы при низких температурах. Немонотонное поведение теоретической зависимости 1 связано с тем, что УС (8) и выражение (10) содержат члены, пропорциональные ${{\left( {{{\omega \left( \tau \right)} \mathord{\left/ {\vphantom {{\omega \left( \tau \right)} \tau }} \right. \kern-0em} \tau }} \right)}^{S}},$ влияние которых оказывается доминирующим при уменьшении температуры.

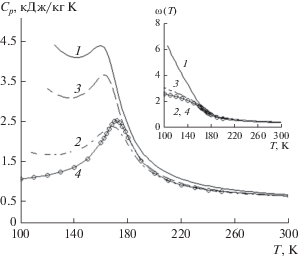
Расчеты плотности $\omega \left( \tau \right)$ по уравнениям (8), Редлиха–Квонга и Бертло, показанные на фрагменте рис. 2, качественно согласуются с данными измерений. Однако зависимость $\omega \left( T \right),$ полученная по УС (8), отличается значительно более резким возрастанием при понижении температуры T, следствием чего является неверное поведение изобарной теплоемкости. Слабо выраженный минимум существует и на кривой 2. Интересно отметить, что подобная картина поведения ${{C}_{P}}\left( T \right)$ наблюдается в ксеноне при P ≥ 10 МПа [16].

Из рис. 3 видно, что все теоретические кривые 1–3 качественно согласуются с данными эксперимента [17]. При низких температурах результаты расчетов коэффициента Джоуля–Томсона ${{\alpha }_{P}}\left( T \right)$ хорошо описывают реальную ситуацию. Это обусловлено тем, что влияние упомянутых выше членов вида ${{\left( {{{\omega \left( \tau \right)} \mathord{\left/ {\vphantom {{\omega \left( \tau \right)} \tau }} \right. \kern-0em} \tau }} \right)}^{S}},$ отвечающих за аномальное поведение изобарной теплоемкости и входящих в (11), компенсируется вкладом ${{C}_{P}}\left( T \right)$ в знаменателе формулы (11). Относительная погрешность значения $\alpha _{P}^{{\max }}$ для кривой 1 составляет ~18%.

На рис. 4 показаны данные измерений [14] и результаты расчетов скорости звука в аргоне при постоянном давлении P = 10 МПа. Видно, что отклонения кривой 1, построенной по формуле (12, от экспериментальной 4 возрастают при понижении температуры. Количественные расхождения при качественно верном воспроизведении зависимости ${{u}_{P}}\left( T \right)$ можно объяснить конкуренцией сомножителей ${{C}_{V}}\left( T \right)$ и $\left( {{{\partial \Pi } \mathord{\left/ {\vphantom {{\partial \Pi } {\partial \tau }}} \right. \kern-0em} {\partial \tau }}} \right)_{\varphi }^{2}$ и наличием множителя ${1 \mathord{\left/ {\vphantom {1 {\omega \left( \tau \right)}}} \right. \kern-0em} {\omega \left( \tau \right)}}$ в (12). Относительная погрешность $u_{P}^{{\min }}$ для кривой 1 составляет ~15%.

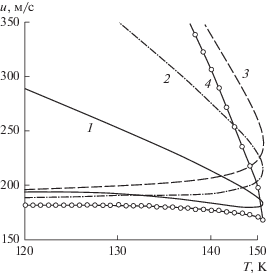
Для расчета свойств модельной системы, в частности скорости звука, на бинодали необходимо определить плотности ${{\omega }_{1}},{{\omega }_{2}}$ сосуществующих фаз, которые являются решениями системы нелинейных уравнений, отвечающих условиям равновесия фаз:

где $\mu \left( {\omega ,\tau } \right) = {{\left( {\frac{{\partial F}}{{\partial N}}} \right)}_{{\omega ,\tau }}}$ = $\frac{\tau }{{{{\beta }_{c}}}}\left[ {\ln \left( {\frac{\omega }{{{{\tau }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{n}_{c}}\lambda _{c}^{3}} \right) + \frac{{{{x}_{c}}\omega }}{\tau }D} \right.$ – ‒ $\left. {\frac{{q_{c}^{2}}}{{\tau {{x}_{c}}{{J}_{1}}\left( {{{x}_{c}}} \right)}}\left( {\frac{3}{2}\left( {1 - \varepsilon \delta } \right) + {{J}_{3}}\left( {\omega ,\tau } \right)} \right)} \right],$ ${{J}_{3}}\left( {\omega ,\tau } \right)$ = = $3\left[ {\delta \left( {q(x){{Q}_{1}}(x) + Q(x){{q}_{1}}(x)} \right) - {{Q}^{2}}(x){{Q}_{1}}(x)} \right],$ x = $ = {{{{x}_{c}}\omega } \mathord{\left/ {\vphantom {{{{x}_{c}}\omega } \tau }} \right. \kern-0em} \tau }.$ При решении системы (16) в Е-пределе необходимо сделать замену ${{x}_{c}}D = {{c}_{1}}\left( m \right)$ и ${{x}_{c}}d = {{c}_{2}}\left( m \right).$ Скорость звука вычисляется по формуле (12) с учетом найденных решений ${{\omega }_{1}},{{\omega }_{2}}$ системы.

Результаты расчета скорости звука на линии равновесия фаз в аргоне приведены на рис. 5 в сопоставлении с данными наблюдений [14]. Видно, что теоретическая кривая 1 для скорости звука в модельной системе демонстрирует не только качественные особенности эксперимента почти всюду в расчетном диапазоне температур, но и неплохое количественное согласие с экспериментом с погрешностью не более 10% для газовой ветви (нижняя часть кривой 1), исключая узкую окрестность КТ, где можно заметить участок, на котором функция $u\left( T \right)$ возрастает. Подобное возрастание, но в более широком температурном интервале, наблюдается для газовых ветвей кривых 2 и 3, построенных по уравнениям Редлиха–Квонга и Бертло, что не соответствует данным измерений.

ЗАКЛЮЧЕНИЕ

Для описания равновесных термодинамических свойств системы, моделирующей простую жидкость с DY-потенциалом, применяется один из распространенных статистических способов учета взаимодействия, основанный на вычислении КИ.

Определение значений четырех параметров потенциала взаимодействия, обеспечивающих воспроизведение данных измерений с минимально возможными для рассматриваемой модели погрешностями, удается свести к нахождению одного управляющего параметра, что позволяет обойти известные трудности, возникающие при решении систем нелинейных уравнений. Оптимальное значение этого параметра установлено с учетом трех экспериментальных величин ${{Z}_{c}},$ ${{T}_{{\text{B}}}},$ ${{\left( {{{\partial \Pi } \mathord{\left/ {\vphantom {{\partial \Pi } {\partial \tau }}} \right. \kern-0em} {\partial \tau }}} \right)}_{c}}$ и использовано для расчета зависимостей ${{C}_{P}}\left( T \right),$ ${{\alpha }_{P}}\left( T \right),$ ${{u}_{P}}\left( T \right).$

Как видно из приведенных результатов, в надкритической области наилучшее согласие с экспериментом имеет зависимость ${{\alpha }_{P}}\left( T \right),$ для скорости звука ${{u}_{P}}\left( T \right)$ расхождение с экспериментом увеличивается с уменьшением температуры и ростом плотности, поведение ${{C}_{P}}\left( T \right)$ при низких температурах не соответствует экспериментальной картине.

Теоретическая зависимость скорости звука $u\left( T \right)$ на газовой ветви бинодали воспроизводит данные измерений с погрешностью не более 10%, однако расхождения возрастают на ветви жидкой фазы при понижении температуры.

Сопоставление полученных результатов с экспериментом и более точными решениями [6, 10] позволяет установить область, в которой приближение (2) в сочетании с DY-потенциалом становится неприменимым. Расчеты модели в рамках рассмотренного формализма не дают адекватного описания жидкого состояния, что, по-видимому, является следствием влияния многочастичных сил, которые проявляются и в области высоких давлений. Кроме того, можно ожидать, что модель окажется непригодной в области чрезвычайно высоких температур, где происходит ионизация нейтральных частиц. Поэтому, возможно, для корректировки результатов с целью улучшения их согласия с экспериментом необходимо рассмотрение более сложной модели потенциала, учитывающей зависимости его параметров от плотности и температуры.

Автор выражает искреннюю благодарность проф. А.Ю. Захарову за полезные дискуссии и обсуждение результатов.