Теплофизика высоких температур, 2020, T. 58, № 1, стр. 113-122
Идентификация излучательной способности и теплового сопротивления экранно-вакуумной тепловой изоляции в математической модели теплообмена с сосредоточенными параметрами
А. Г. Викулов 1, *, А. В. Ненарокомов 1
1 Московский авиационный институт
(национальный исследовательский университет)
Москва, Россия
* E-mail: viarticle@yandex.ru
Поступила в редакцию 10.07.2019
После доработки 30.09.2019
Принята к публикации 22.10.2019
Аннотация
Решена задача идентификации комплекса разнородных теплофизических свойств, входящих в систему обыкновенных дифференциальных уравнений математической модели с сосредоточенными параметрами. Для регуляризации неустойчивого решения обратной задачи теплообмена использован разработанный ранее итерационно-вариационный метод. Полученные результаты подтверждают работоспособность этого метода регуляризации и позволяют исследовать температурные зависимости излучательной способности и термического сопротивления экранно-вакуумной тепловой изоляции.
ВВЕДЕНИЕ
Обыкновенными дифференциальными уравнениями или их системами (модели с сосредоточенными параметрами) можно описать не только задачи теплообмена, но и многие другие: задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, сопротивления материалов. Ряд задач для уравнений в частных производных также сводится к задачам для обыкновенных дифференциальных уравнений. Например, это возможно, если многомерная задача допускает разделение переменных (задачи на нахождение собственных колебаний упругих балок и мембран простейшей формы или определение собственных значений энергии частицы в сферически симметричном поле) или ее решение зависит от некоторой комбинации переменных (автомодельные решения) [1].
Конкретная прикладная задача может приводить к дифференциальному уравнению любого порядка или к системе уравнений любого порядка. Однако известно, что обыкновенное дифференциальное уравнение N-го порядка [1]
Для определения вектора z достаточно начального условия (задача Коши)
Такими математическими моделями с сосредоточенными параметрами (МСП), основанными на обыкновенных дифференциальных уравнениях, и описываются теплофизические системы [2]:
(1)
$\frac{{d{{T}_{i}}}}{{d\tau }} = {{f}_{i}}\left( {{{T}_{1}},{{T}_{2}},...,{{T}_{N}}} \right),\,\,\,\,i = 1,2, \ldots ,N.$В [3] построен аналитический метод решения дифференциального уравнения теплового баланса применительно к математическим моделям с сосредоточенными параметрами (1) при наличии теплового излучения. Используя конечно-разностную аппроксимацию по времени, имеем
(2)
$\begin{gathered} \frac{{{{T}_{{i,j + 1}}} - {{T}_{{i,j}}}}}{{{{\tau }_{{j + 1}}} - {{\tau }_{j}}}} = {{f}_{i}}\left( {{{T}_{{1,j}}},{{T}_{{2,j}}},...,{{T}_{{N,j}}}} \right), \\ ~i = 1,2, \ldots ,N;\,\,\,\,j = 0,1,2, \ldots ,M. \\ \end{gathered} $Выражая из (2) Ti, j+ 1, получаем квазилинейную нестационарную дискретную динамическую систему следующего вида:
Рассмотрен детерминированный подход к параметрической идентификации такой системы, определены условия разрешимости поставленной задачи, сформулирован критерий существования решения, и построен алгоритм его поиска, возможности которого продемонстрированы на численных примерах [4, 5].
При достаточно подробном разбиении на элементы с однородной температурой точность МСП сопоставима с точностью, обеспечиваемой методом конечных разностей, как в стационарном, так и в переходном процессе. Тем не менее по мере увеличения количества узлов МСП усложняются задачи решения системы обыкновенных дифференциальных уравнений и идентификации тепловых связей между узлами [6].
МСП могут применяться в рамках двухмодельного метода для решения обратной задачи при условии, что оператор перехода от модели с распределенными параметрами к ее конечномерной аппроксимации в виде МСП является сжимающим [7, 8].
В [9] исследовано влияние внутреннего тепловыделения и числа Био на точность и применимость моделей с сосредоточенными параметрами в нестационарных одномерных задачах теплообмена. Для получения средней температуры и плотности теплового потока в пространственном направлении применены классическая МСП на основе объемной теплоемкости и усовершенствованная модель на основе эрмитовой и полиномиальной аппроксимации. Введены количественные критерии оценки применимости моделей с сосредоточенными параметрами.
В [10] технологическая система сложного вида рассмотрена как “черный ящик” со входом и выходом. Описан тепломассоперенос в этой системе при помощи обыкновенных дифференциальных уравнений с постоянными коэффициентами определенного порядка. Предложена методика использования “неустойчивых” уравнений для описания практических задач. Под неустойчивостью понимается тот факт, что полученный дифференциальный оператор имеет характеристические числа с положительной вещественной частью. Определены коэффициенты уравнения на основе анализа кривой отклика системы на возмущение в виде “ступеньки”. Рассмотрен конкретный пример реализации данного алгоритма.
Предложен экспериментально-аналитический метод, дающий возможность сформировать на базе результатов тепловакуумных испытаний космического устройства его математическую узловую модель, позволяющую распространить полученные результаты на тепловые режимы, невоспроизводимые при испытаниях. Метод основан на решении обратной задачи по восстановлению тепловых параметров узловой модели из известных значений температур, тепловыделений и внешних тепловых потоков. Представлены данные экспериментальной проверки метода, подтверждающие его практическую применимость и показывающие некоторые особенности использования [11].
Метод итерационной регуляризации адаптирован для математических моделей теплообмена с сосредоточенными параметрами: построены аналитические выражения для расчета неопределенных множителей Лагранжа при определении градиента функционала невязки температуры и расчета шага спуска, работоспособность которых подтверждена численными экспериментами. Полученные результаты обобщены для технических систем космических аппаратов [12, 13].
Анализ вариационного метода регуляризации [14] и метода итерационной регуляризации [15–17] позволил разработать модифицированный вариационный метод итерационной регуляризации (итерационно-вариационный метод) решения задач идентификации математических моделей с сосредоточенными параметрами на основе минимизации сглаживающего функционала и функционала температурной невязки [18, 19]. Полученные результаты применены для идентификации математических моделей составных частей космического аппарата (КА), в частности теплового сопротивления и излучательной способности экранно-вакуумной тепловой изоляции (ЭВТИ) [19, 20].
В [19] тепловое сопротивление ЭВТИ определялось прямым алгебраическим методом решения обратной задачи, который позволил найти корректное решение только для отдельных экспериментальных режимов. В [19, 20] излучательная способность ЭВТИ определялась из решения задачи идентификации, получаемого с использованием модифицированного итерационно-вариационного метода регуляризации и искусственной фильтрации [21], заключающейся во введении в вектор измерений дополнительных параметров модели. В частности, искусственная фильтрация позволяет изолировать от системы уравнение с излучательной способностью путем замены некоторых расчетных температур экспериментальными.
В настоящей работе задача идентификации комплекса теплофизических характеристик, включающего излучательную способность ЭВТИ, тепловое сопротивление ЭВТИ и тепловое сопротивление сотовой панели (СП), решена с использованием модифицированного итерационно-вариационного метода регуляризации без искусственной фильтрации.
ЭКВИВАЛЕНТНАЯ ТЕПЛОВАЯ СХЕМА И МАТЕМАТИЧЕСКАЯ МОДЕЛЬ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ СОТОВОЙ ПАНЕЛИ И ЭКРАННО-ВАКУУМНОЙ ТЕПЛОИЗОЛЯЦИИ
Рассмотрим характерный элемент конструкции КА в виде многослойной теплопередающей стенки, состоящей из последовательно расположенных ЭВТИ и СП. СП устанавливается на силовом каркасе и вместе с ним образует несущую конструкцию КА.
Расчет проводимостей ЭВТИ и СП проводится по показаниям двух групп аналоговых датчиков температуры (АДТ) в режимах тепловых вакуумных испытаний (ТВИ), имитирующих предельные условия эксплуатации (рис. 1): “Д1” – внешний нагрев инфракрасными имитаторами (ИКИ); “Д2”, “Д4” – охлаждение криоэкранами с температурой 83 К; “Д3” – внутренний нагрев опытного образца за счет тепловыделений аппаратуры и электронагревателей.
Рис. 1.
Размещение аналоговых датчиков температуры на экранно-вакуумной тепловой изоляции и сотовой панели “БI”: R17, R22 – АДТ снаружи ЭВТИ; R19, R20 – АДТ под ЭВТИ; R18, R21 – АДТ под СП.
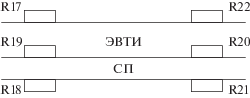
Прямой расчет проводимостей невозможен из-за отсутствия экспериментальных значений плотности теплового потока, проходящего через многослойную стенку, поэтому проводимости ЭВТИ и СП уточняются решением задачи идентификации МСП в удельных величинах, включающих три узла, соответствующих физическим поверхностям: узел 7 – внешняя поверхность ЭВТИ, узел 8 – внешняя поверхность СП, узел 9 – внутренняя поверхность СП (рис. 2).
Рис. 2.
Эквивалентная тепловая схема математической модели с сосредоточенными параметрами экранно-вакуумной тепловой изоляции и сотовой панели “БI”.
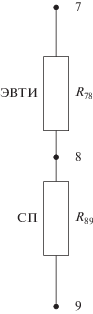
Узел 7 – модельная оболочка ЭВТИ толщиной 2.59 мм (толщина ЭВТИ в сжатом состоянии), имеющая с изолируемой поверхностью тепловой контакт, проводимость которого соответствует проводимости ЭВТИ в поперечном направлении. Плотность модельной оболочки равна
Узлы 8, 9 моделируют две алюминиевые пластины толщиной
Удельная теплоемкость модельных поверхностей СП равна
Удельное сопротивление ЭВТИ имеет начальное значение
Соответствующие удельные проводимости:
Система уравнений математической модели с сосредоточенными параметрами записывается в следующем виде:
(3)
$\left\{ \begin{gathered} {{\rho }_{7}}{{c}_{7}}{{\delta }_{7}}\frac{{d{{T}_{7}}\left( \tau \right)}}{{d\tau }} = \hfill \\ = {{q}_{{s,7}}} + \sigma {{\varepsilon }_{7}}\left( {T_{R}^{4} - {{T}_{7}}{{{\left( \tau \right)}}^{4}}} \right) + {{\alpha }_{{78}}}\left( {{{T}_{8}}\left( \tau \right) - {{T}_{7}}\left( \tau \right)} \right), \hfill \\ {{\rho }_{8}}{{c}_{8}}{{\delta }_{8}}\frac{{d{{T}_{8}}\left( \tau \right)}}{{d\tau }} = \hfill \\ = {{\alpha }_{{78}}}\left( {{{T}_{7}}\left( \tau \right) - {{T}_{8}}\left( \tau \right)} \right) + {{\alpha }_{{89}}}\left( {{{T}_{9}}\left( \tau \right) - {{T}_{8}}\left( \tau \right)} \right), \hfill \\ {{\rho }_{9}}{{c}_{9}}{{\delta }_{9}}\frac{{d{{T}_{9}}\left( \tau \right)}}{{d\tau }} = {{\alpha }_{{89}}}\left( {{{T}_{8}}\left( \tau \right) - {{T}_{9}}\left( \tau \right)} \right) + {{q}_{9}}\left( \tau \right) \hfill \\ \end{gathered} \right\},$ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ТЕПЛООБМЕНА МОДИФИЦИРОВАННЫМ ИТЕРАЦИОННО-ВАРИАЦИОННЫМ МЕТОДОМ
Будем искать излучательную способность ЭВТИ ε7 = ε7(τ) и удельные тепловые проводимости ЭВТИ α78 = α78(τ) и СП α89 = α89(τ) как функции времени на временнóй сетке τj (j = 0, 1, 2, …, M + 1): εj = = ε7(τj), α78j = α78(τj), α89j = α89(τj). Тогда система уравнений (3) запишется следующим образом:
(4)
$\left\{ \begin{gathered} {{\rho }_{7}}{{c}_{7}}{{\delta }_{7}}\frac{{d{{T}_{{7j}}}}}{{d\tau }} = \hfill \\ = {{\varepsilon }_{{7j}}}{{q}_{{7j}}} + \sigma {{\varepsilon }_{{7j}}}\left( {T_{R}^{4} - T_{{7j}}^{4}} \right) + {{\alpha }_{{78j}}}\left( {{{T}_{{8j}}} - {{T}_{{7j}}}} \right), \hfill \\ {{\rho }_{8}}{{c}_{8}}{{\delta }_{8}}\frac{{d{{T}_{{8j}}}}}{{d\tau }} = {{\alpha }_{{78j}}}\left( {{{T}_{{7j}}} - {{T}_{{8j}}}} \right) + {{\alpha }_{{89j}}}\left( {{{T}_{{9j}}} - {{T}_{{8j}}}} \right), \hfill \\ {{\rho }_{9}}{{c}_{9}}{{\delta }_{9}}\frac{{d{{T}_{{9j}}}}}{{d\tau }} = {{\alpha }_{{89j}}}\left( {{{T}_{{8j}}} - {{T}_{{9j}}}} \right) + {{q}_{{9j}}} \hfill \\ \end{gathered} \right\}$(5)
${{T}_{i}}\left( {{{\tau }_{0}}} \right) = {{T}_{{i0}}}\,\,\,\,\left( {i = 7,\,\,8,\,\,9} \right)$(6)
$\begin{gathered} \left\{ \begin{gathered} {{T}_{i}}\left( {{{\tau }_{j}} - 0} \right) = {{T}_{i}}\left( {{{\tau }_{j}} + 0} \right) \hfill \\ {{\tau }_{0}} = {{\tau }_{{\min }}},\,\,{{\tau }_{{M + 1}}} = {{\tau }_{{\max }}} \hfill \\ \end{gathered} \right\} \\ (i = {\text{7}},\,\,{\text{8}},\,\,{\text{9;}}\,\,\,\,j = {\text{1}},{\text{2}}, \ldots ,M). \\ \end{gathered} $Для построения итерационного процесса методом Ньютона преобразуем систему уравнений к следующему виду:
Производные функций равны
Тогда выражения метода Ньютона и соответствующие им приращения искомых функций запишутся как
Для регуляризации решения используется дополнительная информация в виде экспериментальных температур
Регуляризированное решение выражается через решение на текущей итерации l, его приращение относительно итерации (l – 1) и безразмерный шаг спуска βij (i = 7, 8, 9; j = 1, 2, …, M):
Шаг спуска определяется из решения следующей задачи для вариаций искомых функций.
Пусть искомые параметры получили вариации
Тогда температуры Tij изменятся на некоторую величину υij(τ) (i = 1, …, N; j = 1, …, M), а вариация температуры υij(τ) удовлетворяет краевой задаче:
(7)
$\left\{ \begin{gathered} {{\rho }_{7}}{{c}_{7}}{{\delta }_{7}}\frac{{d{{\upsilon }_{{7j}}}}}{{d\tau }} = \delta {{\varepsilon }_{{7j}}}{{q}_{{7j}}} + \sigma \delta {{\varepsilon }_{{7j}}}\left( {T_{R}^{4} - T_{{7j}}^{4}} \right) - \hfill \\ - \,\,4\sigma {{\varepsilon }_{{7j}}}T_{{7j}}^{3}{{\upsilon }_{{7j}}} - {{\alpha }_{{78j}}}{{\upsilon }_{{7j}}}, \hfill \\ {{\rho }_{8}}{{c}_{8}}{{\delta }_{8}}\frac{{d{{\upsilon }_{{8j}}}}}{{d\tau }} = \delta {{\alpha }_{{78j}}}\left( {{{T}_{{7j}}} - {{T}_{{8j}}}} \right) - \left( {{{\alpha }_{{78j}}} + {{\alpha }_{{89j}}}} \right){{\upsilon }_{{8j}}}, \hfill \\ {{\rho }_{9}}{{c}_{9}}{{\delta }_{9}}\frac{{d{{\upsilon }_{{9j}}}}}{{d\tau }} = \delta {{\alpha }_{{89j}}}\left( {{{T}_{{8j}}} - {{T}_{{9j}}}} \right) - {{\alpha }_{{89j}}}{{\upsilon }_{{9j}}} \hfill \\ \end{gathered} \right\}$Функционал температурной невязки на итерации l запишется как
(8)
$\begin{gathered} \left\{ \begin{gathered} J\left( {{{\varepsilon }_{{7j}}}} \right) = \sum\limits_{j = 1}^M {{{{\left( {{{T}_{{7j}}} - T_{{7j}}^{{\left( 0 \right)}}} \right)}}^{2}}} , \hfill \\ J\left( {{{\alpha }_{{78j}}}} \right) = \sum\limits_{j = 1}^M {{{{\left( {{{T}_{{8j}}} - T_{{8j}}^{{\left( 0 \right)}}} \right)}}^{2}}} , \hfill \\ J\left( {{{\alpha }_{{89j}}}} \right) = \sum\limits_{j = 1}^M {{{{\left( {{{T}_{{9j}}} - T_{{9j}}^{{\left( 0 \right)}}} \right)}}^{2}}} \hfill \\ \end{gathered} \right\} \Rightarrow \\ \Rightarrow J = \sum\limits_{i = 7}^9 {\sum\limits_{j = 1}^M {{{{\left( {{{T}_{{ij}}} - T_{{ij}}^{{\left( 0 \right)}}} \right)}}^{2}}} } . \\ \end{gathered} $Следовательно, приращения компонент функционала равны
(9)
${{\upsilon }_{{ij}}} = T_{{ij}}^{{\left( 0 \right)}} - {{T}_{{ij}}}\,\,\,\,(i = {\text{7}},\,\,{\text{8}},\,\,{\text{9}};\,\,\,\,j = {\text{1}},{\text{2}}, \ldots ,M).$Подставляя вариации температуры из (9) в (7), получаем уравнение для определения βij (i = 7, 8, 9; j = 1, 2, …, M):
(10)
$\left\{ \begin{gathered} - {{\rho }_{7}}{{c}_{7}}{{\delta }_{7}}\frac{{d{{T}_{{7j}}}}}{{d\tau }} = - \beta _{{7j}}^{\varepsilon }\Delta {{\varepsilon }_{{7j}}}{{q}_{{7j}}} - \hfill \\ - \,\,\sigma \beta _{{7j}}^{\varepsilon }\Delta {{\varepsilon }_{{7j}}}\left( {T_{R}^{4} - T_{{7j}}^{4}} \right) - \hfill \\ - \,\,4\sigma {{\varepsilon }_{{7j}}}T_{{7j}}^{3}\left( {T_{{7j}}^{{\left( 0 \right)}} - {{T}_{{7j}}}} \right) - {{\alpha }_{{78j}}}\left( {T_{{7j}}^{{\left( 0 \right)}} - {{T}_{{7j}}}} \right), \hfill \\ - {{\rho }_{8}}{{c}_{8}}{{\delta }_{8}}\frac{{d{{T}_{{8j}}}}}{{d\tau }} = - \beta _{{8j}}^{\alpha }\Delta {{\alpha }_{{78j}}}\left( {{{T}_{{7j}}} - {{T}_{{8j}}}} \right) - \hfill \\ - \,\,\left( {{{\alpha }_{{78j}}} + {{\alpha }_{{89j}}}} \right)\left( {T_{{8j}}^{{\left( 0 \right)}} - {{T}_{{8j}}}} \right), \hfill \\ - {{\rho }_{9}}{{c}_{9}}{{\delta }_{9}}\frac{{d{{T}_{{9j}}}}}{{d\tau }} = - \beta _{{9j}}^{\alpha }\Delta {{\alpha }_{{89j}}}\left( {{{T}_{{8j}}} - {{T}_{{9j}}}} \right) - \hfill \\ - \,\,{{\alpha }_{{89j}}}\left( {T_{{9j}}^{{\left( 0 \right)}} - {{T}_{{9j}}}} \right), \hfill \\ \end{gathered} \right\}$Так как в знаменателе выражений шага спуска находятся приращения искомых функций на текущей итерации, они сокращаются в выражениях вариаций, и вариации этих функций могут быть найдены непосредственно без дополнительного итерационного процесса.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ И РЕЗУЛЬТАТЫ ИДЕНТИФИКАЦИИ
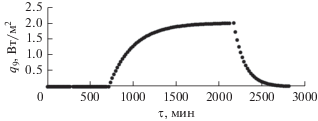
Экспериментальные температуры узлов математической модели показаны на рис. 3, плотность потока излучения от инфракрасных имитаторов – на рис. 4, а плотность теплового потока, имитирующего внутреннюю тепловую мощность в узле 9, – на рис. 5.
Рис. 3.
Распределение экспериментальных температур в зависимости от времени: 0–290 мин – режим “Д1”, 300–700 – “Д2”, 710–2150 – “Д3”, 2160–2830 – “Д4”.
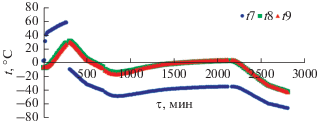
Рис. 4.
Распределение плотности теплового потока от инфракрасных имитаторов в зависимости от времени: описание режимов – как на рис. 3.
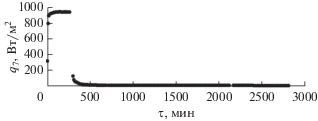
Рис. 5.
Распределение плотности теплового потока, имитирующего внутреннее тепловыделение на СП, в зависимости от времени: описание режимов – как на рис. 3.
Дисперсия экспериментальной температуры $T_{i}^{{(0)}}$ равна
Следовательно, дисперсия температуры одинакова для всех трех узлов математической модели, но изменяется в зависимости от количества M = (M1, M2, M3, M4) = (25, 37, 69, 31) точек временнóй сетки в различных режимах: Di = (Di1, Di2, Di3, Di4) = (0.167, 0.111, 0.059, 0.133) К2 (i = 7, 8, 9; второй индекс определяет номер режима). Среднеквадратичная ошибка температурных измерений для всей системы равна
т.е. в зависимости от экспериментального режима δi = (δi1, δi2, δi3, δi4) = (0.501, 0.333, 0.177, 0.399) К2.Для проверки устойчивости решения на распределения экспериментальных температур накладывается нормальное возмущение со средним квадратичным отклонением 0.4 К, соответствующим дисперсии температуры 0.16 К2. Устойчивость решений проверяется сопоставлением функций, определенных по возмущенному температурному полю, с функциями, идентифицированными по исходным распределениям экспериментальных температур.
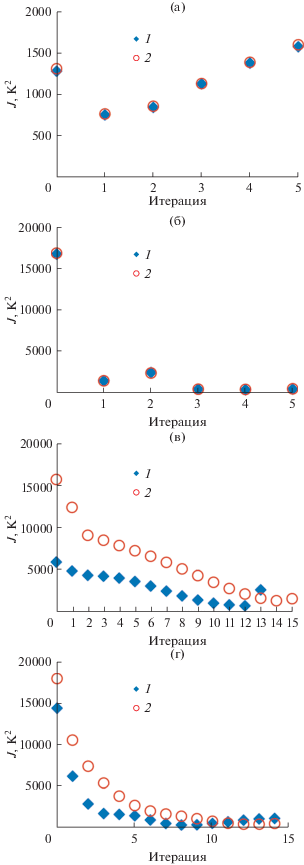
Распределение значений температурного функционала (8) в зависимости от номера итерации показано на рис. 6. Наименьшие значения функционала, соответствующие наилучшему решению, достигаются (в скобках для возмущенного решения): в режиме “Д1” – 763.2 К2, на первой итерации (775.3 К2, на первой итерации); в режиме “Д2” – 376.8 К2, на четвертой итерации (418.1 К2, на четвертой итерации); в режиме “Д3” наименьшее значение функционала, равное 676.0 К2, достигается на двенадцатой итерации, но после девятой итерации со значением функционала 1362 К2 гладкость решения ухудшается, поэтому решение считается оптимальным на девятой итерации (4282 К2, на девятой итерации); в режиме “Д4” – 374.0, на восьмой итерации (454.0 К2, на тринадцатой итерации).
Рис. 6.
Распределение суммарного функционала невязки температуры в зависимости от номера итерации: 1 – по экспериментальным температурам, 2 – по возмущенным температурам; (а) – режим “Д1”, (б) – “Д2”, (в) – “Д3”, (г) – “Д4”.
Начальные приближения задавались следующие (в скобках для возмущенного решения): в режимах “Д1”, “Д2” – $\varepsilon _{7}^{{\left( 0 \right)}}$ = 0.01, $\alpha _{{78}}^{{\left( 0 \right)}}$ = 0.1 Вт/(м2 К), $\alpha _{{89}}^{{\left( 0 \right)}}$ = 1.0 Вт/(м2 К) (те же); в режиме “Д3” – $\varepsilon _{7}^{{\left( 0 \right)}}$ = = 0.008815 (0.009587), $\alpha _{{78}}^{{\left( 0 \right)}}$ = 0.03866 (0.04246) Вт/(м2 К), $\alpha _{{89}}^{{\left( 0 \right)}}$ = 0.1452 (0.07836) Вт/(м2 К); в режиме “Д4” – $\varepsilon _{7}^{{\left( 0 \right)}}$ = 0.01268 (0.01187), $\alpha _{{78}}^{{\left( 0 \right)}}$ = 0.05503 (0.04915) Вт/(м2 К), $\alpha _{{89}}^{{\left( 0 \right)}}$ = 0.3948 (0.2002) Вт/(м2 К). В режимах “Д1”, “Д2” начальные приближения определены по предварительной теоретической оценке, в режимах “Д3”, “Д4” – по последней временнóй точке предыдущего участка для обеспечения лучшей гладкости решения на границе режимов.
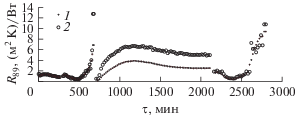
Идентифицированные функции представлены на следующих рисунках: излучательная способность ЭВТИ ε7 – на рис. 7, удельное тепловое сопротивление ЭВТИ R78 – на рис. 8, удельное тепловое сопротивление СП R89 – на рис. 9.
Рис. 7.
Распределение идентифицированной излучательной способности ЭВТИ в зависимости от времени: 1 – по экспериментальным температурам, 2 – по возмущенным температурам; описание режимов – как на рис. 3.
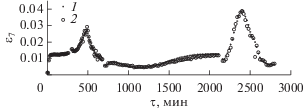
Рис. 8.
Распределение идентифицированного теплового сопротивления ЭВТИ в зависимости от времени: обозначения – см. на рис. 7.
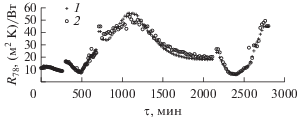
Рис. 9.
Распределение идентифицированного теплового сопротивления СП в зависимости от времени: обозначения – см. на рис. 7.
Излучательная способность ЭВТИ имеет глобальный минимум 0.00446 (0.00458) в режиме “Д3” и глобальный максимум 0.0389 (0.03883) в режиме “Д4”, на два–три порядка отличаясь от излучательной способности наружного слоя (0.63) и являясь некоторой суперпозицией свойств внутренних слоев. Значение ε7(τ) зависит не только от температуры T7 наружного слоя, но и от температуры T8 внутреннего слоя, а также от разности этих температур и теплового сопротивления R78, т.е. от величины и направления плотности теплового потока. В результате, характер излучательной способности ЭВТИ сложен и нелинеен.
Тепловое сопротивление ЭВТИ R78 имеет глобальный минимум 6.2 (6.2) м2 К/Вт в режиме “Д4” и глобальный максимум 55.6 (54.3) м2 К/Вт в режиме “Д3”. Глобальные и локальные максимумы теплового сопротивления ЭВТИ соответствуют глобальным и локальным минимумам излучательной способности ЭВТИ и наоборот.
Тепловое сопротивление СП R89 имеет глобальный минимум 0.411 (0.397) м2 К/Вт в режиме “Д2” и глобальный максимум 9.4 м2 К/Вт в режиме “Д4” (12.8 м2 К/Вт в режиме “Д2”). Качественно поведение теплового сопротивления СП совпадает с характером временнóй зависимости термического сопротивления ЭВТИ, имея при этом точку разрыва на границе режимов “Д2”, “Д3”. По всей видимости, наличие точки разрыва объясняется изменением величины и направления теплового потока через сотовую панель в результате включения внутренних источников тепла. Причем если теоретическое значение плотности теплового потока от внутренних источников изменяется по экспоненте (рис. 5), то экспериментальная тепловая мощность практически сразу же достигает номинального уровня.
Экстремумы идентифицированных функций излучательной способности ЭВТИ, тепловых сопротивлений ЭВТИ и сотовой панели находятся в окрестностях одних и тех же моментов времени. Анализ их временны́х распределений с учетом границ экспериментальных режимов показывает, что экстремумы функций следуют за сменой режима, смещаясь при этом во времени из-за тепловой инерции ЭВТИ и СП.
Гладкость решений оценивается по условию обеспечения его устойчивости. Устойчивость проверяется решением той же самой обратной задачи по распределениям экспериментальных температур с дополнительным малым возмущением, дисперсия 1.6 К2 которого соответствует максимальной из измеренных.
Под гладкостью понимается уровень рассеяния идентифицированных функций, который также можно оценивать количественно средним квадратичным отклонением (дисперсией) или визуально (качественно). Зачастую достаточно визуальной оценки решений, последовательно появляющихся на одном и том же графике. Но можно использовать и количественную оценку, особенно при разработке универсальных программ.
Итерационный процесс продолжается до достижения минимального значения температурного функционала. Чаще всего ему соответствует наиболее гладкое решение. Тем не менее возможна ситуация, когда минимуму функционала соотносится решение с неприемлемой дисперсией, как, например, в режиме “Д3”. Тогда необходимо найти итерацию с минимальной дисперсией решения, после которой она возрастает, и определить наилучшее соотношение между гладкостью решения (значением дисперсии) и значением температурного функционала.
В итерационной регуляризации не всегда удается достичь значения функционала, сопоставимого по точности с исходными данными. Итерационный процесс останавливается по условиям достижения минимума функционала или замедления его сходимости к минимуму. В редких случаях (функционал считается квазимонотонным) возможно получение нескольких локальных минимумов и сравнение их между собой.
ЗАКЛЮЧЕНИЕ
1. Применение итерационно-вариационного метода регуляризации позволяет получить условно устойчивое решение задачи идентификации вектора неизвестных характеристик математической модели теплообмена с сосредоточенными параметрами. Число компонент вектора равно количеству узлов МСП или, что то же самое, количеству строк в связанной с ней системе обыкновенных дифференциальных уравнений.
2. Найдено регуляризованное решение задачи идентификации математической модели с сосредоточенными параметрами, описывающей конструктивный элемент космического аппарата в виде последовательно расположенных экранно-вакуумной тепловой изоляции и сотовой панели и состоящей из трех уравнений, относительно вектора характеристик, включающего временны́е функции излучательной способности ЭВТИ, и тепловых сопротивлений ЭВТИ и СП.
3. Излучательная способность ЭВТИ изменяется от 0.00446 до 0.03889, увеличивается при нагреве внешнего или внутреннего слоев. Локальные и глобальные экстремумы распределения излучательной способности ЭВТИ во времени соответствуют локальным и глобальным экстремумам противоположного характера теплового сопротивления ЭВТИ – минимумы соответствуют максимумам и наоборот.
4. Термическое сопротивление ЭВТИ изменяется от 6.2 до 55.6 м2 К/Вт и зависит от величины и направления теплового потока.
5. Термическое сопротивление сотовой панели изменяется от 0.41 до 9.4 м2 К/Вт и имеет точку разрыва на границе режимов охлаждения криоэкранами внешней поверхности ЭВТИ и нагрева внутренней поверхности сотовой панели.
6. Наложение на распределения экспериментальных температур дополнительного малого возмущения, примерно равного экспериментальному, не нарушает характер идентифицированных функций. Глобальные экстремумы функций сохраняются приблизительно в том же временнóм диапазоне, за исключением сопротивления сотовой панели, глобальный максимум которого переходит из режима охлаждения “Д4” в аналогичный режим “Д2”.
Работа выполнена в рамках госзадания № 9.9074.2017/БЧ Минобрнауки России.
Список литературы
Калиткин Н.Н. Численные методы. Учеб. пособ. 2-e изд., испр. СПб.: БХВ–Петербург, 2011. 592 с.
Викулов А.Г., Ненарокомов А.В. Идентификация тепловых связей в математических моделях космических систем // Тепловые процессы в технике. 2014. № 6. С. 274.
Кузнецов В.Е. Упрощение решения дифференциального уравнения теплового баланса путем преобразования его в алгебраическое уравнение применительно к математическим моделям с сосредоточенными параметрами // Тепловые процессы в технике. 2017. № 1. С. 13.
Зубов Н.Е., Микрин Е.А., Рябченко В.Н. Об одном подходе к идентификации дискретной системы на основе матричных делителей нуля // Вестн. Моск. гос. техн. ун-та им. Н.Э. Баумана. Сер. Приборостроение. 2017. № 3. С. 20.
Микрин Е.А., Зубов Н.Е., Рябченко В.Н., Ефанов Д.Е., Поклад М.Н. Идентификация дискретной системы на основе матричных делителей нуля // Автоматизация. Современные технологии. 2017. Т. 71. № 6. С. 269.
Балаковский С.Л. Идентификация параметров эквивалентных тепловых схем электродвигателей в нестационарном режиме // ИФЖ. 1989. Т. 56. № 4. С. 657.
Балаковский С.Л., Дилигенский Н.В. О двухмодельном итерационном методе решения граничной обратной задачи теплообмена // ИФЖ. 1989. Т. 56. № 2. С. 313.
Балаковский С.Л. Решение обратных задач теплообмена двухмодельным методом // ИФЖ. 1989. Т. 57. № 3. С. 500.
Behrooz Abbasi Souraki, Assareh N., Omidi M. Effect of Internal Heat Generation on the Applicability of Different Lumped Models with Unsteady One-dimensional Conduction // Heat Transfer Res. 2014. V. 45. № 8. P. 767.
Мошинский А.И., Маркова А.В., Рубцова Л.Н., Сорокин В.В., Ганин П.Г. Использование уравнений идентификации модели типа “черный ящик” в случае неустойчивости // ИФЖ. 2016. Т. 89. № 6. С. 1365.
Семена Н.П., Сербинов Д.В. Математическая интерпретация теплового эксперимента, имитирующего условия космического пространства // Тепловые процессы в технике. 2016. № 9. С. 423.
Викулов А.Г., Ненарокомов А.В. Экстремальный метод идентификации тепловых математических моделей с сосредоточенными параметрами // Тепловые процессы в технике. 2015. № 7. С. 307.
Викулов А.Г., Ненарокомов А.В. Уточненное решение вариационной задачи идентификации математических моделей теплообмена с сосредоточенными параметрами // ТВТ. 2019. Т. 57. № 2. С. 234.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Изд. 2-е. М.: Наука; Физматлит, 1979. 288 с.
Алифанов О.М. Идентификация процессов теплообмена летательных аппаратов. М.: Машиностроение, 1979. 216 с.
Алифанов О.М. Обратные задачи теплообмена. М.: Машиностроение, 1988. 280 с.
Алифанов О.М., Артюхин Е.А., Румянцев С.В. Экстремальные методы решения некорректных задач и их приложения к обратным задачам теплообмена. М.: Физматлит, 1988. 288 с.
Викулов А.Г., Ненарокомов А.В. Вариационный метод идентификации тепловых математических моделей с сосредоточенными параметрами // Тепловые процессы в технике. 2016. № 5. С. 214.
Викулов А.Г., Ненарокомов А.В. Идентификация математических моделей теплообмена в космических аппаратах // ИФЖ. 2019. Т. 92. № 1. С. 32.
Викулов А.Г., Ненарокомов А.В. Идентификация редуцированной модели экранно-вакуумной тепловой изоляции // Тепловые процессы в технике. 2016. № 11. С. 488.
Мацевитый Ю.М., Мултановский А.В., Немировский Н.А. Оптимизация теплотехнических процессов с использованием методов управления и идентификации // ИФЖ. 1990. Т. 59. № 2. С. 298.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур


