1. На главную
  2. Электронные версии
  3. Теплофизика высоких температур
  4. T. 58, № 2, 2020

Теплофизика высоких температур, 2020, T. 58, № 2, стр. 179-187

Малопараметрическое уравнение состояния алюминия

С. Д. Гилев *

Институт гидродинамики им. М.А. Лаврентьева СО РАН
г. Новосибирск, Россия

* E-mail: gilev@hydro.nsc.ru

Поступила в редакцию 10.12.2018
После доработки 17.10.2019
Принята к публикации 22.10.2019

Полный текст (PDF)

Аннотация

Построено малопараметрическое уравнение состояния алюминия, основанное на предложенной зависимости коэффициента Грюнайзена от удельного объема и температуры. Определены характеристики состояния алюминия в области высоких давлений и температур: нулевая и нормальная изотермы; теплоемкость; изоэнтропический модуль объемного сжатия; семейство ударных адиабат, соответствующих различной начальной плотности; кривые вторичного сжатия и разгрузки; скорость звука. Рассчитанные значения оказываются близки к имеющимся экспериментальным данным. Это указывает на адекватность предложенного подхода к построению термодинамически согласованного уравнения состояния алюминия до сжатия в 3–4 раза.

ВВЕДЕНИЕ

Для прогнозирования воздействия высокоэнергетических потоков на вещество необходимо знать уравнение состояния среды [1–5]. В настоящее время широкое распространение получили полуэмпирические широкодиапазонные уравнения состояния (см., например, [6–10] и цитируемую там литературу). Современные уравнения состояния [8–12] характеризуются широким рабочим диапазоном и точностью, соответствующей первичным экспериментальным данным. В значительной степени это достигается рассмотрением нескольких областей фазовой диаграммы, в каждой из которых используются дополнительные модельные зависимости между величинами. В результате такого подхода увеличивается количество свободных (так называемых подгоночных) параметров. В прецизионных уравнениях состояния общее число свободных параметров достигает нескольких десятков. При этом нахождение численных их значений превращается в отдельную вычислительную задачу, которая часто не имеет однозначного решения. Наличие нескольких рабочих областей требует аккуратного согласования величин при переходе вещества из одной области в другую.

Малопараметрические уравнения состояния [13–24] отличаются более узким диапазоном применимости, меньшей точностью, но часто демонстрируют прозрачные физические результаты. Это важно, в частности, при решении сложных магнитогидродинамических задач. В таких задачах, как ударно-волновая магнитная кумуляция [25], кроме теплофизических характеристик необходимо задавать электрофизические параметры вещества (известные, как правило, не очень хорошо), вследствие чего требования к точности уравнения состояния получаются менее строгими. В то же время важными становятся такие качества модели, как простота, непротиворечивость и термодинамическая согласованность.

В работе [26] предложено новое полуэмпирическое уравнение состояния вещества, в основе которого лежит построение коэффициента Грюнайзена как функции удельного объема и температуры. Функция Грюнайзена [26] качественно описывает эксперименты по ударному сжатию металлов в области высоких давлений. В подходе [26] “холодная” составляющая давления находится из обобщенного модельного уравнения [27], связывающего холодное давление с коэффициентом Грюнайзена. Ранее такая идея использовалась для уравнений Дугдала–Мак-Доналда [28] и Слэтера–Ландау [18, 19] (при других зависимостях коэффициента Грюнайзена от удельного объема и температуры). Уравнение состояния [26] характеризуется небольшим количеством предположений о поведении вещества, малым числом свободных параметров и достаточно широким рабочим диапазоном. В частности, уравнение состояния [26] удовлетворительно описывает имеющиеся на сегодняшний день экспериментальные данные по ударно-волновому сжатию меди в области высоких плотностей энергии. По сравнению с малопараметрическим уравнением состояния [18, 19] область описания состояний меди по давлению и удельной внутренней энергии значительно расширена.

В настоящей работе проводится апробация нового уравнения состояния на другом веществе – алюминии. Алюминий, так же как медь, является эталонным материалом в области высоких давлений и температур. Построение малопараметрического уравнения состояния алюминия важно как для выяснения возможностей подхода [26], так и для решения прикладных задач физики высоких плотностей энергии.

УРАВНЕНИЕ СОСТОЯНИЯ

Главная особенность уравнения состояния [26] состоит в том, что коэффициент Грюнайзена $\Gamma $ при сжатии вещества полагается зависящим от удельного объема $V$ и температуры $T$ в следующем виде:

(1)
$\Gamma \left( {V,T} \right) = {{\Gamma }_{\infty }} + {{\left( {\frac{V}{{{{V}_{0}}}}} \right)}^{\alpha }}\frac{{{{\Gamma }_{0}} - {{\Gamma }_{\infty }}}}{{1 + \beta T}}\left( {1 + \beta {{T}_{0}}} \right).$
Здесь ${{\Gamma }_{\infty }}$ – коэффициент Грюнайзена в предельном случае сильного сжатия и нагрева ($V \to 0,$ $T \to \infty $); ${{\Gamma }_{0}}$ – коэффициент Грюнайзена при нормальных условиях; ${{V}_{0}}$ – удельный объем при нормальных условиях (${{V}_{0}} = {1 \mathord{\left/ {\vphantom {1 {{{\rho }_{0}},}}} \right. \kern-0em} {{{\rho }_{0}},}}$ ${{\rho }_{0}}$ – плотность при нормальных условиях); ${{T}_{0}}$ – нормальная температура. В зависимости (1) имеется два свободных параметра: $\alpha $ и $\beta $ ($\alpha > 0,$ $\beta > 0$). Параметр $\alpha $ описывает влияние удельного объема, параметр $\beta $ – температуры. Зависимость (1) полагается справедливой при сжатии вещества, т.е. при $V < {{V}_{0}}.$

Зная функцию Грюнайзена, можно найти ряд фундаментальных характеристик твердого тела. Кривая холодного сжатия ${{p}_{c}}\left( V \right)$ находится из обобщенного модельного уравнения [27], связывающего коэффициент Грюнайзена и холодное давление:

$\Gamma = - \frac{V}{2}\frac{{{{{{\partial }^{2}}\left( {{{p}_{c}}{{V}^{{{{2t} \mathord{\left/ {\vphantom {{2t} 3}} \right. \kern-0em} 3}}}}} \right)} \mathord{\left/ {\vphantom {{{{\partial }^{2}}\left( {{{p}_{c}}{{V}^{{{{2t} \mathord{\left/ {\vphantom {{2t} 3}} \right. \kern-0em} 3}}}}} \right)} {\partial {{V}^{2}}}}} \right. \kern-0em} {\partial {{V}^{2}}}}}}{{{{\partial \left( {{{p}_{c}}{{V}^{{{{2t} \mathord{\left/ {\vphantom {{2t} 3}} \right. \kern-0em} 3}}}}} \right)} \mathord{\left/ {\vphantom {{\partial \left( {{{p}_{c}}{{V}^{{{{2t} \mathord{\left/ {\vphantom {{2t} 3}} \right. \kern-0em} 3}}}}} \right)} {\partial V}}} \right. \kern-0em} {\partial V}}}} + \frac{{t - 2}}{3}.$
Эта формула при $t = 0$ соответствует модели Слэтера–Ландау, при $t = 1$ – модели Дугдала–Мак-Доналда, при $t = 2$ – модели Зубарева–Ващенко. Используя данную формулу и выражение для коэффициента Грюнайзена (1) при $T = 0,$ получим дифференциальное уравнение для функции ${{p}_{c}}\left( V \right).$ Решая полученное уравнение, запишем выражение для холодного давления как
(2)
$\begin{gathered} {{p}_{c}}\left( V \right) = {{V}^{{ - \frac{{2t}}{3}}}}\left( {{{C}_{1}} + {{C}_{2}}\int\limits_1^{\frac{V}{{{{V}_{0}}}}} {{{\tau }^{{ - 2{{\Gamma }_{\infty }} + \frac{2}{3}\left( {t - 2} \right)}}}} } \right. \times \\ \left. {^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}} \times \,\,\exp \left( { - \frac{{2\left( {{{\Gamma }_{0}} - {{\Gamma }_{\infty }}} \right)}}{\alpha }\left( {1 + \beta {{T}_{0}}} \right){{\tau }^{\alpha }}} \right)d\tau } \right). \\ \end{gathered} $
В этой формуле $C_{1}^{{}}$ и ${{C}_{2}}$ являются константами интегрирования. Функция (2) монотонно возрастает при уменьшении удельного объема и не имеет каких-либо особенностей. При помощи численного интегрирования холодное давление в форме (2) может быть найдено для любых имеющих физический смысл коэффициентов $\alpha ,$ $\beta .$ Условие равенства нулю потенциальной части давления ${{p}_{c}}\left( {{{V}_{{0K}}}} \right) = 0$ определяет соответствующий удельный объем ${{V}_{{0K}}}.$

В области растяжения ($V > {{V}_{0}}$) зависимость коэффициента Грюнайзена от удельного объема (1) нуждается в корректировке. Самый простой способ состоит в замене в формуле (1) коэффициента $\alpha $ на новый коэффициент $\delta ,$ причем $\delta < 0.$ Тогда при большом росте удельного объема можно обеспечить предельный переход к случаю идеального газа. Коэффициент $\delta $ является свободным параметром модели для области растяжения.

Формула (2) используется при $V \leqslant {{V}_{{0K}}}.$ Для области $V > {{V}_{{0K}}}$ такая зависимость оказывается неадекватной. При $V > {{V}_{{0K}}}$ функция холодного давления имеет вид

(3)
$\begin{gathered} {{p}_{c}}\left( V \right) = {{\left( {\frac{{{{V}_{0}}}}{V}} \right)}^{\varepsilon }}{{V}^{{ - \frac{{2t}}{3}}}}\left( {{{C}_{1}} + {{C}_{2}}\int\limits_1^{\frac{V}{{{{V}_{0}}}}} {{{\tau }^{{ - 2{{\Gamma }_{\infty }} + \frac{2}{3}\left( {t - 2} \right)}}}} \times } \right. \\ \left. {^{{^{{^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}}}}}} \times \,\,\exp \left( { - \frac{{2\left( {{{\Gamma }_{0}} - {{\Gamma }_{\infty }}} \right)}}{\alpha }\left( {1 + \beta {{T}_{0}}} \right){{\tau }^{\alpha }}} \right)d\tau } \right). \\ \end{gathered} $
Эта формула отличается от (2) лишь сомножителем ${{\left( {{{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} V}} \right. \kern-0em} V}} \right)}^{\varepsilon }}$ и удовлетворяет условию, что при бесконечно большом расширении ($V \to \infty $) холодное давление стремится к нулю. Показатель степени $\varepsilon $ определяется из дополнительного соотношения, которое обсуждается ниже.

Характеристическая температура ${{\theta }_{D}}$ в приближении Дебая находится в квазигармоническом случае из соотношения $\Gamma = - {{\left( {\frac{{\partial \ln {{\theta }_{D}}}}{{\partial \ln V}}} \right)}_{T}}.$ Интегрирование этого уравнения дает зависимость ${{\theta }_{D}}$ от удельного объема и абсолютной температуры. Для области сжатия ($V < {{V}_{0}}$)

(4)
$\begin{gathered} {{\theta }_{D}}\left( {V,T} \right) = {{\theta }_{{D0}}}{{\left( {\frac{{{{V}_{0}}}}{V}} \right)}^{{{{\Gamma }_{\infty }}}}} \times \\ \times \,\,\exp \left[ {\frac{{\left( {{{\Gamma }_{0}} - {{\Gamma }_{\infty }}} \right)\left( {1 + \beta {{T}_{0}}} \right)}}{{\alpha \left( {1 + \beta T} \right)}}\left( {1 - {{{\left( {\frac{V}{{{{V}_{0}}}}} \right)}}^{\alpha }}} \right)} \right]. \\ \end{gathered} $
Константа интегрирования ${{\theta }_{{D0}}}$ полагается равной температуре Дебая при нормальных условиях ($T = {{T}_{0}},$ $V = {{V}_{0}}$). В области растяжения $V > {{V}_{0}}$ формула для температуры Дебая ${{\theta }_{D}}\left( {V,T} \right)$ имеет аналогичный вид, но с заменой в (4) коэффициента $\alpha $ на $\delta .$

Свободная энергия Гельмгольца твердого тела (изохорно-изотермический потенциал) представлена в традиционном виде, как сумма слагаемых, выражающих вклад холодного сжатия кристаллической решетки, а также тепловых компонент, обусловленных движением ядер и электронов

(5)
$\begin{gathered} F\left( {V,T} \right) = {{E}_{c}}\left( V \right) + \frac{9}{8}R{{\theta }_{D}} + \\ + \,\,RT{\kern 1pt} \left\{ {3\ln \left[ {1 - \exp \left( { - \frac{{{{\theta }_{D}}}}{T}} \right)} \right] - D\left( {\frac{{{{\theta }_{D}}}}{T}} \right)} \right\} - \frac{{{{\gamma }_{0}}{{T}^{2}}}}{2}{\kern 1pt} {{\left( {\frac{V}{{{{V}_{0}}}}} \right)}^{{{{\Gamma }_{e}}}}}{\kern 1pt} . \\ \end{gathered} $
Здесь $R$ – удельная газовая постоянная, ${{\gamma }_{0}}$ – коэффициент электронной теплоемкости, ${{\Gamma }_{e}}$ – аналог функции Грюнайзена для электронов (полагается постоянным), $D\left( x \right)$ – функция Дебая
$D\left( {\frac{{{{\theta }_{D}}}}{T}} \right) = \frac{{3{{T}^{3}}}}{{\theta _{D}^{3}}}\int\limits_0^{{{{{\theta }_{D}}} \mathord{\left/ {\vphantom {{{{\theta }_{D}}} T}} \right. \kern-0em} T}} {\frac{{{{z}^{3}}dz}}{{{{e}^{z}} - 1}}} ,$
${{E}_{c}}\left( V \right)$ – холодная энергия вещества:

${{E}_{c}}\left( V \right) = - \int\limits_{{{V}_{{0K}}}}^V {{{p}_{c}}\left( V \right)dV} .$

Свободная энергия является термодинамическим потенциалом, поэтому, зная свободную энергию, можно найти давление, внутреннюю энергию, энтропию:

(6)
$\begin{gathered} p\left( {V,T} \right) = - \frac{{\partial F}}{{\partial V}} = {{p}_{c}}\left( V \right) + \frac{{\Gamma \left( {V,T} \right)}}{V} \times \\ \times \,\,R\left[ {\frac{9}{8}{{\theta }_{D}} + 3TD\left( {\frac{{{{\theta }_{D}}}}{T}} \right)} \right] + {\text{ }}\frac{{{{\Gamma }_{e}}{{\gamma }_{0}}{{T}^{2}}}}{{2V}}{{\left( {\frac{V}{{{{V}_{0}}}}} \right)}^{{{{\Gamma }_{e}}}}}, \\ \end{gathered} $
(7)
$\begin{gathered} E\left( {V,T} \right) = F - T\frac{{\partial F}}{{\partial T}} = {{E}_{c}}\left( V \right) + \frac{9}{8}\left( {1 + M} \right)R{{\theta }_{D}} + \\ + \,\,3\left( {1 + M} \right)RTD\left( {\frac{{{{\theta }_{D}}}}{T}} \right) + \frac{{{{\gamma }_{0}}{{T}^{2}}}}{2}{{\left( {\frac{V}{{{{V}_{0}}}}} \right)}^{{{{\Gamma }_{e}}}}}, \\ \end{gathered} $
(8)
$\begin{gathered} S\left( {V,T} \right) = - \frac{{\partial F}}{{\partial T}} = R\left[ {\frac{9}{8}M\frac{{{{\theta }_{D}}}}{T} + \left( {3M + 4} \right)D\left( {\frac{{{{\theta }_{D}}}}{T}} \right) - } \right. \\ \left. { - \,\,3\ln \left( {1 - {{e}^{{{{ - {{\theta }_{D}}} \mathord{\left/ {\vphantom {{ - {{\theta }_{D}}} T}} \right. \kern-0em} T}}}}} \right)} \right] + {{\gamma }_{0}}T{{\left( {\frac{V}{{{{V}_{0}}}}} \right)}^{{{{\Gamma }_{e}}}}} \\ \end{gathered} $
и другие термодинамические параметры вещества.

В формулах (7), (8) использована вспомогательная функция

$M\left( {V,T} \right) = - {{\left( {\frac{{\partial \ln {{\theta }_{D}}}}{{\partial \ln T}}} \right)}_{V}},$
отражающая зависимость характеристической температуры ${{\theta }_{D}}$ от абсолютной температуры.

Нетрудно показать, что в силу соотношений (6) и (7), давление можно представить в форме обобщенного уравнения Ми–Грюнайзена

$\begin{gathered} p\left( {V,T} \right) = {{p}_{c}}\left( V \right) + \frac{{\Gamma \left( {V,T} \right)}}{V}\frac{9}{8}R{{\theta }_{D}} + \\ + \,\,\frac{{\Gamma \left( {V,T} \right)}}{{V\left( {1 + M} \right)}}{{E}_{a}}\left( {V,T} \right) + \frac{{{{\Gamma }_{e}}}}{V}{{E}_{e}}\left( {V,T} \right), \\ \end{gathered} $
где ${{E}_{a}}\left( {V,T} \right)$ и ${{E}_{e}}\left( {V,T} \right)$ – тепловая энергия ядер и электронов соответственно.

Константы интегрирования $C_{1}^{{}}$ и ${{C}_{2}}$ в (2), (3) находятся из следующих физических условий:

(9)
$p\left( {{{V}_{0}},{{T}_{0}}} \right) = {{p}_{0}},$
(10)
${{\left. { - V{{{\left( {\frac{{\partial p}}{{\partial V}}} \right)}}_{T}}} \right|}_{\begin{subarray}{l} V = {{V}_{0}} \\ T = {{T}_{0}} \end{subarray} }} = {{K}_{{T0}}}.$
Уравнение (9) показывает, что давление $p$ при нормальных условиях равно атмосферному давлению ${{p}_{0}}.$ Уравнение (10) означает, что изотермический модуль объемного сжатия при нормальных условиях соответствует своему экспериментальному значению ${{K}_{{T0}}}.$

Показатель степени $\varepsilon $ определяется из условия, что энергия связи, найденная для холодного давления в форме (3), совпадает со своим табличным значением ${{E}_{s}}{\text{:}}$

$ - \int\limits_{{{V}_{{0K}}}}^\infty {{{p}_{c}}\left( V \right)dV} + \frac{9}{8}R{{\theta }_{D}}\left( {\infty ,0} \right) - \frac{9}{8}R{{\theta }_{D}}\left( {{{V}_{{0K}}},0} \right) = {{E}_{s}}.$
Соотношения (1)–(5) определяют предлагаемое полуэмпирическое уравнение состояния конденсированного вещества. В уравнении состояния используются значения величин при начальных условиях ${{V}_{0}},$ ${{\Gamma }_{0}},$ ${{\theta }_{{D0}}},$ ${{K}_{{T0}}},$ ${{p}_{0}},$ ${{T}_{0}},$ а также констант $R,$ ${{\Gamma }_{\infty }},$ ${{\gamma }_{0}},$ ${{\Gamma }_{e}},$ ${{E}_{s}},$ $\alpha ,$ $\beta ,$ $\delta ,$ $t.$

С целью уменьшения количества свободных параметров в модели положим, что $t = 0,$ т.е. для связи коэффициента Грюнайзена с холодным давлением будем использовать уравнение Слэтера–Ландау. Отметим, что хотя модель Слэтера–Ландау является приближенной, она обладает прозрачным физическим смыслом. В случае необходимости величину $t$ можно рассматривать как дополнительный параметр модели.

Таким образом, настоящая модель имеет два свободных параметра $\alpha ,$ $\beta $ для области сжатия ($V < {{V}_{0}}$). Параметрами для области растяжения ($V > {{V}_{0}}$) являются $\delta ,$ $\beta .$ Значения свободных параметров $\alpha ,$ $\beta ,$ $\delta $ определялись из условия согласования модельных зависимостей с имеющимися экспериментальными и расчетными данными о сжимаемости вещества при высоких давлениях и температурах. В качестве опорных данных при таком сравнении служили нулевая и нормальная изотермы, а также ударные адиабаты сплошного и пористого вещества. Коэффициент ${{\Gamma }_{e}}$ находился по экспериментальной ударной адиабате сплошного вещества при максимальных параметрах сжатия.

Параметры уравнения состояния алюминия приведены в таблице. Значение коэффициента ${{\Gamma }_{\infty }}$ принято равным ${2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$, что соответствует квантово-статистической модели Томаса–Ферми при сильном сжатии, а также модели идеального газа при сильном расширении. В расчетах использованы параметры нормального состояния ${{T}_{0}} = 293\,\,{\text{K,}}$ ${{p}_{0}} = 100\,\,{\text{кПа}}{\text{.}}$

Таблица 1.  

Значения коэффициентов состояния алюминия

$\begin{gathered} {{\rho }_{0}}, \\ {{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}} \\ \end{gathered} $ $\begin{gathered} R, \\ {{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {\left( {{\text{г K}}} \right)}}} \right. \kern-0em} {\left( {{\text{г K}}} \right)}} \\ \end{gathered} $ ${{\Gamma }_{0}}$ ${{\Gamma }_{\infty }}$ ${{\theta }_{{D0}}}$,
K 		${{K}_{{{{T}_{0}}}}}$, ГПа ${{\gamma }_{0}}$, ${{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {({\text{г }}{{{\text{К}}}^{{\text{2}}}})}}} \right. \kern-0em} {({\text{г }}{{{\text{К}}}^{{\text{2}}}})}}$ ${{E}_{s}}$, ${{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {\text{г}}}} \right. \kern-0em} {\text{г}}}$ Γe $C_{1}^{{}}$, ГПа $C_{2}^{{}}$, ГПа ε ${{\rho }_{{0K}}}$, г/см3 α β,
10–6 K–1		 δ
2.71 $3.08 \times {{10}^{{ - 4}}}$ 2.14 [29] ${2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}$ 390 [20] 72.2 [30, 31] $5.03 \times {{10}^{{ - 8}}}$ [29] 11.9 [29] 0.5 –1.76313 –412.653 1.425 2.76974 1.8 100 –2

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

На рис. 1 представлена полученная нулевая изотерма алюминия. Она сравнивается с данными Альтшулера [7], результатами квантово-механических расчетов по модели Томаса-Ферми с градиентными поправками [32] и широкодиапазонными моделями [8, 12]. При небольшом сжатии модельная кривая неплохо соответствует данным [7], а при сильном – данным [8, 12], которые оказываются близки между собой. Отметим, что результаты [7] и [12] несколько различаются, а данные [8] располагаются между [7] и [12].

Рис. 1.

Модельная нулевая изотерма алюминия (сплошная кривая) и результаты расчетов других авторов: 1 – модель Томаса–Ферми с градиентными поправками [32]; 2 – полуэмпирическая модель Альтшулера [7]; широкодиапазонные модели: 3 – [12], 4 – [8].

На рис. 2 представлена полученная нормальная изотерма алюминия вместе с данными других авторов.

Рис. 2.

Модельная нормальная изотерма (сплошная кривая), данные экспериментов по статическому сжатию (1–3) и расчетов (4–6): 1 – [33], 2 – [34], 3 – [35], 4 – [36], 5 – [12], 6 – [8].

На рис. 3 показаны зависимости теплоемкости и плотности от температуры. Согласие между моделью и экспериментальными данными [37–39] удовлетворительное. Расхождение между моделью и экспериментом наблюдается в окрестности температуры плавления (${{T}_{m}} \approx 933\,\,{\text{K}}$). Настоящая модель не описывает фазовые переходы, поэтому при $T > {{T}_{m}}$ разница в плотности оказывается заметной.

Рис. 3.

Зависимости безразмерной теплоемкости при постоянном давлении (1–3) и плотности (4–6) от температуры при $p = {{p}_{0}}{\text{:}}$ 1, 4 – расчет; 2, 5 – экспериментальные данные [37]; 3 – [38]; 6 – аппроксимация данных по тепловому расширению [39].

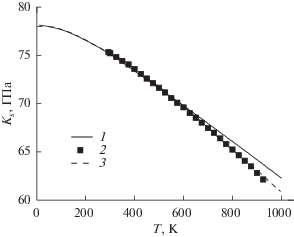
На рис. 4 показана зависимость изоэнтропического модуля объемного сжатия при изобарическом нагреве. Изоэнтропический модуль объемного сжатия ${{K}_{S}}$ определялся по формуле

${{K}_{S}} = {{K}_{T}} + \frac{{TV}}{{{{c}_{V}}}}\left( {\frac{{\partial p}}{{\partial T}}} \right)_{V}^{2},$
где ${{c}_{V}}$ – теплоемкость при постоянном объеме. Согласие модельной зависимости с экспериментальными данными можно оценить как хорошее. Отличие модели от экспериментальных данных увеличивается с ростом температуры и при максимальной температуре (925 К), близкой к температуре плавления, составляет 2.5%.

Рис. 4.

Зависимость изоэнтропического модуля объемного сжатия при изобарическом нагреве: 1 – модель, 2 – экспериментальные данные [40], 3 – расчеты [41].

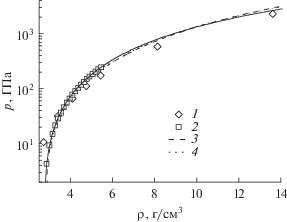
Важным тестом модели является поведение вещества при сжатии в сильных ударных волнах. На рис. 5 в переменных $p{\kern 1pt} - {\kern 1pt} \rho $ показаны модельные ударные адиабаты алюминия, соответствующие различным значениям коэффициента пористости $m = {{{{\rho }_{0}}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}} {{{\rho }_{{00}}}}}} \right. \kern-0em} {{{\rho }_{{00}}}}}$ (${{\rho }_{{00}}}$ – начальная плотность пористого вещества). Здесь же представлены известные на сегодняшний день экспериментальные данные по ударно-волновому сжатию алюминия [42], а также широкодиапазонная ударная адиабата сплошного алюминия [43].

Рис. 5.

Зависимости давления ударной волны от плотности для образцов алюминия различной пористости: сплошные кривые – модель, точки – экспериментальные данные [42], штриховая линия – широкодиапазонная ударная адиабата [43].

Для данных, соответствующих максимальным давлениям, на рис. 5 приведены погрешности плотности из оригинальных работ [44, 45]. Для ударной адиабаты с коэффициентом пористости $m = 8$ погрешности оценены в предположении, что измерения массовой и волновой скоростей выполнены с относительной погрешностью 1.5%.

Согласие между моделью и экспериментом можно оценить как хорошее вплоть до давления $p \approx {{10}^{5}}\,\,{\text{ГПа}}{\text{.}}$ При $p > {{10}^{5}}\,\,{\text{ГПа}}$ модельная ударная адиабата отклоняется от данных [43], так же как от данных модели Томаса–Ферми [21], которые в этой области демонстрируют более сложное поведение (уменьшение плотности при росте давления).

Значительное расхождение между моделью и экспериментом наблюдается для высокопористых образцов ($m \gg 1$) в области относительно малых давлений ($p < 5\,\,{\text{ГПа}}$). Для описания ударной сжимаемости в этой области необходимо привлекать модели, описывающие процесс закрытия пор при сжатии.

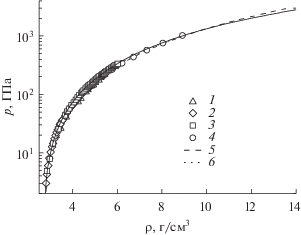
Дополнительным тестом модели является сравнение состояний вещества, достигаемых при вторичном ударном сжатии и разгрузке. На рис. 6 показаны расчетные зависимости давления от массовой скорости при вторичном сжатии, а также экспериментальные данные [42].

Рис. 6.

Зависимость давления от массовой скорости при вторичном ударном сжатии: сплошные кривые – модель, точки – экспериментальные данные [42], штриховая линия – главная ударная адиабата алюминия.

На рис. 7 показаны зависимости давления от массовой скорости при разгрузке вещества из первоначально сжатого состояния. При сильной разгрузке модельные зависимости дают несколько меньшие значения массовой скорости, чем эксперимент. При разгрузке из состояния, соответствующего давлению ударной волны $p = 407\,\,{\text{ГПа,}}$ отличие в массовой скорости составляет около 5%. Для сравнения на рис. 7 показана кривая, соответствующая зеркальному отражению ударной адиабаты при $p = 407\,\,{\text{ГПа}}{\text{.}}$ Такое приближение хорошо работает при малых давлениях ударной волны, но, как видно из рисунка, приводит к заметным ошибкам при большом давлении.

Рис. 7.

Зависимость давления от массовой скорости при разгрузке ударно-сжатого вещества: сплошные кривые – модель; точки – экспериментальные данные: 1 – [46, 47], 2 – [48]; штриховая линия – главная ударная адиабата алюминия; пунктир – кривая разгрузки из состояния с $p = 407\,\,{\text{ГПа,}}$ полученная из условия зеркального отражения ударной адиабаты.

Как видно из рис. 6 и 7, настоящая модель удовлетворительно описывает вторичное ударное сжатие и разгрузку алюминия.

На рис. 8 показана зависимость объемной скорости звука в ударно-сжатом образце от давления. Настоящая модель дает результаты, которые хорошо соответствуют экспериментальным данным [49] и модели [9], но несколько отличается от данных [50] и модели [12].

Рис. 8.

Зависимость объемной скорости звука в ударно-сжатом алюминии от давления: сплошная кривая – модель; точки – экспериментальные данные: 1 – [49], 2 – [50], 3 – [51]; предсказания широкодиапазонных моделей: 4 – [12], 5 – [9].

ОБСУЖДЕНИЕ

Представленные выше результаты показывают, что малопараметрическая модель (1)–(5) описывает разнообразные эксперименты с алюминием в области больших давлений и температур. Настоящая модель дает удовлетворительные результаты при определении нулевой и нормальной изотерм, теплоемкости, изоэнтропического модуля объемного сжатия, семейства ударных адиабат, вторичного сжатия и разгрузки, объемной скорости звука. Отклонения в давлении от данных других авторов во всей исследованной области, как правило, не превышают разброса между известными данными и экспериментальных погрешностей. Основываясь на рис. 5, а также на сравнении полученных данных с результатами расчетов по широкодиапазонным уравнениям состояния [8–10, 12], можно оценить рабочий диапазон настоящей модели: плотность – $1.5{\kern 1pt} - {\kern 1pt} 13\,\,{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{{\text{3}}}}}},$ температура – до 20 кK, давление ударного сжатия при $m = 1$ до $\sim {\kern 1pt} {{10}^{5}}\,\,{\text{ГПа}}{\text{.}}$

Сравним настоящую модель с малопараметрическим уравнением состояния [18, 19]. Как отмечается в [18, 19], эта модель справедлива в диапазоне давления до $\sim {\kern 1pt} {{10}^{2}}\,\,{\text{ГПа,}}$ сжатия до двух раз, температуры до нескольких тысяч градусов. Модель [18, 19] неприменима для области пониженных плотностей ($ < {\kern 1pt} 80\% $ относительно нормальной плотности). Таким образом, по сравнению с малопараметрическим уравнением состояния [18, 19], диапазон по плотности у настоящей модели увеличен в 3–4 раза, а максимальное давление – на два-три порядка величины.

Разумеется, предлагаемое малопараметрическое уравнение состояния не может обеспечить диапазон и точность, характерную для современных широкодиапазонных уравнений состояния. Настоящее уравнение состояния использует в качестве опорного состояние конденсированного вещества при стандартных условиях и основывается на моделях Дебая или твердого тела. В случае фазовых переходов, большого отклонения от стандартного состояния конденсированного вещества, данный подход может оказаться некорректным. В частности, модель не учитывает эффекты ангармонизма, уменьшение теплоемкости вещества при экстремально больших температурах, плавление, испарение, снятие вырождения электронного газа и т.д.

ЗАКЛЮЧЕНИЕ

Построено малопараметрическое уравнение состояния алюминия, основанное на предложенной зависимости коэффициента Грюнайзена от удельного объема и температуры. Достоинство настоящей модели состоит в малом количестве произвольных допущений, термодинамической согласованности, относительной простоте, предсказуемости результатов. Это позволяет использовать настоящее уравнение состояния при решении сложных задач физики высоких плотностей энергии, где требования к модели включают в себя непротиворечивость и простоту.

Список литературы

  1. Жарков В.Н., Калинин В.А. Уравнения состояния твердых тел при высоких давлениях и температурах. М.: Наука, 1968.

  2. Eliezer S., Ghatak A., Hora H. Fundamentals of Equations of State. New Jersey: World Scientific, 2002.

  3. Фортов В.Е. Уравнения состояния вещества от идеального газа до кварк-глюонной плазмы. М.: Физматлит, 2012.

  4. Бушман А.В., Фортов В.Е. Модели уравнений состояния веществ // УФН. 1983. Т. 140. № 2. С. 177.

  5. Godwal B.K., Sikka S.K., Chidambaram R. Equation of State Theories of Condensed Matter up to about 10 TPa // Phys. Rep. 1983. V. 102. № 3. P. 121.

  6. Альтшулер Л.В., Бушман А.В., Жерноклетов М.В. и др. Изэнтропы разгрузки и уравнения состояния металлов при высоких плотностях энергии // ЖЭТФ. 1980. Т. 78. № 2. С. 741.

  7. Альтшулер Л.В., Брусникин С.Е., Кузьменков Е.А. Изотермы и функции Грюнайзена 25 металлов // ПМТФ. 1987. № 1. С. 134.

  8. Гордеев Д.Г., Гударенко Л.Ф., Каякин А.А и др. Полуэмпирическая модель уравнения состояния металлов с эффективным учетом ионизации. Ч. 2. Уравнение состояния алюминия // ВАНТ. Сер. Теор. и прикл. физика. 2010. № 3. С. 26.

  9. Гордеев Д.Г., Гударенко Л.Ф., Каякин А.А., Куделькин В.Г. Модель уравнения состояния металлов с эффективным учетом ионизации. Уравнения состояния Ta, W, Al, Be // ФГВ. 2013. Т. 49. № 1. С. 106.

  10. Ломоносов И.В., Фортова С.В. Широкодиапазонные полуэмпирические уравнения состояния вещества для численного моделирования высокоэнергетических процессов // ТВТ. 2017. Т. 55. № 4. С. 596.

  11. Khishchenko K.V., Fortov V.E., Lomonosov I.V. Multiphase Equation of State for Carbon over Wide Range of Temperatures and Pressures // Int. J. Thermophys. 2005. V. 26. № 2. P. 479.

  12. Lomonosov I.V. Multi-phase Equation of State for Aluminum // Laser and Particle Beams. 2007. V. 25. P. 567.

  13. Vinet P., Rose J.H., Ferrante J., Smith J.R. Universal Features of the Equation of State of Solids // J. Phys.: Condens. Matter. 1989. V. 1. № 11. P. 1941.

  14. Taravillo M., Baonza V.G., Núñez J. et al. Simple Equation of State for Solids under Compression // Phys. Rev. B. 1996. V. 54. P. 7034.

  15. Roy S.B., Roy P.B. An Equation of State Applied to Solid up to 1 TPa // J. Phys.: Condens. Matter. 1999. V. 11. № 50. P. 10375.

  16. Holzapfel W.B. Equations of State and Thermophysical Properties of Solids under Pressure. In: High Pressure Crystallography / Eds. Katrusiak A., McMillan P. Dordrecht: Kluwer Acad. Publ., 2004. P. 217.

  17. Sun J.X., Wu Q., Cai L.C. et al. Equation of State for Solids with High Accuracy and Satisfying the Limitation Condition at High Pressure // Phys. B. Condens. Matter. 2006. V. 371. № 2. P. 257.

  18. Молодец А.М. Уравнение состояния твердых химических элементов // Докл. РАН. 1997. Т. 353. № 5. С. 610.

  19. Молодец А.М. Изохорно-изотермический потенциал и термодинамика ударного сжатия твердых тел // Хим. физика. 1997. Т. 16. № 9. С. 132.

  20. Хищенко К.В. Уравнение состояния магния в области высоких давлений // Письма в ЖТФ. 2004. Т. 30. № 19. С. 65.

  21. Shemyakin O.P., Levashov P.R., Khishchenko K.V. Equation of State of Al Based on the Thomas–Fermi Model // Contrib. Plasma Phys. 2012. V. 52. № 1. P. 37.

  22. Кинеловский С.А., Маевский К.К. Модель поведения алюминия и смесей на его основе при ударно-волновом воздействии // ТВТ. 2014. Т. 52. № 6. С. 843.

  23. Khishchenko K.V. Equation of State for Tungsten over a Wide Range of Densities and Internal Energies // J. Phys.: Conf. Ser. 2015. V. 653. 012081.

  24. Kraus E.I., Shabalin I.I. A Few-parameter Equation of State of the Condensed Matter // J. Phys.: Conf. Ser. 2016. V. 774. P. 012009.

  25. Gilev S.D. Model of Shock-wave Magnetic Cumulation // J. Phys. D: Appl. Phys. 2009. V. 42. № 2. 025501.

  26. Гилев С.Д. Малопараметрическое уравнение состояния меди // ФГВ. 2018. Т. 54. № 4. С. 107.

  27. Ващенко В.Я., Зубарев В.Н. О коэффициенте Грюнайзена // ФТТ. 1963. Т. 5. С. 886.

  28. Баканова А.А., Дудоладов И.П., Трунин Р.Ф. Сжатие щелочных металлов сильными ударными волнами // ФТТ. 1965. Т. 7. № 6. С. 1615.

  29. Gschneidner K.A. Physical Properties and Interrelationships of Metallic and Semimetallic Elements // Solid State Physics. 1964. V. 16. P. 275.

  30. Францевич И.Н., Воронов С.С., Бакута С.А. Упругие постоянные и модули упругости металлов и неметаллов. Спр. Киев: Наукова думка, 1982.

  31. Киттель Ч. Введение в физику твердого тела. М.: Наука, 1978.

  32. Perrot F. Zero-temperature Equation of State of Metals in the Statistical Model with Density Gradient Correction // Phys. A: Statist. Mech. Its Appl. 1979. V. 98. № 3. P. 555.

  33. Greene R.G., Luo H., Ruoff A.L. Al as Simple Solid: High Pressure Study to 220 GPa (2.2 Mbar) // Phys. Rev. Lett. 1994. V. 73. P. 2075.

  34. Dewaele A., Loubeyre P., Mezouar M. Equations of State of Six Metals above 94GPa // Phys. Rev. B. 2004. V. 70. 094112.

  35. Akahama Y., Nishimura M., Kinoshita K., Kawamura H., Ohishi Y. Evidence of a fcc-hcp Transition in Aluminum at Multimegabar Pressure // Phys. Rev. Lett. 2006. V. 96. 045505.

  36. Nellis W.J., Moriarty J.A., Mitchell A.C. et al. Metals Physics at Ultrahigh Pressure: Aluminum, Copper, and Lead as Prototypes // Phys. Rev. Lett. 1988. V. 60. P. 1414.

  37. Зиновьев В.Е. Теплофизические свойства металлов при высоких температурах. М.: Металлургия, 1989.

  38. Физические величины. Спр. / Под ред. Григорьева И.С., Мейлихова Е.3. М.: Энергоатомиздат, 1991.

  39. Новикова С.И. Тепловое расширение твердых тел. М.: Наука, 1974.

  40. Simmons G., Wang H. Single Crystal Elastic Constants and Calculated Aggregate Properties. Cambridge: MIT Press, 2009.

  41. Sjostrom T., Crockett S., Rudin S. Multiphase Aluminum Equations of State Via Density Functional Theory // Phys. Rev. B. 2016. V. 94. № 14. 144101.

  42. Levashov P.R., Khishchenko K.V., Lomonosov I.V., Fortov V.E. Database on Shock-wave Experiments and Equations of State Available Via Internet // AIP Conf. Proc. 2004. V. 706. P. 87. http://www.ihed.ras.ru/rusbank/

  43. Kalitkin N.N., Kuzmina L.V. Wide-range Characteristic Thermodynamic Curves. In: Shock Waves and Extremal Conditions of Matter / Ed. Fortov V.E. et al. N.Y.: Springer, 2004. P. 109.

  44. Владимиров А.С., Волошин Н.П., Ногин В.Н. и др. Ударная сжимаемость алюминия при давлениях p > 1 Гбар // Письма в ЖЭТФ. 1984. Т. 39. Вып. 2. С. 69.

  45. Симоненко В.А., Волошин H.П., Владимиров А.С. и др. Абсолютные измерения ударной сжимаемости алюминия при давлениях Р > 1 ТПа // ЖЭТФ. 1985. Т. 88. № 4. С. 1452.

  46. Баканова А.А., Дудоладов И.П., Жерноклетов М.В., Зубарев В.Н., Симаков Г.В. Об испарении ударно-сжатых металлов при расширении // ПМТФ. 1983. № 2. С. 76.

  47. Глушак Б.Л., Жарков А.П., Жерноклетов М.В., Терновой В.Я., Филимонов А.С., Фортов В.Е. Экспериментальное изучение плотной плазмы металлов при высоких концентрациях энергии // ЖЭТФ. 1989. Т. 96. № 4. С. 1301.

  48. Knudson M.D., Desjarlais M.P., Pribram-Jones A. Adiabatic Release Measurements in Aluminum between 400 and 1200 GPa: Characterization of Aluminum as a Shock Standard in the Multimegabar Regime // Phys. Rev. B. 2015. V. 91. 224105.

  49. Альтшулер Л.В., Кормер С.Б., Бражник М.И., Владимиров Л.А., Сперанская М.П., Фунтиков А.И. Изэнтропическая сжимаемость алюминия, меди, свинца и железа при высоких давлениях // ЖЭТФ. 1960. Т. 38. С. 1061.

  50. Neal T. Mach Waves and Reflected Rarefactions in Aluminum // J. Appl. Phys. 1975. V. 46. P. 2521.

  51. Mcqueen R.G., Fritz J.N., Morris C.E. The Velocity of Sound behind Strong Shock Waves in 2024 Al. In: Shock Waves in Condensed Matter – 83 / Ed. Asay J.R., Graham R.A., Straub G.K. Amerstdam: North Holland, 1984. P. 95.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал