Теплофизика высоких температур, 2020, T. 58, № 2, стр. 244-248

Расчет прогрева и уноса теплозащитного материала в осесимметричной постановке

Д. Н. Минюшкин¹, И. А. Крюков^1, 2, *

¹ Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

² Московский авиационный институт
Москва, Россия

^* E-mail: ikryukov@gmail.com

Поступила в редакцию 07.10.2019
После доработки 12.11.2019
Принята к публикации 24.12.2019

DOI: 10.31857/S0040364420020143

Полный текст (PDF)

Аннотация

В работе изложен метод расчета на подвижных сетках прогрева и уноса теплозащитного материала. Конвективный тепловой поток получен из расчета внешнего течения по уравнениям Навье–Стокса. Валидация проведена на экспериментальных данных, полученных для уноса образца из POCO-графита в плазмотроне. Расчеты показали, что в процессе уноса присутствует как диффузионный, так и сублимационный режимы.

ВВЕДЕНИЕ

Высокоскоростные летательные аппараты (ЛА) испытывают аэродинамический нагрев элементов конструкции. На практике особенно теплонапряженные участки конструкции ЛА усиливаются тепловой защитой. Проектирование тепловой защиты высокоскоростных летательных аппаратов требует расчета аэродинамического нагрева, прогрева и разрушения теплозащитного покрытия (ТЗП). Одним из основных способов тепловой защиты ЛА при высоких уровнях тепловых нагрузок является использование пассивной уносимой тепловой защиты. Она может устанавливаться на носовую часть ЛА и на управляющие элементы (кромки рулей, крыльев). Поэтому актуальной задачей является расчет уноса ТЗП и прогрева конструкции сложной формы. Для оценки прочности, аэродинамических свойств и других характеристик ЛА нужно тщательно оценивать не только внешние силовые и тепловые нагрузки, но и прогрев конструкции с учетом разрушения ТЗП. Необходимость учета многих подобных факторов для решения задачи требует комплексного подхода [1, 2].

Данная работа посвящена методу расчета уноса и прогрева ТЗП в осесимметричной постановке в допущении изотропности свойств конструкционных материалов. Использовалась равновесная модель разрушения углерода (механический унос не учитывается). Давление и тепловые потоки определялись решением уравнений Навье–Стокса. Валидация проведена на основе сравнения полученных результатов с экспериментальными данными.

РАСЧЕТ ТЕПЛОВЫХ И СИЛОВЫХ НАГРУЗОК

Полная система уравнений Навье–Стокса, описывающая нестационарные двумерные течения сжимаемого вязкого многокомпонентного химически реагирующего газа [3]:

(1)

$\frac{{\partial Q}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} = \frac{{\partial {{F}_{{v}}}}}{{\partial x}} + \frac{{\partial {{G}_{{v}}}}}{{\partial y}} + R,$

(2)

${\mathbf{Q}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u} \\ {\rho {v}} \\ \begin{gathered} E \\ \rho {{b}_{i}} \\ \end{gathered} \end{array}} \right],\,\,{\mathbf{F(Q)}} = \left[ {\begin{array}{*{20}{c}} {\rho u} \\ {\rho {{u}^{2}} + p} \\ {\rho u{v}} \\ \begin{gathered} (E + p)u \\ \rho {{b}_{i}}u \\ \end{gathered} \end{array}} \right],\,\,{\mathbf{G(Q)}} = \left[ {\begin{array}{*{20}{c}} {\rho {v}} \\ {\rho u{v}} \\ {\rho {{{v}}^{2}} + p} \\ \begin{gathered} (E + p){v} \\ \rho {{b}_{i}}{v} \\ \end{gathered} \end{array}} \right],$

$\begin{gathered} {{{\mathbf{F}}}_{{\mathbf{v}}}}{\mathbf{(Q)}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{{\tau }_{{xx}}}} \\ {{{\tau }_{{xy}}}} \\ \begin{gathered} {{q}_{x}} + u{{\tau }_{{xx}}} + {v}{{\tau }_{{xy}}} \\ \rho {{D}_{i}}\frac{{\partial {{b}_{i}}}}{{\partial x}} \\ \end{gathered} \end{array}} \right],\,\,{{{\mathbf{G}}}_{{\mathbf{v}}}}{\mathbf{(Q)}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{{\tau }_{{xy}}}} \\ {{{\tau }_{{yy}}}} \\ \begin{gathered} {{q}_{y}} + u{{\tau }_{{yx}}} + {v}{{\tau }_{{yy}}} \\ \rho {{D}_{i}}\frac{{\partial {{b}_{i}}}}{{\partial y}} \\ \end{gathered} \end{array}} \right], \\ {\mathbf{R}} = - \frac{\rho }{y}{\text{ }}\left[ {\begin{array}{*{20}{c}} {v} \\ {u{v}} \\ \begin{gathered} {{{v}}^{2}} \hfill \\ {v}h \hfill \\ \end{gathered} \\ {{v}{{b}_{i}}} \end{array}} \right] + {\text{ }}\left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ \begin{gathered} 0 \\ {{W}_{i}} \\ \end{gathered} \end{array}} \right]. \\ \end{gathered} $

Система уравнений (1) выражает законы сохранения в некотором замкнутом объеме пространства массы, импульса и энергии как смеси газов (первые четыре уравнения), так и отдельных компонент смеси (следующие N уравнений, где N − количество компонент в смеси).

Вектор Q называется вектором консервативных переменных. Векторы F(Q), G(Q) – векторы потоков сохраняемых величин по соответствующим координатам (потоки массы, импульса, энергии), обусловленные конвективными процессами.

Векторы F_v(Q), G_v(Q) – векторы “вязких” потоков, обусловленных диффузионными процессами: вязким трением, диффузией, теплопроводностью; R – вектор источниковых членов, предназначен для учета осесимметричности течения и учета протекания химических реакций W_i (W_i – скорость образования i-й компоненты за счет химических реакций).

В (1)–(3) ρ, p, E – плотность, давление и полная энергия смеси в единице объема соответственно; u, v – компоненты вектора скорости в декартовой системе координат x, y; b_i – мольно-массовая концентрация i-й компоненты смеси; h_i – энтальпия i-й компоненты. Полная энергия единицы объема представляет собой сумму внутренней энергии e и кинетической энергии этого объема.

Компоненты тензора вязких напряжений в (1)–(3) записываются следующим образом:

$\begin{gathered} {{\tau }_{{xx}}} = 2\mu \frac{{\partial u}}{{\partial x}} - \frac{2}{3}\mu \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \alpha \frac{{v}}{r}} \right), \\ {{\tau }_{{yy}}} = 2\mu \frac{{\partial {v}}}{{\partial y}} - \frac{2}{3}\mu \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \alpha \frac{{v}}{r}} \right), \\ {{\tau }_{{xy}}} = \mu \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial {v}}}{{\partial x}}} \right), \\ \end{gathered} $

где α = 1 для осесимметричного течения, α = 0 для плоского, µ – коэффициент динамической вязкости.

Компоненты вектора плотности потока энергии q_x, q_y (тепловой поток) с учетом переноса энергии за счет теплопроводности и переноса массы вещества посредством всех видов диффузии и при условии пренебрежения потоком энергии, обусловленным диффузионным термоэффектом, выглядят следующим образом:

${{q}_{x}} = - \lambda \frac{{\partial T}}{{\partial x}} + \sum\limits_{i = 1}^N {{{J}_{{xi}}}{{h}_{i}}} ,\,\,\,\,{{q}_{y}} = - \lambda \frac{{\partial T}}{{\partial y}} + \sum\limits_{i = 1}^N {{{J}_{{yi}}}{{h}_{i}}} .$

Здесь ${{{\mathbf{J}}}_{i}} = ({{J}_{{xi}}},{{J}_{{yi}}})$ – вектор плотности потока массы i-й компоненты (диффузионный поток), λ – коэффициент теплопроводности, Т – температура. Для описания диффузионных потоков используется закон Фика:

${{J}_{{xi}}} = - \rho {{D}_{i}}\frac{{\partial {{b}_{i}}}}{{\partial x}},\,\,\,\,{{J}_{{yi}}} = - \rho {{D}_{i}}\frac{{\partial {{b}_{i}}}}{{\partial y}},$

где D_i – эффективный коэффициент диффузии i-й компоненты смеси [4, 5].

Для численного решения системы уравнений (1)–(3) использовался метод, описанный в [6–9]. В качестве базовой схемы для аппроксимации конвективной части системы уравнений используется схема Годунова повышенного порядка точности. Члены уравнений, описывающие диффузионный перенос, аппроксимируются с помощью аналога схемы центральных разностей для неравномерных сеток, источниковые члены уравнений – с помощью явно-неявного алгоритма [7]. На основе описанного метода разработан авторский программный комплекс nt2D для расчета двумерных нестационарных течений вязкого многокомпонентного газа [6–9], который использовался в данной работе.

На стенках задавались условия прилипания, на плоскости симметрии – условия симметрии (непротекания), на свободных границах – условия отсутствия отражения возмущений. Во входном сверхзвуковом потоке задавались компоненты вектора скорости, температура, давление и мольно-массовые концентрации всех компонент смеси.

МОДЕЛЬ РАЗРУШЕНИЯ ГРАФИТА

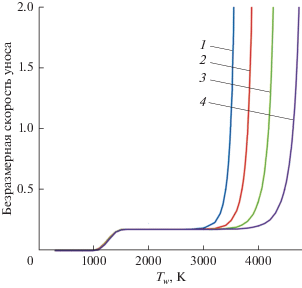
В расчетах использовалась модель разрушения графита в равновесной постановке [10], т.е. концентрации химических компонент в каждый момент времени зависели от местных значений температуры и давления. Моделируется скорость разрушения углерода для трех основных режимов уноса: кинетического, диффузионного и сублимационного. Безразмерная скорость уноса представлена на рис. 1. При высоких температурах, где реализуется сублимационный режим, скорость разрушения сильно зависит от температуры стенки. Поэтому точный расчет температуры на поверхности материала имеет большое значение при расчете изменения формы ЛА.

Рис. 1.

Зависимость безразмерной скорости уноса от температуры стенки и давления: 1 – P = 0.1 атм, 2 – 1.0, 3 – 10, 4 – 100.

В рамках данной постановки модель разрушения является входным параметром и передается вычислительному модулю расчета прогрева и уноса как набор двух двумерных таблиц: 1) безразмерная скорость уноса в зависимости от температуры стенки и давления, 2) энтальпия смеси от температуры стенки и давления.

РАСЧЕТ ПРОГРЕВА И УНОСА ТЗП

Расчет прогрева конструкции с уносимой теплозащитой проводился на подвижных сетках, поэтому в уравнении теплопроводности появляется дополнительный конвективный член:

$\frac{{\partial T}}{{\partial t}} = \frac{1}{{\rho c}}\nabla (\lambda \nabla T) - {{{\mathbf{V}}}_{m}} \cdot \nabla T.$

Здесь ρ – плотность материала, c – теплоемкость, V_m – вектор скорости движения расчетной сетки.

Для получения скорости движения узлов сетки V_m решалась вспомогательная задача деформации твердого тела. Предполагалось, что вершины ячеек сетки соединены упругими связями и на поверхности двигаются со скоростью уноса.

Для решения задачи прогрева на внешней границе задаются граничные условия:

$\nabla T = - \frac{{{{q}_{l}}}}{\lambda }.$

Величина q_l, т.е. тепловой поток, идущий на прогрев ТЗП, рассчитывается из уравнения баланса энергии на границе.

Условие сохранения энергии на границе теплозащитного материала складывается из баланса подведенного извне конвективного теплового потока, который расходуется на прогрев, разрушение и излучение с поверхности:

${{q}_{c}} = \dot {m}\Delta {{Q}_{{{\text{раз}}}}} + \varepsilon \sigma T_{w}^{4} + {{q}_{l}}.$

Здесь q_с – конвективный тепловой поток с учетом вдува; $\dot {m}$ – массовая скорость уноса поверхности, в кг/м^–2 с^–1; $\Delta {{Q}_{{{\text{раз}}}}}$ – теплота разрушения теплозащитного материала; $\varepsilon \sigma T_{w}^{4}$ – лучистый поток с поверхности материала; T_w – температура стенки. Для расчета скорости уноса используется равновесная модель разрушения графита [10]. Более подробно алгоритм расчета прогрева и уноса описан в работе [11]. В процессе горения теплозащитного материала происходит интенсивный массообмен с пограничным слоем. Структура пограничного слоя меняется и, как следствие, меняется тепловой поток к поверхности аппарата. Для учета этого влияния использованы соотношения [12]

$\frac{{{{q}_{{wl}}}}}{{q_{{wl}}^{0}}} = 1 - 0.68B + 0.66{{B}^{2}},\,\,\,\,B = \frac{{\dot {m}}}{{{{a_{l}^{0}} \mathord{\left/ {\vphantom {{a_{l}^{0}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}}}$

для ламинарного теплообмена и

$\frac{{{{q}_{{wt}}}}}{{q_{{wt}}^{0}}} = \sqrt {1 + \frac{1}{4}{{B}^{2}}} - \frac{1}{2}B,\,\,\,\,B = \frac{{\dot {m}}}{{{{a_{t}^{0}} \mathord{\left/ {\vphantom {{a_{t}^{0}} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}}}$

для турбулентного. Здесь a⁰, c_p – турбулентный и ламинарный коэффициенты теплообмена на непроницаемой поверхности.

ВАЛИДАЦИЯ РАСЧЕТА УНОСА

Валидация метода расчета проводилась путем сравнения с экспериментальными данными из работы [13]. В эксперименте был достигнут сублимационный режим уноса графита, что позволило протестировать расчет уноса при условии сильной зависимости скорости уноса от температуры поверхности. Исследуемый образец представлял собой модель со сферическим затуплением радиусом 1.905 см. В плазмотроне был реализован режим течения с полной энтальпией потока 27 MДж/кг, тепловым потоком в критической точке 2100 Вт/см² и давлением торможения 76 кПа (0.75 атм). Длительность эксперимента составляла 30 с. Модель была изготовлена из POCO-графита, теплофизические свойства которого взяты из [14] и представлены в таблице.

Таблица 1.

Теплофизические свойства POCO-графита

T, К	λ, Вт/(м К)	c, Дж/(кг К)	ε
300	106	702	0.8
400	97.2	957	0.8
500	89.2	1168	0.8
600	82.8	1282	0.8
700	77.3	1520	0.8
800	72.5	1636	0.8
900	67.3	1726	0.8
1000	62.8	1797	0.8
1100	58.6	1859	0.8
1200	54.7	1905	0.8
1300	51.2	1942	0.8
1400	48.2	1975	0.787
1500	45.6	2002	0.793
1600	43.6	2028	0.799
1700	42.1	2050	0.805
1800	40.8	2070	0.811
1900	39.8	2087	0.817
2000	38.8	2100	0.823
2100	38	2111	0.829
2200	37.4	2127	0.835
2300	37	2140	0.841
2400	36.5	2155	0.847
2900	35	2180	0.853
4000	32	2200	0.92

Необходимо отметить, что в [14] значения представлены только до 2900 К, в то время как в эксперименте были достигнуты температуры более 3500 К, поэтому в таблице на отрезке значений 2900–4000 К проведена экстраполяция данных.

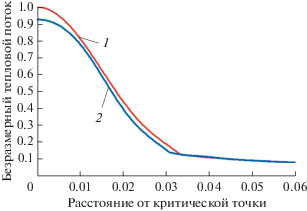
На рис. 2 представлены распределения для моментов времени эксперимента 0 и 30 с. В критической точке тепловой поток в момент времени 30 с ниже, чем в начальный момент времени, из-за затупления образца в процессе уноса. На рис. 2 тепловой поток отнесен к значению теплового потока к холодной стенке в критической точке в начале эксперимента q₀ = 2100 Вт/см².

Рис. 2.

Тепловой поток при t = 0 (1) и 30 с (2).

На рис. 3 приводится сравнение результатов расчета величин уноса в данной работе (линии) с экспериментальными данными [13] (маркеры) для двух точек на поверхности. В каждый момент времени режим течения был ламинарным, температура поверхности быстро достигла высоких значений и был реализован сублимационный режим уноса графита.

Рис. 3.

Сравнение распределений величины уноса при q_s = 2.1 Вт/м², P = 0.75 атм, H = 27 МДж/кг в критической точке (1) и в точке 45° (2); маркеры – экспериментальные данные.

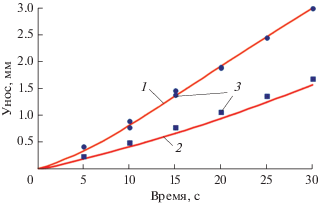
Общий линейный унос в критической точке при t = 30 с испытания составил 3 мм, а в точке 45° – около 1.65 мм.

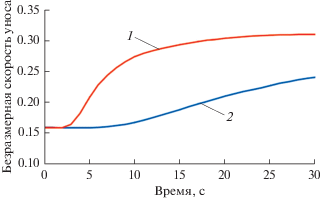
На рис. 4 представлены зависимости безразмерной скорости уноса для критической точки и точки 45°. В критической точке диффузионный режим горения сохраняется около 2 с, далее унос переходит в сублимационный режим и к концу эксперимента безразмерная скорость достигает значения 0.3. В точке 45° диффузионный режим горения сохраняется около 6 с, далее он становится сублимационным и к концу эксперимента безразмерная скорость уноса достигает значения 0.25.

Рис. 4.

Безразмерная скорость уноса от времени в критической точке (1) и в точке 45° (2).

На рис. 5 приведено сравнение результатов расчета температуры на поверхности в точке 45° с экспериментальными данными, полученными с помощью инфракрасной камеры и пирометра [13]. Рассчитанная температура на поверхности превышает измеренную: для 30 с рассчитанная температура равна 3420 К, измеренная камерой – 3300 К и измеренная пирометром – 3360 К. Разница между результатами расчета и результатами измерений составила менее 5%.

Рис. 5.

Сравнение температуры, рассчитанной по 3D-модели в точке 45° (1), c экспериментальными данными [9], полученными с помощью пирометра (2) и инфракрасной камеры (3).

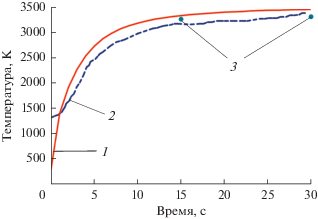
Из рис. 3 и 5 видно, что результаты сравнения расчета с экспериментальными данными имеют удовлетворительное совпадение.

ЗАКЛЮЧЕНИЕ

Предложенный в данной работе метод расчета уноса теплозащитного материала позволяет получить удовлетворительный результат в точке поверхности сферы 45° с погрешностью не более 10% в рассмотренном диапазоне определяющих параметров. В эксперименте был достигнут сублимационный режим уноса, а следовательно, скорость уноса имела сильную зависимость от температуры поверхности. Нужно отметить, что рассчитанные значения температуры на боковой поверхности сферы в точке 45° совпали с экспериментом с погрешностью не более 5%.

Список литературы

Страхов В.Л., Кузьмин И.А., Бакулин В.Н. Комплексное математическое моделирование теплозащиты из высоконаполненных эластомеров // ТВТ. 2019. Т. 57. № 2. С. 278.
Зинченко В.И., Гольдин В.Д., Зверев В.Г. Численное моделирование влияния материалов пассивной тепловой защиты на характеристики сопряженного тепломассообмена при пространственном обтекании затупленных тел // ТВТ. 2018. Т. 56. № 5. С. 747.
Anderson J.D., Jr. Hypersonic and High Temperature Gas Dynamics. N.Y.: The McGraw-Hill Company, 1989. 690 p.
Poling B.E., Prausnitz J.M., O’Connell J.P. Properties of Gases and Liquids. 5th ed. N.Y.: McGraw-Hill, 2001. 768 p.
Shang J.S., Surzhikov S.T. Nonequilibrium Radiative Hypersonic Flow Simulation // Prog. Aeronaut. Sci. 2012. V. 53. P. 46.
Иванов И.Э., Крюков И.А. Квазимонотонный метод повышенного порядка точности для расчета внутренних и струйных течений невязкого газа // Матем. моделирование РАН. 1996. Т. 8. № 6. С. 47.
Глушко Г.С., Иванов И.Э., Крюков И.А. Метод расчета турбулентных сверхзвуковых течений // Матем. моделирование РАН. 2009. Т. 21. № 12. С. 103.
Гидаспов В.Ю., Иванов И.Э., Кpюков И.А., Набоко И.М., Петухов В.А., Стрельцов В.Ю. Исследование процессов распространения волн горения и детонации в кумулирующем объеме // Матем. моделирование РАН. 2004. Т. 16. № 6. С. 118.
Иванов И.Э., Кpюков И.А. Численное моделирование течений многокомпонентного газа с сильными разрывами свойств среды // Матем. моделирование РАН. 2007. Т. 19. № 11. С. 89.
Scala S.M., Gilbert L.M. Sublimation of Graphite at Hypersonic Speeds // AIAA J. 1965. V. 3. № 9. P. 1635.
Минюшкин Д.Н. Трехмерный расчет прогрева и уноса теплозащитного материала с использованием платформы OpenFOAM и неструктурированной сетки // Космонавтика и ракетостроение. 2018. № 5(104). С. 101.
Конвективный теплообмен летательных аппаратов / Под науч. ред. Землянского Б.А. М.: Физматлит, 2014. 377 с.
Chen Y.-K., Milos F.S., Reda D.C., Stewart D.A. Graphite Ablation and Thermal Response Simulation Under Arc-Jet Flow Conditions // AIAA Paper 2003-4042.
Touloukian Y.S., Powell R.W., Ho C.Y., Klemens P.G. Thermal Conductivity Nonmetallic Solid // Thermophys. Properties of Matter. 1970. V. 2. P. 21.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теплофизика высоких температур

Архивы выпусков Информация о журнале Отправить рукопись в журнал