Теплофизика высоких температур, 2020, T. 58, № 3, стр. 355-364
Исследование границы фазового перехода для C6F6 и SF6 в условиях микрогравитации
В. С. Воробьев 1, Е. Е. Устюжанин 2, *, В. Ф. Очков 2, В. В. Шишаков 2, Аунг Ту Ра Тун 2, В. А. Рыков 3, С. В. Рыков 3
1 Объединенный институт высоких температур РАН
Москва, Россия
2 Национальный исследовательский университет “МЭИ”
Москва, Россия
3 Национальный исследовательский университет ИТМО
Санкт-Петербург, Россия
* E-mail: evgust@gmail.com
Поступила в редакцию 06.06.2019
После доработки 22.11.2019
Принята к публикации 24.12.2019
Аннотация
Обсуждаются две группы экспериментальных данных, полученных в окрестности критической точки. Первая группа I описывает уровень ht, на котором расположен мениск, разделяющий две фазы вещества в ячейке. Измерения выполнены для SF6 в условиях g = 9.8 м с–2 в ходе эксперимента, проведенного в космической лаборатории. Вторая группа II включает данные о плотности жидкости и пара, которые измерены на линии насыщения в условиях g = 9.8 м с–2 для C6F6. В обоих случаях исследуемый двухфазный образец находится в горизонтальной цилиндрической ячейке. Во втором эксперименте на изотермах измерялся также гравитационный эффект как зависимость плотности образца от высоты h, отсчитываемой от дна ячейки. В данной работе построено уравнение, которое связывает уровень ht (эксперимент I) с такими функциями, как параметр порядка fs и средний диаметр fd. Полученное уравнение описывает исходные экспериментальные данные при относительных температурах τ = (Т – Tc)/Tc = 2 × 10–6–0.01. Рассмотрен подход, который учитывает влияние микрогравитации (g = gM ⪡ 9.8 м с–2) на высоту h (эксперимент II). Получены зависимости, которые представляют fs и fd, а также плотности жидкой и газовой фаз на линии насыщения указанных веществ. Данные зависимости удовлетворительно согласуются с результатами экспериментов I и II в широком диапазоне температур и отвечают масштабной теории критических явлений.
ВВЕДЕНИЕ
Объектом данного исследования выбраны (ρl, ρg, τ)-данные, а также функции ρl(τ), ρg(τ), fd(τ), fs(τ) и др., которые относятся к C6F6 и SF6. Здесь ρl, ρg – плотности жидкой и газовой фаз, fd – средний диаметр бинодали, fs – параметр порядка, τ = (Т – Tc)/Tc – относительная температура, Tc – критическая температура. Измерение (ρl, ρg, τ)-данных для C6F6 выполнено в [1]. Поведение плотности на бинодали SF6 исследовалось в ряде работ [2–13], среди них имеются и экспериментальные исследования [9, 10]. Скейлинговые модели, предложенные в данных источниках, представляют собой функции ρl(τ), ρg(τ), fd(τ), fs(τ) и др., которые отвечают масштабной теории критических явлений (МТ).
В отношении отмеченных моделей анализ показывает, что модели ρl(τ), ρg(τ) можно разделить на две группы: первая обобщает результаты [9], а вторая строится на основе данных [10]. Выявлено расхождение между уравнениями, включенными в первую группу, и однотипными уравнениями, включенными во вторую группу; данное различие касается как структуры уравнений, так и соответствующих расчетных данных, полученных на основе указанных функций. Так, для области относительных температур (τ = 2 × 10–4–0.01) имеются:
• система уравнений [6], включающая fd(τ), fs(τ) и содержащая линейные и сингулярные компоненты; средний диаметр fd(τ) = ${{B}_{{{\text{1}} - \alpha }}}{{\tau }^{{{\text{1}} - \alpha }}}$ + + ${{B}_{{2\beta }}}{{\tau }^{{2\beta {\text{ }}}}} + {{B}_{1}}\tau + ...,$ входящий в эту систему, получен с помощью данных [10]; его структура содержит пять компонентов, в том числе скейлинговые члены (${{B}_{{2\beta }}}{{\tau }^{{2\beta }}},$ B1 – α${{\tau }^{{{\text{1}} - \alpha }}}$), отражающие так называемую “кривизну” этого диаметра (линия 2, рис. 1а), здесь B1–α, B2β, B1 – коэффициенты;
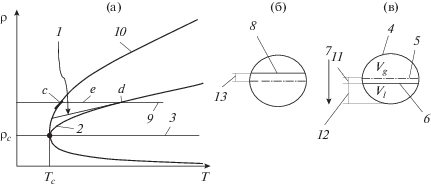
Рис. 1.
Бинодаль на фазовой плоскости для SF6 (а): 1 – функция Dm= ${{A}_{0}} + {{A}_{1}}\tau ;$ 2 – функция Dm, построенная с помощью (ρl, ρg, T)-данных [10]; 3 – изохора ρ = ρcell= ρc; 9 – изохора ρ = ρcell> ρc; 10 – бинодаль; (б), (в) – ячейка и положение мениска в экспериментах II и I соответственно: 4 – сечение ячейки, имеющей форму горизонтального цилиндра; 5 – виртуальная горизонтальная плоскость, размещенная вдоль оси цилиндра и соответствующая смещению ht0 и высоте hM0; 6 – уровень мениска при ρcell < ρc; 7 – направление силы тяжести в ячейке; 8 – уровень мениска при ρcell> ρc.
• система уравнений [4], содержащая только сингулярные компоненты, при этом диаметр fd отвечает равенству fd(τ) = ${{B}_{{2\beta }}}{{\tau }^{{2\beta }}},$ полученному с помощью данных [10];
• диаметр fd(τ) = ${{B}_{{{\text{1}} - \alpha }}}{{\tau }^{{{\text{1}} - \alpha }}} + {{B}_{1}}\tau $ [12], который включает два компонента, полученные с помощью данных [10];
• диаметр fd(τ) = ${{B}_{0}} + {{B}_{1}}\tau $ [12] в форме прямолинейного диаметра, который построен по (ρl, ρg, T)-данным, относящимся к регулярной области температур и измеренным в [10];
• функции, отвечающие линейной форме fd(τ) = ${{B}_{1}}\tau $ и рекомендованные в работах [8, 9], коэффициенты которых найдены с помощью результатов [9].
В отношении известных экспериментальных (ρl, ρg, T)-данных в [2, 3] сделан вывод, который свидетельствует о заметном расхождении между источниками [9] и [10]. В работе [9] (ρl, ρg, T)-данные получены прямым методом, т.е. в пьезометрическом эксперименте на первом этапе измерялись (ρ, Р, Т)-данные на изотерме, здесь Р – давление в пьезометре, например, в жидкой фазе вблизи линии насыщения. На втором этапе находилось значение ρl путем экстраполяции (ρ, Р)-данных до линии кипения при Р = Рs.
В работе [10] (ρl, ρg, T)-данные получены косвенным путем, при этом в качестве исходных данных для плотности использовались прямые измерения в форме (εl, εg, T)-данных. Здесь εl, εg – диэлектрические проницаемости, измеряемые двумя датчиками в жидкой и газовой фазах. Анализ показывает, что величины εl, εg существенно зависят от высот hl, hg, на которых размещены датчики диэлектрической проницаемости в ячейке. Здесь hl, hg – расстояния по вертикали до датчиков от дна ячейки (ср. с высотой h, которая отсчитывается от нижней образующей цилиндра и определяет положение датчика плотности в эксперименте II). В работе [10] отсутствует информация о значениях hl, hg, на которых расположены два датчика, регистрирующие (εl, εg, T)-данные.
Указанная несогласованность приводит, с одной стороны, к тому, что размерный средний диаметр Dm= (ρl + ρg)/2 = ρc(1 + fd(τ)) (линия 2, рис. 1а) содержит функцию fd(τ) = ${{B}_{{{\text{1}} - \alpha }}}{{\tau }^{{{\text{1}} - \alpha }}}$ + $ + \,\,{{B}_{{2\beta }}}{{\tau }^{{2\beta }}}~ + \,{{B}_{1}}\tau + ...$ [6], построенную с помощью (ρl, ρg, T)-данных [10]. Кривизну этого диаметра впервые в 1974 г. отметил Weiner в своей диссертации11. Линия 2 существенно отклоняется от линии 1 (рис. 1а), которая представляет собой диаметр Dm = ${{D}_{0}} + {{D}_{1}}\tau $ [12].
С другой стороны, авторами выявлена дополнительная информация о диаметре fd(τ) для SF6. В работе [8] поставлен специальный эксперимент I, указывающий на то, что причиной кривизны диаметра fd(τ) [10] является гравитационный эффект. Для подтверждения этого вывода в рамках эксперимента I ячейка [8], имеющая форму горизонтального цилиндра (рис. 1б) и содержащая двухфазный образец SF6, размещалась в условиях (g = = 9.8 м/с2) в космической лаборатории. В экспериментах определялось смещение мениска ht как расстояние от оси цилиндра до уровня мениска, разделяющего фазы (линия 8, рис. 1б). Данные о ht, Т измерялись на нескольких околокритических изотермах. Для обобщения этих данных в [8] предложено уравнение ht(τ) =A(–B(fd/fs) + С/fs), в которое входят функции fd, fs и константы A, B, C. Значения A, B, C определены с помощью калибровочных экспериментов. В [8] рассмотрено несколько вариантов функции ht(τ) и сделан ряд выводов о диаметре fd(τ), в том числе:
• диаметр fd существенно влияет на функцию ht(τ) и поэтому погрешность, которую имеет модель fd(τ), в значительной степени определяет погрешность ht(τ);
• ht(τ) (вариант A) включает зависимость fd(τ), полученную в [6] на основе (ρl, ρg, T)-данных [10]; этот вариант существенно отклоняется от упомянутых экспериментальных (ht, T)-данных; измерения [10] и зависимость fd(τ) [6] связаны с гравитационным эффектом; в условиях микрогравитации (g = gM) зависимость fd(τ) [6] является причиной того, что ht(τ) (вариант A) не согласуется с экспериментальными (ht, T)-данными [8];
• в ht(τ) (вариант В) используется линейная зависимость fd(τ) = ${{B}_{1}}\tau $ [8], основанная на (ρl, ρg, T)-данных [9]; этот вариант позволяет уменьшить отклонение от экспериментальных (ht, τ)-данных [8] по сравнению с вариантом A; отмеченное улучшение косвенно свидетельствует, что (ρl, ρg, T)-данные [10] содержат погрешность, которая является источником кривизны (см. линию 2, рис. 1а) и существенно превышает погрешность соответствующих результатов [9].
Для детального исследования вопроса о роли гравитации авторами привлечены результаты эксперимента II, поставленного в работе [1]. В экспериментах [1] получены данные о гравитационном эффекте, который реализуется в двухфазном образце C6F6, помещенном в ячейку, изготовленную в форме горизонтального цилиндра (рис. 1в). Гравитационный эффект имеет вид зависимости ρ(h), которая включает плотность ρ вещества на фиксированных высотах h, отсчитываемых от нижней образующей цилиндра (линия 11, рис. 1в), при температурах 515.98, 516.28, 516.57 К (рис. 2, 3).
Рис. 2.
Распределение плотности C6F6 ρ(h – hM) на изотермах в области высоких плотностей (ρ > ρc): a, b, c – точки пересечения изотерм ρmid(h – hM) с локальными уровнями мениска (рядом указаны расчетные значения ρl(Т)); 1, 2, 6 – значения (h – hM), отвечающие смещениям ht; 3, 4, 5 – экспериментальные (ρ, h – hM)-данные; 7, 8, 9 – значения ρmidl; 1, 3, 7 – при 515.98 К; 2, 4, 8 – 516.28; 6, 5, 9 – 516.57.

Рис. 3.
Распределение плотности C6F6 ρ(h – hM) при 516.28 К: a, a' – точки пересечения аппроксимирующих функций с линией (h = hM); 1 – экспериментальные (ρ, h – hM)-данные при ρ > ρc; 2 – экспериментальные (ρ, h – hM)-данные в интервале 2Δh; 3 – при ρ < ρc.

В [1] представлены также экспериментальные (ρl, ρg, T)-данные в диапазоне температур 298.79–516.57 К и данные о давлении насыщения P. Эксперимент II показал, что гравитационная составляющая давления (Pg ≈ ρgh), которая является компонентом в измеряемой величине P, приводит к следующему выводу: очевидное распределение ρ(h), которое в условиях микрогравитации (g = gM) на изотерме содержит участки ρl = const, ρg= const и скачок ρl – ρg, превращается в непрерывную зависимость ρ(h) (рис. 2, 3), при этом в образце фактически отсутствует граница между жидкой и газовой фазами в виде мениска, располагающегося на высоте hM. На рис. 3 показана зависимость ρ(h), которая относится к Т = 516.28 К, здесь виден интервал 2Δh (Δh ≈ ±2.2 мм) вблизи оси цилиндра, где гравитационный эффект является существенным.
Планируемый в данном исследовании совместный анализ результатов, полученных в экспериментах I и II, даст возможность оценить количественное влияние гравитационной составляющей Pg на (ρl, ρg, T)-данные для C6F6 и SF6. Так, эксперимент II показал, что гравитационный эффект существенно влияет на функцию ρ(h) применительно к C6F6 при постоянных внешних Р, Т. Отклонение локальной плотности ρ(h) при ρ > ρc может отличаться от соответствующей плотности ρl(Т) на ±(2–10)% в зависимости от высоты. Эти отклонения свидетельствуют об уровне ошибок, которые могут присутствовать в (ρl, ρg, T)-данных [10] для SF6.
Представленная информация о SF6 (разнообразие моделей, расхождения в экспериментальных данных о плотности и др.) не дает возможности пользователю отдать предпочтение результатам [9] перед результатами [10], а также выделить уравнения, включенные в первую группу, как более точные по сравнению с аналогичными функциями, входящими во вторую группу. Построение адекватных моделей, которые в критической области описывают бинодаль, диаметр fd(τ) и другие функции, следует рассматривать как актуальную проблему для SF6.
В настоящей работе проводится совместный анализ результатов, которые получены в экспериментах I и II и связаны с количественным влиянием гравитационной составляющей Pg на (ρl, ρg, T)-данные для C6F6 и SF6. Исследуется положение мениска и соответственно корректируются (ρl, ρg, T)-данные для C6F6 при условии пониженного гравитационного эффекта в ячейке [1]. Вычисляются (ρl, ρg, T)-данные для SF6 в окрестности Tc, не охваченной экспериментом, с привлечением экспериментальных значений (ht, Т) [8].
Для C6F6 и SF6 находятся новые выражения функций ρl(τ), ρg(τ), fd(τ) и др. с существенным уточнением ранее известных результатов в околокритической области.
ПОЛОЖЕНИЕ МЕНИСКА В ЯЧЕЙКЕ
В эксперименте II фактически не оценивается положение мениска в ячейке, а предлагается метод, в котором выбирается виртуальная плоскость Sv, имеющая высоту hM (линия 4, рис. 3). Данная высота составляет hM = 19.1 мм и располагается в окрестности Δh вблизи оси ячейки (рис. 2, 3). Ячейка имеет длину L = 140.0 мм и диаметр d = 40.0 мм. В этом методе выбраны экспериментальные (ρ, h)-данные, относящиеся, например, к изотерме Т = 516.28 К (линия 1, рис. 3) при высоких плотностях (ρ > ρc) и размещенные вне Δh. Затем (ρ, h)-данные экстраполировались до точки a пересечения с линией 4 (рис. 3). В данной точке (ρl = 644.8 кг/м3) (табл. 1). Аналогичным образом выбирались экспериментальные данные (ρ, h) (линия 3, рис. 3), которые относятся к низким плотностям (ρ < ρc) и размещены за пределами Δh. Эти (ρ, h)-данные экстраполировались до точки пересечения a' с линией 4 (рис. 3), чтобы вычислить значение ρg = 455.8 кг/м3 (табл. 1).
Таблица 1.
Некоторые результаты второго этапа расчетов для C6F6
| ρl, кг/м3 | ρg, кг/м3 | τ | ρl, кг/м3 | ρg, кг/м3 | urexp | ht exp, мм | ht, мм |
|---|---|---|---|---|---|---|---|
| 670.3 | 433.7 | 0.00131 | 675.54 | 437.23 | 0.01268 | 0.191 | 0.207 |
| 644.8 | 455.8 | 0.000731 | 640.29 | 453.49 | –0.00212 | –0.031 | 0.157 |
| 610.1 | 491.5 | 0.000168 | 609.27 | 496.73 | 0.005059 | 0.079 | 0.078 |
Представляет интерес найти, на каком уровне hMT будет размещаться мениск в ячейке (рис. 1в). Для этого граничные условия выбраны следующими:
• средняя плотность ρcell = M/V, которую имеет образец, определяется равенством ρcell= ρc, т.е. линия 3 (рис. 1а) является критической изохорой; температура T удовлетворяет неравенству T < Tc (например, T = 516.28 К);
• гравитационный эффект значительно снижен; равновесная плотность в верхней части цилиндра равна ρg(Т), а в нижней части цилиндра – ρl(Т); в ячейке образуется мениск из-за конечной разности плотностей (ρl – ρg).
Отмеченное условие микрогравитации (g = gM) можно создать, например, за счет перемешивания вещества в верхней части до состояния, которому отвечает равновесная величина ρg(Т), и такого же перемешивания вещества в нижней части до достижения плотности ρl(Т).
Для определения уровня мениска рассмотрим изохорный процесс в ячейке, имеющей объем V (рис. 1в). Пусть в начальном состоянии вещество имеет параметры ρ = ρc, Т1 = Тc. Разместим виртуальную горизонтальную плоскость Sv (линия 5, рис. 1в) вдоль оси цилиндра. Это положение принято за начало отсчета ht0 (рис. 2), для смещения ht, (линия 12, рис. 1в), которое имеет мениск, разделяющий две фазы при понижении или повышении температуры ячейки. Выделим верхнюю и нижнюю части ячейки (Vg, Vl), которые имеют объем V/2 (рис. 1в).
Переведем вещество в состояние II. В этом процессе выполняются следующие условия: ρcell= = ρc = const, ТП = Тc + ΔТ. Здесь ${{\rho }_{{{\text{cell}}}}}$ – средняя плотность вещества в ячейке, ∆T > 0. В результате происходит перегрев вещества в ячейке по отношению к критической температуре, и мениска не возникает.
Переведем вещество в состояние I. В этом процессе выполняются следующие условия: реализована микрогравитация (g = gM), ρcell= ρc = const, T2 = Tc – ∆T, ∆T > 0. В результате происходят:
• конденсация в ячейке, и масса вещества в верхней части уменьшается (∆M > 0),
• плотность газовой фазы ρg отличается от плотности жидкой фазы ρl; благодаря микрогравитации и конечной разности (ρl – ρg) образуется мениск, расположенный ниже оси ячейки и разделяющий две фазы;
• смещение плоскости Sv вниз до мениска (линия 6, рис. 1в); это смещение ht отмечено линией 12 (рис. 1в).
Плотности фаз можно записать как (ρg, ρl) = = (ρc + ∆ρgρc, ρc + ∆ρl ρc), где ∆ρl = (ρl – ρc)/ρc, ∆ρg = (ρg – ρc)/ρc. Запишем объем V образца как функцию ряда аргументов, включая (∆M, ∆ρg, ∆ρl), в виде
(1)
$\begin{gathered} V = \left( {\frac{M}{2} - \Delta M} \right)\frac{1}{{{{\rho }_{c}} + \Delta {{\rho }_{g}}{{\rho }_{c}}}} + \\ + \,\,\left( {\frac{M}{2} + \Delta M} \right)\frac{1}{{{{\rho }_{c}} + \Delta {{\rho }_{l}}{{\rho }_{c}}}}. \\ \end{gathered} $Из (1) функция ΔM/M выражается как
(2)
$\frac{{\Delta M}}{M} = \left( {\frac{{\Delta {{\rho }_{l}} + \Delta {{\rho }_{g}}}}{2} + \Delta {{\rho }_{l}}\Delta {{\rho }_{g}}} \right)\frac{1}{{\Delta {{\rho }_{g}} - \Delta {{\rho }_{l}}}}.$Функции fd, fs вводятся в виде
(3)
${{f}_{d}} = ({{\rho }_{l}} + {{\rho }_{g}}){{(2{{\rho }_{c}})}^{{--1}}}--1{\text{ }} = {{(\Delta {{\rho }_{l}} + \Delta {{\rho }_{g}})} \mathord{\left/ {\vphantom {{(\Delta {{\rho }_{l}} + \Delta {{\rho }_{g}})} 2}} \right. \kern-0em} 2},$(4)
${{f}_{s}} = ({{\rho }_{l}} - {{\rho }_{g}}){{(2{{\rho }_{c}})}^{{ - 1}}} = {{(\Delta {{\rho }_{l}} - \Delta {{\rho }_{g}})} \mathord{\left/ {\vphantom {{(\Delta {{\rho }_{l}} - \Delta {{\rho }_{g}})} 2}} \right. \kern-0em} 2}.$После некоторых преобразований подстановка (3), (4) в (2) c учтем равенства (∆ρg – ∆ρl = –2 fs, ∆ρg∆ρl = $f_{d}^{2} - f_{s}^{2}$) дает
(5)
$\frac{{\Delta M}}{M} = \frac{{{{f}_{s}}}}{2} - \frac{{{{f}_{d}}}}{{2{{f}_{s}}}} - \frac{{f_{d}^{2}}}{{2{{f}_{s}}}}.$Изменение объема верхней части представляется как
(6)
$\Delta {{V}_{g}} = \left( {\frac{M}{2} - \Delta M} \right)\frac{1}{{{{\rho }_{g}}}} - \frac{V}{2}.$Используя (5) и (6), после преобразований относительное изменение объема ΔVg/V можно записать в виде
(7)
$\begin{gathered} \frac{{\Delta {{V}_{g}}}}{V} = \left( {\frac{{{{\rho }_{c}}}}{2} - \frac{{\Delta M}}{M}{{\rho }_{c}}} \right)\frac{1}{{{{\rho }_{c}}(1 + \Delta {{\rho }_{g}})}} - \frac{1}{2} \simeq \\ \simeq \left( {\frac{1}{2} - \frac{{\Delta M}}{M}} \right)(1 - \Delta {{\rho }_{g}}) - \frac{1}{2}. \\ \end{gathered} $Используя равенство ∆ρg = fd – fs и уравнения (5), (7), функцию $\frac{{\Delta {{V}_{g}}}}{V}$ можно представить как
(8)
$\begin{gathered} \frac{{\Delta {{V}_{g}}}}{V} = \frac{{({{f}_{d}} + f_{d}^{2} - f_{s}^{2})(1 + {{f}_{s}} - {{f}_{d}})}}{{2{{f}_{s}}}} - \frac{{{{f}_{d}} - {{f}_{s}}}}{2} = \\ = \frac{{{{f}_{d}}}}{{{{f}_{s}}}}\left( {\frac{1}{2} + \frac{{{{f}_{d}}{{f}_{s}}}}{2} + \frac{{{{f}_{d}}f_{s}^{2}}}{2} + ...} \right). \\ \end{gathered} $Рассмотрим следующие условия: fs > 0 [7] и ΔVg/V > 0, т.е. относительный объем верхней части увеличивается в изохорном процессе, тогда в асимптотической температурной области (∆T > 0 мало) из уравнения (8) можно получить следующее неравенство:
Вывод (9) получен впервые и является справедливым для любой формы функций fd(τ), fs(τ) в указанных условиях. Представим ΔVg как элементарный объем образца , имеющего высоту ht, и запишем отношение ΔVg/V как приближенную функцию с аргументом ht в виде
Смещение ht можно с использованием (8) и (10) представить в виде
где ur = fd/fs – комплекс, зависящий от температуры.Из уравнения (11) следует, что смещение ht не является единственным значением, которое отвечало бы высоте (hM = 19.1 мм), предложенной в [1].
ОЦЕНКА ПОЛОЖЕНИЯ МЕНИСКА В ЭКСПЕРИМЕНТЕ II И НЕКОТОРЫЕ ЧИСЛЕННЫЕ ДАННЫЕ О ПЛОТНОСТИ С6F6
Для построения функции ht(T) применительно к температурным условиям, которые реализованы в эксперименте II [1], предлагается следующий подход. На первом этапе выбираются комбинированные модели fs(C, D, τ), fd(C, D, τ) для представления fs, fd в виде [2, 3, 13]:
(12)
${{f}_{s}} = {{B}_{{s0}}}{{\tau }^{\beta }} + {{B}_{{s1}}}{{\tau }^{{\beta + \Delta }}} + {{B}_{{s2}}}{{\tau }^{{\beta + 2\Delta }}} + {{B}_{{s3}}}{{\tau }^{2}} + {{B}_{{s4}}}{{\tau }^{3}},$(13)
$\begin{gathered} {{f}_{d}} = {{B}_{{d0}}}{{\tau }^{{1 - \alpha }}} + {{B}_{{d\exp }}}{{\tau }^{{2\beta }}} + \\ + \,\,{{B}_{{d1}}}{{\tau }^{{1 - \alpha + \Delta }}} + {{B}_{{d3}}}{{\tau }^{2}} + {{B}_{{d4}}}{{\tau }^{3}}, \\ \end{gathered} $Подчеркнем, во-первых, то, что в литературе отсутствуют скейлинговые модели, описывающие функции fs, fd и др. в критической области для C6F6. Значения C и D (12), (13) определялись на основе нелинейного метода наименьших квадратов (NRMS) [5, 13] и экспериментальных (ρl, ρg, T)-данных для C6F6 [1]. Во-вторых, структура моделей (12), (13) содержит лидирующие скейлинговые компоненты Bd0τ1 – α, Bd0τ2β, которые отражают современные тенденции МТ [2, 3, 6, 13].
В методе NRMS на первом этапе выбирается следующая информация:
• начальное приближение для D таково: Tc = = 516.62 К [1], ρс = 550.9 кг/м3 [1], α = 0.11 [7], β = = 0.325 [7], Вs0 = 2.0 [7], Bd0 = 0.5 [7], Bdexp = 0.2;
• лидирующий компонент fd (13) отвечает неравенству Bdexp > 0 (см. условие (9)).
На втором рассчитываются значения C, D: Tc = = 516.65 К, ρс = 550.43 кг/м3, α = 0.131, β = 0.348, Bs0 = 2.145, Bd0 = 0.595, Bdexp = 0.1005.
Полученные модели (12), (13) послужили основой для функций ρl(τ, D, C), ρg(τ, D, C) в следующем виде:
(14)
${{\rho }_{l}} = ({{f}_{d}} + {{f}_{s}} + 1){{\rho }_{c}},\,\,\,\,{{\rho }_{g}} = ({{f}_{d}}--{{f}_{s}} + 1){{\rho }_{c}}.$На основе уравнений (11)–(14) получены некоторые численные величины. Рассчитаны (ρg, ρl, T)-данные на изотермах [1]. Результаты согласуются с (ρl, ρg, Т)-данными [1] с приемлемой точностью в интервале (2 × 10–4 < τ < 0.2). Средние квадратические отклонения (СКО) Sg, Sl для (ρl, ρg, T)-данных [1] от результатов уравнений (14) составили: Sg = 0.52%, Sl = 0.12%.
Подход NRMS [5, 13] дал возможность определить коэффициенты для скейлинговой части – fs scale= Bs0τβ+ Bs1τβ + Δ+ Bs2τβ + 2Δ, fd scale= Bd0τ1 – α+ + Bdexpτ2β+ Bd1τ1 – α + Δ, входящей в (12), (13). Соответствующие им функции ρl(τ, D), ρg(τ, D) дают удовлетворительное согласование с экспериментом [1] в интервале (2 × 10–4 < τ < 0.1), при этом СКО составляют Sg = 0.31%, Sl = 0.16%.
Часть численных результатов можно видеть в табл. 1. Там же представлены экспериментальные величины плотности и данные о urexp, ht exp, T. При вычислении последних привлекались (ρl, ρg, T)-данные [1], уравнение (11) и значения D, найденные на втором этапе.
Сравнение показывает, что экспериментальные значения ρl, ρg заметно отклоняются от соответствующих расчетных величин (табл. 1). Из анализа следует, что выявленные отклонения экспериментальных значений плотностей приводят к тому, что (urexp, htexp, T)-данные являются немонотонными. Расчетные (ht, T)-данные монотонно убывают с ростом температуры (табл. 1). На рис. 2 качественно показаны линии (1, 2, 6), отвечающие смещениям ht при температурах 515.98, 516.28, 516.57 К.
Рассчитанные (ur, ht, T)-данные существенно зависят от лидирующих компонентов Bs0τβ, Bd0τ2β в соответствии с уравнением (11). При приближении к Тс значения ur и ht положительны и стремятся к нулю.
Данные о ht, T (табл. 1) использованы для оценки средней интегральной плотности ρmidl в объеме Vl с помощью распределения ρ(h – hM) на изотермах (рис. 2). Для этого принято, что высота мениска hМV = 19.1 мм отвечает следующим граничным условиям:
• соответствующая температура образца составляет T = 516.57 К (максимальная температура в эксперименте [1]);
• соответствующее смещение мениска составляет ht1 = 0.083 мм (табл. 1); указанное состояние отвечает аргументу (hi – hM = 0, i = 1) и линии 6 (рис. 2).
На втором шаге из распределения ρ(hi – hM) (например, линия 5, T = 516.57 К, рис. 2) получены распределения ρ(hti) при температурах 515.98, 516.28, 516.57 К.
На третьем шаге рассмотрена гипотеза А, которая объясняет влияние гравитации (g = 9.8 м с–2) на распределение ρ(ht) при заданной температуре. В рамках гипотезы А в образце создается ряд условий. Во-первых, температура образца отвечает значению 516.57 К, его плотность ρcell ≈ ρc = const, мениск имеет смещение ht1 = 0.083 мм, которое реализовано выше в условиях микрогравитации (g = gM).
Во-вторых, повышается гравитация в ячейке, в результате чего начальное распределение ρ(h), которое отвечает микрогравитации (g = gM) и имеет скачок (ρl – ρg), будет изменяться. Согласно гипотезе А, градиент давления, возникающий по высоте ячейки при гравитации (g = 9.8 м/с2), вызывает процесс, благодаря которому происходит перераспределение молекул, находящихся в объеме Vl. Так, существенно уменьшится количество молекул в элементарном объеме, который расположен снизу вблизи плоскости Sv, имеющей смещение ht1 = 0.083 мм. Начальная плотность ρl, соответствующая микрогравитации (g = gM), уменьшается до конечного значения ρ(ht1) (рис. 2) при g = 9.8 м/с2, т.е. эффект Δρ(T, h) = ρ(ht1) – ρl, который вызван гравитацией (g = 9.8 м/с2), является отрицательным.
В связи с перераспределением молекул в элементарном объеме, который расположен вблизи нижней образующей цилиндра, существенно меняется начальная плотность ρl: она увеличивается до значения ρ(ht), так как эффект Δρ(T, h) является положительным при h – hM = 0.
В целом начальный профиль плотности превращается в непрерывную зависимость ρ(h) (линия 5, рис. 2), при этом в соответствии с гипотезой А средняя плотность ρmidl в объеме Vl не меняется в связи с указанными процессами, и выполняется условие ρmidl = ρl.
На основании гипотезы А найдены:
а) элементарные массы Δhti Ls(hti)ρ(hti), i = 1 … N, здесь Δhti = (ht (i+ 1) – hti) – высота элементарного объема, s(hti) – длина секущей, которая относится к сечению ячейки и отстоит на hti от оси цилиндра, N – число участков на интервале (19.1 мм – ht1),
б) элементарные объемы ΔhtiLs(hti), i = 1 … N в интервале от ht1 до htN.
На четвертом шаге было выполнено численное интегрирование указанных масс и объемов в интервале от ht1 до htN. В итоге этой обработки определены: Mmidl, Vmidl и их отношение ρmidl = = 606.49 кг/м3 (линия 9, рис. 2, табл. 2), которое представляет собой плотность образца в объеме Vl.
Таблица 2.
Плотности (ρmidl, ρmidg) на околокритических изотермах C6F6
| Т, К | ρmidl, кг/м3 | ρmid g, кг/м3 |
|---|---|---|
| 515.98 | 668.94 | 435.03 |
| 516.28 | 646.49 | 456.29 |
| 516.57 | 606.49 | 494.93 |
Аналогичным образом рассчитаны Mmidg, Vmidg и их отношение ρmidg = 456.29 кг/м3 (табл. 2), которое представляет собой среднюю плотность образца в объеме Vg.
На рис. 3 показан пример экспериментального распределения ρ(h) (линии 1–3) от нижней цилиндра до верхней образующей при T = 516.28 К.
На пятом шаге из распределений ρ(h – hM), которые получены в эксперименте II при температурах 515.98, 516.28 К, и с помощью схемы вычисления, рассмотренной выше, определены ρmidl, ρmidg на указанных изотермах (табл. 2).
В целом данные результаты дали возможность сформировать модифицированный массив (ρl, ρg, Т)-данных, в который внесены:
• экспериментальные (ρl, ρg, T)-данные [1] при температурах 298.79–516.57 К, из которых исключены точки, относящиеся к температурам 515.98, 516.28, 516.57 К;
• (ρl, ρg, T)-данные, которые содержатся в табл. 2.
На основе модифицированного массива данных и методики NRMS вычислены параметры C, D, входящие в (12), (13) (табл. 3).
Таблица 3.
Параметры модели (12), (13) для C6F6
| ρc, кг/м3 | Tc, К | α | β | Bs0 | Bs1 | Bs2 |
|---|---|---|---|---|---|---|
| 550.77 | 516.65 | 0.12985 | 0.34799 | 2.14345 | 0.134753 | –1.253085 |
| Bs3 | Bs4 | Bd0 | Bdexp | Bd2 | Bd3 | Bd4 |
| 1.40842 | –0.897481 | 0.59485 | 0.09995 | 0.042626 | 1.490123 | –2.520365 |
Рассчитаны плотности ρi и локальные отклонения δρ = 100(ρi – ρ(14)i/ρi, где ρ(14)i – значение плотности, рассчитанное с помощью уравнений (14), ρi – плотность, входящая в модифицированные (ρl, ρg, Т)-данные.
Анализ показал, что уравнения (14) представляют экспериментальные (ρl, ρg, Т)-данные [1] с приемлемой точностью в интервале (2 × 10–4 < τ < < 0.2). СКО для (ρl, ρg, T)-данных [1] от значений, полученных по уравнению (14), определены как Sg = 0.48%, Sl = 0.12%.
Представляет интерес расположение мениска при граничных условиях эксперимента I:
• ρcell следует неравенству ρcell> ρc (рис. 1а, линия 3);
• температура T отвечает неравенству T < TCX, где TCX – температура, которая относится к точке c (рис. 1а), лежащей на линии насыщения; плотность в точке с отвечает равенству ρl = ρcell;
• гравитационный эффект значительно снижен в ячейке, например, благодаря ее размещению в космической лаборатории (условия микрогравитации, g = gM).
Рассмотрим состояние III для образца в ячейке, когда его параметры отвечают равенствам $T = {{T}_{{{\text{cross}}}}},$ ρ = ρcell (точка d, рис. 1а); смещение мениска ht = 0; верхняя и нижняя части имеют объем V/2. Плотности вещества отвечают равенствам: ${{\rho }_{g}} = {{\rho }_{g}}({{T}_{{{\text{cross}}}}}),$ ${{\rho }_{l}} = {{\rho }_{l}}({{T}_{{{\text{cross}}}}}).$
Переведем образец в состояние IV, его параметры таковы: TCX > T > Tcross, ρ = ρcell (точка e, рис. 1а). В состоянии IV мениск отвечает линии 8 (рис. 1б). Для состояния IV используется массовый баланс и Vg/V записывается в виде
(15)
${{V}_{g}}{{\rho }_{g}} + (V - {{V}_{g}}){{\rho }_{l}} = V{{\rho }_{{{\text{cell}}}}},\,\,\,\,\frac{{{{V}_{g}}}}{V} = \frac{{{{\rho }_{{{\text{cell}}}}} - {{\rho }_{l}}}}{{{{\rho }_{g}} - {{\rho }_{l}}}}.$Введя в (15) функции Δρl, Δρg, Δρсell = $\frac{{{{\rho }_{{{\text{cell}}}}} - {{\rho }_{c}}}}{{{{\rho }_{c}}}},$ можно выразить Vg/V в форме
(16)
$\frac{{{{V}_{g}}}}{V} = \frac{{\Delta {{\rho }_{l}}}}{{\Delta {{\rho }_{l}} - \Delta {{\rho }_{g}}}} - \frac{{\Delta {{\rho }_{{{\text{cell}}}}}}}{{\Delta {{\rho }_{l}} - \Delta {{\rho }_{g}}}}.$Можно записать функцию Δρсell, относящуюся к состоянию IV, в виде
(17)
$\Delta {{\rho }_{{{\text{cell}}}}} = \frac{1}{2}(\Delta {{\rho }_{l}}({{T}_{{{\text{cross}}}}}) + \Delta {{\rho }_{g}}({{T}_{{{\text{cross}}}}})) = {{f}_{d}}({{T}_{{{\text{cross}}}}}).$Введя смещение мениска ht в отношение Vg/V, используя (10), (16) и (17), получим
(18)
$\frac{{\Delta {{V}_{g}}}}{V} = \frac{{4{{h}_{t}}Ld}}{{\pi {{d}^{2}}L}} = \frac{1}{2} - \frac{{{{f}_{s}} + {{f}_{d}}}}{{2{{f}_{s}}}}ur - \frac{{{{f}_{d}}\left( {{{T}_{{{\text{cross}}}}}} \right)}}{{2{{f}_{s}}}}.$Используя (18), запишем ht(T) в форме
(19)
${{h}_{t}} = \frac{{{\pi }d}}{8}\left( { - ur + \frac{{{{f}_{d}}\left( {{{T}_{{{\text{cross}}}}}} \right)}}{{{{f}_{s}}}}} \right).$Формула (19) показывает, что смещение ht существенно зависит не только от комплекса ur, но и от плотности образца ρсell.
НЕКОТОРЫЕ ЧИСЛЕННЫЕ ДАННЫЕ О ПЛОТНОСТИ SF6 И ОЦЕНКА ПОЛОЖЕНИЯ МЕНИСКА В ЭКСПЕРИМЕНТЕ I
В эксперименте I используется цилиндрическая ячейка, имеющая d = (10.606 ± 0.005) мм и эффективный объем V = 221.7 мм3. В эксперименте проводится ряд измерений, в том числе определяются смещение ht (линия 13, рис. 1б) и температура двухфазного образца в заданном интервале при условии ρcell > ρc. В статье [8] представлены результаты, среди которых:
• график экспериментальной функции y = ht/r в диапазоне температур от 308 К до температур, очень близких к Tc, при этом минимальное отклонение от Tc составляет ~1 мК;
• аналитическая форма для функции y(τ) в виде
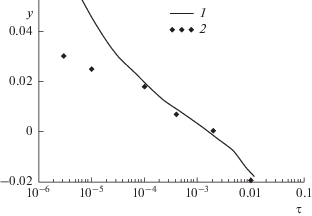
где 0.002 = Δρсell = $\frac{{{{\rho }_{{{\text{cell}}}}} - {{\rho }_{c}}}}{{{{\rho }_{c}}}},$ x = 0.06 – поправочный член, связанный с эффективным объемом ячейки.В [8] представлены такие значения, как Tc = = 318.707297 К, TCX = 318.707270 К, 317.823 > Tcross > > 318.123 К, ρc = (742.0 ± 1.5) кг/м3. Функция y(τ) показана на рис. 4 при относительных температурах τ = 10–6–10–2.
Интересной задачей является построение (ρg, ρl, T)-данных на основе значений (y, T) [8] при относительных температурах τ = 10–3–10–6. На первом этапе решения этой задачи выбраны комбинированные модели (12), (13) для представления функций fs, fd со значениями C и D, опубликованными в [3] для SF6. В работе [3] использовались экспериментальные (ρg, ρl, T)-данные [9] для вычисления значений C, D при температурах τ = = 2 × 10–4–0.3. Также в [3] представлены такие значения D, как Tc = 318.7095 К, ρс= 741.61 кг/м3, α = 0.1098, β = 0.34745, Bd0 = 0.25491, Bs0 = 1.9569, Bdexp = 0.08499.
Отметим, что авторы [9] оценили ошибку δρexp ≤ 0.1% для своих (ρg, ρl, T)-данных и определили такие значения D, как Tc = 318.723 К и ρc = = 742.26 кг/м3.
Далее выбираются экспериментальные данные yexpi, Ti, i = 1 … N, которые имеются в [8] при τ = 10–3–10–6 (рис. 4). С использованием этих значений и функции fs (12), коэффициенты которой приведены в [3], рассчитаны некоторые величины, часть которых показана в табл. 4:
Таблица 4.
Некоторые результаты второго этапа расчетов для SF6
| T, К | yexp | fs | ur | fd | ρg, кг/м3 | ρl, кг/м3 |
|---|---|---|---|---|---|---|
| 318.583 | 0.00712 | 0.12897 | 0.00713 | 0.000923 | 646.65 | 837.92 |
| 318.678 | 0.0185 | 0.07964 | 0.00351 | 0.000281 | 682.76 | 800.86 |
| 318.707 | 0.0251 | 0.03576 | 0.0260 | 0.000935 | 715.78 | 768.81 |
| 318.709 | 0.0315 | 0.02353 | 0.0488 | 0.00115 | 725.02 | 759.91 |
• данные о fsi, Ti, i = 1…4;
• значения uri, Ti, i = 1…4, полученные с помощью уравнения (20), и данные yexpi, Ti и fsi, Ti;
• данные fdi, Ti, i = 1…4, полученные с помощью uri, Ti и fsi, Ti;
• ρgi, ρli, Ti, i = 1…4, полученные с использованием уравнений (14), fdi, Ti; fsi, Ti и ρc [3].
Сформированы комбинированные (ρg, ρl, T)-данные. Этот массив объединил данные из табл. 4 и экспериментальные данные [9]. С помощью этого массива и NRMS определены параметры C, D, входящие в модели (12), (13) (табл. 5).
Таблица 5.
Параметры моделей (12), (13) для SF6
| ρc, кг/м3 | Tc, К | α4 | β4 | Bs0 | Bs1 | Bs2 |
|---|---|---|---|---|---|---|
| 741.645 | 318.7101 | 0.1112 | 0.3477 | 1.95825 | 0.021714 | –0.060572 |
| Bs3 | Bs4 | Bd0 | Bdexp | Bd2 | Bd3 | Bd4 |
| –0.938958 | 1.211974 | 0.25941 | 0.08521 | 1.02283 | –0.84764 | 0.620608 |
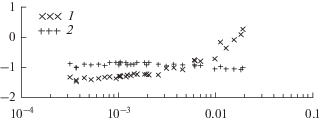
Сравним результаты, которые основываются на функциях ρl(τ, D, C), ρg(τ, D, C), содержащих параметры D, С (табл. 5). Во-первых, подсчитаны локальные отклонения δρl = 100(ρi – ρl(τ, D, C)/ρl, δρg = 100 (ρg – ρg(τ, D, C)/ρg. В этом сравнении используются комбинированные (ρg, ρl, T)-данные. СКО от соответствующих функций ρl(τ, D, C), ρg(τ, D, C) определены как Sg = 0.067% и Sl = = 0.029%. Во-вторых, анализ показал, что уравнения ρl(τ, D, C), ρg(τ, D, C) передают комбинированные (ρg, ρl, T)-данные с приемлемой точностью в интервале (2 × 10–6 < τ < 0.3) (рис. 5). Отметим, что (ρg, ρl, T)-данные [9] имеют погрешность, оцениваемую в [9] как δρexp ≤ 0.1%.
Рис. 5.
Сравнение комбинированных (ρl, ρg, T)-данных с функциями ρl(τ, D, C) и ρg(τ, D, C): 1 – δρg, 2 – δρl.

В-третьих, получены локальные отклонения δρl, δρg (рис. 6), которые относятся к (ρg, ρl, T)-массиву [10]. Эти экспериментальные результаты использованы в работах [2–6, 11, 12] для построения скейлинговых моделей fs(τ), fd(τ), Dm(τ) и др. для SF6. Анализ позволил оценить:
а) среднее арифметическое отклонение δρlM = = (Σδρli)/N2, i = 1… N2, N2 = 33 для (ρl, T)-данных [10] как δρlM = –0.95%;
б) среднее арифметическое отклонение δρgM = = (Σδρgi)/N2, i = 1… N2 для (ρg, T) [10] в δρgM = = ‒1.05%.
Существует несколько моделей в упомянутых исследованиях, в том числе:
1) модель средней относительной плотности на бинодали Fd = (ρl + ρg)(2ρc)–1 в виде Fd = = ${{A}_{0}} + {{A}_{1}}\tau $ [12], где A0 = 1.0024, A1 – α = 1.018, Tc = = 318.707 К, ρc = 733 кг/м3;
2) Fd = ${{A}_{0}} + {{A}_{{{\text{1}} - \alpha }}}{{\tau }^{{{\text{1}} - \alpha }}}$ [12], где A0 = 1.0012, A1 – α = = 0.6909, α = 0.11;
3) fd =${{B}_{{2\beta }}}{{\tau }^{{2\beta }}}$ [4], где 2β = 0.78, Tc = 318.707 К, ρc = 733 кг/м3;
4) fd = ${{B}_{{{\text{1}} - \alpha }}}{{\tau }^{{{\text{1}} - \alpha }}} + {{B}_{{2\beta }}}{{\tau }^{{2\beta {\text{ }}}}}~ + {{B}_{1}}\tau + ...$ [6] (результаты данной модели соответствуют линии 2, рис. 1а), где B2β = 1.0864, B1 – α = −7.990, B1 = 9.770, α = 0.11, β = 0.325, Tc = 318.707 К, ρc = 733 кг/м3.
Модели (12), (13) и (14), построенные для SF6, дают независимую основу для оценки погрешности приведенных литературных моделей. Как отдельную важную проблему следует рассматривать вопрос о методе, позволяющем уменьшить систематические ошибки (ρg, ρl, T)-данных [10], рассмотренных выше. Данный вопрос заслуживает отдельного рассмотрения.
ЗАКЛЮЧЕНИЕ
Исследовано высотное распределение плотности ρ(h) для образца C6F6, погруженного в ячейку [1] при гравитации (g = 9.8 м/с2). Предложено уравнение ht(T), которое описывает положение мениска в ячейке при граничных условиях ρcell = ρc, на околокритических изотермах в условиях микрогравитации (g = gM). Полученное уравнение показывает, что ht(T) существенно зависит от комплекса ur и параметра порядка fs.
Рассчитаны некоторые численные данные, которые относятся к температурам от 515.92 до 516.57 К и включают: а) смещения ht в интервале от 0.208 мм до 0.079 мм, б) (ρl, ρg, Т)-данные. На основе комбинированного массива (ρl, ρg, Т)-данных построены модели (12), (13), применимые в интервале 2 × 10–4 < τ < 0.2 для С6F6.
Предложено уравнение ht(T), описывающее положение мениска в ячейке с двухфазным образцом SF6 применительно к эксперименту I в условиях микрогравитации (g = gM). Выбраны экспериментальные данные, включающие значения (yi = hti/r, Ti, i = 1… N) [8] в диапазоне температур τ = 10–2–10–6 и интервале ht от –0.101 до 0.159 мм. Разработан метод, который дает возможность:
• вычислить (ρl, ρg, Т)-данные с помощью отмеченных (y, T)-значений;
• сформировать комбинированный массив (ρl, ρg, Т)-данных, которые включают новые значения и точки [9] в интервале 2 × 10–6 < τ < 0.3;
• получить параметры D, C моделей (12), (13) для SF6.
Анализ показал, что полученные функции ρl(τ, D, C), ρg(τ, D, C) для SF6 и C6F6 удовлетворительно описывают соответствующие исходные (ρl, ρg, Т)-данные. Так, отклонение комбинированных (ρl, ρg, Т)-данных, включая точки [9], является удовлетворительным (Sg = 0.067%, Sl = = 0.029%) в интервале 2 × 10–6 < τ < 0.3. Из сравнения видно, что (ρl, ρg, T)-данные [10] содержат систематическое отклонение δρM ≈ –1.0% в интервале τ = 2 × 10–4–0.02. Интересно, что функция fd (13) содержит скейлинговый компонент ${{B}_{{d\exp }}}{{\tau }^{{2\beta }}}$ (Bdexp > 0) и не включает линейного члена. Эти особенности отражают современные тенденции МТ [2, 3, 6, 13].
Список литературы
Stankus S.V., Khairulin R.A. Properties of Perfluorobenzene near the Critical Point // Int. J. Thermophys. 2006. V. 27. № 4. P. 1110.
Vorob’ev V.S., Rykov V.A., Ustyuzhanin E.E., Shishakov V.V., Popov P.V., Rykov S.V. Comparison of the Scaling Mo-dels for Substance Densities Along Saturation Line // J. Phys.: Conf. Ser. 2016. V. 774. 012017.
Vorob’ev V.S., Ochkov V.F., Rykov V.A., Rykov S.V., Ustyuzhanin E.E., Pokholchenko V.A. Development of Combined Scaling Models for Liquid and Gas Densities at the Saturation Line: Structures and Numerical Data for SF6 // J. Phys.: Conf. Ser. 2019. V. 1147. 012016.
Losada-Pérez P., Cerdeiriña C.A. Coexisting Densities and Critical Asymmetry between Gas and Liquid // J. Chem. Thermodynamics. 2017. V. 109. P. 56.
Устюжанин Е.Е., Шишаков В.В., Попов П.В., Рыков В.А., Френкель М.Л. Скейлинговые модели для описания термодинамических свойств веществ на линии насыщения: перспективы и ограничения // Вестник МЭИ. 2011. № 6. С. 167.
Fisher M.E., Orkoulas G. The Yang–Yang Anomaly in Fluid Criticality: Experiment and Scaling Theory // Phys. Rev. Lett. 2000. V. 85. P. 696.
Анисимов М.А. и др. Термодинамика критического состояния индивидуальных веществ. М.: Энергоиздат, 1990. 125 с.
Garrabos Y., Lecoutre C., Marre S., Beysens D., Hahn I. Liquid-vapor Rectilinear Diameter Revisited // Phys. Rev. E. 2018. V. 97. P. 020101(R).
Funke M., Kleinrahm R., Wagner W. Measurement and Correlation of the (p, ρ, T) Relation of Sulphur Hexafluoride (SF6). II. Saturated-liquid and Saturated-vapour Densities and Vapour Pressures Along the Entire Coexistence Curve // J. Chem. Thermod. 2001. V. 34. P. 735.
Weiner J., Langley K.H., Ford Jr. N.C. Experimental Evidence for a Departure from the Law of the Rectilinear Diameter // Phys. Rev. Lett. 1974. V. 32. P. 879.
Anisimov M.A., Wang J. Nature of Asymmetry in Fluid Criticality // Phys. Rev. E. 2007. 051107.
Pestak M.W., Goldstein R.E., Chan M.H.W., de Bruyn J.R., Balzarini D.A., Ashcroft N.W. Three-body Interactions, Scaling Variables, and Singular Diameters in the Coexistence Curves of Fluids // Phys. Rev. 1987. V. 36. P. 599.
Ochkov V.F., Rykov V.A., Rykov S.V., Ustyuzhanin E.E., Znamensky B.E. Extrapolation of IAPWS-IF97 Data: The Liquid and Gas Densities on the Saturation Line near the Critical Point of H2O // J. Phys.: Conf. Ser. 2018. V. 946. 012119.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур