Теплофизика высоких температур, 2021, T. 59, № 1, стр. 100-108
Численное исследование влияния колебаний сферически затупленного конуса при обтекании сверхзвуковым потоком воздуха на характеристики сопряженного тепломассообмена
К. Н. Ефимов 1, В. А. Овчинников 1, А. С. Якимов 1, *
1 Национальный исследовательский Томский государственный университет
Томск, Россия
* E-mail: yakimovas@mail.ru
Поступила в редакцию 06.11.2019
После доработки 15.05.2020
Принята к публикации 14.10.2020
Аннотация
Работа посвящена изучению воздействия флуктуаций тела, обтекаемого сверхзвуковым потоком воздуха, на сопряженный тепломассообмен в теплозащитном материале при наличии вдува продуктов термохимического разрушения и тепломассообмена между телом и набегающим потоком. Представлены результаты численного исследования пространственного сверхзвукового потока около сферически затупленного конуса, совершающего колебательное движение в плоскости тангажа. Рассматривается влияние колебаний тела с угловой скоростью в диапазоне 0–100 градус/с на температуру поверхности и теплообменные характеристики.
ВВЕДЕНИЕ
Летательные аппараты при движении с гиперзвуковыми скоростями в плотных слоях атмосферы Земли подвергаются сильному тепловому воздействию, приводящему к изменению их формы и аэродинамических характеристик. Колебательные движения меняют условия обтекания и тепловое состояние тела по сравнению со случаем его отсутствия. Ранее, например в работах [1, 2], были проведены исследования влияния переменных углов атаки на аэродинамические характеристики обтекаемых осесимметричных тел. В связи с этим интересно проанализировать влияние таких колебательных движений на тепловое состояние тела при взаимодействии с высокоэнтальпийными потоками. При обтекании тела с постоянным углом атаки [3, 4] разница тепловых потоков на подветренной и наветренной сторонах может быть очень значительной, что приводит к неравномерному нагреву. Для уменьшения этого эффекта сверхзвуковым летательным аппаратам могут придавать вращательные и колебательные движения. Взаимосвязанный характер протекания тепловых и аэродинамических процессов приводит к необходимости при математическом моделировании решать задачу в сопряженной постановке [5]. В публикациях [6–8] проведено исследование влияния вращения тела вокруг оси на характеристики сопряженного тепломассопереноса при пространственном сверхзвуковом обтекании.
В настоящей работе движение газового потока описывается уравнениями пограничного слоя с учетом ламинарного и турбулентного режимов течения. Для описания теплового состояния тела выписывается система уравнений сохранения для пористой среды. Учитываются различные процессы разрушения на конической части поверхности обтекаемого тела и фильтрация охлаждающего газа в порах на сферическом затуплении. Задача решается в сопряженной постановке [5, 9], так как это позволяет существенно повысить точность определения аэродинамических и тепловых характеристик по сравнению с раздельными оценками аэродинамики, термохимического разрушения, параметров движения тела.
ПОСТАНОВКА ЗАДАЧИ
В работах [5, 9] проведены оценки времен релаксации в газовой и конденсированной фазах. На основании этих оценок характеристики сопряженного тепломассообмена находятся из решения квазистационарных уравнений пространственного пограничного слоя при различных режимах течения. Тепловое состояние пористой оболочки определяется из решения нестационарного уравнения сохранения энергии для пористого сферического затупления и квазистационарного уравнения для скорости фильтрации охлаждающего газа в порах в рамках однотемпературной модели.
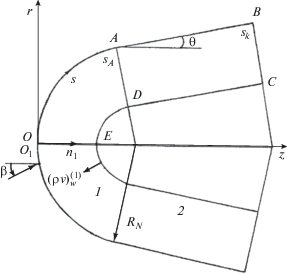
Для модели химически равновесного воздуха по гипотезе “пассивности” и равенства единице чисел Льюиса для всех компонентов система уравнений пространственного пограничного слоя в естественной системе координат, связанной с внешней поверхностью обтекаемой оболочки, имеет вид [3, 8] (рис. 1)
(1)
$\frac{\partial }{{\partial s}}\left( {\rho u{{r}_{w}}} \right) + \frac{\partial }{{\partial n}}\left( {\rho v{{r}_{w}}} \right) + \frac{\partial }{{\partial \eta }}(\rho w) = 0,$(2)
$\begin{gathered} \rho \left( {u\frac{{\partial u}}{{\partial s}} + v\frac{{\partial u}}{{\partial n}} + \frac{w}{{{{r}_{w}}}}\frac{{\partial u}}{{\partial \eta }} - \frac{{{{w}^{2}}}}{{{{r}_{w}}}}\frac{{\partial {{r}_{w}}}}{{\partial s}}} \right) = \\ = - \frac{{\partial {{P}_{e}}}}{{\partial s}} + \frac{\partial }{{\partial n}}\left( {{{\mu }_{\Sigma }}\frac{{\partial u}}{{\partial n}}} \right), \\ \end{gathered} $(3)
$\begin{gathered} \rho \left( {u\frac{{\partial w}}{{\partial s}} + v\frac{{\partial w}}{{\partial n}} + \frac{w}{{{{r}_{w}}}}\frac{{\partial w}}{{\partial \eta }} + \frac{{uw}}{{{{r}_{w}}}}\frac{{\partial {{r}_{w}}}}{{\partial s}}} \right) = \\ = - \frac{1}{{{{r}_{w}}}}\frac{{\partial {{P}_{e}}}}{{\partial \eta }} + \frac{\partial }{{\partial n}}\left( {{{\mu }_{\Sigma }}\frac{{\partial w}}{{\partial n}}} \right), \\ \end{gathered} $(4)
$\begin{gathered} \rho \left( {u\frac{{\partial H}}{{\partial s}} + v\frac{{\partial H}}{{\partial n}} + \frac{w}{{{{r}_{w}}}}\frac{{\partial H}}{{\partial \eta }}} \right) = \\ = \frac{\partial }{{\partial n}}\left\{ {\frac{{{{\mu }_{\Sigma }}}}{{{{{\Pr }}_{\Sigma }}}}\left[ {\frac{{\partial H}}{{\partial n}} + \left( {{{{\Pr }}_{\Sigma }}\, - 1} \right)\frac{\partial }{{\partial n}}\left( {\frac{{{{u}^{2}} + {{w}^{2}}}}{2}} \right)} \right]} \right\}, \\ \end{gathered} $(5)
$\begin{gathered} P = {{\rho h({{\gamma }_{{{\text{ef}}}}} - 1)} \mathord{\left/ {\vphantom {{\rho h({{\gamma }_{{{\text{ef}}}}} - 1)} {{{\gamma }_{{{\text{ef}}}}},\,\,\,\,P = {{P}_{e}}(s,\eta )}}} \right. \kern-0em} {{{\gamma }_{{{\text{ef}}}}},\,\,\,\,P = {{P}_{e}}(s,\eta )}}, \\ H = h + {{({{u}^{2}} + {{w}^{2}})} \mathord{\left/ {\vphantom {{({{u}^{2}} + {{w}^{2}})} 2}} \right. \kern-0em} 2}, \\ {{\mu }_{\Sigma }} = \mu + \Gamma {{\mu }_{T}},\,\,\,\,{{\Pr }_{\Sigma }} = \frac{{(\mu + Г{{\mu }_{T}})\Pr {{{\Pr }}_{T}}}}{{\mu {{{\Pr }}_{T}}\, + Г{{\mu }_{Т}}\Pr }}. \\ \end{gathered} $(7)
$\begin{gathered} {{(\rho {{c}_{p}})}_{1}}(1 - \varphi )\frac{{\partial {{T}_{1}}}}{{\partial t}} = \frac{1}{{{{r}_{1}}{{H}_{1}}}}\left\{ {\frac{\partial }{{\partial {{n}_{1}}}}\left[ {{{r}_{1}}{{H}_{1}}{{\lambda }_{1}}(1 - \varphi )\frac{{\partial {{T}_{1}}}}{{\partial {{n}_{1}}}}} \right] + } \right. \\ + \,\,\frac{\partial }{{\partial s}}\left[ {\frac{{{{r}_{1}}{{\lambda }_{1}}}}{{{{H}_{1}}}}(1 - \varphi )\frac{{\partial {{T}_{1}}}}{{\partial s}}} \right] + \left. {\frac{\partial }{{\partial \eta }}\left[ {\frac{{{{H}_{1}}{{\lambda }_{1}}}}{{{{r}_{1}}}}\left( {1 - \varphi } \right)\frac{{\partial {{T}_{1}}}}{{\partial \eta }}} \right]} \right\} + \\ + \,\,{{c}_{{p2}}}\left( {\rho v} \right)_{w}^{{(1)}}\frac{{{{r}_{{1w}}}}}{{{{r}_{1}}{{H}_{1}}}}\frac{{\partial {{T}_{1}}}}{{\partial {{n}_{1}}}}, \\ \end{gathered} $(8)
$A\mu {v} + B{{\rho }_{2}}\varphi v\left| v \right| = - \frac{{\partial P}}{{\partial {{n}_{1}}}},$(9)
$\begin{gathered} P = \frac{{{{\rho }_{2}}R{{T}_{1}}}}{M},\,\,\,\,{{H}_{1}} = \frac{{{{R}_{N}} - {{n}_{1}}}}{{{{R}_{N}}}},\,\,\,\,\bar {s} = \frac{s}{{{{R}_{N}}}}, \\ {{r}_{1}} = ({{R}_{N}} - {{n}_{1}})\sin (\bar {s}),\,\,\,\,\mu \sim \sqrt {{{T}_{1}}} ,\,\,\,\,{{\lambda }_{1}}\sim \sqrt {{{T}_{1}}} , \\ \varphi = {\text{const}}{\text{.}} \\ \end{gathered} $(10)
$\begin{gathered} {{\rho }_{c}}{{c}_{p}}\left( {\frac{{\partial T}}{{\partial t}} - \psi \frac{{\partial T}}{{\partial {{n}_{1}}}}} \right) + {{c}_{{p2}}}G\frac{{\partial T}}{{\partial {{n}_{1}}}} = \frac{\partial }{{\partial {{n}_{1}}}}\left( {\lambda \frac{{\partial T}}{{\partial {{n}_{1}}}}} \right) + \\ + \,\,\frac{\partial }{{\partial s}}\left( {\lambda \frac{{\partial T}}{{\partial s}}} \right) + \frac{1}{{r_{2}^{2}}}\frac{\partial }{{\partial \eta }}\left( {\lambda \frac{{\partial T}}{{\partial \eta }}} \right) - {{Q}_{c}}\frac{{d{{\rho }_{c}}}}{{dt}}, \\ \end{gathered} $(11)
$\begin{gathered} \frac{{d{{\rho }_{c}}}}{{dt}} = \left( {\frac{{\partial {{\rho }_{c}}}}{{\partial t}} - \psi \frac{{\partial {{\rho }_{c}}}}{{\partial {{n}_{1}}}}} \right) = \\ = \left\{ \begin{gathered} - {{k}_{c}}{{\rho }_{{c0}}}\left( {\frac{{{{\rho }_{c}} - {{\rho }_{{c*}}}}}{{{{\rho }_{{c0}}}}}} \right)\exp \left( { - \frac{{{{E}_{c}}}}{{RT}}} \right),\,\,\,{{\rho }_{c}} > {{\rho }_{{c*}}}, \hfill \\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{\rho }_{c}} \leqslant {{\rho }_{{c*}}}, \hfill \\ \end{gathered} \right. \\ G = \int\limits_0^{{{l}_{1}}} {\frac{{d{{\rho }_{c}}}}{{dt}}d{{n}_{1}},} \,\,\,\,{{r}_{2}} = \left( {{{R}_{N}} - {{n}_{1}}} \right)\cos \theta + \left( {s - {{s}_{A}}} \right)\sin \theta , \\ l = L - x(t),\,\,\,\,x(t) = \int\limits_0^t {\psi d\tau } ,\,\,\,\,{{(\rho v)}_{{1w}}} = {{G}_{w}}, \\ \end{gathered} $(12)
$\begin{gathered} (\rho v)_{w}^{{(2)}} = {{(\rho v)}_{{1w}}} + {{(\rho v)}_{{2w}}} + {{(\rho v)}_{{3w}}}, \\ \psi = \sum\limits_{i = 2}^3 {\frac{{(\rho v)_{{iw}}^{{}}}}{{{{\rho }_{{cw}}}}}} . \\ \end{gathered} $Рис. 1.
Схема обтекания тела: 1 – пористое сферическое затупление, 2 – коническая часть тела из углепластика или графита.
В отличие от работ [6–8] в данной статье рассматриваются периодические колебания угла атаки в плоскости тангажа. Это движение описывается выражением
(13)
$\beta (t) = \left\{ \begin{gathered} {{\beta }_{m}} - \left| {{{\omega }_{f}}t - {{\beta }_{m}}} \right| - (i - 1){{B}_{f}}, \hfill \\ (i - 1){{B}_{f}} \leqslant t < {{B}_{f}}{i \mathord{\left/ {\vphantom {i 2}} \right. \kern-0em} 2}, \hfill \\ \left| {{{\omega }_{f}}t - 3{{\beta }_{m}}} \right| - {{\beta }_{m}} - {{B}_{f}}{i \mathord{\left/ {\vphantom {i 2}} \right. \kern-0em} 2}, \hfill \\ {{B}_{f}}{i \mathord{\left/ {\vphantom {i 2}} \right. \kern-0em} 2} \leqslant t < {{B}_{f}}i. \hfill \\ \end{gathered} \right.$В формуле (13) t – длительность процесса, i = = 1, 2…, ${{B}_{f}} = {{{{4{{\beta }_{m}}} \mathord{\left/ {\vphantom {{4{{\beta }_{m}}} \omega }} \right. \kern-0em} \omega }}_{f}}$ – период флуктуации, ${{\omega }_{f}}$ – угловая скорость изменения угла атаки β, βm – максимальный угол атаки.
Вводятся следующие допущения: 1) характерная линейная скорость колебания тела много меньше скорости набегающего потока: Ωf = $ = {{\omega }_{f}}{{{{R}_{N}}} \mathord{\left/ {\vphantom {{{{R}_{N}}} {{{V}_{\infty }}}}} \right. \kern-0em} {{{V}_{\infty }}}} \ll 1$; 2) характерное время колебательного процесса много больше времени релаксации газовой фазы (tω $ \gg $ ta, tω = 4βm/ωf , ta = RN/V∞). Это позволяет использовать уравнения пограничного слоя в квазистационарном виде.
Начальные условия:
(14)
${{\left. {{{T}_{1}}} \right|}_{{t = 0}}} = {{\left. T \right|}_{{t = 0}}} = {{T}_{0}},\,\,\,\,{{\rho }_{c}}\left| {_{{t = 0}}} \right. = {{\rho }_{{c0}}}.$(15)
$u \to {{u}_{e}}\left( {s,\eta } \right),\,\,\,\,w \to {{w}_{e}}\left( {s,\eta } \right),\,\,\,\,h \to {{h}_{e}}\left( {s,\eta } \right),$на поверхности обтекаемого тела при $n = 0$
(16)
$u\left( {s,\eta } \right) = 0,\,\,\,\,w = 0,\,\,\,\,v = {{v}_{w}},\,\,\,\,\left( {0 < s < {{s}_{A}}} \right).$(17)
$\begin{gathered} {{\left. {\frac{\mu }{{\Pr }}\left( {\frac{{\partial h}}{{\partial n}}} \right)} \right|}_{w}} - (1 - \varphi ){{\varepsilon }_{1}}\sigma T_{{1w}}^{4} = {{\left. { - {{\lambda }_{1}}\left( {1 - \varphi } \right)\left( {\frac{{\partial {{T}_{1}}}}{{\partial {{n}_{1}}}}} \right)} \right|}_{w}}, \\ 0 < s < {{s}_{A}}, \\ \end{gathered} $(18)
$\begin{gathered} {{\left. { - \lambda \frac{{\partial T}}{{\partial {{n}_{1}}}}} \right|}_{{{{n}_{1}} = 0 - x(t)}}} = {{\left. {\frac{\mu }{{\Pr }}\left( {\frac{{\partial h}}{{\partial n}}} \right)} \right|}_{w}} - \left( {{{h}_{w}} - {{h}_{c}}} \right)\sum\limits_{i = 2}^3 {\left( {\rho v} \right)_{{iw}}^{{}}} - \\ - \,\,\left( {\rho v} \right)_{{1w}}^{{}}\left( {{{h}_{w}} - {{h}_{g}}} \right) - \varepsilon \sigma T_{w}^{4},\,\,\,\,{{s}_{A}} \leqslant s \leqslant {{s}_{k}}. \\ \end{gathered} $На внутренней поверхности полусферы и конической части выписываются соотношения [9]:
(19)
${{\left. { - {{\lambda }_{1}}\left( {1 - \varphi } \right)\frac{{\partial {{T}_{1}}}}{{\partial {{n}_{1}}}}} \right|}_{{{{n}_{1}} = L}}} = \delta \left( {{{T}_{{1,L}}} - {{T}_{0}}} \right),\,\,\,\,0 < s < {{s}_{A}},$(20)
${{\left. {{{\rho }_{c}}} \right|}_{{{{n}_{1}} = l}}} = {{\rho }_{{c0}}},\,\,\,\,{{\left. {\lambda \frac{{\partial T}}{{\partial {{n}_{1}}}}} \right|}_{{{{n}_{1}} = \ell }}} = 0,\,\,\,\,{{s}_{A}} \leqslant s \leqslant {{s}_{k}}.$(21)
$\begin{gathered} {{\left. {\frac{{{{\lambda }_{1}}\left( {1 - \varphi } \right)}}{{{{H}_{1}}}}\frac{{\partial {{T}_{1}}}}{{\partial s}}} \right|}_{{s = {{s}_{A}} - 0}}} = {{\left. {\lambda \frac{{\partial T}}{{\partial s}}} \right|}_{{s = {{s}_{A}} + 0}}}, \\ {{\left. {{{T}_{1}}} \right|}_{{s = {{s}_{A}} - 0}}} = {{\left. T \right|}_{{s = {{s}_{A}} + 0}}},\,\,\,\,{{\left. {\frac{{\partial T}}{{\partial s}}} \right|}_{{s = {{s}_{k}}}}} = 0. \\ \end{gathered} $На внешней и внутренней поверхностях области сферического затупления имеет место равенство давлений в порах и во внешней среде
(22)
${{\left. {{{P}_{w}}} \right|}_{{{{n}_{1}} = 0}}} = {{P}_{e}}(s,\eta ),\,\,\,\,{{\left. P \right|}_{{{{n}_{1}} = L}}} = {{P}_{L}}.$При отсутствии плоскости симметрии течения имеют место условия периодичности
(23)
$\begin{gathered} {{T}_{1}}(t,{{n}_{1}},s,\eta ) = {{T}_{1}}(t,{{n}_{1}},s,\eta + 2\pi ), \\ T(t,{{n}_{1}},s,\eta ) = T(t,{{n}_{1}},s,\eta + 2\pi ). \\ \end{gathered} $На границе раздела сред при $s \geqslant {{s}_{A}}$ рассматривалась следующая кинетическая схема протекания неравновесных химических реакций (${{T}_{w}} \leqslant 4000$ К) [9, 10, 12]:
(24)
$\begin{gathered} C\, + {{O}_{2}} \to C{{O}_{2}},\,\,\,\,2C\, + {{O}_{2}} \to 2CO, \\ C\, + O \to CO,\,\,\,\,C\, + C{{O}_{2}} \to 2CO, \\ 2O\, + C \to {{O}_{2}}\, + C,\,\,\,\,2N\, + C \to {{N}_{2}}\, + C, \\ C \leftrightarrow {{C}_{1}},\,\,\,\,C \leftrightarrow {{C}_{3}}. \\ \end{gathered} $Молярные и массовые скорости протекания данных химических реакций (24) и выражение для массовой скорости уноса подробно описаны в [5, 9], а формулы для ${{(\rho v)}_{{2w}}}$, ${{(\rho v)}_{{3w}}}$ из (12) имеют вид
(25)
$\begin{gathered} {{(\rho v)}_{{2w}}} = {{\rho }_{w}}\left[ {\left( {\frac{{{{m}_{6}}}}{{{{m}_{2}}}} - 1} \right){{c}_{{2w}}}{{B}_{1}} + \left( {2\frac{{{{m}_{5}}}}{{{{m}_{2}}}} - 1} \right){{c}_{{2w}}}{{B}_{2}}} \right. + \\ + \,\,\left. {\left( {\frac{{{{m}_{5}}}}{{{{m}_{1}}}} - 1} \right){{c}_{{1w}}}{{B}_{3}} + \left( {2\frac{{{{m}_{5}}}}{{{{m}_{6}}}} - 1} \right){{c}_{{6w}}}{{B}_{4}}} \right], \\ {{(\rho v)}_{{3w}}} = \sum\limits_{i = 7}^8 {\frac{{{{m}_{i}}{{A}_{{ci}}}(P_{{ci}}^{*} - {{P}_{{ci}}})}}{{{{{(2\pi R{{T}_{w}}{{m}_{i}})}}^{{0.5}}}}}} ,\,\,\,\,i = 7,8, \\ P_{{ci}}^{*} = {{10}^{5}}\exp ({{D}_{i}} - {{{{E}_{i}}} \mathord{\left/ {\vphantom {{{{E}_{i}}} {{{T}_{w}}}}} \right. \kern-0em} {{{T}_{w}}}}), \\ {{B}_{i}} = {{k}_{{iw}}}\exp \left( {{{ - {{E}_{{iw}}}} \mathord{\left/ {\vphantom {{ - {{E}_{{iw}}}} {R{{T}_{w}}}}} \right. \kern-0em} {R{{T}_{w}}}}} \right),\,\,\,\,i = \overline {1,4} , \\ {{P}_{{ci}}} = {{P}_{e}}{{c}_{{iw}}}{{{{m}_{w}}} \mathord{\left/ {\vphantom {{{{m}_{w}}} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}},\,\,\,\,i = 7,8, \\ {{\rho }_{w}} = {{{{P}_{e}}{{m}_{w}}} \mathord{\left/ {\vphantom {{{{P}_{e}}{{m}_{w}}} {(R{{T}_{w}})}}} \right. \kern-0em} {(R{{T}_{w}})}},\,\,\,\,{{h}_{w}} = \sum\limits_{i = 1}^8 {{{h}_{i}}{{c}_{{iw}}}} , \\ m_{w}^{{ - 1}} = \sum\limits_{i = 1}^8 {{{{{c}_{{iw}}}} \mathord{\left/ {\vphantom {{{{c}_{{iw}}}} {{{m}_{i}}}}} \right. \kern-0em} {{{m}_{i}}}}} ,\,\,\,\,{{c}_{{p2}}} = {{b}_{1}} + b_{2}^{{}}T,\,\,\,\,{{h}_{g}} = \int\limits_0^T {{{c}_{{p2}}}dT} . \\ \end{gathered} $В (24), (25) порядковый номер компонентов соответствует следующему порядку их перечисления: $O,\;{{O}_{2}},\;N,\;{{N}_{2}},\;CO,\;C{{O}_{2}},{{C}_{1}},{{C}_{3}}$. C – обозначение твердофазного углерода, который принадлежит материалу теплозащитного покрытия. В пограничном слое имеются четыре компонента: $O,\;{{O}_{2}},\;N,\;{{N}_{2}}$, которые участвуют в двух равновесных химических реакциях: ${{O}_{2}} \leftrightarrow 2O$, ${{N}_{2}} \leftrightarrow 2N$. На границе конденсированной и газовой фаз присутствуют четыре компонента: $CO,\;C{{O}_{2}},{{C}_{1}},{{C}_{3}}$, которые возникают в шести гетерогенных реакциях горения и сублимации из (24). Учитываются также две реакции каталитической рекомбинации компонентов ${{O}_{2}},{{N}_{2}}$.
Балансовые соотношения для массовых концентраций компонент (${{c}_{{iw}}}$) запишем, используя закон Фика для диффузионных потоков и аналогию процессов тепло- и массообмена [10]:
Здесь и ниже $u,v,w$ − компоненты вектора среднемассовой скорости в естественной системе координат ($s,n,\eta $); Г – коэффициент перемежаемости; H, m – полная энтальпия и молекулярная масса; ${{R}_{N}}$ – радиус сферического затупления; ${{r}_{w}},{{r}_{i}}{\text{ (}}i = 1,2),{{H}_{1}}$ − коэффициенты Ламе; h и $\left( {\rho v} \right)_{w}^{{(1)}}$ − энтальпия и расход газа-охладителя с поверхности сферического затупления; ρ − плотность; μ − динамическая вязкость; P − давление; T – температура; $\left( {\rho v} \right)_{w}^{{(2)}}$ − полный массовый унос с углеродной поверхности конической части тела; A и B − вязкостный и инерционный коэффициенты в нелинейном законе Дарси (8); v − скорость фильтрации; φ − пористость сферического затупления; ${{c}_{p}}$ – коэффициент теплоемкости при постоянном давлении; λ – коэффициент теплопроводности; R – универсальная газовая постоянная; M – молекулярная масса газа в пористой оболочке; L – толщина оболочки; θ − угол конусности; β – угол атаки; ${{n}_{1}}$ – нормаль к поверхности направлена в глубь оболочки; ψ − линейная скорость перемещения поверхности разрушения; $x(t)$ − граница раздела газообразной и конденсированной фаз (глубина выгорания); ${{E}_{{iw}}},{{k}_{{iw}}}$ (i = 1, …, 4) – энергия активации и предэкспонент i-й гетерогенной реакции оболочки конической части тела; ${{k}_{c}}$, ${{E}_{c}}$ и ${{Q}_{c}}$ − предэкспонент, энергия активации и тепловой эффект реакции пиролиза; ${{H}_{\infty }}$, V∞ − высота и скорость набегающего потока на бесконечности; σ − постоянная Стефана‒Больцмана; ε − излучательная способность поверхности; G − массовый унос продуктов пиролиза углепластика; δ − коэффициент теплоотдачи на внутренней холодной поверхности сферической оболочки; Pr − число Прандтля.
Индексы e, e0 и w соответствуют величинам на внешней границе пограничного слоя, на внешней границе в точке торможения и на поверхности обтекаемого тела; (1), (2) внизу − характеристики каркаса и газа на сфере; g – газовая фаза на конической части поверхности; ∞ − величина набегающего газового потока на бесконечности; T, 0 – характеристика турбулентного переноса и начальные условия; L – внутренняя оболочка сферической части тела; $k$ – периферийный участок оболочки; (1), (2) вверху − характеристики, связанные с расходом охладителя на пористой полусфере и поверхностные химические реакции на конической части тела; черта вверху – безразмерный параметр; z – время окончания теплового воздействия; ef − эффективная величина; m – максимальное значение; с – углепластик.
МЕТОД РАСЧЕТА И ИСХОДНЫЕ ДАННЫЕ
Система уравнений (1)−(4), (6)−(8), (10), (11) с начальными и граничными условиями (14)−(23) решена численно. Система уравнений пространственного пограничного слоя решалась в переменных типа Дородницына с учетом ламинарной, переходной и турбулентной областей течения. Для описания турбулентного течения применялась двухслойная модель турбулентного пограничного слоя [13, 14]. Рассматриваемая трехслойная алгебраическая модель турбулентности учитывает наличие ламинарного вязкого подслоя, внутренней области турбулентного ядра, которая описывается формулой Ван-Дрийста‒Себечи [14], и внешней области, в которой используется формула Сполдинга [13]. Коэффициент перемежаемости и переход от ламинарного к турбулентному режиму течения описывался с помощью формулы Дхаваны‒Нарасимхи [15]. При численном интегрировании Pr = 0.72, ${{\Pr }_{T}} = 1$. Для уравнений пограничного слоя с помощью итерационно-интерполяционного метода [16] были получены комбинированные разностные схемы, обеспечивающие сращивание искомых характеристик на границе ламинарного подслоя и турбулентного ядра и учитывающие характер изменения ${{\mu }_{Т}}$ поперек пограничного слоя. Параметры методики [15], в том числе положение точек потери устойчивости ламинарного и перехода к турбулентному течению, подбирались исходя из экспериментальных данных [17, 18], которые также использовались для тестирования описанной модели пограничного слоя, показав ее хорошую работоспособность.
Численное решение трехмерных уравнений (7), (10) проводится методом расщепления [19]. Использована неявная, абсолютно устойчивая, монотонная разностная схема с суммарной погрешностью аппроксимации О(τ + $H_{{{{n}_{1}}}}^{2} + H_{s}^{2}$ + $H_{\eta }^{2}$), где ${{H}_{{{{n}_{1}}}}}$, ${{H}_{s}}$, ${{H}_{\eta }}$– шаг по пространству вдоль координат ${{n}_{1}}$, s, η соответственно; τ − шаг по времени. Для проверки программы численного расчета в пористом теле использовалась последовательность сгущающихся сеток по пространству: ${{h}_{1}} = $ = ${{h}_{{{{n}_{1}}}}}$ = ${{10}^{{ - 3}}}$ м, ${{h}_{2}} = {{h}_{{s1}}}$ = 0.925 × ${{10}^{{ - 2}}}$ (на сфере), ${{h}_{3}} = {{h}_{{s2}}}$ = ${{10}^{{ - 2}}}$ (на конусе), ${{h}_{4}} = {{h}_{\eta }}$ = 0.087 и бралось ${{H}_{{1,i}}} = 2{{h}_{i}}$, ${{H}_{{2,i}}} = {{h}_{i}}$, ${{H}_{{3,i}}} = {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} 2}} \right. \kern-0em} 2}$, ${{H}_{{4,i}}} = {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} 4}} \right. \kern-0em} 4}$, i = 1‒4. Температура каркаса фиксировалась по глубине тела в различные моменты времени. Во всех вариантах задача решалась с переменным шагом по времени, который выбирался из условия заданной точности, одинаковой для всех шагов по пространству. Различие относительной погрешности по температуре падало и к моменту времени t = ${{t}_{z}}$ составляло ${{\Delta }_{1}}$ = 10.3%, ${{\Delta }_{2}}$ = 6.5%, ${{\Delta }_{3}}$ = 3.4%. Ниже результаты расчета получены для шагов по пространству ${{H}_{{3,i}}} = {{{{h}_{i}}} \mathord{\left/ {\vphantom {{{{h}_{i}}} 2}} \right. \kern-0em} 2}$, i = 1‒4.
Для тестирования процессов взаимодействия высокоэнтальпийных потоков воздуха с графитовыми поверхностями использовались результаты теоретических [20] и обобщенных экспериментальных исследований [21].
Квазистационарное уравнение неразрывности (6) ${{{{{(\rho v)}}_{w}}{{r}_{{1w}}}} \mathord{\left/ {\vphantom {{{{{(\rho v)}}_{w}}{{r}_{{1w}}}} {({{H}_{1}}{{r}_{1}})}}} \right. \kern-0em} {({{H}_{1}}{{r}_{1}})}}$ = $ - {{\rho }_{2}}\varphi v$ (знак минус обусловлен тем, что нормальная координата ${{n}_{1}}$ направлена в глубь тела (см. рис. 1), а охладитель течет в противоположном направлении) совместно с первым выражением (9), нелинейным законом Дарси (8) и граничными условиями (22) можно проинтегрировать и найти расход газа и давление в области 1 [9]:
Давление на внутренней “холодной” поверхности пластины $L$ задано в виде
где k – некоторая постоянная. Это обеспечивало необходимый расход охладителя (в частности, не была достигнута температура плавления каркаса из пористого металла [10, 22]) на участке теплового воздействия от t = 0 до t = ${{t}_{z}}$.Расчеты обтекания конуса, затупленного по сфере, с углом полураствора θ = 15° потоком химически равновесного воздуха с переменным углом атаки – βm ≤ β ≤ βm, βm = 10° проводились для следующих условий [11], которые соответствуют параметрам: ${{H}_{\infty }}$ = 2.3 × ${{10}^{4}}$ м, V∞ = 3000, 5000 м/с, ${{R}_{N}}$ = 0.1 м, ${{L}_{0}}$ = 0.02 м, k = 2. При данных параметрах задачи характерными являются время колебательного процесса tω= 0.4 c, время релаксации газовой фазы ta = 3.3 × ${{10}^{{ - 5}}}$ c, число Струхаля St = ta/tω= 8.25 × ${{10}^{{ - 5}}}$. Кинетические константы (25) гетерогенных реакций (24) брались из [9], энтальпия графита ${{h}_{c}}$ рассчитывалась по формуле [23]. Эффективный показатель адиабаты ${{\gamma }_{{{\text{ef}}}}}$ в первой формуле (5) определялся согласно работе [11]. Для углеродного материала конической оболочки теплофизические коэффициенты известны из [9], для пористой стали – из [24]. Для графита конической части тела решается уравнение (10) при ${{Q}_{c}}$ = 0, G = 0.
Приводимые ниже результаты получены при ${{h}_{{e0}}}$ = 4.7197 × 106 и 1.272 × 107 Дж/кг, $\varphi $ = 0.34, ${{T}_{0}}$ = = 300 К, ${{b}_{1}} = 965.5,\,\;{{b}_{2}} = 0.147$, М = 29 кг/кмоль, σ = 5.67 × ${{10}^{{ - 8}}}$ Вт/(${{{\text{м}}}^{{\text{2}}}}\,{{{\text{К}}}^{{\text{4}}}}$), $\varepsilon = 0.9$, ${{\rho }_{{c0}}}$ = 1400 кг/${{м}^{3}}$, ${{\rho }_{{c*}}}$ = 1300 кг/${{м}^{3}}$, ${{k}_{c}}$ = 3.15 × ${{10}^{6}}$ ${{c}^{{ - 1}}}$, ${{E}_{c}}$ = 8.38 × × ${{10}^{4}}$ Дж/моль, ${{Q}_{c}}$ = 1.26 × ${{10}^{6}}$ Дж/кг, ${{t}_{z}}$ = 40 с. Теплофизические характеристики пористого затупления соответствовали пористой стали: ${{\varepsilon }_{1}} = 0.8$, ${{\lambda }_{1}}$ = 2.92 + 4.5 × ${{10}^{{ - 3}}}$${{T}_{1}}$ Вт/(м К), ${{\rho }_{1}}{{c}_{{p1}}}$ = = (1252 + 0.544${{T}_{1}}$) × ${{10}^{3}}$ Дж/(K ${{{\text{м}}}^{{\text{3}}}}$) [24], A = 2.3 × × ${{10}^{{11}}}$ 1/${{м}^{2}}$, B = 5.7 × ${{10}^{5}}$ 1/м. Теплофизические характеристики конической части тела отвечают углепластику [4, 9] или сплошному графиту ВПП [25].
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО РЕШЕНИЯ И ИХ АНАЛИЗ
В дальнейшем результаты относятся к сечению ${s \mathord{\left/ {\vphantom {s {{{R}_{N}}}}} \right. \kern-0em} {{{R}_{N}}}}$ = 5.0, находящемуся на конической части тела. При таком выборе координаты сечения на подветренной части тела не наблюдались предотрывные состояния во все время процесса. В силу малых времен тепловой релаксации углепластика [7] для иллюстрации нестационарных тепловых процессов (рис. 2–7), возникающих вследствие колебательного движения и сильного аэродинамического нагрева, удобнее использовать графит. Тем не менее результаты на рис. 2–7 качественно отражают влияние колебаний на углепластик. Интегральные количественные сравнения графита с углепластиком представлены на рис. 8.
Рис. 2.
Зависимость температуры поверхности графита в сечении ${s \mathord{\left/ {\vphantom {s {{{R}_{N}}}}} \right. \kern-0em} {{{R}_{N}}}}$ = 5.0 при V∞ = 5000 м/с: 1, 2 ‒ ${{\omega }_{f}}$ = 0 градус/с; 3‒5 – 5.
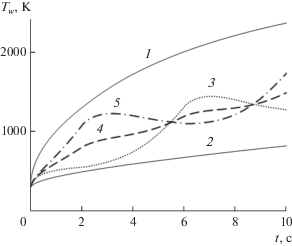
Рис. 3.
Распределение температуры поверхности графита по окружной координаты при V∞ = 5000 м/с: 1 ‒ ${{\omega }_{f}}$ = 0 градус/с, 2 ‒ 5, 3 ‒ 10, 4 ‒ 100.
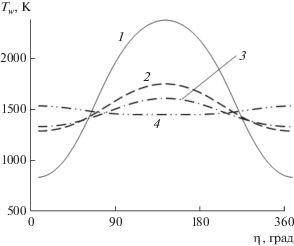
Рис. 4.
Образующие семейства кривых ${{T}_{{w\eta }}}(t)$ при V∞ = 5000 м/с и ${{\omega }_{f}}$ = 5 градус/с для материала графита на конической части оболочки.
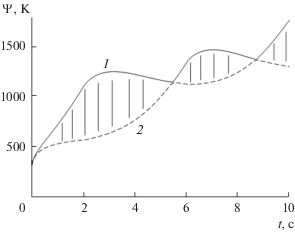
Рис. 5.
Образующие семейства кривых ${{T}_{{w\eta }}}(t)$ при V∞ = 5000 м/с и ${{\omega }_{f}}$ = 40 градус/с для графита.
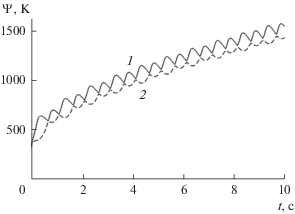
Рис. 6.
Временнáя зависимость угла атаки: точки ‒ моменты времени перехода в изотермический режим при V∞ = 5000 м/с и ${{\omega }_{f}}$ = 40 градус/с для графита.
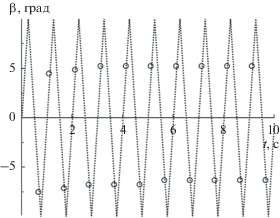
Рис. 7.
Модуль угла атаки в моменты времени перехода в изотермический режим при ${{\omega }_{f}}$ = 40 градус/с и V∞ = 5000 м/с для графита: 1 ‒ β > 0, 2 – β < 0.
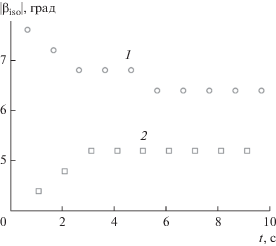
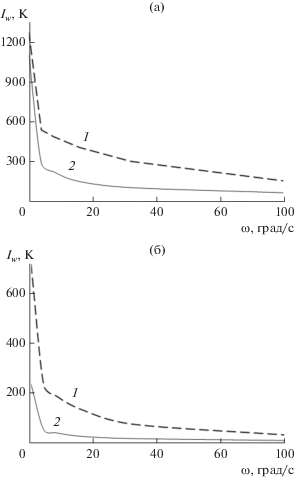
Рис. 8.
Зависимость интегрального перепада температуры поверхности от угловой скорости колебаний тела при V∞ = 5000 (а) и 3000 м/с (б).
На рис. 2 показана временнáя зависимость температуры поверхности тела из графита при скорости набегающего потока V∞ = 5000 м/с и фиксированном угле атаки β = βm = 10° (${{\omega }_{f}}$ = 0): кривые 1−2 и ${{\omega }_{f}}$ = 5 градус/с (кривые 3−5). В отсутствие колебательного процесса наблюдается монотонный рост температуры в точках η = 180° (кривая 1) и η = 0° (кривая 2). При наличии осциллирующего движения (кривые 3–5) происходит немонотонное изменение температуры поверхности в точках с координатами η = 0, 90, 180°, которым соответствуют кривые 3‒5. При этом происходит одновременное периодическое пересечение кривых 3−5 в определенные моменты времени. Как видно из рис. 2, колебательное движение приводит к снижению перепада температур с 1563 до 463 К при t = 10 c.
Это также может быть продемонстрировано посредством распределений температуры поверхности графита вдоль окружной координаты, показанным на рис. 3 для момента времени t = 10 с. Здесь кривым 1‒4 соответствуют ${{\omega }_{f}}$ = 0, 5, 10, 100 градус/с. Из рис. 3 видно, что в этот момент времени η = 180° соответствует наветренной стороне для кривых 1‒3 и подветренной для кривой 4. Максимальный перепад температуры в 1538 К на поверхности по окружной координате достигается в отсутствие осцилляций тела ${{\omega }_{f}}$ = 0 градус/с (см. рис. 3, кривая 1). С увеличением угловой скорости колебаний ${{\omega }_{f}}$ до 100 градус/с происходит снижение перепада температур до 83 К.
Рассмотрим 37 временны́х кривых ${{T}_{{w\eta }}}(t)$, описывающих изменение температур поверхности конической части из графита в точках η = 0, 5, …, 175, 180° исследуемого сечения s. Введем функции Ψmin(t) и Ψmax(t), которые являются огибающими семейства 37 кривых${{T}_{{w\eta }}}(t)$, полученных из решения сопряженной задачи, при фиксированных ${{\omega }_{f}}$ и ${s \mathord{\left/ {\vphantom {s {{{R}_{N}}}}} \right. \kern-0em} {{{R}_{N}}}}$.На рис. 4 и 5 показаны зависимости Ψmax(t) (кривая 1) и Ψmin(t) (кривая 2) для угловых скоростей колебаний тела ${{\omega }_{f}}$ = 5 и 40 градус/с соответственно. Из рис. 4 и 5 видно, что в определенные моменты времени сплошные и штриховые кривые имеют точки соприкосновения друг с другом. Это означает, что поверхность в сечении ${s \mathord{\left/ {\vphantom {s {{{R}_{N}}}}} \right. \kern-0em} {{{R}_{N}}}}$ в эти моменты времени становится близкой к изотермической.
Как известно, при ${{\omega }_{f}}$ = 0 температура поверхности постоянна вдоль окружной координаты η при нулевом угле атаки [3]. В случае колебательного движения температура приближается к постоянному значению через некоторый промежуток времени, после того как угол атаки β проходит через нулевое значение (см. рис. 6). Как видно из рис. 4‒6, переход в локальный изотермический режим носит циклический характер и зависит от угловой скорости колебаний ${{\omega }_{f}}$. Из результатов расчетов при ${{\omega }_{f}}$ = 40 градус/с следует, что поверхность становится близкой к изотермической с нерегулярной цикличностью при различных углах атаки βiso, представленных на рис. 7. Как видно из этого рисунка, значение |βiso| уменьшается с течением времени и на величину |βiso| влияет знак угла атаки. При β < 0 значение |βiso| меньше, чем при положительных углах атаки β. Максимальное время между изотермическими режимами наблюдается в начальные моменты времени и составляет 5.4 и 0.7 с для ${{\omega }_{f}}$ = 5 и 40 градус/с соответственно (см. рис. 4 и 5). Причиной затянувшегося процесса перехода в изотермический режим по сравнению с последующими является сильный аэродинамический нагрев, действующий на тело в начальные моменты времени, который также определяет разницу в значениях |βiso| для положительных и отрицательных углов атаки в последующие моменты времени.
В целях более детального изучения влияния осцилляций тела на теплообмен в теплозащитном материале введем следующую величину:
Как видно из приведенной выше формулы, величина${{I}_{w}}$ численно равна площади области (заштрихованной на рис. 4) между образующими, ограничивающими решение задачи и характеризующими интегральный перепад температур на поверхности тела, отнесенной к промежутку времени полета. На рис. 8 показаны зависимости интегрального перепада температур поверхности тела от скорости колебаний в течение рассматриваемого промежутка времени от t =${{t}_{0}}$ до t =${{t}_{z}}$ для V∞ = 3000 и 5000 м/с соответственно. Данные зависимости построены по результатам серии из 24 расчетов, соответствующих варьированию скорости набегающего потока V∞ = 3000 и 5000 м/с, угловой скорости${{\omega }_{f}}$ = 0, 5, 10, 20, 40, 100 градус/с и материалов (углепластика и графита). Кривые 1 на рис. 8 соответствуют углепластику, кривые 2 – графиту. Как видно из рис. 8, даже при малых угловых скоростях колебаний (${{\omega }_{f}}$ = 5 градус/с) происходит сильное снижение перепада температур (для УП ‒ на 58–67%, для графита ‒ до 74–76%) по сравнению со случаем движения с постоянным углом атаки. Для достижения уровня перепада температур поверхности графита, например,${{I}_{w}}$ < 300 К при использовании углепластика в качестве теплозащитного материала требуется более высокая скорость колебаний тела ${{\omega }_{f}}$ = 40 градус/с, тогда как для графита достаточно${{\omega }_{f}}$ = = 5 градус/с (см. рис. 8).
В результате при наличии осцилляций изменение формы тела вследствие линейного уноса материала с поверхности, обусловленного аэродинамическим нагревом, будет более равномерным (см. рис. 9). Кривые 1‒3 на рис. 9 отвечают углепластику и ${{\omega }_{f}}$ = 0, 5, 40 градус/с. При наличии колебаний ${{\omega }_{f}}$ = 5–100 средние значения функций распределения глубины выгорания x(η), представленных на рис. 9, по сравнению с ${{\omega }_{f}}$ = = 0 градус/с будут меньше на 18–19%. Максимальное отклонение функции x(η) от своих средних значений 76% для ${{\omega }_{f}}$ = 0 уменьшается до 1.5% для ${{\omega }_{f}}$ = 40 градус/с. Это говорит о том, что осцилляции в целом приводят к меньшему изменению формы летательного аппарата как в качественном, так и количественном отношении.
ЗАКЛЮЧЕНИЕ
В рамках сопряженной постановки задачи оценено интегральное влияние регулярного колебательного движения тела на перетекание тепла в теплозащитном покрытии. Показано, что даже при небольших значениях угловой скорости колебаний значительно уменьшается перепад температур (на 58–78% в зависимости от материала и условий обтекания) на поверхности тела. Показано, что изотермические режимы поверхности тела возникают с нерегулярной цикличностью. Скорость изменения угла атаки ${{\omega }_{f}}$ ≥ 5 градус/с приводит к более равномерному и меньшему (на 18–19%) изменению формы летательного аппарата по сравнению с движением с постоянным углом атаки. Тем самым обеспечивается лучшее сохранение аэродинамических характеристик летательного аппарата и меньший линейный унос теплозащитного материала.
Работа выполнена при поддержке фонда Д.И. Менделеева (грант № 8.2.15.2018).
Список литературы
Hoffman G.H., Plastzer M.F. On Supersonic Flow Past Oscillating Bodies of Revolution // AIAA J. 1966. V. 4. № 2. P. 370.
Telionis D., Gupta T. Compressible Oscillating Boun-dary Layers // AIAA J. 1977. V. 15. № 7. P. 974.
Зинченко В.И., Ефимов К.Н., Якимов А.С. Исследование характеристик сопряженного тепло- и массообмена при вдуве газа и термохимическом разрушении обтекаемого тела // ТВТ. 2007. Т. 45. № 5. С. 749.
Ефимов К.Н., Овчинников В.А., Якимов А.С., Гаар С.А. Численный анализ характеристик теплообмена при радиационно-конвективном нагреве конуса, затупленного по сфере // ТВТ. 2019. Т. 57. № 1. С. 83.
Гришин А.М., Фомин В.М. Сопряженные и нестационарные задачи механики реагирующих сред. Новосибирск: Наука; СО АН СССР, 1984. 319 с.
Ефимов К.Н., Овчинников В.А., Якимов А.С. Математическое моделирование влияния вращения на характеристики сопряженного тепломассообмена при высокоэнтальпийном обтекании затупленного по сфере конуса под углом атаки // Теплофизика и аэромеханика. 2017. Т. 24. № 5. С. 677.
Efimov K.N., Ovchinnikov V.A., Yakimov A.S. Rotation Influence on Heat Transfer at Supersonic Flow around a Blunted Body // AIAA J. 2018. V. 56. № 2. P. 743.
Ефимов К.Н., Овчинников В.А., Якимов А.С. Численное исследование влияния вращения на характеристики сопряженного тепломассообмена при сверхзвуковом обтекании конуса, затупленного по сфере под углом атаки и массовом уносе с поверхности // ТВТ. 2018. Т. 56. № 2. С. 253.
Гришин А.М., Голованов А.Н., Зинченко В.И., Ефимов К.Н., Якимов А.С. Математическое и физическое моделирование тепловой защиты. Томск: Изд-во Томск. ун-та, 2011. 358 с.
Полежаев Ю.В., Юревич Ф.П. Тепловая защита. М.: Энергия, 1976. 392 с.
Лунев В.В., Магомедов К.М., Павлов В.Г. Гиперзвуковое обтекание притупленных конусов с учетом равновесных физико-химических превращений. М.: ВЦ АН СССР, 1968. 203 с.
Горский В.В., Запривода А.В. О применении полной термохимической модели разрушения углерода к задаче разрушения углепластика в условиях нестационарного нагрева // ТВТ. 2014. Т. 52. № 2. С. 240.
Патанкар С., Сполдинг Д. Тепло- и массообмен в пограничных слоях. М.: Энергия, 1970. 127 с.
Cebeci T. Behavior of Turbulent Flow near a Porouswall with Pressure Gradient // AIAA J. 1970. V. 8. № 12. P. 48.
Dhawan D., Narasimha R. Some Properties of Boundary Layer Flow During the Transition from Laminar to Turbulent Motion // J. Fluid Mechanics. 1958. № 3. P. 418.
Гришин А.М., Зинченко В.И., Ефимов К.Н., Субботин А.Н., Якимов А.С. Итерационно-интерполяционный метод и его приложения. Томск: Изд-во Томск. ун-та, 2004. 320 с.
Feldhuhn R.N. Heat Transfer from a Turbulent Boundary Layer on a Porous Hemisphere // AIAA Paper 76-119. 1976.
Уидхопф Дж.Ф., Холл Р. Измерение теплопередачи на затупленном конусе под углом атаки при переходном и турбулентном режимах течения // РТК. 1972. Т. 10. № 10. С. 71.
Самарский А.А. Введение в теорию разностных схем. М.: Наука, 1971. 552 с.
Гофман А.Г., Гришин А.М. Теоретическое исследование термохимического разрушения графита в высокоэнтальпийном воздухе // ПМТФ. 1984. № 4. С. 107.
Бейкер Р.Л. Влияние неравновесных химических процессов на сублимацию графита // РТК. 1977. Т. 15. № 10. С. 21.
Андриевский Р.А. Пористые металлокерамические материалы. М.: Металлургия, 1964. 187 с.
Бучнев Л.М., Смыслов А.И., Дмитриев И.А. и др. Экспериментальное исследование энтальпии квазимонокристалла графита и стеклоуглерода в интервале температур 300−3800 К // ТВТ. 1987. Т. 25. № 6. С. 1120.
Алифанов О.М., Трянин А.П., Ложкин А.Л. Экспериментальное исследование метода определения коэффициента внутреннего теплообмена из решения обратной задачи // ИФЖ. 1987. Т. 52. № 6. С. 461.
Соседов В.П. Свойства конструкционных материалов на основе углерода. Спр. М.: Металлургия, 1975. 335 с.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур