Теплофизика высоких температур, 2021, T. 59, № 1, стр. 109-115
Снижение максимальных температур поверхности при сверхзвуковом обтекании затупленного по сфере конуса
В. И. Зинченко 1, *, В. Д. Гольдин 1, **
1 Томский государственный университет
Томск, Россия
* E-mail: vladislav.zinchenko@bk.ru
** E-mail: vdg@math.tsu.ru
Поступила в редакцию 28.11.2019
После доработки 28.11.2019
Принята к публикации 10.03.2020
Аннотация
Рассмотрена сопряженная задача нестационарного теплообмена при сверхзвуковом обтекании затупленного по сфере конуса при большом числе Маха (M∞ = 9.9). В этом случае максимальные температуры обтекаемой оболочки могут достигать температуры разрушения материала и важно оценить возможные способы их снижения. Обобщенные критериальные зависимости, полученные на основе численных расчетов нестационарной задачи в сопряженной постановке, позволяют оценить необходимое снижение максимальной температуры поверхности тела за счет выбора геометрических характеристик тела и теплофизических характеристик материалов для сферической и конической областей тела.
ВВЕДЕНИЕ
Требование сохранения геометрии летательного аппарата при больших временах движения вызывает необходимость использования различных материалов, в том числе высокотеплопроводных, обеспечивающих наряду с переизлучением поверхности тела снижение максимальных температур лобовой части [1–5].
Используя отработанную технологию решения задач в сопряженной постановке [6, 7], важно оценить возможности управления температурными режимами обтекаемых тел и получить критериальные зависимости для инженерных оценок максимальных температур Tw.
ПОСТАНОВКА ЗАДАЧИ
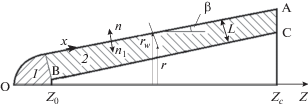
Рассматривается сверхзвуковое обтекание затупленных по сфере конических тел с углом полураствора 5°, радиусом сферического затупления RN и различными длинами zc = 5, 10, 20 при нулевом угле атаки. Лобовая часть тела выполнена из сплошного материала, а на боковой части (при z > z0) имеется коническая оболочка постоянной толщины L, причем материалы в этих областях могут быть различными (рис. 1). Внутренняя часть тела представляет собой конус с торцевым затуплением. Все линейные размеры отнесены к RN. Расчет течения в ламинарном пограничном слое проводился как в [1, 6], а тепловое поле в обтекаемой оболочке описывалось уравнениями теплопроводности, которые в предположении постоянства теплофизических характеристик материала имеют вид
(1)
$\frac{1}{{{{S}_{1}}}}\frac{{\partial {{\theta }_{1}}}}{{\partial \tau }} = \frac{1}{r}\frac{\partial }{{\partial \tau }}\left( {r\frac{{\partial {{\theta }_{1}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{\theta }_{1}}}}{{\partial {{z}^{2}}}},$(2)
$\frac{{{{\lambda }_{{s1}}}}}{{{{\rho }_{{s1}}}{{c}_{{s1}}}}}\frac{{{{\rho }_{{s2}}}{{c}_{{s2}}}}}{{{{\lambda }_{{s2}}}}}\frac{1}{{{{S}_{1}}}}\frac{{\partial {{\theta }_{2}}}}{{\partial \tau }} = \frac{1}{r}\frac{\partial }{{\partial \tau }}\left( {r\frac{{\partial {{\theta }_{2}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{z}^{2}}}}.$В начальный момент времени задается температура тела
(3)
${{\tilde {q}}_{w}} - {{\pi }_{\sigma }}\theta _{{wi}}^{4} = - {\kern 1pt} {{S}_{i}}\frac{{\partial {{\theta }_{i}}}}{{\partial {{n}_{1}}}}.$В переменных Дородницына–Лиза
Для случая единого материала в областях 1, 2 наряду с решением двумерного уравнения теплопроводности температура тела рассчитывалась по одномерной модели в естественной системе координат [1]:
При этом остаются прежними начальные и граничные условия. Здесь R – радиус кривизны образующей поверхности тела, α – угол между касательной к телу и осью симметрии, rw – расстояние от поверхности тела до оси симметрии.
Решение уравнений теплопроводности определяется в основном параметрами сопряженности Si и параметром πσ, характеризующим излучение поверхности тела. В предельном случае (Si = 0) решение системы уравнений пограничного слоя с граничным условием (3) дает распределение радиационно-равновесной температуры поверхности θwr(ξ). Случай Si → ∞ соответствует материалу с бесконечной теплопроводностью, при этом температура тела зависит только от времени, и уравнение для ее определения приведено в [1, 4].
МЕТОДИКА РЕШЕНИЯ И ИСХОДНЫЕ ДАННЫЕ
Методика решения и алгоритм численного расчета краевой задачи в сопряженной постановке подробно представлены в [1]. Здесь отличительным моментом явилось сквозное определение поля температур в теле при различных коэффициентах λsi в областях 1, 2.
При проведении серийных численных расчетов использовались следующие входные данные: M∞ = 9.9, pe0 = 1.6 бар, Tini = 293 К, ε = 0.8, z0 = = 0.96, L = 0.5. Радиус затупления RN принимался равным 0.005, 0.01, 0.04 м, базовая температура торможения Te0 – 3250 К. Также проводились расчеты при Te0 = 1000, 1500, 2000 К. Теплофизические характеристики материалов приведены в табл. 1 [8]. В случае различных материалов для сферической части использовалась сталь, а для конической – медь с характеристиками из табл. 1.
АНАЛИЗ РЕЗУЛЬТАТОВ ЧИСЛЕННОГО РЕШЕНИЯ
Рассмотрим вначале случай обтекания тела, выполненного из единого материала. В работе [1] при M∞ = 6.1, Te0 = 562 К, pe0 = 2.2 бар проведено сравнение расчетных и экспериментальных значений [9] коэффициента ${{C}_{h}} = \frac{{{{q}_{w}}}}{{{{\rho }_{\infty }}{{V}_{\infty }}{{c}_{p}}\left( {{{T}_{{e0}}} - {{T}_{{w,{\text{ini}}}}}} \right)}}$ в зависимости от z в начальный момент времени, а затем рассмотрена эволюция температурного поля обтекаемых тел, выполненных из различных материалов, вплоть до выхода на стационарный режим. При этом значения определяющего параметра πσ не превышали 0.38. При возрастании чисел Маха до 10 и высоте полета H = 30 км [2] значения πσ могут возрастать в несколько раз, поэтому необходимо дать оценку возможности управления температурными режимами тела для данных практически важных условий.
Для zc = 5, RN = 0.01 м при указанных выше параметрах торможения на рис. 2 приведены значения температур поверхности тела, выполненного из представленных в табл. 1 материалов. Здесь же показано распределение температуры стенки Twr(ξ) при S = 0 (кривая 9) и в предельном случае материала с бесконечной теплопроводностью – S → ∞ (кривые 4, 8). Серия кривых 5–8 отвечает стационарным значениям Tw(ξ) в момент времени t = 250 с, а кривые 1–4 соответствуют значениям Tw(ξ) при t = 10 с.
Рис. 2.
Температура поверхности тела из сталей Ст1 (1, 5) и Ст2 (2, 6), меди (3, 7) и материала с бесконечной теплопроводностью (4, 8) в моменты времени t = 10 (1–4) и 250 с (5–8); 9 – радиационно-равновесная температура.
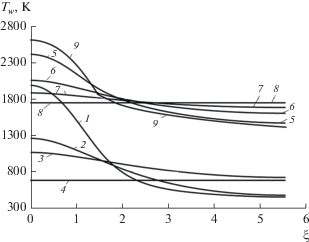
Представленные результаты иллюстрируют возможности снижения максимальной температуры поверхности при выборе высокотеплопроводных материалов и носят модельный характер для уровня высоких температур, превышающих температуры разрушения материалов. Отметим, что максимальная температура достигается в критической точке.
Для оценки максимальной температуры при t → ∞ в критериальном виде на рис. 3, 4 представлены зависимости безразмерной температуры в критической точке
(4)
${{\varphi }_{{{\text{st}}}}} = \frac{{{{\theta }_{{w0r}}} - {{\theta }_{{w0}}}}}{{{{\theta }_{{w0r}}} - {{\theta }_{{w0}}}\left( {{{\lambda }_{s}} \to \infty } \right)}}$Рис. 3.
Зависимость безразмерной температуры φst от параметра сопряженности S: при πσ = 0.53 и zc = 5 (1), 10 (2), 20 (3); 4 – πσ = 0.38, 5 – 1.06; и для составного материала при πσ = 0.53, S1 = 2, 4, S2 = 13 и zc = 5 (6), 20 (7).
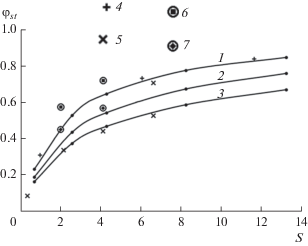
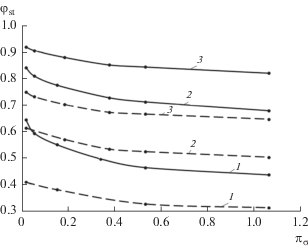
Рис. 4.
Зависимость безразмерной температуры φst от параметра πσ при S = 2 (1), 6 (2), 13 (3); сплошные кривые – zc = 5, штриховые – 20.
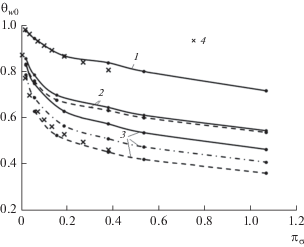
Для предельных условий по S (λs = 0 и λs → ∞) на рис. 5 приведены максимальные температуры в зависимости от параметра πσ для различных удлинений конической части. При πσ ≥ 0.4 θw0 в случае λs → ∞ оказывается ниже радиационно-равновесной температуры θw0r на 30–50% в зависимости от zc. При πσ < 0.4 результаты расчета согласуются с данными [1]. Здесь же для примера приведены данные расчетов для S = 6 (кривые 2), из которых следует, что при данных и меньших значениях параметра сопряженности S максимальная температура в критической точке слабо зависит от удлинения конической части, а ее снижение по отношению к θw0r при πσ ≥ 0.4 составляет около 25%.
Рис. 5.
Стационарная температура в критической точке при S = 0 (1), 6 (2), ∞ (3); сплошные линии – zc = 5, штриховые – 20, штрихпунктирные – 10; 4 – результаты [1].
Отметим, что, используя критериальные зависимости, приведенные на рис. 3, 4, а также значения температуры, найденные для предельных условий по S (θw0r, θw0(λs → ∞)), из выражения (4) можно определить значение θw0 в расчетном диапазоне S, πσ. Погрешность нахождения θw0 с учетом возможной линейной интерполяции по определяющим критериям не превышает 2%. Такой подход позволяет избежать массовых точных расчетов двумерной задачи теплопроводности в теле, в том числе при усложнении внутренней геометрии обтекаемой оболочки.
Влияние относительной толщины оболочки L на максимальную температуру θw0 представлено в табл. 2 для различных значений πσ и S. Как и для базовой толщины L = 0.5, при двух других значениях имеет место слабое влияние длины тела на θw0 при S ≤ 6 практически во всем расчетном диапазоне πσ. При возрастании L (≥0.5) наблюдается слабое уменьшение температуры θw0 для фиксированных значений S. В то же время в диапазоне 0.1 ≤ L ≤ 0.5 при возрастании L происходит существенное снижение θw0, что приводит в данных условиях к уменьшению максимальной температуры тела. Снижение температур θw0 может достигать 25–30% (табл. 2) от максимальных значений в зависимости от выбора определяющих параметров задачи.
Таблица 2.
Максимальная температура поверхности θw0
| πσ | 0.53 | 1.06 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | 4.3 | 13 | 4.1 | 13 | ||||||||
| L | 0.1 | 0.5 | 0.8 | 0.1 | 0.5 | 0.8 | 0.1 | 0.5 | 0.8 | 0.1 | 0.5 | 0.8 |
| θw0, zc = 5 | 0.67 | 0.63 | 0.62 | 0.62 | 0.58 | 0.57 | 0.60 | 0.57 | 0.56 | 0.55 | 0.51 | 0.51 |
| θw0, zc = 20 | 0.67 | 0.63 | 0.61 | 0.61 | 0.55 | 0.53 | 0.60 | 0.56 | 0.55 | 0.54 | 0.49 | 0.48 |
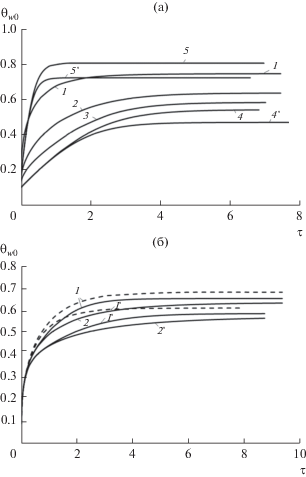
Рассмотрим далее температурный режим в окрестности лобовой критической точки для нестационарных условий и однородного материала обтекаемой оболочки. На рис. 6а показана зависимость от времени безразмерной температуры θw0(τ) для различных материалов (кривые 1–4), а также приведены данные одномерных расчетов (кривые 5, 5 '). Здесь и ниже кривые со штрихами отвечают πσ = 1.06. В принятых переменных результаты одномерных расчетов для различных материалов ложатся практически на одну кривую при S > 2. На нестационарном участке эффективность использования высокотеплопроводных материалов может значимо возрастать.
Рис. 6.
Временнáя зависимость безразмерной температуры в критической точке тела с однородным (а) и составным покрытием (б) при πσ = 0.53 (1, 2) и 1.06 (1 ', 2 '): (а) zc = 5, 1 – S = 0.69, 2 – 4.3, 3 – 13, 4 – ∞, 5 – одномерный расчет; (б) 1 – zc = 5, S1 = 2, S2 = 13; 2 – 20, 2, 13; штриховые линии – однородный материал при S = 2.
Как и в [1], введем нестационарный аналог функции φst
(5)
${{\varphi }_{{{\text{nst}}}}} = \frac{{{{\theta }_{{w01}}}\left( {\tau ,{{\lambda }_{s}}} \right) - {{\theta }_{{w02}}}\left( {\tau ,{{\lambda }_{s}}} \right)}}{{{{\theta }_{{w01}}}\left( {\tau ,{{\lambda }_{s}}} \right) - {{\theta }_{{w02}}}\left( {\tau ,{{\lambda }_{s}} \to \infty } \right)}},$Рис. 7.
Временнáя зависимость φnst в критической точке при πσ = 0.53 (1–4) и 1.06 (1 '–4 '): 1 – S = 2, zc = 5; 2 – 13, 5; 3 – 2, 20; 4 – 13, 20.
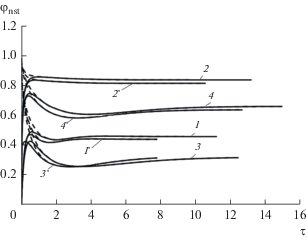
Учитывая поведение функции φnst, можно заметить, что для τ ≥ 1 ее максимальное отличие от своего стационарного значения ${{\varphi }_{{{\text{st}}}}}$ не превышает 10%, что позволяет приравнять эти величины в расчетном диапазоне τ. Тогда из (5) вытекает
(6)
$\begin{gathered} {{\theta }_{{w02}}}\left( {\tau ,{{\lambda }_{s}}} \right) = {{\theta }_{{w01}}}\left( {\tau ,{{\lambda }_{s}}} \right) - \\ - \,\,{{\varphi }_{{{\text{st}}}}}\left[ {{{\theta }_{{w01}}}\left( {\tau ,{{\lambda }_{s}}} \right) - {{\theta }_{{w02}}}\left( {\tau ,{{\lambda }_{s}} \to \infty } \right)} \right]. \\ \end{gathered} $На рис. 8 для условий рис. 7 дано сравнение нестационарного численного решения (сплошные кривые) и приближенного, найденного из (6), (штриховые кривые). Видно, что приближенное решение дает высокую точность при zc = 5, которая снижается при τ < 8 и zc = 20.
Рис. 8.
Температура в критической точке в зависимости от времени при πσ = 0.53 (1–4) и 1.06 (1 '–4 '): 1–4 – то же, что на рис. 7; штриховые линии – приближенное решение.
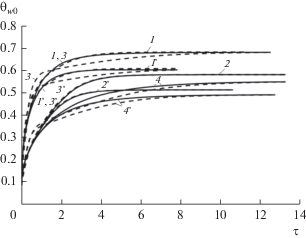
Таким образом, для нестационарных условий обтекания тела может быть использован приближенный способ определения его максимальных температур, включающий определение φst в стационарном случае и температуры поверхности тела в предельных случаях нетеплопроводного материала θw0r и абсолютно теплопроводного тела θw02(τ, λs → ∞), а также результаты одномерного расчета температуры поверхности при отсутствии продольного перетекания тепла по ней θw01(τ, λs). Как указывалось выше, при τ ≥ 1 значения θw01(τ, λs) могут быть заменены значением θw0r.
Рассмотрим далее случай различных материалов сферической и конической частей. На рис. 6б представлена зависимость θw0(τ) для двух значений zc (5, 20), двух значений πσ (0.53, 1.06) при S1 = 2, S2 = 13. Здесь же для сравнения приведены соответствующие зависимости θw0 для однородного материала S1 = S2 = 2 при zc = 5 (штриховые линии). Таким образом, получается комбинация высокотемпературного (область 1) и высокотеплопроводного (область 2) материалов; такая комбинация обеспечивает снижение максимальной температуры по отношению к однородному материалу на 4–7% в зависимости от zc.
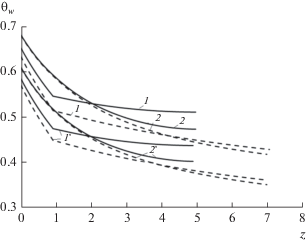
Распределение стационарной температуры поверхности θw(z) для различных длин тела показано на рис. 9. Кривые 1, 1 ', имеющие разрыв производной, соответствуют различным материалам (S1 = 2, S2 = 13), а кривые 2, 2 ' отвечают однородному материалу при S1 = S2 = 2. Как и выше, кривые без штрихов и со штрихами построены для πσ = 0.53 и 1.06 соответственно. Как и следовало ожидать, для однородного материала при S = 2 максимальная температура в окрестности критической точки при различных πσ не зависит от длины тела zc. В то же время использование различных материалов позволяет управлять снижением температуры поверхности θw0. На периферийной конической части тела рост S2 вследствие повышения коэффициента теплопроводности материала обеспечивает рост температуры поверхности и выполаживание зависимости θw(z). Качественно такое поведение температуры в этой области отвечает зависимостям θw(ξ) для различных λs, которые рассматривались при анализе рис. 2.
Рис. 9.
Распределение стационарной температуры вдоль поверхности тела из составного (1) и однородного (2) материалов при πσ = 0.53 (1, 2) и 1.06 (1 ', 2 '): сплошные линии – zc = 5, штриховые – 20.
Интересно оценить влияние коэффициента теплопроводности в области 1 высокотемпературного материала и параметра S1 на максимальное значение θw0 при заданном значении S2 в области высокотеплопроводного материала. На рис. 3 для двух длин zc (5, 20) показано значение φst при S1 = 2, 4 (значки внутри кружков). Такая обработка отражает факт заметного снижения температуры θw0 по отношению к однородному материалу обтекаемого тела. Так, для zc = 5 значения θw0 составляют 0.95 и 0.9 от максимальной температуры однородного материала при S1 = 2 и S1 = 4. Если zc = 20, то это отношение равно 0.93 и 0.87 соответственно.
На рис. 10 показана зависимость θw0 от параметра S1 при заданном значении S2 = 13 для различных величин πσ и zc. При S1 ≥ 6 максимальная температура меняется слабо в пределах 5%. Отсюда вытекает близкий к оптимальному уровню диапазон значений S1 (2–5), при котором заметно снижается уровень максимальных температур при соответствующем выборе высокотемпературного материала сферического затупления.
Рис. 10.
Зависимость максимальной стационарной температуры от параметра сопряженности S1 при πσ = 0.53 (1, 2) и 1.06 (1 ', 2 '): 1, 1 ' – zc = 5; 2, 2 ' – 20.
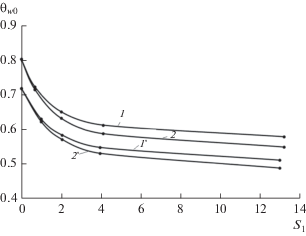
Таким образом, меняя соотношение коэффициентов теплопроводности материалов сферической и конической частей, можно влиять на снижение максимальной температуры в окрестности критической точки. При этом, как вытекает из рис. 6б, для нестационарного участка процесса это снижение может быть заметно бόльшим.
ЗАКЛЮЧЕНИЕ
Для нулевого угла атаки в области больших значений чисел Маха (до 10.0) и высоких температур торможения (до 3250 К) на высотах порядка 30 км рассмотрена задача снижения максимальной температуры поверхности затупленного по сфере конуса ниже температуры разрушения материала тела. На основе нестационарной задачи в сопряженной постановке изучены возможные способы управления температурными режимами за счет выбора теплофизических характеристик материала и геометрических характеристик модели: радиуса RN, длины zc и толщины оболочки L. Показано, что использование высокотеплопроводных материалов тела в целом либо комбинации высокотемпературных материалов на затуплении и высокотеплопроводных на конической части дает возможность существенно снизить максимальную температуру лобовой критической точки. Построенные критериальные зависимости позволяют оценивать максимальные значения Tw0 во всем диапазоне времен движения.
Оценено применение часто используемой одномерной модели распространения тепла в теле и показана возможность кратной ошибки в определении максимальных температур для перспективных высокотеплопроводных материалов.
Список литературы
Зинченко В.И., Гольдин В.Д. Решение сопряженной задачи нестационарного теплообмена при сверхзвуковом обтекании затупленного по сфере конуса // ИФЖ. 2019. Т. 92. № 1. С. 137.
Гешеле В.Д., Полежаев Ю.В., Раскатов И.П., Стоник О.Г., Габбасова Г.В. Возможности повышения скорости полета гиперзвуковых летательных аппаратов // ТВТ. 2013. Т. 51. № 5. С. 798.
Башкин В.А., Решетько С.М. Температурный режим затупленных клиньев и конусов в сверхзвуковом потоке с учетом теплопроводности материала // Уч. зап. ЦАГИ. 1990. Т. XXI. № 4. С. 11.
Зинченко В.И., Лаева В.И., Сандрыкина Т.С. Расчет температурных режимов обтекаемых тел с различными теплофизическими характеристиками // ПМТФ. 1996. Т. 37. № 5. С. 105.
Зинченко В.И., Гольдин В.Д., Зверев В.Г. Численное моделирование влияния материалов тепловой защиты на характеристики сопряженного тепломассообмена при пространственном обтекании затупленных тел // ТВТ. 2018. Т. 56. № 5. С. 747.
Зинченко В.И. Математическое моделирование сопряженных задач тепломассообмена. Томск: Изд-во Томск. ун-та, 1985. 222 с.
Гришин А.М., Голованов А.Н., Зинченко В.И., Ефимов К.Н., Якимов А.С. Математическое и физическое моделирование тепловой защиты. Томск: Изд-во Томск. ун-та, 2011. 358 с.
Физические величины. Спр. / Под. ред. Григорьева И.С., Мейлихова Е.3. М.: Энергоатомиздат, 1991. 1232 с.
Бражко В.Н., Ваганов А.В., Ковалева Н.А., Колина Н.П., Липатов И.И. Экспериментальные и расчетные исследования перехода в пограничном слое на затупленных конусах при сверхзвуковом обтекании // Уч. зап. ЦАГИ. 2009. Т. XL. № 3. С. 21.
Дополнительные материалы отсутствуют.
Инструменты
Теплофизика высоких температур