Теплофизика высоких температур, 2021, T. 59, № 1, стр. 86-99

ВВЕДЕНИЕ

Волновые течения тонких слоев жидкости или ее пара (газа) по вертикальной или наклонной твердой поверхностям под действием силы тяжести часто встречаются в природе и многих технических приложениях. В механике жидкости, газа и плазмы существует три больших класса задач, связанных с движением жидкости или ее пара по вертикальной поверхности, которые представляют большой интерес как для теории, так и для ее приложений. Общее для всех трех типов течения по вертикальной или наклонной твердой поверхностям (слой жидкости, граничащей с газом; слой конденсата, граничащего с паром; пленка пара, граничащая с жидкостью) заключается в том, что эти течения являются волновыми, несмотря на их различную физическую природу.

Первые два класса задач относятся к течениям жидкости, но отличаются способом образования самой жидкости и поддержанием ее расхода. В работах П.Л. Капицы [1–3], относящихся к первому классу задач, теоретически и экспериментально исследовано течение слоя вязкой жидкости по вертикальной стенке при заданном расходе G = const. В теоретическом анализе автор показал, что волновой режим поверхности стекающего слоя жидкости является более устойчивым по сравнению со слоем постоянной толщины [1]. В волновом режиме толщина слоя $h = {{h}_{0}} + \delta h(z,t)$ состоит из постоянной части h₀ = const и волны $\delta h\cos [k(z + ct)],$ ${{\delta h} \mathord{\left/ {\vphantom {{\delta h} h}} \right. \kern-0em} h} \ll 1,$ движущейся с постоянной фазовой скоростью c. Фазовая скорость и величины h₀, k, δh зависят от физических свойств жидкости и ее расхода через слой G = const.

Необходимость анализа устойчивости стационарного режима подтверждается примером последующих исследований задачи П.Л. Капицы. Более детальный математический анализ этой задачи, выполненный в работе [4], показал: при заданном расходе стекающей в слое жидкости G = const существует бесконечное множество волновых режимов, отличающихся длинами волн. Поэтому перенос результатов работы [1] (особенно зависимости усредненной толщины слоя жидкости от расхода) на другие задачи без дополнительного анализа может привести к ошибочным выводам [5].

Второй близкий класс задач связан с анализом двухфазных сред (жидкость и ее пар) [5, 6]. В этих задачах конденсация пара на твердой холодной поверхности приводит к образованию стекающего по стенке слоя жидкости. Типичная проблема для таких явлений сводится к нахождению зависимости стационарной толщины слоя жидкости x_f(z) от расстояния z. Отличие работ этого класса от [1–5] состоит в том, что расход в стекающей жидкости $G(z,J)$ изменяется по высоте и зависит от интенсивности конденсации пара J на холодной стенкe. Задача о границе между паром, находящимся в объеме, и сконденсировавшейся на холодной поверхности жидкостью ${{x}_{f}}(z) \approx {{z}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}$ впервые была решена Нуссельтом (W. Nusselt). Полученное на основе этого решения значение среднего по высоте коэффициента теплоотдачи, несмотря на некоторые поправки, учитывающие реальный волновой характер границы раздела пар–жидкость, широко используется в различных технологиях (ссылки на работы в данной области можно найти в [7, 8]). В задаче, рассмотренной Нуссельтом, и последующих исследованиях конденсации пара на различных поверхностях детальный анализ устойчивости полученных стационарных решений остался до конца не выполненным.

Третий большой класс задач, к которому относится и настоящая, так же, как и второй, связан с двухфазными средами (жидкость и ее пар). Изучаются явления, связанные с пленочными режимами кипения обычных и криогенных жидкостей на нагретых до высокой температуры цилиндрических или сферических металлических поверхностях (при различных значениях недогрева охлаждающей жидкости). Эти процессы наблюдаются в технологических установках, при изучении механизмов кипения в лабораториях и в природе при извержении подводных вулканов, когда лава вытекает в морскую воду. Особенностью задач третьего класса является то, что режим пленочного кипения сопровождается постоянным истечением пара в окружающую среду. Истечение пара в окружающую среду может быть либо периодическим, если нагреватель целиком окружен охлаждающей жидкостью и расход пара происходит за счет отрывающихся от фазовой поверхности паровых пузырей, либо постоянным, если паровая полость соприкасается с окружающей средой непосредственно. Большинство проблем в рассмотренных задачах этого класса [3–13] сводятся к определению формы стационарной фазовой границы на нагретых цилиндрических или сферических поверхностях (при наличии вынужденной или естественной конвекции жидкости) и расчету среднего по периметру значения коэффициента теплоотдачи. Теоретический анализ, проведенный в этих задачах, связан с рассмотрением стационарных состояний и детально не затрагивает вопросов анализа единственности и устойчивости этих режимов относительно малых и конечных возмущений.

Рассматриваемый в данной работе режим пленочного кипения на плоской, вертикальной стенке существенно отличается от режимов, рассмотренных в [3–13], в которых отсутствует вынужденное обтекание нагревателя жидкостью. В нашем случае паровая полость соприкасается с окружающей средой непосредственно и существует постоянный расход пара. Здесь поток теплоты от горячей стенки идет на нагрев и испарение новых порций жидкости и на поддержание непрерывного расхода пара. Истечение пара здесь происходит не под воздействием силы Архимеда, а за счет того, что давление в паровой пленке превышает давление в окружающей среде, когда пар вытекает. При пленочном кипении на горизонтальных трубах или сферах объем пара, находящегося возле нагревателя, окружен охлаждающей жидкостью. Поэтому пар из замкнутого объема, ограниченного фазовой поверхностью, расходуется малыми порциями из-за отрывающихся и затем всплывающих в жидкости за счет силы Архимеда паровых пузырей. При этом тепловой поток от нагревателя тратится на небольшое квазипериодическое воспроизводство ушедшего с пузырями пара и на поддержание конвекции в жидкости.

Вторая проблема, рассматриваемая в данной работе, относится к анализу устойчивости стационарного пленочного кипения на вертикальной поверхности. Необходимость анализа устойчивости квазистационарных состояний можно видеть и на примерах распространения плоских ударных волн [14] и одномерной задачи Стефана (Jožef Stefan). В этих задачах плоская фазовая граница перемещается в горизонтальном направлении (в задаче Стефана по закону ${{x}_{f}}(t) \approx \sqrt {\chi t} ,$ $\chi $ – коэффициент температуропроводности). Хотя эта задача относится к одномерной нестационарной постановке, она демонстрирует необходимость анализа устойчивости простейших решений. Задачи Стефана возникают при плавлении твердых тел и кристаллизации жидкости и демонстрируют неустойчивость плоского фронта кристаллизации. Именно анализ двумерных нестационарных возмущений позволяет реализовывать технологии обеспечения гладкой фазовой поверхности. В двумерной геометрии определение положения и формы фазовой границы требует более тонкого анализа. Аналогичные соображения относятся и к стационарным решениям, полученным в [5–13].

Главной целью работы является более детальный и математически более строгий анализ решений о пленочном кипении на плоской вертикальной поверхности. Первая часть данной работы посвящена анализу стационарных распределений специального вида в двухфазной системе и определению формы границы, отделяющей пар от жидкости. Решение гидродинамических уравнений проводится методом многомасштабных асимптотических разложений. Часто авторы качественных инженерных решений полагают, что полученные ими решения единственны, даже для вполне конкретной экспериментальной ситуации. Однако, как показывает анализ целого ряда гидродинамических задач [14], частные стационарные решения могут быть не единственными и не устойчивыми даже к малым возмущениям и не реализовываться в эксперименте. В отличие от других задач пленочного кипения особенностью данного подхода является представление о том, что толщина паровой пленки в таких процессах состоит из стационарной части и поверхностных волн, распространяющихся по фазовой границе. Это относится к режимам пленочного кипения как на плоских горизонтальных и вертикальных поверхностях, так и на трубах и сферах. Поэтому отдельный раздел данной работы специально посвящен исследованию устойчивости стационарной конфигурации пара, жидкости и разделяющей их фазовой границы. В этом разделе показаны отличия волн на фазовой поверхности от хорошо известных гравитационно-капиллярных волн на поверхности изотермической жидкости [14].

СТАЦИОНАРНЫЕ РАСПРЕДЕЛЕНИЯ СВОЙСТВ СРЕДЫ В ДВУХФАЗНОЙ СИСТЕМЕ. ФОРМА ФАЗОВОЙ ГРАНИЦЫ ПАР–ЖИДКОСТЬ (ЧАСТНЫЙ РЕЖИМ)

Постановка задачи

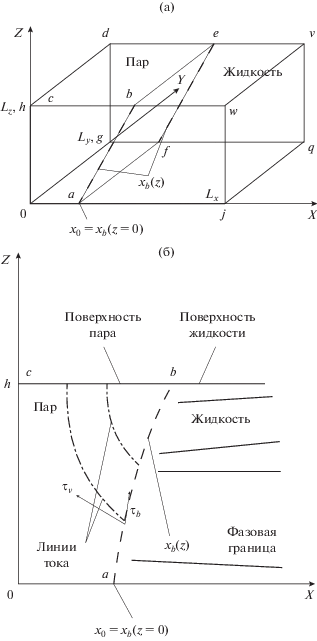
Исследование пленочного кипения на вертикальной нагретой поверхности проводится для открытого сверху прямоугольного сосуда. Сосуд с характерными размерами L_x, L_y, L_z в направлении осей X, Y, Z заполнен жидкостью до уровня h < L_z (рис. 1), а его левая плоская вертикальная стенка $0gdc0$ нагрета до температуры T_w, существенно превышающей температуру кипения (T_b(P_b) < T_w) жидкости при постоянном давлении в области над жидкостью. Считается, что остальные стенки адиабатически изолированы – нормальный к стенке градиент температуры равен нулю. При нагреве жидкости после переходного режима на стенке образуется паровая область, отделенная от жидкости фазовой поверхностью abefa (рис. 1а). Проекция фазовой поверхности на плоскость Z0X – $x = {{x}_{b}}(z)$ изображена на рис. 1б. В процессе решения задачи находится форма границы, отделяющей жидкость от пара ${{x}_{b}}(z),$ $0 \leqslant z \leqslant h,$ а также распределения температуры, давления и скорости течения в паре и жидкости. Решение задачи позволяет найти расход пара ${{G}_{ - }},$ вытекающего из паровой области через поверхность bcdeb. Считается, что уход испарившейся жидкости компенсируется дополнительным ее поступлением в сосуд ${{G}_{l}}$ через поверхность jwvqj так, чтобы уровень жидкости оставался постоянным h = const.

Рис. 1.

Схема (а) расположения пара и жидкости в бассейне размером ${{L}_{x}} \times {{L}_{y}} \times {{L}_{z}}{\text{:}}$ 0abcdefg0 – область, заполненная паром; ajwbevqfa – жидкостью; afeba – фазовая поверхность; б) плоскость $X0Y$ бассейна ${{L}_{x}} \times {{L}_{y}} \times {{L}_{z}}{\text{:}}$ ab – след проекции фазовой плоскости на плоскость X0Y; 0abc0 – область пара; область справа от линии ab – жидкость; штрихпунктирные линии – линии тока пара; τ_v(x_b(z)), τ_b(x_b(z)) – касательные векторы к линии тока и фазовой границе соответственно, взятые в произвольной точке фазовой границы x_b(z).

Область пара. Следуя идее, высказанной в работе [15] и используемой ее автором для определения критического потока теплоты, при анализе процессов в паровой пленке можно ограничиться рассмотрением невязкого вихревого течения пара.

Система уравнений, описывающая распределение свойств пара, сводится к решению уравнений

(1)

$\begin{gathered} \nabla \cdot {{\rho }_{{v}}}{{U}_{{v}}} = 0,\,\,\,\,\left[ {\nabla \times {{U}_{{v}}} \times {{U}_{{v}}}} \right] = \\ = - \left( {\frac{1}{{{{\rho }_{{v}}}}}\nabla {{P}_{{v}}} + \frac{1}{2}\nabla U_{{v}}^{2}} \right) - g + {{\mu }_{{v}}}\Delta {{U}_{{v}}}, \\ {{c}_{{p{v}}}}{{\rho }_{{v}}}({{U}_{{v}}} \cdot \nabla ){{T}_{{v}}}--{{\lambda }_{{v}}}\Delta {{T}_{{v}}} = 0,\,\,\,\,{{P}_{{v}}} = {{R}_{{v}}}{{\rho }_{{v}}}{{T}_{{v}}}. \\ \end{gathered} $

Система уравнений, описывающая распределение параметров жидкости пара, сводится к решению уравнений

(2)

$\begin{gathered} \nabla \cdot {{U}_{l}} = 0,\,\,\,\,\left( {\frac{1}{{{{\rho }_{l}}}}\nabla {{P}_{l}} + \frac{1}{2}\nabla U_{l}^{2}} \right) - g + {{\mu }_{l}}\Delta {{U}_{l}} = 0, \\ {{c}_{{pl}}}{{\rho }_{l}}({{U}_{l}} \cdot \nabla ){{T}_{l}}--{\text{ }}{{\lambda }_{l}}\Delta {{T}_{l}} = 0,\,\,\,\,{{\rho }_{l}} = {\text{const}}. \\ \end{gathered} $

Здесь P_j, ρ_j, T_j, U_v = (u, 0, w), U_l = (u_l, 0, w_l) – давление, плотность, температура и скорость соответственно; ${{\lambda }_{j}},$ ${{c}_{{pj}}}$ – коэффициенты теплопроводности и теплоемкости; g = g(0, 0, 1) – сила тяжести; ${{\mu }_{j}}$ – коэффициент кинематической вязкости; ∆ – оператор Лапласа; j = v, l – нижний индекс ${v}$ соответствует пару, $l$ – жидкости.

При решении поставленной задачи используется метод многомасштабных асимптотических разложений [16, 17]. Далее рассматривается плоская задача, в которой зависимые переменные $f(x,z)$ являются функциями только от координат $x,z$ (рис. 1а). В данной задаче существует малый параметр $\varepsilon < 1,$ численное значение которого будет установлено позже, поэтому выбирается следующий скейлинг для производных от функций $f(x,z){\text{:}}$

(3)

${{\frac{{\partial f}}{{\partial z}}} \mathord{\left/ {\vphantom {{\frac{{\partial f}}{{\partial z}}} {\frac{{\partial f}}{{\partial x}}}}} \right. \kern-0em} {\frac{{\partial f}}{{\partial x}}}} \approx {{\varepsilon }^{4}} \ll 1.$

При решении системы уравнений (1), (2) считается, что нормальные к твердым стенкам компоненты скорости обращаются в ноль (более детально это будет записано при решении конкретной задачи).

На стационарной фазовой границе ${{x}_{b}}(z),$ которая находится в процессе решения, должно выполняться условие непрерывности потоков массы

(4)

${{\rho }_{{v}}}{{U}_{{{v}n}}} = {{\rho }_{l}}{{U}_{{ln}}},$

где ${{U}_{{jn}}}$ – нормальная к фазовой границе компонента скорости среды j.

Граничные условия, используемые при решении уравнений системы (1), (2), описывающих распределение температуры в паре и жидкости на твердых стенках, представлены далее при решении конкретной задачи.

На фазовой границе $x = {{x}_{b}}(z)$ должны выполняться следующие условия.

Равенства нормальных и касательных напряжений в паре и жидкости

${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{{{v}n}}} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{{ln}}} = 0,\,\,\,\,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{{{v}{{\tau }}}}} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{{l{{\tau }}}}} = 0$

для рассматриваемого вида течения сводятся к

(5)

${{P}_{{v}}} = {{P}_{l}} = {{P}_{b}}({{T}_{b}}).$

Равенства температур и нормальных к фазовой границе потоков:

(6)

$\begin{gathered} {{T}_{{v}}} = {{T}_{l}} = {{T}_{b}},\,\,\,\,{{\rho }_{b}}{{i}_{b}}{{U}_{b}}({{x}_{b}}(z),z) = \\ = {{\left[ { - {{\lambda }_{{v}}}\frac{{\partial {{T}_{{v}}}}}{{\partial n}} + {{\lambda }_{l}}\frac{{\partial {{T}_{l}}}}{{\partial n}}} \right]}_{{{{x}_{b}}(z),z}}}. \\ \end{gathered} $

Здесь ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{j}}$ – тензор напряжений; ${{P}_{b}}({{T}_{b}})$ – давление насыщения пара, зависящее от температуры кипения ${{T}_{b}};$ ${{i}_{b}}$ – теплота парообразования (конденсации); $\frac{{\partial {{T}_{{v}}}}}{{\partial n}}$ – градиент температуры в направлении нормали к фазовой поверхности; ${{U}_{b}}({{x}_{b}}(z),z)$ – интенсивность парообразования на фазовой границе.

Уравнение (6) демонстрирует то, что разность между потоком теплоты, приходящим на фазовую поверхность, и потоком, уходящим с нее, идет на испарение жидкости.

Распределение параметров пара. Рассмотрим распределение параметров пара в области между стенкой $0cdg0$ и фазовой плоскостью $abefa,$ считая, что имеет место следующее неравенство:

${{U}_{{{v}n}}} \ll {{a}_{{{v}s}}} \equiv {{a}_{s}},$

где ${{a}_{{{v}s}}}$ – скорость звука в паре.

Плотность пара может быть представлена в виде суммы

${{\rho }_{{v}}} = {{\rho }_{b}} + \delta \rho (x,z),$

где ρ_b = const – плотность пара при температуре кипения ${{T}_{b}}$ и давлении ${{P}_{b}}({{T}_{b}}),$ ${{\delta \rho } \mathord{\left/ {\vphantom {{\delta \rho } {{{\rho }_{b}}}}} \right. \kern-0em} {{{\rho }_{b}}}} \approx \varepsilon \ll 1.$ Использование условий

(7)

${{\rho }_{{v}}} = {{\rho }_{b}} = {\text{const}}\,\,{\text{и}}\,\,\nabla \cdot {\mathbf{u}} = 0$

можно оправдать тем, что в стационарном случае из уравнения u ⋅ $\frac{{\partial \ln \rho }}{{\partial {\mathbf{r}}}}$ = $ - \frac{\partial }{{\partial {\mathbf{r}}}}$ ⋅ u следует оценка $\left| {\Delta \ln \rho } \right| < \frac{{\Delta u}}{u},$ где $\Delta f$ – характерное изменение величины f. Таким образом, с учетом (7) первое уравнение системы (1) с точностью до малого параметра $\varepsilon $ принимает вид

(8)

$\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}} = 0.$

Это уравнение решается с граничными условиями

на твердых стенках

(9)

$\begin{gathered} u(x = 0,z) = 0,\,\,\,\,w(0 \leqslant x \leqslant {{x}_{b}}(z = 0),z = 0) = 0, \\ {{U}_{b}}({{x}_{b}}(z),z) = \sqrt {u_{b}^{2} + w_{b}^{2}} \equiv {{U}_{{v}}}({{x}_{b}}(z),z), \\ \end{gathered} $

на фазовой границе $x = {{x}_{b}}(z),z.$

Здесь ${{u}_{b}} = u(x = {{x}_{b}}(z),z),$ ${{w}_{b}} = w(x = {{x}_{b}}(z),z),$ $0 \leqslant z \leqslant h.$

Рассмотрим специальный вид течения. Несмотря на то что в области пара ρ_v ≈ const, на фазовой границе приходящий от горячей стенки тепловой поток вызывает интенсивную генерацию пара и при $x = {{x}_{b}}(z)$ $\nabla \mathop \rho \nolimits_{v} = \delta {\text{(}}(x - {{x}_{b}}(z)){\text{)}} \ne 0$. Наличие $\nabla \mathop \rho \nolimits_{v} (x = {{x}_{b}}(z)) \ne 0$ приводит к генерации вихревого движения пара ${\mathbf{\Omega }} = \nabla \times {\mathbf{u}}$ согласно известному механизму

$\left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{\Omega }} = \nabla {{\rho }_{{v}}}\left( {{{x}_{b}}\left( z \right)} \right) \times {\mathbf{g}}{\kern 1pt} .$

В невязком вихревом течении вихрь Ω = ∇ × × u ≠ 0 переносится вдоль линий тока (u ⋅ ∇)Ω = 0. Именно поэтому коэффициент вязкости так же, как и в рассмотренной в [15] задаче, не входит в окончательные решения. Сила Архимеда участвует в создании вихря только на фазовой границе. Далее пар продолжает двигаться по инерции согласно принципу минимальности сопротивления. Проходя вдоль стенки, пар выходит в окружающее пространство, где давление P₊ ниже, чем давление в паровой пленке P_b: P₊ < P_b.

В этом случае решение уравнения (8) с граничными условиями (9) выражается через функцию тока

${\mathbf{u}}\left( {x,z} \right) = \nabla \times {\mathbf{\Psi }}\left( {x,~z} \right).$

Здесь Ψ = e_yΨ(x, z) = ε^mu₀zx/h, e_y – единичный вектор в направлении оси y, Ω = ∇ × u = –∆Ψ.

В этом случае компоненты скорости пара U_v = = (u, 0, w) имеют вид

(10)

$u = - \frac{{\partial \psi }}{{\partial z}} = - {{\varepsilon }^{m}}{{u}_{0}}\frac{x}{h},\,\,\,\,w = \frac{{\partial \psi }}{{\partial x}} = {{\varepsilon }^{m}}{{u}_{0}}\frac{z}{h}.$

Множитель ${{u}_{0}} \approx 1$ и показатель степени $m$ определяются в ходе решения задачи.

Для безвихревого течения (10) выполняются следующие равенства:

$\left[ {\nabla \times {{{\mathbf{U}}}_{{v}}} \times {{{\mathbf{U}}}_{{v}}}} \right] = 0,\,\,\,\,{{\mu }_{j}}\Delta {{{\mathbf{U}}}_{j}} = 0,\,\,\,\,j = {v},l,$

которые означают, что вязкость не оказывает влияния на данный вид течения и граничные условия для давления на фазовой границе сводятся к уравнению (5). При этом решение уравнения сохранения импульса системы (1), записанное в форме Громеки–Лэмба, с граничным условием на фазовой границе (9) сводится к виду

$\begin{gathered} {{P}_{{v}}}(x = {{x}_{b}}(z),z) = {{P}_{b}}--({{{{\rho }_{b}}} \mathord{\left/ {\vphantom {{{{\rho }_{b}}} {\text{2}}}} \right. \kern-0em} {\text{2}}}){\mathbf{U}}_{b}^{2} + {{\rho }_{b}}gz, \\ 0 \leqslant z \leqslant h. \\ \end{gathered} $

Таким образом, с точностью до малого параметра ${{\varepsilon }^{{2m}}} \ll 1$ и учетом неравенства ${{{{\rho }_{b}}gh} \mathord{\left/ {\vphantom {{{{\rho }_{b}}gh} P}} \right. \kern-0em} P} < 1$ распределение давления пара сводится к виду

${{P}_{{v}}}\left( {x,y} \right) = {{P}_{b}} = {\text{const}}.$

С учетом ранее полученных решений для скорости пара (10) уравнение сохранения энергии системы (1) имеет вид

(11)

$\begin{gathered} {{c}_{{p{v}}}}{{\rho }_{b}}\left( { - {{\varepsilon }^{m}}{{u}_{0}}\frac{x}{h}\frac{{\partial {{T}_{{v}}}}}{{\partial x}} + {{\varepsilon }^{m}}{{u}_{0}}\frac{z}{h}\frac{{\partial {{T}_{{v}}}}}{{\partial z}}} \right) = \\ = {{\lambda }_{{{v}1}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}} \right){{T}_{{v}}}. \\ \end{gathered} $

Это уравнение должно решаться со следующими граничными условиями:

на твердых стенках

$\begin{gathered} {{T}_{{v}}}(x = 0,\,\,0 \leqslant z \leqslant h) = {{T}_{w}} = {\text{const}} > {{T}_{b}}, \\ \frac{{\partial {{T}_{{v}}}}}{{\partial z}}(0 \leqslant x \leqslant {{x}_{0}},\,\,z = 0) = 0, \\ \end{gathered} $

на фазовой границе

${{T}_{{v}}}({{x}_{b}}(z),z){{T}_{b}} = {\text{const,}}$

на границe выхода пара в пространство над жидкостью

$\frac{{\partial {{T}_{{v}}}}}{{\partial z}}(0 \leqslant x \leqslant {{x}_{b}}(z = h),z = h) = 0.$

Здесь ${{T}_{w}} > {{T}_{b}}$ – температура горячей стенки, λ_v1 = const – коэффициент теплопроводности пара при температуре ${{T}_{{v}}} = {{({{T}_{w}} + {{T}_{b}})} \mathord{\left/ {\vphantom {{({{T}_{w}} + {{T}_{b}})} 2}} \right. \kern-0em} 2}.$

С учетом граничных условий (9) и малых параметров, входящих в уравнение (11), распределение температуры пара в области 0 ≤ x ≤ x_b(z), 0 ≤ z ≤ h имеет вид

(12)

${{T}_{{v}}}(x,z) = {{T}_{w}} - ({{T}_{w}} - {{T}_{b}})\frac{x}{{{{x}_{b}}(z)}}.$

Распределение параметров жидкости. При расчете распределений параметров жидкости учтем следующее неравенство:

${{\rho }_{{v}}} \ll {{\rho }_{l}} = {\text{const}}.$

В этом случае первое уравнение системы (2) сводится к

(13)

$\frac{{\partial {{u}_{l}}}}{{\partial x}} + \frac{{\partial {{w}_{l}}}}{{\partial z}} = 0.$

Это уравнение решается с граничными условиями

на дне сосуда и на свободной поверхности жидкости

(14)

$\begin{gathered} {{w}_{l}} = 0\,\,\,{\text{при}}\,\,\,\,{{x}_{0}} \leqslant x \leqslant {{L}_{x}},\,\,\,\,z = 0, \\ \,\,\,\,{{x}_{b}}(z = h) \leqslant x \leqslant {{L}_{x}},\,\,\,\,z = h, \\ \end{gathered} $

и на фазовой границе – условие (4).

С учетом неравенства (3) и граничного условия (14) решение уравнения (13) принимает вид

${{u}_{l}}(z) \ne 0,\,\,\,\,{{w}_{l}} = 0.$

Используя условие (4), находим

$\begin{gathered} {{u}_{l}}(x = {{x}_{b}}(z),z) = \\ = \frac{{{{\rho }_{b}}}}{{{{\rho }_{l}}}}u(x = {{x}_{b}}(z),z) = - {{\varepsilon }^{m}}\frac{{{{\rho }_{b}}}}{{{{\rho }_{l}}}}{{u}_{0}}\frac{{{{x}_{b}}(z)}}{h}. \\ \end{gathered} $

С учетом неравенства (3) уравнение сохранения энергии системы (2) записывается так

$\begin{gathered} {{\lambda }_{l}}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}{{T}_{l}} + {{c}_{{pl}}}{{\rho }_{l}}{{u}_{l}}\frac{{\partial {{T}_{l}}}}{{\partial z}} = {{\lambda }_{l}}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}{{T}_{l}} + \\ + \,\,{{c}_{{pl}}}{{\rho }_{b}}{{u}_{l}}{{\varepsilon }^{m}}{{u}_{0}}\frac{{{{x}_{b}}}}{h}\frac{{\partial {{T}_{{v}}}}}{{\partial z}} = 0. \\ \end{gathered} $

Это уравнение решается со следующими граничными условиями:

(15)

${{T}_{l}}(x \to \infty ) \to {{T}_{0}} < {{T}_{b}},\,\,\,\,{{T}_{l}}(x = {{x}_{b}}) = {{T}_{b}}$

на фазовой границе.

Здесь ${{T}_{0}}$ – температура жидкости, недогретой до кипения; ${{\lambda }_{l}}$ – коэффициент теплопроводности жидкости при температуре ${{T}_{l}}.$

С учетом граничных условий (15) распределение температуры в жидкости выглядит как

(16)

$\begin{gathered} {{T}_{l}}(x,z) = ({{T}_{b}} - {{T}_{0}}) \times \\ \times \,\,\exp [ - {{c}_{{pl}}}{{\rho }_{b}}{{\varepsilon }^{m}}{{u}_{0}}({{x - {{x}_{b}}(z))} \mathord{\left/ {\vphantom {{x - {{x}_{b}}(z))} {h{{\lambda }_{l}}}}} \right. \kern-0em} {h{{\lambda }_{l}}}}] + {{T}_{0}}. \\ \end{gathered} $

Для скорости генерации пара на фазовой границе

(17)

${{U}_{b}}(x = {{x}_{b}}(z),z) = \frac{1}{{{{\rho }_{b}}{{i}_{b}}}}{{\left[ { - {{\lambda }_{{v}}}\frac{{\partial {{T}_{{v}}}}}{{\partial x}} + {{\lambda }_{l}}\frac{{\partial {{T}_{l}}}}{{\partial x}}} \right]}_{{x = {{x}_{0}},z}}},$

с учетом уравнений (12) и (16) из (17) и с точностью до малого параметра ${{\varepsilon }^{{m + n}}} \ll 1$ получается

${{U}_{b}}(x = {{x}_{b}}(z),z) = {{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{{{x}_{b}}(z)\mathop {{{\rho }_{b}}i}\nolimits_b }}.$

Подчеркнем еще раз, в данной модели сила Архимеда участвует в создании вихря на фазовой границе, но далее пар начинает двигаться по инерции согласно принципу минимальности сопротивления вдоль стенки и выходить в окружающее пространство.

Истечение пара происходит не за счет силы Архимеда, а вследствие того, что образовавшийся пар начинает двигаться согласно принципу минимальности сопротивления вдоль стенки и выходить в окружающее пространство. Именно поэтому коэффициент вязкости так же, как и в рассмотренной в [15] задаче, не входит в окончательные решения.

Стационарная граница раздела фаз

Перейдем к нахождению фазовой границы, отделяющей жидкость от пара (линия ab на рис. 1б). Дальнейший анализ базируeтся только на предположении о том, что толщина пленки пара ${{x}_{b}}(z)$ меньше высоты сосуда h:

${{x}_{b}}(z) \ll h,\,\,\,\,0 \leqslant z \leqslant h.$

Уравнение фазовой границы ищется в виде

(18)

$\begin{gathered} {{F}_{b}} = x - {{\varepsilon }^{n}}{{x}_{b}}(z) = 0,\,\,\,\,{{x}_{b}}(z = 0) = {{x}_{0}}, \\ \varepsilon < 1,\,\,\,\,n > 1. \\ \end{gathered} $

Здесь ${{x}_{b}}(z)$ – уравнение проекции фазовой поверхности afeba на плоскость X0Z (рис. 1б), которое, как и показатель степени n, должнo быть определенo в процессe решения задачи.

Образование пара, происходящее при испарении жидкости, и начало движения пара происходят на фазовой границе. Линии тока пара, начинающиеся на фазовой границе, уходят на линию $0 \leqslant x \leqslant {{x}_{b}}$ $(z = h)$ (cb на рис. 1б) и затем переходят в свободное пространство z > h. В таком случае существует связь между положением фазовой границы и линиями тока, начинающимися на ней. Поэтому в качестве гипотезы, позволяющей найти уравнение фазовой границы, принимается предположение о том, что вектор τ_v, касательный к линии тока пара в точке (x_b(z), z), 0 ≤ z ≤ h, перпендикулярен вектору τ_b, касательному к фазовой границе в этой же точке. Другими словами, нормаль к фазовой границе в точке (${{x}_{b}}(z),z$) совпадает с вектором τ_v, касательным к линии тока пара в этой же точке.

Согласно соотношению (10), уравнение линии тока пара на плоскости X0Z имеет вид

$\psi \left( {x,z} \right){\text{ }} = C,\,\,\,\,C = {\text{ const}}\,\,{\text{или}}\,\,z = {{hC} \mathord{\left/ {\vphantom {{hC} {x.}}} \right. \kern-0em} {x.}}$

Отсюда находится касательный к линии тока вектор, взятый на фазовой границе в точке ($x = {{x}_{b}}(z),z$):

${{\tau }_{u}}(x = {{x}_{b}}(z),z) = - \frac{z}{{{{x}_{b}}}}(\cos {{\varphi }_{u}},0,\sin {{\varphi }_{u}}).$

Соответственно, касательный к линии фазовой границы (18) вектор, взятый в точке (x = x_b(z), z), имеет вид

(19)

${{\tau }_{b}}(x = {{x}_{b}}(z),z) = \frac{1}{{({{d{{x}_{b}}} \mathord{\left/ {\vphantom {{d{{x}_{b}}} {dz}}} \right. \kern-0em} {dz}})}}(\cos {{\varphi }_{b}},0,\sin {{\varphi }_{b}}).$

Здесь

(20)

$\begin{gathered} \sin {{\varphi }_{u}} = \frac{{{\text{tg}}{{\varphi }_{u}}}}{{\sqrt {1 + \mathop {({\text{tg}}{{\varphi }_{u}})}\nolimits^2 } }},\,\,\,\,\cos {{\varphi }_{u}} = \frac{1}{{\sqrt {1 + \mathop {({\text{tg}}{{\varphi }_{u}})}\nolimits^2 } }}, \\ {\text{tg}}{{\varphi }_{u}} = {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}_{u}} = - \frac{z}{{{{x}_{b}}}},\,\,\,\,\sin {{\varphi }_{b}} = \frac{{{\text{tg}}{{\varphi }_{b}}}}{{\sqrt {1 + \mathop {({\text{tg}}{{\varphi }_{b}})}\nolimits^2 } }}, \\ \cos {{\varphi }_{b}} = \frac{1}{{\sqrt {1 + \mathop {({\text{tg}}{{\varphi }_{b}})}\nolimits^2 } }},\,\,\,\,{\text{tg}}{{\varphi }_{b}} = {{\left( {\frac{{\partial z}}{{\partial x}}} \right)}_{b}} = \\ = {{ - \frac{{\partial {{F}_{b}}}}{{\partial x}}} \mathord{\left/ {\vphantom {{ - \frac{{\partial {{F}_{b}}}}{{\partial x}}} {\frac{{\partial {{F}_{b}}}}{{\partial z}}}}} \right. \kern-0em} {\frac{{\partial {{F}_{b}}}}{{\partial z}}}} = \frac{1}{{{{d{{x}_{b}}} \mathord{\left/ {\vphantom {{d{{x}_{b}}} {dz}}} \right. \kern-0em} {dz}}}}. \\ \end{gathered} $

Согласно высказанной выше гипотезе о расположении в точке (x = x_b(z), z) векторов τ_u, τ_b, касательных к линии тока и фазовой границе, имеем

(21)

${{{\mathbf{\tau }}}_{u}}\left( {x = {{x}_{b}}\left( z \right),z} \right) \cdot {{{\mathbf{\tau }}}_{b}}\left( {x = {{x}_{b}}\left( z \right),z} \right) = 0$

и

(22)

${{\varphi }_{u}} = {{\varphi }_{b}} + {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$

С использованием уравнений (19)–(22) получается уравнение для фазовой границы, отделяющей область пара от жидкости:

${{x}_{b}}\frac{{d{{x}_{b}}}}{{dz}} = z,$

решение которого с граничным условием

${{x}_{b}}(z = 0) = {{x}_{0}}$

имеет вид

(23)

${{x}_{b}}(z) = {{\varepsilon }^{n}}\sqrt {{{z}^{2}} + x_{0}^{2}} .$

Величины x₀, u₀, ε так же, как и показатели степеней $n,m$, должны быть определены из условий сохранения потоков массы и энергии пара.

Условие сохранения потока массы пара сводится к равенству потока массы ${{G}_{ + }},$ возникающего при испарении жидкости на фазовой плоскости $abefa,$ потоку массы ${{G}_{ - }},$ уходящей из области пара через плоскость $abdf.$

Поток массы ${{G}_{ + }}$ рассчитывается как

(24)

$\begin{gathered} {{G}_{ + }} \equiv {{L}_{y}}{{\rho }_{b}}\int\limits_a^b {{{U}_{b}}(x = {{x}_{b}}(z),z)dl} = \\ = {{L}_{y}}{{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{\mathop {{{\varepsilon }^{n}}{{\rho }_{b}}i}\nolimits_b }}{{I}_{1}}({{{\tilde {x}}}_{0}}). \\ \end{gathered} $

Здесь

$dl = \sqrt {1 + {{{\left( {{{\varepsilon }^{n}}\frac{{d{{x}_{b}}}}{{dz}}} \right)}}^{2}}} dz = \left[ {1 + {{\varepsilon }^{{2n}}}\frac{{{{z}^{2}}}}{{2\left( {{{z}^{2}} + x_{0}^{2}} \right)}}} \right]dz$

– элемент длины фазовой границы,

${{I}_{1}}({{\tilde {x}}_{0}}) = \int\limits_0^h {\frac{1}{{\sqrt {{{z}^{2}} + x_{0}^{2}} }}dz} = {\text{l}}n\left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right).$

Аналогично записывается поток массы G_–

(25)

${{G}_{ - }} \equiv {{L}_{y}}{{\rho }_{b}}\int\limits_0^{{{\varepsilon }^{n}}x_{b}^{{(h)}}} {w(x,z = h)dx} = {{L}_{y}}{{\rho }_{b}}{{\varepsilon }^{m}}{{u}_{0}}h\sqrt {1 + \tilde {x}_{0}^{2}} .$

С помощью уравнений (24), (25) равенство потоков ${{G}_{ + }} = {{G}_{ - }}$ сводится к виду

$\begin{gathered} {{G}_{ + }} \equiv {{L}_{y}}{{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{{{\varepsilon }^{n}}{{\rho }_{b}}{{i}_{b}}}}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right) = {{G}_{ - }} \equiv \\ \equiv {{L}_{y}}{{\rho }_{b}}{{\varepsilon }^{m}}{{u}_{0}}h\sqrt {1 + \tilde {x}_{0}^{2}} . \\ \end{gathered} $

Полученное уравнение может быть преобразовано к следующему соотношению, связывающему величины u₀, x₀ и индексы m, n:

(26)

${{\varepsilon }^{{m + 2n}}}{{\tilde {u}}_{0}}\sqrt {1 + {{{({{{\tilde {x}}}_{0}})}}^{2}}} = \Lambda \ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right).$

Здесь $\tilde {u}$ = u₀/a_s, ${{\tilde {x}}_{0}}$ = x₀/h, безразмерный параметр

(27)

$\Lambda = {{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{{{a}_{s}}{{\rho }_{b}}{{i}_{b}}h}}.$

Безразмерный параметр $\Lambda $ аналогичен критерию Стентона St, но отличается от последнего тем, что в знаменателe дроби $\frac{{{{{{\lambda }_{{v}}}({{T}_{w}} - {{T}_{b}})} \mathord{\left/ {\vphantom {{{{\lambda }_{{v}}}({{T}_{w}} - {{T}_{b}})} h}} \right. \kern-0em} h}}}{{{{a}_{s}}{{\rho }_{b}}{{i}_{b}}}}$ фигурирует скорость звука ${{a}_{s}}$ и теплота парообразования ${{i}_{b}} \equiv {{h}_{{\lg }}}.$ Для характерных параметров пленочного кипения $\Lambda $ можно представить в виде

$\Lambda = {{\Lambda }_{0}} \times {\text{1}}{{0}^{{--s}}} \ll {\text{1}},\,\,\,\,s > {\text{1}},\,\,\,\,{{\Lambda }_{0}} \approx {\text{1}}.$

Величины Λ₀, s зависят от рода кипящей жидкости, ее давления и температур T_w, T_b.

Рассмотрим теперь условие сохранения потоков энергии в паре. Это условие сводится к тому, что энергетический поток от горячей поверхности (твердой стенки) ${{S}_{w}}$ тратится на: 1) нагрев и превращение жидкости в пар ${{S}_{b}};$ 2) унос с энтальпией торможения пара, уходящего через поверхность $bcdeb$ (рис. 1а) в свободное пространство ${{S}_{ - }};$ 3) унос энергии в жидкость за счет теплопроводности через поверхность $abefa$ (рис. 1а) ${{S}_{{l - }}};$ 4) унос энергии из области пара во все стороны за счет излучения ${{S}_{r}}{\text{:}}$

(28)

${{S}_{w}} = {{S}_{b}} + {{S}_{ - }} + {{S}_{{l - }}} + {{S}_{r}}.$

Входящие в уравнение (28) потоки имеют следующий вид:

(29)

$\begin{gathered} {{S}_{w}} \equiv {{L}_{y}}{{\lambda }_{{v}}}({{T}_{w}} - {{T}_{b}})\int\limits_0^h {\frac{1}{{{{\varepsilon }^{n}}\sqrt {{{z}^{2}} + x_{0}^{2}} }}dz} = \\ = {{\varepsilon }^{{ - n}}}{{L}_{y}}{{\lambda }_{{v}}}({{T}_{w}} - {{T}_{b}}){{I}_{1}}({{{\tilde {x}}}_{0}}) \\ \end{gathered} $

– поток энергии, идущий в область пара с горячей стенки;

(30)

$\begin{gathered} {{S}_{b}} \equiv {{L}_{y}}{{\rho }_{b}}{{c}_{p}}{{T}_{b}}\int\limits_a^b {{{U}_{b}}(x = {{x}_{b}}(z),z)} dl = \\ = {{L}_{y}}{{\lambda }_{{v}}}{{\varepsilon }^{{ - n}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{{{i}_{b}}}}{{c}_{p}}{{T}_{b}}{{I}_{1}}({{{\tilde {x}}}_{0}}) \\ \end{gathered} $

– поток энергии, идущий на образование пара на фазовой плоскости $abde;$

(31)

$\begin{gathered} {{S}_{ - }} \equiv {{\rho }_{b}}\int\limits_c^b {{{c}_{p}}{{T}_{{v}}}w\left| {(x,z} \right. = h)dx} = {{L}_{y}}{{\rho }_{b}}{{\varepsilon }^{{m + n}}}{{u}_{0}}{{c}_{p}} \times \\ \times \,\,\frac{{{{T}_{w}} + {{T}_{b}}}}{2}\sqrt {1 + \tilde {x}_{0}^{2}} \\ \end{gathered} $

– поток энергии, уносимый через плоскость $cbdf$ уходящим паром;

(32)

$\begin{gathered} {{S}_{{l - }}} = - {{L}_{y}}\int\limits_a^b {{{{\left. {{{\lambda }_{l}}\frac{{\partial {{T}_{l}}}}{{\partial x}}} \right]}}_{{x = {{x}_{0}},z}}}} dl = \\ = ({{T}_{b}} - {{T}_{0}}){{c}_{{pl}}}{{\rho }_{0}}{{\varepsilon }^{{m + n}}}{{u}_{0}}{{I}_{2}}({{{\tilde {x}}}_{0}}), \\ {{I}_{2}}({{{\tilde {x}}}_{0}}) = \int\limits_0^1 {\sqrt {{{\xi }^{2}} + {{{({{{\tilde {x}}}_{0}})}}^{2}}} } d\xi \\ \end{gathered} $

– поток энергии, уходящий с фазовой плоскости в жидкость, находимый с учетом распределения температуры в жидкости (16).

Расчет энергии, уносимой излучением из области пара в область над паром и жидкостью, в саму жидкость и на стенки сосуда, представляет отдельную задачу. Согласно работе [18], лучистый теплообмен между горячей стенкой и фазовой границей может быть оценен по уравнению

${{\sigma \left( {T_{w}^{4} - T_{b}^{4}} \right)} \mathord{\left/ {\vphantom {{\sigma \left( {T_{w}^{4} - T_{b}^{4}} \right)} {\left( {\frac{1}{{{{\varepsilon }_{w}}}} + \frac{1}{{{{\varepsilon }_{l}}}} - 1} \right)}}} \right. \kern-0em} {\left( {\frac{1}{{{{\varepsilon }_{w}}}} + \frac{1}{{{{\varepsilon }_{l}}}} - 1} \right)}},$

где $\sigma $ – постоянная Стефана–Больцманa; ε_w, ε_l – степени черноты стенки и жидкости соответственно. Лучистый теплообмен между объемом пара, боковыми стенками и днищем сосуда может быть оценен аналогичным образом.

Здесь суммарные потоки энергии с учетом излучения увеличиваются посредством множителей $\varsigma > 1,$ ${{\varsigma }_{l}} > 1$ (т.е. доля излучения в потоках ${{S}_{ - }},$ ${{S}_{l}},$ уходящих из области пара, составляет величины $\varsigma - 1,$ ${{\varsigma }_{l}} - 1$). С учетом этого поток, уносимый излучением из области пара, учитывается следующим образом:

${{S}_{r}} = \varsigma {{S}_{ - }} + {{\varsigma }_{l}}{{S}_{l}}.$

Более точное значение коэффициентов $\varsigma - 1,$ ${{\varsigma }_{l}} - 1$ может быть установлено в эксперименте.

Проводя вычисления по уравнениям (29)–(32) и подставляя эти результаты в уравнение (30), представим условие сохранения суммарного потока энергии в виде

$\begin{gathered} {{\varepsilon }^{{m + 2n}}}{{{\tilde {u}}}_{0}}\left[ {\sqrt {1 + \tilde {x}_{0}^{2}} + 2\frac{{{{c}_{{pl}}}({{T}_{b}} - {{T}_{0}})}}{{\varsigma {{c}_{p}}({{T}_{w}} + {{T}_{b}})}}{{I}_{2}}({{{\tilde {x}}}_{0}})} \right] = \\ = 2\Lambda \frac{{{{i}_{b}} - {{c}_{p}}{{T}_{b}}}}{{{{c}_{p}}({{T}_{w}} + {{T}_{b}})}}{{I}_{1}}({{{\tilde {x}}}_{0}}), \\ \end{gathered} $

где ${{I}_{2}}({{\tilde {x}}_{0}}) = \frac{1}{2}\left[ {{{{\sqrt {1 + \tilde {x}_{0}^{2}} }}^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}} \right.$ + $\tilde {x}_{0}^{2}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{{{{\tilde {x}}}_{0}}}}} \right].$

Для характерных параметров пленочного кипения безразмерный комплекс (27) можно представить в виде Λ = Λ₀ × 10^–s, где $7 \geqslant s > 1.$ Поэтому для обеспечения одинакового порядка по параметру $\varepsilon < 1$ всех величин, входящих в (26) и (29), выбираются следующие значения $\varepsilon $ и связи между показателями степени m, n, s:

$\varepsilon = {{\Lambda }^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}} = {{10}^{{ - 1}}},\,\,\,\,m + 2n = s.$

Для рассматриваемой физической системы и конкретного значения параметра s выбор величин m, n не однозначен. Поэтому нужны либо априорная информация, получаемая на основе эксперимента, либо анализ устойчивости стационарных состояний, позволяющий отобрать устойчивые режимы пленочного кипения на вертикальной стенке.

Для кипения воды при атмосферном давлении и T_b = 373 К, T_w = 383 К параметры $\Lambda $ и $s$ принимают значения Λ = 4 × 10⁵, тогда Λ₀ = 4, s = 5, ε = = 4^1/5 × 10^–1 < 1. Поэтому далее с ориентировкой на многочисленные экспериментальные данные для воды выбираются

$\varepsilon = {{10}^{{ - 1}}},\,\,\,\,m = 2,\,\,\,\,n = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}.$

При таком выборе условие сохранения потока массы (27) сводится к

(33)

${{\tilde {u}}_{0}}\sqrt {1 + \tilde {x}_{0}^{2}} = {{\Lambda }_{0}}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right),$

а условие сохранения потока энергии (28) принимает вид

$\begin{gathered} {{{\tilde {u}}}_{0}}\left\{ {\sqrt {1 + \tilde {x}_{0}^{2}} + \frac{{{{c}_{{pl}}}({{T}_{b}} - {{T}_{0}})}}{{\varsigma {{c}_{p}}({{T}_{w}} + {{T}_{b}})}}} \right.\left[ {\sqrt {1 + \tilde {x}_{0}^{2}} {{ + }^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}}}} \right. \\ \left. { + \,\,\tilde {x}_{0}^{2}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{{{{\tilde {x}}}_{0}}}}} \right]} \right\} = \\ = 2{{\Lambda }_{0}}\frac{{\mathop i\nolimits_b - {{c}_{p}}{{T}_{b}}}}{{\varsigma {{c}_{p}}({{T}_{w}} + {{T}_{b}})}}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right). \\ \end{gathered} $

Уравнение (33) позволяет выразить ${{\tilde {u}}_{0}}$ через функцию параметра ${{\tilde {x}}_{0}}$

(34)

${{\tilde {u}}_{0}} = {{\Lambda }_{0}}\ln {{\left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right)} {\sqrt {1 + \tilde {x}_{0}^{2}} }}} \right. \kern-0em} {\sqrt {1 + \tilde {x}_{0}^{2}} }}.$

Используя уравнение (34), подставим величину ${{\tilde {u}}_{0}}$ в (33), сведя его к уравнению для определения ${{\tilde {x}}_{0}},$

(35)

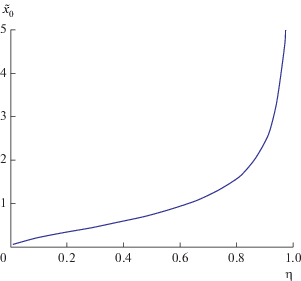
${{\tilde {x}_{0}^{2}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{\mathop {\tilde {x}}\nolimits_0 }}} \right)} \mathord{\left/ {\vphantom {{\tilde {x}_{0}^{2}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{\mathop {\tilde {x}}\nolimits_0 }}} \right)} {\sqrt {1 + \tilde {x}_{0}^{2}} }}} \right. \kern-0em} {\sqrt {1 + \tilde {x}_{0}^{2}} }} = \eta ,$

где $\eta = \frac{{2{{i}_{b}} - {{c}_{p}}[\varsigma {{T}_{w}} + (2 + \varsigma ){{T}_{b}}]}}{{{{\varsigma }_{l}}{{c}_{{pl}}}({{T}_{b}} - {{T}_{0}})}} - 1.$

При $\eta > 1$ уравнение (35) не имеет решения (${{\tilde {x}}_{0}} \to \infty $ при $\eta \to 1$). Это означает, что режимы пленочного кипения на вертикальной плоскости могут реализовываться лишь при вполне определенных условиях. При $\eta < 1$ решения существуют и зависимость ${{\tilde {x}}_{0}}$ от свойств пара и жидкости (от параметра η) представлена на рис. 2. Например, для кипения воды при атмосферном давлении, температурах T_b = 373 К, T_w = 400 К, T_b – T₀ = = 40 К, выбирая $\varsigma = 1.5,$ ${{\varsigma }_{1}} = 1.25,$ $m = 5,$ находим ${{\tilde {x}}_{0}} \approx 30.3.$ При приведенных выше данных для кипения воды при атмосферном давлении характерная толщина пленки составляет величины порядка 10² мкм.

Рис. 2.

Зависимость параметра ${{\tilde {x}}_{0}}$ от параметра η.

Используя уравнение (34), находим характерную скорость движения пара ${{\tilde {u}}_{0}},$ которая через параметры ${{\tilde {x}}_{0}},$ ${{\Lambda }_{0}}$ зависит от свойств испаряющейся жидкости, пара и температуры горячей стенки. На рис. 3 красным цветом представлена зависимость ${{{{{\tilde {u}}}_{0}}} \mathord{\left/ {\vphantom {{{{{\tilde {u}}}_{0}}} {{{\Lambda }_{0}}}}} \right. \kern-0em} {{{\Lambda }_{0}}}}$ от параметра η. С помощью формулы (34) для ${{\tilde {u}}_{0}}$ можно рассчитать зависимость безразмерного потока массы пара G_–/(L_yhρ_ba₀), уходящего через плоскость $abdf$ (рис. 1а), от параметров ${{\Lambda }_{0}}$ и η по формуле (35)

${{{{G}_{ - }}} \mathord{\left/ {\vphantom {{{{G}_{ - }}} {\left( {{{L}_{y}}h{{\rho }_{b}}{{a}_{s}}} \right)}}} \right. \kern-0em} {\left( {{{L}_{y}}h{{\rho }_{b}}{{a}_{s}}} \right)}} = {{\varepsilon }^{{m + n}}}{{\Lambda }_{0}}\ln \left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right).$

Рис. 3.

Зависимость от параметра η параметра ${{\tilde {u}}_{0}}$/Λ₀ (1) и уходящего потока пара G_–/(L_yhρ_ba_sε^{m + n}) для двух значений Λ₀: 2 – 0.1, 3 – 0.9.

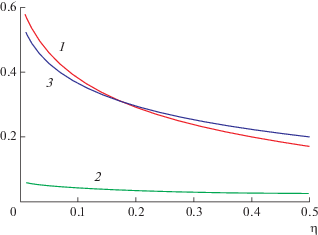
Зависимость комплекса G_–/(L_yhρ_ba_sε^{m + n}) от η для двух значений параметра Λ₀ = 0.1, 0.9 показана на рис. 3.

Для кипения воды при атмосферном давлении и температурах T_b = 373 К, T_w = 383 К фазовая граница и скорости течения пара в размерной форме имеют вид

${{x}_{b}} = {{\left( {{{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{\mathop {{{a}_{s}}{{\rho }_{b}}i}\nolimits_b h}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 {10}}} \right. \kern-0em} {10}}}}}h\sqrt {{{{\tilde {z}}}^{2}} + \tilde {x}_{0}^{2}(\eta )} ,\,\,\,\,0 \leqslant \tilde {z} \leqslant 1,$

$u = \mathop {{{{\tilde {u}}}_{0}}(\eta ){{a}_{s}}\left( {{{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{\mathop {{{a}_{s}}{{\rho }_{b}}i}\nolimits_b h}}} \right)}\nolimits^{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0em} 5}} \left( { - \frac{x}{h},0,\frac{z}{h}} \right).$

Важно подчеркнуть, что, кроме размеров слоя жидкости h, скорости звука в паре ${{a}_{s}}$ и безразмерного комплекса $\left( {{{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{\mathop {{{a}_{f}}{{\rho }_{b}}i}\nolimits_b h}}} \right),$ на форму фазовой поверхности и скорость течения пара оказывает влияние комплекс $\eta = \frac{{2{{i}_{b}} - {{c}_{p}}[\varsigma {{T}_{w}} + (2 + \varsigma ){{T}_{b}}] - {{\varsigma }_{l}}{{c}_{{pl}}}({{T}_{b}} - {{T}_{0}})}}{{{{\varsigma }_{l}}{{c}_{{pl}}}({{T}_{b}} - {{T}_{0}})}},$ от которого зависят безразмерные величины ${{\tilde {x}}_{0}},{{\tilde {u}}_{0}}.$

Следуя [9, 11], используем следующее значение для локального коэффициента теплоотдачи $\alpha (z)$ при пленочном кипении на вертикальной поверхности:

${{\lambda }_{{v}}}\frac{{{{T}_{w}} - {{T}_{b}}}}{{{{x}_{b}}(z)}} = \alpha (z)({{T}_{w}} - {{T}_{{l\infty }}}),$

где ${{T}_{w}} - {{T}_{{l\infty }}} = ({{T}_{w}} - {{T}_{b}})$ + $({{T}_{b}} - {{T}_{{l\infty }}}) \equiv \Delta {{T}_{ + }} + \Delta {{T}_{ - }}$, ${{T}_{{l\infty }}}$ – температура жидкости на входе в резервуар, $\Delta {{T}_{ + }}$ – перегрев пара, $\Delta {{T}_{ - }}$ – недогрев жидкости до температуры кипения.

Теперь, используя уравнение (29), можно рассчитать среднее по высоте фазовой поверхности значение числа Нуссельта

$\begin{gathered} \left\langle {{\text{Nu}}} \right\rangle \equiv \frac{{{{T}_{w}} - {{T}_{b}}}}{{\Delta {{T}_{ + }} + \Delta {{T}_{ - }}}}\int\limits_0^h {\frac{1}{{\mathop \varepsilon \nolimits^n \sqrt {\mathop z\nolimits^2 + x_{0}^{2}} }}} {\kern 1pt} dz = \\ = \mathop \varepsilon \nolimits^{ - n} \frac{{{{T}_{w}} - {{T}_{b}}}}{{\Delta {{T}_{ + }} + \Delta {{T}_{ - }}}}{\text{ln}}\left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right). \\ \end{gathered} $

Для кипения воды при атмосферном давлении и температурах T_b = 373 К, T_w = 383 К осредненное значение числа Нуссельта при пленочном кипении на вертикальной поверхности может быть представлено в виде

$\begin{gathered} \left\langle {{\text{Nu}}} \right\rangle = {{\left[ {\frac{{\mathop {{{a}_{s}}{{\rho }_{b}}i}\nolimits_b h}}{{{{\lambda }_{{v}}}({{T}_{w}} - {{T}_{b}})}}} \right]}^{{{3 \mathord{\left/ {\vphantom {3 {10}}} \right. \kern-0em} {10}}}}} \times \\ \times \,\,\left( {\frac{{{{T}_{w}} - {{T}_{b}}}}{{\Delta {{T}_{ + }} + \Delta {{T}_{ - }}}}} \right){\text{ln}}\left( {\frac{{1 + \sqrt {1 + \tilde {x}_{0}^{2}} }}{{1 + {{{\tilde {x}}}_{0}}}}} \right). \\ \end{gathered} $

Однако, как это будет показано далее, при пленочном кипении на вертикальной поверхности локальный коэффициент теплоотдачи при колебании пленки зависит и от времени $\alpha (z,t)$ и его необходимо осреднять и по высоте пленки, и по времени. Особенностью данного процесса является постоянное истечение пара в окружающую среду и представление о том, что толщина паровой пленки состоит из стационарной части и волн, распространяющихся по фазовой поверхности. В стационарном анализе исследован специальный режим, для которого методом многомасштабных асимптотических разложений построены решения гидродинамических уравнений, найдена форма фазовой границы, которая отделяет пар, примыкающий к горячей вертикальной стенке, от холодной жидкости. Найденное решение позволяет рассчитать характеристики теплообмена.

УСТОЙЧИВОСТЬ СТАЦИОНАРНОЙ ЗАДАЧИ ОТНОСИТЕЛЬНО МАЛЫХ И КОНЕЧНЫХ ВОЗМУЩЕНИЙ

Проведем теперь краткий анализ устойчивости полученных выше стационарных решений о течениях пара и жидкости, находящихся по разные стороны от фазовой границы ${{x}_{b}}(z,t) = \tilde {x}(\tilde {z}) + \delta \tilde {x}(\tilde {z},t),$ $\tilde {x}(\tilde {z}) = \sqrt {{{{\tilde {z}}}^{2}} + \tilde {x}_{0}^{2}} ,$ и устойчивости самой плоской границы.

Необходимость анализа устойчивости стационарного режима подтверждается примером последующих исследований задачи П.Л. Капицы [4, 5]. Многочисленные эксперименты по стекающим по наклонным стенкам слоям жидкости свидетельствуют о том, что в зависимости от организации течения (эксперимента) имеют место волновые режимы разной природы (см. работы [5, 7, 19–26] и библиографию к ним). Аналогичная картина наблюдается в экспериментах с горизонтальными паровыми пленками и пленками на поверхности нагретых сфер, опускаемых в холодную жидкость [27, 28], и горизонтальных трубах [23–26]. Достаточно подробный анализ колебаний паровой пленки на горизонтальной трубке с использованием лазерной диагностики получен в работе [26]. Однако несмотря на богатый экспериментальный материал, представленный в этих работах, трактовка механизма, приводящего к колебанию пленки пара, была неадекватной. В [26] сказано, что “при колебании границы раздела фаз одним из механизмов … является нелинейная зависимость термического сопротивления от толщины парового слоя”. Зависимость термического сопротивления от толщины парового слоя не может приводить к колебаниям фазовой границы. Как показано в [27, 29–33] и подробно разбирается ниже применительно к рассматриваемой здесь задаче, причиной колебаний является механизм, связанный с зависимостью давления насыщения от температуры. Кроме того, в экспериментах [24–26] на колебания фазовой границы на горизонтальной трубке мог оказывать влияние отрыв паровых пузырей в верхней части трубы, аналогично тому, что наблюдается в [28].

Для рассматриваемой здесь задачи при анализе устойчивости полученного стационарного решения воспользуемся результатами работ [27, 29–33], посвященных анализу устойчивости режимов пленочного кипения. В этих работах проведены исследования устойчивости плоской, горизонтальной фазовой границы в поле сил тяжести при различных расположениях пара и тяжелой жидкости. Из-за стационарного потока теплоты q(r) = –λ∇T(r) ≠ 0 при искривлении границы раздела фаз, кроме гравитационно-капиллярных сил, оказывают влияние изменения потоков теплоты и массы, вызванные изменением толщины паровой пленки. Искривление и смещение фазовой поверхности приводит к изменению температуры кипения и, соответственно, давления насыщения, зависящего от температуры. Это явление аналогично известному эффекту Гиббса–Томсона: деформация фазовой поверхности приводит к изменению температуры кипения и давления насыщения. При больших тепловых потоках через фазовую поверхность вариации температуры кипения и давления насыщения вызывают возмущения, превышающие аналогичные эффекты, связанные с силой тяжести и поверхностным натяжением. В этих случаях именно вариации температуры кипения и давления насыщения приводят к генерации поверхностных волн, отличающихся от известных гравитационно-капиллярных волн. Фазовая скорость этих волн при интенсивных потоках теплоты может намного превышать скорость капиллярно-гравитационных волн и приводить к возникновению “ряби, не связанной с поверхностным натяжением”. Эти волны играют определяющую роль в волновых процессах на границе раздела жидкость–пар и проявляются, как отмечено в [5], при любой стратификации фаз.

При анализе устойчивости стационарного состояния пренебрежем изменением толщины стационарной пленки по высоте сосуда, т.е. стационарная толщина паровой пленки ${{x}_{{sb}}}$ считается постоянной:

Изменение толщины пленки по высоте сосуда можно искать в виде

При таких условиях с учетом неравенства (38) для анализа устойчивости полученного выше стационарного решения (23) можно воспользоваться результатами работ [29, 30], где описан метод получения дифференциального уравнения для функции $\xi (t).$ В линейном приближении по $\xi (t)$ получается

Решая уравнение (39), для возмущений толщины пленки $\delta x(z,t),$ обращающихся в ноль при $z = h$ и $z = h,$ получаем

Здесь частота колебаний границы паровой пленки вычисляется как

Данное выражение отличается от формулы

С учетом характерных параметров задачи при условии ${{g}_{f}} > {{\sigma \mathop {{\text{(}}{{k}_{{\min }}}{\text{ }})}\nolimits^2 } \mathord{\left/ {\vphantom {{\sigma \mathop {{\text{(}}{{k}_{{\min }}}{\text{ }})}\nolimits^2 } {{{\rho }_{\Sigma }}}}} \right. \kern-0em} {{{\rho }_{\Sigma }}}}$ можно пренебречь поверхностным натяжением. В этих случаях частоту колебаний границы пленки пара, находящейся на твердой горячей вертикальной поверхности, можно рассчитать по формуле

С учетом неравенства (38) и малой толщины стационарной паровой пленки (36) частота колебаний поверхности пленки для кипения воды при атмосферном давлении и перепадах температур ${{T}_{w}} - T \approx 100$ К лежит в пределах (10–100) Гц. Поэтому для наблюдения таких волн в экспериментах требуются прецизионные измерения.

В рамках линейной задачи (39) определить амплитуду поверхностной волны невозможно. Ее можно получить, учтя нелинейные эффекты [33], опущенные в (39). В работе [33] получено нелинейное уравнение, описывающее более медленное колебание, чем период колебания пленки пара.

С учетом нелинейных членов уравнение (39) имеет вид

Уравнение имеет свой малый параметр

С использованием метода, предложенного в [34], можно найти амплитуду волны

Для кипения воды при атмосферном давлении и T_b = 373 К, T_w = 383 К, где Λ = 4 × 10^–5, с учетом (27) и n = 3/2 амплитуда волны в размерном виде:

Из (42) следует, что результаты [33], полученные для горизонтальной паровой пленки, можно использовать и для паровой пленки на вертикальной поверхности. Параметры, входящие в (42), зависят от состояния стационарной паровой пленки, но, согласно (37), не учитывают изменения толщины паровой пленки по высоте (длине), как в [33]. В [33] показано, что нелинейные эффекты, связанные с изменением толщины паровой пленки, могут также приводить к периодически повторяющемуся взрывному разрушению паровой пленки и выбросу пузырьков пара в жидкость. В таких режимах за конечное время происходит взрывное разрушение паровой пленки и жидкость приближается к горячей поверхности на очень малое расстояние. Происходит интенсивное испарение и восстановление – паровая пленка на вертикальной поверхности существует в режиме периодического разрушения и восстановления.

Эксперименты, проводимые при опускании раскаленной металлической сферы в недогретую до кипения жидкость, явно демонстрируют колебания фазовой границы пар–жидкость [27, 28]. На рис. 4 показано изменение во времени формы фазовой поверхности жидкость–пар, возникающей при опускании нагретой до 1500 К металлической сферы диаметром 20 мм в жидкий аргон [28]. Эти результаты аналогичны колебаниям, возникающим при опускании нагретой металлической полусферы в воду [27]. Однако детальных экспериментальных измерений характеристик волн на плоских, вертикальных нагретых до высоких температур металлических поверхностях автору не известно.

Рис. 4.

Формы фазовой поверхности, возникающей при опускании нагретой до 1500 К металлической сферы диаметром 20 мм в жидкий аргон [12]; время отсчитывается от момента опускания сферы в жидкость.

Характеристики волновых течений на вертикальной фазовой поверхности, полученные здесь, существенно отличаются от волновых явлений, рассмотренных в работах [1, 4, 5, 7, 9, 10, 23–26]. Это связано с тем, что основным механизмом является не сила тяжести, а зависимость давления насыщения ${{P}_{b}}({{T}_{b}})$ от температуры и искривление фазовой поверхности, приводящее к изменению температуры кипения T_b.

Качественный и количественный анализ данных, полученных в [9–15, 18–26], позволяет предположить, что явления, наблюдавшиеся в ряде экспериментов по пленочному кипению, могут быть связаны с образованием и распространением специфических нелинейных волн – солитонов, их последующим разрушением и выбросом пузырьков пара в жидкость. Судя по осциллограммам колебаний паровой пленки, приведенным в работе [35], эти режимы пленочного кипения подобны волновой турбулентности, развитой В.Е. Захаровым для гидродинамических волн [35].

ЗАКЛЮЧЕНИЕ

Исследован частный режим стационарного пленочного кипения на плоской вертикальной поверхности. Особенностью данного процесса является постоянное истечение пара в окружающую среду и представление о том, что толщина паровой пленки состоит из стационарной части и волн, распространяющихся по фазовой поверхности. В стационарном анализе исследован специальный режим, для которого методом многомасштабных асимптотических разложений построены решения гидродинамических уравнений и найдена форма фазовой границы для слоя конечной толщины h. Изменяющаяся по высоте бассейна фазовая граница x_b(z), 0 ≤ z ≤ h, отделяет находящийся на вертикальной стенке пар от недогретой до кипения жидкости, заполняющей остальную часть открытого сверху прямоугольного сосуда. Решение плоской задачи в декартовой системе координат, построенное методом многомасштабных асимптотических разложений, позволяет рассчитать характеристики теплообмена, включая средние значения коэффициента теплоотдачи и числа Нуссельта.

Исследована устойчивость полученной стационарной конфигурации границы пар–жидкость и показано, что вдоль границы распространяются волны, которые аналогичны волнам, исследованным в работах [29–33]. Найдено решение нелинейной задачи о колебании фазовой поверхности, и определена амплитуда распространяющейся волны. Волны, возникающие в неизотермических системах, к которым относятся поверхности фазового перехода жидкость–пар, отличаются от известных гравитационно-капиллярных волн в жидкости. Генерация этих поверхностных волн связана с изменением температуры кипения, возникающим при искривлении и смещении фазовой поверхности, и зависимостью давления насыщения от температуры. Изменение температуры кипения при искривлении или смещении фазовой поверхности, по существу, есть эффект Гиббса–Томсона – влияние деформации фазовой поверхности на изменение температуры фазового перехода.

Полученное решение позволяет рассчитать характеристики теплообмена при пленочном режиме кипения на плоской вертикальной поверхности.

Автор благодарит Ю.П. Ивочкина и В.В. Глазкова за полезные обсуждения данной работы.

Работа посвящается памяти П.Л. Капицы.