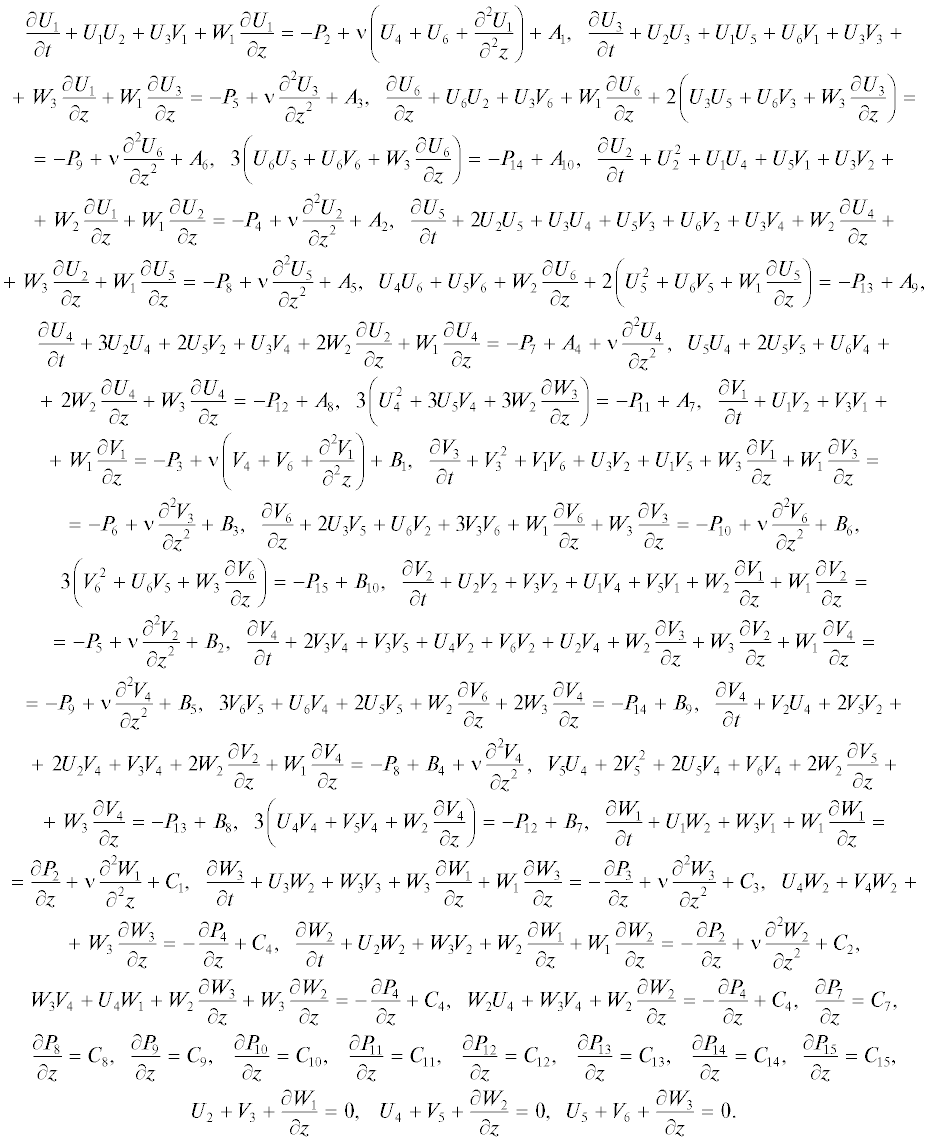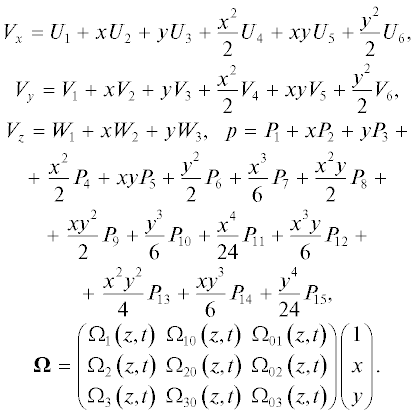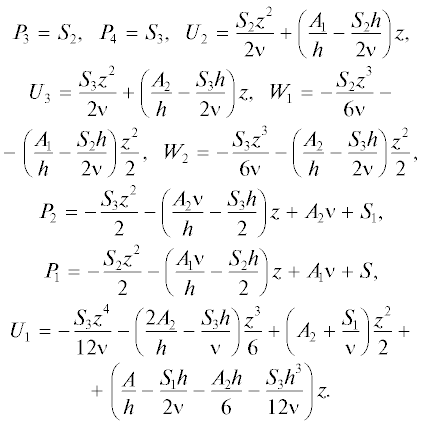Теоретические основы химической технологии, 2019, T. 53, № 1, стр. 112-120
Новый класс точных решений уравнений Навье–Стокса со степенной зависимостью скоростей от двух пространственных координат
Е. Ю. Просвиряков *
Институт машиноведения УрО РАН
Екатеринбург, Россия
* E-mail: evgen_pros@mail.ru
Поступила в редакцию 14.04.2017
После доработки 06.12.2017
Принята к публикации 11.10.2017
Аннотация
Предложен новый класс точных решений нелинейных и линеаризованных уравнений Навье–Стокса, обобщающий известное семейство точных решений, в котором скорость линейна по части координат. Подробно рассмотрен случай квадратичной зависимости скоростей от двух горизонтальных (продольных) координат с коэффициентами, являющимися функциями от вертикальной (поперечной) координаты и времени. Приведены обобщения найденных решений для вращающихся жидкостей. Получены формулы для построения точных решений с произвольной зависимостью скоростей от горизонтальных координат.
ВВЕДЕНИЕ
Непрерывное развитие химических и нефтехимических технологий требует поиска новых подходов для расширения методов математического моделирования процессов, лежащих в их основе. Углубленное теоретическое исследование физических процессов всегда сопровождается анализом и уточнением математических моделей, что приводит к более сложным определяющим уравнениям, описывающим физико-химические процессы. Это непосредственно относится к явлениям движения несжимаемых сред (жидкостей или газов), которые описываются уравнениями Навье–Стокса. Нелинейность уравнения движения жидкости способствовала появлению различных упрощенных представлений системы Навье–Стокса для того, чтобы получить теоретические сведения о потоке жидкости для дальнейшего использования в практической деятельности.
В данном направлении очень трудно переоценить роль точных решений уравнений Навье–Стокса. Несмотря на определенные успехи в вычислительной гидродинамике, построении большого числа моделей турбулентности, используемых в прикладных расчетах потоков несжимаемых сред, остается открытым вопрос о способах передачи импульсов в жидкости. Представляется, что именно точные решения и их дальнейшее обобщение с подробнейшим исследованием их области применимости позволят ответить на многие вопросы, которые ждут своего ответа.
Известно, что не существует алгоритмов аналитического решения системы уравнений Навье–Стокса, поэтому на первый план при интегрировании уравнений движения вышли классы точных решений. Под классами решений понимают определенную структуру гидродинамических полей, которая определяется непосредственно из уравнений Навье–Стокса. Понятно, что в запасе у исследователя всегда только небольшое количество частных решений уравнений движения, но даже в этом случае бывает чрезвычайно затруднительно исследовать редуцированную систему дифференциальных уравнений с различными свойствами, наследовавших нелинейные свойства уравнений Навье–Стокса.
Важную роль при исследовании изотермических течений вязких несжимаемых жидкостей играет класс точных решений, который характеризуется линейной зависимостью скоростей от части координат [1]. Данный класс, предложенный изначально для уравнений магнитной гидродинамики Ц.Ц. Линем [2], по крайней мере, дважды был заново описан в работах [3, 4] для точного интегрирования уравнений естественной конвекции несжимаемой жидкости.
Большинство известных точных решений уравнений Навье–Стокса принадлежит этому классу. В последнем обзоре [1], в котором рассматривались точные решения, линейно зависящие от части координат, содержалось описание не только известных к тому времени классических результатов, но и много новых точных решений, полученных авторами публикации. После публикации обзора [1] появилось некоторое количество работ, в которых развиты идеи дальнейшего использования класса Линя–Сидорова–Аристова. Укажем только некоторые направления дальнейшего обобщения изотермического класса решений.
Структура класса Линя–Сидорова–Аристова была использована при построении точных решений уравнений термодиффузии [5]. Важно отметить использование точных решений при описании реологических жидкостей [6–8] и сред, в которых ярко проявляются эффекты запаздывания [9, 10]. В статьях [12, 13] было показано, что благодаря этому классу оказалось возможным построить точные решения уравнений Навье–Стокса, которые описывают возникновение закрутки в жидкости и формирование противотечений в изотермических потоках. Исследования конвективных и концентрационных течений вязкой несжимаемой жидкости в рамках этого класса осуществлялось в работах [13–22].
В данной статье предложено обобщение класса решений, в котором скорости линейно зависят от части координат. Решения приводятся для изотермической жидкости.
КЛАСС РЕШЕНИЙ ДЛЯ ПОЛНОЙ СИСТЕМЫ
Уравнения Навье–Стокса вязкой несжимаемой жидкости или газа, как известно, являются квадратично нелинейными [1]:
(1)
$\frac{{\partial V}}{{\partial t}} + \left( {V \cdot \nabla } \right)V = - \nabla P + \nu \Delta V + F{\text{,}}$В системе (1), (2) использованы следующие обозначения: ${\mathbf{V}}\left( {t,x,y,z} \right) = \left( {{{V}_{x}},{{V}_{y}},{{V}_{z}}} \right)$ – скорость жидкости; $\nu $ – кинематическая (молекулярная) вязкость; $P$ – давление, нормированное на постоянную плотность несжимаемой среды; F(t, x, y, z) = (A, B, C) – поле массовых сил.
Построение нового класса точных решений системы (1) начнем с задания структуры горизонтальных (продольных) скоростей ${{V}_{x}}$ и ${{V}_{y}},$ обобщающей класс решений, в котором скорости линейно зависят от части координат [1–5]. Рассмотрим скорости ${{V}_{x}}$ и ${{V}_{y}}$ в виде квадратичной формы по горизонтальным координатам:
(3)
$\begin{gathered} {{V}_{x}} = {{U}_{1}} + x{{U}_{2}} + y{{U}_{3}} + \frac{{{{x}^{2}}}}{2}{{U}_{4}} + xy{{U}_{5}} + \frac{{{{y}^{2}}}}{2}{{U}_{6}}, \\ {{V}_{y}} = {{V}_{1}} + x{{V}_{2}} + y{{V}_{3}} + \frac{{{{x}^{2}}}}{2}{{V}_{4}} + xy{{V}_{5}} + \frac{{{{y}^{2}}}}{2}{{V}_{6}}. \\ \end{gathered} $Отметим, что коэффициенты квадратичных форм (3) ${{U}_{k}},$ ${{V}_{k}},$ где $k = \overline {1;6} $ зависят от поперечной координаты $z$ и времени t.
Для определения скорости ${{V}_{z}}$ подставим полиномиальные представления скоростей (3) в уравнение несжимаемости (2), получим
(4)
${{U}_{2}} + x{{U}_{4}} + y{{U}_{5}} + {{V}_{3}} + x{{V}_{5}} + y{{V}_{6}} + \frac{{\partial {{V}_{z}}}}{{\partial z}} = 0.$Из уравнения (4) следует представление вертикальной (поперечной) скорости в потоке вязкой несжимаемой жидкости:
где ${{W}_{l}} = {{W}_{l}}\left( {z,t} \right),$ $l = \overline {1;3} .$Для определения структуры выражения, описывающего давление P и массовые силы $F$ в вязкой несжимаемой жидкости, проанализируем степени многочленов по горизонтальным координатам в системе (1). Для начала заметим, что после дифференцирования функций ${{V}_{x}}$ и ${{V}_{y}}$ по координатам x и y степень многочленов (3) равняется единице. Таким образом, степень многочлена в левой части в уравнении (1), спроецированном на оси $Ox$ и $Oy,$ равняется трем. Очевидно, что решение (3) и (5) формируют поле давления в следующем виде:
(6)
$\begin{gathered} P = {{P}_{1}} + x{{P}_{2}} + y{{P}_{3}} + \frac{{{{x}^{2}}}}{2}{{P}_{4}} + xy{{P}_{5}} + \\ + \,\,\frac{{{{y}^{2}}}}{2}{{P}_{6}} + \frac{{{{x}^{3}}}}{6}{{P}_{7}} + \frac{{{{x}^{2}}y}}{2}{{P}_{8}} + \frac{{x{{y}^{2}}}}{2}{{P}_{9}} + \frac{{{{y}^{3}}}}{6}{{P}_{{10}}} + \\ + \,\,\frac{{{{x}^{4}}}}{{24}}{{P}_{{11}}} + \frac{{{{x}^{3}}y}}{6}{{P}_{{12}}} + \frac{{{{x}^{2}}{{y}^{2}}}}{4}{{P}_{{13}}} + \frac{{x{{y}^{3}}}}{6}{{P}_{{14}}} + \frac{{{{y}^{4}}}}{{24}}{{P}_{{15}}}. \\ \end{gathered} $Здесь ${{P}_{i}} = {{P}_{i}}\left( {z,t} \right),$ $i = \overline {1;15} .$
Уточним вид зависимости коэффициентов в выражении (6) для давления от координаты и времени. Подставляя в проекцию уравнения сохранения импульсов (1) на ось $Oz$ гидродинамические поля (3), (5), (6), получим зависимость этого уравнения только от слагаемых, у которых степень горизонтальных координат не превосходит двух. Таким образом, при отсутствии массовых сил $F = 0{\text{,}}$ коэффициенты, стоящие перед одночленами (6) степени три и четыре, зависят только от времени. При изучении стационарных процессов эти коэффициенты становятся постоянными числами и определяются граничными значениями, если вектор $F$ определяется формулами
(7)
$\begin{gathered} A = {{A}_{1}} + x{{A}_{2}} + y{{A}_{3}} + \frac{{{{x}^{2}}}}{2}{{A}_{4}} + xy{{A}_{5}} + \frac{{{{y}^{2}}}}{2}{{A}_{6}} + \\ + \,\,\frac{{{{x}^{3}}}}{6}{{A}_{7}} + \frac{{{{x}^{2}}y}}{2}{{A}_{8}} + \frac{{x{{y}^{2}}}}{2}{{A}_{9}} + \frac{{{{y}^{3}}}}{6}{{A}_{{10}}}, \\ B = {{B}_{1}} + x{{B}_{2}} + y{{B}_{3}} + \frac{{{{x}^{2}}}}{2}{{B}_{4}} + xy{{B}_{5}} + \frac{{{{y}^{2}}}}{2}{{B}_{6}} + \\ + \,\,\frac{{{{x}^{3}}}}{6}{{B}_{7}} + \frac{{{{x}^{2}}y}}{2}{{B}_{8}} + \frac{{x{{y}^{2}}}}{2}{{B}_{9}} + \frac{{{{y}^{3}}}}{6}{{B}_{{10}}}, \\ C = {{C}_{1}} + x{{C}_{2}} + y{{C}_{3}} + \frac{{{{x}^{2}}}}{2}{{C}_{4}} + xy{{C}_{5}} + \frac{{{{y}^{2}}}}{2}{{C}_{6}} + \\ + \,\,\frac{{{{x}^{3}}}}{6}{{C}_{7}} + \frac{{{{x}^{2}}y}}{2}{{C}_{8}} + \frac{{x{{y}^{2}}}}{2}{{C}_{9}} + \frac{{{{y}^{3}}}}{6}{{C}_{{10}}} + \\ + \frac{{{{x}^{4}}}}{{24}}{{C}_{{11}}} + \frac{{{{x}^{3}}y}}{6}{{C}_{{12}}} + \frac{{{{x}^{2}}{{y}^{2}}}}{4}{{C}_{{13}}} + \frac{{x{{y}^{3}}}}{6}{{C}_{{14}}} + \frac{{{{y}^{4}}}}{{24}}{{C}_{{15}}}. \\ \end{gathered} $В (7) ${{A}_{i}} = {{A}_{i}}\left( {z,t} \right),$ ${{B}_{i}} = {{B}_{i}}\left( {z,t} \right),$ $i = \overline {1;10} ;$ Cj = Cj(z, t), $j = \overline {1;15} .$
Таким образом, выражения для скоростей (3), (5) и полей давления (6) и массовых сил (7) формируют новый класс точных решений уравнений Навье–Стокса.
Для нахождения неизвестных функций, определяющих поле скоростей (3), (5) и давления (6), необходимо подставить их в систему уравнений (1), (2). После подстановки неизвестных функций, входящих в (3), (5), (6), с учетом массовых сил (7) получим систему уравнений
Система уравнений (8) состоит из тридцати восьми уравнений для определения тридцати неизвестных функций. Следовательно, система (8) является сильно переопределенной. Таким образом, для нахождения точных решений уравнений Навье–Стокса необходимо найти нетривиальное решение системы (8).
Отметим, что при равенстве нулю конвективной производной в уравнении (1) система уравнений (8) будет состоять из тридцати уравнений, поскольку функции ${{C}_{{11}}},$ ${{C}_{{12}}},$ ${{C}_{{13}}},$ ${{C}_{{14}}},$ ${{C}_{{15}}}$ в (7) будут тождественно равны нулю.
КЛАСС ТОЧНЫХ РЕШЕНИЙ ДЛЯ ВРАЩАЮЩИХСЯ ЖИДКОСТЕЙ
Характерной особенностью класса точных решений (3), (5)–(7) является зависимость вертикальной компоненты завихренности ${{\Omega }_{z}}$ от горизонтальных координат:
Остальные две компоненты вектора завихренности зависят от горизонтальных координат по квадратичному закону. Для примера приведем
Данное свойство поля скоростей (3) означает, что класс (3), (5)–(7) справедлив для описания вихревых движений жидкостей, в том числе и вертикально завихренных.
Запишем далее уравнения движения, связывающие силу Кориолиса, градиенты давления, вязкие при отсутствии массовых сил, которые описывают вращение вязкой несжимаемой жидкости. В этом случае уравнение (1) модифицируется следующим образом:
(9)
$\frac{{\partial V}}{{\partial t}} + r \times \frac{{\partial \Omega }}{{\partial t}} + 2\Omega \times V = - \nabla p + \nu \Delta V{\text{.}}$Здесь $\Omega $ определяет вектор угловой скорости вращения жидкости $\Omega \left( {t,x,y,z} \right)$ = $\left( {{{\Omega }_{x}},{{\Omega }_{y}},{{\Omega }_{z}}} \right),$ а r = = (x, y, z) – радиус-вектор, описывающий положение жидкой частицы; $p = P - \frac{1}{2}\left( {\Omega \times r,\Omega \times r} \right)$ – модифицированное давление.
Анализируя уравнение (9), получим класс точных решений:
В (10) решение для угловой скорости записано в векторно-матричном виде. Следовательно, представление каждой компоненты вектора угловой скорости (9) совпадает с выражением для вертикальной скорости (5). Наличие слагаемых с четвертой степенью относительно координат x и y обусловлено yналичием в линейных уравнениях (9) сил инерции $2\Omega \times V{\text{.}}$ Если вычислить векторное произведение $2\Omega \times V$ в силу формул (10) для линейных скоростей и вектора угловой скорости, то получим зависимость силы инерции от координат x и y по кубическому закону. Интегрирование по этим координатам позволяет построить решение (10) для давления.
Для нахождения тридцати девяти неизвестных функций, формирующих класс точных решений (10), получим систему уравнений, аналогичную системе (8), состоящую также из тридцати девяти уравнений. Таким образом, полученная система уравнений будет определенной и совместной, а ее решение позволяет описывать неоднородно вращающуюся жидкость в аппаратах химической технологии, при перемешивании металлов или при моделировании морских и океанических течений.
Отметим, что класс точных решений (10) справедлив при описании вращающихся вязких несжимаемых жидкостей при наличии сил инерции:
(11)
$\frac{{\partial V}}{{\partial t}} + r \times \frac{{\partial \Omega }}{{\partial t}} + \left( {V \cdot \nabla } \right)V + 2\Omega \times V = - \nabla p + \nu \Delta V{\text{.}}$При необходимости учета поля массовых сил в системах (9) или (11) точные решения (10) могут быть представлены аналогично формулам (7).
Отметим некоторую двойственность класса решений (3), (5)–(7), (10). При помощи точного решения (8) уравнения (1) можно осуществлять исследование движения вращающейся жидкости. Непосредственной подстановкой (8) в (1) можно получить условия, при которых данные формулы описывают вращение жидкости, совпадающие с системой, которая может быть получена при использовании гидродинамических полей (8), (10) при решении (9). Двойственность при интегрировании уравнений движения жидкости посредством классов точных решений (8), (10) возникает из-за того, что существует обратимое преобразование перехода из инерциальной системы координат в неинерциальную систему [1].
ТОЧНОЕ РЕШЕНИЕ, ОПИСЫВАЮЩЕЕ ПОЛЗУЩИЕ ТЕЧЕНИЯ
Рассмотрим пример точного решения (3), (5), (6), (7), описывающего стационарное плоское движение вязкой несжимаемой жидкости в приближении Стокса при отсутствии массовых сил. В этом случае система (1) редуцируется к векторному уравнению вида
Уравнение несжимаемости жидкости (2) остается без изменений.
Движение жидкости в бесконечном слое характеризуется гидродинамическими полями вида
Граничные условия, необходимые для вычисления частного решения системы (8), записываются следующим образом. На горизонтальной границе $z = 0$ выполнено условие прилипания:
Верхняя граница $z = h$ является плоской, на которой задана скорость и давление:
Точное решение краевой задачи имеет следующий вид:
Полученное решение (13) не может быть использовано при описании движения идеальных сред, поскольку оно зависит от диссипативного параметра $\nu $ по гиперболическому закону.
Поле скоростей (13) в безразмерных переменных записывается следующим образом:
(14)
$\begin{gathered} {{U}_{2}} = \frac{{{{\delta }^{2}}Ga}}{{2\operatorname{Re} }}{{Z}^{2}} + \left( {{{a}_{1}} - \frac{{{{\delta }^{2}}Ga}}{{2\operatorname{Re} }}} \right)Z,\,\,\,\,{{U}_{3}} = \frac{{{{\delta }^{2}}Ga{{b}_{1}}}}{{2\operatorname{Re} }}{{Z}^{2}} + \\ + \,\,\left( {{{a}_{2}} - \frac{{{{\delta }^{2}}Ga{{b}_{1}}}}{{2\operatorname{Re} }}} \right)Z,\,\,\,\,{{W}_{1}} = - \frac{{{{\delta }^{2}}Ga}}{{6\operatorname{Re} }}{{Z}^{3}} - \\ - \,\,\left( {{{a}_{1}} - \frac{{{{\delta }^{2}}Ga}}{{2\operatorname{Re} }}} \right)\frac{{{{Z}^{2}}}}{2},\,\,\,\,{{W}_{2}} = - \frac{{{{\delta }^{2}}Ga{{b}_{1}}}}{{6\operatorname{Re} }}{{Z}^{3}} - \\ - \,\,\left( {{{a}_{2}} - \frac{{{{\delta }^{2}}Ga{{b}_{1}}}}{{2\operatorname{Re} }}} \right)\frac{{{{Z}^{2}}}}{2},\,\,\,\,{{U}_{1}} = - \frac{{{{\delta }^{4}}Ga{{b}_{1}}}}{{12\operatorname{Re} }}{{Z}^{4}} - \\ - \,\,\left( {2{{\delta }^{2}}{{a}_{2}} - \frac{{{{\delta }^{4}}Ga{{b}_{1}}}}{{\operatorname{Re} }}} \right)\frac{{{{Z}^{3}}}}{6} + \left( {{{\delta }^{2}}{{a}_{2}} + \frac{{{{\delta }^{2}}Ga{{b}_{2}}}}{{\operatorname{Re} }}} \right)\frac{{{{Z}^{2}}}}{2} + \\ + \,\,\left( {1 - \frac{{{{\delta }^{2}}Ga{{b}_{2}}}}{{2\operatorname{Re} }} - \frac{{{{\delta }^{2}}{{a}_{2}}}}{6} - \frac{{{{\delta }^{4}}Ga{{b}_{1}}}}{{12\operatorname{Re} }}} \right)Z. \\ \end{gathered} $Здесь $\operatorname{Re} = \frac{{Al}}{\nu },$ $Ga = \frac{{{{S}_{2}}{{l}^{4}}}}{{{{\nu }^{2}}}}$ – число Рейнольдса и Галилея соответственно; $\delta = \frac{h}{l},$ ${{a}_{1}} = \frac{{{{A}_{1}}l}}{A},$ ${{a}_{2}} = \frac{{{{A}_{2}}{{l}^{2}}}}{A},$ ${{b}_{1}} = \frac{{{{S}_{3}}l}}{{{{S}_{2}}}},$ ${{b}_{2}} = \frac{{{{S}_{1}}}}{{{{S}_{2}}l}},$ $Z = \frac{z}{h},$ где h – толщина слоя, l – характерный горизонтальный масштаб.
Исследуя свойства скоростей (14), получим, что противотечения относительно скоростей ${{U}_{1}}X$ и ${{U}_{2}}{{X}^{2}}$ $\left( {X = \frac{x}{l}} \right)$ возможны при выполнении следующих неравенств, связывающих управляющие параметры краевой задачи:
При выполнении данных неравенств у соответствующих скоростей возможно существование только одной застойной точки. Аналогично можно получить оценки на безразмерные параметры
для скоростей ${{W}_{1}}$ и ${{W}_{2}}X$ соответственно, при выполнении которых существует одна застойная точка. Два нулевых значения, как показывает анализ выражений (14), может принимать скорость ${{U}_{1}}.$ Таким образом, обобщение класса решений с пространственным ускорением позволяет моделировать противотечения в вязкой несжимаемой жидкости при постоянной температуре.
ОБОБЩЕНИЕ КЛАССА РЕШЕНИЙ
После построения нового класса точных решений (3), (5), (6), (7), обобщающего известное семейство, характеризующееся линейностью скоростей по части координат [1], естественным оказывается вопрос о возможности учета мономов по горизонтальным координатам более высокого порядка.
Для начала рассмотрим конвективную производную в уравнении (1) в виде $\left( {U \cdot \nabla } \right)V{\text{,}}$ где $U = \left( {\alpha ,\beta ,\gamma } \right)$ – постоянный вектор. Данная аппроксимация соответствует приближению Озеена и, как частный случай, течению Стокса. Система уравнений (1), (2) в этом случае является линейной, поэтому справедливо следующее точное решение:
(15)
$\begin{gathered} {{V}_{x}} = \sum\limits_{k = 0}^n {{{U}_{k}}} ,\,\,\,\,{{V}_{y}} = \sum\limits_{k = 0}^n {{{V}_{k}}} , \\ {{V}_{z}} = \sum\limits_{k = 0}^{n - 1} {{{W}_{k}}} ,\,\,\,\,P = \sum\limits_{k = 0}^{n + 1} {{{P}_{k}}} . \\ \end{gathered} $Здесь формы ${{U}_{k}},$ ${{V}_{k}},$ ${{W}_{k}},$ ${{P}_{k}}$ определяются выражениями
При нахождении точного решения нелинейной системы Навье–Стокса (1), (2) поле скоростей соответствует точному решению (15), а давление в этом случае имеет следующий вид:
Очевидно, что вектор массовых сил $F$ будет иметь такую же структуру: для линеаризованной системы (1), (2)–(15), для полной системы (1), (2)–(16). Таким образом, при построении точных решений нелинейных уравнений Навье–Стокса степень горизонтальных координат силовых полей намного больше увеличивается по сравнению с гидродинамическими полями линеаризованной системой. Заметим, что если рассматривать точное решение (15), (16) для уравнений вращающейся жидкости (9) или (11), то, как было показано, каждая компонента вектора угловой скорости записывается аналогично представлению (10) относительно вертикальной скорости ${{V}_{z}}.$
В качестве последнего замечания по анонсированным новым точным решениям уравнений движений несжимаемых сред (в том числе неоднородно вращающихся) укажем обобщения приведенных решений относительно кинематической (динамической) вязкости. Существует возможность замены диссипативного постоянного коэффициента ν тензором второго ранга $\nu = {{\nu }_{{ik}}},$ где $i,k = \overline {1,3} ,$ определяющим вязкие свойства жидкости или газа. В этом случае решения (3), (5)–(7), (10) и (15), (16) будут также удовлетворять уравнениям Навье–Стокса (1), (9), (11), (12) и уравнению несжимаемости (2).
ЗАКЛЮЧЕНИЕ
В настоящей работе приведен ряд новых классов точных решений уравнений Навье–Стокса, полученных в результате обобщения класса решений относительно скоростей, линейных по двум координатам. Сначала приведено семейство точных решений, которое характеризуется квадратичными формами горизонтальных скоростей и линейной формой вертикальной скорости для нелинейных и линеаризованных уравнений. Приведены решения для вращающихся жидкостей. Характерной особенностью полученных в статье решений является учет массовых сил в уравнениях движения вязкой несжимаемой жидкости.
Работа выполнена в рамках комплексной про-граммы УрО РАН “Математические основы вычислительных и информационных технологий” (проект № 18-1-1-5).
ОБОЗНАЧЕНИЯ
| A | значение скорости на верхней границе в формулах (13), м/с |
| ${{A}_{1}}$ | градиент скорости ${{V}_{x}}$ на верхней границе в формулах (13), 1/с |
| ${{A}_{2}}$ | коэффициент при ${{x}^{2}}$ скорости ${{V}_{x}}$ на верхней границе в формулах (13), 1/(м с) |
| ${{A}_{1}},$${{A}_{2}},$ …, ${{A}_{{10}}},$${{B}_{1}},$${{B}_{2}},$ …,${{B}_{{10}}},$${{C}_{1}},$${{С }_{2}},$ …,${{C}_{{15}}}$ | функции, определяющие структуру точного решения поля массовых сил |
| ${{a}_{1}},$${{a}_{2}}$ | безразмерные параметры, характеризующие отношения скоростей на верхней границе слоя жидкости |
| ${{b}_{1}},$${{b}_{2}}$ | безразмерные параметры, характеризующие отношения давления на верхней границе слоя жидкости |
| $C_{k}^{i}$ | число сочетаний без повторений |
| F(t, x, y, z) = = (A, B, C) | плотность поля массовых сил и его компоненты, м/с2 |
| h, l | толщина и характерный горизонтальный размер слоя жидкости, м |
| $P$ | давление, нормированное на постоянную плотность несжимаемой среды |
| ${{P}_{1}},$${{P}_{2}},$ …, ${{P}_{{15}}}$ | функции, определяющие структуру точного решения для давления |
| S | значение приведенного давления на верхней границе, м2/с2 |
| ${{S}_{1}}$ | градиент приведенного давления на верхней границе, м/с2 |
| ${{S}_{2}}$ | коэффициент при ${{x}^{2}}$ приведенного давления на верхней границе, 1/с2 |
| ${{S}_{3}}$ | коэффициент при ${{x}^{3}}$ приведенного давления на верхней границе, 1/(м с2) |
| $U = \left( {\alpha ,\beta ,\gamma } \right)$ | вектор скорости для конвективной производной в приближении Озеена, м/с |
| ${{U}_{k}}$ | полиномиальная форма скорости ${{V}_{x}}$ |
| ${{U}_{1}},$${{U}_{2}},$ …, ${{U}_{6}}$ | функции, определяющие структуру точного решения для скорости ${{V}_{x}}$ |
| $\begin{gathered} V\left( {t,x,y,z} \right) = \hfill \\ = \,\,\left( {{{V}_{x}},{{V}_{y}},{{V}_{z}}} \right) \hfill \\ \end{gathered} $ | вектор скорости течения жидкости и его компоненты, м/с |
| ${{V}_{k}}$ | полиномиальная форма скорости ${{V}_{y}}$ |
| ${{V}_{1}},$${{V}_{2}},$ …, ${{V}_{6}}$ | функции, определяющие структуру точного решения для скорости ${{V}_{y}}$ |
| ${{W}_{k}}$ | полиномиальная форма скорости ${{V}_{z}}$ |
| ${{W}_{1}},$${{W}_{2}},$${{W}_{3}}$ | функции, определяющие структуру точного решения для скорости ${{V}_{z}}$ |
| X, Z | безразмерные прямоугольные декартовы координаты, |
| x, y, z | прямоугольные декартовы координаты, м |
| $\delta $ | показатель геометрической анизотропии слоя жидкости |
| $\nu $ | кинематическая (молекулярная) вязкость жидкости, м2/с |
| $\nu = {{\nu }_{{ik}}}$ | тензор кинематической или турбулентной вязкости, м2/с |
| $\begin{gathered} \Omega \left( {t,x,y,z} \right) = \hfill \\ = \,\,\left( {{{\Omega }_{x}},{{\Omega }_{y}},{{\Omega }_{z}}} \right) \hfill \\ \end{gathered} $ | вектор угловой скорости вращения жидкости и его компоненты |
| ${{\Omega }_{1}},$${{\Omega }_{2}},$${{\Omega }_{3}},$${{\Omega }_{{10}}},$${{\Omega }_{{01}}},$${{\Omega }_{{20}}},$${{\Omega }_{{02}}},$${{\Omega }_{{30}}},$${{\Omega }_{{03}}}$ | функции, определяющие структуру точного решения для угловой скорости вращения жидкости |
| $Ga$ | модифицированное число Галилея |
| $\operatorname{Re} $ | число Рейнольдса |
ИНДЕКСЫ
Список литературы
Aristov S.N., Knyazev D.V., Polyanin A.D. Exact solutions of the Navier-Stokes equations with the linear dependence of velocity components on two space variables // Theor. Found. Chem. Eng. 2009. V. 43. № 5. P. 642. [Аристов С.Н., Князев Д.Е., Полянин А.Д. Точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двух пространственных переменных // Теорет. основы хим. технологии. 2009. Т. 43. № 5. С. 547.]
Lin C.C. Note on a class of exact solutions in magneto-hydrodynamics // Arch. Rational Mech. Anal. 1958. V. 1. P. 391.
Sidorov A.F. Two classes of solutions of the fluid and gas mechanics equations and their connection to traveling wave theory // J. Appl. Mech. Tech. Phys. 1989. V. 30. № 2. P. 197. [Сидоров А.Ф. О двух классах решений уравнений механики жидкости и газа и их связи с теорией бегущих волн // Прикл. мех. и техн. физ. 1989. № 2. С. 34.]
Аристов С.Н. Вихревые течения в тонких слоях жидкости. Автореф. … дис. докт. физ.-мат. наук. Владивосток, 1990.
Aristov S.N., Prosviryakov E.Y. A new class of exact solutions for three-dimensional thermal diffusion equations // Theor. Found. Chem. Eng. 2016. V. 50. № 3. P. 286. [Аристов С.Н., Просвиряков Е.Ю. Новый класс точных решений трехмерных уравнений термодиффузии // Теорет. основы хим. технологии. 2016. Т. 50. № 3. С. 294.]
Pukhnachev V.V. Mathematical model of an incompressible viscoelastic Maxwell medium // Journal of Applied Mechanics and Technical Physics. 2010. V. 51. № 4. P. 546. [Пухначев В.В. Математическая модель несжимаемой вязкоупругой среды Максвелла // Прикл. мех. и техн. физ. 2010. Т. 51. № 4 (302). С. 116.]
Pukhnachev V.V., Pukhnacheva T.P. The Couette problem for a Kelvin–Voigt medium // J. Mathematical Sciences. 2012. V. 186. № 3. P. 495. [Пухначев В.В., Пухначева Т.П. Задача Куэтта для среды Кельвина–Фойхта // Сиб. журн. чист. и прикл. матем. 2010. Т. 10. № 3. С. 94.]
Pukhnachev V.V. Exact solutions of the equations of motion for an incompressible viscoelastic Maxwell medium // J. Applied Mechanics and Technical Physics. 2009. V. 50. № 2. P. 181. [Пухначев В.В. Точные решения уравнений движения несжимаемой вязкоупругой среды максвелла // Прикл. мех. и техн. физ. 2009. Т. 50. № 2(294). С. 16.]
Polyanin A.D., Vyazmin A.V. Decomposition of three-dimensional linearized equations for Maxwell and Oldroyd viscoelastic fluids and their generalizations // Theor. Found. Chem. Eng. 2013. V. 47. № 4. P. 321. Полянин А.Д., Вязьмин А.В. декомпозиция трехмерных линеаризованных уравнений вязкоупругих жидкостей Максвелла, Олдройда и их обобщений // Теорет. основы хим. технологии. 2013. Т. 47. № 4. С. 386.
Polyanin A.D. Exact solutions to new classes of reaction-diffusion equations containing delay and arbitrary functions // Theor. Found. Chem. Eng. 2015. V. 49. № 2. P. 169. [Полянин А.Д. Точные решения новых классов реакционно-диффузионных уравнений, содержащих запаздывание и произвольные функции // Теорет. основы хим. технологии. 2015. Т. 49. № 2. С. 175.]
Polyanin A.D., Sorokin V.G., Vyazmin A.V. Exact solutions and qualitative features of nonlinear hyperbolic reaction-diffusion equations with delay // Theor. Found. Chem. Eng. 2015. V. 49. № 5. P. 622. [Полянин А.Д., Сорокин В.Г., Вязьмин А.В. Точные решения и качественные особенности нелинейных гиперболических реакционно-диффузионных уравнений с запаздыванием // Теорет. основы хим. технологии. 2015. Т. 49. № 5. С. 527.]
Aristov S.N., Prosviryakov E.Y. Large-scale flows of viscous incompressible vortical fluid // Russian Aeronautics. 2015. V. 58. № 4. P. 413. [Аристов С.Н., Просвиряков Е.Ю. Крупномасштабные течения завихренной вязкой несжимаемой жидкости // Известия высших учебных заведений. Авиационная техника. 2015. № 4. С. 50.]
Aristov S.N., Prosviryakov E.Y. Unsteady layered vortical fluid flows // Fluid Dynamics. 2016. V. 51. № 2. P. 148. [Аристов С.Н., Просвиряков Е.Ю. Нестационарные слоистые течения завихренной жидкости // Известия Российской академии наук. Механика жидкости и газа. 2016. № 2. С. 25.]
Aristov S.N., Prosviryakov E.Y., Spevak L.F. Unsteady-state Bénard–Marangoni convection in layered viscous incompressible flows // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 132.
Knyazev D.V. Two-dimensional flows of a viscous binary fluid between moving solid boundaries // J. Appl. Mech. Tech. Phys. 2011. V. 52. № 2. P. 212. [Князев Д.В. Плоские течения вязкой бинарной жидкости между подвижными твердыми границами // Прикл. мех. и техн. физ. 2011. Т. 52. № 2 (306). С. 66.]
Aristov S.N., Prosviryakov E.Y. Nonuniform convective Couette flow // Fluid Dynamics. 2016. V. 51. № 5. P. 581. [Аристов С.Н., Просвиряков Е.Ю. Неоднородное конвективное течение Куэтта // Известия Российской академии наук. Механика жидкости и газа. 2016. № 5. С. 3.]
Aristov S.N., Shvarts K.G. Convective heat transfer in a locally heated plane incompressible fluid layer // Fluid Dynamics. 2013. V. 48. № 3. P. 330. [Аристов С.Н., Шварц К.Г. Конвективный теплообмен при локализованном нагреве плоского слоя несжимаемой жидкости // Известия Российской академии наук. Механика жидкости и газа. 2013. № 3. С. 53.]
Andreev V.K., Bekezhanova V.B. Stability of nonisothermal fluids (Review) // J. Appl. Mech. Tech. Phys. 2013. V. 54. № 2. P. 171. [Андреев В. К., Бекежанова В. Б. Устойчивость неизотермических жидкостей (обзор) // Прикл. мех. техн. физ. 2013. № 2. С. 3.]
Goncharova O.N., Rezanova E.V. Modeling of two layer fluid flows with evaporation at the interface in the presence of the anomalous thermocapillary effect // J. Sib. Fed. Univ. Math. Phys. 2016. V. 9. № 1. P. 48.
Efimova M.V. On one two-dimensional stationary flow of a binary mixture and viscous fluid in a plane layer // J. Sib. Fed. Univ. Math. Phys. 2016. V. 9. № 1. P. 30.
Goncharova O.N., Kabov O.A., Pukhnachov V.V. Solutions of special type describing the three dimensional thermocapillary flows with an interface // Int. J. Heat Mass Transfer. 2012. V. 55. № 4. P. 715.
Goncharova O.N., Rezanova E.V. Mathematical modelling of the evaporating liquid films on the basis of the generalized interface conditions // MATEC Web of Conferences. 2016. V. 84. P. 00013.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии