Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 174-188
Непрерывное смешивание сыпучих материалов при импульсном воздействии на сегрегированный поток порционно дозируемого компонента
В. Н. Долгунин 1, *, О. О. Иванов 1, Е. А. Рябова 1
1 Тамбовский государственный технический университет
Тамбов, Россия
* E-mail: dolgunin-vn@yandex.ru
Поступила в редакцию 28.02.2017
После доработки 28.08.2018
Принята к публикации 04.05.2018
Аннотация
Принцип управления сегрегированными технологическими потоками используется для организации процесса непрерывного смешивания сыпучих материалов в условиях порционного дозирования микрокомпонента. Анализируются технологические возможности процесса смешивания при обратном импульсном воздействии на сегрегированный поток компонента в барабанном смесителе. Методами экспериментального и аналитического исследования динамики процесса смешивания установлено, что путем избирательного воздействия на сегрегированный поток микрокомпонента каскадом встречных импульсов обеспечивается возможность многократного снижения вариации состава смеси по сравнению со смесителем, структура потока в котором соответствует идеальному перемешиванию.
ВВЕДЕНИЕ
Непрерывные технологии получают все большее распространение в связи с возрастающей технологической культурой и перспективами повышения качества продукции и снижения его себестоимости [1]. Вместе с тем при организации непрерывных процессов ужесточаются регламентные требования к выполнению загрузочно-разгрузочных операций [2], которые часто становятся сдерживающим фактором для внедрения непрерывных технологий. В первую очередь это относится к технологиям сыпучих материалов.
Высокие показатели эффективности процесса непрерывного смешивания сыпучих материалов достигаются при выполнении двух основных условий [3, 4]: обеспечение контакта компонентов смеси с их интенсивным взаимным проникновением и достаточно высокой точности дозирования. Однако, несмотря на очевидные достоинства непрерывного смешивания, его широкое распространение, во многих случаях, сдерживается высокими требованиями по точности дозирования. Точность дозирования определяет состав смеси и при непрерывном и при периодическом смешивании. Однако при периодическом смешивании точность дозирования не является фактором, ограничивающим качество смеси, поскольку для достижения требуемой точности периодического дозирования практически не существует никаких технических препятствий. Точность же непрерывного дозирования сыпучих материалов во всех случаях прямо влияет на качество получаемой [4] смеси, определяя вариацию ее состава. При этом особой технической сложностью характеризуется технологическая задача организации процесса непрерывного смешивания при микродозировании компонентов [4] с высокой склонностью к сегрегации. В первую очередь это объясняется технической сложностью организации надежного непрерывного дозирования сыпучих микрокомпонентов.
Решение такого рода проблемы является актуальным, например, в производствах композиционных и строительных материалов, медицинских и химических препаратов, пищевых концентратов, пластмасс, резиновых смесей и многих других производствах, когда содержание либо целевого компонента, либо модифицирующей добавки в смеси строго регламентируется и соответствует по величине микродозе. В связи с низкой технологической надежностью непрерывно действующих микродозаторов сыпучих материалов, в таких случаях, возникает необходимость применения высокоточного весового порционного дозирования компонента смеси с использованием, соответственно, периодического смешивания. Однако, условия периодического смешивания в наибольшей мере способствуют проявлению негативных последствий сегрегации, в том числе на этапе выгрузки готовой смеси [1, 2]. В связи с этим использование периодически действующего смесителя для приготовления смесей материалов с высокой склонностью к сегрегации является технологически нецелесообразным. Несмотря на то, что общепризнанной универсальной оценки склонности смесей сыпучих материалов к сегрегации не существует, можно обозначить предельные случаи, в которых сформировать смесь в режиме периодического смешивания практически невозможно. Например, невозможно ни получить и ни использовать в периодическом процессе бинарную смесь несвязных частиц, различающихся по размеру более чем в ~6 раз, вследствие спонтанной миграции мелких частиц в направлении силы тяжести даже в неподвижной среде [5].
Сегрегация (лат. segregatio – отделение) – эффект взаимодействия неоднородных частиц сыпучего материала, при котором происходит их перераспределение с образованием областей, отличающихся более однородными свойствами частиц, чем среда в целом. В технологиях сыпучих материалов проявление эффектов сегрегации имеет глобальный характер [6] и является столь существенным, что, по крайней мере, в промышленных условиях получение идеально однородных смесей не представляется возможным [7, 8].
В этом случае альтернативным технологическим решением может быть применение непрерывного смешивания с использованием смесителя с высокой сглаживающей способностью [4]. Необходимую сглаживающую способность смесителя традиционно обеспечивают за счет увеличения его рабочего объема и интенсификации продольного перемешивания. Однако использование таких приемов сопровождается пропорциональным возрастанием диссипации механической энергии и увеличением капитальных и эксплуатационных затрат на организацию процесса.
Задача, решаемая в рамках настоящей работы, заключается в повышении качества непрерывно получаемой смеси в условиях, когда повышенные требования по точности дозирования микрокомпонента, как одного из компонентов смеси, обеспечиваются путем порционной его подачи, в то время как остальные компоненты смеси подаются непрерывно. Для решения этой технологической задачи в настоящей работе предлагается использование принципа управления сегрегированными потоками [9–11]. Сегрегированные потоки зарождаются вследствие проявления эффектов сегрегации в рабочем объеме оборудования и являются частями единого технологического потока, частицы в котором различаются по степени проявления того или иного свойства или комплексу физико-механических свойств. Принцип управления сегрегированными потоками может быть реализован при использовании либо спонтанно образованных, либо искусственно организованных сегрегированных потоков.
Сущность принципа заключается в оказании направленного сконцентрированного воздействия на сегрегированный поток или некоторую его часть для достижения определенной технологической цели. При наличии в смеси склонного к сегрегации микрокомпонента будет наблюдаться его преимущественное перемещение в одной из частей сегрегированного технологического потока. Вследствие этого, неоднородность дозирования микрокомпонента в наибольшей степени будет проявляться в неоднородности состава части сегрегированного потока, обогащенной этим компонентом, оказывая определяющее влияние на однородность смеси в целом.
В соответствии с принципом управления сегрегированными потоками для достижения наиболее высокого эффекта сглаживания пульсаций порционно дозируемого компонента целесообразно сконцентрировать сглаживающее воздействие на части сегрегированного технологического потока с наиболее высоким проявлением неоднородности. Очевидно, что такое сглаживающее воздействие является более рациональным по сравнению с традиционными экстенсивными способами в связи с его целенаправленным характером и энергосберегающим эффектом.
Реализация принципа управления сегрегированными потоками предполагает выбор варианта импульсного воздействия на технологический поток, наиболее подходящий для достижения технологического эффекта. При анализе возможных вариантов импульсного сглаживающего воздействия с использованием поперечных и продольных импульсов [9] можно сделать вывод, что наибольший эффект сглаживания пульсаций порционной подачи компонента могут обеспечить продольные импульсы. Вместе с тем очевидно, что использование продольно уравновешенных знакопеременных импульсов не может обеспечить эффект сглаживания, который смог бы превысить таковой для аппарата, структура потока в котором соответствует идеальному перемешиванию. В настоящей работе анализируется способ непрерывного смешивания сыпучих материалов с высокой неоднородностью подачи отдельных компонентов, который позволяет преодолеть эффект сглаживания, достигаемый в потоке, структура которого соответствует идеальному перемешиванию.
ОСНОВНАЯ ЧАСТЬ
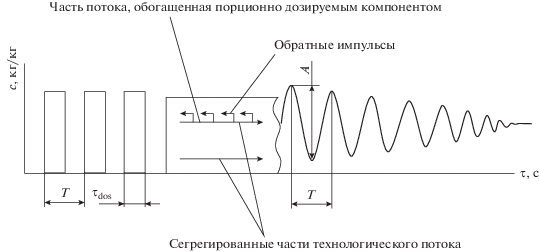
Сущность способа смешивания заключается в воздействии обратными продольными импульсами на сегрегированный поток, обогащенный порционно дозируемым компонентом (рис. 1). Импульсы направлены навстречу технологическому потоку и распределены продольно в объеме соответствующей сегрегированной его части. Такое воздействие должно приводить к двойному сглаживающему эффекту. Во-первых, сглаживание обеспечивается за счет многократного демпфирующего воздействия последовательной цепочки встречных импульсов непосредственно на локальные проявления пульсации подачи компонента. Во-вторых, под воздействием встречных импульсов в головной (загрузочной) части смесителя формируется буферная масса порционно дозируемого компонента, которая также приводит к избирательному повышению сглаживающей функции в отношении компонента смеси с высокой неоднородностью подачи.
Рис. 1.
Схема импульсного воздействия при организации процесса непрерывного смешивания сыпучих материалов с порционной подачей отдельных компонентов: c – концентрация порционно дозируемого компонента; τ – время; τdos – время ввода дозы; T – период подачи доз.
Эффективность предложенного способа смешивания исследована с использованием в качестве экспериментальной базы аппарата с вращающимся барабаном, снабженным периферийными подъемными лопастями. Подобного рода аппараты широко используются для организации тепломассообменных и гидромеханических процессов с участием дисперсной твердой фазы (сушки, гранулирования, смешивания, термовлажностной обработки и др.) и характеризуются образованием ярко выраженных сегрегированных технологических потоков сыпучих материалов [12].
Сегрегированный поток зарождается в скатывающемся слое засыпки материала в нижней части барабана и подъемными лопастями распространяется на падающий слой частиц. В общем случае [12], вследствие сегрегации крупные и менее плотные частицы концентрируются на поверхности скатывающегося слоя засыпки, в первую очередь исчерпываются лопастной насадкой и выпадают из насадки в последней фазе ее опорожнения, образуя падающий слой частиц под опускающимися лопастями. Напротив, мелкие и более плотные частицы концентрируются у основания скатывающегося слоя засыпки и поэтому попадают на лопасти на завершающей стадии их заполнения. Вследствие этого такие частицы в первую очередь выпадают из насадки, принимая участие в образовании падающего слоя, преимущественно, под поднимающимися лопастями.
В результате, в зависимости от физико-механических свойств частиц (размера, плотности, формы, шероховатости, упругости и т.д.) будут наблюдаться траектории их преимущественного перемещения в падающем слое материала в поперечном сечении барабана. Очевидно, что при приготовлении смеси сыпучих материалов с микрокомпонентом, имеющим склонность к сегрегации, его частицы также будут образовывать сегрегированный поток и перемещаться в падающем слое материала преимущественно по характерным для них траекториям. Тогда, в соответствии с предложенным способом смешивания, достаточно воздействовать на сегрегированный поток микрокомпонента каскадом последовательных импульсов, направленных навстречу технологическому потоку в барабане.
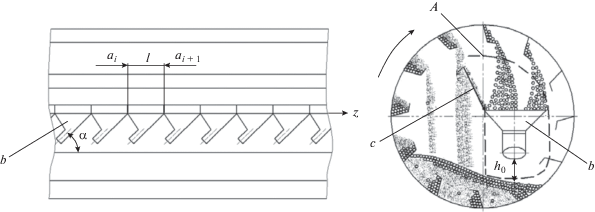
Схема устройства насадки барабанного аппарата, позволяющей реализовать предложенный способ смешивания, изображена на рис. 2. На внутренней поверхности вращающегося барабана закреплены подъемные Г-образные лопасти, а в центральной его части неподвижно, на вынесенных за пределы барабана опорах, установлена насадка, предназначенная для оказания необходимого импульсного воздействия на сегрегированный поток частиц падающего слоя. Насадка представляет собой продольный ряд отклоняющих элементов, выполненных в форме воронок с наклонными течками, при контакте с которыми падающие частицы приобретают продольный импульс, направленный навстречу технологическому потоку. Насадка закреплена с возможностью поперечного перемещения в барабане, а на продольных кромках ее отклоняющих элементов установлены поворотные заслонки. Такая конструкция насадки позволяет обеспечить контакт ее отклоняющих элементов с любой из частей сегрегированного потока падающих частиц, что обеспечивает условия для гибкой адаптации смесителя к изменяющимся условиям протекания процесса при переходе с одной смеси на другую.
Рис. 2.
К разработке математической модели – схема барабанного смесителя с обратным импульсным воздействием на сегрегированный поток компонента с высокой неоднородностью дозирования: A – область сегрегированного потока компонента с высокой неоднородностью дозирования; аi – координата i-го отклоняющего элемента; b – насадка, управляющая сегрегированным потоком; c – поворотная заслонка; h0 – высота расположения нижней кромки отклоняющего элемента над поверхностью засыпки материала в барабане; l – длина отклоняющего элемента; z – направление технологического потока; α – угол наклона отклоняющего элемента к горизонту.
Очевидно, что при формировании смеси пульсации ее концентрации вследствие порционной загрузки микрокомпонента наиболее ярко проявляются в пульсациях концентрации сегрегированного потока. Эта в наибольшей степени неоднородная часть технологического потока при перемещении от загрузочного к разгрузочному торцу барабана периодически вступает в контакт с отклоняющими элементами, которые сообщают ему при контакте импульсы, направленные навстречу технологическому потоку. В результате сегрегированный поток оказывается под воздействием каскада встречных импульсов, которые не только демпфируют в нем пульсации концентрации микрокомпонента, но и приводят к накапливанию некоторой буферной его массы в загрузочной части смесителя. Формирование буферной массы микрокомпонента увеличивает среднее время его пребывания в аппарате и, как следствие, вносит дополнительный вклад в повышение эффективности сглаживания. Таким образом, названные эффекты сконцентрированного импульсного воздействия способствуют избирательному возрастанию сглаживающей функции барабанного смесителя в отношении компонента с высокой неоднородностью дозирования.
С целью исследования влияния обратного импульсного воздействия на характеристики структуры сегрегированных потоков и динамику формирования смеси сыпучих материалов в барабанном смесителе разработана математическая модель, описывающая эволюцию продольного распределения контрольного компонента в аппарате при его порционной подаче. Одной из основных прикладных задач, подлежащих решению методом математического моделирования, является определение параметров импульсного воздействия на сегрегированный поток компонента с высокой неоднородностью подачи, необходимого и достаточного для получения смеси с заданной степенью однородности.
Описание динамики продольного распределения концентрации c(z, τ) контрольного (порционно дозируемого) компонента смеси проведено с использованием в качестве базы основного уравнения массопереноса [9, 13]. В отличие от уравнения в его традиционной формулировке, предложенное уравнение учитывает изменение локальных значений концентрации контрольного компонента не только вследствие наличия потоков конвекционного переноса и квазидиффузионного перемешивания, но и под влиянием эффектов управления сегрегированными потоками при совокупном воздействии подъемных лопастей и обратных импульсов.
При описании эффекта воздействия обратных импульсов на технологический поток приняты во внимание эффекты избирательного исчерпывания компонентов подъемными лопастями из засыпки, задержки компонента при транспортировании его лопастями над засыпкой материала и направленное перемещение компонента в составе его сегрегированного потока под действием отклоняющих элементов. При анализе эффектов задержки принято допущение о том, что время контакта частиц материала с отклоняющими элементами является пренебрежимо малым по сравнению с продолжительностью периода между их исчерпыванием из засыпки и возвратом в засыпку в отсутствие отклоняющих элементов. При описании потока, формируемого отклоняющими элементами, сделано допущение о полном его перемешивании на каждом из элементов. Принятому допущению может быть дано следующее феноменологическое обоснование. Частицы разреженного падающего слоя, движущиеся с высокой и примерно одинаковой скоростью, сталкиваются с некоторым разбросом по времени с расположенной под углом отражательной поверхностью отклоняющего элемента. Вследствие этого частицы резко изменяют направление движения и продолжают свое перемещение по пересекающимся траекториям с интенсивным хаотическим взаимным перемещением. С учетом относительно небольшой длины отклоняющих элементов, которая, в общем случае [14], для достижения высокой эффективности определяется в соответствии с длиной ячейки идеального перемешивания ячеечной модели структуры потока в аппарате, правомерно допущение об идеальном перемешивании потока частиц на каждом из таких элементов.
Кроме того, с учетом малых значений концентрации микрокомпонента в смеси сделано допущение о том, что его порционная подача не влияет на продольное распределение материала и площадь поперечного сечения засыпки материала в барабане S(z) зависит только от координаты в направлении потока.
С учетом функций источников, описывающих эффекты избирательного исчерпывания компонентов из их сегрегированного потока в засыпке барабана $I_{B}^{ - },$ их задержки лопастями $I_{B}^{ + },$ а также направленного перемещения компонентов под действием каскада обратных импульсов $I_{0}^{ + },$ уравнение динамики продольного распределения концентрации c(z,τ) контрольного (порционно дозируемого) компонента записано в следующем виде:
(1)
$\begin{gathered} S(z){{\rho }_{b}}(z)\frac{{\partial c(z,\tau )}}{{\partial \tau }} = - \frac{{\partial \left( {c(z,\tau {\text{)}}\left( {G(z) + {{G}_{0}}(z)} \right)} \right)}}{{\partial z}} + \\ + \,\,{{D}_{{dif}}}\frac{\partial }{{\partial z}}\left( {{{\rho }_{b}}(z)S(z)\frac{{\partial c(z,\tau )}}{{\partial z}}} \right) + S(z)\left( {I_{B}^{ - } + I_{B}^{ + } + I_{0}^{ + }} \right). \\ \end{gathered} $В уравнении (1) поток конвекции контрольного компонента, в отличие от традиционной его формулировки, учитывает наличие дополнительной составляющей G0(z), обусловленной действием обратных импульсов. Поскольку обратные импульсы, сообщаемые сегрегированному потоку компонента отклоняющими элементами, приводят к противоточному перемещению материала, то реакцией на их воздействие будет соответствующее усиление конвекционного переноса.
Граничные условия для уравнения (1) записаны в традиционном для этого случая виде с учетом импульсного характера изменения концентрации контрольного компонента в технологическом потоке на входе в смеситель при его порционной загрузке в следующей формулировке:
(2)
$\left\{ \begin{gathered} {{\partial c} \mathord{\left/ {\vphantom {{\partial c} {\partial z}}} \right. \kern-0em} {\partial z}} = 0,\,\,z = 0,L; \hfill \\ c(0,\tau {\text{)}} = {{c}_{1}},{\text{ (}}k - 1)T < \tau \leqslant (k - 1)T + {{\tau }_{{{\text{dos}}}}}; \hfill \\ с (0,\tau {\text{)}} = 0{\text{, (}}k - 1)T + {{\tau }_{{{\text{dos}}}}} < \tau \leqslant kT, \hfill \\ \end{gathered} \right.$На первом этапе моделирования динамики процесса смешивания начальные условия для уравнения (1) сформулированы без детального учета их влияния на динамические характеристики смесителя в предположении отсутствия подачи порционно дозируемого микрокомпонента до полной загрузки рабочего объема смесителя базовым компонентом:
Интенсивность избирательного исчерпывания компонентов смеси подъемными лопастями из сегрегированного потока засыпки материала вращающегося барабана описывается [9] функцией отрицательного источника, имеющей следующий вид:
(4)
$I_{B}^{ - } = {{\omega nF{{\rho }_{b}}{{K}_{e}}c(\tau ,z)} \mathord{\left/ {\vphantom {{\omega nF{{\rho }_{b}}{{K}_{e}}c(\tau ,z)} {(2\pi S(z))}}} \right. \kern-0em} {(2\pi S(z))}},$(5)
${{K}_{e}} = {{c}_{b}}{{(\tau ,z)} \mathord{\left/ {\vphantom {{(\tau ,z)} {c(\tau ,z)}}} \right. \kern-0em} {c(\tau ,z)}}.$Эффект задержки частиц, обусловленный временной потерей их контакта с засыпкой при исчерпывании материала лопастями, определяется [9] с учетом среднего значения времени задержки частиц τd. Интенсивность потока частиц контрольного компонента, возвращаемых в засыпку без контакта с отклоняющими элементами, описывается функцией источника в следующем виде:
(6)
$I_{B}^{ + } = {{\omega n(F - {{F}_{0}}){{\rho }_{b}}{{c}_{B}}(\tau - {{\tau }_{d}},z)} \mathord{\left/ {\vphantom {{\omega n(F - {{F}_{0}}){{\rho }_{b}}{{c}_{B}}(\tau - {{\tau }_{d}},z)} {(2\pi S(z))}}} \right. \kern-0em} {(2\pi S(z))}},$Среднее значение времени задержки частиц, исчерпываемых подъемными лопастями из засыпки, определяется экспериментально с учетом суммарного времени их транспортирования лопастями и падения следующим образом:
(7)
${{\tau }_{d}} = {{\sum\limits_1^n {{{\tau }_{{dj}}}{{m}_{j}}} {{c}_{j}}} \mathord{\left/ {\vphantom {{\sum\limits_1^n {{{\tau }_{{dj}}}{{m}_{j}}} {{c}_{j}}} {\sum\limits_1^n {{{m}_{j}}{{c}_{j}}} }}} \right. \kern-0em} {\sum\limits_1^n {{{m}_{j}}{{c}_{j}}} }},$Средняя концентрация частиц контрольного компонента в потоке материала, выпадающего из лопастей и не контактирующего с отклоняющими элементами, вычисляется с использованием следующего соотношения:
(8)
$\begin{gathered} {{c}_{B}} = ({{K}_{e}}с (\tau - {{\tau }_{d}},z)F - \\ {{ - \,\,{{K}_{s}}c(\tau - {{\tau }_{d}},z){{F}_{0}})} \mathord{\left/ {\vphantom {{ - \,\,{{K}_{s}}c(\tau - {{\tau }_{d}},z){{F}_{0}})} {(F - {{F}_{0}}),}}} \right. \kern-0em} {(F - {{F}_{0}}),}} \\ \end{gathered} $Интенсивность потока контрольного компонента вследствие обратного импульсного воздействия отклоняющих элементов на сегрегированный технологический поток определяется функцией источника, записанной в следующем виде:
(9)
$I_{0}^{ + } = {{\omega n{{F}_{0}}{{\rho }_{b}}(z)g{}_{i}(z)lK{}_{s}c(\tau - {{\tau }_{d}},z)} \mathord{\left/ {\vphantom {{\omega n{{F}_{0}}{{\rho }_{b}}(z)g{}_{i}(z)lK{}_{s}c(\tau - {{\tau }_{d}},z)} {(2\pi S(z))}}} \right. \kern-0em} {(2\pi S(z))}},$Очевидно, что вид функции распределения gi(z) зависит от конструкции отклоняющих элементов. Адекватная формулировка этой функции позволяет не только определить величину встречного сегрегированного потока под действием каскада импульсов, но и смоделировать обусловленный этим потоком эффект дополнительного конвекционного перемешивания. Для элементов, использованных в настоящем исследовании, распределение сегрегированного потока частиц по длине барабана после его контакта с отклоняющими элементами описано кусочно-линейной зависимостью. Такое распределение основывается на виртуальном предположении о том, что при ссыпании с отклоняющих элементов в засыпку материала вращающегося барабана сегрегированный поток формирует насыпку в виде призмы с треугольным основанием, лежащей на одной из боковых граней. С учетом геометрических параметров отклоняющих элементов и их расположения в барабане (рис. 2) функция продольного распределения сегрегированного потока частиц под действием обратных импульсов записана в следующем виде:
(10)
${{g}_{i}}(z) = \left\{ \begin{gathered} 0,\,\,{\text{п р и }}\,\,z \leqslant {{a}_{i}} - h - \frac{l}{2}; \hfill \\ \frac{1}{{{{l}^{2}}}}(z - {{a}_{i}} + h + \frac{l}{2}),\,\,{\text{п р и }}\,\,{{a}_{i}} - h - \frac{l}{2} \leqslant z \leqslant {{a}_{i}} - h + \frac{l}{2}; \hfill \\ \frac{1}{{{{l}^{2}}}}(z - {{a}_{i}} + h - \frac{3}{2}l),\,\,{\text{п р и }}\,\,{{a}_{i}} - h + \frac{l}{2} \leqslant z \leqslant {{a}_{i}} - h + \frac{3}{2}l; \hfill \\ 0,\,\,{\text{п р и }}\,\,z \geqslant {{a}_{i}} - h + \frac{3}{2}l, \hfill \\ \end{gathered} \right.$Средняя величина продольного смещения частиц сегрегированного потока под действием отклоняющего элемента рассчитывается следующим образом:
где: h0(z) – высота расположения нижней кромки отклоняющего элемента над засыпкой материала в барабане; α – угол наклона отклоняющего элемента к горизонту (рис. 2).Очевидно, что под действием каскада обратных импульсов в рабочем объеме смесителя формируется дополнительный сегрегированный поток материала, направленный навстречу основному технологическому потоку. С учетом насыпной плотности материала, его объемного расхода и средней величины продольного смещения (11) частиц во встречном сегрегированном потоке h(z) его величина рассчитывается следующим образом:
(12)
${{G}_{0}}(z) = {{\omega n{{F}_{0}}{{\rho }_{b}}(z)h(z)} \mathord{\left/ {\vphantom {{\omega n{{F}_{0}}{{\rho }_{b}}(z)h(z)} {(2\pi )}}} \right. \kern-0em} {(2\pi )}}.$Таким образом, каскад обратных импульсов формирует циркуляционный контур материала с противоточным перемещением частиц в падающем слое и с прямоточным их перемещением в засыпке материала в барабане. Прямоточное перемещение частиц в составе циркуляционного контура приводит к усилению конвекционного переноса в рабочем объеме смесителя. Однако, усиление прямоточного перемещения частиц не оказывает определяющего влияния на сглаживающий эффект в отношении потока частиц порционно дозируемого компонента. Это объясняется тем, что концентрация частиц компонента в сегрегированном потоке противоточного конвекционного переноса существенно больше, чем в прямоточном конвекционном потоке в любом произвольном сечении барабана. Вследствие этого поток противоточного конвекционного переноса порционно дозируемого компонента усиливается в направлении, обратном направлению технологического потока, что сопровождается эффектами сглаживания пульсаций концентрации компонента, которые будут детально объяснены при анализе результатов моделирования (рис. 9). Соответствующий эффект циркуляционного контура с расходом материала ${{G}_{0}}(z)$ учтен при определении потока конвекционного переноса в уравнении динамики продольного распределения концентрации c(z,τ) контрольного (порционно дозируемого) компонента (1).
Динамика распределения концентрации порционно дозируемого компонента в смесителе смоделирована путем решения уравнения (1) с краевыми условиями (2) и (3) численным методом с использованием неявной разностной схемы Кранка-Николсон [15]. При реализации разностной схемы шаг по координате выбран кратным длине рабочей зоны барабана и его участков, соответствующих длине отклоняющих элементов. Полученная с использованием разностных аналогов система линейных уравнений решалась методом факторизации.
Адекватность математической модели проверена в два этапа. На первом этапе проверка адекватности выполнена путем сравнения расчетных и экспериментальных распределений концентрации идеального и неидеального трассеров (индикаторов) в потоке модельного материала
Исследование технологических характеристик процесса непрерывного смешивания сыпучих материалов при порционном дозировании одного из компонентов проведено на экспериментальной установке с вращающимся барабаном. Барабан диаметром 0.3 м и длиной 1.2 м с помощью бандажей установлен на роликовых опорах и связан с приводом, обеспечивающим его вращение с регулируемой скоростью. По торцам барабана смонтированы загрузочная и разгрузочная камеры. В загрузочной камере закреплена течка, связанная патрубками с дозаторами для подачи компонентов смеси в барабан. Конструкция внутренних узлов барабана аналогична таковой для насадочных устройств, изображенных на рис. 2. Насадка состоит из 11 установленных в один ряд отклоняющих элементов и закреплена в торцевых камерах с возможностью поперечного перемещения в барабане.
Модельными материалами служили смеси частиц, различающихся по размеру, а также частиц, имеющих различный размер и плотность. В качестве основного модельного материала использована смесь гранул полипропилена (фракция +3.0–4.0 мм) с насыпной плотностью 605 кг м–3 и керамзита (фракция +4.0–5.0 мм) с насыпной плотностью 515 кг м–3. При таком сочетании свойств частиц (крупных и менее плотных частиц керамзита с мелкими и более плотными частицами полипропилена) смесь приобретает высокую склонность к сегрегации несмотря на относительно небольшое различие частиц по размеру. Основным (базовым) компонентом смеси являлись гранулы полипропилена, а в качестве микрокомпонента смеси использовались гранулы керамзита.
Возможности избирательного воздействия обратных импульсов на сегрегированные потоки компонентов смеси наглядно продемонстрированы результатами экспериментального исследования концентрации индикаторов (трассеров) каждого из компонентов в потоке на выходе из смесителя в зависимости от времени их пребывания в аппарате (рис. 3). Для оказания противоточного импульсного воздействия на сегрегированный поток условного микрокомпонента (керамзита) отклоняющие элементы устанавливались под опускающимися лопастями.
Рис. 3.
Зависимости концентрации трассеров гранул полипропилена (1) и керамзита (2) от времени их пребывания в барабанном аппарате при обратном импульсном воздействии на сегрегированный поток, обогащенный керамзитом: точки – эксперимент; линии – расчет.
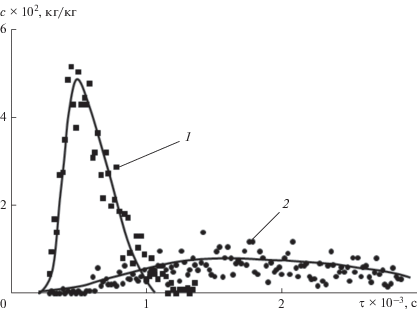
Исследование проведено при одновременном импульсном вводе индикаторов, в качестве которых использовались окрашенные гранулы компонентов смеси. Идеальным трассером служили окрашенные гранулы полипропилена, а в качестве неидеального трассера использованы гранулы порционно дозируемого компонента смеси (керамзита). Отбор проб материала на выходе из смесителя осуществлялся полным потоком в течение каждых 20 с при производительности 0.025 кг/с. Пробы анализировались на содержание в них частиц индикатора и микрокомпонента весовым методом после разделения их визуальным способом. Содержание микрокомпонента выражалось относительной его долей в отношении к общей массе пробы. С целью снижения случайной погрешности и статистической оценки достоверности результатов каждый опыт повторялся трижды и его результаты после проверки их на статистическую однородность усреднялись. Погрешность полученных результатов оценивалась с использованием среднего квадратичного отклонения, выраженного в процентах в отношении к их средним измеренным значениям, и составляла не более 15%.
Приведенные результаты позволяют сделать вывод о том, что воздействие на сегрегированный поток микрокомпонента противоточными импульсами характеризуется высокой степенью избирательности и позволяет принципиально изменять его структуру, поскольку приводит к многократному увеличению дисперсии распределения времени пребывания и его среднего значения по сравнению со структурой потока базового компонента.
Что касается прикладного значения полученного результата, то следует отметить, что вариант преобразования структуры потока противоточными импульсами сопровождается интенсивными избирательными сглаживающими и задерживающими эффектами. Эти эффекты могут быть использованы не только для сглаживания неоднородностей подачи компонентов технологического потока в непрерывно действующем оборудовании, но и с целью поддержания в его рабочем объеме повышенной концентрации (увеличения среднего времени пребывания) какого-либо компонента дисперсных сред, например, в сушилках, грануляторах, реакторах, дражираторах и др.
Математическое моделирование динамики процесса смешивания на базе уравнения (1) предполагает наличие возможности прогнозирования интенсивности формирования сегрегированных потоков сыпучего материала во вращающемся барабане с подъемными лопастями. В соответствии с выражением (4) интегральным показателем интенсивности сегрегированных потоков в барабане является коэффициент исчерпывания Ke, значение которого зависит от свойств смеси и комплекса конструктивных и режимных параметров смесителя. Для решения сложной многопараметрической задачи определения этой зависимости целесообразно использовать метод математического планирования эксперимента.
В настоящей работе зависимость коэффициента исчерпывания для модельной смеси исследована методом планирования ортогонального эксперимента [16] на плоской модели барабанного аппарата в интервалах варьирования: коэффициентом заполнения барабана 0.16; 0.22, скоростью вращения барабана по числу Фруда (ω2d/(2g)) 0.04; 0.12, диаметром барабана 0.3 и 0.6 м и концентрацией порционно дозируемого компонента 0.01; 0.1 кг/кг. Полученная зависимость позволяет утверждать, что доминирующее влияние на интенсивность формирования сегрегированных потоков в барабане оказывают его диаметр и коэффициент заполнения.
Концентрация трассеров с1 в потоке на входе в смеситель вычислена как отношение массы трассера к суммарной массе материала, поступающего в барабан за время ввода дозы трассера τdos. Для вычисления коэффициента продольного перемешивания использована зависимость, предложенная в работе [17]. Экспериментально измеренное значение коэффициента разделения Ks составило 1.6.
Адекватность экспериментальных и расчетных значений концентрации идеального и неидеального трассеров на выходе из смесителя с обратным импульсным воздействием на сегрегированный поток неидеального трассера (рис. 3) установлена путем оценки статистической однородности дисперсий воспроизводимости и адекватности при 95%-ной доверительной вероятности.
Математическая модель после проверки ее на адекватность использована для моделирования процесса непрерывного смешивания гранул полипропилена и керамзита с порционным дозированием последнего. Моделирование проведено для нестационарной фазы процесса при периоде подачи доз Т = 350 с и длительности операции ввода дозы τdos = 3 с. Результаты моделирования, представленные на рис. 4 в виде кривых 1 и 5, отражают динамику изменения концентрации порционно дозируемого компонента в модельной смеси (Ks = 1.6) для вариантов организации процесса без импульсного воздействия (кривая 5) и при обратном импульсном воздействии на сегрегированный поток порционно дозируемого компонента (кривая 1).
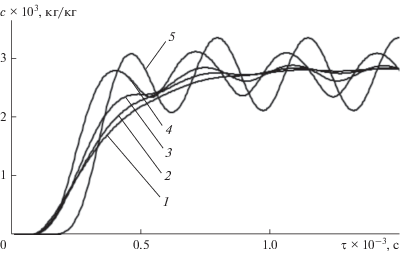
Рис. 4.
Результаты моделирования динамики непрерывного процесса смешивания в аппаратах с импульсным воздействием (1–4) и без импульсного воздействия (5) при периоде ввода дозы 350 с порционно дозируемого компонента с различной склонностью к сегрегации (величиной коэффициента разделения Ks): 1, 5 – Ks = 1.6; 2 – 1.4; 3 – 1.2; 4 – Ks = 1.
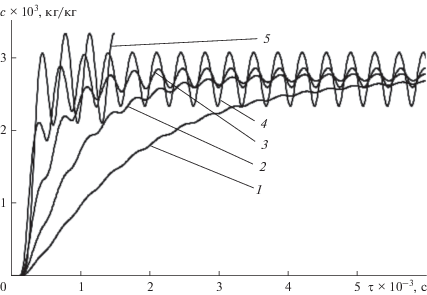
Сравнение кривых 1 и 5 свидетельствует, что избирательное воздействие каскада обратных импульсов на часть сегрегированного потока с наиболее высокой неоднородностью состава позволяет повысить качество смеси с уменьшением коэффициента вариации более чем в 40 раз (с 38.3 до 0.85%). Наблюдаемые технологический и энергосберегающий эффекты являются следствием того, что импульсное воздействие не рассеяно в рабочем объеме среды, а сосредоточено в той части сегрегированного технологического потока, в которой экстремально проявляется технологическая проблема. В связи с этим названные эффекты находятся в прямой зависимости от интенсивности формирования сегрегированного технологического потока, которая в определенных условиях существования потока определяется склонностью его компонентов к сегрегации. Сказанное подтверждается результатами математического моделирования динамики процесса смешивания в условиях обратного импульсного воздействия при различной склонности порционно дозируемого компонента к сегрегации, приведенными на рис. 4 в виде кривых 1–4. Результаты, полученные для периода подачи доз, равного 350 с, свидетельствуют, что вариация состава смеси резко повышается при снижении склонности смеси к сегрегации. Например, для смеси, не склонной к сегрегации (Ks = 1), вариация состава более чем в 30 раз превышает вариацию для модельной смеси с относительно высокой склонностью к сегрегации (Ks = 1.6).
Очевидно, что сглаживающий эффект воздействия обратных импульсов имеет место и в технологическом потоке, не склонном к формированию сегрегированных частей. Однако, как свидетельствуют результаты моделирования, представленные на рис. 4 в виде кривых 5 и 4, эффективность такого воздействия пренебрежимо мала по сравнению с импульсным воздействием на соответствующий сегрегированный поток. Действительно, на фоне более чем 30-тикратного снижения вариации состава смеси при воздействии импульсов на сегрегированный поток порционно дозируемого компонента аналогичное по интенсивности импульсное воздействие на технологический поток, не склонный к сегрегации, приводит к незначительному снижению вариации всего в 1.7 раза. Этот результат моделирования, свидетельствующий о локальном характере продольного перемешивания технологического потока обратными импульсами, можно рассматривать также как дополнительное подтверждение энергосберегающего эффекта предложенного способа смешивания.
Однако, наряду с ярким эффектом повышения однородности смеси при импульсном воздействии наблюдается значительное увеличение продолжительности нестационарной фазы процесса (кривые 1–4 на рис. 4). Этот, очевидно, негативный эффект проявляется тем сильнее, чем выше склонность смеси к сегрегации и объясняется большой длительностью накапливания равновесной (буферной) массы порционно дозируемого компонента в загрузочной части барабана.
В таком случае, увеличение продолжительности нестационарной фазы процесса под действием обратных импульсов возможно предотвратить путем предварительного размещения в головной части барабана буферной массы порционно дозируемого компонента. При реализации такого подхода возникают задачи определения величины буферной массы и рационального размещения последней в аппарате. В соответствии с физическим механизмом формирования этой массы ее величина определяется свойствами частиц компонента, определяющими их склонность к сегрегации, и интенсивностью импульсного воздействия на сегрегированный поток компонента. Поскольку представленная математическая модель отражает механизм формирования буферной массы порционно дозируемого компонента, то искомую величину возможно прогнозировать в результате моделирования продольного распределения концентрации компонента в стационарных (равновесных) условиях. При этом буферная масса определяется путем интегральной оценки содержания компонента в аппарате. Что касается задачи размещения буферной массы в аппарате, то одним из рациональных вариантов начального условия является [18] равномерное распределение массы на определенном участке головной части аппарата, а именно
(13)
$\begin{gathered} c(z,0) = {{c}_{0}}\,\,({\text{п р и }}0 < z < {{z}_{1}}); \\ c(z,0) = 0\,\,({\text{п р и }}{{z}_{1}} \leqslant z). \\ \end{gathered} $Эффективность такого решения подтверждена методами экспериментального исследования и математического моделирования процесса на базе уравнения (1) с граничными и начальными условиями (2) и (13). Сравнение результатов, представленных на рис. 4 и 5, свидетельствует, что предварительное размещение буферной массы порционно дозируемого компонента на 1/3 длины барабана в его головной части позволяет (кривые 1–4) почти на порядок уменьшить продолжительность нестационарной фазы процесса. В результате этот показатель приходит в соответствие с таковым для варианта организации процесса без импульсного воздействия (кривая 5). В дополнение необходимо отметить, что с повышением склонности порционно дозируемого компонента к сегрегации увеличивается не только сглаживающий эффект, но и продолжительность нестационарной фазы процесса (рис. 4), связанной с накапливанием равновесной массы компонента в смесителе. Эта закономерность нашла свое отражение в процедуре моделирования динамики процесса при начальном условии размещения буферной массы (рис. 5). Действительно, для обеспечения динамических характеристик процесса, представленных на рис. 5, требуется повышение концентрации компонента в засыпке барабана по месту размещения буферной массы с 0.0015 кг/кг при Кs = 1.0 до 0.0186 кг/кг при Кs = 1.6.
Рис. 5.
Результаты моделирования динамики непрерывного процесса смешивания в аппаратах с импульсным воздействием (1–4) и без импульсного воздействия (5) при начальном условии с размещением буферной массы (13) порционно дозируемого компонента с различной склонностью к сегрегации: 1 – Ks = 1.6; 2 – 1.4; 3 – 1.2; 4, 5 – Ks = 1.0.
При технологическом использовании способа наиболее принципиальными вопросами являются определение длины барабана и числа отклоняющих элементов, при которых выполняются регламентные требования по однородности состава смеси. В связи с этим важно оценить влияние на сглаживающую способность смесителя числа отклоняющих элементов при фиксированной длине его рабочей зоны, с одной стороны, и длины рабочей зоны при фиксированном расстоянии между элементами – с другой. В качестве базовой конструкции смесителя во всех вариантах моделирования использован барабанный аппарат ранее описанной экспериментальной установки. Варианты моделирования отличаются друг от друга либо длиной барабана и соответственно числом отклоняющих элементов фиксированной длины, либо числом отклоняющих элементов в смесителе с фиксированной длиной барабана.
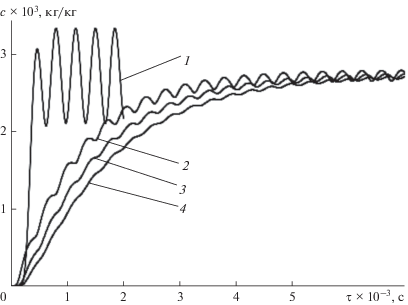
Результаты моделирования динамики процесса приготовления модельной смеси (Ks = 1.6) при периоде ввода дозы 350 с и различной частоте установки отклоняющих элементов в аппарате фиксированной длины (1.2 м) приведены на рис. 6. В соответствии с конструкцией отклоняющих элементов они начинают терять транспортирующую функцию в барабане диаметром 0.3 м и длиной 1.2 м при общем их числе менее 5. Результаты моделирования (рис. 6) наглядно демонстрируют эффект повышения сглаживающей способности смесителя с увеличением количества (частоты установки) отклоняющих элементов. Повышение сглаживающей способности при этом является следствием увеличения встречного сегрегированного потока порционно дозируемого компонента $I_{0}^{ + }$ (9) под действием более интенсивного импульсного воздействия. Очевидным ограничением при назначении числа отклоняющих элементов является их пропускная способность, которая убывает с повышением частоты установки отклоняющих элементов.
Рис. 6.
Результаты моделирования динамики непрерывного процесса приготовления модельной смеси (Ks = 1.6) в аппарате с фиксированной длиной барабана (1.2 м) при различном числе отклоняющих элементов: 1 – 0; 2 – 5; 3 – 8; 4 – 11 элементов.
Оценка влияния длины рабочей зоны смесителя на его сглаживающую способность проведена путем моделирования динамики процесса в аппаратах, которые по технологическим параметрам, за исключением длины барабана, тождественны экспериментальному аппарату. В вариантах моделирования, представленных на рис. 7, длина барабана варьировалась пропорционально числу отклоняющих элементов фиксированной длины с учетом того, что в барабане экспериментальной установки длиной 1.2 м размещено 11 таких элементов.
Рис. 7.
Результаты моделирования динамики непрерывного процесса приготовления модельной смеси (Ks = 1.6) в аппарате с импульсным воздействием при длине рабочей зоны барабана, соответствующей различному числу отклоняющих элементов фиксированной длины: 1 – 3; 2 – 6; 3 – 8; 4 – 11 элементов.
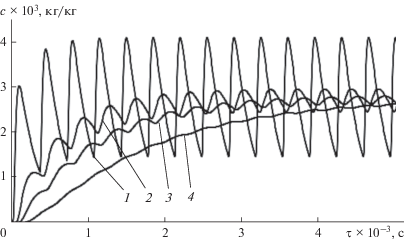
Приведенные результаты свидетельствуют, что экстенсивное повышение обратного импульсного воздействия на сегрегированный поток порционно дозируемого компонента путем увеличения числа импульсов с фиксированной интенсивностью в их каскаде, является эффективным способом повышения сглаживающей способности смесителя. В соответствии с результатами моделирования, представленными на рис. 7, с увеличением числа отклоняющих элементов амплитуда пульсаций концентрации порционно дозируемого компонента в готовой смеси уменьшается по экспоненциальному закону (рис. 8).
Рис. 8.
Зависимость амплитуды пульсаций концентрации порционно дозируемого компонента в смеси от числа отклоняющих элементов фиксированной длины (0.11 м).
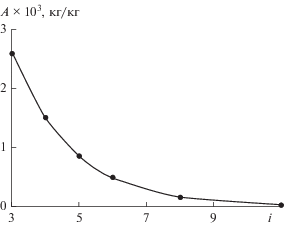
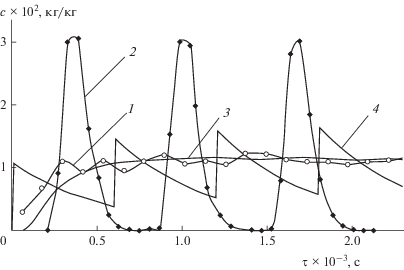
Рис. 9.
Динамика процесса непрерывного смешивания фракций +3.0–4.0 и +6.0–7.0 мм гранул полипропилена при порционном дозировании последней в аппарате с воздействием (1, 3) и без воздействия (2, 4) обратными импульсами: 1, 2 – эксперимент; 3, 4 – результаты моделирования в аппарате с импульсным воздействием (3) и в аппарате идеального перемешивания (4).
Таким образом, сглаживающий эффект обратных импульсов, сообщаемый сегрегированному технологическому потоку отдельным отклоняющим элементом, перемножается с эффектами других элементов каскада и складывается со сглаживающим эффектом вращающегося барабана. Поскольку последний относительно небольшой, то наблюдается экспоненциальное возрастание сглаживающей способности смесителя с увеличением числа отклоняющих элементов (рис. 8). Показатель экспоненты в такой зависимости определяется в первую очередь склонностью смеси к сегрегации (рис. 4). Таким образом, в соответствии с регламентным требованием по максимально допустимому отклонению концентрации смеси от номинального ее значения, можно определить допустимую величину амплитуды пульсаций концентрации. Затем путем моделирования зависимости амплитуды от числа отклоняющих элементов, аналогичной приведенной на рис. 8, установить необходимое число элементов, при котором амплитуда пульсаций будет меньше предельно допустимой.
С целью дополнительной прямой оценки эффективности предложенных технических решений и проверки адекватности математической модели проведено экспериментальное и аналитическое исследование динамики процесса непрерывного смешивания в экстремальных условиях его организации. Экстремальные условия смешивания организованы путем назначения периода подачи доз порционно дозируемого компонента настолько большим (600 с), чтобы он существенно превосходил среднее время пребывания материала смеси в аппарате (360 с). Исследование динамики процесса смешивания проведено для вариантов его организации с воздействием и без воздействия обратных импульсов, а также в гипотетическом аппарате со структурой потока идеального перемешивания. Для приготовления смеси фракций +3.0–4.0 мм и +6.0–7.0 мм гранул полипропилена использован ранее описанный аппарат с вращающимся барабаном диаметром 0.3 м и длиной 1.2 м.
С целью снижения случайной погрешности экспериментальных результатов и статистической оценки адекватности математического описания динамики процесса смешивания каждый из опытов повторялся трижды. Результаты опытов (рис. 9) после проверки их на статистическую однородность усреднялись. Адекватность математического описания установлена путем сравнения дисперсий адекватности и воспроизводимости по критерию Фишера при 95%-ной доверительной вероятности.
Во всех вариантах организации процесса, в том числе и при воздействии каскада обратных импульсов, наблюдаются пульсации концентрации состава получаемой смеси, обусловленные порционной подачей микрокомпонента, с периодом пульсаций, соответствующим периоду подачи доз указанного компонента. Однако, при смешивании в условиях обратного импульсного воздействия амплитуда пульсаций существенно подавляется и выглядит пренебрежимо малой даже на фоне пульсаций, имеющих место в аппарате со структурой потока идеального перемешивания. Пилообразная форма кривой изменения концентрации смеси во времени для аппарата с идеальным перемешиванием потока объясняется практически мгновенным увеличением концентрации компонента в объеме смесителя в течение непродолжительной (в течение 3 с) операции ввода каждой его новой порции.
Сравнение результатов, представленных на рис. 9, свидетельствует, что назначенный период порционной подачи компонента настолько велик, что в отсутствие импульсного сглаживающего воздействия (кривая 2) частицы компонента, принадлежащие двум следующим друг за другом порциям, практически не вступают в контакт друг с другом. Сравнение экспериментально полученных зависимостей 1 и 2 свидетельствует о том, что воздействие обратных импульсов на сегрегированный поток порционно дозируемого компонента позволяет в несколько десятков раз снизить вариацию состава смеси по сравнению с вариантом смешивания без импульсного воздействия. Сглаживающий эффект каскада обратных импульсов обусловлен следующими факторами. Во-первых, названный эффект является следствием демпфирования всплесков концентрации порционно дозируемого компонента за счет наиболее интенсивного переноса его частиц в сегрегированном потоке из областей с повышенной концентрацией в области с низким содержанием компонента. Во-вторых, увеличение концентрации порционно дозируемого компонента в направлении потока противоточного конвекционного переноса материала приводит к формированию буферной массы компонента в загрузочной зоне барабана, что способствует усилению сглаживающего эффекта. Кроме того, результаты моделирования, представленные зависимостями 3 и 4, позволяют заключить, что сглаживающий эффект обратных импульсов настолько значителен, что почти на порядок превышает сглаживающий эффект, достигаемый в аппарате с потоком идеального перемешивания. Очевидно, что этот результат является подтверждением не только высокого технологического, но и энергосберегающего эффекта предложенных технических решений.
ЗАКЛЮЧЕНИЕ
Описан способ снижения неоднородностей подачи отдельных компонентов в непрерывных процессах переработки сыпучих материалов путем воздействия на их сегрегированный поток каскадом встречных импульсов. Способ реализован в устройстве для непрерывного смешивания сыпучих материалов при порционной подаче микрокомпонента, которое разработано на базе аппарата с вращающимся барабаном, снабженным периферийными подъемными лопастями.
Представлена математическая модель, описывающая динамику продольного распределения порционно дозируемого компонента в рабочем объеме аппарата в зависимости от комплекса технологических параметров и склонности компонентов смеси к сегрегации. Результаты исследования структуры сегрегированного технологического потока свидетельствуют о высоком избирательном сглаживающем эффекте обратных импульсов, которые при воздействии на сегрегированный поток порционно дозируемого компонента позволяют многократно увеличить дисперсию распределения его частиц по времени пребывания в аппарате.
Исследованы динамические характеристики процесса непрерывного смешивания модельных материалов с порционной подачей микрокомпонента в барабанном смесителе в условиях обратного импульсного воздействия на сегрегированный поток порционно дозируемого компонента, а также в отсутствие импульсного воздействия и в том числе в смесителе со структурой потока идеального перемешивания. Установлено, что склонность компонентов смеси к сегрегации является определяющим фактором в обеспечении эффективности предложенного способа сглаживания неоднородностей подачи компонентов технологического потока.
Проведена оценка влияния на сглаживающую способность смесителя числа отклоняющих элементов при фиксированной длине барабана и длины его рабочей зоны при фиксированной длине отклоняющих элементов. Отмечена существенная значимость числа отклоняющих элементов, с увеличением которого амплитуда пульсаций порционно дозируемого компонента в смеси снижается по экспоненциальному закону. Установлено, что под действием каскада обратных импульсов обеспечивается возможность многократного снижения пульсаций концентрации порционно дозируемого компонента в смеси по сравнению с аппаратом, структура потока в котором соответствует идеальному перемешиванию.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 14-08-97531).
ОБОЗНАЧЕНИЯ
| A | амплитуда пульсации концентрации контрольного компонента, кг/кг |
| a | координата границы между ячейками отклоняющих элементов, м |
| c, $\bar {c}$ | концентрация и средняя концентрация компонента, кг/кг |
| Ddif | коэффициент продольного перемешивания, м2/с |
| d | диаметр барабана, м |
| F | площадь поперечного сечения засыпки материала на лопасти, м2 |
| G | массовая скорость движения материала вдоль барабана, кг/с |
| $g{}_{i}(z)$ | функция плотности распределения потока частиц вдоль барабана после i-го отклоняющего элемента, м–1 |
| h | продольное смещение материала, вызванное действием отклоняющих элементов, м |
| $I_{B}^{ - },$$I_{B}^{ + },$$I_{0}^{ + }$ | функции источников (стоков) целевого компонента, кг/(м3 с) |
| K, Ke, Ks | коэффициенты пропорциональности, определяющие концентрацию контрольного компонента в сегрегированных потоках |
| L | длина барабана, м |
| l | длина ячейки отклоняющего элемента, м |
| n | количество подъемных лопастей в барабане, шт |
| S | площадь поперечного сечения засыпки материала в барабане, м2 |
| w | скорость продольного поступательного движения частицы, м/с |
| z | декартова координата по длине барабана, м |
| α | угол наклона отклоняющих элементов к горизонту, рад |
| β | коэффициент заполнения барабана, м3/м3 |
| ρb | насыпная плотность материала, кг/м3 |
| τ | время, с |
| ω | угловая скорость вращения барабана, с–1 |
| Fr | число Фруда, ω2d/(2g). |
ИНДЕКСЫ
Список литературы
Ortega-Rivas E. Unit operations of particulate solids: Theory and Practice. CRC Press, 2012.
Plumb K. Continuous processing in the pharmaceutical industry: Changing the mind set // Chem. Eng. Res. Des. 2005. V. 83. 6A. P. 730.
Williams J.C., Rahman M.A. The continuous mixing of particulate solids // Journal of the Society of Cosmetic Chemists. 1970. V. 21. № 1. P. 3.
Williams J.C. Mixing of particulate solids // Mixing: Theory and Practice / Eds. Uhl V.W., Gray J.B. Orlando, Florida: Academic Press, 1986. V. 3. Chapter 16.
Savage S.B. Interparticle percolation and segregation in granular materials: A review // in A.P.S. Selvaduraj (ed.) Development in Engineering Mechanics, Elsevier Science Publishers B.V., Amsterdam, 1987. P.347.
Bates L. User Guide to Segregation // British Materials Handling Boards: Elsinore house, United Kingdom, 1997.
Marikh K., Berthiaux H., Mizonov V., Barantseva E. Experimental study of the stirring conditions taking place in a pilot plant continuous mixer of particulate solids // Powder Technology. 2005. P. 138.
Mizonov V., Berthiaux H., Gatumel C. Theoretical search for solutions to minimize negative influence of segregation in mixing of particulate solids // Particuology. 2016. V. 25. P. 36.
Dolgunin V.N., Ivanov O.O., Ukolov A.A., Kudi A.N. Processing of granular materials in controlled segregated flows // Theor. Found. Chem. Eng. 2014. V. 48. № 4. P. 404. [Долгунин В.Н., Иванов О.О., Уколов А.А., Куди А.Н. Процессы переработки зернистых материалов в управляемых сегрегированных потоках // Теорет. основы хим. технологии. 2014. Т. 48. № 4. С. 404.]
Dolgunin V.N., Ivanov O.O., Kudi A.N., Ukolov A.A., Karev V.I. Technological possibilities of flow structure control in barrel heat-mass exchange reactor // Khimicheskaya Tekhnologiya. 2012. № 10. P. 600. [Долгуни В.Н., Иванов О.О., Куди А.Н., Уколов А.А., Карев В.И. Технологические возможности управления структурой потоков в барабанном тепломассообменном аппарате // Химическая технология. 2012. № 10. С. 600.]
Иванов О.О., Пронин В.А., Рябова Е.А. Управление сегрегированными потоками сыпучих материалов для их обработки методами разделения и соединения // Вестник ТГТУ. 2016. Т. 22. № 3. С. 397.
Ivanov O.O., Borschov V.Ya., Dolgunin V.N. Effect of particle separation in the curtain of a packed drum vessel // Chem. and Petroleum Eng. 2009. V. 45. № 7–8. P. 468. [Иванов О.О., Борщев В.Я., Долгунин В.Н. Эффект разделения частиц в завесе барабанного насадочного аппарата // Хим. и нефтегаз. машиностроение. 2009. Т. 45. № 8. С. 13.]
Лыков А.В. Тепломассообмен. Справочник. 2-е изд., перераб. и доп. М.: Энергия, 1978.
Долгунин В.Н, Борщев В.Я., Уколов А.А., Буданцев В.И., Кузнецов В.И., Сенаторов Ю.П., Волков В.В. Оценка гидромеханики движения материала в барабанном грануляторе–сушилке и совершенствование его конструкции // Хим. пром-сть. 1986. № 7. С. 422.
Марчук Г.И. Методы вычислительной математики. М.: Наука, 1977.
Адлер Ю.П., Маркова Е.В., Грановский Ю.А. Планирование эксперимента при поиске оптимальных условий. 2-е изд., перераб. и доп. М.: Наука, 1976.
Вершинина Н.П. Исследование влияния продольного перемешивания материала на длительность сушки его в барабанной сушилке. Автореф. дис. … канд. тех. наук. Харьков: Ин-т, 1975.
Dolgunin V.N., Ivanov O.O., Ukolov A.A., Pronin V.A., Ryabova E.A., Larionova E.P. Organization of mixing process of granular materials with portion dosage of some components // Trans. of TSTU. 2012. V. 18. № 1. P. 108. [Долгунин В.Н., Иванов О.О., Уколов А.А., Пронин В.А., Рябова Е.А., Ларионова Е.П. Организация процесса смешения зернистых материалов при порционном дозировании отдельных компонентов // Вестник ТГТУ. 2012. Т. 18. № 1. С. 108].
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


