Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 168-173

Моделирование процесса ультрафильтрации с учетом продольного перемешивания очищаемого раствора

А. Б. Голованчиков¹, Н. А. Прохоренко^1, *, Доан Минь Кыонг¹

¹ Волгоградский государственный технический университет
Волгоград, Россия

^* E-mail: natasha292009@yandex.ru

Поступила в редакцию 13.03.2017
После доработки 16.08.2018
Принята к публикации 21.06.2018

DOI: 10.1134/S0040357119010044

Аннотация

На основании дифференциальных уравнений материального баланса выведены формулы технологических и геометрических параметров ультрафильтрационного процесса с учетом продольной диффузии молекул растворенного вещества в очищаемом растворе. Проведена оценка влияния продольной диффузии на концентрацию молекул растворенного вещества в пермеате и ретентате в сравнении с режимами идеального вытеснения и смешения.

Ключевые слова: пермеат, ретентат, ультрафильтрация, ультрафильтрационные мембраны, продольная диффузия, идеальное вытеснение, идеальное смешение

ВВЕДЕНИЕ

Типовые методы расчета ультрафильтрационных мембран основаны на режиме идеального вытеснения по очищаемому раствору, движущемуся под полупроницаемой перегородкой [1–3]. Для нейтрализации эффекта концентрационной поляризации часто применяют вибрацию, статические и динамические перемешивающие устройства, приводящие к значительному отклонению структуры потока очищаемого раствора от идеального вытеснения [4–8].

Аналогичные гидромеханические процессы в массообменных аппаратах и химических реакторах, занимающие промежуточное положение по структуре потоков между идеальным вытеснением и смешением, описываются так называемой однопараметрической диффузионной моделью или моделью с продольной диффузией [3, 4, 9–11].

Целью настоящей работы моделирование и создание алгоритма расчетов технологических и геометрических параметров ультрафильтрационного аппарата со структурой потока продольной диффузии очищаемого раствора.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

На рис. 1 изображена схема ультрафильтрационного аппарата с материальными потоками и их концентрациями.

Рис. 1.

Схема ультрафильтрационного аппарата с материальными потоками и их концентрациями (обозначения параметров смотри в табл. 1).

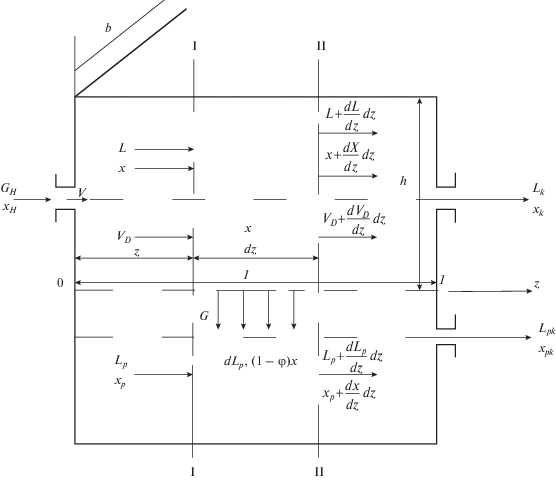
Выделим на длине z от входа аппарата сечения I–I и II–II с расстоянием между ними dz.

Составим элементарный материальный баланс по раствору для выделенного объема $dV = bhdz$ (обозначения параметров приведены в табл. 1):

$L = L + \frac{{dL}}{{dz}}dz + bGdz,$

где $G = ({{a}_{m}}{{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} \mu }} \right. \kern-0em} \mu })\Delta p$ – удельная производительность по пермеату.

Таблица 1.

Исходные и справочные данные и расчетные параметры процесса ультрафильтрации с учетом продольного перемешивания (справочные данные взяты из [1])

№	Наименование параметра	Размерность	Обозна-чение	Величина
Исходные данные
1	Производительность по исходному раствору	кг/с	G_H	0.2
2	Начальная концентрация молекул ацилазы в исходном растворе	кг(А)/кг(G_H), %	Х_H	0.015
3	Конечная концентрация молекул ацилазы в исходном растворе	кг(А)/кг(L_k), %	Х_k	0.15
				Идеальный вытеснитель ${\text{P}}{{{\text{e}}}_{0}} \to \infty $	Продольное перемешивание ${\text{P}}{{{\text{e}}}_{0}} = 100$	Идеальный смеситель ${\text{P}}{{{\text{e}}}_{0}} \to 0$
Расчетные параметры
1	Производительность по пермеату на выходе	кг/с	L_рk	1.802 × 10^–1	1.805 × 10^–1	1.809 × 10^–1
2	Производительность по ретентату на выходе	кг/с	L_k	1.977 × 10^–2	1.955 × 10^–1	1.9095 × 10^–2
3	Концентрация молекул ацилазы в пермеате на выходе	кг(А)/кг(L_pk), %	x_рk	1.915 × 10^–4	5.26 × 10^–4	7.5 × 10^–4
4	Концентрация молекул ацилазы в ретентате на выходе	кг(А)/кг(L_k), %	x_k	0.15	0.15	0.15
5	Поверхность мембраны	м²	F_m	668.7	670.6	671.2

Решение после алгебраических преобразований и интегрирования с учетом граничного условия: z = 0, L = G_H принимает вид

(1)

$L = {{G}_{Н }} - bGz.$

Аналогичный элементарный материальный баланс по молекулам растворенного вещества с учетом скорости продольной диффузии V_D принимает следующий вид:

$\begin{gathered} {{L}_{x}} + bh{{V}_{D}} = \left( {L + \frac{{dL}}{{dz}}dz} \right)\left( {x + \frac{{dx}}{{dz}}dz} \right) + \\ + \,\,bh\left( {{{V}_{D}} + \frac{{d{{V}_{D}}}}{{dz}}dz} \right) + bGdz(1 - \varphi )x. \\ \end{gathered} $

Проведя алгебраические преобразования и отбрасывая бесконечно малые высших порядков, приходим к выражению

(2)

$\begin{gathered} x\frac{{dL}}{{dz}}dz + L\frac{{dx}}{{dz}}dz + bh\frac{{d{{V}_{D}}}}{{dz}}dz + \\ + \,\,bGdz(1 - \varphi )x = 0. \\ \end{gathered} $

По аналогии с уравнением скорости молекулярной диффузии (первым законом Фика), заменяя коэффициент молекулярной диффузии коэффициентом продольной диффузии D_l [3, 4], получаем

${{V}_{D}} = - {{D}_{l}}\rho \frac{{dx}}{{dz}}.$

Тогда вышеупомянутое выражение (2) с учетом уравнения скорости продольной диффузии после алгебраических преобразований принимает форму неоднородного дифференциального уравнения II порядка [12]:

(3)

$bh{{D}_{l}}\rho \frac{{{{d}^{2}}x}}{{d{{z}^{2}}}} = L\frac{{dx}}{{dz}} - bGx + bG{{x}_{{pz}}}{\text{.}}$

Так как расходы пермеата и ретентата связаны интегральным уравнением

(4)

${{G}_{H}} = {{L}_{{pk}}} + {{L}_{k}},$

общий расход пермеата описывается формулой

(5)

${{L}_{{pk}}} = blG,$

а концентрации в пермеате и ретентате молекул растворенного вещества уравнением

(6)

${{x}_{{pz}}} = x(1 - \varphi ),$

то, переходя к безразмерной длине $Z = {z \mathord{\left/ {\vphantom {z l}} \right. \kern-0em} l},$ получаем неоднородное дифференциальное уравнение II порядка [10]:

(7)

$\frac{1}{{{\text{P}}{{{\text{e}}}_{{\text{0}}}}}}\frac{{{{d}^{2}}x}}{{d{{Z}^{2}}}} = \left( {1 - \frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}Z} \right)\frac{{dx}}{{dZ}} - \frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}\phi x,$

где безразмерный критерий Пекле продольной диффузии для очищаемого раствора

${\text{P}}{{{\text{e}}}_{{\text{0}}}} = {{{{V}_{0}}l} \mathord{\left/ {\vphantom {{{{V}_{0}}l} {{{D}_{l}}}}} \right. \kern-0em} {{{D}_{l}}}}.$

Особенностью выражения для Пекле Pe₀ в отличие от числа Пекле продольной диффузии при расчете массообменных процессов и химических реакторов [7–9] является то, что скорость ${{V}_{0}} = {{{{G}_{H}}} \mathord{\left/ {\vphantom {{{{G}_{H}}} {\rho bh}}} \right. \kern-0em} {\rho bh}},$ т.е. относится к начальному участку Z = 0 с известными граничными условиями [7–9, 11, 12]:

(8)

$Z = 0,\,\,{{x}_{H}} = {{x}_{b}} - \frac{1}{{{\text{P}}{{{\text{e}}}_{0}}}}\left( {\frac{{dx}}{{dZ}}} \right),$

где ${{x}_{b}} > {{x}_{H}}.$

При ${\text{P}}{{{\text{e}}}_{0}} \to \infty $ или ${{D}_{l}} \to 0$ режим течения соответствует идеальному вытеснению, тогда ${{x}_{b}} = {{x}_{H}},$ т.е. скачка концентрации на входе нет. При ${\text{P}}{{{\text{e}}}_{0}} \to 0$ или ${{D}_{l}} \to \infty $ режим течения соответствует идеальному смешению ${{x}_{b}} = {{x}_{k}},$ т.е. скачок концентрации на входе наибольший.

Второе граничное условие:

(9)

$Z = 1,\,\,x = {{x}_{k}}.$

Неоднородное дифференциальное уравнение II порядка (7) с граничными условиями (8) и (9) не имеет аналитического решения.

Алгоритм численного решения уравнения (7) может быть следующий.

I. Сначала решаем уравнение (7) при Re_l → ∞, ${{D}_{l}} \to 0,$ т.е. для идеального вытеснения по раствору:

(10)

$\left( {1 - \frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}Z} \right)\frac{{dx}}{{dz}} = \left( {\frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}} \right){{\varphi }^{2}}x,$

с граничным условием $Z = 0,\,\,x = {{x}_{H}}.$

Собственный интеграл последнего дифференциального уравнения имеет следующий вид:

(11)

$x = {{{{x}_{H}}} \mathord{\left/ {\vphantom {{{{x}_{H}}} {{{{\left[ {1 - \left( {\frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}} \right)Z} \right]}}^{\phi }}}}} \right. \kern-0em} {{{{\left[ {1 - \left( {\frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}} \right)Z} \right]}}^{\phi }}}}.$

При $Z = 1,\,\,x = {{x}_{K}},$ и последнее уравнение решается относительно расхода пермеата на выходе:

(12)

${{L}_{{pk}}} = {{G}_{H}}\left[ {1 - {{{\left( {\frac{{{{x}_{H}}}}{{{{x}_{k}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 \varphi }} \right. \kern-0em} \varphi }}}}} \right].$

Тогда необходимая площадь ультрафильтрационной мембраны определяется по уравнению

(13)

$F = \frac{{{{L}_{{pk}}}}}{G},$

а концентрация молекул растворенного вещества в пермеате на выходе:

(14)

${{x}_{{pk}}} = {{\left[ {{{G}_{H}}{{x}_{H}} - ({{G}_{H}} - {{L}_{{pk}}}){{x}_{k}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{G}_{H}}{{x}_{H}} - ({{G}_{H}} - {{L}_{{pk}}}){{x}_{k}}} \right]} {{{L}_{{pk}}}}}} \right. \kern-0em} {{{L}_{{pk}}}}}.$

Для определения зависимости концентрации молекул растворенного вещества от координаты z в пермеате составим материальный баланс для произвольного сечения от начала координат:

${{x}_{p}} = \frac{{\int\limits_0^Z {Gb(1 - \varphi )xdz} }}{{Gbz}},$

где в числителе массовый расход молекул растворенного вещества, прошедших сквозь мембрану при ее истинной селективности φ, в знаменателе – массовый расход пермеата.

После подстановки значения х из выражения (13) и интегрирования получаем уравнение зависимости концентрации молекул растворенного вещества в пермеате от безразмерной координаты длины Z:

(15)

${{x}_{p}} = \frac{{\frac{{{{x}_{H}}}}{{\left( {{{{{L}_{{pk}}}} \mathord{\left/ {\vphantom {{{{L}_{{pk}}}} {{{G}_{H}}}}} \right. \kern-0em} {{{G}_{H}}}}} \right)}}\left[ {1 - {{{\left( {1 - \frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}Z} \right)}}^{{1 - \varphi }}}} \right]}}{Z}.$

При Z = 1 концентрация на выходе определяется в виде

(16)

${{x}_{{pk}}} = \frac{{{{x}_{H}}}}{{\left( {{{{{L}_{{pk}}}} \mathord{\left/ {\vphantom {{{{L}_{{pk}}}} {{{G}_{H}}}}} \right. \kern-0em} {{{G}_{H}}}}} \right)}}\left[ {1 - {{{\left( {1 - \frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}} \right)}}^{{1 - \varphi }}}} \right].$

Формулы (14) и (16) тождественны и дают одинаковые результаты при расчетах ${{x}_{{pk}}}.$

II. Рассматриваем вариант идеального смешения по раствору, находящемуся над ультрафильтрационной мембраной, т.е. при ${\text{P}}{{{\text{e}}}_{0}} \to 0,\,\,{{D}_{l}} \to \infty .$ В этом случае

(17)

$x = {{x}_{k}},\,\,{{x}_{p}} = {{x}_{{pk}}}\,\,{\text{и }}\,\,{{x}_{{pk}}} = {{x}_{k}}(1 - \varphi ).$

Из совместного решения общих уравнений материального баланса

${{G}_{H}} = {{L}_{{pk}}} + {{L}_{k}}\,\,{\text{и }}\,\,{{G}_{H}}{{x}_{H}} = {{L}_{{pk}}}{{x}_{{pk}}} + {{L}_{k}}{{x}_{k}}$

получаем расчетные формулы для расходов пермеата

(18)

${{L}_{{pk}}} = \frac{{{{G}_{H}}({{x}_{k}} - {{x}_{H}})}}{{\varphi {{x}_{k}}}}$

и ретентата

(19)

${{L}_{k}} = {{G}_{H}} - {{L}_{{pk}}}.$

Поверхность ультрафильтрационной мембраны определяется для режима идеального смешения по формуле (13). При селективности мембраны $\varphi \to 1$ расчеты расходов пермеата по формуле (12) для идеального вытеснения и (16) для идеального смешения дают практически одинаковые результаты, а значит, это же касается и расходов ретентата и поверхности мембраны (см. табл. 1). Отличие связано с концентрациями растворенного вещества пермеата на выходе, рассчитываемыми по формулам (14) или (16) для идеального вытеснения и (17) для идеального смешения. Проскок молекул растворенного вещества в пермеат при идеальном вытеснении в несколько раз меньше, чем при идеальном смешении (см. результаты расчетов в табл. 1). Поэтому, когда целевым продуктом является пермеат с допускаемой концентрацией молекул растворенного вещества, продольная диффузия ухудшает качество пермеата по концентрации этих молекул.

III. Рассматриваем вариант продольного смешения для $0 < {\text{P}}{{{\text{e}}}_{0}} < \infty .$

Переводим дифференциальное уравнение (7) в численный вид:

(20)

$\begin{gathered} {{g}_{{i + 1}}} = {{g}_{i}} + {\text{P}}{{{\text{e}}}_{0}}\left( {1 - \frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}{{Z}_{i}}} \right){{g}_{i}}\Delta Z - \\ - \,\,\left( {\frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}} \right){\text{P}}{{{\text{e}}}_{0}}\varphi {{x}_{i}}\Delta Z, \\ \end{gathered} $

где ${{g}_{i}} = \left( {\frac{{dx}}{{dz}}} \right)i$ – градиент концентрации молекул растворенного вещества в ретентате по безразмерной длине Z. Задаемся интервалом по безразмерной длине, например $\Delta Z = 0.001,$ т.е. числом итераций n = 1000. С учетом граничного условия на входе (9) для входной итерации $i = 1$ принимаем

${{x}_{H}} < {{x}_{b}} < {{x}_{k}}$

и определяем ${{g}_{1}} = ({{x}_{b}} - {{x}_{H}}){\text{P}}{{{\text{e}}}_{l}}{\text{:}}$

${{Z}_{1}} = i\Delta Z$ и ${{x}_{1}} = {{x}_{b}}.$

Тогда

$\begin{gathered} {{g}_{2}} = {{g}_{1}} + {\text{P}}{{{\text{e}}}_{0}}\left( {1 - \frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}{{Z}_{i}}} \right){{g}_{i}}\Delta Z - \\ - \,\,\left( {\frac{{{{L}_{{pk}}}}}{{{{G}_{H}}}}} \right){\text{P}}{{{\text{e}}}_{0}}y{{x}_{i}}\Delta Z. \\ \end{gathered} $

Правильный выбор ${{x}_{b}}$ определяется из условия

(21)

${{x}_{n}} \approx {{x}_{k}}$

с заданной точностью. Это можно сделать, используя метод половинного деления. Концентрации ${{x}_{{i + 1}}}$ на каждой итерации можно определить следующим образом: ${{x}_{{i + 1}}} = {{x}_{i}} + {{g}_{i}}\Delta Z.$

Для определения зависимости концентрации молекул растворенного вещества в пермеате от безразмерной длины Z составим элементарный материальный баланс в выбранном сечении длиной dZ (рис. 1) и возьмем определенные интегралы от левой и правой частей:

$\int\limits_{(1 - \varphi ){{x}_{H}}}^{{{x}_{p}}} {d{{x}_{p}} = \frac{{\int\limits_0^Z {Gb(1 - \varphi )xdz} }}{{\int\limits_0^Z {Gbdz} }}} ,$

или в численном виде:

${{x}_{{pj}}} = (1 - \varphi )\frac{{\sum\limits_{i = 1}^j {{{x}_{i}}} }}{k}.$

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Результаты расчетов по вышеприведенному алгоритму в виде графиков зависимостей концентрации молекул в пермеате и входной концентрации этих молекул в ретентате от числа Пекле Pe₀ приведены на рис. 2. Как видно из первого графика, концентрация молекул в пермеате в значительной степени зависит от числа Пекле Pe₀ и продольной диффузии, т.е. перемешивание исходного раствора в процессе ультрафильтрации, с одной стороны, снижает концентрационную поляризацию, а с другой, ухудшает качество пермеата.

Рис. 2.

Зависимости конечной концентрации молекул от числа Пекле Pe₀ (индекс относится к идеальному смешению, индекс b – к идеальному вытеснению): 1 – в пермеате; 2 – в исходном растворе на выходе в аппарат.

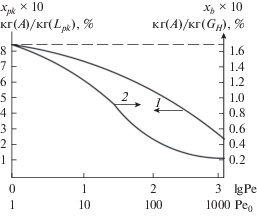
Другая особенность продольной диффузии связана со скачком концентрации исходного раствора на входе. Величина этого скачка тем больше, чем меньше число Pe₀, и изменяется от нуля для режима идеального вытеснения до наибольшего значения в режиме идеального смешения ${{x}_{b}} = {{x}_{k}}$ (рис. 2, кривая 2). Профили концентраций молекул ацилазы в ретентате и пермеате в зависимости от относительной длины мембраны приведены на рис. 3 и 4 . Как видно из этих рисунков, с уменьшением числа Pe₀ (увеличением коэффициента продольной диффузии D_l) эти концентрации в обоих случаях возрастают с ростом относительной длины Z, при этом градиент концентрации молекул ацилазы в ретентате на выходе при Z = 1 не равен нулю, как это имеет место в массообменных и реакторных процессах (это одно из граничных условий $\frac{{dc}}{{dz}} = 0$ при решении дифференциальных уравнений второго порядка, аналогичных дифференциальному уравнению (7) в массообменных и реакторных процессах, учитывающих продольную диффузию [7–12]). Однако мы в работах [11, 12] показали, что вместо безградиентного условия (21) можно использовать градиентное граничное условие при Z = 1. Последнее и имеет место в мембранных процессах с диффузионной структурой потока. Нельзя не обратить внимания и еще на одну особенность, связанную с резким возрастанием концентрации молекул ацилазы в пермеате по длине мембраны при режимах, близких к идеальному вытеснению. Поэтому для получения раствора пермеата повышенной чистоты можно помимо использования мембраны с высокой селективностью и снижением степени концентрирования ретентата провести секционирование приемной камеры, в которую отбирается пермеат. Тогда в первых секциях по ходу течения ретентата будет отбирать пермеат с концентрациями растворенных молекул в 2–3 раза меньше, чем на выходе.

Рис. 3.

Профили концентраций молекул ацилазы в ретентате по относительной длине ультрафильтрационной мембраны: 1 – режим идеального вытеснения ${\text{P}}{{{\text{e}}}_{0}} \to \infty ;$ 2 – режим с обратным перемешиванием ${\text{P}}{{{\text{e}}}_{0}} \to 500;$ 3 – режим с обратным перемешиванием ${\text{P}}{{{\text{e}}}_{0}} \to 100;$ 4 – режим идеального смешения ${\text{P}}{{{\text{e}}}_{0}} \to 0.$

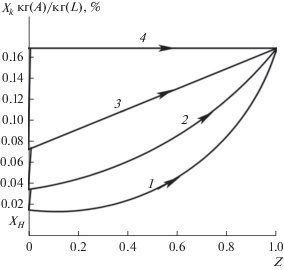
Рис. 4.

Профили концентраций молекул ацилазы в пермеате по относительной длине ультрафильтрационной мембраны: 1 – режим идеального вытеснения ${\text{P}}{{{\text{e}}}_{0}} \to \infty ;$ 2 – режим с обратным перемешиванием ${\text{P}}{{{\text{e}}}_{0}} \to 500;$ 3 – режим с обратным перемешиванием ${\text{P}}{{{\text{e}}}_{0}} \to 100;$ 4 – режим идеального смешения ${\text{P}}{{{\text{e}}}_{0}} \to 0.$

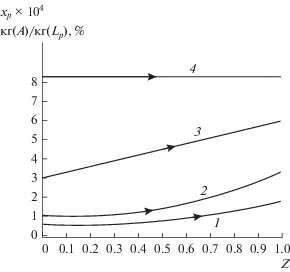
ОБОЗНАЧЕНИЯ

a	константа проницаемости мембраны по чистой воде, кг/(м² с МПа)
D_l	продольная диффузия, м²/с
F	площадь ультрафильтрационной мембраны, м²
F_m	поверхность мембраны, м²
G	удельная производительность по растворителю, кг/м²
G_H	производительность по исходному раствору, кг/с
g_b	градиент концентрации молекул ацилазы в ретентате на входе, %
g_i	градиент концентрации молекул растворенного вещества в ретентате
h	высота ретентата над мембраной, м
L_k	производительность по ретентату на выходе, кг/с
L_рk	производительность по пермеату на выходе, кг/с
l	общая длина, м
p	рабочий перепад давления, МПа
t	рабочая температура, °С
V_D	скорость продольной диффузии, м/с
Х_H	начальная концентрация молекул ацилазы в исходном растворе, %
Х_k	конечная концентрация молекул ацилазы в исходном растворе, %
х	техническая концентрация ретентата, %
х_pz	локальная концентрация молекул растворенного вещества под мембраной, %
x_рk	концентрация молекул ацилазы в пермеате на выходе, %
x_k	концентрация молекул ацилазы в ретентате на выходе, %
x_b	концентрация молекул ацилазы в ретентате на входе, %
y	истинная селективность мембраны УАМ-150 по молекулам ацилазы
Z	безразмерная длина
$\mu $	динамическая вязкость раствора, Па с
${{\mu }_{0}}$	динамическая вязкость чистой дистиллированной воды, Па с
$\nu $	кинематическая вязкость раствора, м²/с
ρ	плотность водного раствора ацилазы, кг/м³
φ	истинная селективность
Pe₀	число Пекле

Список литературы

Дытнерский Ю.И. Основные процессы и аппараты химической технологии. Пособие по проектированию. М.: Химия, 1983.
Левеншпиль О. Инженерное оформление химических процессов. М.: Химия, 1969.
Кафаров В.В. Методы кибернетики в химии и химической технологии. М.: Химия, 1976.
Лобасенко Б.А., Семенов А.Г. Математическая модель ультрафильтрации с учетом гелеобразования в условиях периодической очистки мембраны // Техника и технология пищевых производств. 2010. № 3. С. 137.
Масленников В.А., Осадчий Ю.П., Маркелов А.В., Гришута А.С. Математическая модель процесса разделения отработанного моторного масла на компоненты ультрафильтрацией // Приволжский научный журнал. 2013. № 3. С. 39.
Яцун С.Ф., Локтионова О.Г., Кудрявцев В.А., Кувардина Е.М. Моделирование процесса ультрафильтрации диффузионного сока сахарной свеклы // Известия вузов. Пищевая технология. 2004. № 2–3. С. 74.
Лисовой В.В. Математическое моделирование процесса ультрафильтрации в малоотходной технологии переработки водных биоресурсов // Новые технологии. 2011. № 2. С. 39.
Богомолов В.Ю., Кочетов В.И., Лазарев С.И. Расчет элементов мембранного агрегата для очистки промышленных растворов и стоков методом ультрафильтрации // Вопросы современной науки и практики. Университет им. В.И. Вернадского. 2015. № 2(56). С. 195.
Голованчиков А.Б., Коберник А.А., Залипаева О.А., Меренцов Н.А. Ионообмен в аппарате непрерывного действия с диффузионной структурой потока по жидкости // Известия Волгоградского государственного технического университета. 2015. Т. 8. № 1(154). С. 39.
Голованчиков А.Б., Прохоренко Н.А., Карев В.Н. Алгоритм расчета насадочной ректификационной колонны с учетом продольного перемешивания по жидкой фазе // Известия Волгоградского государственного технического университета. Сер. Актуальные проблемы управления, вычислительной техники и информатики в технических системах. 2016. № 3(182). С. 14.
Голованчиков А.Б., Меренцов Н.А. Моделирование насадочной экстракционной колонны с диффузионной структурой потока по сплошной фазе // Химическая технология. 2016. Т. 17. № 8. С. 377.
Выгодский М.Я. Справочник по высшей математике. 12-е изд. М.: Наука, 1977.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал