Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 160-167

Анализ параметров обратных токов и газосодержания в жидкости за выступом шероховатости

Н. А. Войнов^1, *, А. С. Фролов¹, О. П. Жукова¹

¹ Сибирский государственный университет науки и технологий им. академика М.Ф. Решетнева
Красноярск, Россия

Поступила в редакцию 24.01.2018
После доработки 15.06.2018
Принята к публикации 31.05.2018

DOI: 10.1134/S0040357119010172

Аннотация

На основании экспериментальных исследований показано влияние газосодержания в жидкости за выступами искусственной винтовой шероховатости на толщину пленки и величину коэффициента теплоотдачи. Представлены результаты численного моделирования распределения скоростей обратных токов и перепадов давления по высоте выступа и длине впадины, а также экспериментальные значения газосодержания в отрывной зоне жидкости, возникающей при обтекании регулярной шероховатости. Показано, что масштаб обратных токов, их расположение за выступом шероховатости, так же как и величина газосодержания, зависят от высоты и формы выступа, плотности орошения, физических свойств жидкости. Сделано заключение, что формирование пузырьков газа в жидкости происходит в зонах обратных токов во впадинах искусственной шероховатости из-за пониженного давления в них по сравнению с давлением газа на межфазной поверхности и обеспечения тем самым подсоса газа из зоны межфазной границы. Предложена зависимость для расчета газосодержания по толщине слоя жидкости во впадине шероховатости.

Ключевые слова: численное моделирование, искусственная шероховатость, газосодержание, пленка жидкости, диаметр пузырька

ВВЕДЕНИЕ

Аппараты со стекающей пленкой жидкости, снабженные трубами с крупномасштабной винтовой искусственной шероховатостью, нашли применение в химической промышленности для осуществления процессов тепло- и массопереноса. Они обладают большой пропускной способностью по жидкости, развитой межфазной поверхностью, высокими тепло- и массообменными характеристиками.

Так, представляют интерес разработанные пленочные газожидкостные реакторы, снабженные трубами с винтовой шероховатостью, обладающие большой производительностью и низкими удельными энергозатратами [1]. Апробирована конструкция высокопроизводительного пленочного скруббера, в трубах которого установлена винтовая шероховатость [2]. Разработаны пеногаситель и флотатор [3], обеспечивающие развитую межфазную поверхность за счет наличия на пленкообразующей поверхности винтовой шероховатости, что позволило при низких энергозатратах проводить процессы гашения пены и концентрирования суспензии. Исследован конденсатор, в котором отвод не сконденсировавшегося в водяном паре газа с межфазной поверхности осуществляется в пленку жидкости, стекающей по поверхности с винтовой шероховатостью, что позволило интенсифицировать теплоотдачу при конденсации. Разработана конструкция пленочного теплообменника [4], выполненного из профилированных пластин, образующих цилиндрические трубы, в которых устойчивое течение пленки жидкости, как на внутренней, так и на наружной поверхности, обеспечивается винтовой шероховатостью, что обусловливает компактность установки и высокие значения коэффициентов теплопередачи.

Внедрение рассмотренных пленочных аппаратов с искусственной шероховатостью в инженерную практику сдерживается, в том числе, из-за недостаточной изученности распределения газосодержания в пленке и отсутствия данных об условиях формирования пузырьков газа в жидкости.

Влияние газосодержания на толщину пленки жидкости, стекающей по поверхности труб с винтовой искусственной шероховатостью, показано в работах [1–3]. Установлено, что средняя толщина пленки жидкости, стекающей по виткам шероховатости, измеренная методом отсечки питания, составляет на 30–50% меньшую величину, чем толщина, рассчитанная методом контактной иглы, что обусловлено наличием пузырьков газа в жидкости, объем которых не учитывается при использовании способа отсечки. С увеличением высоты выступа шероховатости и коэффициента динамической вязкости толщина стекающего слоя жидкости возрастает. Как установлено, толщина слоя жидкости во впадине δ_d ~ h^0,4 и зависит как от силы вязкого трения, так и от величины газосодержания.

Толщину слоя жидкости во впадине винтовой шероховатости δ_d предложено рассчитывать с учетом газосодержания по зависимости [3]

(1)

$\begin{gathered} {{{\delta }}_{{\text{d}}}}\left( {1 \pm \frac{{{{{\delta }}_{{\text{d}}}}}}{{2R}}} \right) = \left( {1 \pm \frac{h}{{2R}}} \right)\frac{{hs}}{{s + e}} + \\ + \,\,{{\left\{ {\frac{{{{G}^{2}}(1 + {h \mathord{\left/ {\vphantom {h R}} \right. \kern-0em} R})}}{{{{{\rho }}^{2}}g}}\left[ {\frac{{{\lambda }e}}{{8(s + e)}} + \frac{s}{{32(s + e)\sqrt {\pi } }}} \right]} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $

Плотность газожидкостной смеси в уравнении (1) определяется по зависимости

(2)

$\rho = {{\rho }_{{\text{l}}}}(1 - \varphi ) + {{\rho }_{{\text{g}}}}\varphi ,\quad$

где φ – газосодержание; ρ_g, ρ_l– плотность газа и жидкости соответственно.

Результаты исследования теплоотдачи при нагревании в пленке жидкости, стекающей по теплообменной поверхности с винтовой шероховатостью [3], также выявили существенное влияние газосодержания на теплообмен. Показано, что с увеличением высоты выступа шероховатости величина коэффициента теплоотдачи при нагревании возрастает и достигает максимальных значений при высоте выступа 0.13–0.5 мм, а затем уменьшается, что обусловлено образованием пузырьков газа в жидкости и уменьшением, вследствие этого, теплопроводности газожидкостной среды, которую предложено рассчитывать в виде

(3)

${{\lambda }_{{\text{m}}}} = {{\lambda }_{{\text{l}}}}(1 - \varphi ) + {{\lambda }_{{\text{g}}}}\varphi ,$

где λ_l, λ_g – коэффициент теплопроводности жидкости и газа соответственно, Вт/(м К); λ_m – эффективный коэффициент теплопроводности, Вт/(м К).

Величина коэффициента теплоотдачи в пленке жидкости рассчитывается согласно

(4)

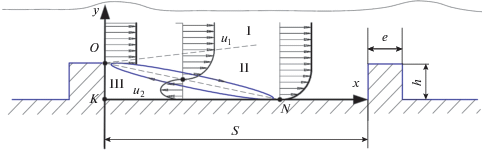
$\alpha = 1.2{\text{ }} \times {{10}^{{--2}}}{\text{R}}{{{\text{e}}}^{{0.8}}}{\text{P}}{{{\text{r}}}^{{0.6}}}{{{{\lambda }_{{\text{m}}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{\text{m}}}}} {{{\delta }_{{\text{d}}}}}}} \right. \kern-0em} {{{\delta }_{{\text{d}}}}}}.$

Среди моделей и схем течения жидкости во впадине шероховатости [4–6] наибольшее распространение получила схема, рассматривающая отрыв потока с позиций эжекции струи, возникающей в точке отрыва на выступе. Например, согласно [7], поток жидкости, обтекающей элемент шероховатости, срывается с задней кромки выступа (точка 0, рис. 1) и далее продолжает распространяться в том же направлении как свободная струя в невозмущенной зоне I. За счет эжектирующего действия струи во впадине возникает зона обратных токов III, размеры которой определяются скоростью набегания потока и геометрическими размерами впадины. На границе двух встречных потоков образуется турбулентный пограничный слой II, представляющий собой зону интенсивного турбулентного смешения [8, 9], внутренняя граница которой (линия 0–1) направлена в сторону свободной поверхности потока жидкости, а внешняя – к ограничивающей течение стенке впадины.

Рис. 1.

Схемы течения жидкости на фиксированной длине впадины.

Граница струи в точке N, расположенной на некотором расстоянии х от выступа, достигает задней стенки или дна впадины. Линии тока, находящиеся за этой границей, являются замкнутыми и образуют циркуляционную зону, часть которой 0–N–K, примыкающая к стенкам впадины, заполнена жидкостью, движущейся со скоростью u₂, противоположной по направлению скорости u₁ в струе. На линии 0–N продольная составляющая скорости равна нулю.

Целью настоящей работы является определение посредством численного моделирования распределения давлений и скоростей токов жидкости по высоте выступа и длине впадины шероховатости и установления их влияния на формирование пузырьков газа.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Эксперименты проводились на системе воздух–вода в трубах с внутренним диаметром 0.037–0.051 м и длиной до 2.0 м, в которых устанавливалась винтовая шероховатость, выполненная из проволоки диаметром h = 1.5–4.0 мм в виде спирали с параметром шероховатости s/h = 3–12. Среднерасходная скорость пленки определялась при помощи трассера, вводимого в стекающий слой жидкости. Средняя величина газосодержания определялась объемным методом с использованием измеренной методами отсечки питания и контактной иглы толщины стекающего слоя. Величина газосодержания по высоте слоя жидкости определялась во впадине на расстоянии x/s = 0.5 объемным методом путем отвода газожидкостной смеси с определенного расстояния от стенки трубы через полую иглу, снабженную прозрачной трубкой диаметром 3.5 мм и длиной 0.2 м. В качестве рабочей среды использовалась вода, а также смесь этанол–вода, при их вязкости 0.00047–0.0012 Па с, при этом осуществлялась рециркуляция жидкости и дегазация из нее растворенного воздуха перед подачей в трубу. Среднеповерхностный диаметр пузырьков газа во впадине шероховатости рассчитывался согласно [10]

(5)

${{d}_{п }} = \sqrt {\frac{{\sum {{{n}_{i}}d_{i}^{2}} }}{{\sum {{{n}_{i}}} }}} ,$

где n_i – количество пузырей определенного размера; d_i – диаметр пузыря, м.

Поверхностное натяжение смеси этанол–вода изменялось путем изменения концентрации этанола в ней и принималось согласно [11].

Расчеты были выполнены в диапазоне скоростей u_av = 0.5–1.0 м/с, шаг между выступами шероховатости s = 4–120 мм, высота выступа h = = 1.5–6.0 мм, плотность жидкости 800–999 кг/м³, коэффициент динамической вязкости 0.0005–0.002 Па с.

Численное моделирование проводилось с помощью программы Comsol Multiphysics, которая использует обобщенную версию уравнений Навье–Стокса:

(6)

$\begin{gathered} \rho \frac{{\partial u}}{{\partial t}} - \nabla \left[ {\eta \left( {\nabla u + {{{\left( {\nabla u} \right)}}^{T}}} \right)} \right] + \rho \left( {u\nabla } \right)u + \nabla p = F, \\ \nabla u {\text{ = 0,}} \\ \end{gathered} $

где η – динамическая вязкость, Па с; u – векторное поле скоростей; p – давление, Па; F – объемная плотность силы, Н/м³.

Интерактивная среда программы основана на дифференциальных уравнениях переноса количества движения и неразрывности потока для несжимаемой жидкости.

Программное обеспечение пакета поддерживает конечно-элементную технологию вместе с адаптивным построением сетки и контролем ошибок. В построении расчетной сетки были использованы треугольные элементы со стандартной сеткой типа Normal, обеспечивающей разбиение на элементы и увеличение их количества в зоне искусственной шероховатости.

В работе использовалась алгебраическая турбулентная модель, которая охватывала всю исследуемую область течения жидкости. В параметрах решателя, отвечающих за точность (relative tolerance), было выбрано значение 0.001, что позволило описать экспериментальные данные с доверительным интервалом ±15%.

В процессе исследования применялся режим, позволяющий исследовать временные процессы (time-dependent), происходящие за выступом различной высоты и формы. Данные фиксировались на участке стабилизации, который наблюдался при времени расчета, равном одной секунде.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Результаты численного моделирования. Исходя из принятого предположения [12] о механизме образования пузырьков газа в пленке, стекающей по поверхности с крупномасштабной искусственной шероховатостью, заключающемся во внедрении струй газа с межфазной поверхности в зону обратных токов, проведены оценки формы обратных токов, скоростей и давлений во впадине шероховатости.

Согласно расчетным данным, при одинаковых входных параметрах потока жидкости формирование обратных токов за прямоугольным выступом шероховатости осуществляется на большей длине впадины, чем на выступе круглого профиля, что согласуется с известными исследованиями, например [13, 14]. Так, согласно расчетам, при h = 4 мм в первом случае максимальная длина обратных токов во впадине достигается при s/h = 4 (рис. 2д), а во втором – при s/h = 10 (рис. 2е). Это подтверждается экспериментальными данными, полученными при исследовании гидродинамики пленочного течения [3, 15], где авторы установили оптимальный параметр s/h, определяющий длину обратных токов жидкости во впадине при котором достигаются максимальные значения толщины пленки и коэффициента массоотдачи.

Рис. 2.

Расчетный контур обратных токов жидкости во впадине шероховатости при µ = 0.001 Па с, u_ср = 0.5 м/с, h = 4 мм, L = 1.5 м. Геометрические параметры шероховатости: (а) – s = 6 мм, s/h = 1.5; (б) – s = 6 мм, s/h = 1.5; (в) – s = 12 мм, s/h = 3; (г) – s = 12 мм, s/h = 3; (д) – s = 16 мм, s/h = 4; (е) – s = 40 мм, s/h = 10; (ж) – s = 40 мм, s/h = 10; (з) – s = 120 мм, s/h = 30.

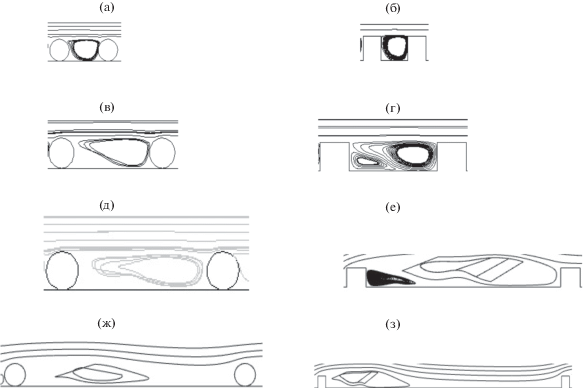
При параметре шероховатости s/h > 2 форма обратных токов вытянута во впадине и соответствует модели течения, представленной на рис. 1 [5].

Распределение давления по сечению трубы с выступом круглого профиля показано на рис. 3.

Рис. 3.

Распределение давления по сечению трубы (d = 45 мм, L = 0.53 м, h = 4 мм, ρ = 999 кг/м³, µ = = 0.001 Па с, x/s = 0.5, s = 40 мм): (а) – u_av = 0.5 м/с; (б) – u_av = 1 м/с.

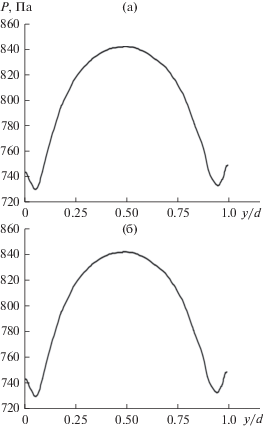
Согласно полученным данным, во впадинах шероховатости на расстоянии y₁ от стенки образуются локальные зоны с наименьшим давлением по сравнению с давлением по оси трубы. С увеличением высоты выступа шероховатости, параметра шероховатости s/h и среднерасходной скорости жидкости при прочих равных условиях происходит рост перепада давлений ∆P (рис. 4).

Рис. 4.

Зависимость перепада давления от высоты выступа круглого профиля (a) и параметра шероховатости s/h (б) при x/s = 0.5: (а) – расчетные линии 1–3: 1 – s/h = 6, u_av = 0.5 м/с; 2 – s/h = 10, u_av = 0.5 м/с; 3 – s/h = 6, u_av = 1.0 м/с; (б) – h = 4 мм, u_av = 0.5 м/с.

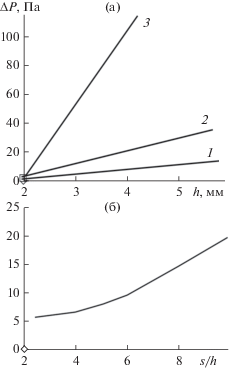
Результаты численного моделирования показали, что увеличение коэффициента динамической вязкости жидкости при прочих равных условиях приводит к снижению перепада давлений ∆P.

Изменение скорости токов жидкости во впадине шероховатости u₂ показано на рис. 5. Увеличение параметра шероховатости s/h и высоты выступа приводит к увеличению скорости обратных токов.

Рис. 5.

Изменение скорости жидкости во впадине от параметра y/h для выступа круглого профиля при x/s = 0.5, d = 45 мм, L = 0.51 м, h = 4 мм, µ = 0.001 Па с, u_av = 0.5 м/c: (а) – s = 16 мм; (б) – s = 40 мм.

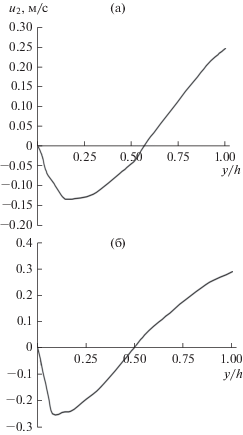
Геометрическая форма выступа (круглая или прямоугольная) при одинаковых параметрах s/h не оказывает существенного влияния на величину скорости обратных токов. Величина максимальной скорости обратных токов жидкости зависит от высоты выступа шероховатости, среднерасходной скорости жидкости и расстояния x во впадине (рис. 6).

Рис. 6.

Изменение максимальной скорости обратных циркуляционных токов от высоты выступа круглого профиля шероховатости (а) и по длине впадины (б): (а) – u_av = 0.5 м/с; x/s = 0.5; линии 1–3: 1 – s/h = 10; 2 – s/h = 4; 3 – s/h = 1.5; (б) – u_av = 0.5 м/с; h = 4 мм; s = 40 мм.

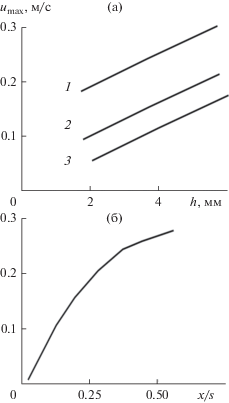
Согласно данным рис. 7а, с увеличением высоты выступа шероховатости и среднерасходной скорости жидкости расстояние y₁ от стенки до локальной зоны с наименьшим давлением возрастает, а также согласно рис. 7б изменяется по длине впадины.

Рис. 7.

Зависимость изменения расстояния l от высоты выступа (а) и отношения x/s (б): (а) – s/h = 6; x/s = 0.5; расчетные линии 1 и 2: 1 – u_av = 1.0 м/с; 2 – u_av = 0.5 м/с; (б) – h = 4 мм; s/h = 10; u_av = 0.5 м/с.

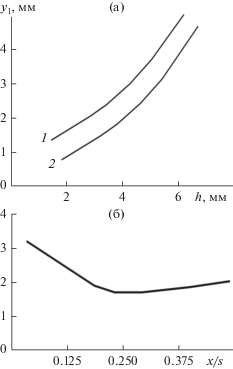
Результаты экспериментальных исследований. При стекании жидкости по внутренней поверхности цилиндрической трубы с винтовой крупномасштабной шероховатостью с параметром s/h = = 4–8 можно выделить три характерных режима течения.

При сравнительно небольших расходах возникает струйный режим, жидкость срывается с витков винтовой шероховатости, образуя несмоченные участки трубы. За выступом затопленных витков винтовой шероховатости наблюдается образование пузырьков газа с определенной частотой и их перемещение со струями жидкости по длине впадины (рис. 8а).

Рис. 8.

Образование стекающей пленки воды на внутренней поверхности трубы с винтовой шероховатостью (d = 37 мм, h = 2.5 мм, µ = 0.00142 Па с, s/h = 10).

С увеличением расхода жидкости (рис. 8б) возникает кольцевой режим течения пленки. Жидкость перемещается между витками винтовой спирали, совершая вращательно-поступательное движение, верхние слои жидкости обтекают выступы шероховатости, образуя регулярные волны. Во впадинах шероховатости наблюдается скопление пузырьков газа, которые формируются на некотором расстоянии от стенки трубы. Причем наибольшее скопление пузырьков наблюдается при x/s = 0.5.

При повышении нагрузки по жидкости пузырьки газа удаляются от стеки трубы (рис. 8в), а на поверхности пленки образуются крупные волны, совершающие вращательно-поступательное движение. При смыкании гребней волн пузырьки газа перемещаются в центральную часть трубы, образуется однофазный поток, возникает режим захлебывания (рис. 8г).

Наблюдение за стекающей жидкостью в трубе с винтовой шероховатостью позволило установить наличие пузырьков воздуха в жидкости и их неравномерное распределение по толщине слоя. Образование пузырьков газа в жидкости визуально наблюдается на стенке трубы с крупномасштабной шероховатостью при h > 1.5 мм.

Как установлено экспериментально, пленка жидкости, стекающей по поверхности трубы с винтовой шероховатостью, состоит из поверхностного газожидкостного слоя и пристенного однофазного слоя.

Толщина пристенного однофазного слоя жидкости δ_о (рис. 9) возрастает с увеличением среднерасходной скорости жидкости и коэффициента динамической вязкости и сопоставима с расчетными значениями y_1, полученными при моделировании (пунктирная линия на рис. 9), которые изменяются по длине впадины и зависят от высоты выступа шероховатости и среднерасходной скорости жидкости (рис. 7). Совпадение величин y₁ и δ_о позволяет предположить, что локальные зоны с пониженным давлением являются местом образования пузырьков газа во впадине. Движущей силой перемещения струй газа является перепад давлений над поверхностью пленки и в обратном токе, который, согласно расчетам, составил 4–100 Па. Так как толщина пленки газожидкостной смеси во впадине над поверхностью обратных токов не превышает 3–5 мм, то, для преодоления давления столба жидкости газом при его движении в область с пониженным давлением, выше указанной величины перепада давлений достаточно.

Рис. 9.

Зависимость толщины пристенного однофазного слоя от числа Рейнольдса пленки воды при d = 45 мм; h = 4 мм; s/h = 4–8; L = 1.6 м. Экспериментальные точки: 1 – µ = 0.00117 Па с; 2 – 0.00067; 3 – µ = 0.00047 Па с.

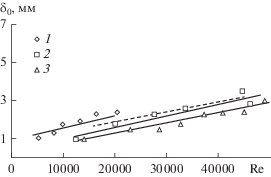
Сформировавшиеся в полостях обратных токов объемы газа имеют различную форму, в частности, приобретают форму эллипсоида, вытянутого по ходу траектории движения жидкости между витками винтовой спирали. В этой связи рассчитывался среднеповерхностный диаметр газовых пузырьков во впадинах шероховатости, который представлен на рис. 10а. Диаметр газовых пузырьков сопоставим с высотой выступа шероховатости и с увеличением h возрастает, что обусловлено увеличением перепада давлений.

Рис. 10.

Изменение среднеповерхностного диаметра пузырька от высоты выступа винтовой шероховатости при Re = 5600, s/h = 6, µ = 0.0014 Па с (а) и средней величины газосодержания (б) при d = 51 мм; s/h = 6; L = 1.9 м; µ = 0.001 Па с; G = 0.006 м³/(с м).

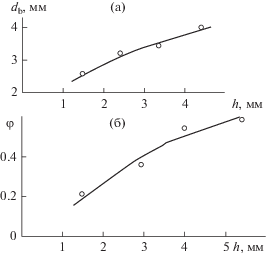
Величина газосодержания в стекающей пленке возрастает с увеличением высоты выступа винтовой шероховатости (рис. 10б). Стабилизация газосодержания в пленке жидкости происходит на длине трубы L = 1.4–1.6 м.

Изменение газосодержания по толщине стекающей пленки жидкости представлено на рис. 11. С увеличением плотности орошения вследствие увеличения толщины пленки жидкости газосодержание уменьшается.

Рис. 11.

Изменение газосодержания по толщине слоя жидкости в зависимости от плотности орошения при h = 4 мм, s/h = 6, µ = 0.00134 Па с. Экспериментальные точки 1–4 для воды: 1 – у = 1 мм; 2 – 2; 3 –4; 4 – у = 5 мм; точки 5–7 для смеси этанол–вода при σ = = 550 × 10^–4 кг/с²: 5 – у = 2.5 мм; 6 – 3.5; 7 – у = 4.5 мм.

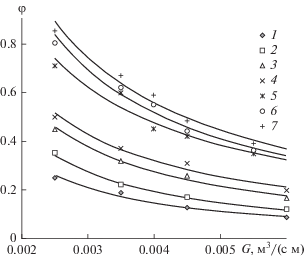
На основании экспериментальных данных получена зависимость для расчета газосодержания по толщине слоя жидкости во впадине в виде

(7)

${{\varphi }_{i}} = 4 \times {{10}^{{--4}}}{{G}^{{--1.2}}}{{({у \mathord{\left/ {\vphantom {у h}} \right. \kern-0em} h})}^{{0.4}}}{{({\sigma \mathord{\left/ {\vphantom {\sigma {{{\sigma }_{{\text{о }}}}}}} \right. \kern-0em} {{{\sigma }_{{\text{о }}}}}})}^{{--1.5}}},\quad$

которое справедливо при µ = 0.00047–0.00140 Па с, σ = (760–550) × 10^–4 кг/с², y/h < 1.25. Толщину пристенного однофазного слоя y₁, которая соответствует минимальному значению (у/h), можно оценить описанным выше методом численного моделирования.

ЗАКЛЮЧЕНИЕ

Газосодержание в пленке жидкости, стекающей по поверхности трубы с искусственной шероховатостью, обусловлено перемещением газа с межфазной поверхности в локальные зоны обратных токов жидкости с пониженным давлением. Масштаб обратных токов и их расположение за выступом шероховатости, так же как и величина газосодержания, зависят от высоты и формы выступа, плотности орошения, физических свойств жидкости. Обратные токи образуются как непосредственно за выступом шероховатости, так и во впадине по ее длине. Расчетный перепад между давлением в локальных зонах обратных токов жидкости и давлением над выступом шероховатости в исследуемом диапазоне конструктивных и кинетических параметров составил 4–100 Па, что, как показывают экспериментальные исследования, является достаточным для преодоления силы поверхностного натяжения при перемещении газа в локальные зоны обратных токов.

При расчете профиля газосодержания по толщине стекающего слоя необходимо методами численного моделирования рассчитать толщину пристенного однофазного слоя y₁, которая соответствует минимальному значению у/h в зависимости (7).

ОБОЗНАЧЕНИЯ

d	диаметр трубы, м
e	ширина выступа элемента шероховатости, м
h	высота выступа, мм
G	плотность орошения, кг/(см)
g	ускорение свободного падения, м/с²
L	длина трубы, м
∆P	разность между давлением по оси трубы и в локальной зоне, Па
R	радиус трубы, м
s	шаг между выступами шероховатости, мм
u	скорость жидкости, м/с
u₂	скорость жидкости во впадине, м/с
x, y	текущие координаты, мм
у₁	расстояние от стенки во впадине до локальной зоны с наименьшим давлением, мм
α	коэффициент теплоотдачи, Вт/(м² К)
δ_d	средняя толщина пленки, м
δ_о	толщина пристенного однофазного слоя жидкости, м
λ	коэффициент трения пленки жидкости на гладкой стенке трубы; коэффициент теплопроводности, Вт/(м К)
µ, η	коэффициент динамической вязкости, Па с
ρ	плотность, кг/м³
σ	коэффициент поверхностного натяжения, кг/с²
σ₀	коэффициент поверхностного натяжения при температуре воды 20°С, кг/с²
φ	газосодержание
Pr	число Прандтля
Re = 4Gρ/µ	число Рейнольдса пленки

ИНДЕКСЫ

av	среднее значение
g	газ
l	жидкость
m	газожидкостная смесь
max	максимальная

Список литературы

Voinov N.A., Zhukova O.P., Nikolaev N.A. Intensification of yeast biomass culturing in a film bioreactor // Foods and Raw Materials. 2013. V. 1. № 2. P. 56.
Войнов Н.А., Николаев Н.А., Еременко Н.А. Пленочный трубчатый аппарат с винтовой шероховатостью // Химическая промышленность. 2006. Т. 83. № 6. С. 285.
Войнов Н.А., Николаев А.Н. Теплосъем при пленочном течении жидкости. Казань: Отечество, 2011.
Лобанов И.Е. Математическое моделирование динамики развития вихревых структур в трубах с турбулизаторами // Вестник ПНИПУ. Аэрокосмическая техника. 2014. № 38. С. 16.
Чжен П. Отрывные течения. Пер. с англ. М.: Мир, 1973.
Ван-Дейк М. Альбом течений жидкости и газа. Пер. с англ. М.: Мир, 1986.
Николаев Н.А., Харин В.Ф. Гидродинамические закономерности пленочного течения жидкости по шероховатой поверхности // Теорет. основы хим. технологии. 1974. Т. 8. № 5. С. 712.
Айвезян О.М. Свойства турбулентных русловых потоков на участках отрывного течения // Изв. АН Арм. ССР. Сер. техн. науки. 1957. № 2. С. 3.
Фридман Б.А. Поле скоростей в водном потоке при внезапном увеличении глубины // Изв. АН СССР. 1953. № 4. С. 365.
Островский Г.М. Прикладная механика неоднородных сред. СПб.: Наука, 2000.
Стабников В.Н., Ройтер И.М., Процюк Т.Б. Этиловый спирт. М.: Пищевая промышленность, 1976.
Isaev S.A., Kharchenko V.B., Chudnovskii Ya.P. Calculation of a three-dimensional flow of a viscous incompressible liquid in the neighborhood of a shallow well on a flat surface // J. Engineering Physics and Thermophysics. 1994. V. 67. № 5–6. P. 1013.
Афанасьев В.Н., Трифонов В.Л., Гетя С.И., Кон Дехай. Выступ в турбулентном пограничном слое // Машиностроение и компьютерные технологии. 2017. № 10. С. 13.
Пядишюс А.А. Динамика интенсификации теплообмена пристенными препятствиями в турбулентном потоке жидкости // Тепломассообмен – VII. Т. 1. Ч. 2. Минск, 1984. С. 149.
Voinov N.A., Konovalov N.M., Nikolaev N.A. Free draining of the liquid film on the inner and outer surfaces of the pipes with a regular screw surface roughness // Theor. Found. Chem. Eng. 1993. V. 27. № 6. P. 641. [Войнов Н.А., Коновалов Н.М., Николаев Н.А. Особенности свободного стекания пленки жидкости по внутренним и наружным поверхностям труб с регулярной винтовой шероховатостью // Теорет. основы хим. технологии. 1993. Т. 27. № 6. С. 638.]

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал