1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 53, № 2, 2019

Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 138-145

Фазовое равновесие реакционных смесей получения эпихлоргидрина в присутствии растворителей

А. В. Фролкова 1, *, Е. А. Охлопкова 1, А. К. Фролкова 1

1 МИРЭА – Российский технологический университет, Институт тонких химических технологий им. М.В. Ломоносова
Москва, Россия

* E-mail: frolkova_nastya@mail.ru

Поступила в редакцию 10.09.2018
После доработки 25.09.2018
Принята к публикации 20.09.2018

Полный текст (PDF)

Аннотация

Осуществлен выбор альтернативного растворителя в процессе получения эпихлоргидрина эпоксидированием аллилхлорида водным раствором пероксида водорода на гетерогенном катализаторе – гранулированном титансодержащем цеолите. Решен вопрос замены токсичного метанола другими растворителями, в присутствии которых в том числе упрощается технологическая схема разделения. Рассмотрены пять пятикомпонентных систем вода–аллилхлорид–эпихлоргидрин–растворитель–тяжелокипящая фракция, где в качестве растворителей выбраны метанол, этанол, пропанол-1, пропанол-2, бутанол-1. Проведены термодинамико-топологический анализ диаграмм фазового равновесия и оценка возможности и целесообразности разделения смесей с применением метода, основанного на сочетании ректификации и расслаивания. Наиболее перспективным с точки зрения разделительной составляющей для реакции эпоксидирования аллилхлорида является пропанол-2.

Ключевые слова: эпихлоргидрин, фазовое равновесие, термодинамико-топологический анализ, растворитель, концентрационный симплекс, азеотроп

ВВЕДЕНИЕ

Одним из перспективных методов получения эпихлоргидрина (ЭХГ), предпочтительным для его промышленной реализации, является эпоксидирование аллилхлорида водным раствором пероксида водорода в среде органического растворителя на гетерогенном катализаторе (гранулированном титансодержащем цеолите) [1–3]. Его преимуществами являются низкое энергопотребление, относительно невысокая токсичность пероксида водорода и отсутствие образования значительных количеств побочных продуктов, загрязняющих окружающую среду или требующих утилизации. В качестве растворителя для данной реакции используется метанол, однако в виду его токсичности актуален вопрос поиска и замены метанола другими растворителями, использование которых позволит также упростить технологическую схему разделения.

В литературе [4] в качестве альтернативных растворителей рассмотрены низшие спирты: этанол, пропанол-2, пропанол-1, бутанол-1. Исследование влияния природы растворителя на процесс эпоксидирования аллилхлорида [5] показало, что все спирты дают близкий по значению выход целевого продукта (при концентрации пероксида водорода в 30%) – 29.1, 28.1, 26.9, 25.9 и 23.9 для метанола, этанола, пропанола-2, пропанола-1 и бутанола-1 соответственно. Наибольшая начальная скорость образования ЭХГ наблюдается для первых трех спиртов из приведенного выше ряда.

Ответ на вопрос, какой из представленных растворителей может составить конкуренцию токсичному метанолу, нельзя получить только на основе анализа реакционной составляющей процесса. Необходима оценка разделительной составляющей технологической схемы получения ЭХГ, для проведения которой требуются данные о фазовых равновесиях реакционных смесей и структуре фазовой диаграммы в целом.

Настоящая работа посвящена исследованию фазового равновесия многокомпонентных систем, образующихся при получении ЭХГ в присутствии различных растворителей. На основе термодинамико-топологического анализа определены структуры диаграмм фазового равновесия жидкость–пар и жидкость–жидкость; выявлены термодинамические ограничения, накладываемые на процессы ректификационного разделения; осуществлен прогноз разделения смесей; выбран альтернативный растворитель.

ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

Объектом исследования выступают пять шестикомпонентных систем, содержащих аллилхлорид (АХ), воду (В), ЭХГ, растворитель (метанол (М), этанол (Э), пропанол-2 (П2), пропанол-1 (П1), бутанол-1 (Б)), 3-хлор-1,2-пропандиол (ХПД) и пероксид водорода (ПВ).

Анализ литературных данных о физико-химических свойствах компонентов и их смесей [6] показал, что указанные системы хорошо изучены: имеются данные о равновесии жидкость–пар в системах метанол–вода, этанол–вода, пропанол-2–вода, пропанол-1–вода, бутанол–вода, эпихлоргидрин–вода, метанол–эпихлоргидрин, аллилхлорид–метанол, аллилхлорид–эпихлоргидрин [7–19], растворимости при различной температуре в системах эпихлоргидрин–вода, бутанол–вода, аллилхлорид–вода [18, 20–23], азеотропные свойства систем аллилхлорид–метанол, аллилхлорид–вода, эпихлоргидрин–вода, аллилхлорид–этанол, этанол–вода, аллилхлорид–пропанол-2, пропанол-2–вода, пропанол-1–вода, бутанол–вода, пропанол–эпихлоргидрин, бутанол–эпихлоргидрин [6, 10, 14, 24]. Этой информации достаточно для проверки адекватности вычислительного эксперимента, основанного на математическом моделировании с применением современных программных средств (AspenOne V.9.0). Поскольку исходные смеси содержат компоненты с ограниченной взаимной растворимостью, в качестве модели описания фазового равновесия выбрано уравнение NRTL [25]. Для систем аллилхлорид–метанол, метанол–вода, этанол–вода, аллилхлорид–вода, метанол–эпихлоргидрин, аллилхлорид–эпихлоргидрин параметры бинарного взаимодействия взяты из базы данных программного комплекса, для остальных систем с использованием экспериментальных данных [14–18] и модели UNIFAC проведена регрессия и получены новые параметры уравнения NRTL. В табл. 1 приведены ошибки описания азеотропных характеристик и составов равновесных жидких слоев.

Таблица 1.  

Ошибки описания азеотропных характеристик при 101.3 кПа и составов равновесных жидких слоев при 101.3 кПа и 293.15 K

Азеотроп x1cal,
мол. д. 		x1 exp,
мол. д. 		u, мол. д. ur, % Тcal, K Тexp, K u, K ur, %
АХ–М 0.7558 0.743 0.0128 1.72 313.27 312.15 1.12 0.36
АХ–В 0.9145 0.913 0.0015 0.16 316.55 316.15 0.40 0.13
В–ЭХГ 0.6584 0.643 0.0154 2.40 362.63 361.65 0.98 0.27
АХ–Э 0.8934 0.92 0.0266 2.89 317.6 317.15 0.45 0.14
Э–В 0.8952 0.9 0.0048 0.53 351.3 351.15 0.15 0.04
АХ–П2 0.9744 0.975 0.0006 0.06 318.38 318.25 0.13 0.04
П2–В 0.6936 0.688 0.0056 0.81 353.24 353.31 0.07 0.02
П1–В 0.4338 0.43 0.0038 0.88 360.78 360.55 0.23 0.06
Б–В 0.2483 0.243 0.0053 2.18 365.65 365.75 0.10 0.03
П1–ЭХГ 0.8380 0.838 0 0 369.15 369.15 0 0
Б–ЭХГ 0.5193 0.515 0.0043 0.83 388.12 385.15 2.97 0.77
Бинарная система $x_{{1\,{\text{cal}},}}^{'}$
мол. д. 		$x_{{1\,{\text{exp}},}}^{'}$
мол. д. 		u,
мол. д. 		ur, %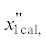
мол. д.
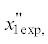мол. д. 		u, мол. д. ur, %
В–ЭХГ 0.9652 0.9861 0.0209 2.12 0.0551 0.0555 0.0058 0.61
В–Б 0.9995 0.9815 0.0180 1.83 0.4412 0.4613 0.0201 4.36
АХ–В 0.9964 0.9966 0.0002 0.02 0.0009 0.0010 0.0501 5.00

Таким образом, получены полные модели описания фазового равновесия в исследуемых многокомпонентных системах, позволяющие воспроизводить физико-химические свойства реальных объектов с относительной ошибкой, не превышающей 3–5%.

В трехкомпонентных системах аллилхлорид–этанол–вода и пропанол-1–вода–эпихлоргидрин обнаружены тройные азеотропы со следующими составами: xАХ = 0.8787, xЭ = 0.0409 и xП1 = 0.2846, xЭХГ = 0.1805 мол. д. соответственно.

Поскольку 3-хлор-1,2-пропандиол и пероксид водорода не образуют азеотропов с остальными компонентами смеси, то они могут быть объединены в одну тяжелокипящую фракцию (ТКФ). Данный прием позволяет снизить размерность решаемой задачи. На следующем этапе необходимо провести термодинамико-топологический анализ диаграмм фазового равновесия пяти пятикомпонентных систем.

ТЕРМОДИНАМИКО-ТОПОЛОГИЧЕСКИЙ АНАЛИЗ ФАЗОВЫХ ДИАГРАММ

На сегодняшний день термодинамико-топологический анализ [26] является наиболее эффективным методом исследования диаграмм фазового равновесия многокомпонентных систем. Концентрационным симплексом пятикомпонентной системы является пентатоп – четырехмерная фигура. При наличии в системе седловидных азеотропов симплекс может содержать сепаратрические многообразия разной размерности, которые ограничивают возможности разделения смеси ректификацией.

Представление геометрической структуры многомерных объектов затруднительно, поэтому их анализ, как правило, начинают с рассмотрения разверток (границ симплекса) различной размерности, в данном случае двухмерной и трехмерной. Анализ граничного пространства позволяет выявить следы сепаратрических многообразий. Так, например, если в концентрационном симплексе пятикомпонентной системы присутствует трехмерное сепаратрическое многообразие, т.е. система содержит два устойчивых или неустойчивых узла, то каждый из указанных узлов на двухмерной развертке пентатопа будет окружен замкнутой линией, состоящей из определенных особых точек (азеотропов и чистых компонентов), одномерных сепаратрис и границ симплекса. Таким образом, можно выделить группы сепаратрических многообразий различной размерности (нулевой и первой), которые будут участвовать в формировании трехмерного сепаратрического многообразия. Анализ трехмерной развертки пентатопа позволяет добавить двухмерные элементы трехмерного сепаратрического многообразия. Следует также отметить, что простейшим трехмерным сепаратрическим многообразием является криволинейная пирамида с треугольным основанием, для формирования которой потребуется минимум четыре двухмерных сепаратрических многообразия.

Если двухмерная развертка содержит один устойчивый и один неустойчивый узел, то в концентрационном пентатопе трехмерное сепаратрическое многообразие будет отсутствовать (система содержит один пучок дистилляционных линий).

Независимо от того, какой размерности рассматривается симплекс или его развертка, любая структура должна подчиняться правилу азеотропии [27, 28]. В настоящей работе рассматривается правило в форме, предложенной Л.А. Серафимовым [29]:

(1)
$\begin{gathered} 2\left( {N_{n}^{ + } + S_{n}^{ + } - N_{n}^{ - } - S_{n}^{ - }} \right) + \\ + \,\,\left( {N_{b}^{ + } + S_{b}^{ + } - N_{b}^{ - } - S_{b}^{ - }} \right) = E. \\ \end{gathered} $
где N – число особых точек типа узел, S – число особых точек типа седло, ± – знак индекса Пуанкаре, индекс n относится к n-компонентным азеотропам, а индекс b – к граничным особым точкам концентрационного симплекса, т.е. к любому азеотропу, содержащему от n – 1 до двух компонентов, и точкам, соответствующим чистым веществам, E – характеристика Эйлера.

Для пятикомпонентных систем данное уравнение может быть упрощено:

(2)
$2({{N}_{5}} + S_{5}^{ + } - S_{5}^{ - }) + ({{N}_{b}} + S_{b}^{ + } - S_{b}^{ - }) = E.$

Для определения полной структуры фазовой диаграммы исследуемых систем построим и проведем анализ двухмерных разверток концентрационных пентатопов [30] (рис. 1).

Рис. 1.

Двухмерные развертки концентрационного симплекса пятикомпонентных систем аллилхлорид (АХ)–вода (В)–растворитель–эпихлоргидрин (ЭХГ)–тяжелокипящая фракция (ТКФ): растворитель – метанол (М), этанол (Э), пропанол-2 (П2), пропанол-1 (П1), бутанол-1 (Б).

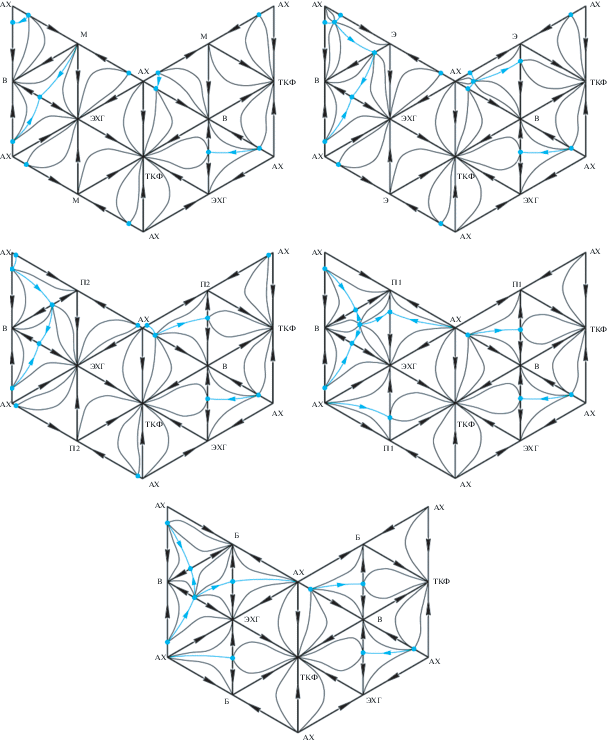
Баланс индексов особых точек приведен в табл. 2. Сумма индексов особых точек для всех разверток равна двум, что свидетельствует о термодинамической непротиворечивости диаграмм.

Таблица 2.  

Типы и индексы особых точек исследуемых систем

Относительно двухмерных разверток концентрационных пентатопов
Система АХ + М + В + + ЭХГ + ТКФ АХ + Э + В + + ЭХГ + ТКФ АХ + П2 + В + + ЭХГ + ТКФ АХ + П1 + В + ЭХГ + ТКФ АХ + Б + В + + ЭХГ + ТКФ
Особая точка тип i тип i тип i тип i тип i
АХ SN 0 SN 0 SN 0 SN 0 SN 0
Р-ль SN 0 SN 0 SN 0 SN 0 SN 0
В SN 0 SN 0 SN 0 SN 0 SN 0
ЭХГ SN 0 SN 0 SN 0 SN 0 SN 0
ТКФ N+ 1 N+ 1 N+ 1 N+ 1 N+ 1
АХ–Р-ль N– 1 SN 0 SN 0 – – – –
АХ–В SN 0 SN 0 N– 1 N– 1 N– 1
В–ЭХГ SN 0 SN 0 SN 0 SN 0 SN 0
Р-ль–В – – SN 0 SN 0 SN 0 SN 0
Р-ль–ЭХГ – – – – – – SN 0 SN 0
АХ–Э–В – – N– 1 – – – – – –
П1–В–ЭХГ – – – – – – SN 0 – –
Σi   2   2   2   2   2

Все диаграммы характеризуются наличием одного неустойчивого узла (азеотроп АХ–М; АХ–Э–В; АХ–В) и одного устойчивого (ТКФ) для систем, содержащих соответственно метанол, этанол, пропанол-2 (пропанол-1, бутанол-1). Остальные особые точки представлены на развертке седло-узлами. Данный факт свидетельствует о том, что в пятикомпонентной системе отсутствует трехмерное сепаратрическое многообразие, т.е. имеется одна область дистилляции, а следовательно, ТКФ может быть отделена от остальных компонентов обычной ректификацией.

Таким образом, на следующем этапе исследования проводится анализ диаграмм систем аллилхлорид–вода–растворитель–эпихлоргидрин. Подробно процедура анализа диаграмм равновесия жидкость–пар четырехкомпонентных систем изложена в работе [31].

На рис. 2 представлены развертки и полные структуры диаграмм фазового равновесия (жидкость–пар и жидкость–жидкость) четырехкомпонентных составляющих.

Рис. 2.

Развертки и полные структуры концентрационных тетраэдров систем аллилхлорид (АХ)–вода (В)–растворитель–эпихлоргидрин (ЭХГ): растворитель – метанол (М), этанол (Э), пропанол-2 (П2), пропанол-1 (П1), бутанол-1 (Б).

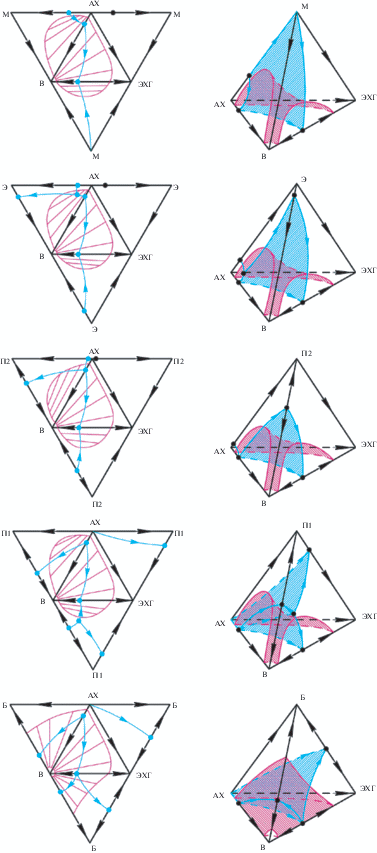
В табл. 3 приведен баланс индексов особых точек, также свидетельствующий о термодинамической непротиворечивости диаграмм: сумма индексов особых точек относительно развертки равна двум, относительно тетраэдра – нулю.

Таблица 3.  

Типы и индексы особых точек четырехкомпонентных составляющих исследуемых систем

Относительно развертки концентрационных тетраэдров
Система АХ + М + В + ЭХГ АХ + Э + В + ЭХГ АХ + П2 + В + ЭХГ АХ + П1 + В + ЭХГ АХ + Б + В + ЭХГ
Особая точка тип i тип i тип i тип i тип i
АХ SN 0 SN 0 SN 0 SN 0 SN 0
Р-ль SN 0 SN 0 SN 0 N+ 1 N+ 1
В N+ 1 N+ 1 N+ 1 N+ 1 N+ 1
ЭХГ N+ 1 N+ 1 N+ 1 N+ 1 N+ 1
АХ–Р-ль N– 1 SN 0 SN 0 – – – –
АХ–В SN 0 SN 0 N– 1 N– 1 N– 1
В–ЭХГ S –1 S –1 S –1 S –1 SN 0
Р-ль–В – – SN 0 SN 0 S –1 S –1
Р-ль–ЭХГ – – – – – – S –1 S –1
АХ–Э–В – – N– 1 – – – – – –
П1–В–ЭХГ – – – – – – N– 1 – –
Σi 2   2 2   2   2
Относительно полной структуры концентрационного тетраэдра
Система АХ + М + В + ЭХГ АХ + Э + В + ЭХГ АХ + П2 + В + ЭХГ АХ + П1 + В + ЭХГ АХ + Б + В + ЭХГ
Особая точка тип i тип i тип i тип i тип i
АХ SN 0 SN 0 SN 0 SN 0 SN 0
Р-ль SN 0 SN 0 SN 0 N+ 1 N+ 1
В N+ 1 N+ 1 N+ 1 N+ 1 N+ 1
ЭХГ N+ 1 N+ 1 N+ 1 N+ 1 N+ 1
АХ–Р-ль N– –1 SN 0 SN 0 – – – –
АХ–В SN 0 SN 0 N– –1 N– –1 N– –1
В–ЭХГ S –1 S –1 S –1 S –1 SN 0
Р-ль–В – – SN 0 SN 0 S –1 S –1
Р-ль–ЭХГ – – – – – – S –1 S –1
АХ–Э–В – – N– –1 – – – – – –
П1–В–ЭХГ – – – – – – S 1 – –
Σi   0   0   0   0   0

Проведем анализ изменения структуры диаграмм для систем с метанолом, этанолом, пропанолом-2, пропанолом-1 и бутанолом-1. В рассматриваемом ряду наблюдается обогащение азеотропа АХ–растворитель аллилхлоридом вплоть до его исчезновения в системе с пропанолом-1 и, соответственно, с бутанолом-1. В бинарной составляющей растворитель–вода во всех системах, за исключением метанольной, присутствует бинарный азеотроп, причем с увеличением молекулярной массы спирта последний обогащается водой.

Системы с метанолом (неустойчивый узел азеотроп АХ–М), этанолом (неустойчивый узел АХ–Э–В) и пропанолом-2 (неустойчивый узел азеотроп АХ–В) характеризуются наличием одной сепаратрической поверхности, разбивающей симплекс на две области дистилляции. Для данных систем устойчивыми узлами являются вода и эпихлоргидрин. В двух других системах присутствуют уже две сепаратрические поверхности и три области дистилляции (неустойчивый узел – азеотроп АХ–В, устойчивые узлы – эпихлоргидрин, вода, растворитель).

На диаграмме фазового равновесия системы с бутанолом-1 имеется область двухфазного расслаивания открытого типа, на остальных – закрытого. Особенность взаимного расположения симплексов расслаивания и сепаратрических многообразий позволяет использовать для разделения смесей метод, основанный на сочетании ректификации и расслаивания [28], однако данный метод будет более эффективен при разделении смеси на отдельные фракции. Использование расслаивания на первом этапе неэффективно, так как это приведет к увеличению числа аппаратов в схеме [32].

Выделение целевого продукта – эпихлоргидрина – в кубе первой колонны возможно для ограниченной области исходных составов для систем с этанолом и пропанолом-2. Для остальных систем такое разделение невозможно.

Использование первого заданного разделения с получением в дистилляте азеотропов АХ–М, АХ–Э–В и АХ–В эффективно для первых трех систем: с метанолом, этанолом и пропанолом-2 соответственно. При этом в кубе колонны в зависимости от исходного состава будут образовываться тройные смеси растворитель–В–ЭХГ или АХ–В–ЭХГ (выделение ЭХГ возможно с применением комплекса колонн и флорентийского сосуда). Такое разделение эффективнее для системы с метанолом и пропанолом-2, поскольку для системы с этанолом при разделении дистиллятного продукта потребуется на одну колонну больше. Для системы с пропанолом-2 возможно разделение смеси АХ–В с использованием флорентийского сосуда, что невозможно для системы с метанолом.

Системы с пропанолом-1 и бутанолом-1 характеризуются более сложной структурой и содержат большее количество термодинамических ограничений (азеотропы и сепаратрические многообразия), а следовательно, схемы их разделения будут априори сложнее.

ЗАКЛЮЧЕНИЕ

На основе термодинамико-топологического анализа диаграмм фазового равновесия систем, содержащих аллилхлорид, воду, растворитель, эпихлоргидрин и тяжелокипящую фракцию, осуществлен выбор альтернативного растворителя (пропанола-2), способного составить конкуренцию метанолу в процессе получения ЭХГ. Выбор обусловлен в первую очередь тем, что фазовая диаграмма системы с пропанолом-2 содержит меньше термодинамических ограничений (азеотропов и сепаратрис) по сравнению с системами с этанолом, пропанолом-1 и бутанолом-1, а также характеризуется благоприятным для разделения взаимным расположением сепаратрис и областей двухфазного расслаивания.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 16-19-10632).

ОБОЗНАЧЕНИЯ

E характеристика Эйлера
i знак индекса Пуанкаре
N особая точка типа узел
S особая точка типа седло
SN особая точка типа седло–узел
T температура, K
u абсолютная ошибка
ur относительная ошибка, %
x мольная доля компонента в жидкой фазе

ИНДЕКСЫ

b граничные особые точки
cal расчетные данные
exp экспериментальные данные
n внутренние особые точки

Список литературы

  1. Gao H., Lu G., Suo J., Li S. Epoxidation of allyl chloride with hydrogen peroxide catalyzed by titanium silicalite 1 // Applied Catalysis A: General. 1996. V. 138. P. 27.

  2. Pandey R.K., Kumar R. Eco-friendly synthesis of epichlorohydrin catalyzed by titanium silicate (TS-1) molecular sieve and hydrogen peroxide // Catal. Commun. 2007. V. 8. P. 379.

  3. Сулимов А.В., Данов С.М., Овчарова А.В., Обрывалина А.Н., Теляшев Р.Г., Овчаров А.А., Балашов А.Л. Инновационные процессы получения эпихлоргидрина // Нефтегазохимия. 2013. № 1. С. 32.

  4. Данов С.М., Сулимов А.В., Сулимова А.В. Влияние природы растворителя на процесс эпоксидирования аллилхлорида пероксидом водорода на титансодержащем силикате // Журн. прикл. химии. 2008. Т. 81. № 11. С. 1847.

  5. Овчарова А.В. Разработка технологии получения эпихлоргидрина. Автореф. дис. … канд. хим. наук. М.: РХТУ им. Д.И. Менделеева, 2012.

  6. Огородников С.K., Лестева T.M., Коган В.Б. Азеотропные смеси. Справочник / Под ред. Когана В.Б. Л.: Химия, 1971.

  7. Yang C., Ma S., Yin X. Organic salt effect of tetramethylammonium bicarbonate on the vapor liquid equilibrium of the methanol water system // J. Chem. Eng. Data. 2011. V. 56. № 10. P. 3747.

  8. Alvarez V.H., Mattedi S., Iglesias M., Gonzalez-Olmos R., Resa J. M. Phase equilibria of binary mixtures containing methyl acetate, water, methanol or ethanol at 101.3 kPa // Phys. Chem. Liq. 2011. V. 49. P. 52.

  9. Tsanas C., Tzani A., Papadopoulos A., Detsi A., Voutsas E. Ionic liquids as entrainers for the separation of the ethanol/water system // Fluid Phase Equilib. 2014. V. 379. P. 148.

  10. Lai H.-S., Lin Y.-F., Tu C.-H. Isobaric (vapor + liquid) equilibria for the ternary system of (ethanol + water + 1,3-propanediol) and three constituent binary systems at P = 101.3 kPa // J. Chem. Thermodyn. 2014. V. 68. P. 13.

  11. Liu X., Lei Z., Wang T., Qunsheng L., Zhu J. Isobaric vapor liquid equilibrium for the ethanol + water + 2-aminoethanol tetrafluoroborate system at 101.3 kPa // J. Chem. Eng. Data. 2012. V. 57. № 12. P. 3532.

  12. Li Q., Zhu W., Wang H., Ran X., Fu Y., Baohuai W. Isobaric vapor liquid equilibrium for the ethanol + water + + 1,3-dimethylimidazolium dimethylphosphate system at 101.3 kPa // J. Chem. Eng. Data. 2012. V. 57. № 3. P. 696.

  13. Kamihama N., Matsuda H., Kurihara K., Tochigi K., Oba S. Isobaric vapor-liquid equilibria for ethanol + + water + ethylene glycol and its constituent three binary systems // J. Chem. Eng. Data. 2012. V. 57. № 2. P. 339.

  14. Lin Y.-F., Tu C.-H. Isobaric vapor-liquid equilibria for the binary and ternary mixtures of 2-propanol, water, and 1,3-propanediol at p = 101.3 kPa: Effect of the 1,3-propanediol addition // Fluid Phase Equilib. 2014. V. 368. P. 104.

  15. Li Q., Zhang J., Lei Z., Zhu J., Wang B., Huang X. Isobaric vapor-liquid equilibrium for (propan-2-ol + water + 1-butyl-3-methylimidazolium tetrafluoroborate) // J. Chem. Eng. Data. 2009. V. 54. № 9. P. 2785.

  16. Orchilles A. V., Miguel P. J., Vercher E., Martinez-Andreu A. Isobaric vapor-liquid equilibria for 1-propanol + + water + 1-ethyl-3-methylimidazolium trifluoromethanesulfonate at 100 kPa // J. Chem. Eng. Data. 2008. V. 53. P. 2426.

  17. Lladosa E., Monton J.B., Burguet M.C., Munoz R. Phase equilibrium for the esterification reaction of acetic acid + + butan-1-ol at 101.3 kPa // J. Chem. Eng. Data. 2008. V. 53. P. 108.

  18. Yue Q., Zhu. J.-W., Wu Y.-Y., Yuan X.-q., Ma L. Liquid–liquid equilibria and vapor–liquid equilibria for the binary system of epichlorohydrin and water // Fluid Phase Equilib. 2009. V. 283. P. 12.

  19. Ding X., Liu H., Li N., Wang S., Wang G., Zhao X., Wang Y. Isobaric vapor−liquid equilibria for the binary and ternary systems of methanol, epichlorohydrin, and glycerol dimethyl ether at 101.3 kPa // J. Chem. Eng. Data. 2015. V. 60. № 3. P. 541.

  20. Wang R., Lu Y., Wang K., Luo G. Liquid−liquid equilibria for the system water + 1,3-dichloro-2-propanol + epichlorohydrin from (283.2 to 303.2) K // J. Chem. Eng. Data. 2013. V. 58. P. 3222.

  21. Benbouzid H., Le Floch S., Stephan L., Olier R., Privat M. Combined effects of salinity and temperature on the solubility of organic compounds // J. Chem. Thermodyn. 2012. V. 48. P. 54.

  22. Naicker P.K., Sandler S.I., Reifsnyder S. Measurement of the liquid-liquid equilibria for mixtures of water + sodium hydroxide + an alkanol or dimethyl ether using near-infrared spectroscopy // J. Chem. Eng. Data. 2002. V. 47. P. 191.

  23. Промышленные хлорорганические продукты / Под ред. Ошина Н.А. М.: Химия, 1978.

  24. Iliuta M.C., Thyrion F.C., Landauer O.M. Effect of calcium chloride on the isobaric vapor-liquid equilibrium of 1-propanol + water // J. Chem. Eng. Data. 1996. V. 41. P. 402.

  25. Renon H., Prausnitz J.M. Local compositions in thermodynamic excess functions for liquid mixtures // AIChE J. 1968. V. 14. № 1. P. 135.

  26. Serafimov L.A. Thermodynamic and topological analysis of liquid-vapor phase equilibrium diagrams and problems of rectification of multicomponent mixtures // Mathematical Methods in Contemporary Chemistry / Ed. Kuchanov S.I. Amsterdam: Gordon and Breach, 1996. Ch. 10. P. 557.

  27. Жаров В.Т., Серафимов Л.А. Физико-химические основы дистилляции и ректификации. Л.: Химия, 1975.

  28. Тимофеев В.С., Серафимов Л.А., Тимошенко А.В. Принципы технологии основного органического и нефтехимического синтеза. 3-е изд. перераб. и доп. М.: Высш. шк., 2010.

  29. Серафимов Л.А., Тациевская Г.И., Медведев Д.В. О различных формах правила азеотропии // Теорет. основы хим. технологии. 2010. Т. 44. № 2. С. 174.

  30. Serafimov L.A., Frolkova A.V. Determination of vapor–liquid equilibrium diagrams of multicomponent systems // Chemical Papers. 2016. V. 70. P. 1578.

  31. Серафимов Л.А., Фролкова А.В., Медведев Д.В., Семин Г.А. Определение структуры диаграммы четырехкомпонентной смеси на основе ее развертки // Теорет. основы хим. технологии. 2012. Т. 46. № 2. С. 154.

  32. Фролкова А.В., Меркульева А.Д., Гаганов И.С. Синтез схем разделения расслаивающихся смесей: современное состояние проблемы // Тонкие химические технологии. 2018. Т. 13. № 3. С. 5.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал